| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.3.3 Локальное управление буферами
Как упоминалось в разделе 6.1, различают статическое и динамическое управление буферами. Последнее полностью обобщает статические стратегии управления, поэтому ниже в первую очередь рассматривается динамическое управление буферами.
Динамическое ситуационное управление, определенное в [42,53], основывается на информации о текущем состоянии УК. Оно состоит в принятии решения о вводе пакета в момент его поступления в зависимости от состояния буферной памяти узла. Сетевая модель УК, описанная в разделе 6.4, в данном случае включает R классов пуассоновских потоков поступлений пакетов с интенсивностями соответственно  , определяемыми потоками в R выходящих из узла каналов.
, определяемыми потоками в R выходящих из узла каналов.
При этом специфика состоит в зависимости интенсивностей входящих в сеть МО потоков от стратегии управления вводом (отказом) пакетов в сеть. Эта зависимость определяется состоянием первого центра «Память» из N приборов обслуживания  буферов, буфер на один пакет), однозначно связанного с состоянием всей сети из М центров обслуживания, и описывается вектором
буферов, буфер на один пакет), однозначно связанного с состоянием всей сети из М центров обслуживания, и описывается вектором  , где
, где  - число пакетов класса
- число пакетов класса  в центре
в центре  . Обозначим
. Обозначим

С каждой стратегией связано допустимое множество состояний. Равнодоступная для всех классов память CS (Complete Sharing) определяет допустимое множество  Полное разделение CP (Complete Partitioning), при котором каждому классу пакетов выделяется изолированная от других классов часть памяти, имеет допустимое множество
Полное разделение CP (Complete Partitioning), при котором каждому классу пакетов выделяется изолированная от других классов часть памяти, имеет допустимое множество  Произвольная стратегия Q определяется только правилом ввода-вывода пакетов в УК, а не их уходом из узла, поэтому
Произвольная стратегия Q определяется только правилом ввода-вывода пакетов в УК, а не их уходом из узла, поэтому

Последнее определяет так называемые координатно-выпуклые множества. Таким образом, стратегия управления буферами может быть охарактеризована вероятностями  ввода в память УК пакетов класса
ввода в память УК пакетов класса  в состоянии
в состоянии  Следует выделить простые стратегии на координатно-выпуклых множествах состояний, определяющие отказ приема пакетов в УК лишь на границе множеств. Для них
Следует выделить простые стратегии на координатно-выпуклых множествах состояний, определяющие отказ приема пакетов в УК лишь на границе множеств. Для них

где  . Такие стратегии однозначно характеризуются своими допустимыми множествами состояний. Справедливо следующее
. Такие стратегии однозначно характеризуются своими допустимыми множествами состояний. Справедливо следующее
Утверждение. Для простой стратегии, определенной на координатно-выпуклом множестве состояний  стационарные вероятности сетевой модели УК имеют мультипликативную форму
стационарные вероятности сетевой модели УК имеют мультипликативную форму

где функции  введены ранее;
введены ранее; 
- нормализующая константа.
Выражение (6.19) непосредственно следует из достаточных условий мультипликативности стационарных вероятностей открытых ло-кально-сбалансированных сетей с зависимостью интенсивностей пуассоновских потоков поступлений от количества пакетов в сети [53,183]. Триггерная функция, определяющая правило ухода из сети пакетов  класса
класса

где  . Условие мультипликативности, имеющее в данном случае вид
. Условие мультипликативности, имеющее в данном случае вид  для
для  очевидным образом выполняется, что обеспечивает справедливость (6.19).
очевидным образом выполняется, что обеспечивает справедливость (6.19).

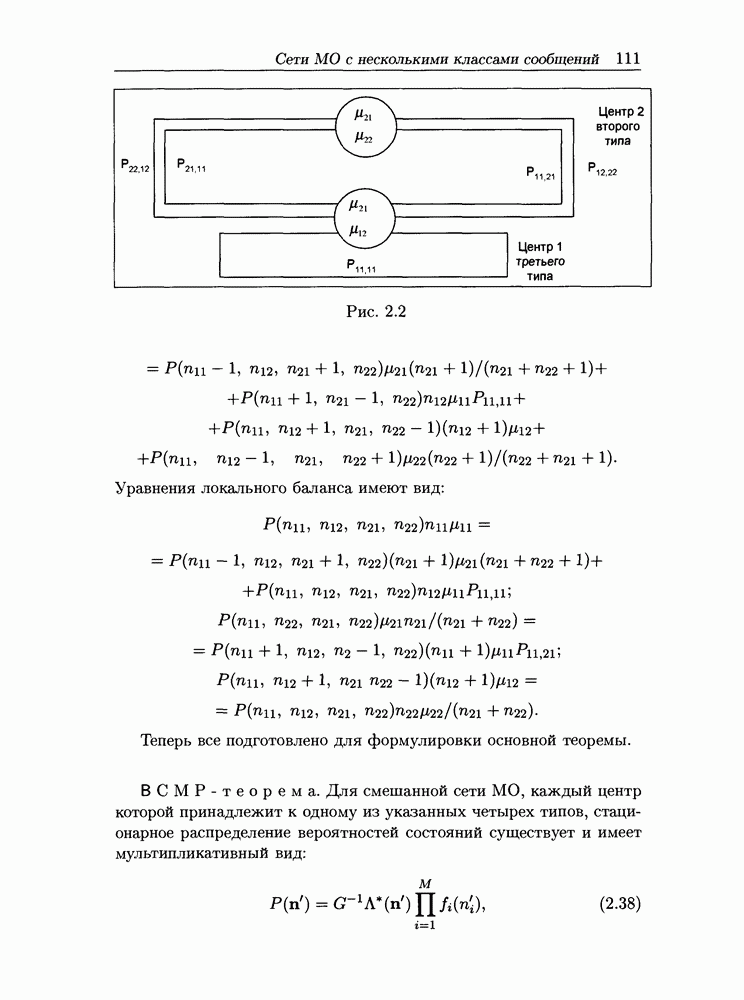
Рис. 6.5
Во избежание громоздких выкладок проиллюстрируем проблему оптимального динамического управления на упрощенной модели УК (рис. 6.5), традиционно рассматриваемой для анализа локального управления буферами. В такой модели УК представляется R выходящими каналами связи и буферной памятью размером в N буферов, каждый канал - однолинейной системой М/М/1 с интенсивностью обслуживания  и дисциплиной обслуживания FCFS («первым пришел - первым обслужен»). Весь узел состоит из набора R таких очередей. Эти очереди имеют N общих мест для ожидания. Пакеты, не принятые в очередь, получают отказ. Поток поступлений в узел представляется R классами пуассоновских потоков, характеризующимися направлением передачи и интенсивностью
и дисциплиной обслуживания FCFS («первым пришел - первым обслужен»). Весь узел состоит из набора R таких очередей. Эти очереди имеют N общих мест для ожидания. Пакеты, не принятые в очередь, получают отказ. Поток поступлений в узел представляется R классами пуассоновских потоков, характеризующимися направлением передачи и интенсивностью 

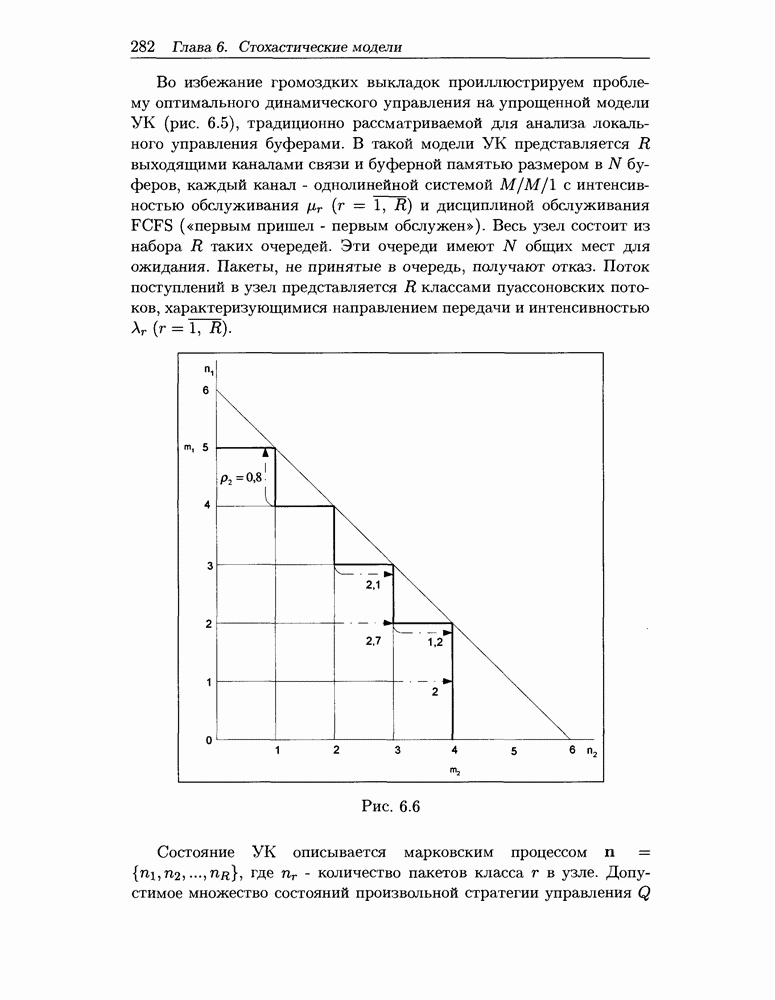
Рис. 6.6
Состояние УК описывается марковским процессом  , где
, где  - количество пакетов класса
- количество пакетов класса  в узле. Допустимое множество состояний произвольной стратегии управления
в узле. Допустимое множество состояний произвольной стратегии управления 

Проблема оптимального управления марковским процессом с конечным числом состояний может быть сформулирована в терминах задачи линейного программирования [42,53]. Пусть доход от передачи через узел пакета класса  равен
равен  . Доход всей системы в единицу времени можно определить в виде
. Доход всей системы в единицу времени можно определить в виде

где  - стационарная вероятность состояния
- стационарная вероятность состояния  . При
. При  выражение (6.20) дает пропускную способность УК.
выражение (6.20) дает пропускную способность УК.
Пусть, как и ранее,  - вероятность приема в память пакета класса
- вероятность приема в память пакета класса  в состоянии
в состоянии  . Тогда оптимальное управление определяется набором вероятностей
. Тогда оптимальное управление определяется набором вероятностей  , доставляющих максимум линейному функционалу D при ограничениях, являющихся уравнениями для стационарных вероятностей состояний узла:
, доставляющих максимум линейному функционалу D при ограничениях, являющихся уравнениями для стационарных вероятностей состояний узла:

В (6.21) используются обозначения 

Введение переменных

преобразует систему (6.21) в линейную систему ограничений задачи линейного программирования относительно  Значения управляющих переменных
Значения управляющих переменных  определяются из (6.21) после решения задачи линейного программирования.
определяются из (6.21) после решения задачи линейного программирования.
Как известно, всякому опорному плану задачи линейного программирования соответствует целочисленный набор вероятностей  состоящий из нулей и единиц. Это поясняет смысл переменных
состоящий из нулей и единиц. Это поясняет смысл переменных  как «разрешений» на ввод пакетов в память узла и позволяет получить из (6.22) дополнительные ограничения для задачи линейного программирования
как «разрешений» на ввод пакетов в память узла и позволяет получить из (6.22) дополнительные ограничения для задачи линейного программирования  .
.
Рассмотрим модель УК с двумя  каналами передачи и
каналами передачи и  буферами памяти (см. рис. 6.5). В этом случае анализ оптимального управления показывает [53], что оптимальные стратегии определены на координатно-выпуклом пространстве состояний
буферами памяти (см. рис. 6.5). В этом случае анализ оптимального управления показывает [53], что оптимальные стратегии определены на координатно-выпуклом пространстве состояний

где граница  (рис. 6.5). При этом переходы управляемого процесса ограничиваются не только на границе
(рис. 6.5). При этом переходы управляемого процесса ограничиваются не только на границе  но и внутри этой области. Увеличение загрузки второго канала
но и внутри этой области. Увеличение загрузки второго канала  при фиксированной
при фиксированной  меняет границы области
меняет границы области  запрещая ввод пакетов обоих классов даже при наличии свободных буферов (штриховые линии на рис. 6.6). Однако общий вид оптимального управления даже в этом случае получить не удается. Для простых стратегий на координатно-выпуклых множествах состояний и трех каналов
запрещая ввод пакетов обоих классов даже при наличии свободных буферов (штриховые линии на рис. 6.6). Однако общий вид оптимального управления даже в этом случае получить не удается. Для простых стратегий на координатно-выпуклых множествах состояний и трех каналов  в [183] получен вид допустимого пространства состояний, соответствующий оптимальной стратегии:
в [183] получен вид допустимого пространства состояний, соответствующий оптимальной стратегии:

где границы  с соответствующими индексами не превосходят N. Оптимальная простая стратегия резервирует часть памяти для пакетов каждого класса, ограничивая, кроме того, общее число пакетов всех комбинаций классов. В общем случае для произвольного R это свойство простых стратегий не доказано.
с соответствующими индексами не превосходят N. Оптимальная простая стратегия резервирует часть памяти для пакетов каждого класса, ограничивая, кроме того, общее число пакетов всех комбинаций классов. В общем случае для произвольного R это свойство простых стратегий не доказано.
Естественным расширением изложенного динамического управления входами узла является ситуационное управление с замещением введенного в буферную память пакета класса i на вновь прибывший пакет класса  на множестве состояний
на множестве состояний 
Пусть  - потери, связанные с вытеснением из памяти пакетов класса
- потери, связанные с вытеснением из памяти пакетов класса  . Тогда в прежних обозначениях функционал (6.34) примет вид
. Тогда в прежних обозначениях функционал (6.34) примет вид

где  для
для  - вероятность замещения пакета
- вероятность замещения пакета  класса
класса  Ограничения задачи линейного программирования в этом случае описываются аналогично. При
Ограничения задачи линейного программирования в этом случае описываются аналогично. При  управление с замещением позволяет получить оценку сверху пропускной способности УК.
управление с замещением позволяет получить оценку сверху пропускной способности УК.
Реализация динамического ситуационного управления буферами связана с трудоемкими измерениями входящей нагрузки. Поэтому, как правило, на практике используют частные стратегии, определяющие статические схемы управления буферами.
Статическое локальное управление буферами определяется фиксированными простыми стратегиями управления на координатновыпуклых пространствах состояний. Такое управление является частным случаем динамического ситуационного управления, рассматривающего в каждом состоянии набор возможных стратегий. Сетевая модель УК, введенная для динамического управления, остается в данном случае без изменений, а зависимость интенсивностей R входящих потоков от состояния сети определяется конкретными стратегиями управления. Простые стратегии однозначно определяются соответствующими пространствами состояний. Поэтому описание схем статического управления осуществляется ниже определением соответствующих координатно-выпуклых множеств.
Наиболее простыми статическими схемами управления являются упомянутые выше равный доступ CS и полное разбиение СР. В последней вся память разделена на R частей, каждая из которых постоянно закрепляется за соответствующим классом пакетов. Очевидно, такая схема будет давать лучшие показатели только при чрезмерных по всем R классам входящих в узел потоков. В иных случаях она не обеспечивает эффективного использования памяти. Во избежание захвата буферов более интенсивными потоками было предложено несколько схем статического управления [233]. Ниже рассматриваются эти схемы с учетом многоэтапного процесса буферизации в УК.
Схема SMXQ. Эта схема управления ограничивает количество буферов, доступных пакетам каждого класса. При этом вводятся границы  , такие, что
, такие, что 
Возможные состояния определяются в виде

Однако эта схема не гарантирует полного использования всех выходящих каналов при тяжелом трафике.
Схема SMA. В этой схеме за каждым классом пакетов закрепляется минимально необходимая память в  буферов, доступных лишь пакетам соответствующего класса. Оставшаяся часть буферного пула в
буферов, доступных лишь пакетам соответствующего класса. Оставшаяся часть буферного пула в  буферов равнодоступна пакетам всех классов. Допустимое множество состояний при этом
буферов равнодоступна пакетам всех классов. Допустимое множество состояний при этом

Схема SMQMA. Данная схема по существу является объединением двух предыдущих схем. В отличие от SMA, в этой схеме налагаются ограничения  на число пакетов каждого класса в общем пуле буферов В. При этом допустимое множество состояний
на число пакетов каждого класса в общем пуле буферов В. При этом допустимое множество состояний

Очевидно, схема SMQMA обобщает все рассмотренные схемы статического управления буферами. Допустимые множества для них могут быть непосредственно получены из (6.23).
При статическом управлении, как и для любой простой стратегии управления на координатно-выпуклых множествах, стационарная вероятность  сетевой модели УК имеет мультипликативный вид (6.33). Вычисление
сетевой модели УК имеет мультипликативный вид (6.33). Вычисление  и требуемых характеристик УК для схем статического управления может быть осуществлено алгоритмами свертки для сетей МО с несколькими классами при некоторой их модификации относительно допустимого пространства состояний, соответствующего схеме управления. Вероятность отказа приема в УК пакетов класса
и требуемых характеристик УК для схем статического управления может быть осуществлено алгоритмами свертки для сетей МО с несколькими классами при некоторой их модификации относительно допустимого пространства состояний, соответствующего схеме управления. Вероятность отказа приема в УК пакетов класса  для общей схемы SMQMA
для общей схемы SMQMA


Характеристики упрощенной модели УК (см. рис. 6.5) могут быть получены в явном виде в терминах нормализующей константы G. Для некоторых схем управления они имеют весьма простой вид [75]. Выбор конкретной схемы статического управления или, что то же самое, параметров схемы SMQMA основывается на компромиссе между пропускной способностью узла и задержкой пакетов в нем. Последние существенным образом зависят от особенностей многоэтапного процесса буферизации УК.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
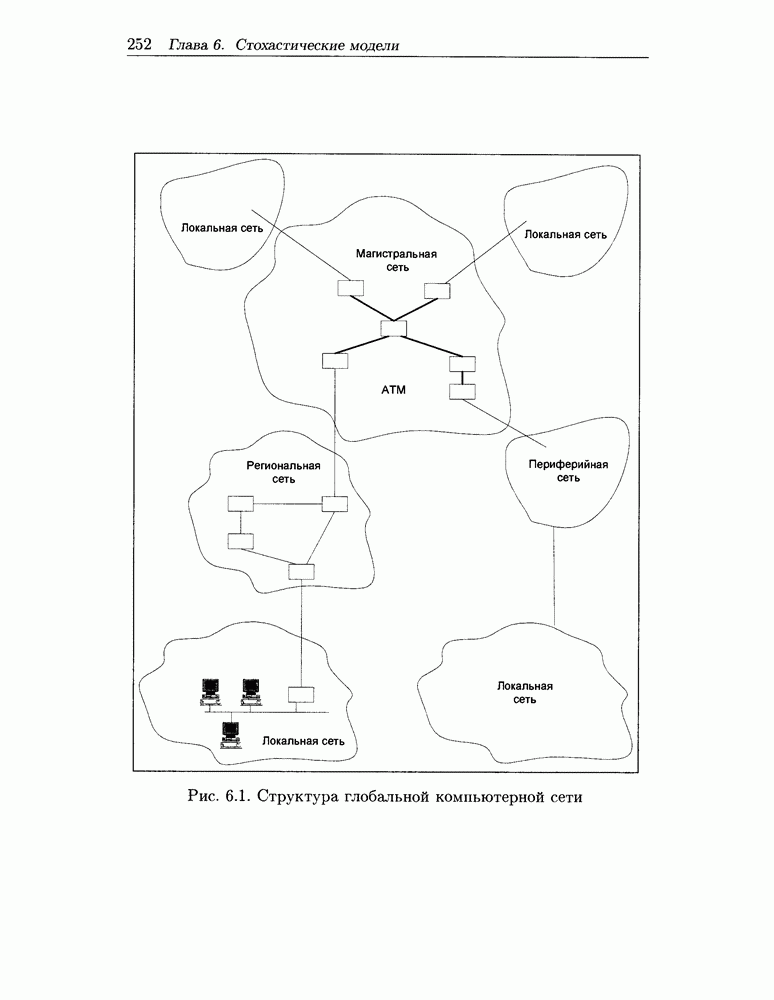
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
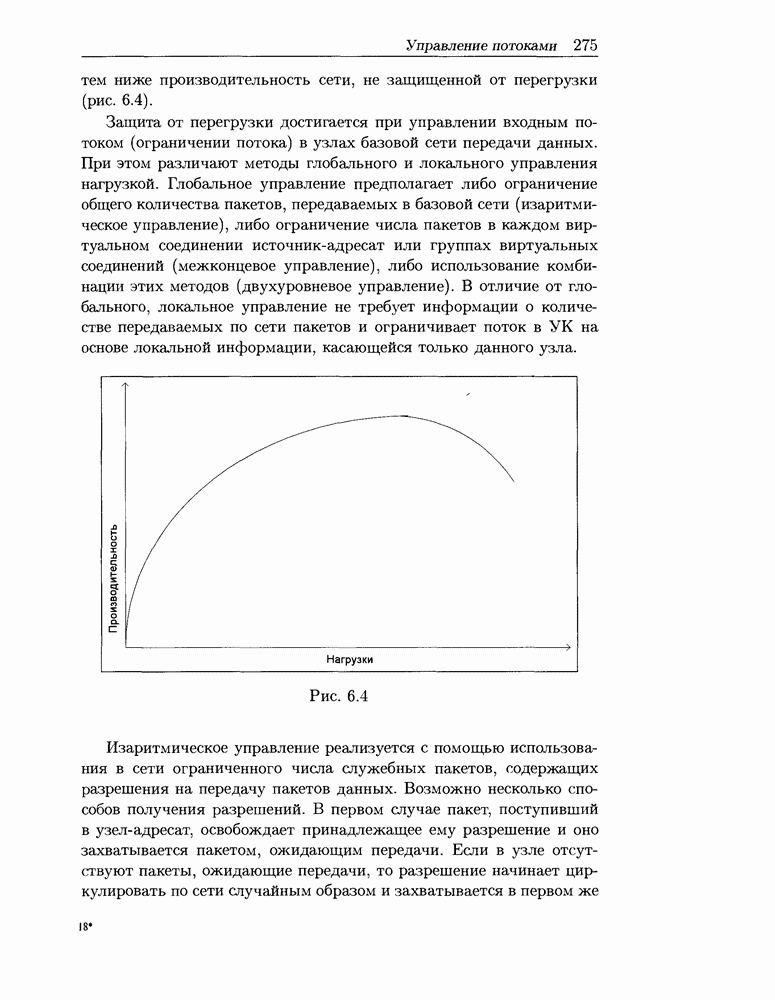
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
- 6.3.3 Локальное управление буферами
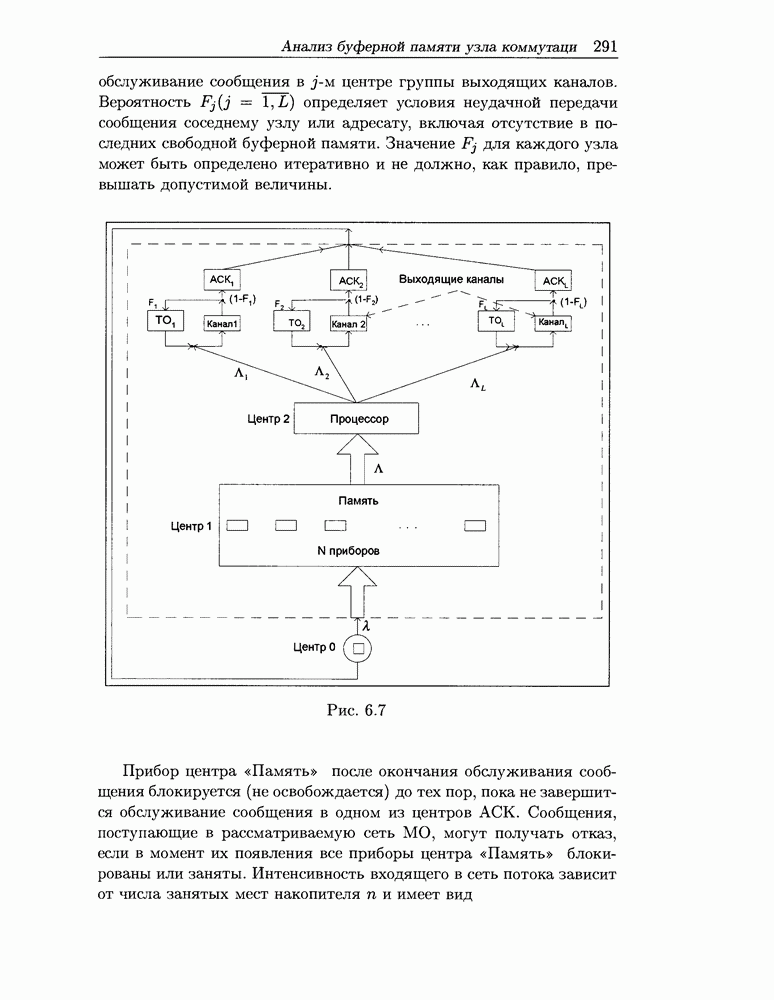
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
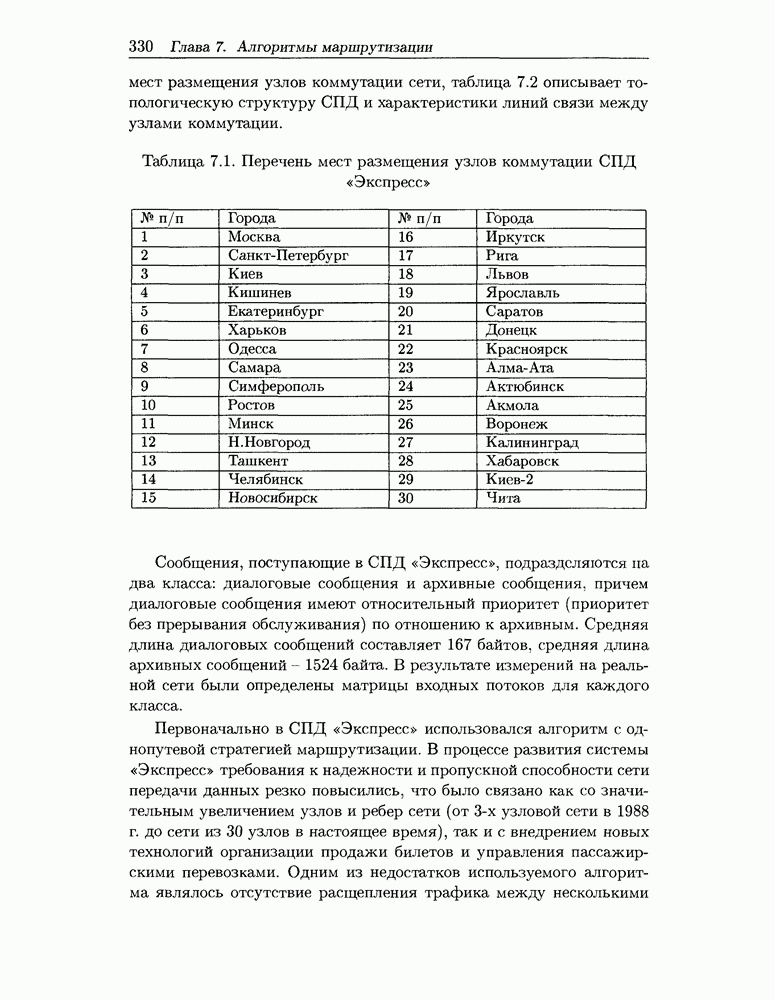
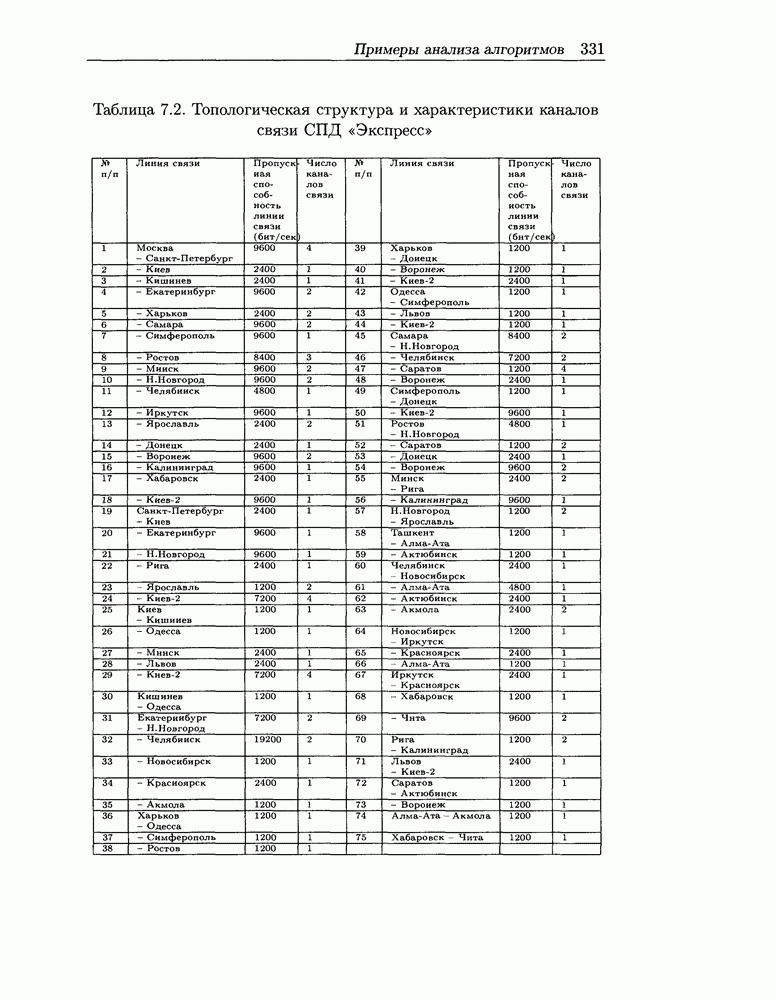
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
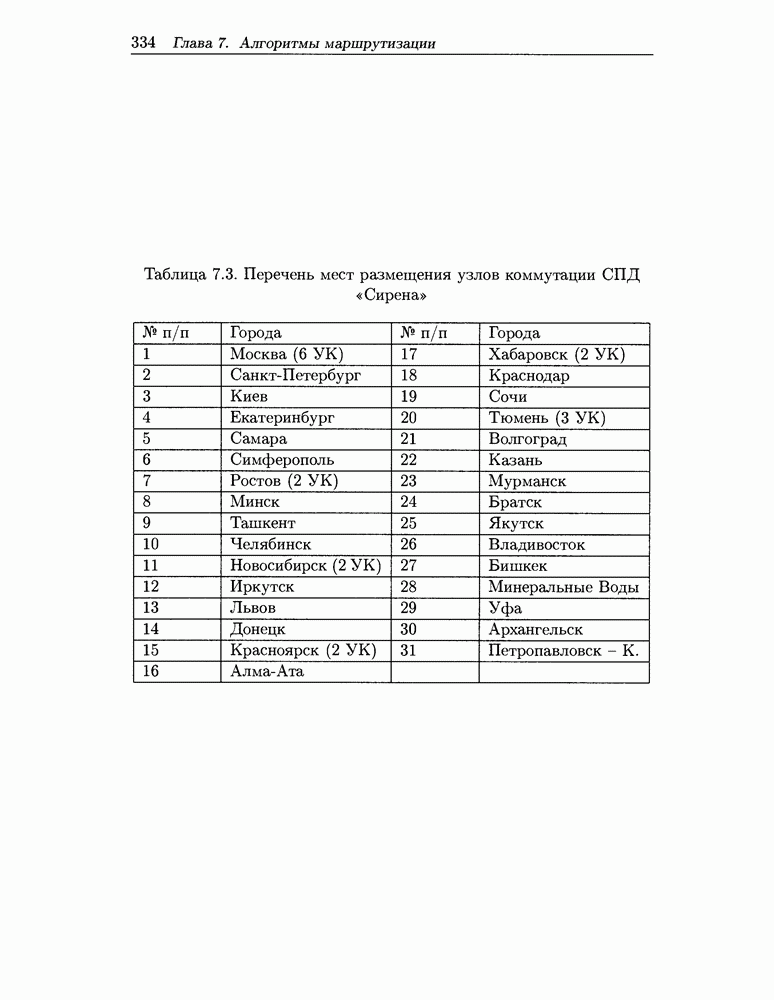
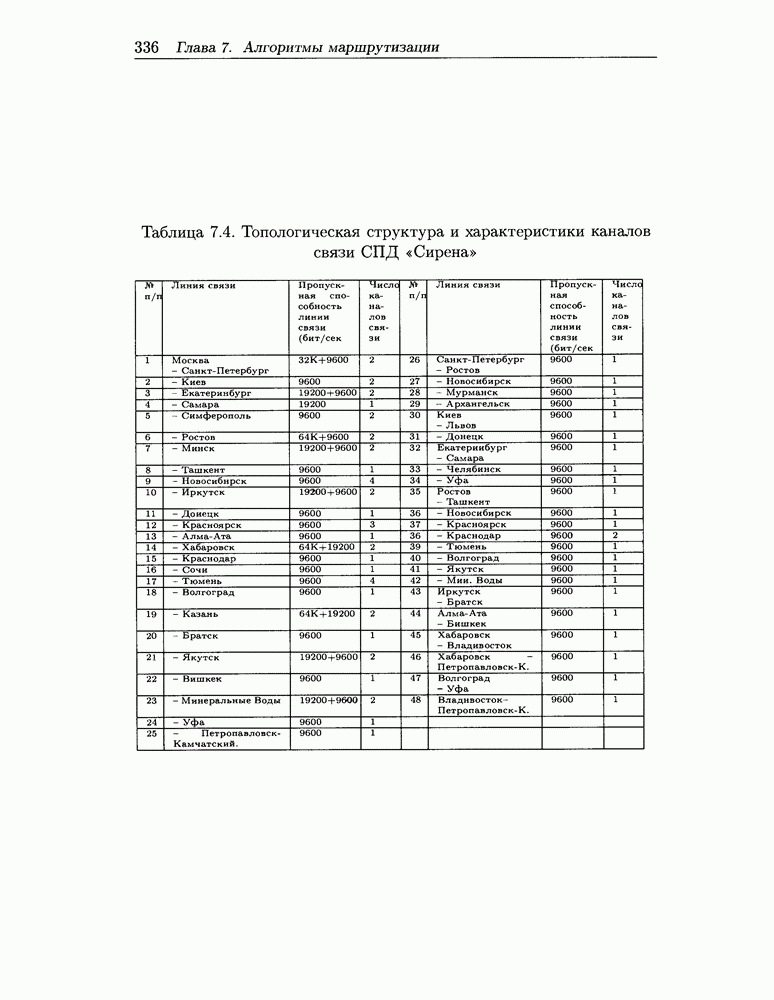
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
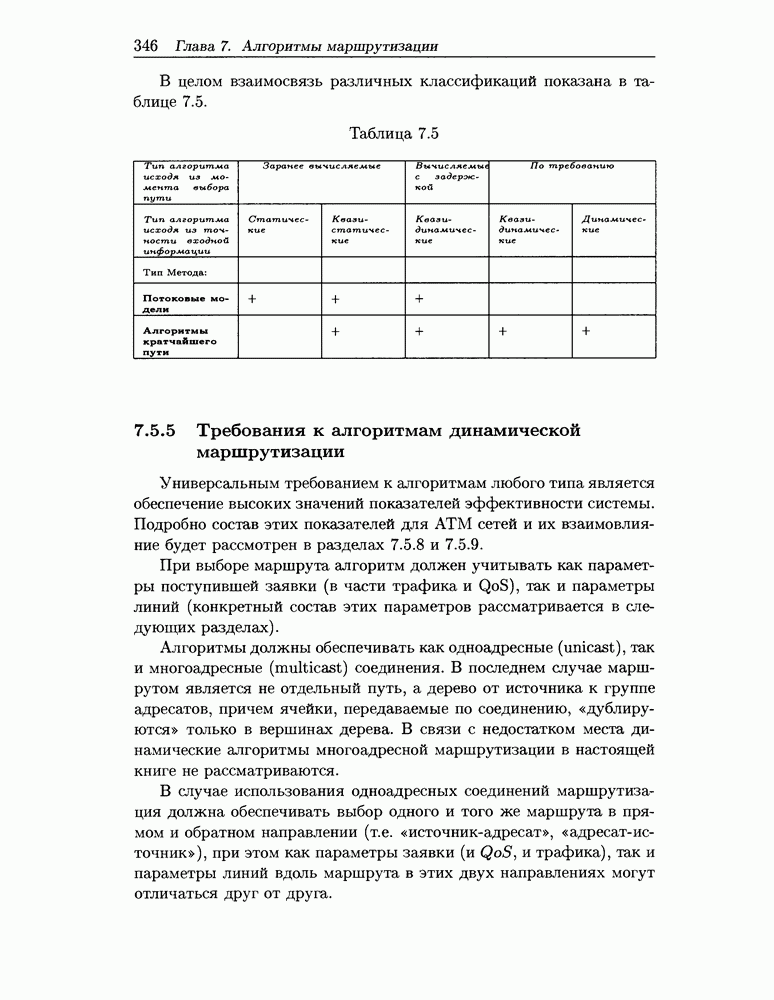
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
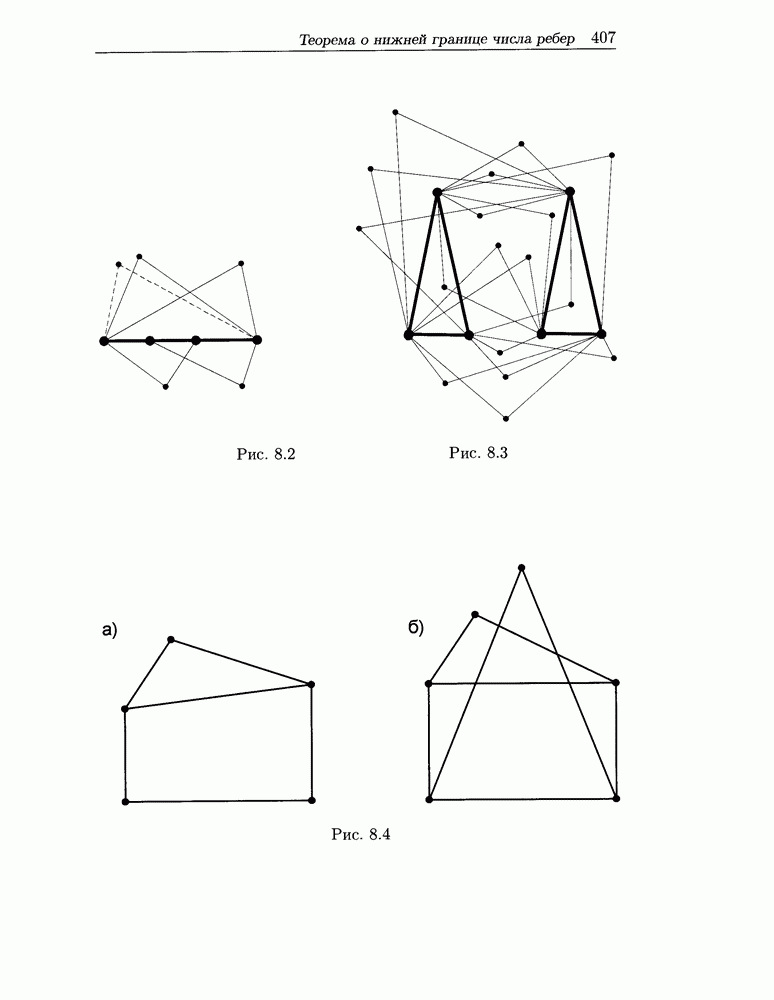
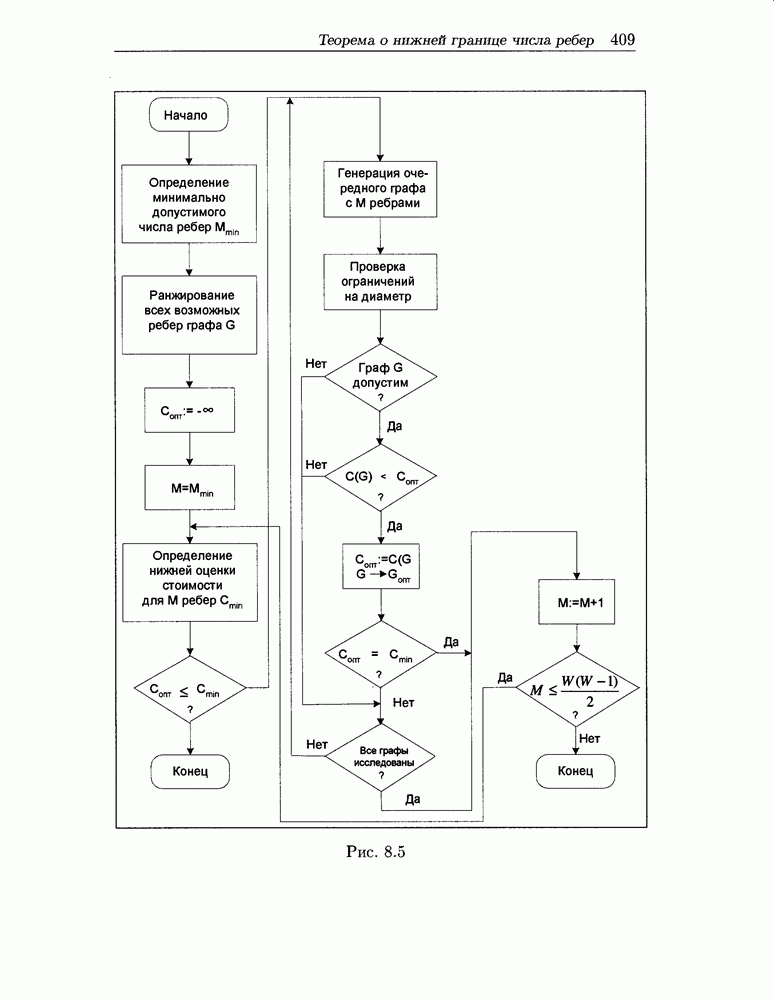
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
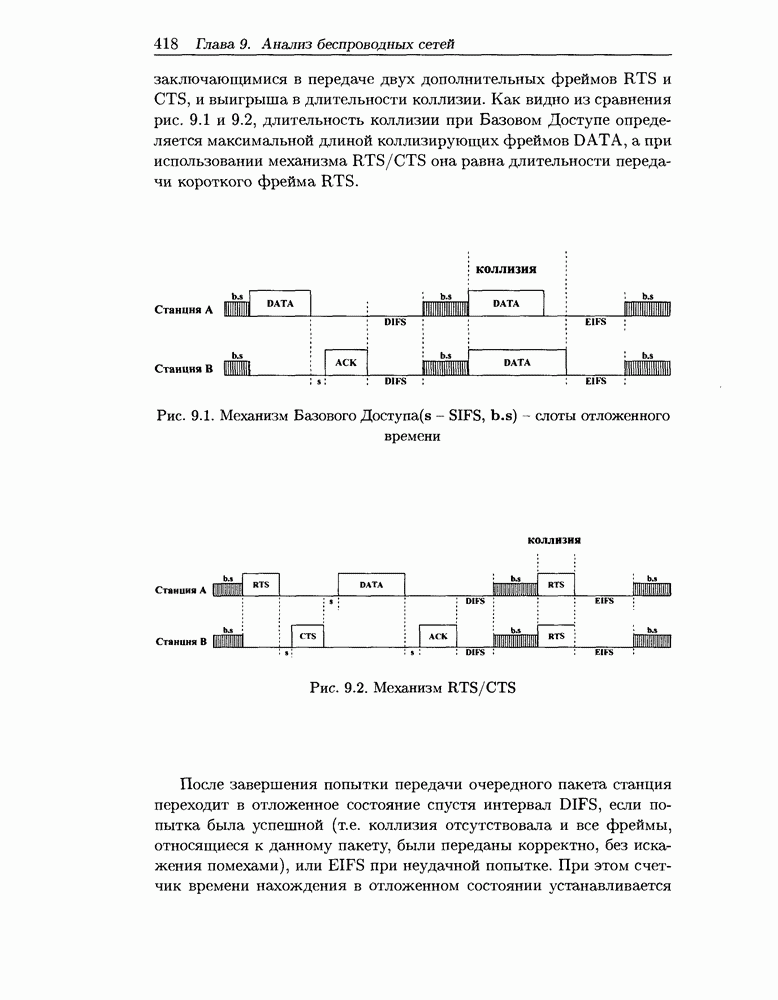
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
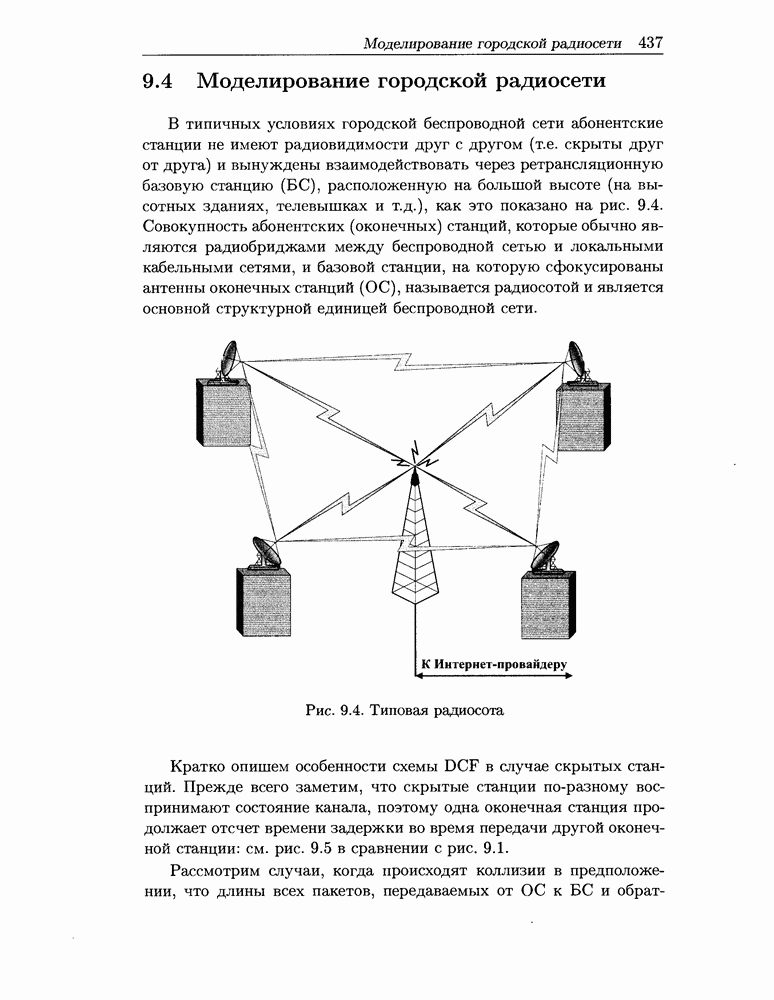
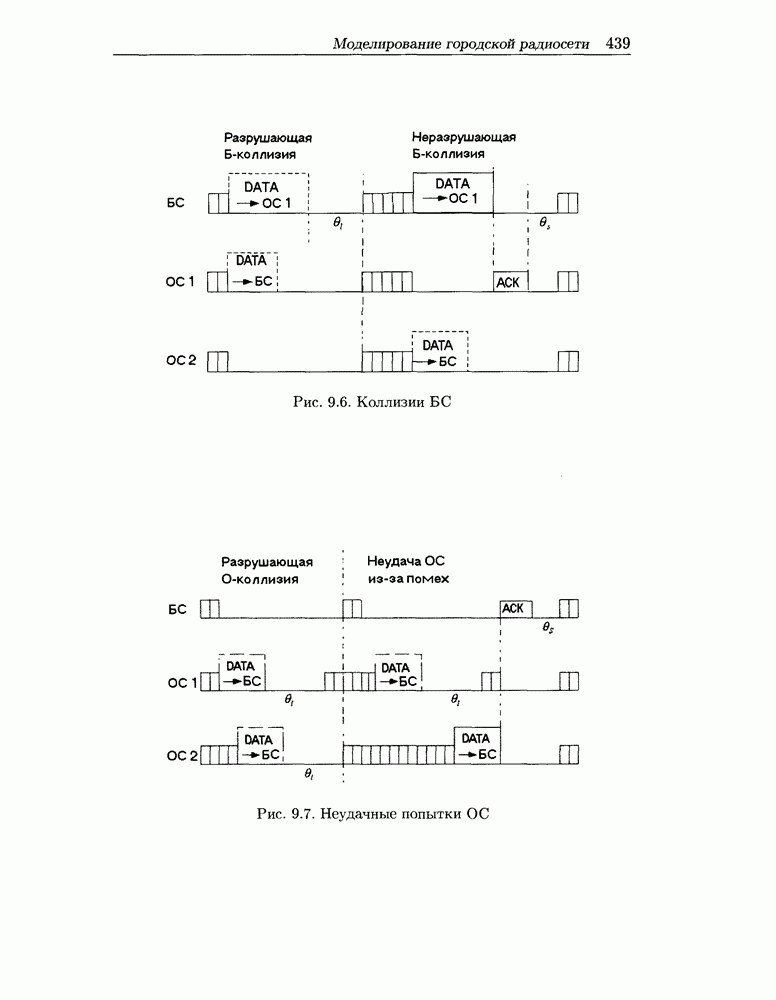
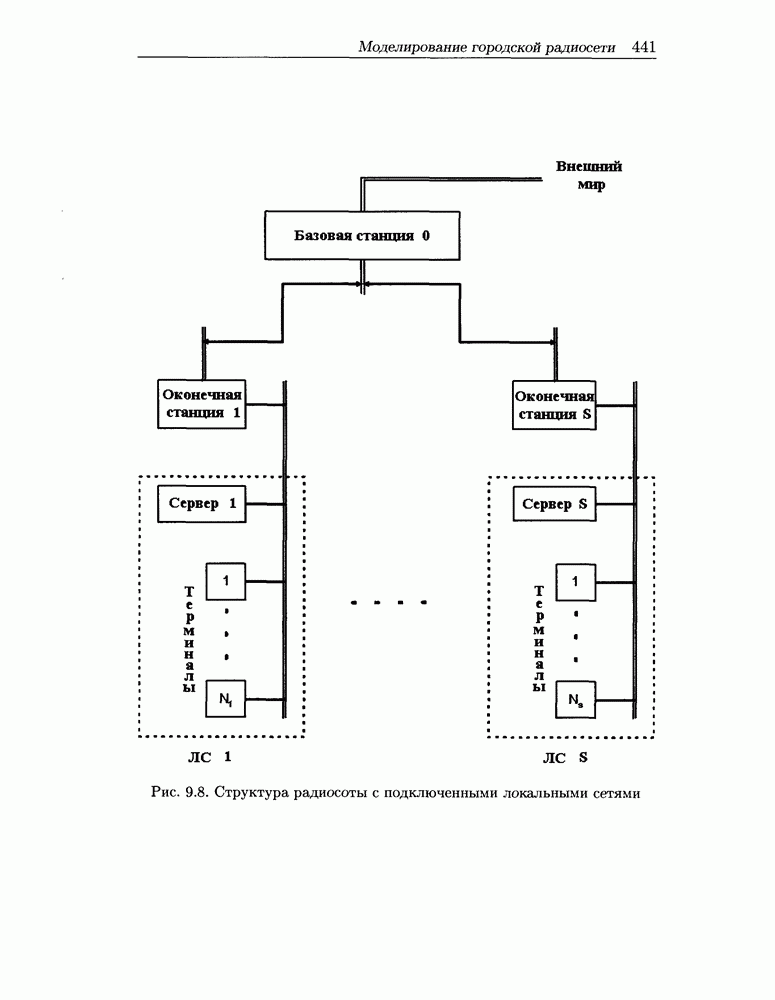
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
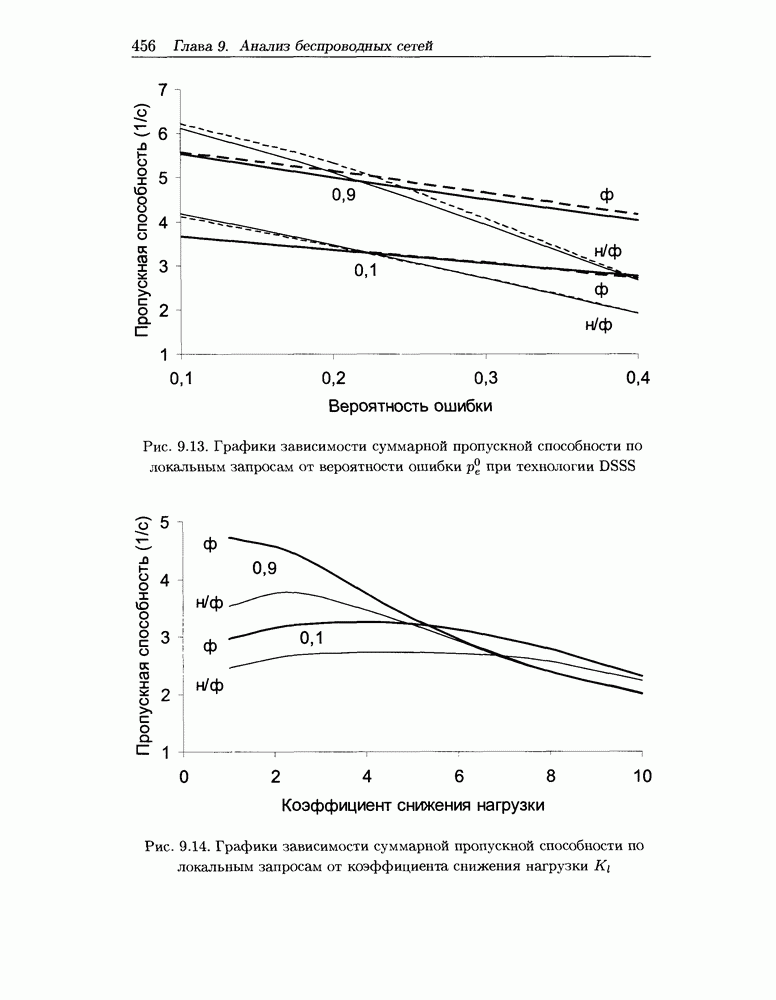
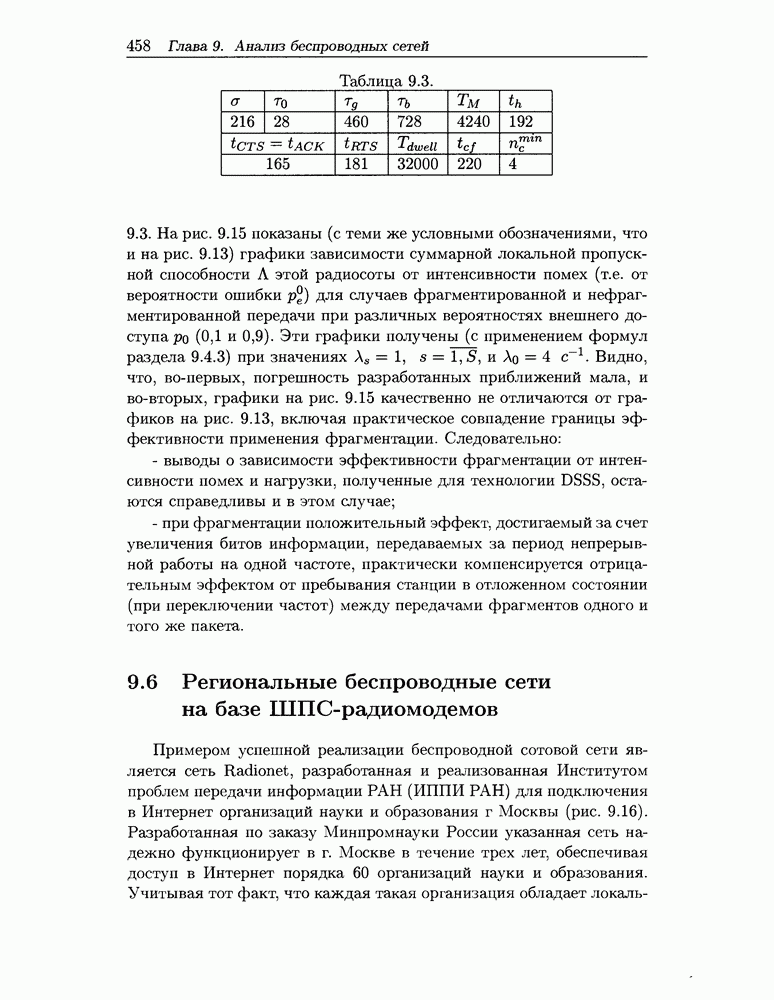
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
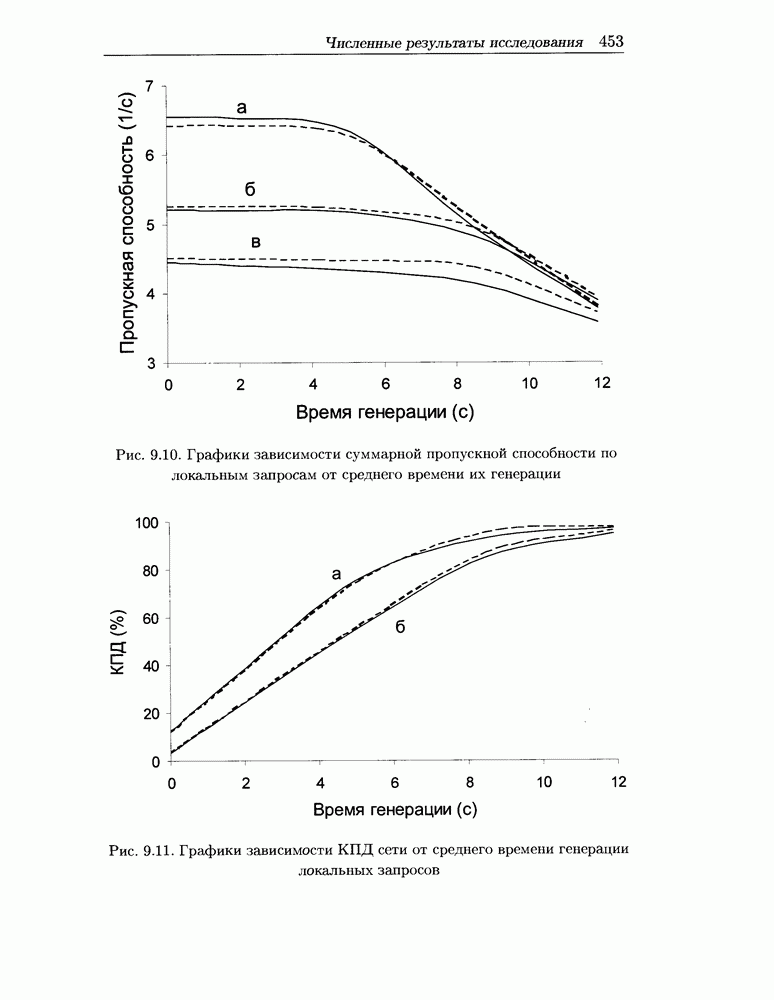
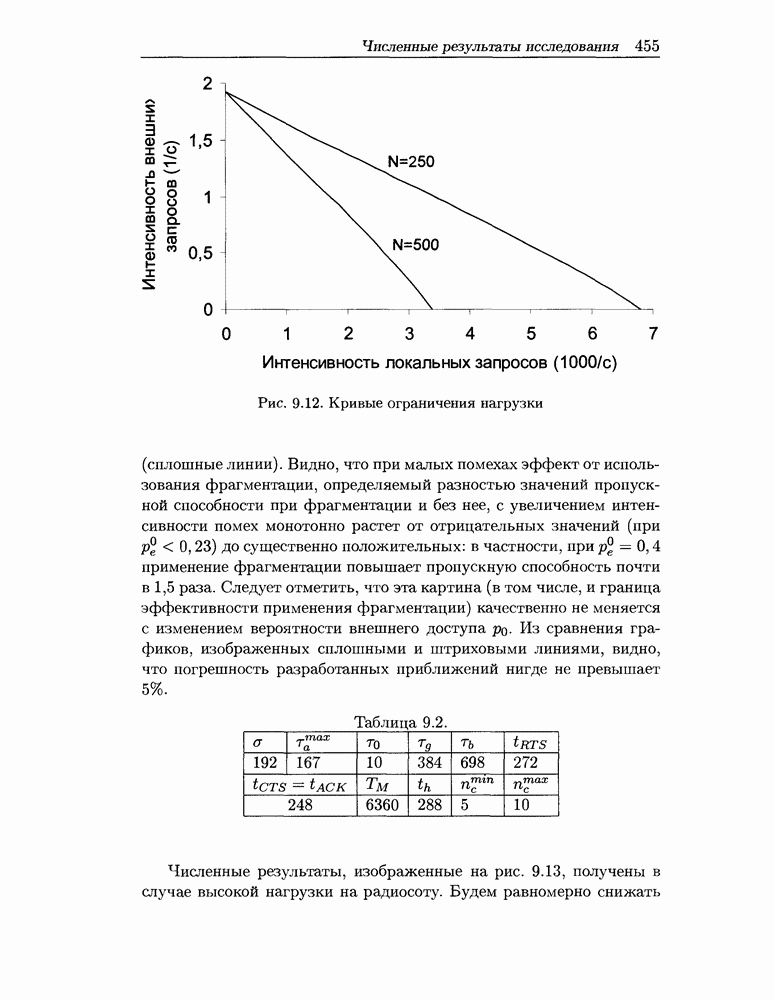
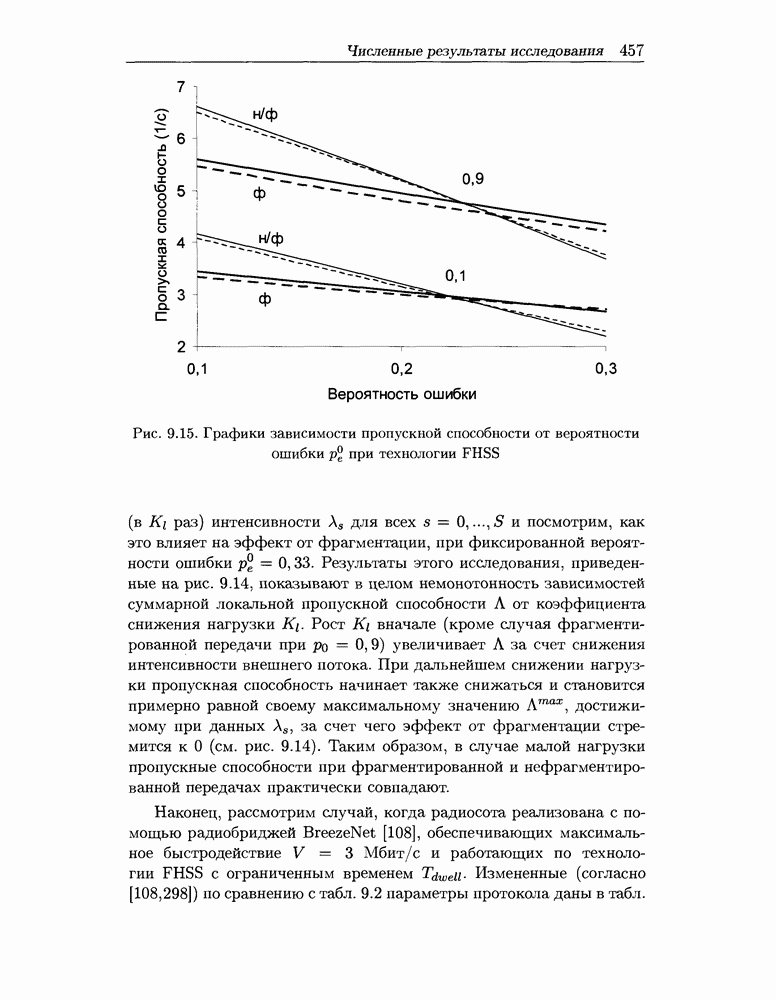
- 9.5 Численные результаты исследования городской радиосоты
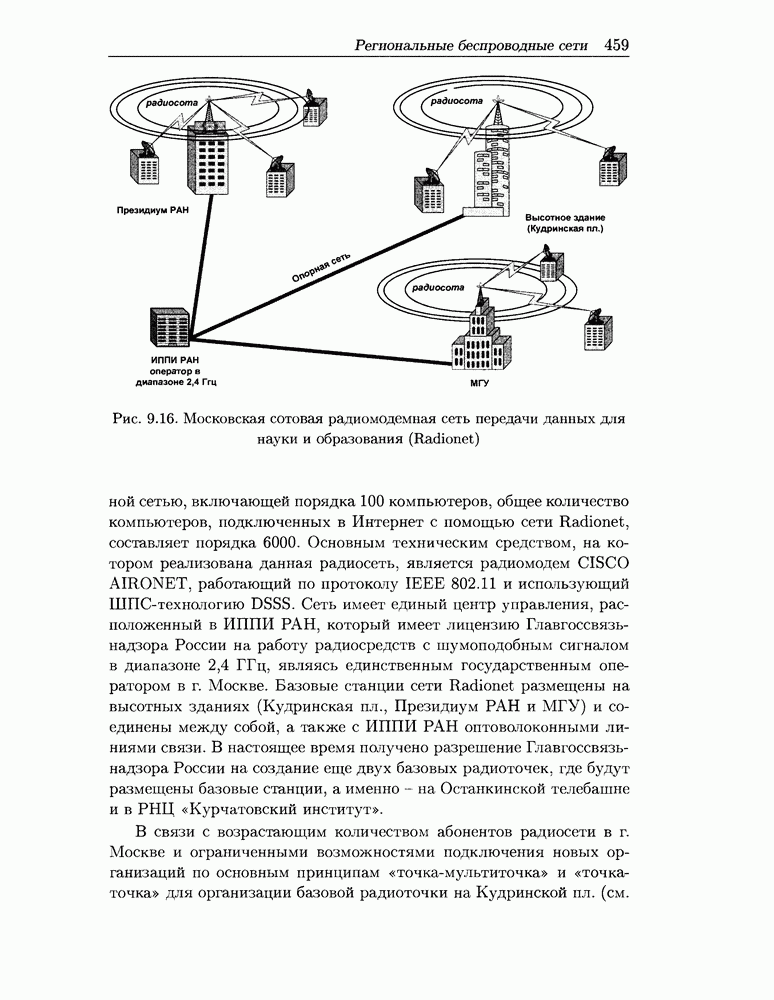
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература