| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
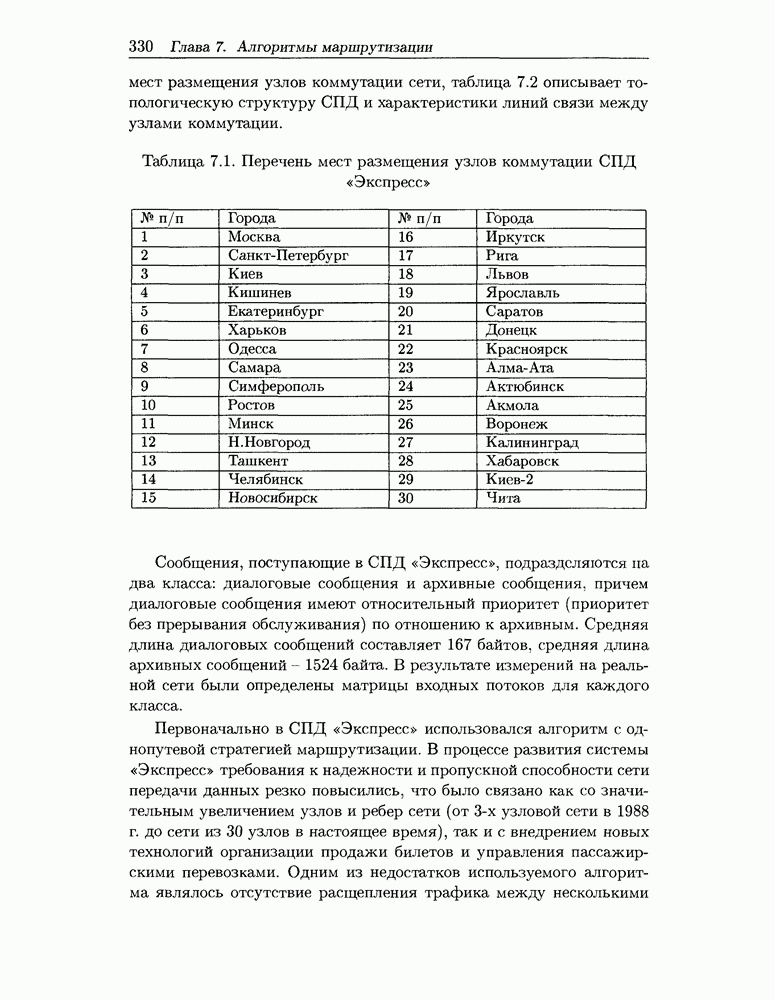
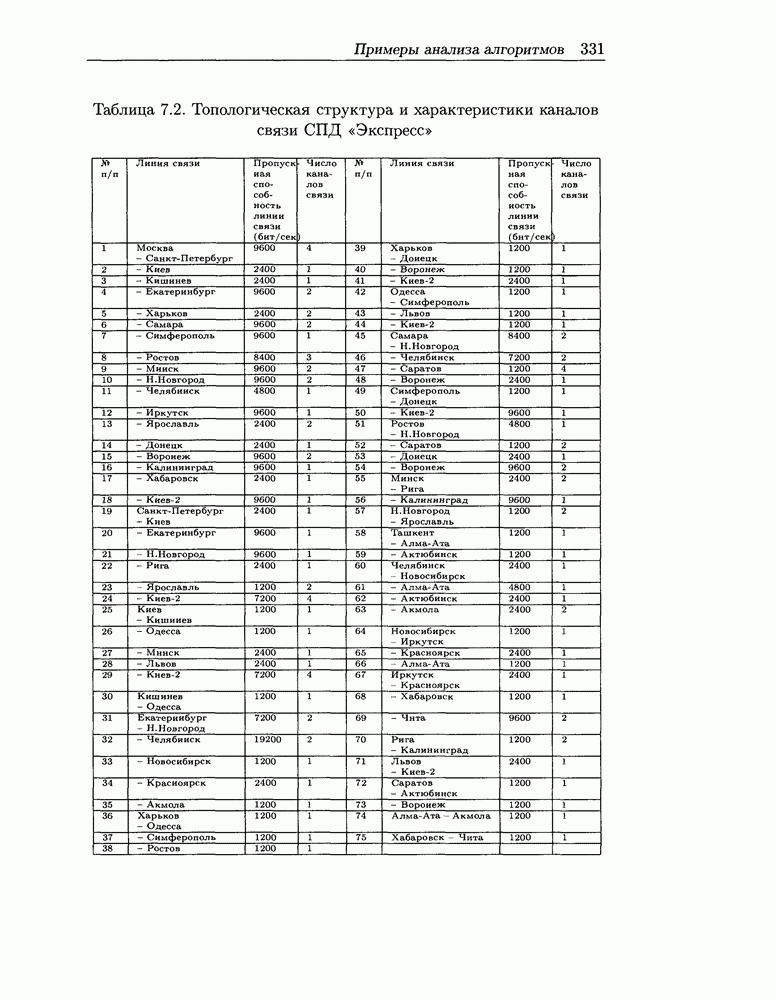
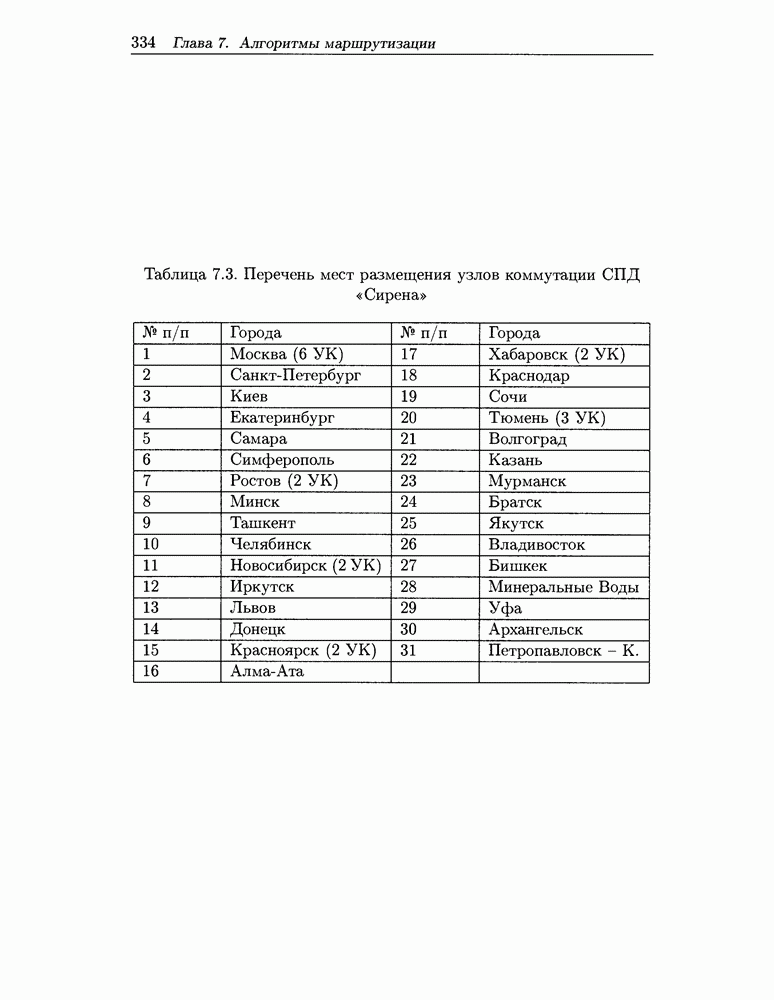
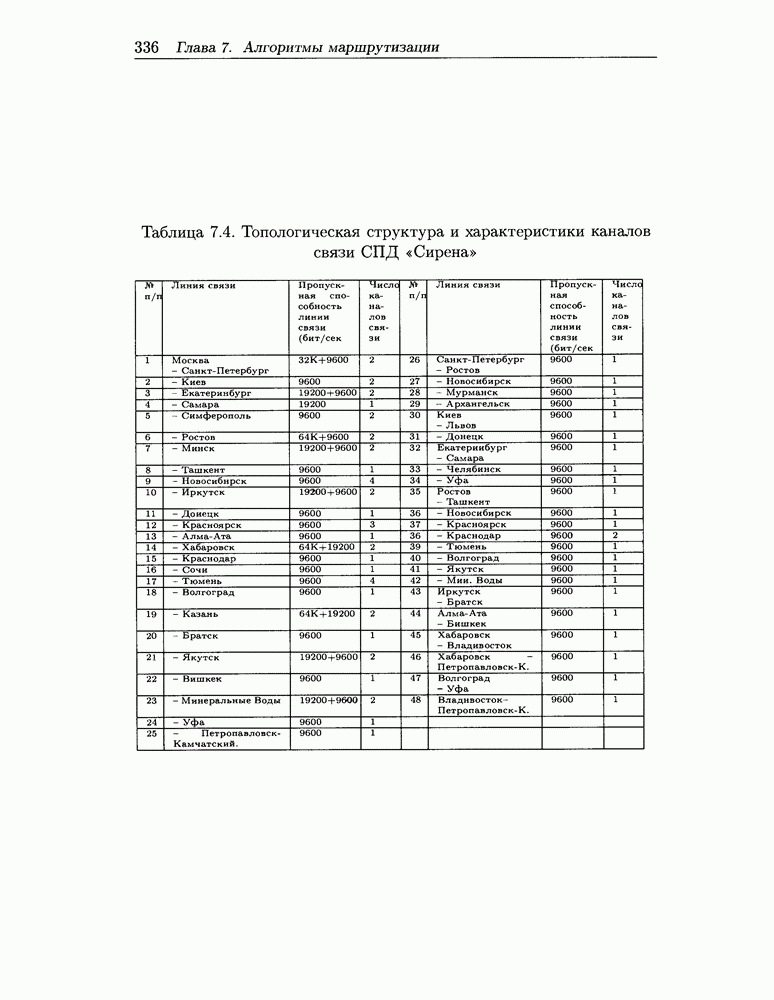
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
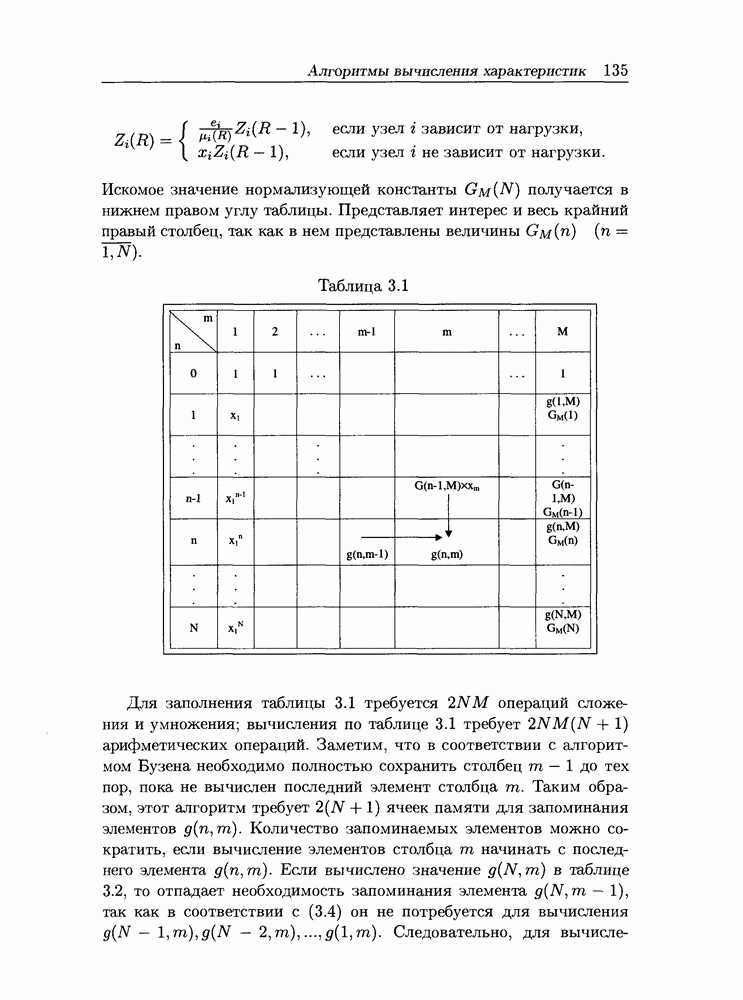
4.2 Декомпозиционные методы на основе теоремы Нортона
4.2.1 Теорема Нортона для анализа замкнутых и разомкнутых локально-сбалансированных сетей массового обслуживания
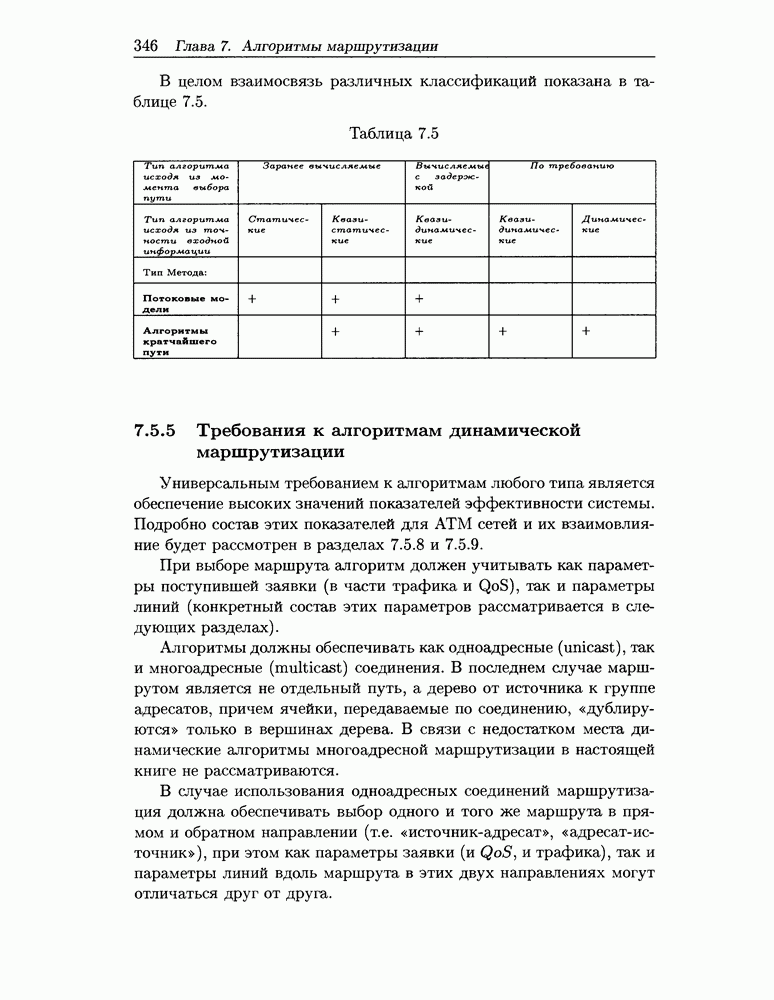
Рассмотрим однородную сеть МО с М центрами обслуживания, удовлетворяющую условиям локального баланса и вероятностями перехода, задаваемыми матрицей маршрутов 
Пусть  - относительная интенсивность потока сообщений в
- относительная интенсивность потока сообщений в  центре, удовлетворяющая векторному уравнению
центре, удовлетворяющая векторному уравнению  Как отмечалось в предыдущих главах,
Как отмечалось в предыдущих главах,  определяется абсолютной интенсивностью поступления сообщений в разомкнутую сеть; в замкнутой сети решение векторного уравнения единственно с точностью до мультипликативной константы.
определяется абсолютной интенсивностью поступления сообщений в разомкнутую сеть; в замкнутой сети решение векторного уравнения единственно с точностью до мультипликативной константы.
Декомпозиция такой сети на основе теоремы Нортона (название дано по аналогии с известным результатом в электрических цепях) позволяет свести исходную сеть МО к эквивалентной с двумя центрами обслуживания. При этом первый центр двухузловой сети совпадает с  центром исходной сети
центром исходной сети  , а второй (композиционный), являющийся эквивалентом оставшейся части сети, обладает экспоненциально распределенным временем обслуживания с параметром
, а второй (композиционный), являющийся эквивалентом оставшейся части сети, обладает экспоненциально распределенным временем обслуживания с параметром  зависящим от числа сообщений в нем.
зависящим от числа сообщений в нем.
Теорема. Маргинальное распределение числа сообщений в  центре исходной сети совпадает с соответствующим распределением эквивалентной сети, если параметр
центре исходной сети совпадает с соответствующим распределением эквивалентной сети, если параметр  композиционного центра равен интенсивности
композиционного центра равен интенсивности  поступления сообщений в
поступления сообщений в  центр исходной сети, в которой
центр исходной сети, в которой 

Рис. 4.1

Рис. 4.2
Рассмотрим более подробно применение этой теоремы для замкнутой сети МО (рис. 4.1). Для вычисления статистических характеристик  центра сети на рис. 4.1 подсеть В заменяется композиционным центром (рис. 4.2).
центра сети на рис. 4.1 подсеть В заменяется композиционным центром (рис. 4.2).

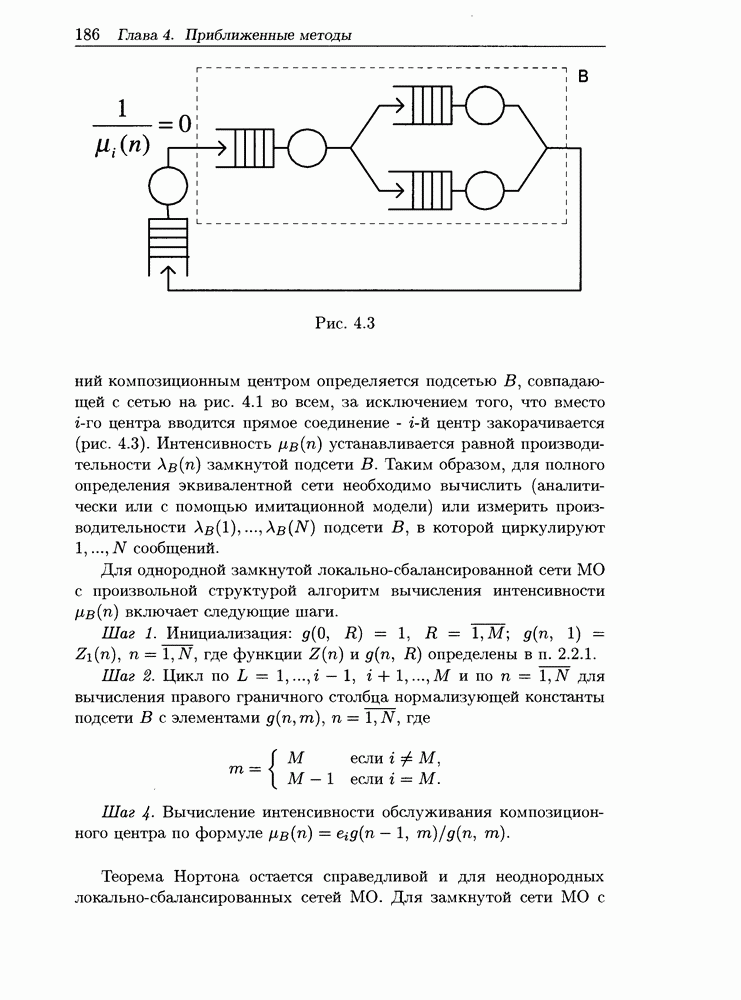
Рис. 4.3
Интенсивность обслуживания сообщений композиционным центром определяется подсетью В, совпадающей с сетью на рис. 4.1 во всем, за исключением того, что вместо  центра вводится прямое соединение -
центра вводится прямое соединение -  центр закорачивается (рис. 4.3). Интенсивность
центр закорачивается (рис. 4.3). Интенсивность  устанавливается равной производительности
устанавливается равной производительности  замкнутой подсети В. Таким образом, для полного определения эквивалентной сети необходимо вычислить (аналитически или с помощью имитационной модели) или измерить производительности
замкнутой подсети В. Таким образом, для полного определения эквивалентной сети необходимо вычислить (аналитически или с помощью имитационной модели) или измерить производительности  подсети В, в которой циркулируют
подсети В, в которой циркулируют  сообщений.
сообщений.
Для однородной замкнутой локально-сбалансированной сети МО с произвольной структурой алгоритм вычисления интенсивности  включает следующие шаги.
включает следующие шаги.
Шаг 1. Инициализация:  где функции
где функции  определены в п. 2.2.1.
определены в п. 2.2.1.
Шаг 2. Цикл по  и по
и по  для вычисления правого граничного столбца нормализующей константы подсети В с элементами
для вычисления правого граничного столбца нормализующей константы подсети В с элементами  , где
, где

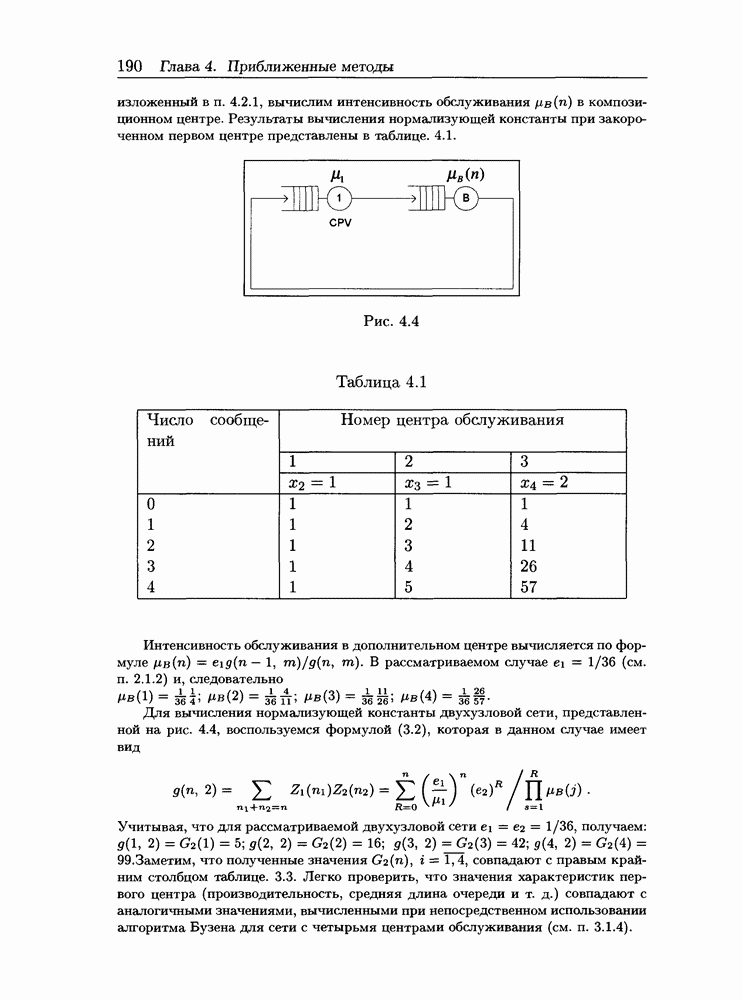
Шаг 4. Вычисление интенсивности обслуживания композиционного центра по формуле  .
.
Теорема Нортона остается справедливой и для неоднородных локально-сбалансированных сетей МО.
Для замкнутой сети МО с  классами сообщений в этом случае с целью построения эквивалентной сети должны быть вычислены для всех
классами сообщений в этом случае с целью построения эквивалентной сети должны быть вычислены для всех  производительности
производительности  подсети В. В разомкнутой сети все центры, за исключением рассматриваемого
подсети В. В разомкнутой сети все центры, за исключением рассматриваемого  центра, заменяются одним композиционным пуассоновским источником, который генерирует сообщения всех классов. Каждый класс генерируется независимо, и интенсивность потока
центра, заменяются одним композиционным пуассоновским источником, который генерирует сообщения всех классов. Каждый класс генерируется независимо, и интенсивность потока  класса сообщений
класса сообщений  , поступающего из композиционного источника, устанавливается равной производительности
, поступающего из композиционного источника, устанавливается равной производительности  подсети В.
подсети В.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
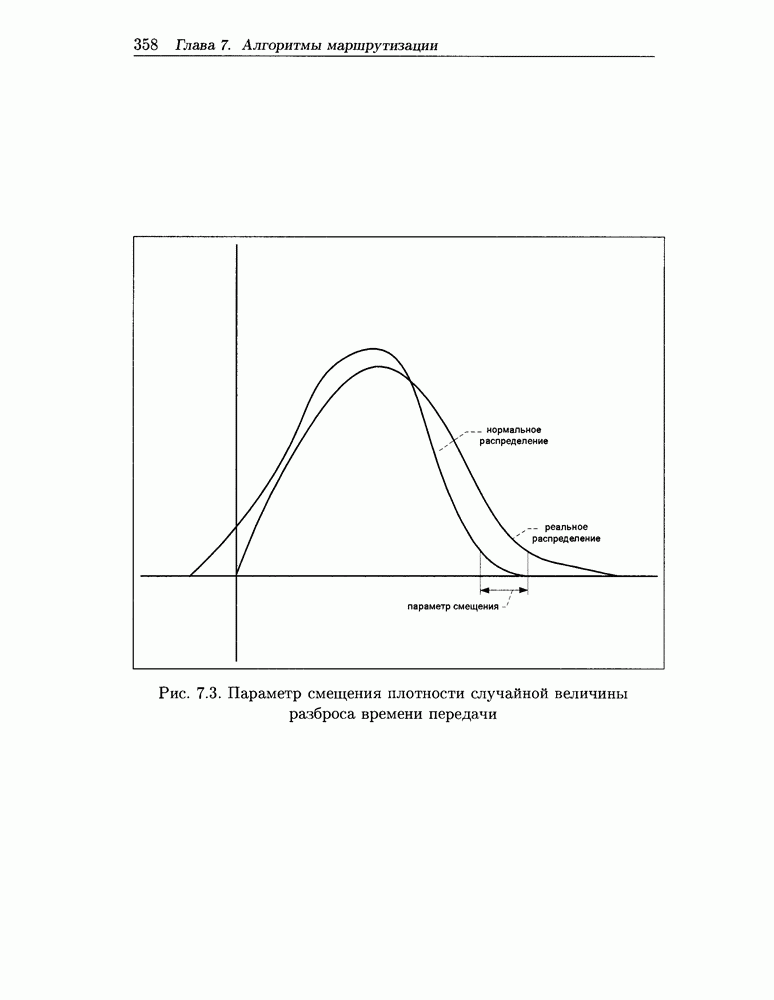
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
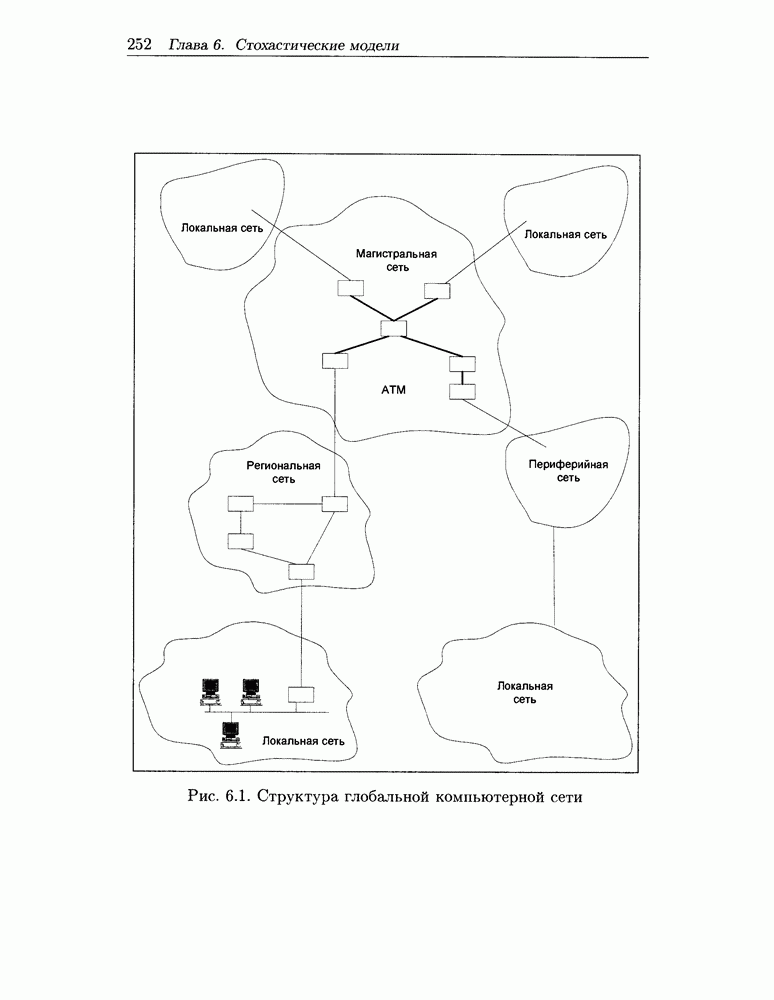
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
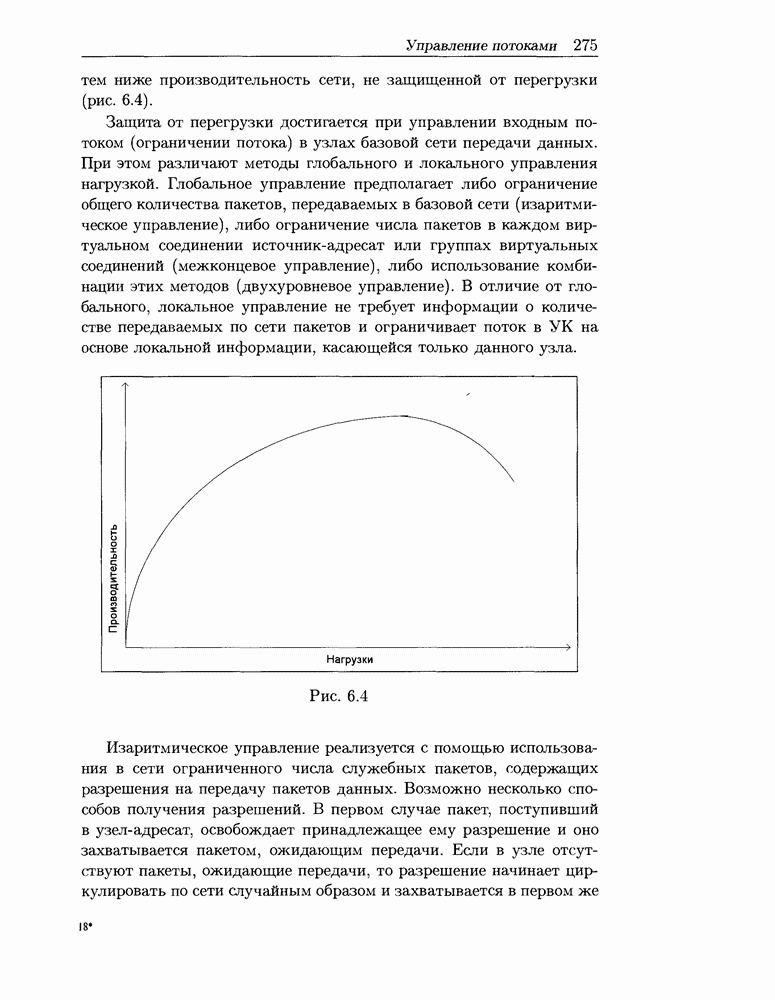
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
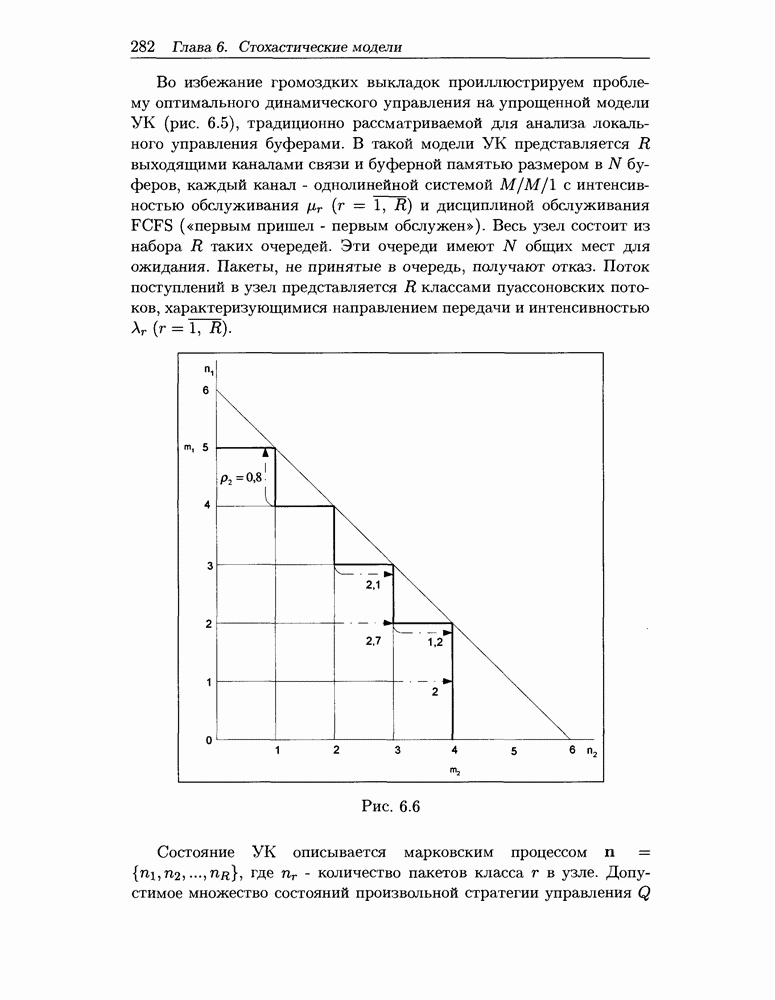
- 6.3.3 Локальное управление буферами
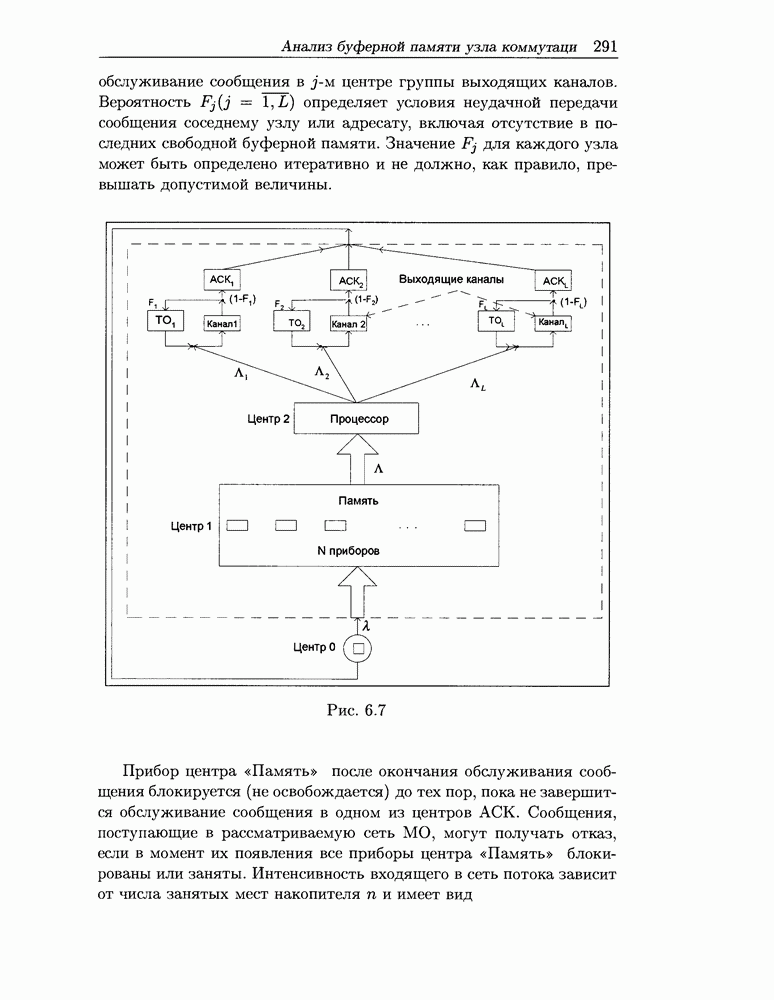
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
- 7.4.2 Анализ развития СПД «Сирена»
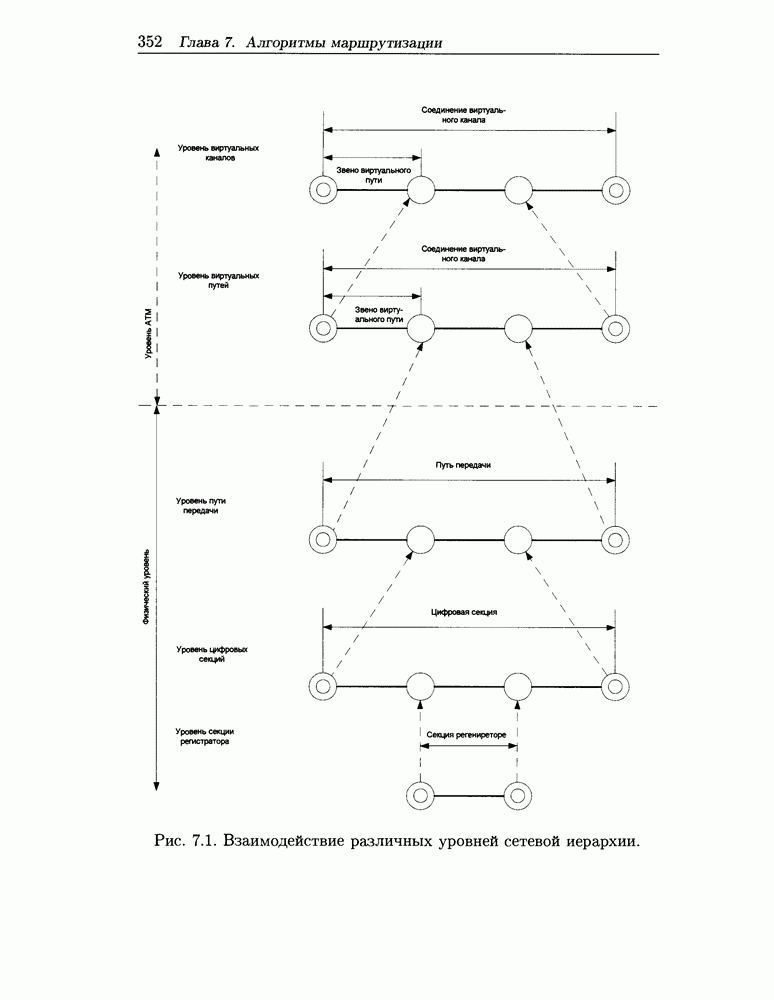
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
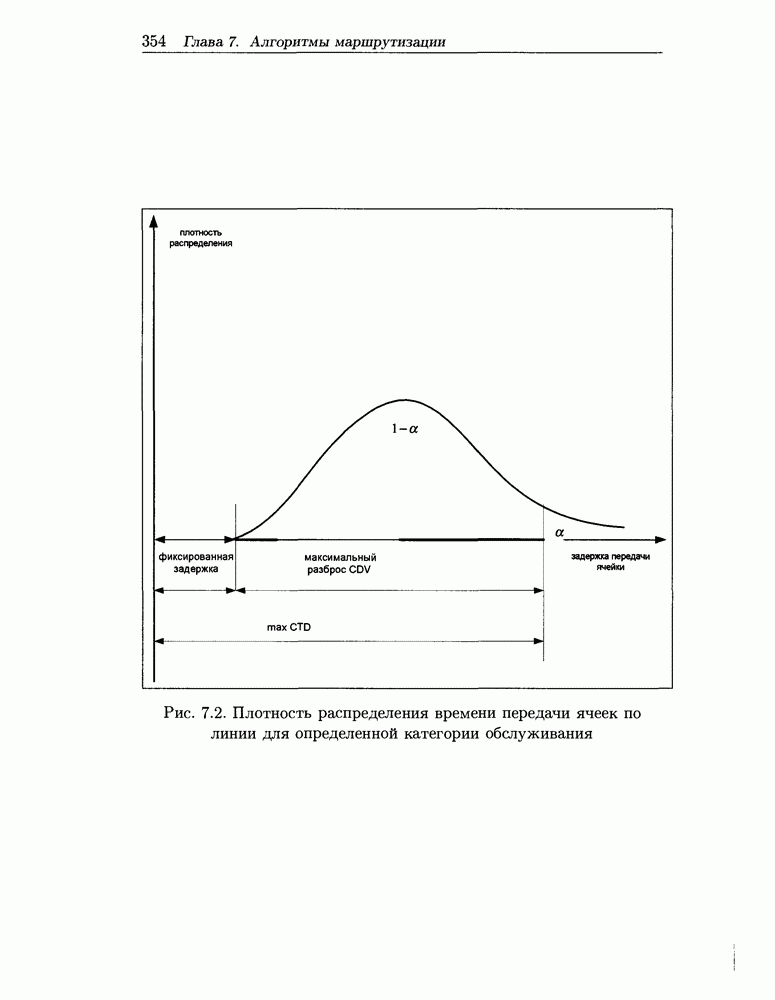
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
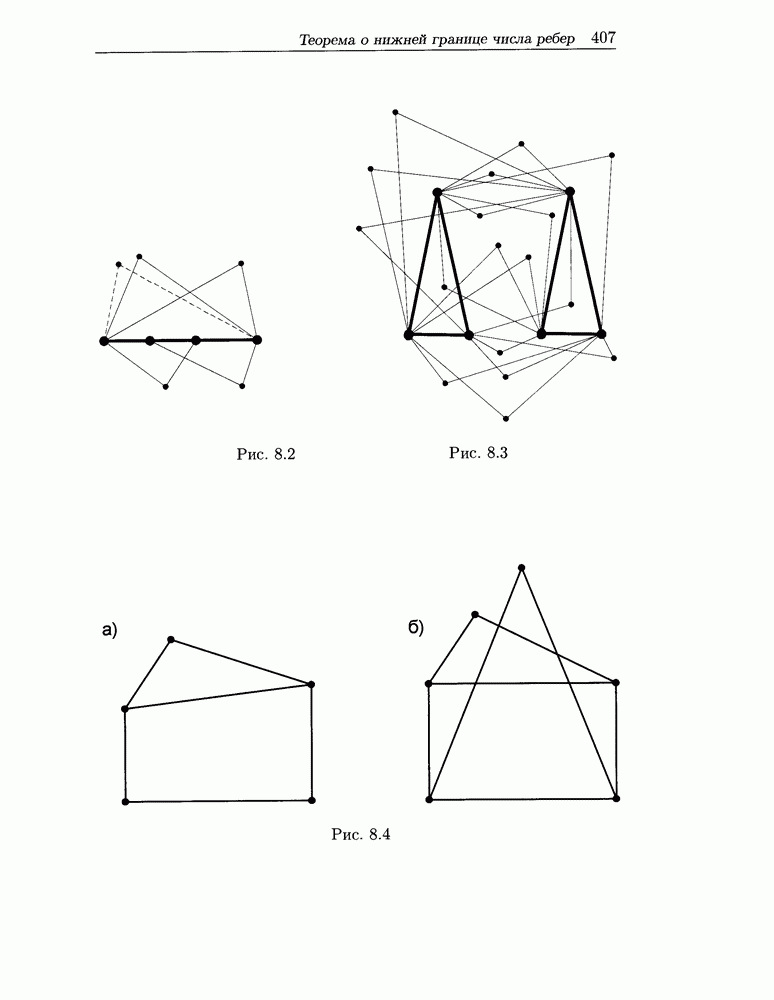
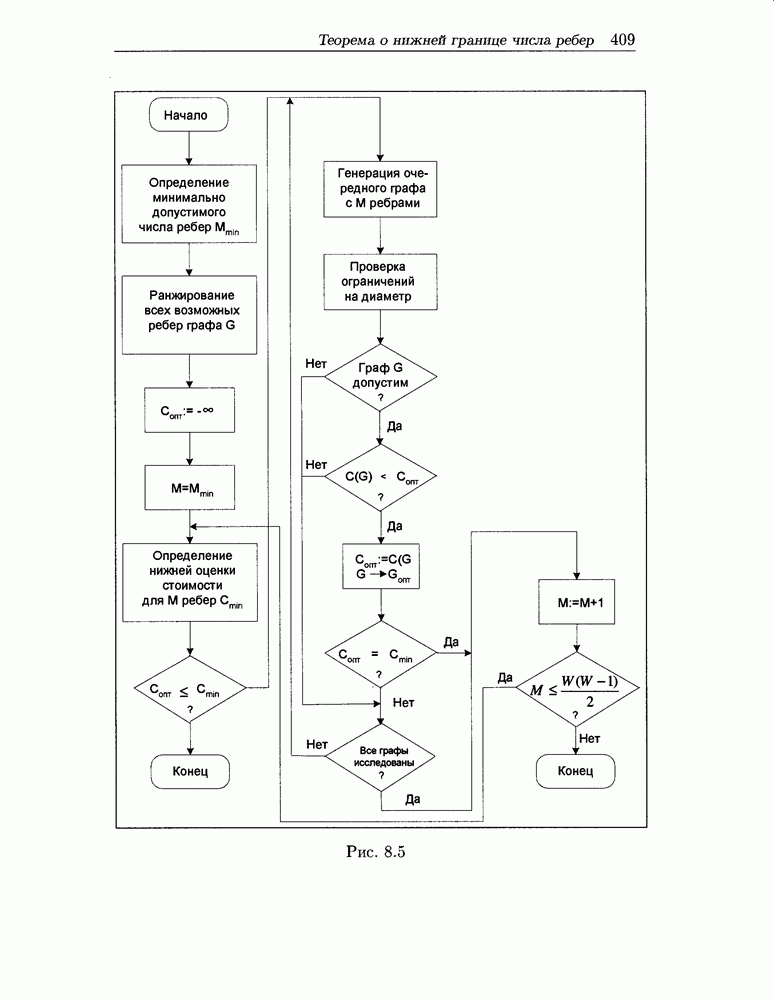
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
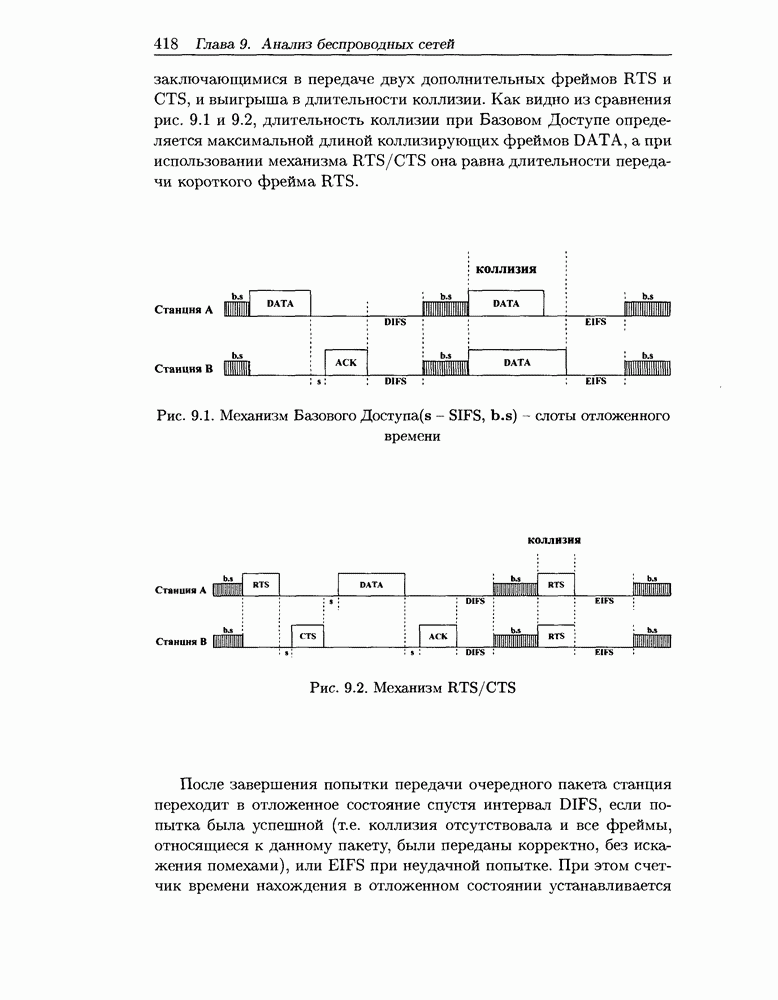
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
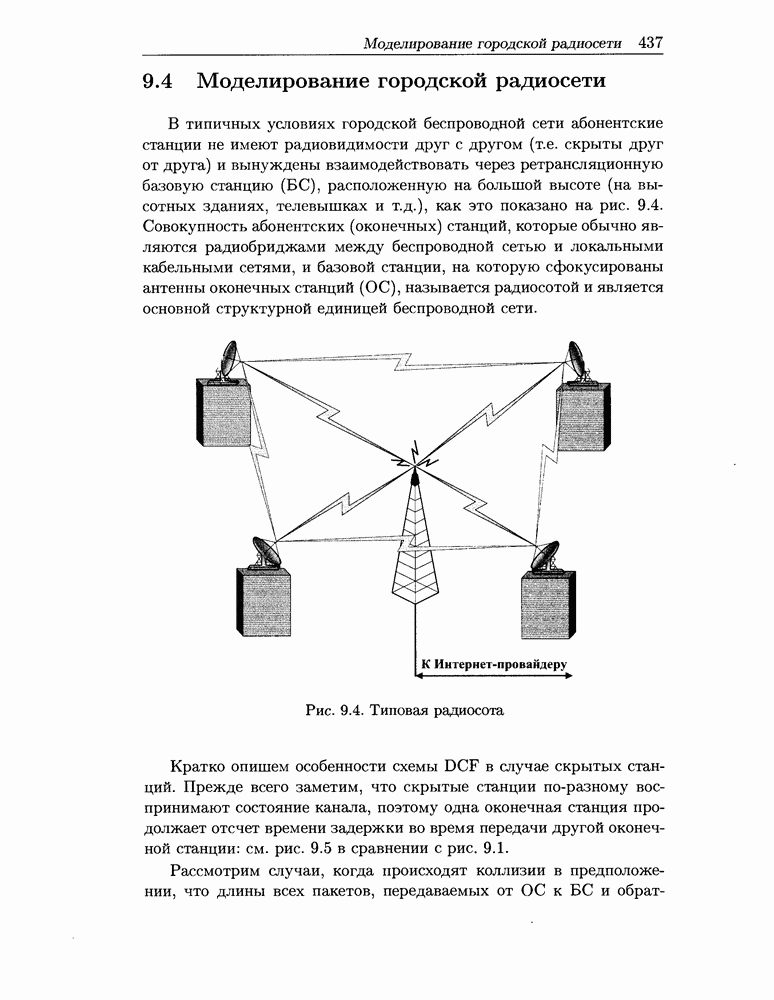
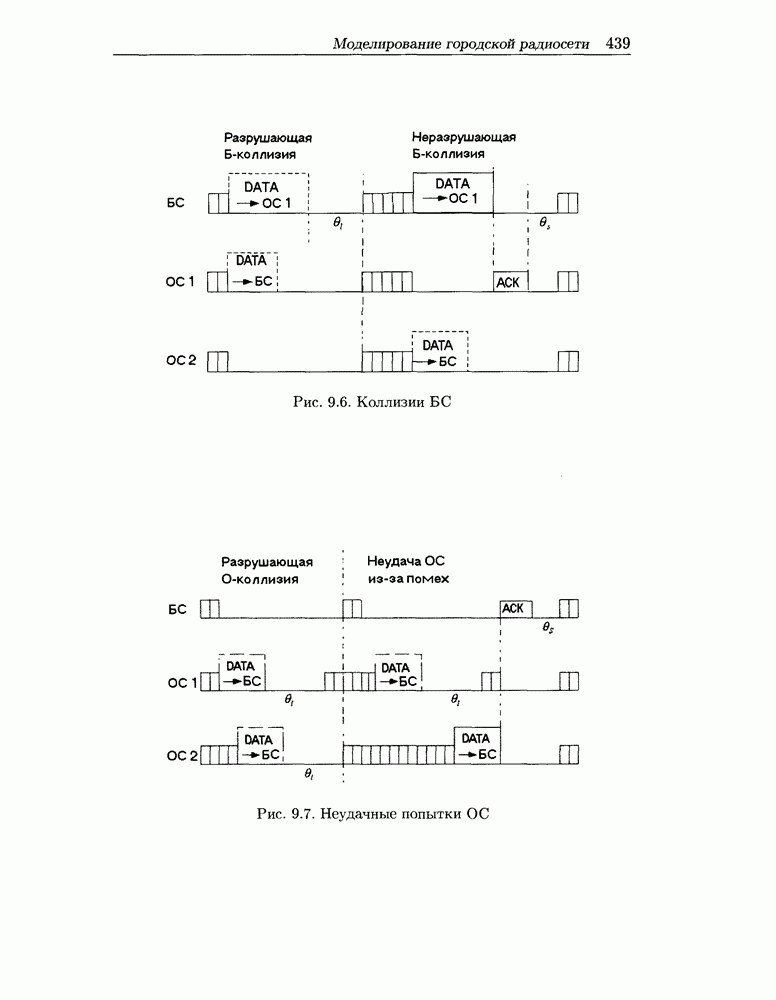
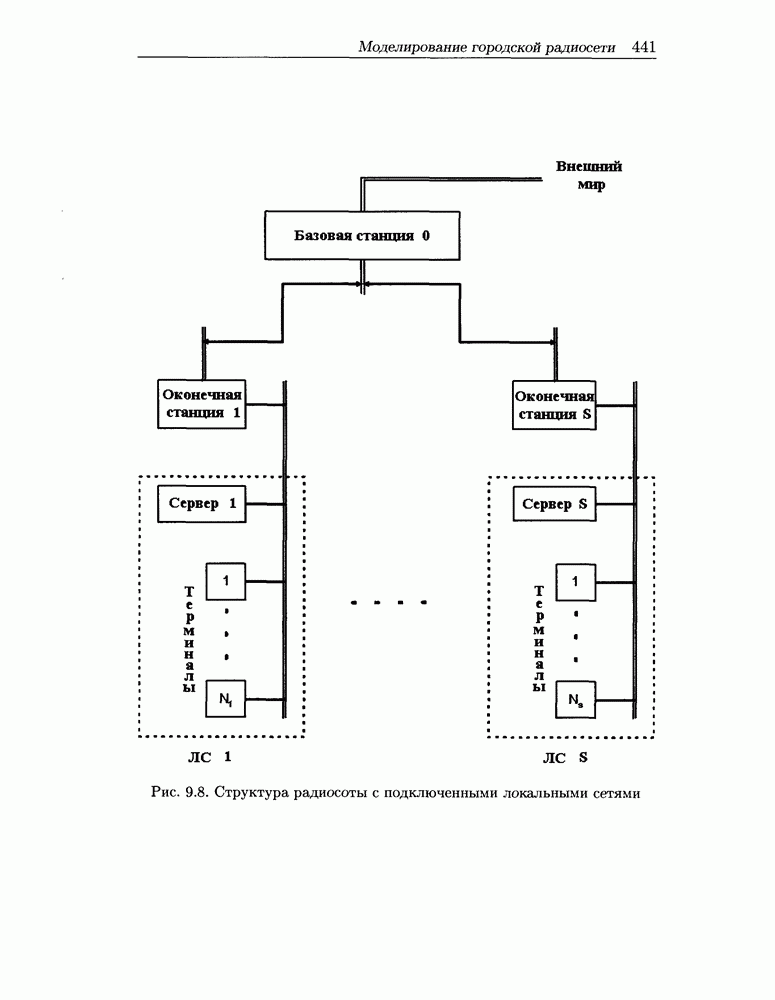
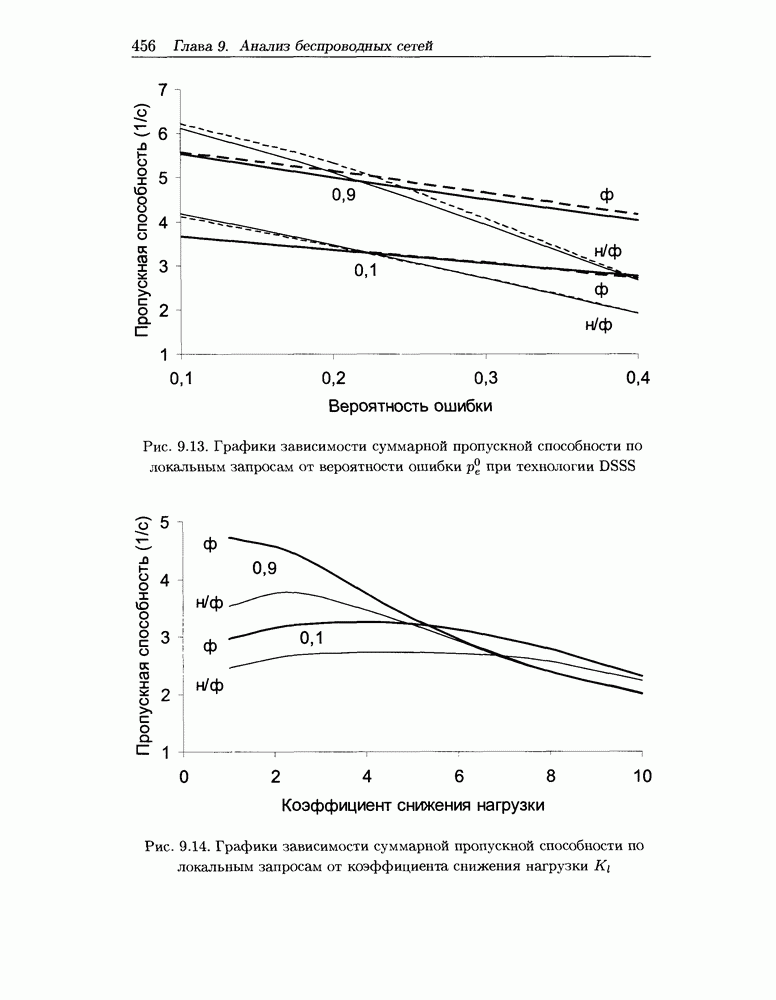
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
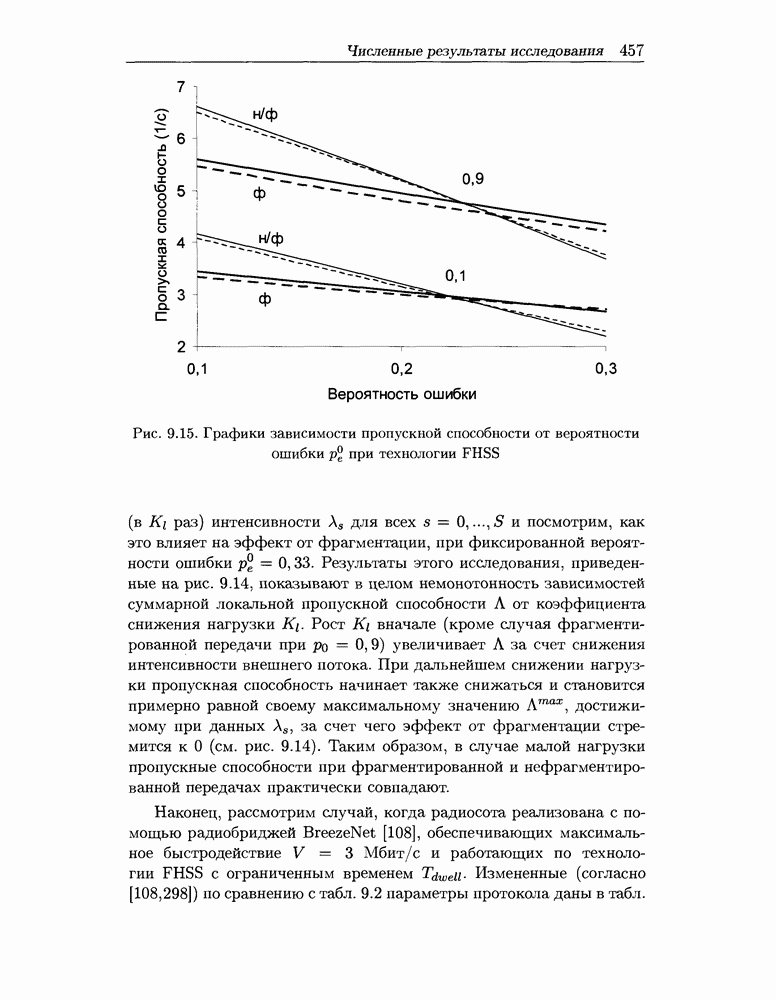
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
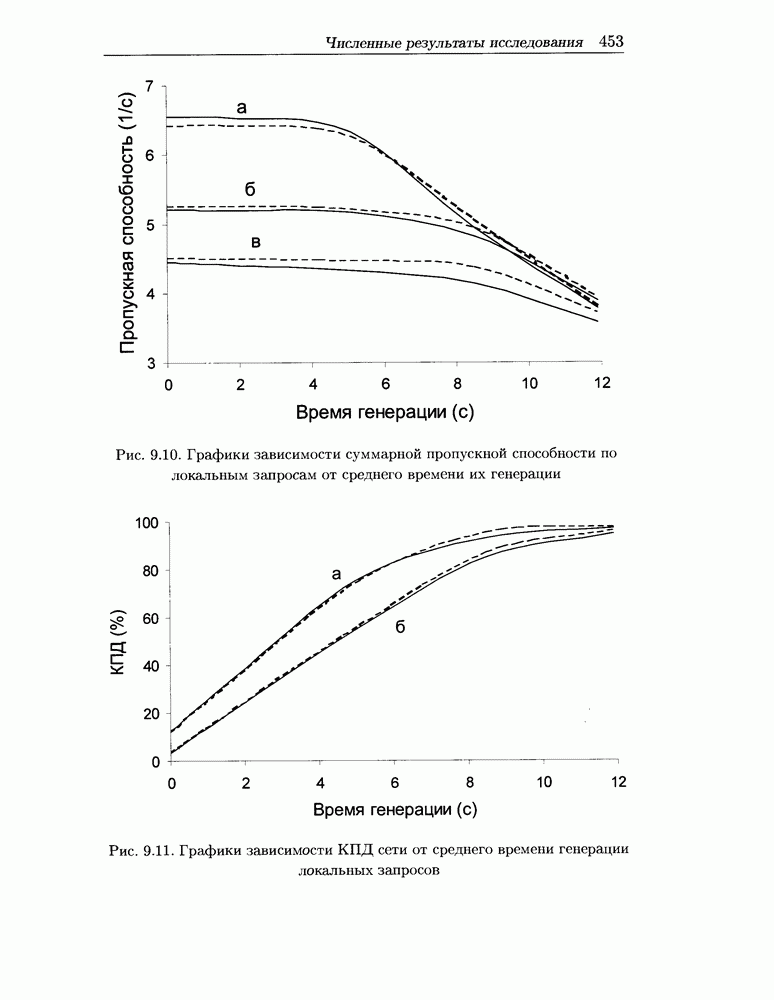
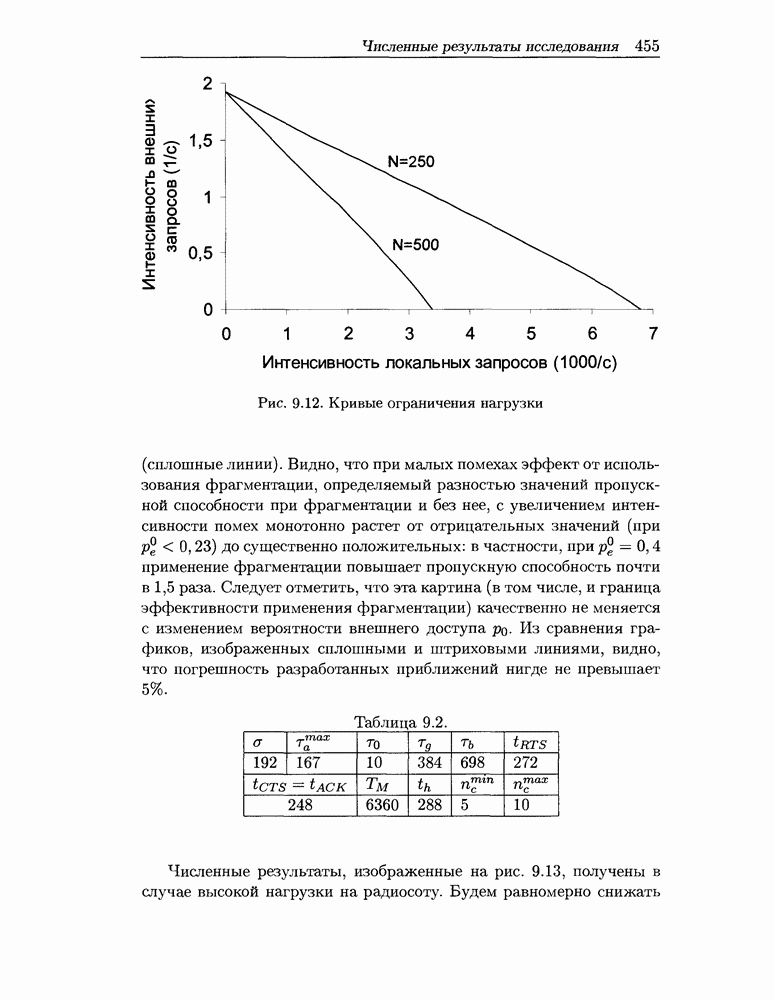
- 9.5 Численные результаты исследования городской радиосоты
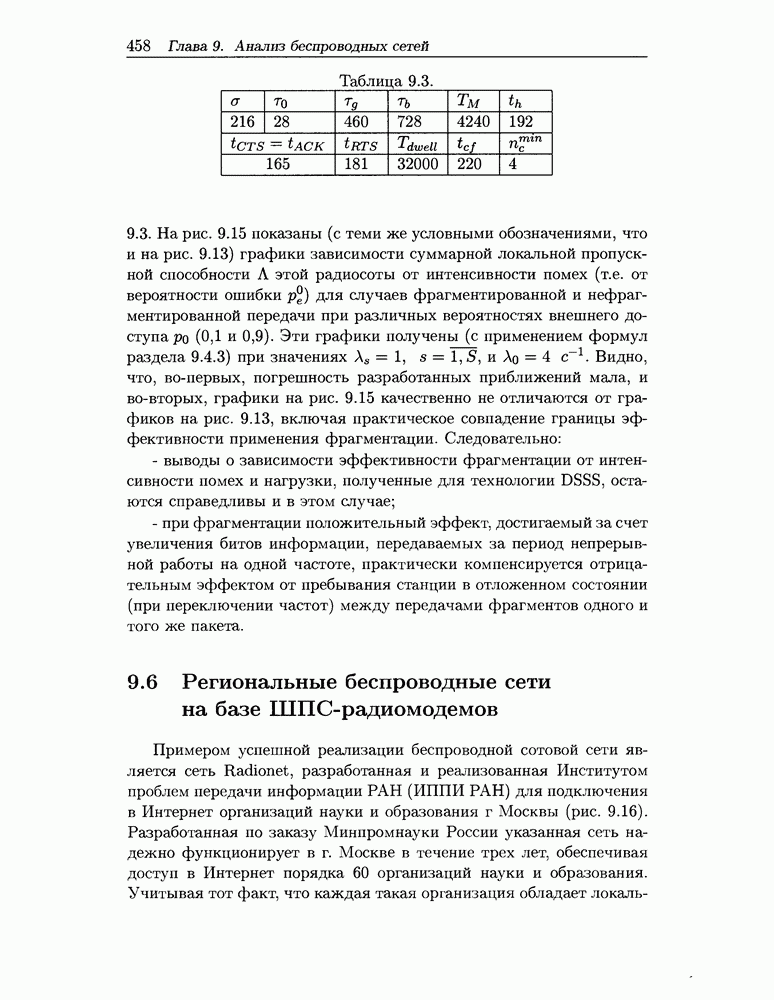
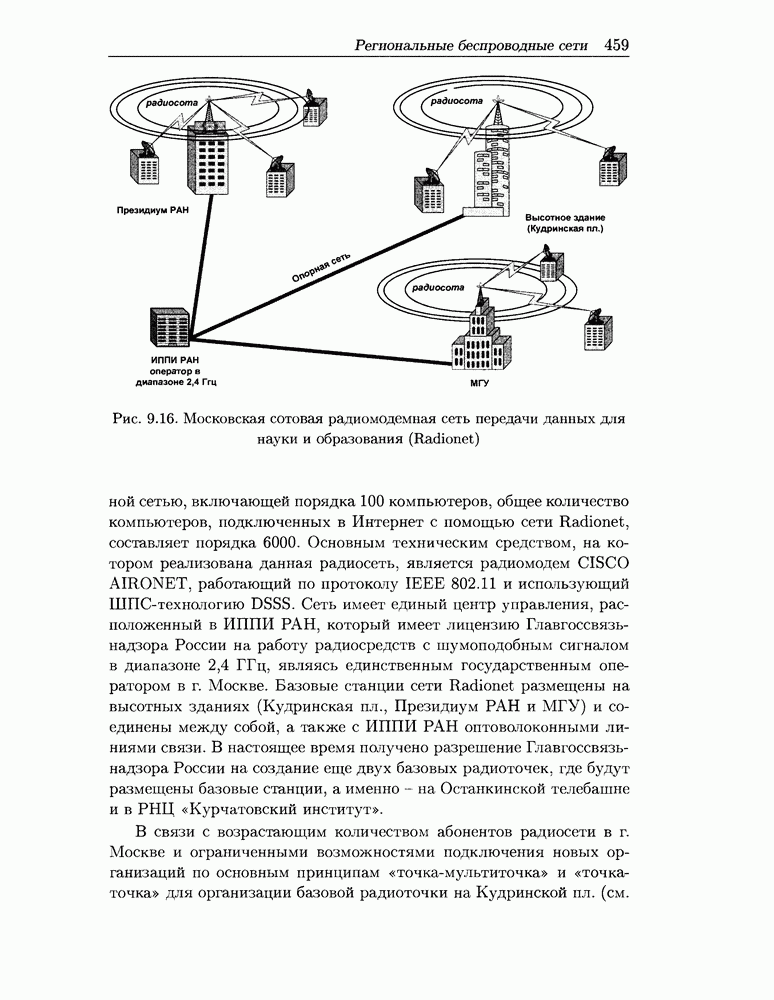
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература