| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.6 Полумарковские однолинейные системы и методы их анализа
Как отмечалось в предыдущем разделе, процесс  - число запросов в системе ММ1 в момент t - является процессом гибели и размножения, то есть, частным случаем цепи Маркова с непрерывным временем. Аналогичный процесс для систем обслуживания типа MG1 с распределением времени обслуживания, отличным от показательного, и типа GIM1 с входящим потоком, отличным от простейшего, уже не является марковским.
- число запросов в системе ММ1 в момент t - является процессом гибели и размножения, то есть, частным случаем цепи Маркова с непрерывным временем. Аналогичный процесс для систем обслуживания типа MG1 с распределением времени обслуживания, отличным от показательного, и типа GIM1 с входящим потоком, отличным от простейшего, уже не является марковским.
Очевидной причиной этого является тот факт, что поведение процесса после некоторого фиксированного момента времени t не определяется, вообще говоря, полностью состоянием этого процесса в этот момент, а зависит также от того, сколь долго уже обслуживается находящийся на приборе в настоящий момент запрос или как давно поступил последний перед данным моментом запрос.
Тем не менее, исследование процесса  может быть сведено к исследованию марковских процессов. Первый способ «маркови-зации» - так называемый метод вложенных цепей Маркова - будет проиллюстрирован на примере системы MG1 в подпункте 6.1 и на примере системы GIM1 - в подпункте 6.2. Одна из разновидностей другого способа «марковизации» - метода введения дополнительной переменной - будет проиллюстрирована в подпункте 6.3. В подпункте 6.4 будет кратко описан и проиллюстрирован на примерах еще один мощный метод исследования СМО - метод введения дополнительного события.
может быть сведено к исследованию марковских процессов. Первый способ «маркови-зации» - так называемый метод вложенных цепей Маркова - будет проиллюстрирован на примере системы MG1 в подпункте 6.1 и на примере системы GIM1 - в подпункте 6.2. Одна из разновидностей другого способа «марковизации» - метода введения дополнительной переменной - будет проиллюстрирована в подпункте 6.3. В подпункте 6.4 будет кратко описан и проиллюстрирован на примерах еще один мощный метод исследования СМО - метод введения дополнительного события.
1.6.1 Метод вложенных цепей Маркова в приложении для системы MG1
Рассмотрим однолинейную СМО с ожиданием, на вход которой поступает простейший поток интенсивности  , а время обслуживания запроса имеет произвольное распределение с функцией распределения
, а время обслуживания запроса имеет произвольное распределение с функцией распределения  преобразованием Лапласа - Стилтьеса
преобразованием Лапласа - Стилтьеса  и конечными начальными моментами
и конечными начальными моментами 
Как было отмечено, процесс  - число запросов в рассматриваемой системе в момент t - не является марковским, поскольку мы не можем описать поведение процесса после произвольного момента времени, не оглядываясь в прошлое.
- число запросов в рассматриваемой системе в момент t - не является марковским, поскольку мы не можем описать поведение процесса после произвольного момента времени, не оглядываясь в прошлое.
Вместе с тем, очевидно, что если мы знаем состояние  процесса
процесса  в момент
в момент  окончания обслуживания к
окончания обслуживания к  запроса, то мы можем предсказать значение процесса
запроса, то мы можем предсказать значение процесса  в момент окончания обслуживания (k + 1)-го запроса, который произойдет через случайное время, и, имеющее распределение B(t). За это время может поступить случайное (распределенное по закону Пуассона с параметром
в момент окончания обслуживания (k + 1)-го запроса, который произойдет через случайное время, и, имеющее распределение B(t). За это время может поступить случайное (распределенное по закону Пуассона с параметром  ) число запросов и один запрос уйдет из системы.
) число запросов и один запрос уйдет из системы.
Фактически мы пришли к идее метода вложенных цепей Маркова. В общем случае, этот метод заключается в следующем. Для немарковского процесса  ищется последовательность моментов времени
ищется последовательность моментов времени  такая, что процесс
такая, что процесс  образует цепь Маркова. Методами теории цепей Маркова исследуют стационарное распределение вложенной цепи и затем по этому распределению восстанавливают стационарное распределение вероятностей исходного процесса. Это обычно делается с использованием теории процессов восстановления или процессов марковского восстановления.
образует цепь Маркова. Методами теории цепей Маркова исследуют стационарное распределение вложенной цепи и затем по этому распределению восстанавливают стационарное распределение вероятностей исходного процесса. Это обычно делается с использованием теории процессов восстановления или процессов марковского восстановления.
Пусть  - момент окончания обслуживания в системе MG1 k-го запроса. Процесс
- момент окончания обслуживания в системе MG1 k-го запроса. Процесс  является однородной цепью Маркова с дискретным временем.
является однородной цепью Маркова с дискретным временем.
Выше отмечалось, что эффективное исследование цепи Маркова с дискретным временем и счетным пространством состояний возможно только в случае, если матрица ее одношаговых переходов имеет какую-либо специальную структуру. Матрица Р одношаговых переходных вероятностей  рассматриваемой вложенной цепи Маркова
рассматриваемой вложенной цепи Маркова  такую структуру имеет. Найдем элементы матрицы Р.
такую структуру имеет. Найдем элементы матрицы Р.
Пусть в некоторый момент окончания обслуживания запроса  число запросов
число запросов  в системе равно
в системе равно  Поскольку в момент
Поскольку в момент  число запросов в системе претерпевает скачок, для определенности будем считать, что
число запросов в системе претерпевает скачок, для определенности будем считать, что  о, то есть, уходящая в данный момент заявка уже не учитывается. Поскольку
о, то есть, уходящая в данный момент заявка уже не учитывается. Поскольку  то на обслуживание немедленно выбирается следующая заявка, которая покинет систему в следующий момент окончания обслуживания запроса
то на обслуживание немедленно выбирается следующая заявка, которая покинет систему в следующий момент окончания обслуживания запроса  Поэтому, для того, чтобы в момент
Поэтому, для того, чтобы в момент  в системе осталось j запросов, необходимо, чтобы за интервал времени
в системе осталось j запросов, необходимо, чтобы за интервал времени  в систему поступило
в систему поступило  запросов. Вероятность этого события есть
запросов. Вероятность этого события есть  где величины
где величины  задаются формулой
задаются формулой

Итак, переходная вероятность  определяется формулой:
определяется формулой:

Пусть теперь в момент  окончания обслуживания запроса число
окончания обслуживания запроса число  запросов в системе равно 0. Очевидно, что система остается пустой до ближайшего момента поступления запроса. Начиная с этого момента, система ведет себя точно так же, как и после момента окончания обслуживания запроса, в который в системе остался один запрос. Поэтому,
запросов в системе равно 0. Очевидно, что система остается пустой до ближайшего момента поступления запроса. Начиная с этого момента, система ведет себя точно так же, как и после момента окончания обслуживания запроса, в который в системе остался один запрос. Поэтому,  откуда следует, что:
откуда следует, что:

Таким образом, мы полностью описали ненулевые элементы матрицы одношаговых вероятностей переходов вложенной цепи. Эта матрица Р имеет специальную структуру:

Наличие такой структуры существенно облегчает исследование данной цепи. Используя известные критерии эргодичности, несложно убедиться, что рассматриваемая вложенная цепь Маркова имеет стационарное распределение тогда и только тогда, когда

где коэффициент загрузки  равен
равен 
Уравнения равновесия (1.16) с учетом вида (1.37) матрицы вероятностей одношаговых переходов можно переписать здесь в виде:

Для решения бесконечной системы линейных алгебраических уравнений (1.39) воспользуемся аппаратом производящих функций. Вводим в рассмотрение производящие функции

Учитывая явный вид (1.35) вероятностей  можно получить явное выражение для производящей функции
можно получить явное выражение для производящей функции 

Умножая уравнения системы (1.39) на соответствующие степени 2 и суммируя их, получаем:

Меняя порядок суммирования, переписываем это соотношение в виде:

Отметим, что нам удалось свернуть двойную сумму в (1.41), благодаря специфике матрицы (1.37) вероятностей переходов, а именно, благодаря тому что переходные вероятности  вложенной цепи Маркова для
вложенной цепи Маркова для  зависят только от величины j — i и не зависят от i и j отдельно. Это свойство матрицы называют квазитеплицевостью. Существенно использовано также то, что все элементы матрицы ниже ее поддиагонали равны нулю.
зависят только от величины j — i и не зависят от i и j отдельно. Это свойство матрицы называют квазитеплицевостью. Существенно использовано также то, что все элементы матрицы ниже ее поддиагонали равны нулю.
Учитывая (1.40), можно переписать формулу (1.41) в следующем виде:

Формула (1.42) определяет искомую производящую функцию стационарного распределения вероятностей вложенной цепи Маркова с точностью до значения неизвестной пока вероятности  того, что рассматриваемая СМО пуста в произвольный момент окончания обслуживания запроса. Для нахождения этой вероятности вспомним, что система уравнений равновесия содержит еще уравнение (1.17) (условие нормировки). Из условия нормировки следует, что
того, что рассматриваемая СМО пуста в произвольный момент окончания обслуживания запроса. Для нахождения этой вероятности вспомним, что система уравнений равновесия содержит еще уравнение (1.17) (условие нормировки). Из условия нормировки следует, что  Поэтому для нахождения вероятности
Поэтому для нахождения вероятности  мы должны подставить в (1.42) z = 1. Однако, простая подстановка не дает результата поскольку и числитель, и знаменатель (1.42) обращаются в нуль.
мы должны подставить в (1.42) z = 1. Однако, простая подстановка не дает результата поскольку и числитель, и знаменатель (1.42) обращаются в нуль.
Для раскрытия неопределенности можно использовать правило Лопиталя. Однако, при вычислении величины L среднего числа запросов в системе в моменты окончания обслуживания запросов потребуется вычислить величину П (1), для чего придется применять правило Лопиталя дважды, при вычислении дисперсии числа запросов в системе придется применять правило Лопиталя трижды и т.д. Во избежание многократного применения правила Лопиталя можно рекомендовать заранее разложить числитель и знаменатель дроби в правой части (1-42) в ряд Тэйлора по степеням (z — 1) (если мы заинтересованы в вычислении  начального момента распределения числа запросов, то разложение нужно провести с точностью до
начального момента распределения числа запросов, то разложение нужно провести с точностью до  ), сократить числитель и знаменатель на (z — 1) и только потом выполнять операции взятия производных и подстановки значения z = 1. Отметим, что если требуется вычислить моменты высокого порядка, при этом можно использовать возможности символьных вычислений, например, с помощью пакета «Mathematica».
), сократить числитель и знаменатель на (z — 1) и только потом выполнять операции взятия производных и подстановки значения z = 1. Отметим, что если требуется вычислить моменты высокого порядка, при этом можно использовать возможности символьных вычислений, например, с помощью пакета «Mathematica».
Используя приведенные соображения, мы получаем следующие выражения для вероятности  среднего числа L запросов в системе и средней длины
среднего числа L запросов в системе и средней длины  очереди в системе в моменты окончания обслуживания запросов:
очереди в системе в моменты окончания обслуживания запросов:
 (1.43)
(1.43)
Подставляя выражение (1.43) в формулу (1.42), получаем:

Формула (1.45) называется формулой Поллячека - Хинчина для производящей функции распределения числа запросов в системе MG1.
Отметим, что в выражения для величин  входит второй начальный момент
входит второй начальный момент  распределения времени обслуживания. Поэтому при одинаковых средние временах обслуживания длины очередей в системах могут существенно отличаться. Так, при показательном распределении времени обслуживания (в этом случае
распределения времени обслуживания. Поэтому при одинаковых средние временах обслуживания длины очередей в системах могут существенно отличаться. Так, при показательном распределении времени обслуживания (в этом случае  - средняя длина
- средняя длина  очереди равна а при детерминированном времени обслуживания
очереди равна а при детерминированном времени обслуживания  средняя длина
средняя длина  очереди в два раза меньше. При эрланговском распределении времени обслуживания средняя длина
очереди в два раза меньше. При эрланговском распределении времени обслуживания средняя длина  очереди принимает промежуточное значение А при гиперэкспоненциальном обслуживании она может принимать существенно большие значения.
очереди принимает промежуточное значение А при гиперэкспоненциальном обслуживании она может принимать существенно большие значения.
Следовательно, оценивание вида распределения времени обслуживания в реальной модели имеет весьма важное значение. Учет только среднего значения может привести к значительной погрешности в оценке характеристик производительности системы.
Итак, проблема нахождения стационарного распределения вложенной цепи Маркова решена. Следует, однако, вспомнить, что нас интересует не эта цепь Маркова, а немарковский процесс  - число запросов в системе в произвольный момент времени. Введем в рассмотрение стационарное распределение этого процесса:
- число запросов в системе в произвольный момент времени. Введем в рассмотрение стационарное распределение этого процесса:

Из теории процессов марковского восстановления (см., например, [171]) следует, что это распределение существует при тех же условиях, что и вложенное распределение (то есть, при выполнении условия (1.38)), и вычисляется через вложенное распределение следующим образом:

Здесь  есть средняя длина интервала между моментами ухода запросов из системы. Для нашей системы (без потери запросов)
есть средняя длина интервала между моментами ухода запросов из системы. Для нашей системы (без потери запросов)  .
.
Введем в рассмотрение производящую функцию 
Умножая соотношения (1.46), (1.47) на соответствующие степени z и суммируя, получаем:


Меняя порядок интегрирования в двойном интеграле, порядок суммирования в двойной сумме и подсчитывая известные суммы, получаем:

Делая замену переменной интегрирования  учитывая равенство
учитывая равенство  и связь между преобразованиями Лапласа и Лапласа-Стилтьеса, отсюда имеем:
и связь между преобразованиями Лапласа и Лапласа-Стилтьеса, отсюда имеем:

Подставляя сюда выражение (1.42) для производящей функции  после элементарных преобразований получаем:
после элементарных преобразований получаем:

В результате мы убедились в справедливости соотношения:

Таким образом, для рассматриваемой системы MG1 распределения вероятностей числа запросов в системе в моменты окончания обслуживания запросов и произвольные моменты времени совпадают. А.Я. Хинчин [118] назвал это утверждение основным законом стационарной очереди.
Затронем проблему нахождения стационарного распределения времени ожидания и пребывания запросов в системе. Предполагаем, что запросы обслуживаются в порядке их поступления в систему (дисциплина выбора из очереди FIFO). Пусть  есть время ожидания,
есть время ожидания,  есть время пребывания в системе запроса, поступившего в нее в момент времени t. Обозначим:
есть время пребывания в системе запроса, поступившего в нее в момент времени t. Обозначим:

и

Условием существования пределов (1-49) является выполнение неравенства (1.38). Поскольку время пребывания запроса в системе равно сумме его времени ожидания и времени обслуживания, а время обслуживания запросов в классических моделях СМО предполагается независимым от состояния системы (и от времени, в течение которого запрос ожидал в очереди), то из свойства 2 преобразования Лапласа - Стилтьеса следует, что:

Популярным методом получения выражения для преобразований Лапласа - Стилтьеса  является вывод интегро-дифференциального уравнения Такача для распределения виртуального времени ожидания (то есть, времени, в течение которого ждал бы начала обслуживания запрос, если бы он поступил в систему в данный момент времени), см., например, [67].
является вывод интегро-дифференциального уравнения Такача для распределения виртуального времени ожидания (то есть, времени, в течение которого ждал бы начала обслуживания запрос, если бы он поступил в систему в данный момент времени), см., например, [67].
Получим эти выражения другим, более простым, способом. Нетрудно видеть, что при дисциплине FIFO число запросов, остающихся в системе в момент окончания обслуживания в ней некоторого запроса, совпадает с числом запросов, пришедших в систему за время пребывания в ней уходящего запроса. Отсюда следуют равенства:

Умножая соотношения (1.51) на соответствующие степени z и суммируя, получаем:

Подставляя в это соотношение явный вид (1.45) производящей функции  используя (1.50) и делая замену переменной:
используя (1.50) и делая замену переменной:  получаем следующую формулу:
получаем следующую формулу:

Формула (1.52) называется формулой Поллячека - Хинчина для преобразования Лапласа - Стилтьеса распределения времени ожидания в системе MG1.
Используя формулу (1.18), из (1.52) получаем следующее выражение для величины среднего времени W ожидания запроса в системе:

Среднее время V пребывания запроса в системе находится как:

Сравнивая формулы (1.44) и (1.53), снова получаем формулу Литтла:

Если имеется настоятельная необходимость нахождения вида функции распределения времени ожидания W(x), а не ее преобразования Лапласа - Стилтьеса, обращение этого проебразования, заданного формулой (1.52), проводится разложением правой части (1.52) на простые дроби (если это возможно) или численными методами (см., например, [176], [261]). Полезной может оказаться также так называемая формула Бенеша:

где  есть свертка
есть свертка  порядка функции распределения
порядка функции распределения

а операция свертки определяется рекуррентным образом:

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
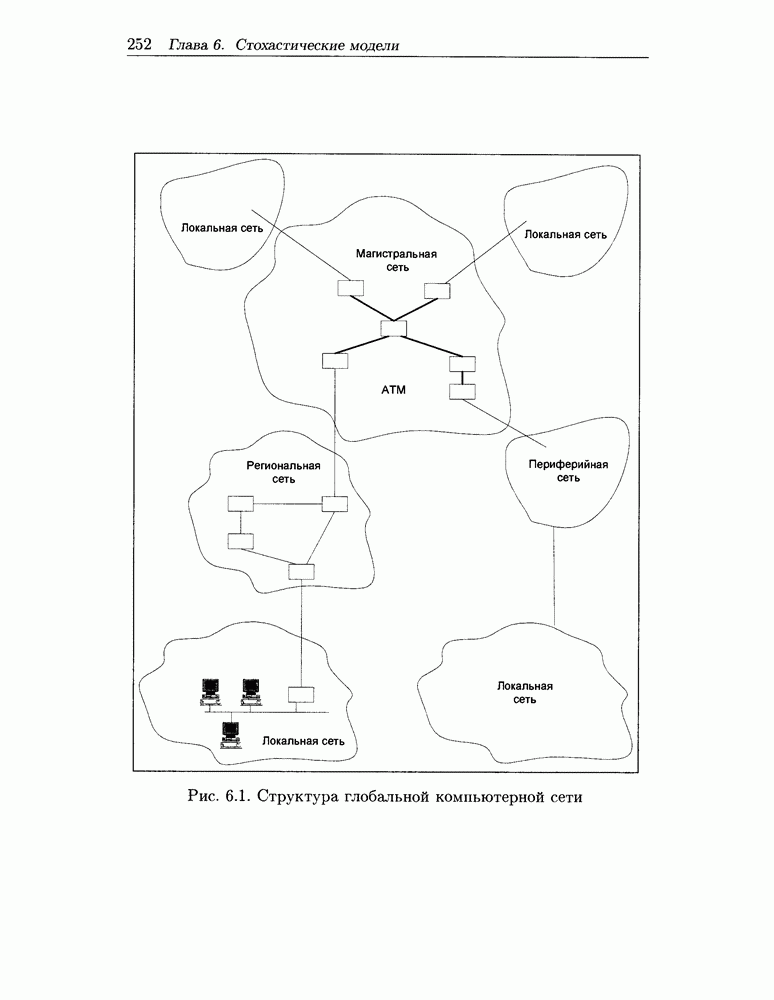
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
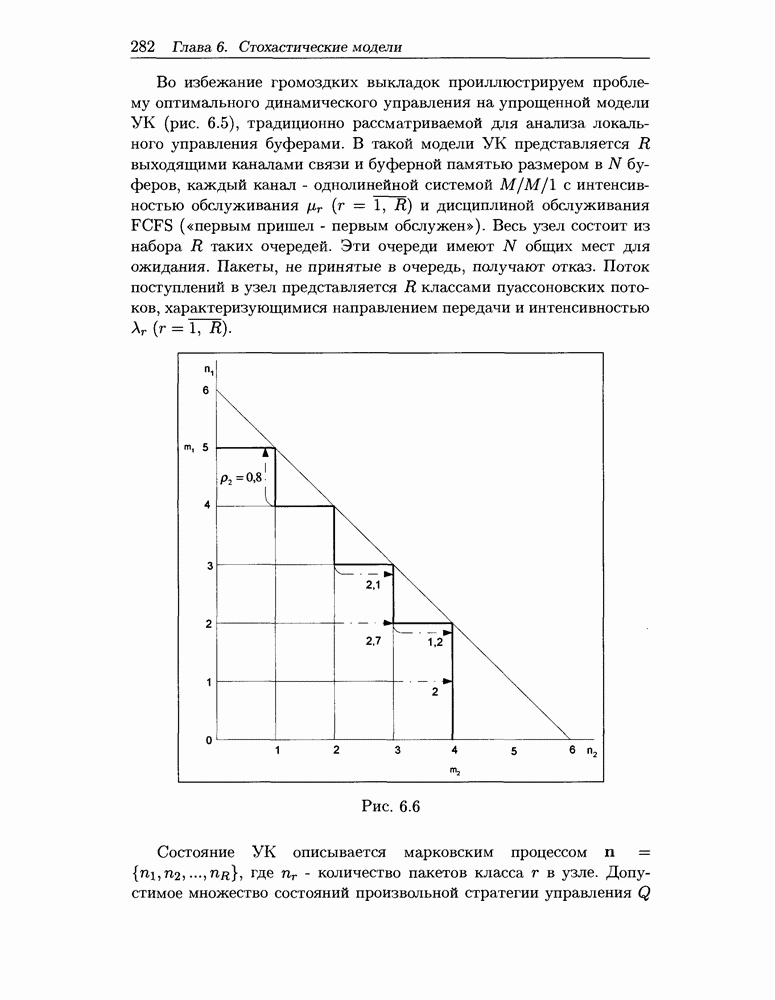
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
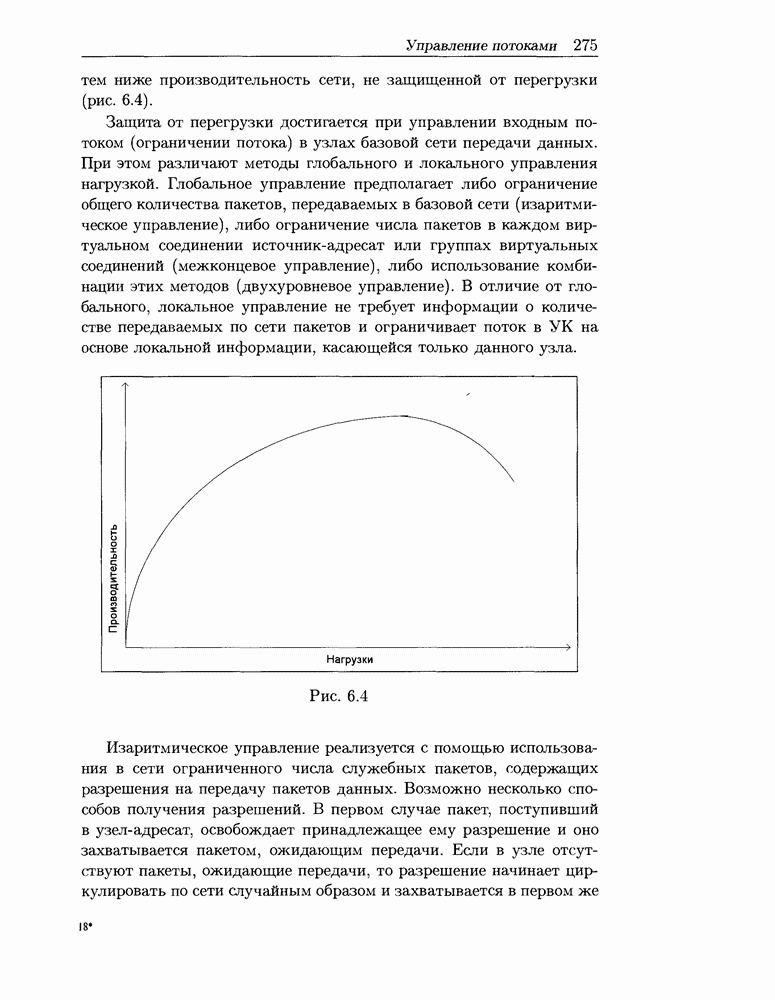
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
- 6.3.3 Локальное управление буферами
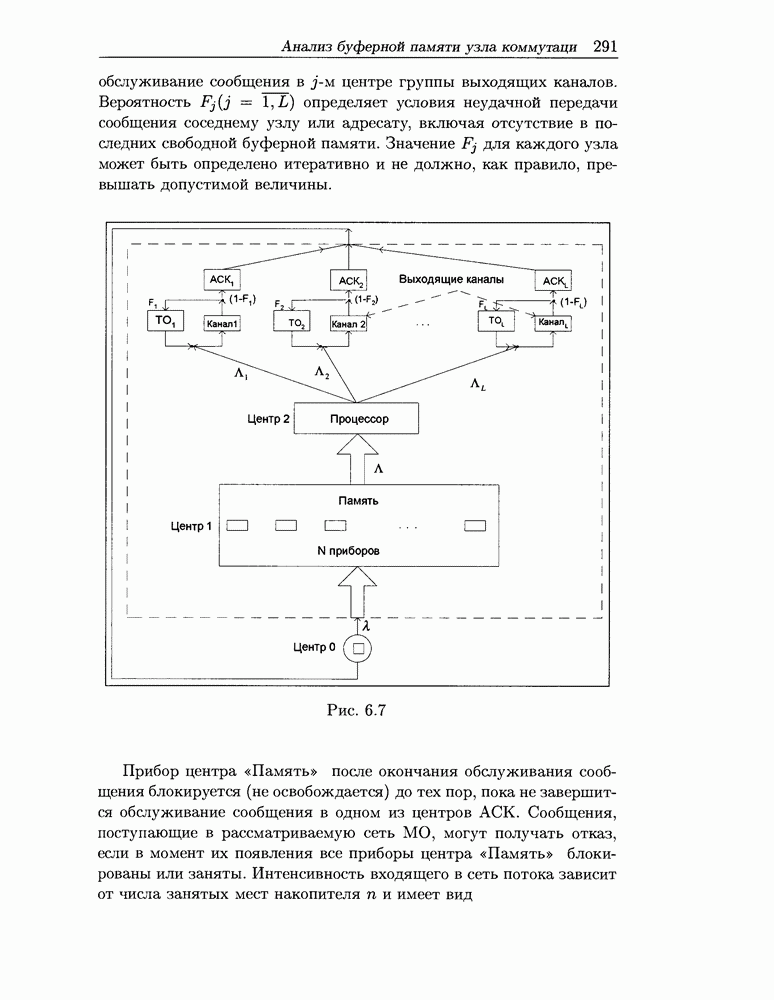
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
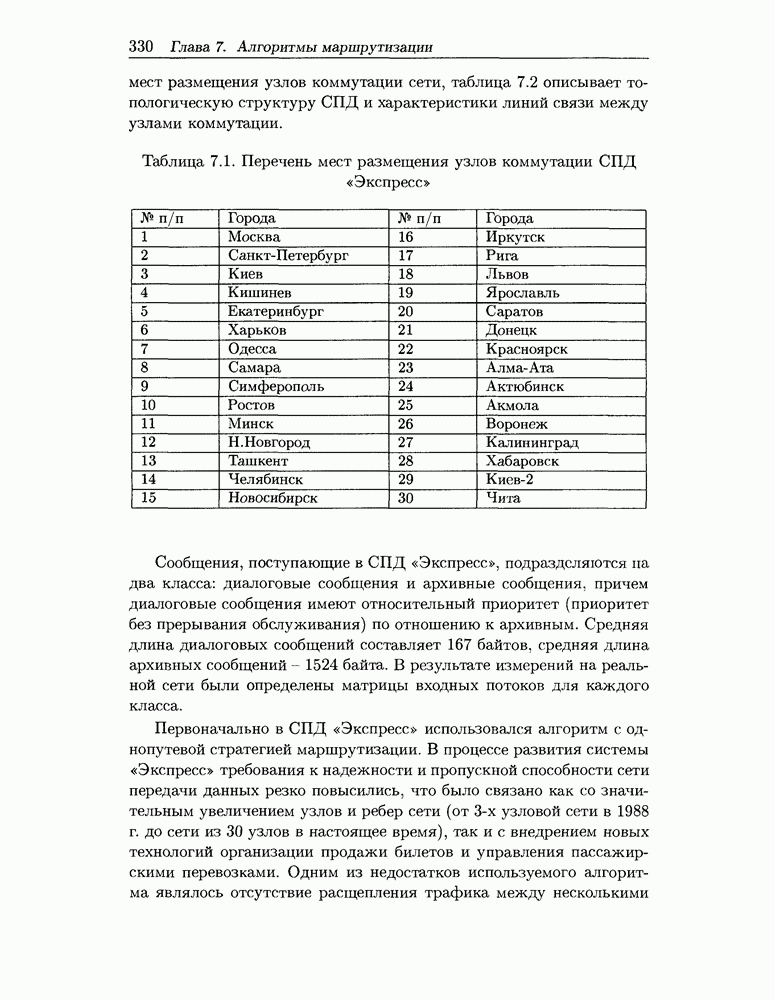
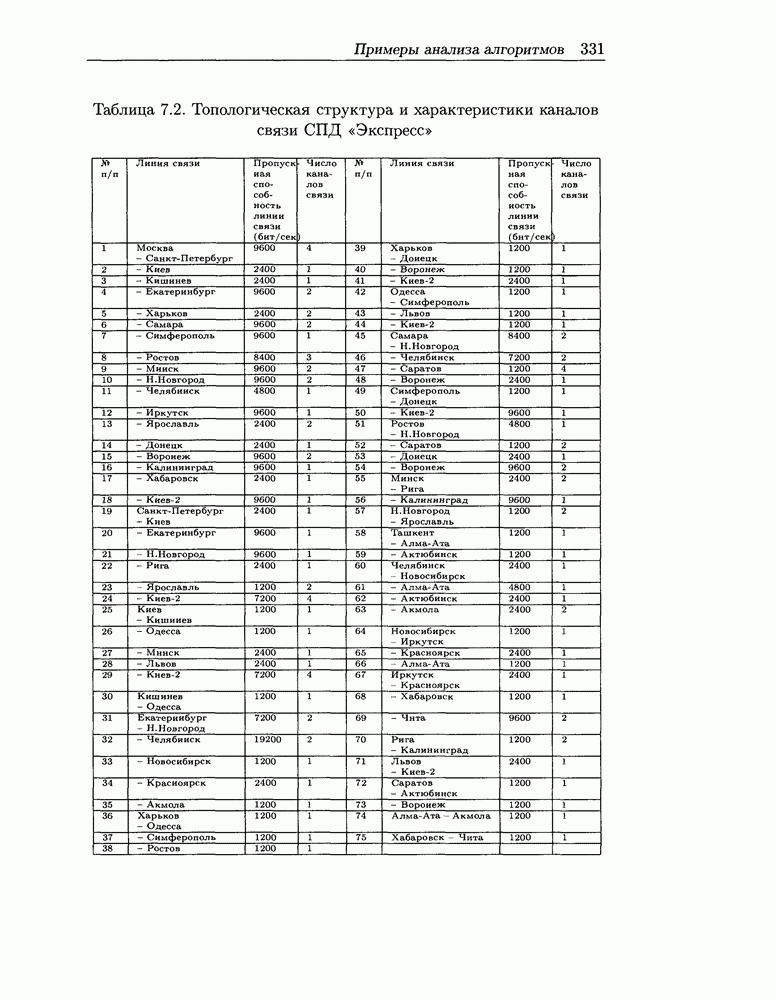
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
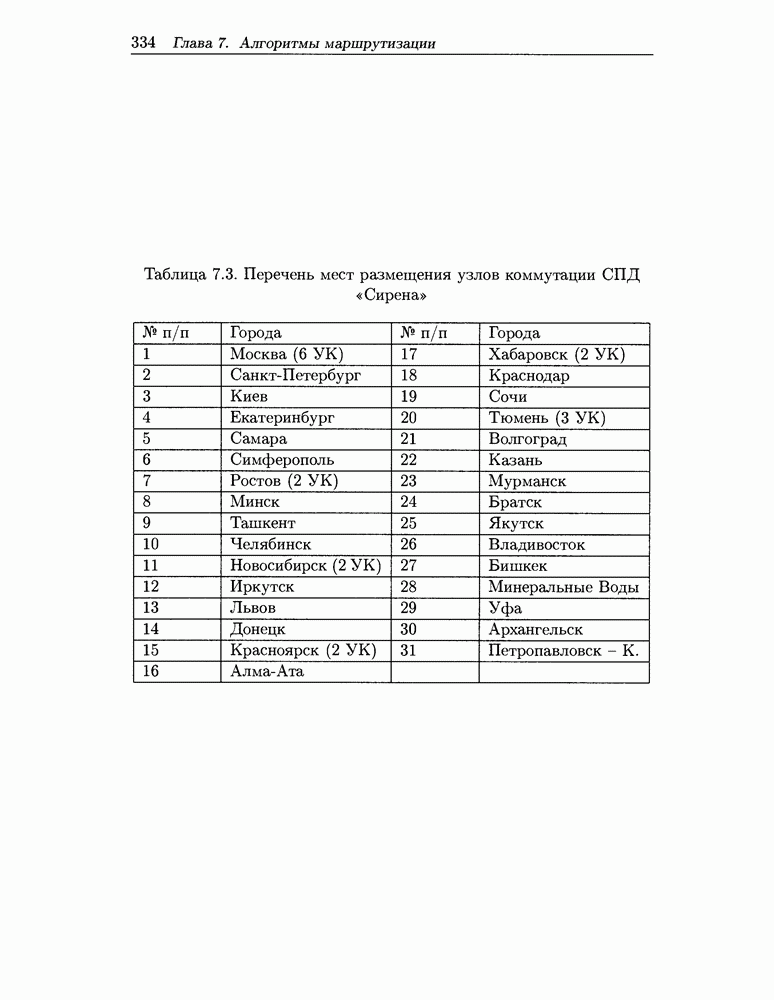
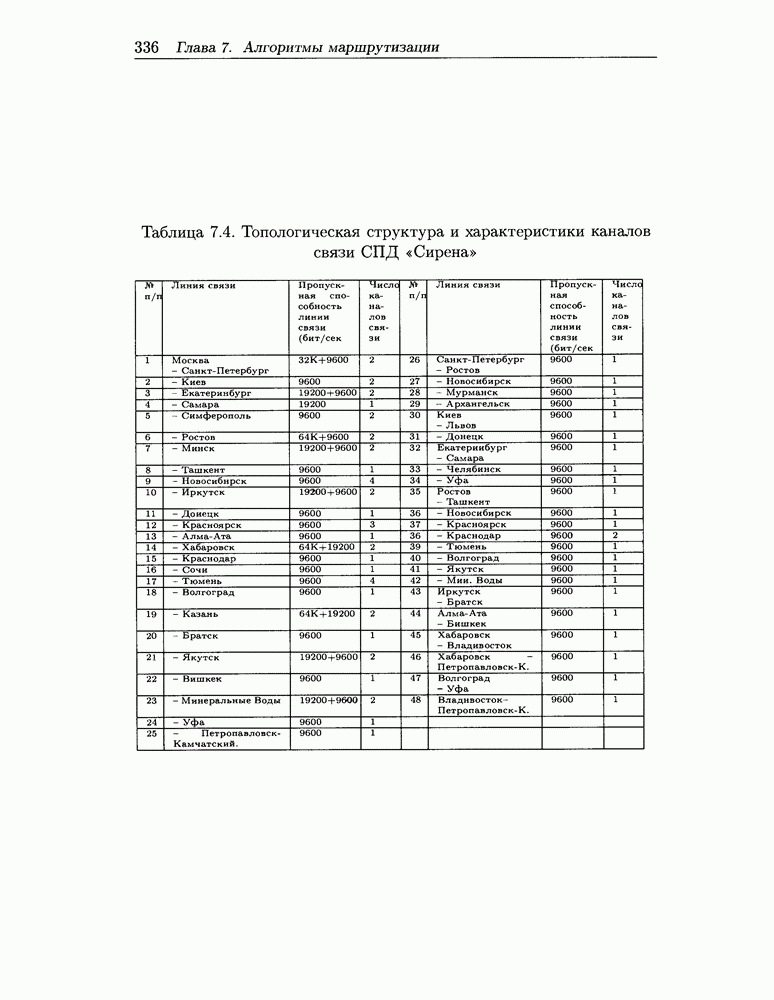
- 7.4.2 Анализ развития СПД «Сирена»
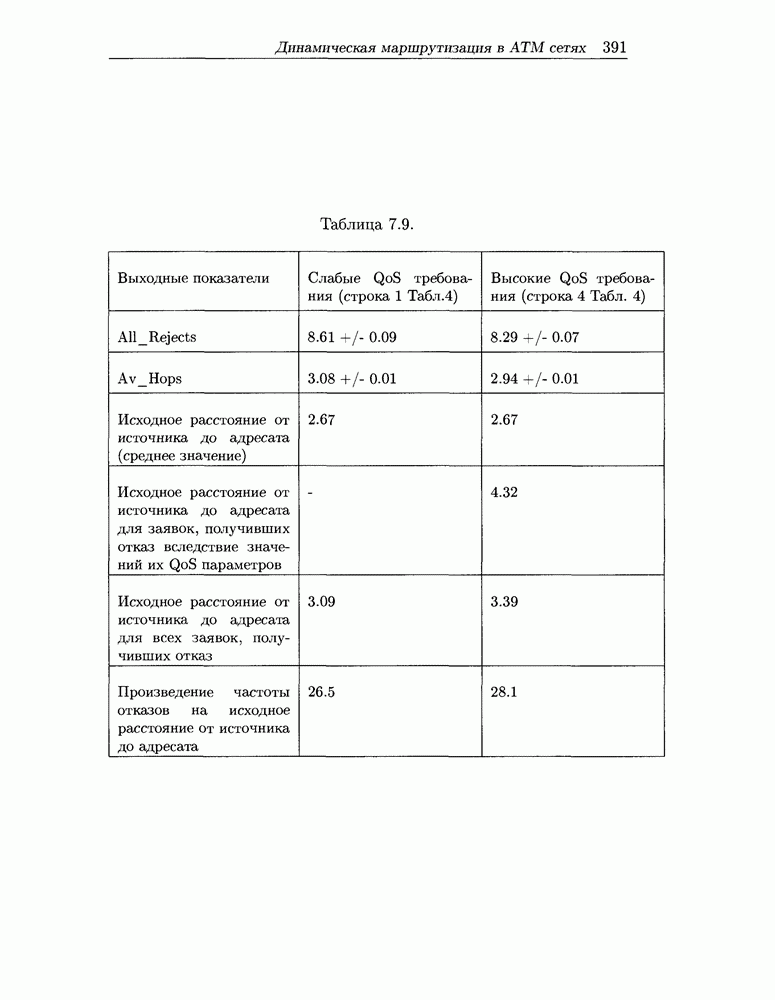
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
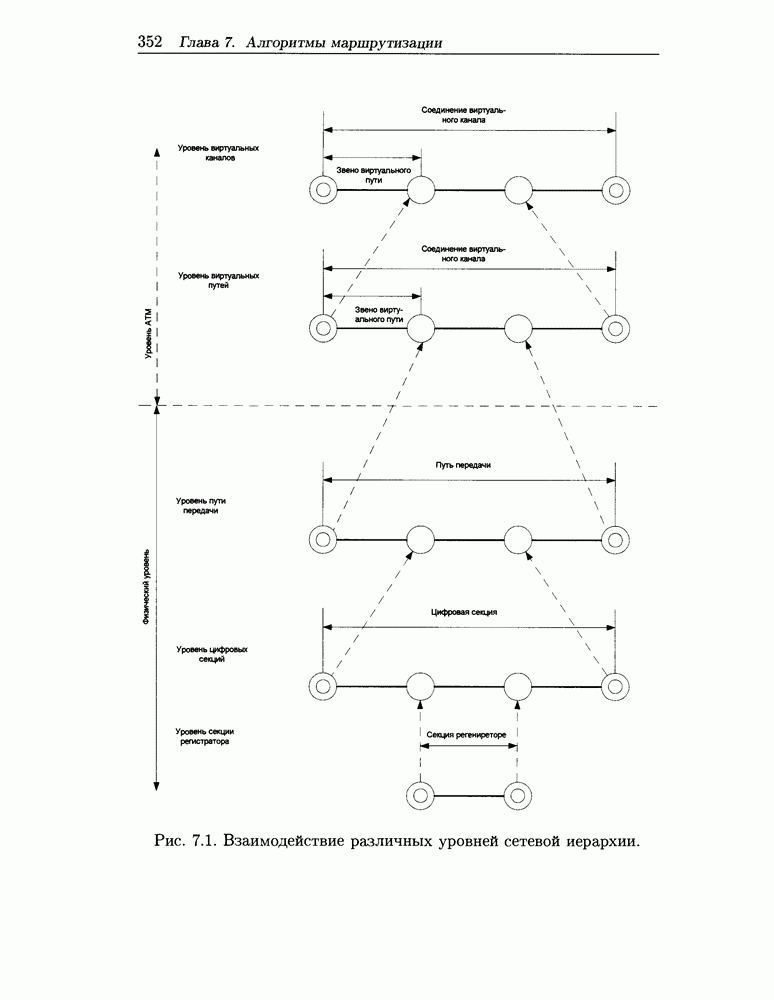
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
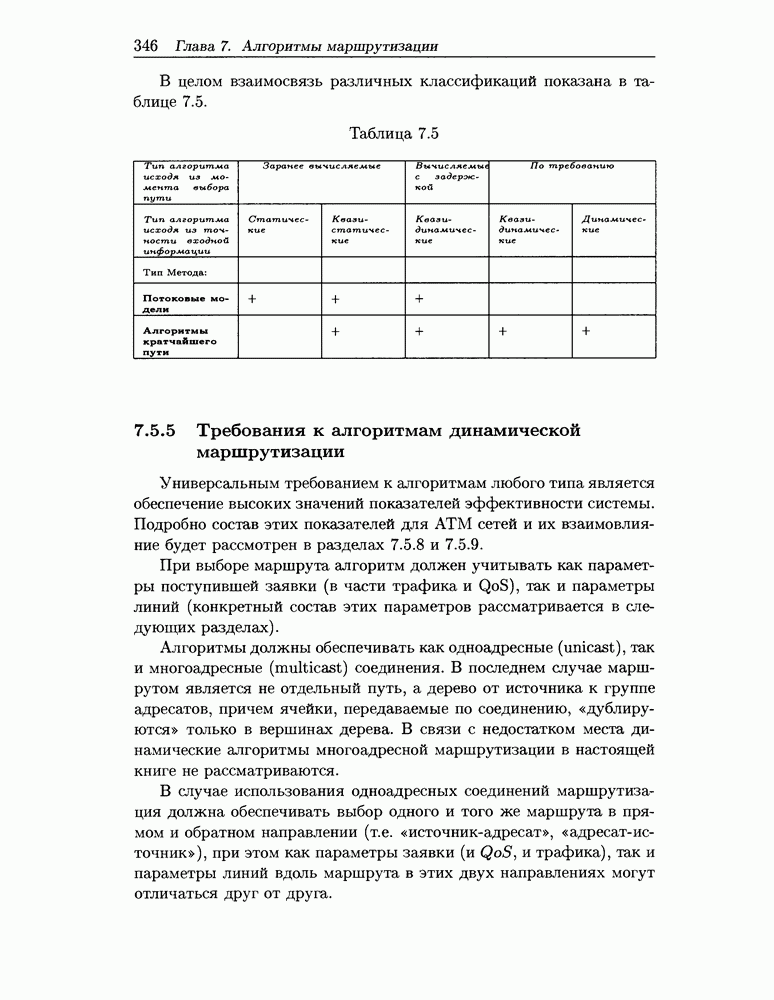
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
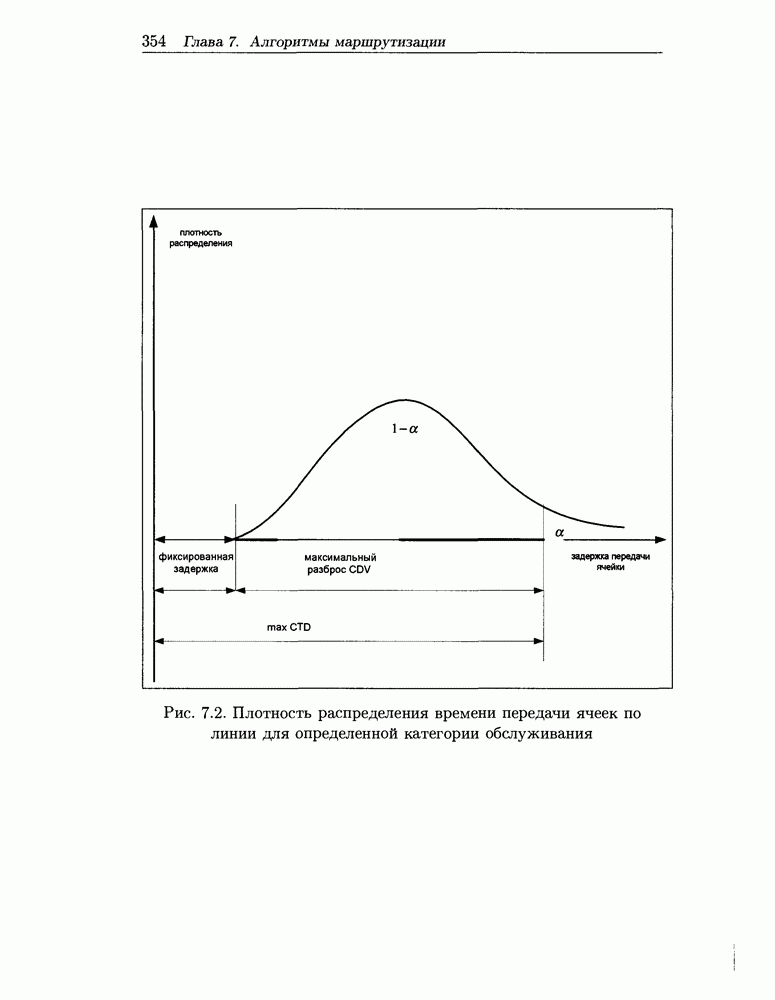
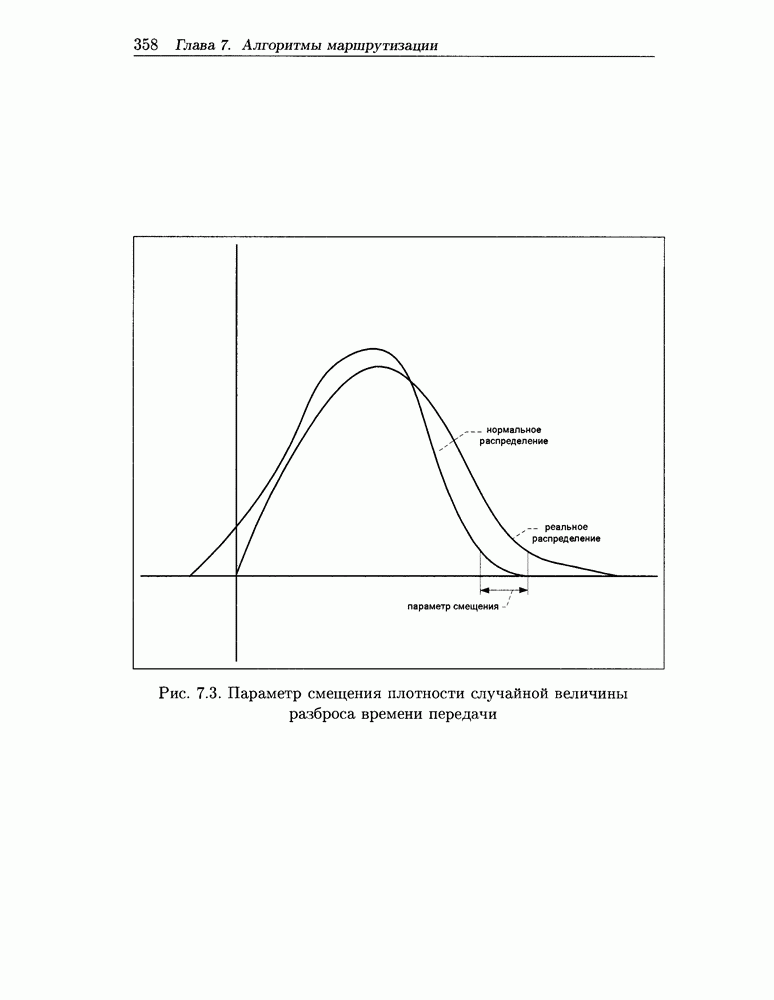
- 7.5.8 Показатели качества маршрутизации
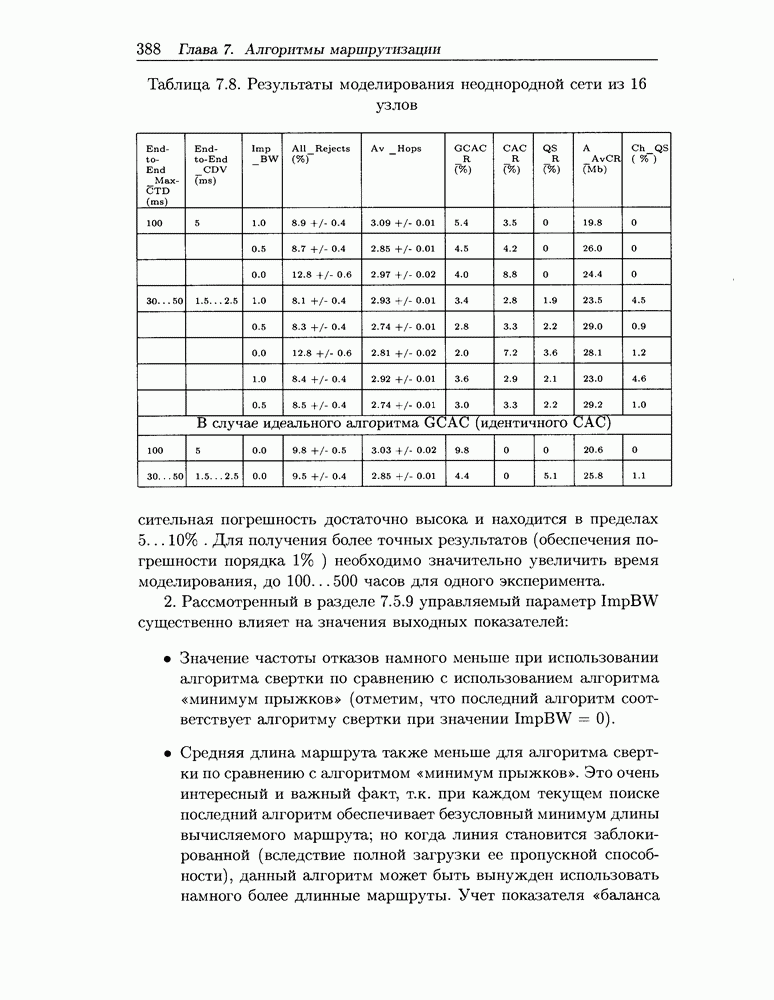
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
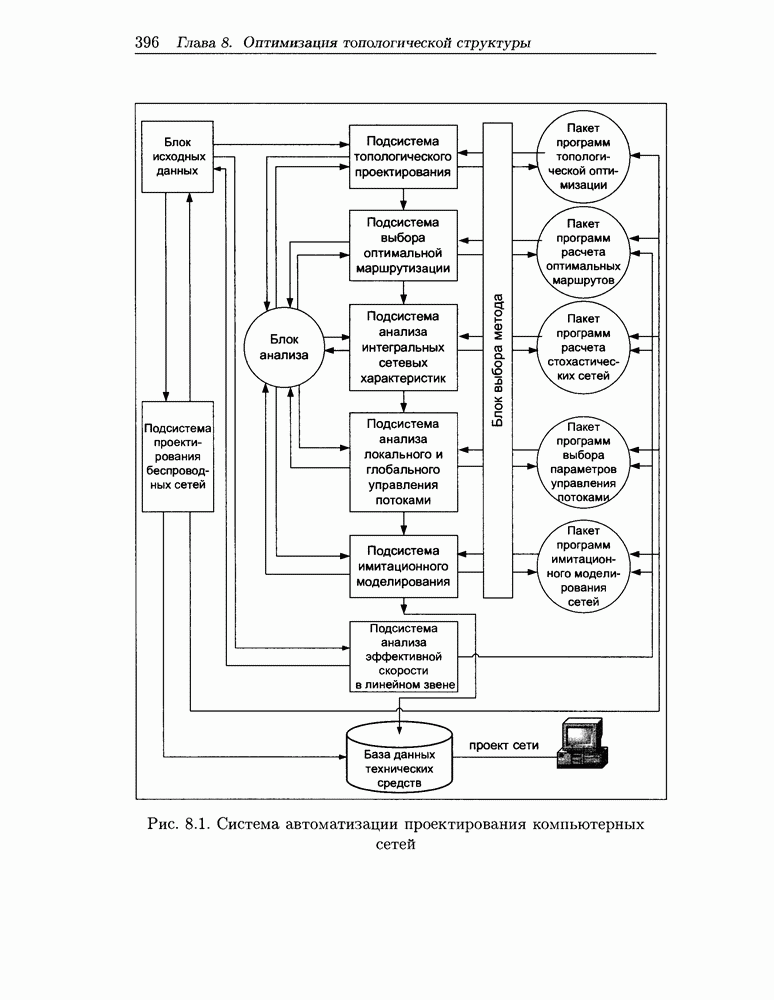
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
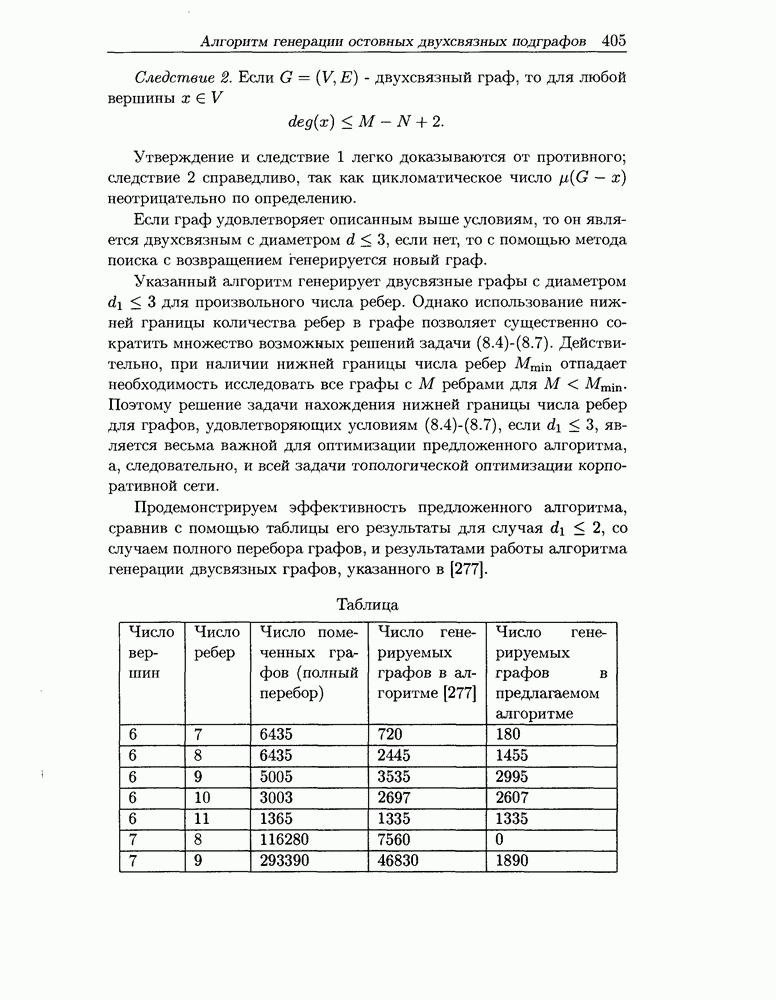
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
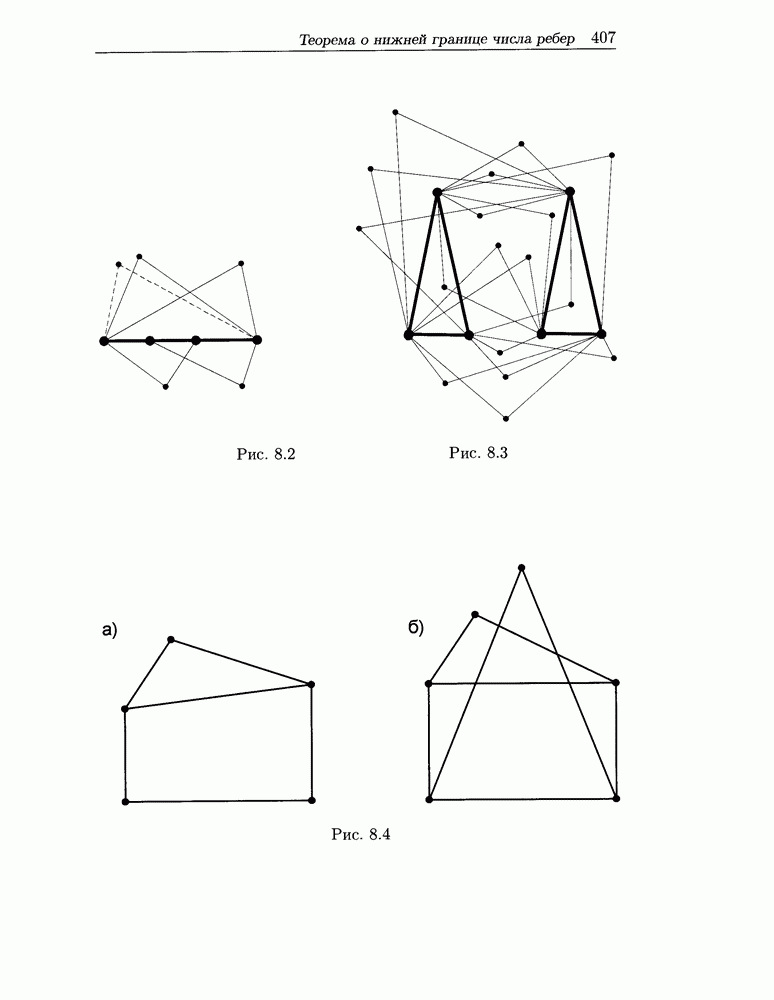
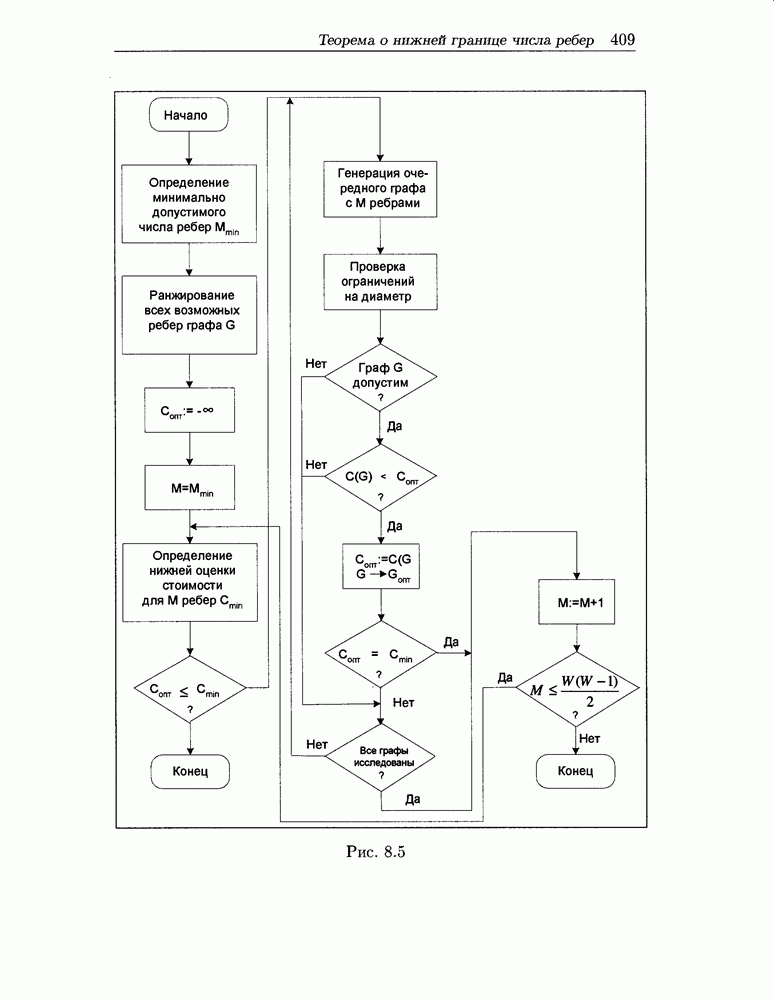
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
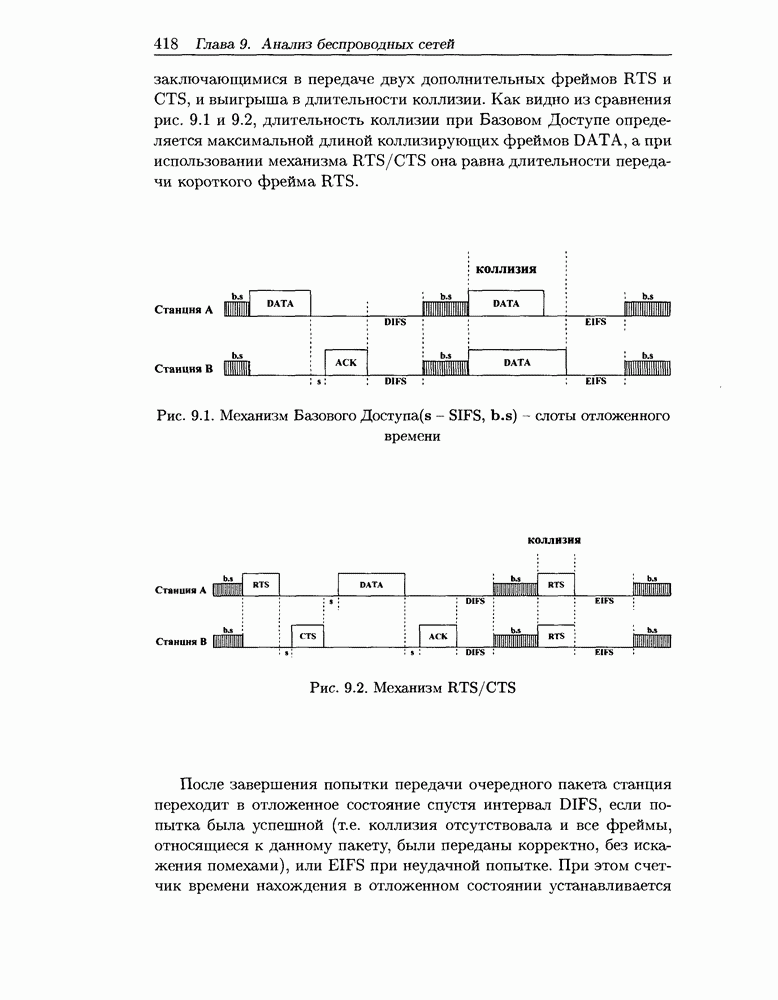
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
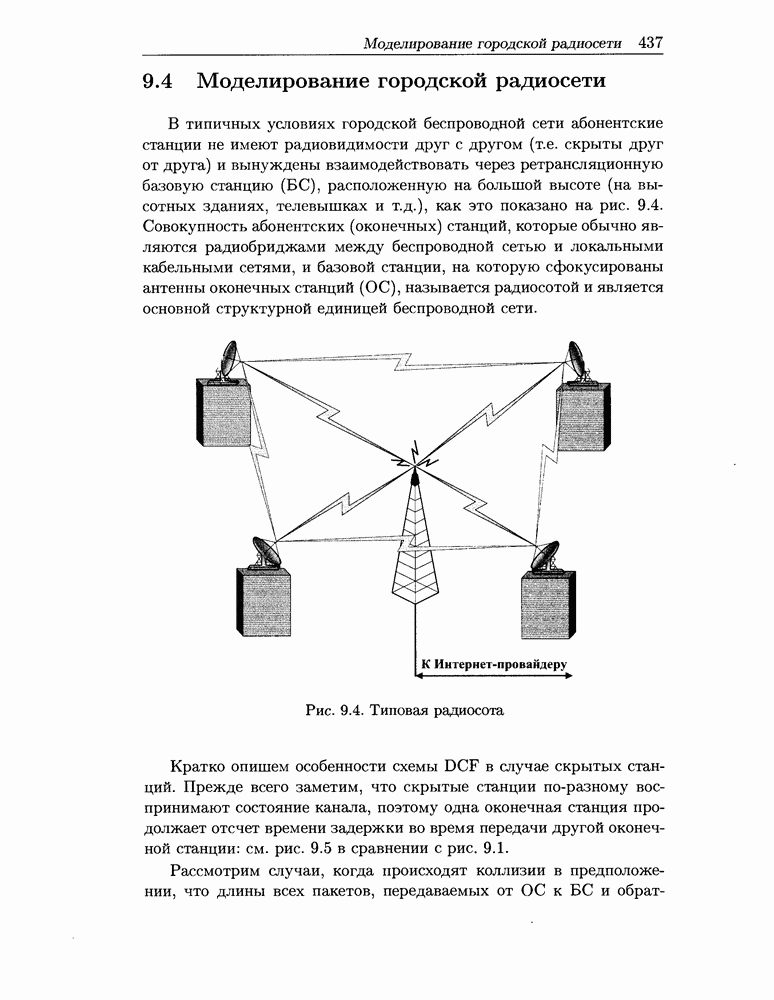
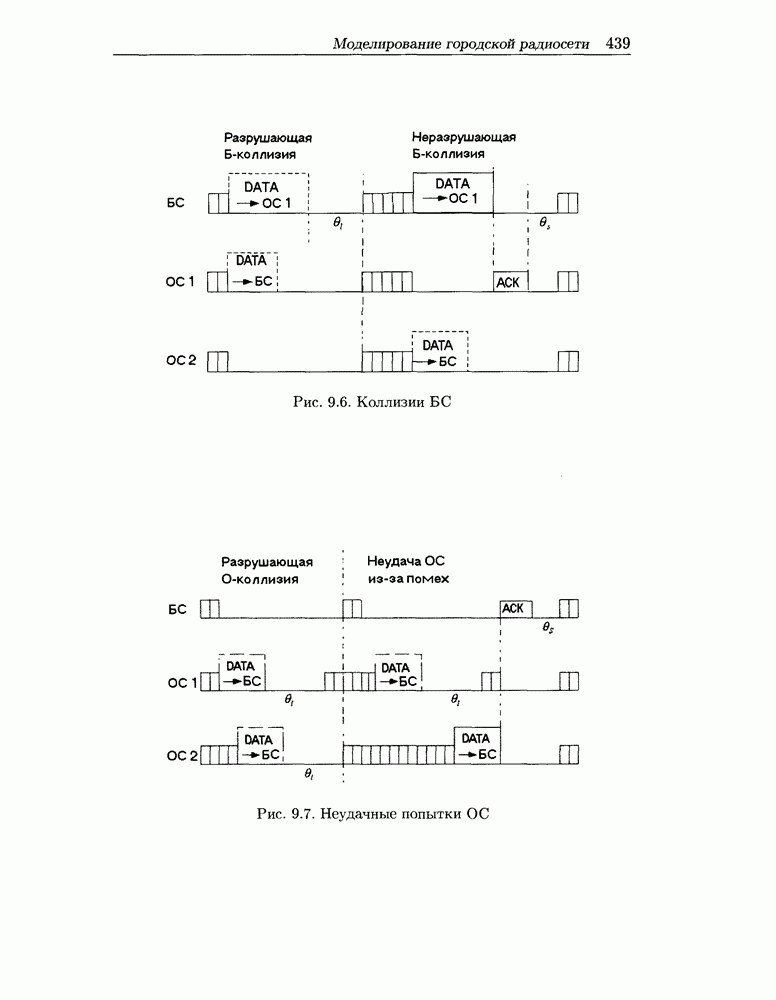
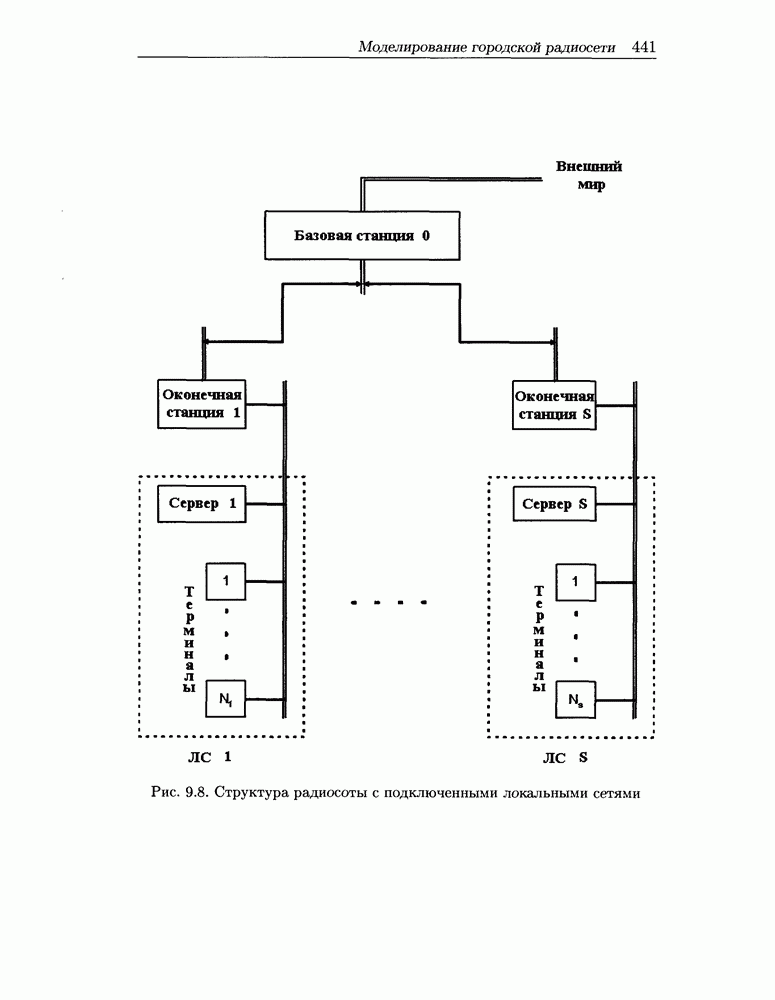
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
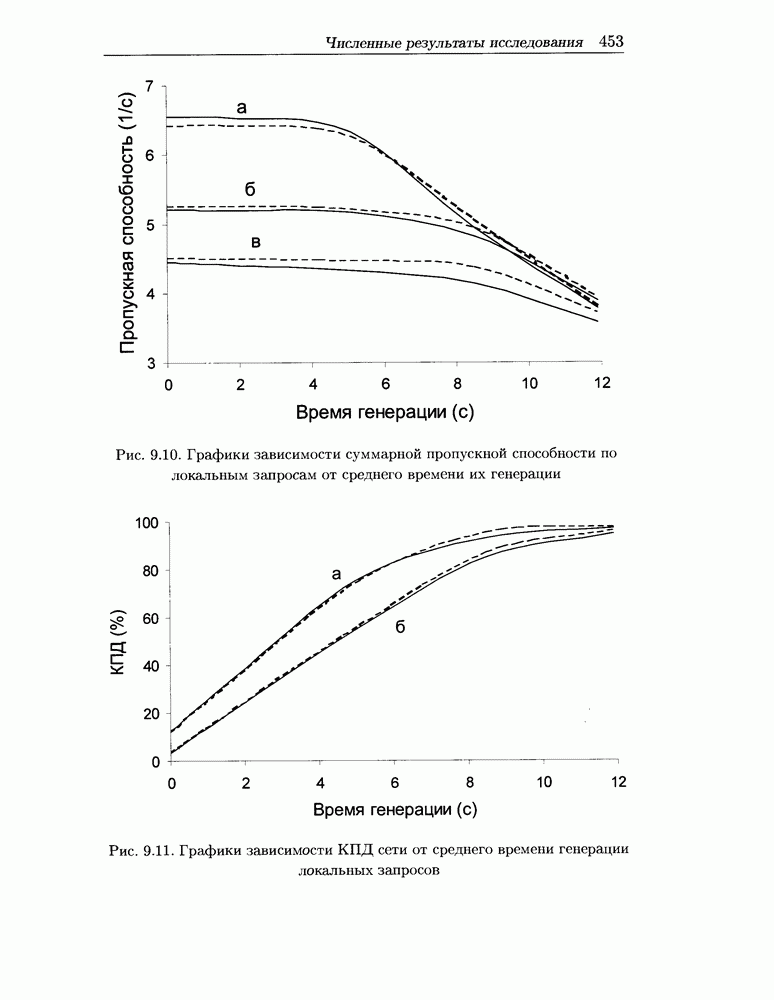
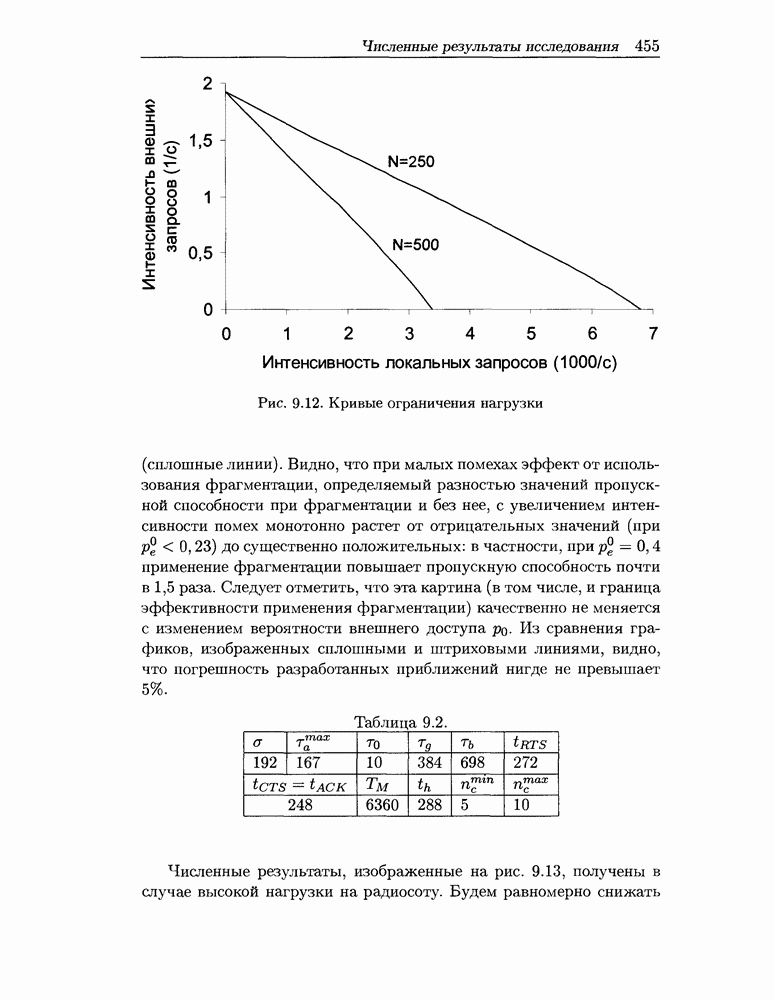
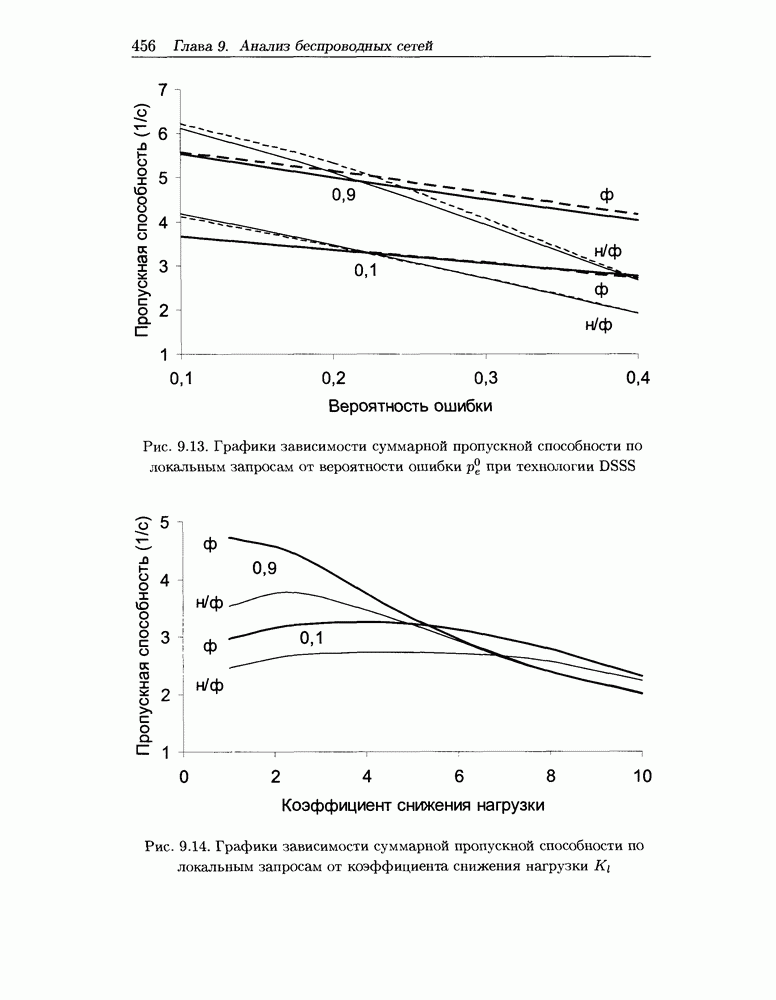
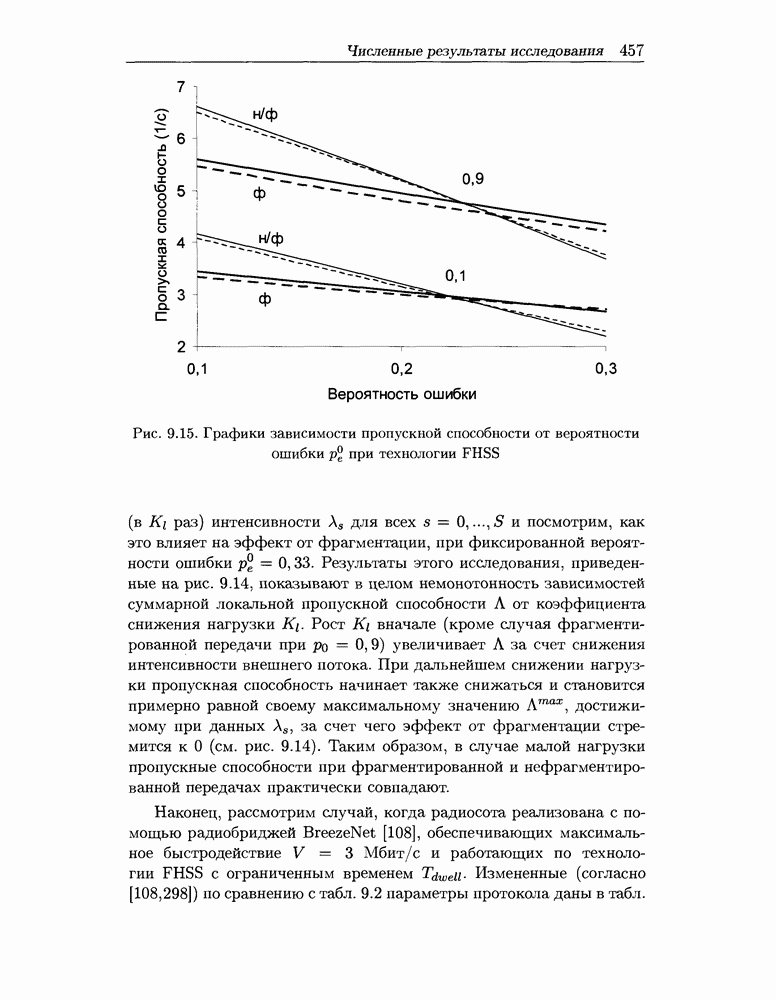
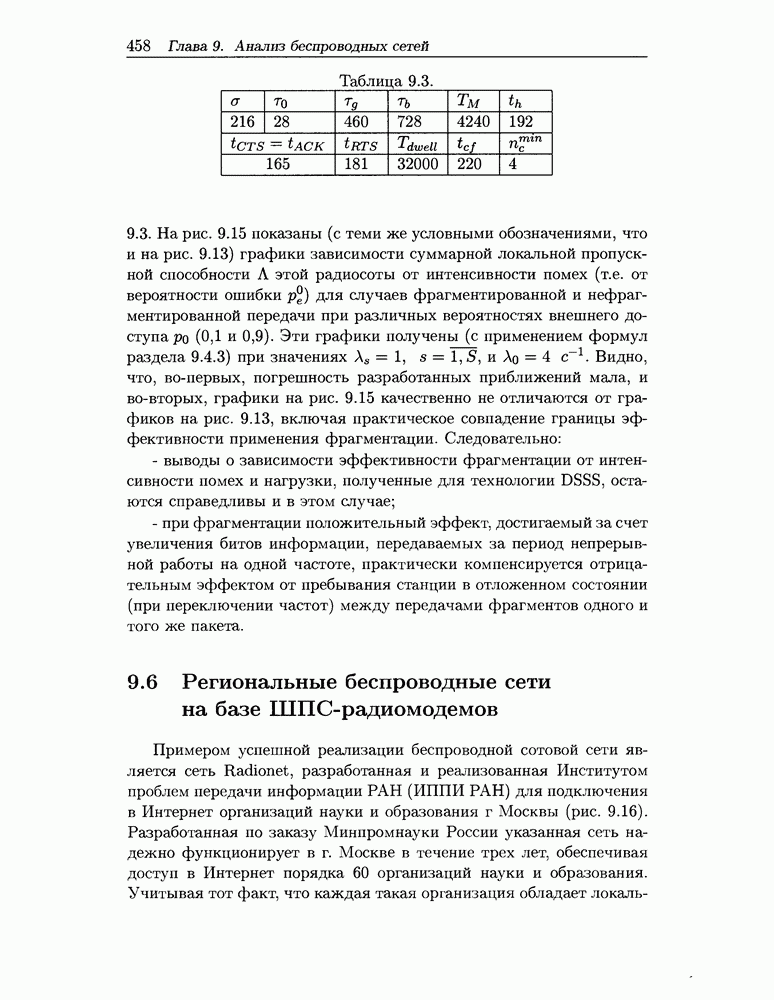
- 9.5 Численные результаты исследования городской радиосоты
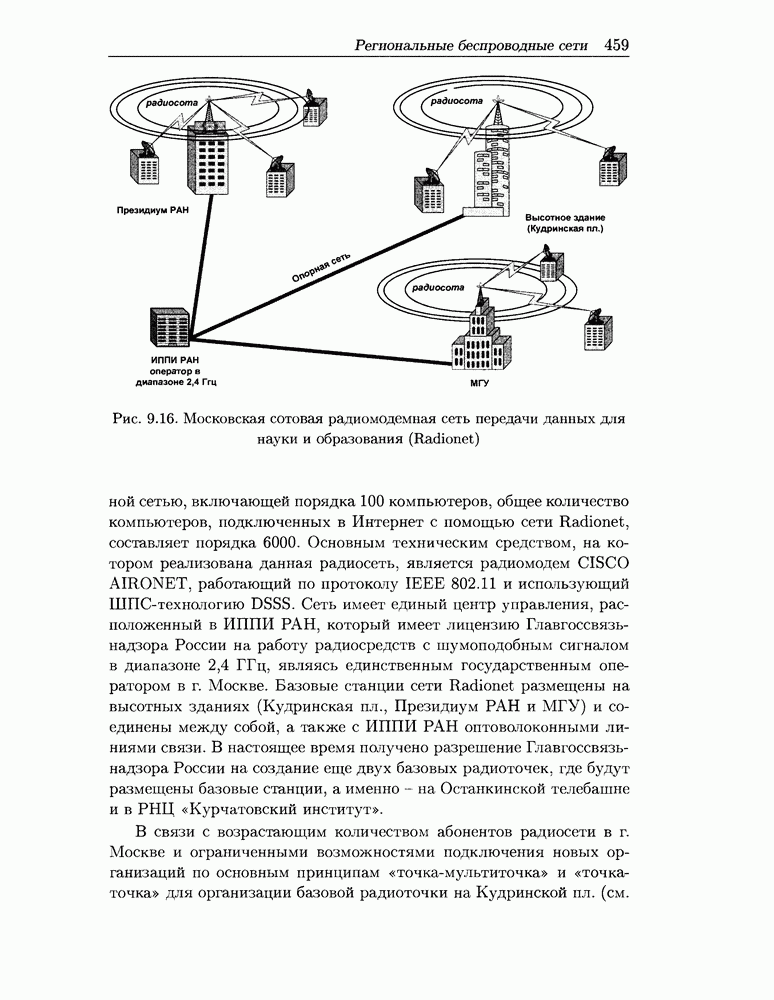
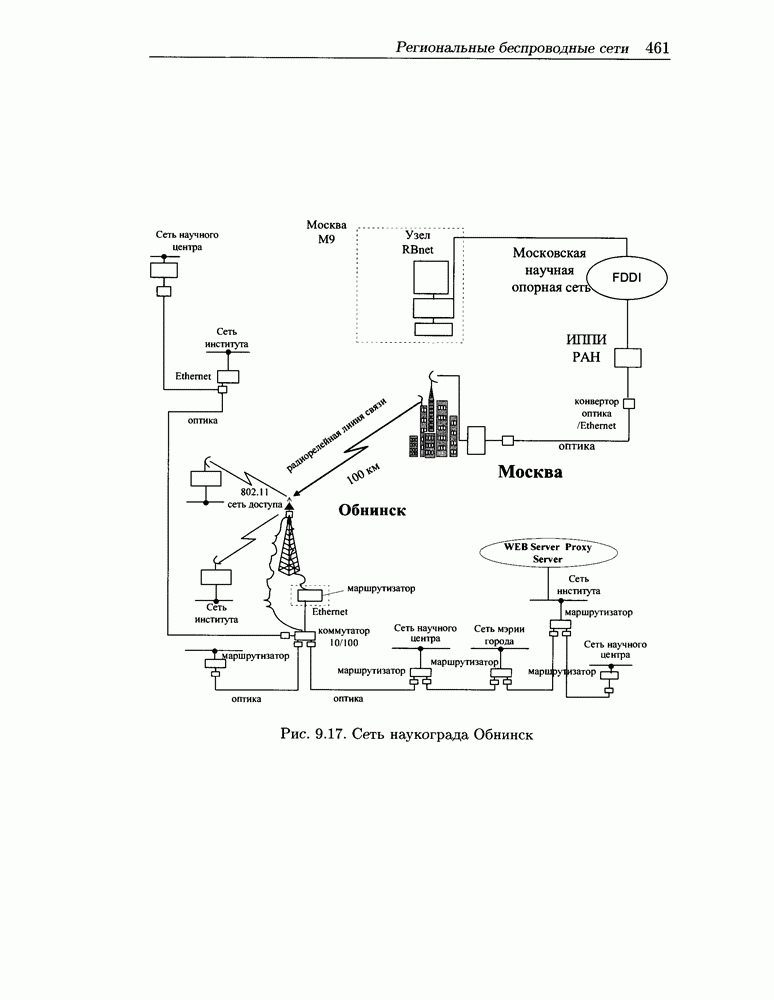
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
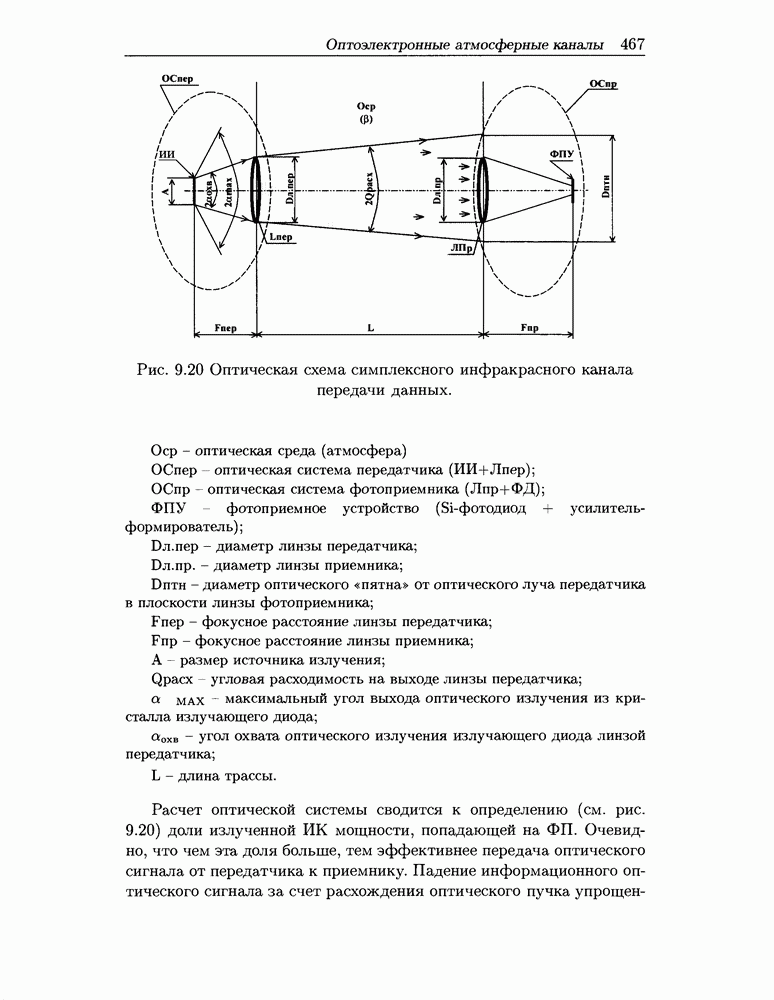
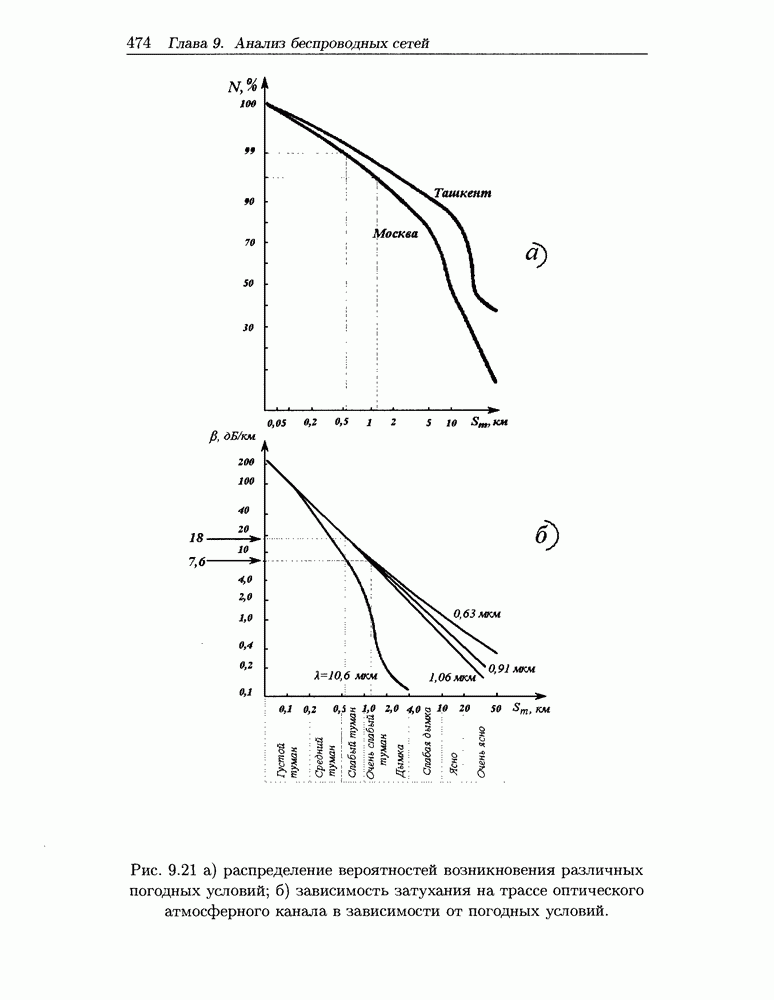
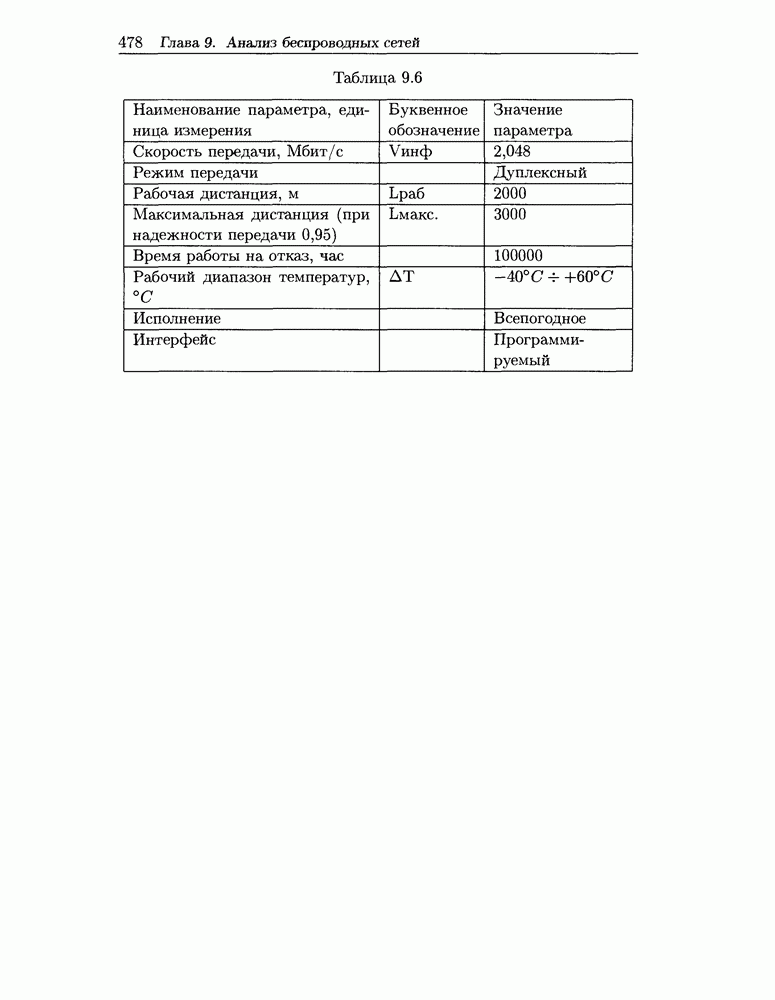
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература