| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.4.4 Анализ динамической памяти с цепочкой буферов
Такая структура буферной памяти наиболее часто используется в узлах коммутации сообщений и весьма эффективна при значительном разбросе длин сообщений. Как отмечалось выше, существуют разновидности такой памяти. В первую очередь различают структуру с резервированием в момент поступления сообщения цепочки буферов под известную его длину. Сведения о длине передаются в начале сообщения, в момент прихода в УК оно может получать отказ в приеме при отсутствии соответствующего количества свободных буферов. Другие схемы памяти с цепочками буферов основаны на формировании цепочек по мере заполнения сообщением очередного буфера. При этом, как правило, не требуется сведений о длине сообщения. Известны различные модификации такой памяти. Допускается частичное резервирование цепочек с учетом известной длины сообщения. Используется динамическое резервирование части памяти для уже принимаемых в УК сообщений, например в зависимости от заполненности памяти или от иных условий [120]. Последнее позволяет снимать вероятность отсутствия дополнительных буферов для принимаемых сообщений, но вызывает дополнительные отказы вновь поступающим сообщениям.
Далее рассматривается сетевая модель памяти с резервированием буферов под известную длину сообщений. Анализ такой памяти в контексте многоэтапного процесса буферизации в УК дает аналитические оценки требуемого объема буферной памяти. Эти оценки во многих случаях могут быть успешно использованы и для других схем цепочек буферов. Последнее объясняется тем, что память, занимаемая принятыми в УК сообщениями, для всех схем цепочек буферов одинакова.
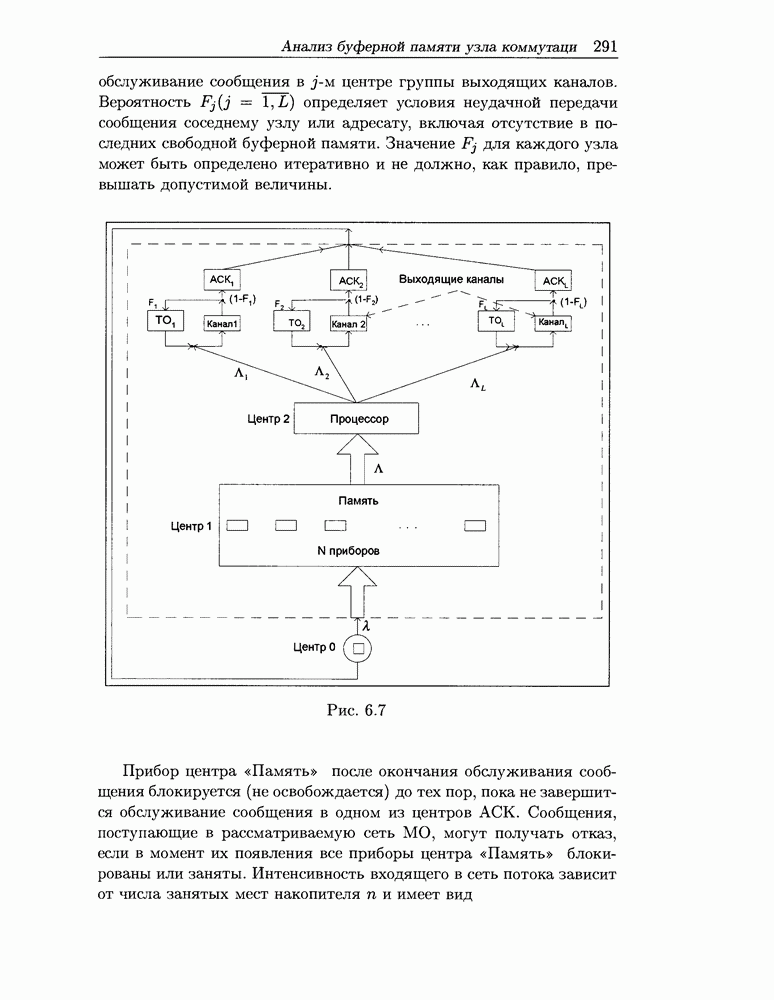
В рассматриваемом случае УК может быть формально представлен моделью открытой сети МО с несколькими классами сообщений, отказами, блокировкой и пуассоновским потоком поступлений интенсивностью  . Сообщения класса
. Сообщения класса  требуют для ввода в сеть
требуют для ввода в сеть  свободных приборов обслуживания первого в сети центра «Память». Этот многолинейный центр состоит из N приборов
свободных приборов обслуживания первого в сети центра «Память». Этот многолинейный центр состоит из N приборов  буферов каждый объемом
буферов каждый объемом 
Очередь в нем отсутствует. Распределение времени обслуживания сообщений класса  , занимающих
, занимающих  приборов
приборов  , определяется распределением длин сообщений этого класса и скоростью передачи по каналу связи.
, определяется распределением длин сообщений этого класса и скоростью передачи по каналу связи.
Число классов R определяется наименьшим целым, удовлетворяющим неравенству  , где
, где  - максимальная длина сообщений. Длина сообщений
- максимальная длина сообщений. Длина сообщений  класса
класса  имеет распределение
имеет распределение

где  - распределение длин сообщений общего потока поступлений,
- распределение длин сообщений общего потока поступлений,  - вероятность того, что сообщению требуются
- вероятность того, что сообщению требуются  буферов. Интенсивность
буферов. Интенсивность  потока
потока  , и, очевидно,
, и, очевидно,  . Остальные центры сети сохраняют структуру, описанную в предыдущем разделе.
. Остальные центры сети сохраняют структуру, описанную в предыдущем разделе.
Приборы центра «Память», занятые сообщением, после окончания обслуживания этого сообщения блокируются до завершения обслуживания сообщения в одном из центров АСК сети. Сообщения класса  , поступающие в первый центр, могут получать отказ, если в момент их появления более
, поступающие в первый центр, могут получать отказ, если в момент их появления более  приборов центра «Память» заняты обслуживанием или блокированы. Интенсивность входящих в сеть потоков зависит от числа занятых приборов первого центра
приборов центра «Память» заняты обслуживанием или блокированы. Интенсивность входящих в сеть потоков зависит от числа занятых приборов первого центра 

где  при
при  при
при 
Таким образом, количество сообщений в рассматриваемой сети МО не превышает N - числа приборов центра «Память». Многолинейные центры АСК, то, состоящие из N приборов, эквивалентны центру «Память». В этих центрах обслуживание прибором сообщения класса  соответствует захвату
соответствует захвату  единиц ресурса (
единиц ресурса ( буферов), ограниченного числом N. Очередь в таких центрах отсутствует, так что они эквивалентны центрам типа IS и допускают произвольное распределение времени обслуживания сообщений всех классов.
буферов), ограниченного числом N. Очередь в таких центрах отсутствует, так что они эквивалентны центрам типа IS и допускают произвольное распределение времени обслуживания сообщений всех классов.
Обозначим, как и раньше,  - вероятность того, что сообщение класса
- вероятность того, что сообщение класса  после окончания обслуживания в
после окончания обслуживания в  центре поступает в центр
центре поступает в центр  - вероятность поступления внешнего потока класса
- вероятность поступления внешнего потока класса  в центр
в центр 

Состояние сети определяется вектором  где
где  - количество сообщений класса
- количество сообщений класса  в центре
в центре  . Обозначим также через
. Обозначим также через  , где
, где  количество сообщений класса
количество сообщений класса  в состоянии сети
в состоянии сети  . Допустимое множество состояний сети
. Допустимое множество состояний сети

Легко видеть, что условие (6.25) при  определяет зависимость потоков, входящих в сеть от ее состояния. Справедливо следующее утверждение.
определяет зависимость потоков, входящих в сеть от ее состояния. Справедливо следующее утверждение.
Утверждение. Если центры рассматриваемой сети МО удовлетворяют условиям теоремы ВСМР, то стационарные вероятности сети имеют мультипликативную форму:

где  - функции, определенные в п. 2.2.1:
- функции, определенные в п. 2.2.1:

и для  приборов обслуживания
приборов обслуживания

Здесь  так же как и раньше, однозначно определяется из системы уравнений
так же как и раньше, однозначно определяется из системы уравнений

Для центра  с дисциплиной обслуживания FCFS предполагается, что
с дисциплиной обслуживания FCFS предполагается, что  . Нормализующая константа имеет вид
. Нормализующая константа имеет вид

Для доказательства (6.26) используем достаточные условия мультипликативности стационарных вероятностей сетей МО, сформулированные в разделе 2.3.4. Пусть  - вектор с неотрицательными компонентами;
- вектор с неотрицательными компонентами; 
Введем функцию потерь, определяющую условия ввода в сеть сообщений класса  ,
,

и «триггерную» функцию, определяющую правило ухода из сети сообщений класса 

Условие мультипликативности имеет вид  тогда и только тогда, когда
тогда и только тогда, когда  для
для  . Для сетевой модели памяти УК с резервированием буферов это условие, очевидно, выполняется, что обеспечивает справедливость (6.26).
. Для сетевой модели памяти УК с резервированием буферов это условие, очевидно, выполняется, что обеспечивает справедливость (6.26).
Для определения вероятностей (6.26) и связанных с ними характеристик могут быть использованы вычислительные алгоритмы, рассмотренные в разделе 3.2 при незначительной их модификации. Однако проблема размерности, проявляющаяся в быстром росте затрат памяти и времени счета при рекуррентных вычислениях по алгоритму свертки, существенно ограничивает применение этого алгоритма. Ниже с целью определения требуемой буферной памяти УК для рассмотренной сети МО получены эффективные вычислительные процедуры, снимающие указанное ограничение для практических расчетов.
Рассмотрим вероятность того, что в сетевой модели УК С приборов центра «Память» заняты обслуживанием или блокированы:

где

Обозначим  , где
, где  имеем
имеем 
Отказ в приеме в буферную память сообщению, требующему  буферов, соответствует множеству состояний
буферов, соответствует множеству состояний

Отсюда вероятность отказа приема сообщений в память из N буферов, каждый объемом 

Таким образом, вероятность отказа  при фиксированном
при фиксированном  может быть определена последовательным вычислением для
может быть определена последовательным вычислением для  функции
функции  которая в свою очередь является
которая в свою очередь является  -кратной сверткой,
-кратной сверткой,
 (6.29)
(6.29)
Здесь  - символ свертки векторов
- символ свертки векторов

где функции

 - маргинальная стационарная вероятность условия
- маргинальная стационарная вероятность условия

для центра  при
при  . Условие (6.30) соответствует количеству приборов (буферов) центра «Память», связанных с
. Условие (6.30) соответствует количеству приборов (буферов) центра «Память», связанных с  центром сети МО. Вероятность
центром сети МО. Вероятность  совпадает с вероятностью условия (6.30) для изолированного от сети центра
совпадает с вероятностью условия (6.30) для изолированного от сети центра  , рассматриваемого при R входящих пуассоновских потоках с интенсивностями, зависящими от состояния центра
, рассматриваемого при R входящих пуассоновских потоках с интенсивностями, зависящими от состояния центра  в виде
в виде

Здесь  определяется из системы уравнений (6.27). При этом допустимое множество состояний имеет вид
определяется из системы уравнений (6.27). При этом допустимое множество состояний имеет вид  . Из (6.26) следует, что для изолированного центра
. Из (6.26) следует, что для изолированного центра  стационарная вероятность определяется выражением
стационарная вероятность определяется выражением

где нормализующая константа имеет вид

Стационарная вероятность условия (6.30) для изолированного центра 


Очевидно,  и с учетом выражения для
и с учетом выражения для  полагать, что
полагать, что  при
при 
Можно показать, что  в центрах типа IS удовлетвлоряет уравнению
в центрах типа IS удовлетвлоряет уравнению

Справедливо следующее утверждение.
Утверждение. Стационарная вероятность  любого изолированного центра
любого изолированного центра  сетевой модели УК удовлетворяет уравнению
сетевой модели УК удовлетворяет уравнению

где  - математическое ожидание числа занятых обслуживающих приборов из R при условии
- математическое ожидание числа занятых обслуживающих приборов из R при условии  (6.30).
(6.30).
Доказательство. Обозначим  . Уравнения локального баланса для центра
. Уравнения локального баланса для центра  могут быть записаны в виде
могут быть записаны в виде

где

 - математическое ожидание количества приборов из R, занятых обслуживанием сообщений класса
- математическое ожидание количества приборов из R, занятых обслуживанием сообщений класса  в состоянии
в состоянии  Суммирование (6.33) по
Суммирование (6.33) по  и по всем
и по всем  дает
дает

Следовательно,

Левая часть (6.34) может быть записана в виде

что и требовалось доказать.
Следствие 1. Для центров типа IS (N приборов) с учетом (6.31)

где  . Это выражение определяет среднее число сообщений в
. Это выражение определяет среднее число сообщений в  центре при фиксированном
центре при фиксированном 
Следствие 2. Для однолинейного центра  , что преобразует (6.32) к виду
, что преобразует (6.32) к виду

Для многолинейного центра  определение
определение  проблематично. В этом случае возможна аппроксимация
проблематично. В этом случае возможна аппроксимация  выражением (6.35) с учетом неравенства
выражением (6.35) с учетом неравенства  что дает приближенный способ вычисления
что дает приближенный способ вычисления 

Для  имеем
имеем  для
для  справедливо
справедливо  Такая аппроксимация дает наилучшие приближения для небольших R, что вполне приемлемо для равнодоступных пучков каналов передачи УК.
Такая аппроксимация дает наилучшие приближения для небольших R, что вполне приемлемо для равнодоступных пучков каналов передачи УК.
Выражения (6.31), (6.36), (6.37) определяют рекурсии для вычисления  что в свою очередь дает возможность определить
что в свою очередь дает возможность определить  и, следовательно, вероятность отказа приема сообщений в память
и, следовательно, вероятность отказа приема сообщений в память  . Эти рекуррентные вычислительные процедуры требуют малой памяти и весьма эффективны для практических расчетов при очень большом числе классов R и количестве буферов N. Общий объем требуемой памяти
. Эти рекуррентные вычислительные процедуры требуют малой памяти и весьма эффективны для практических расчетов при очень большом числе классов R и количестве буферов N. Общий объем требуемой памяти

где  - нелинейная возрастающая функция затрат памяти на адресацию для формирования цепочки буферов и организацию очередей на различных этапах их обслуживания в УК.
- нелинейная возрастающая функция затрат памяти на адресацию для формирования цепочки буферов и организацию очередей на различных этапах их обслуживания в УК.
Во многих случаях  где
где  - ближайшее целое число байт, большее или равное у. Минимальный объем памяти
- ближайшее целое число байт, большее или равное у. Минимальный объем памяти  при допустимой вероятности отказа
при допустимой вероятности отказа  отыскивается последовательным изменением
отыскивается последовательным изменением  с учетом монотонности
с учетом монотонности  по переменной N. При этом для фиксированного
по переменной N. При этом для фиксированного  определяется минимальное
определяется минимальное  удовлетворяющее неравенству
удовлетворяющее неравенству 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
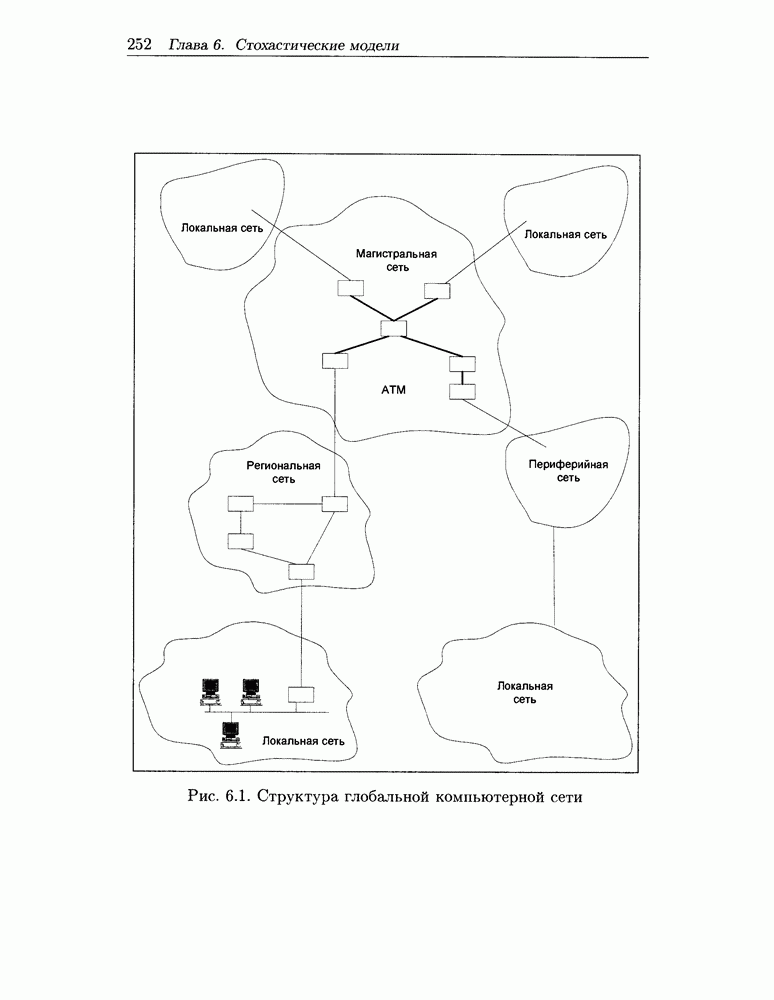
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
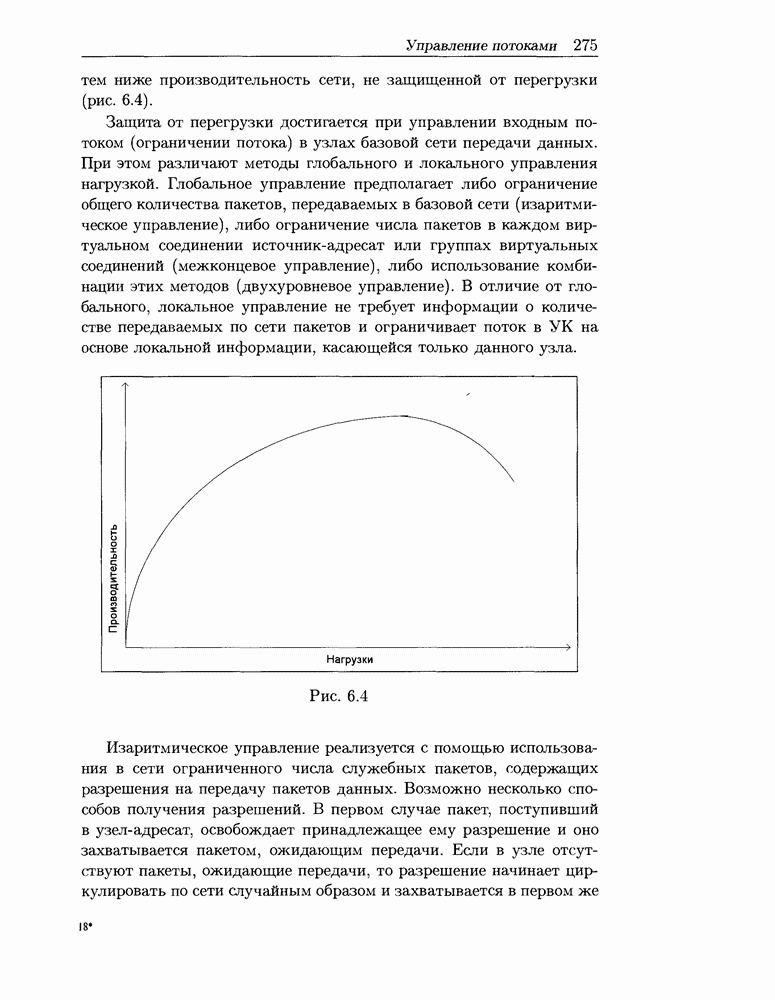
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
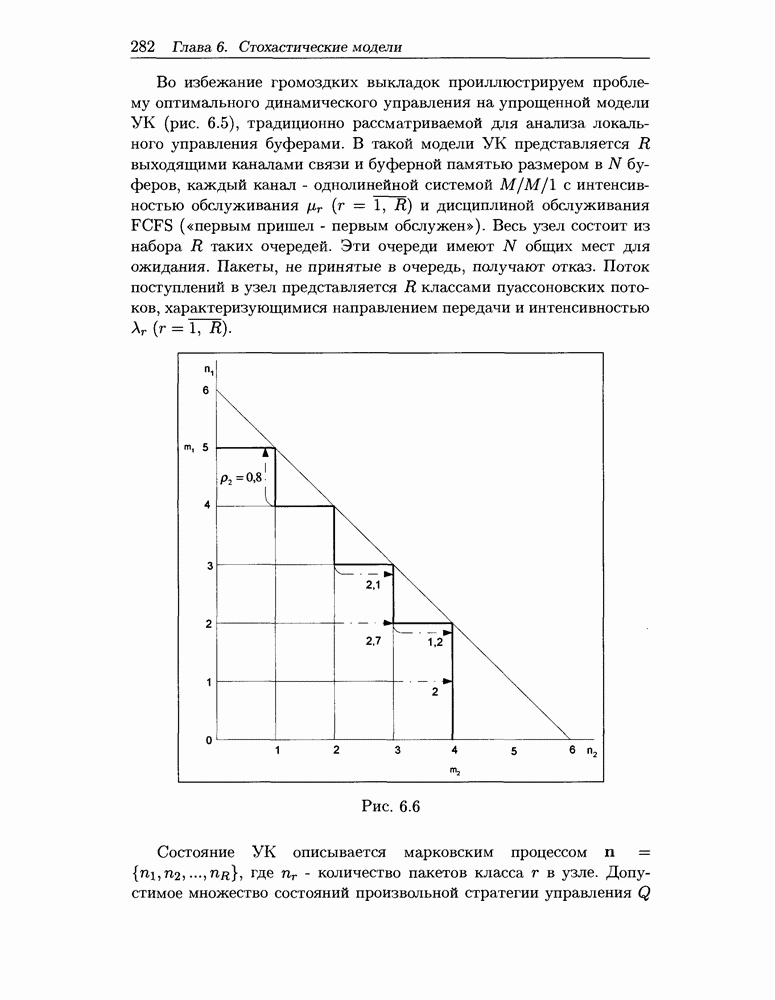
- 6.3.3 Локальное управление буферами
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
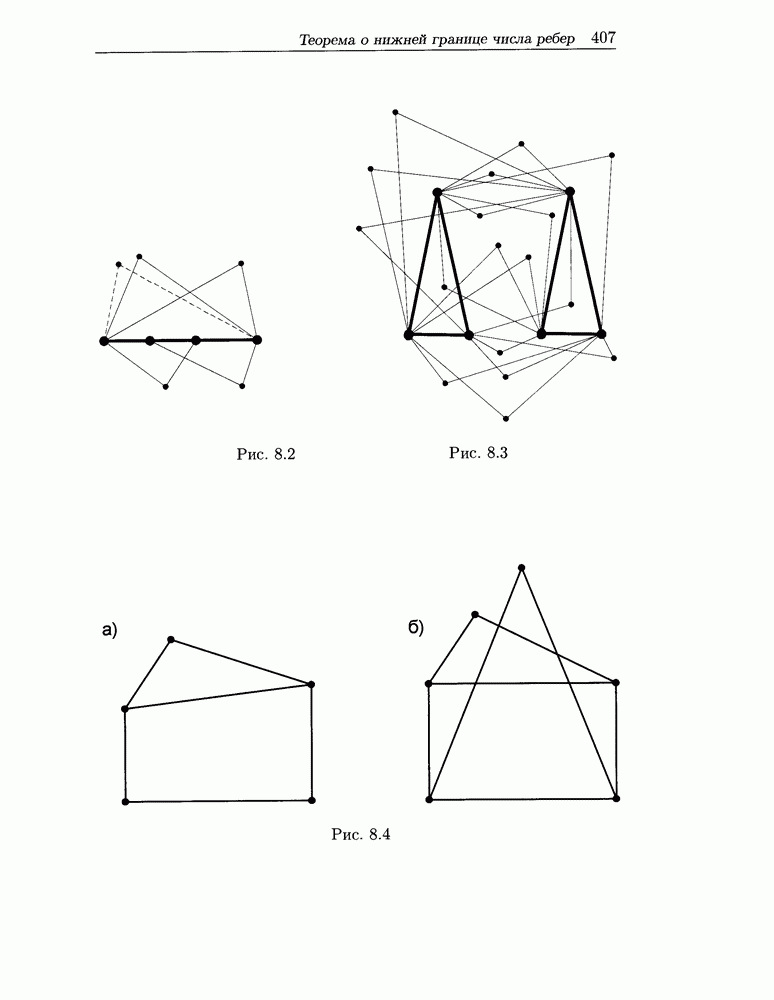
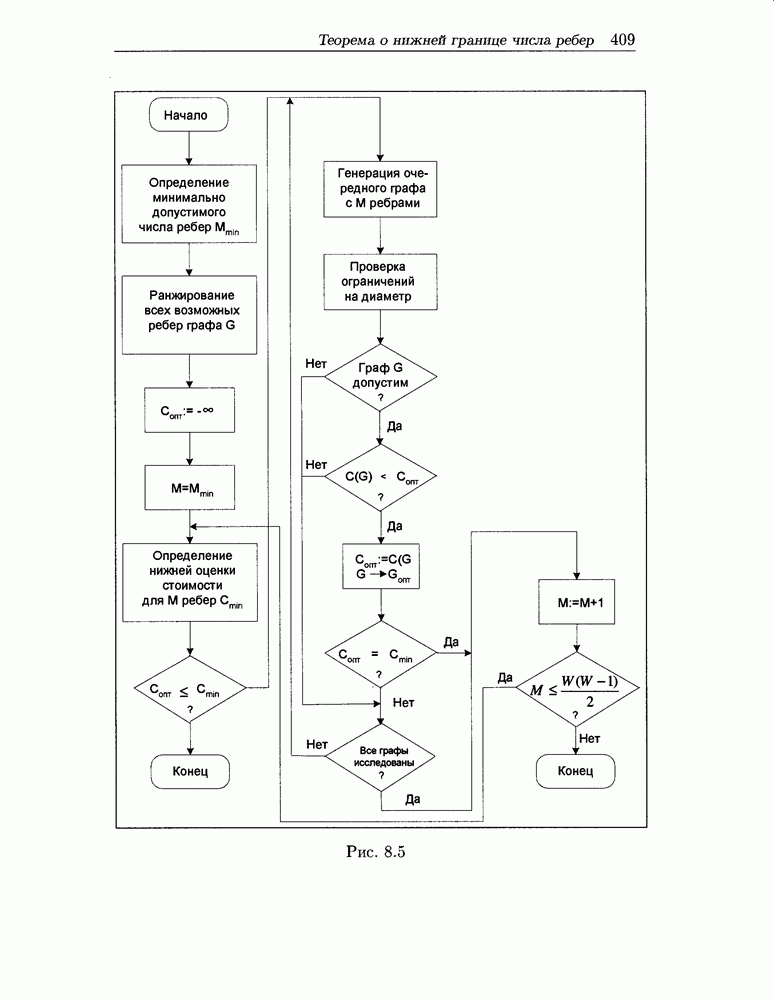
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
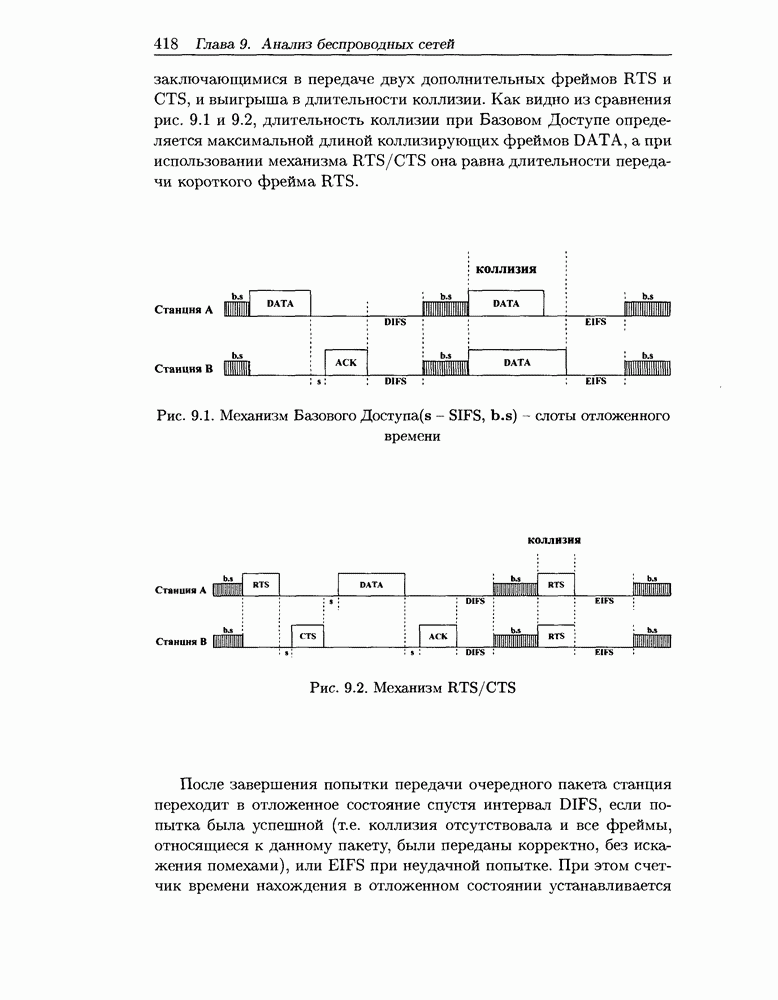
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
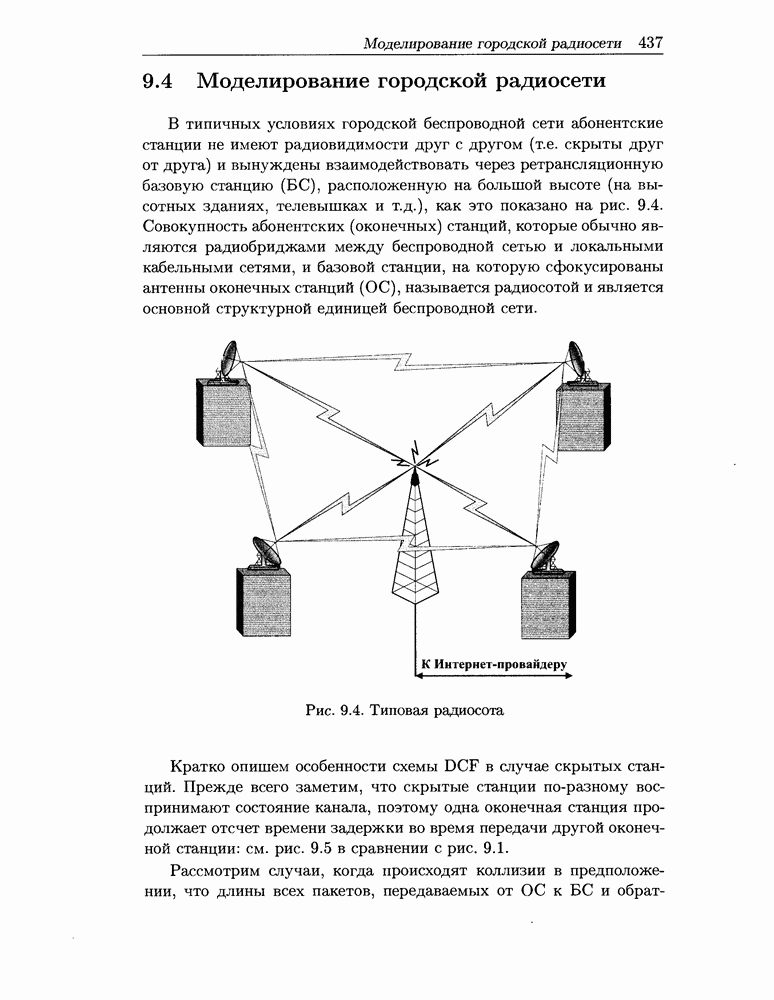
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
- 9.5 Численные результаты исследования городской радиосоты
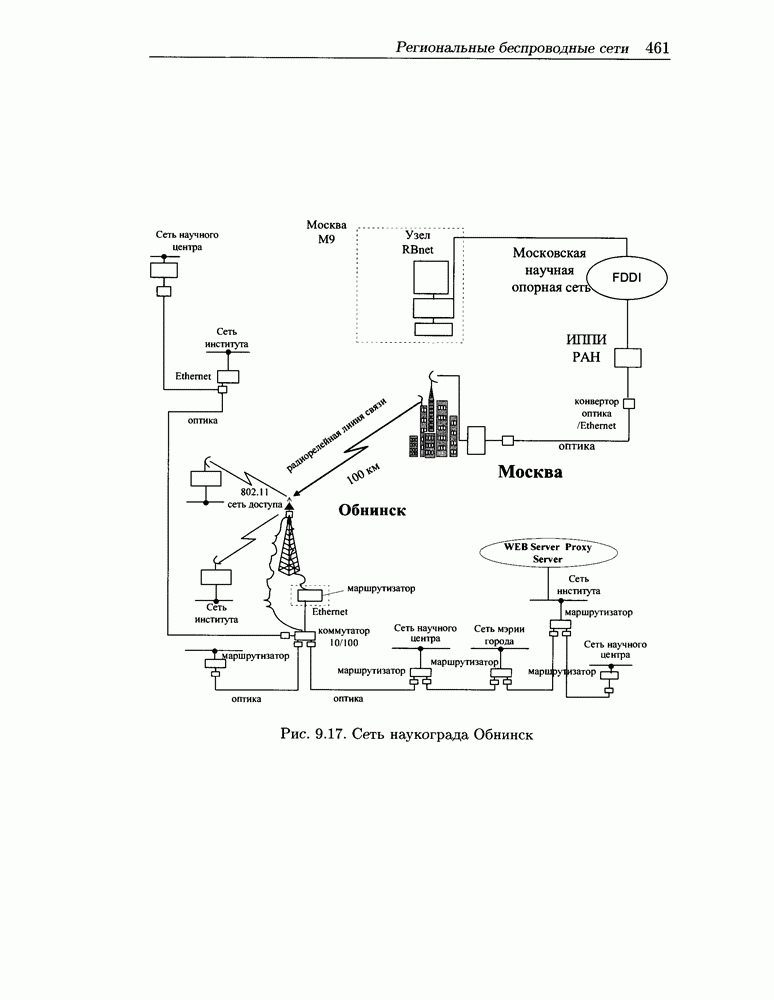
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
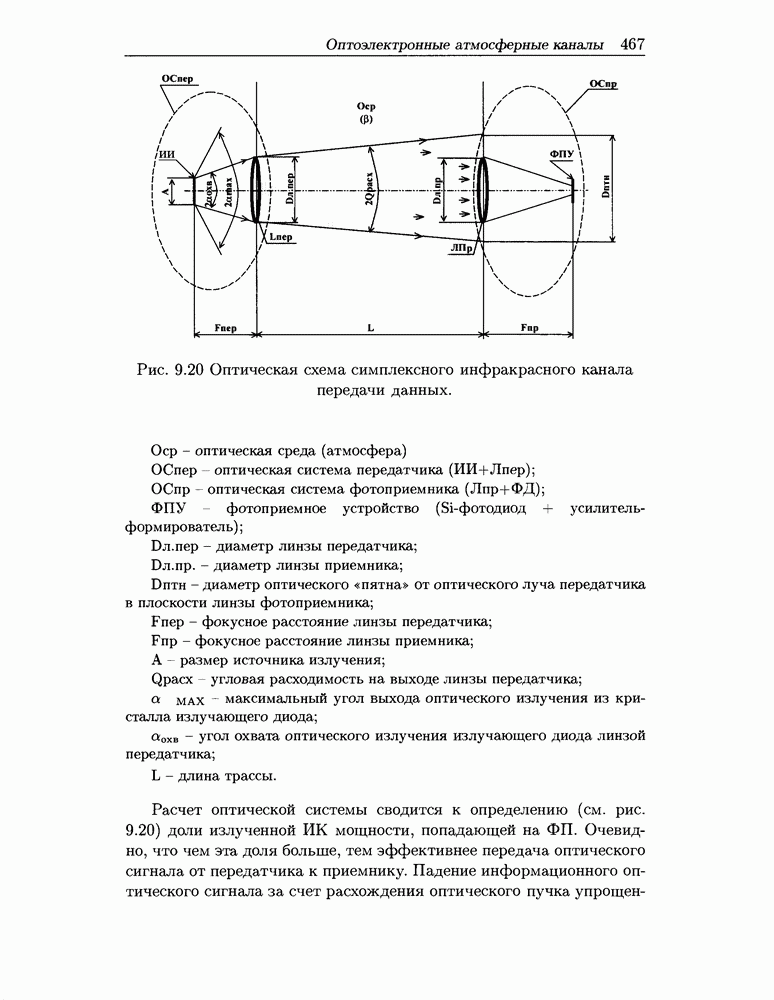
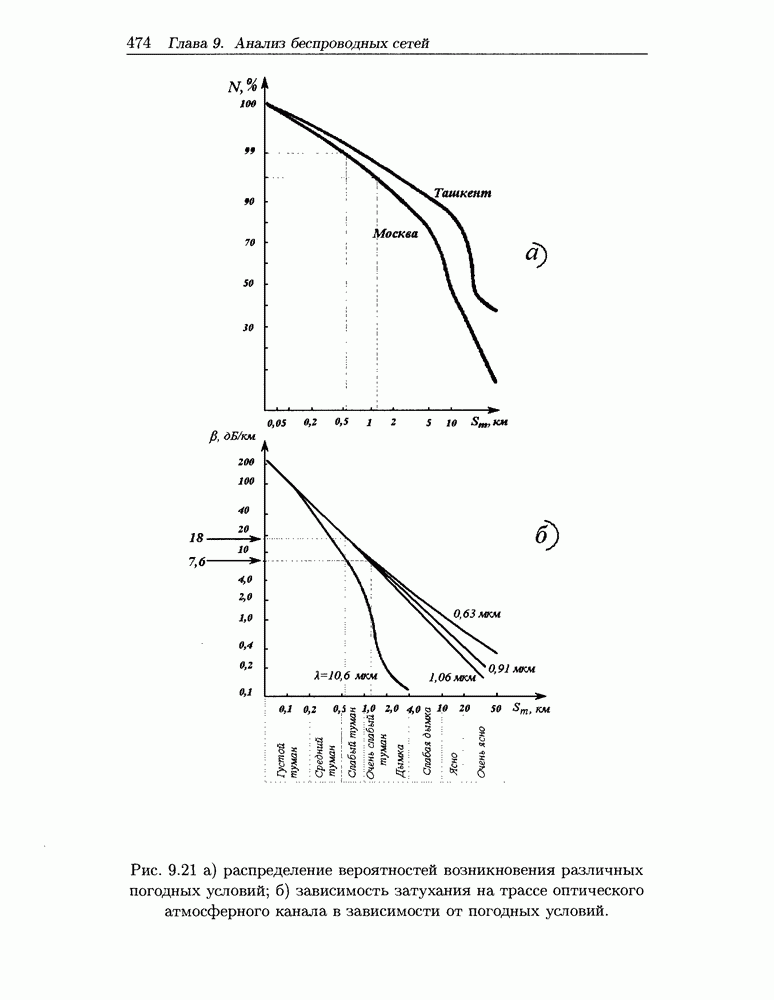
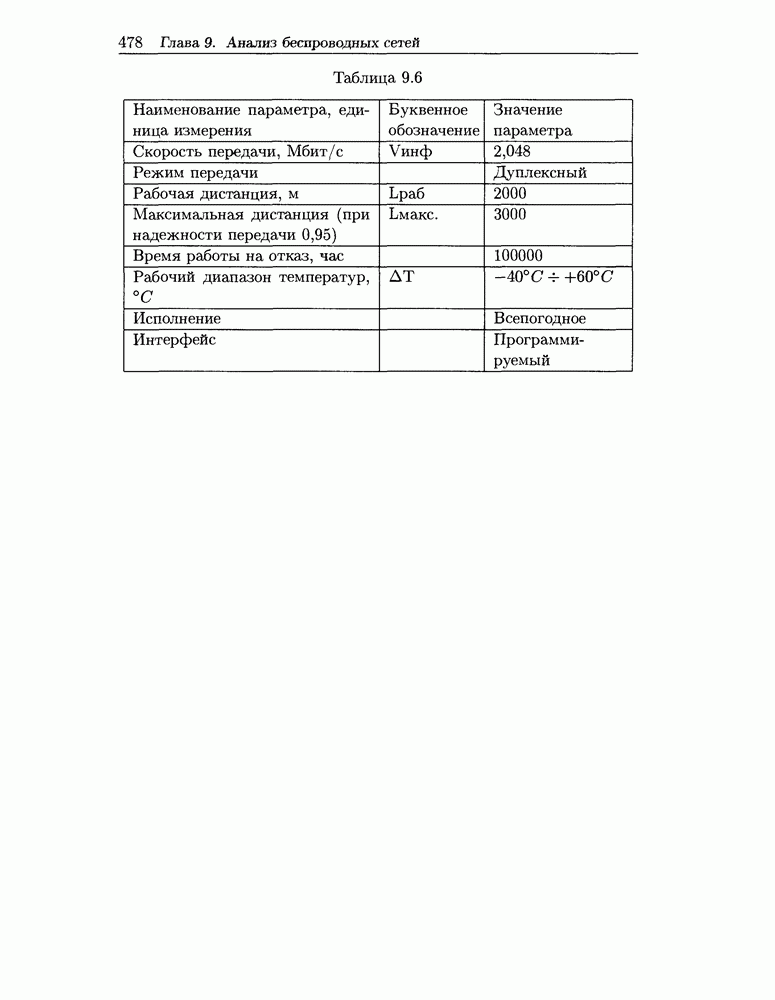
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература