| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.3.3 Случай фрагментации пакетов
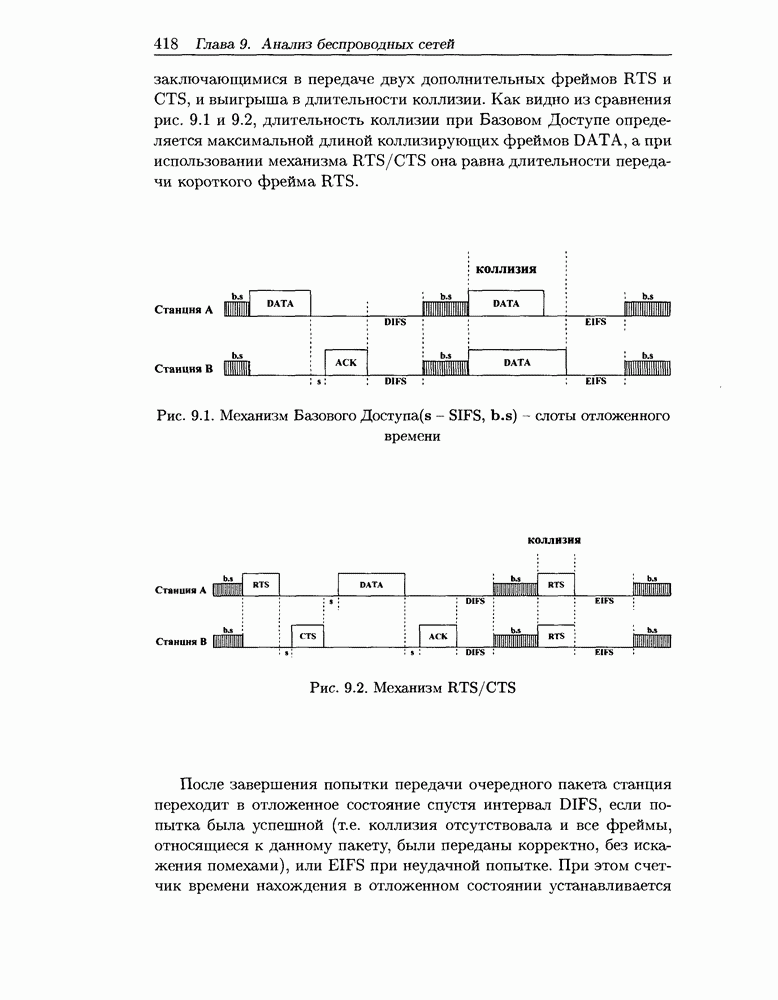
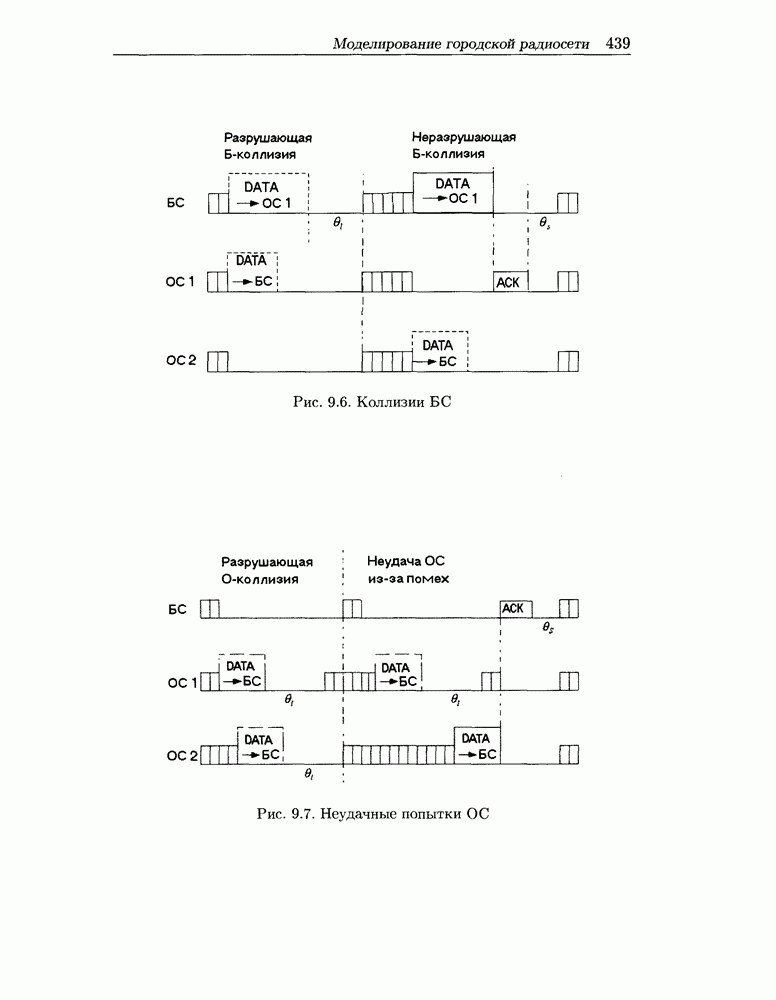
В этом случае пакет, размер которого больше некоторого порога фрагментации  передается в виде цепочки фреймов DATA, содержащих последовательные фрагменты и перемежаемых ответными фреймами АСК, а также короткими межфреймовыми промежутками SIFS. Таким образом, в общем случае процесс передачи пакета можно представить в виде одной или нескольких цепочек фреймов, передаваемых непрерывно. Посылка фрейма DATA с фрагментом, являющимся первым в цепочке и превышающим по длине предел Р, предваряется посылкой фрейма RTS и получением разрешающего фрейма CTS.
передается в виде цепочки фреймов DATA, содержащих последовательные фрагменты и перемежаемых ответными фреймами АСК, а также короткими межфреймовыми промежутками SIFS. Таким образом, в общем случае процесс передачи пакета можно представить в виде одной или нескольких цепочек фреймов, передаваемых непрерывно. Посылка фрейма DATA с фрагментом, являющимся первым в цепочке и превышающим по длине предел Р, предваряется посылкой фрейма RTS и получением разрешающего фрейма CTS.
Для пропускной способности и в случае фрагментации остается справедлива формула (9.3), как и формула (9.2) для входящих в (9.3) вероятностей  .
.
Оценка средних длительностей слотов.
Свяжем каждую попытку передачи с парой  , где l, как и ранее, - длина пакета, к которой относится эта цепочка, а
, где l, как и ранее, - длина пакета, к которой относится эта цепочка, а  - число фрагментов этого пакета, которые осталось передать, причем
- число фрагментов этого пакета, которые осталось передать, причем  , где
, где  - целая часть отношения
- целая часть отношения  . Обозначим также через
. Обозначим также через  длины первого и последнего фрагментов остатка пакета, передаваемого при данной попытке. Пусть вероятность того, что произвольно выбранная попытка передачи связана с конкретной парой
длины первого и последнего фрагментов остатка пакета, передаваемого при данной попытке. Пусть вероятность того, что произвольно выбранная попытка передачи связана с конкретной парой  , равна
, равна  . Тогда формула (9.4) для средней длительности «коллизионного» слота преобразуется в случае фрагментации к виду:
. Тогда формула (9.4) для средней длительности «коллизионного» слота преобразуется в случае фрагментации к виду:

где  - вероятность того, что при данной обычной попытке передается цепочка, длина первого фрагмента которой равна
- вероятность того, что при данной обычной попытке передается цепочка, длина первого фрагмента которой равна  , т.е.
, т.е.

 наименьшее целое число, большее либо равное
наименьшее целое число, большее либо равное  - целая часть отношения
- целая часть отношения  . Кроме того, здесь и далее используется булева функция
. Кроме того, здесь и далее используется булева функция  принимающая единичное значение при выполнении условия
принимающая единичное значение при выполнении условия  .
.
В начале «успешного» слота одна и только одна станция предпринимает попытку передачи, которая с вероятностью  связана с парой
связана с парой  Эта попытка завершится успехом для данной пары (l, к). т.е. успешной передачей всего пакета длиной l, с вероятностью
Эта попытка завершится успехом для данной пары (l, к). т.е. успешной передачей всего пакета длиной l, с вероятностью
 (9.24)
(9.24)
где  при
при  при
при  . Средняя длительность попытки передачи остатка пакета, описываемого парой
. Средняя длительность попытки передачи остатка пакета, описываемого парой  очевидно, составляет:
очевидно, составляет:


При успешном завершении процесса передачи станция выбирает из очереди следующий пакет, длина которого равна I с вероятностью  и с вероятностью
и с вероятностью  может мгновенно приступить к его передаче (ситуация мгновенного повтора). Таким образом, формула (9.5) для средней длительности «успешного» слота остается верной и в случае фрагментации, а формула (9.6), определяющая среднее число байт информации U, успешно переданных в течение «успешного» слота, приобретает вид:
может мгновенно приступить к его передаче (ситуация мгновенного повтора). Таким образом, формула (9.5) для средней длительности «успешного» слота остается верной и в случае фрагментации, а формула (9.6), определяющая среднее число байт информации U, успешно переданных в течение «успешного» слота, приобретает вид:

причем в этих формулах  - усредненные значения вероятности успеха и длительности попытки передачи соответственно при первой попытке
- усредненные значения вероятности успеха и длительности попытки передачи соответственно при первой попытке  и при последующих, мгновенно повторяемых попытках, т.е.
и при последующих, мгновенно повторяемых попытках, т.е.

Оценка вероятности передачи. Как и в предыдущем разделе, рассмотрим процесс передачи пакета длиной l некоторой станцией. После выбора этого пакета из очереди возможны следующие варианты начала процесса его передачи: 1) варианты 0, 2 и 3, определенные в предыдущем разделе, и 2) варианты  на которые «распадается» вариант 1, т.е. при варианте
на которые «распадается» вариант 1, т.е. при варианте  станция мгновенно начинает передачу, но эта передача неудачна из-за искажения помехами либо фрейма DATA, содержащего
станция мгновенно начинает передачу, но эта передача неудачна из-за искажения помехами либо фрейма DATA, содержащего  фрагмент пакета, либо соответствующего фрейма АСК. Очевидно, вероятности вариантов равны
фрагмент пакета, либо соответствующего фрейма АСК. Очевидно, вероятности вариантов равны


а вероятность варианта 0 определена выражением (9.12).
Как и в предыдущем разделе, основная задача состоит в нахождении вероятности  того, что в течение рассматриваемого процесса передачи пакета длиной l, начинающегося в соответствии с вариантом j, происходит ровно
того, что в течение рассматриваемого процесса передачи пакета длиной l, начинающегося в соответствии с вариантом j, происходит ровно  обычных попыток, а также вероятности отказа
обычных попыток, а также вероятности отказа  в передаче пакета длиной l при условии варианта j начала этой передачи. Кроме того, требуется найти для каждой пары (I, к) среднее число
в передаче пакета длиной l при условии варианта j начала этой передачи. Кроме того, требуется найти для каждой пары (I, к) среднее число  попыток передачи остатка пакета, описываемого этой парой; это число определяет вероятность
попыток передачи остатка пакета, описываемого этой парой; это число определяет вероятность 
 (9.32)
(9.32)
В случае  пакет не фрагментируется, т.е.
пакет не фрагментируется, т.е.  поэтому
поэтому  Аналогично для
Аналогично для  имеем
имеем  , причем для нахождения искомых величин используются формулы (9.17), (9.10) и (9.16) при
, причем для нахождения искомых величин используются формулы (9.17), (9.10) и (9.16) при  а при
а при  - формулы (9.9), (9.11) и (9.18)-(9.22).
- формулы (9.9), (9.11) и (9.18)-(9.22).
В процессе передачи фрагментированного пакета длиной  попытки передачи остатка пакета, описываемого парой
попытки передачи остатка пакета, описываемого парой  могут происходить в том и только в том случае, когда
могут происходить в том и только в том случае, когда
1) все предыдущие фрагменты  были успешно переданы, т.е. счетчики
были успешно переданы, т.е. счетчики  не достигли своих предельных значений, и
не достигли своих предельных значений, и
2) при первой попытке передаче фрагмента  начинающего данный остаток, произошло искажение помехами либо фрейма DATA, содержащего этот фрагмент, либо соответствующего фрейма АСК. Поэтому вероятность
начинающего данный остаток, произошло искажение помехами либо фрейма DATA, содержащего этот фрагмент, либо соответствующего фрейма АСК. Поэтому вероятность  для
для  находится следующим рекуррентным способом:
находится следующим рекуррентным способом:

где


и

 для
для  , а для
, а для  , при
, при  , при
, при  наконец,
наконец,  при
при  , а иначе
, а иначе  -Для вероятности отказа при
-Для вероятности отказа при  имеем:
имеем:

Наконец, среднее число попыток для  определяется следующими формулами:
определяется следующими формулами:

где

Теперь мы можем найти значения  определяющие согласно (9.7) вероятность передачи
определяющие согласно (9.7) вероятность передачи  :
:

а также усредненное значение  вероятности отказа:
вероятности отказа:

где номер варианта j в зависимости от I принимает значения  , а также
, а также  при
при 

Таким образом, решая систему уравнений (9.7), (9.12), (9.29)-(9.31), (9.33)-(9.34) и (9.37)-(9.38) с помощью итеративной технологии, аналогичной той, что описана в конце предыдущего подраздела, находим искомую вероятность передачи  . Затем с помощью (9.32), (9.34) и (9.35) определяем распределение d и, наконец, с использованием формул (9.3), (9.5) и 9.23)-(9.28) вычисляем искомую пропускную способность S в случае фрагментации.
. Затем с помощью (9.32), (9.34) и (9.35) определяем распределение d и, наконец, с использованием формул (9.3), (9.5) и 9.23)-(9.28) вычисляем искомую пропускную способность S в случае фрагментации.
Разработанный простой аналитический метод позволяет оценить пропускную способность беспроводной локальной сети, управляемой механизмом DCF протокола IEEE 802.11, в условиях насыщения и помех. Предлагаемый метод позволяет учитывать как ограничения, накладываемые механизмом DCF на число попыток передачи пакета, так и Эффект Захвата, заключающийся в том, что станция, только что успешно закончившая передачу пакета, имеет больше шансов на выигрыш в соревновании с остальными станциями и, соответственно, на захват канала для передачи следующего пакета. Наряду с пропускной способностью оценивается также вероятность отказа в передаче пакета из-за достижения предельных значений, установленных стандартом [298] для числа попыток передачи длинных и коротких фреймов. Кроме того, в отличие от предшествующих работ [146, 155, 294] разработанный метод позволяет оценить пропускную способность и вероятность отказа в условиях использования фрагментации пакетов, рекомендуемой в стандарте [298] для снижения влияния помех.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
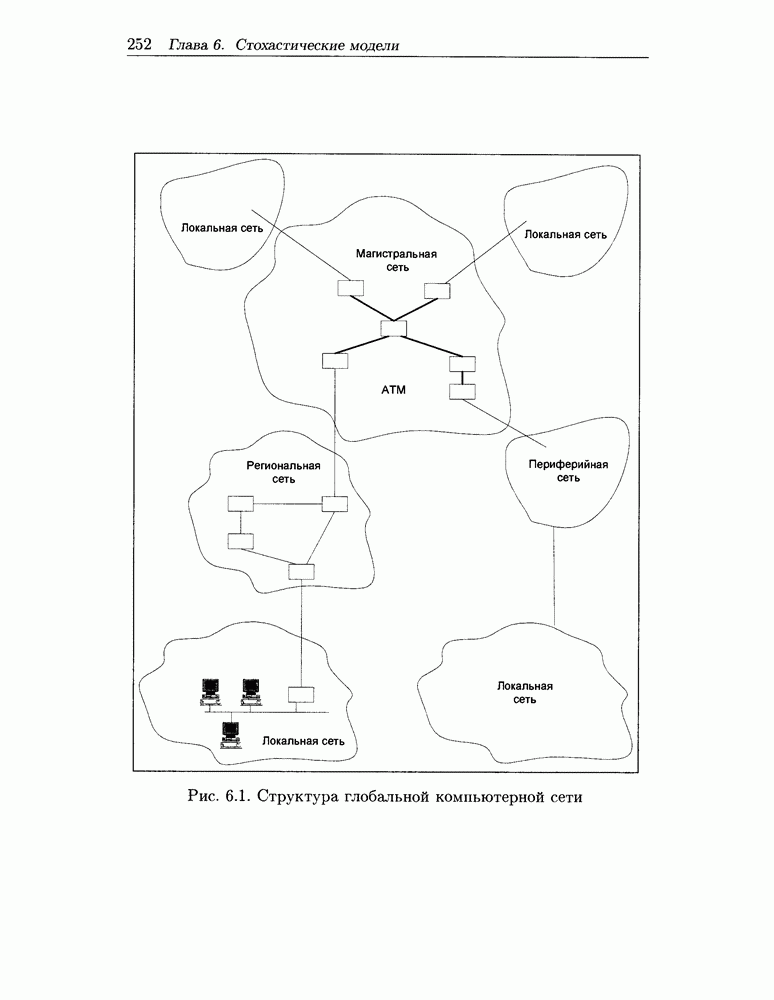
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
- 6.3.3 Локальное управление буферами
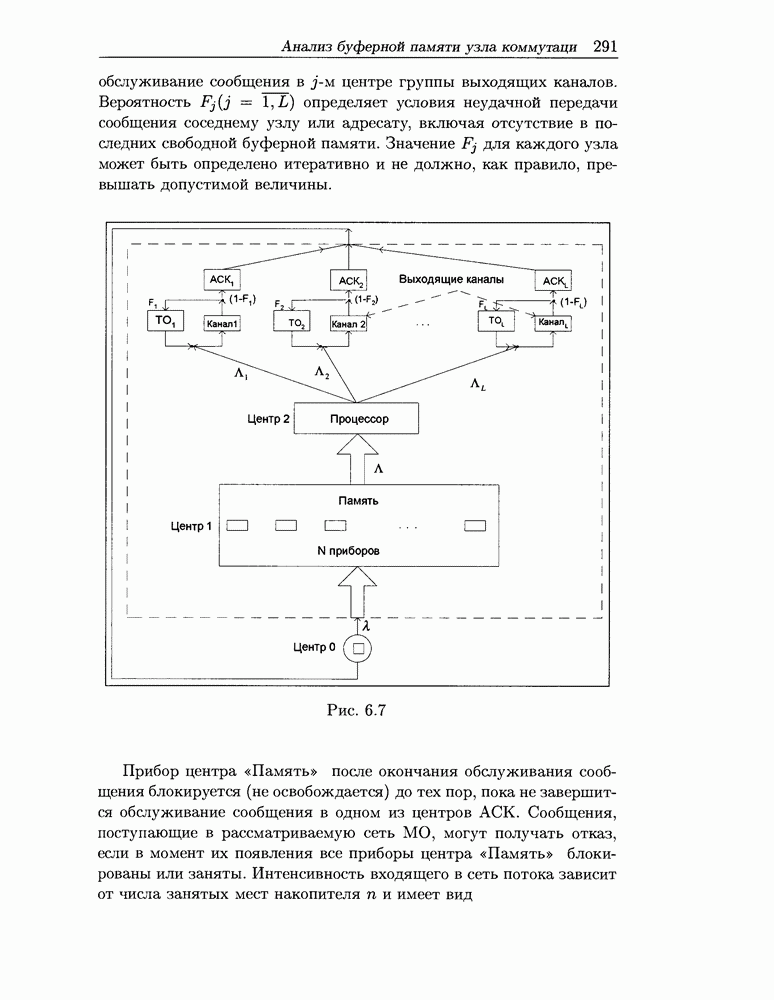
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
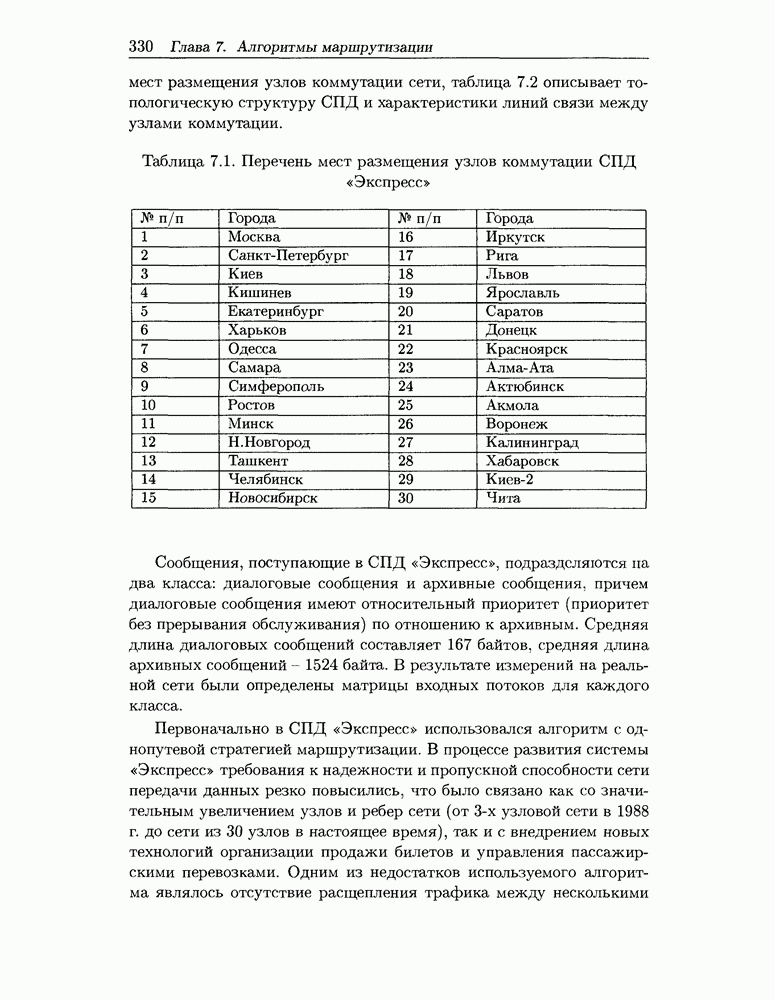
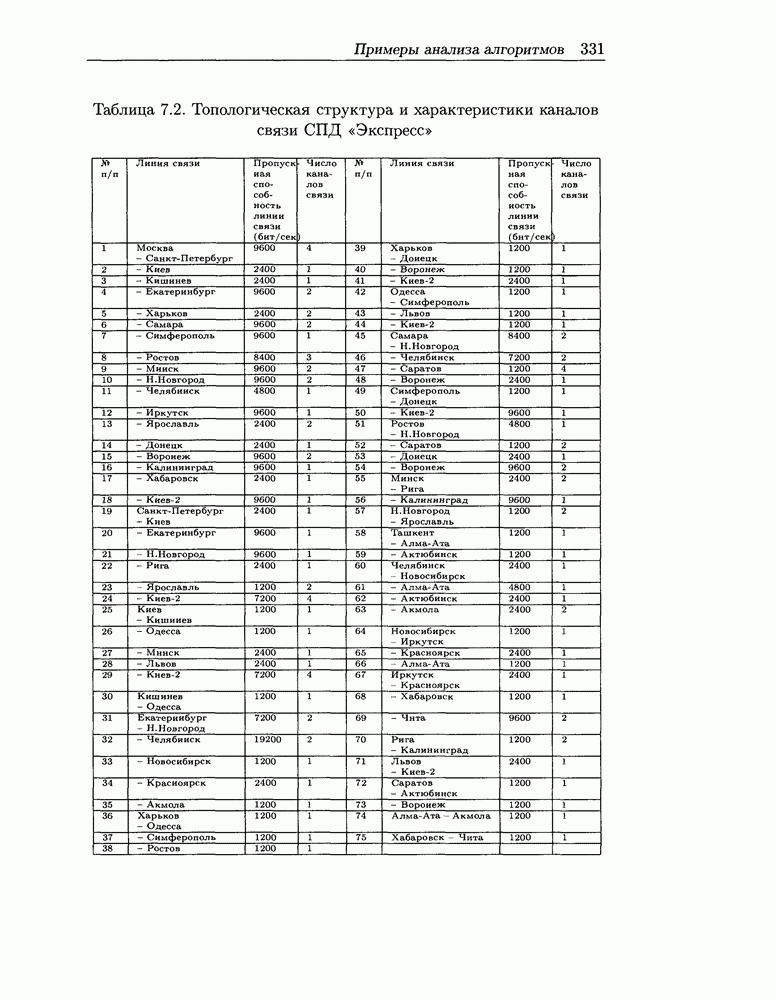
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
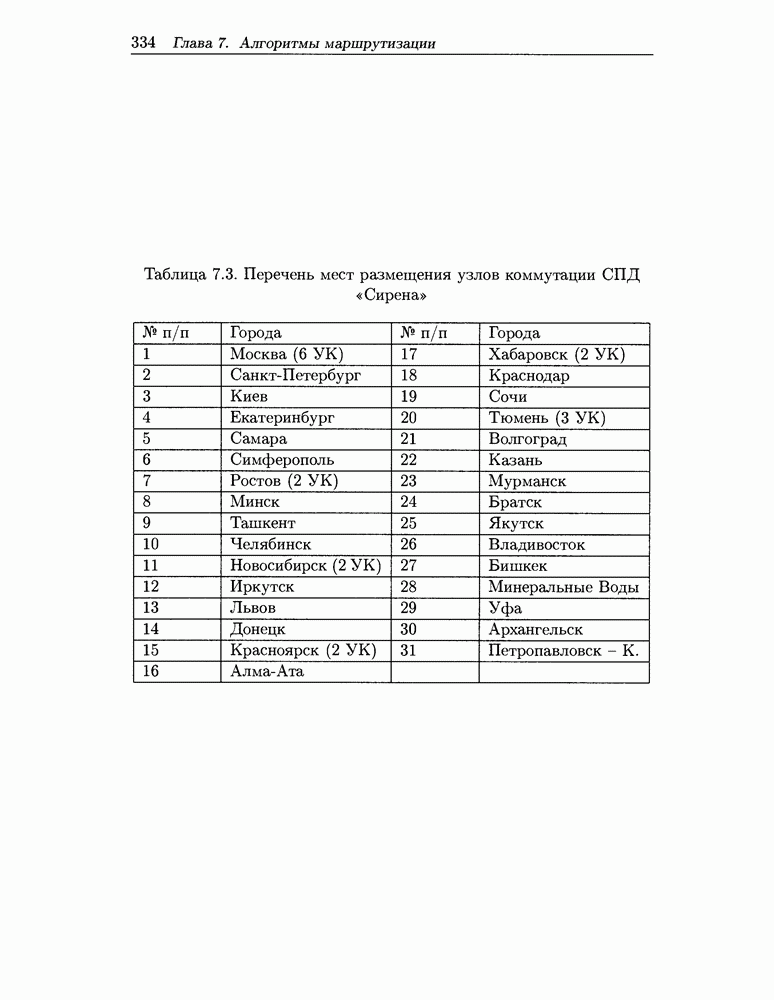
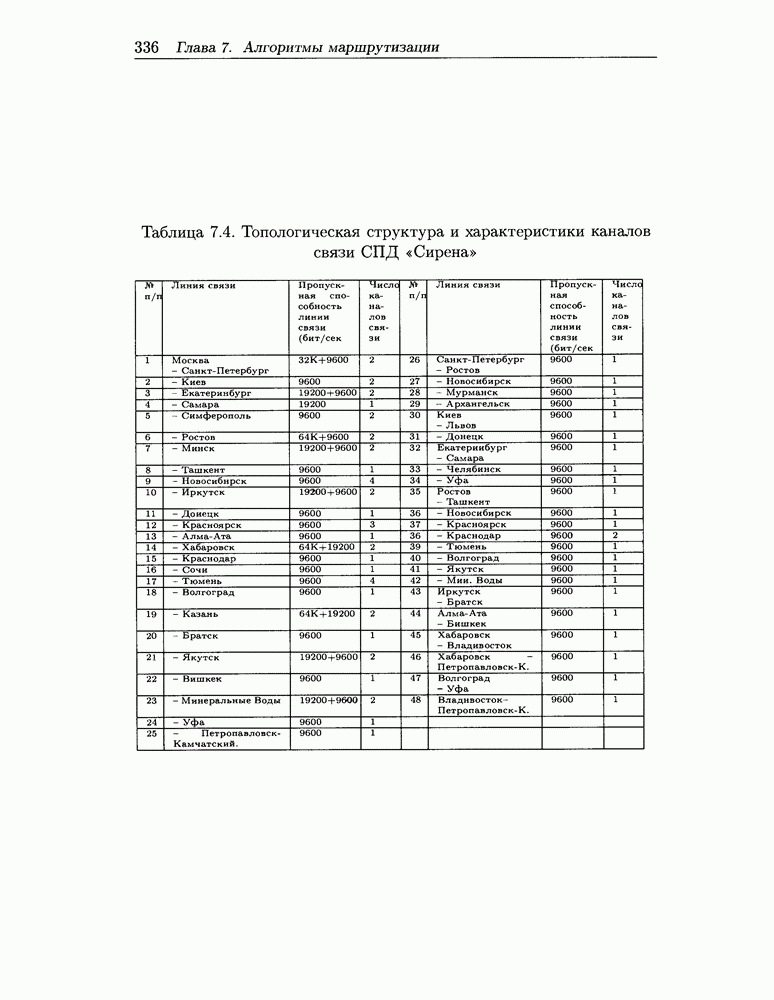
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
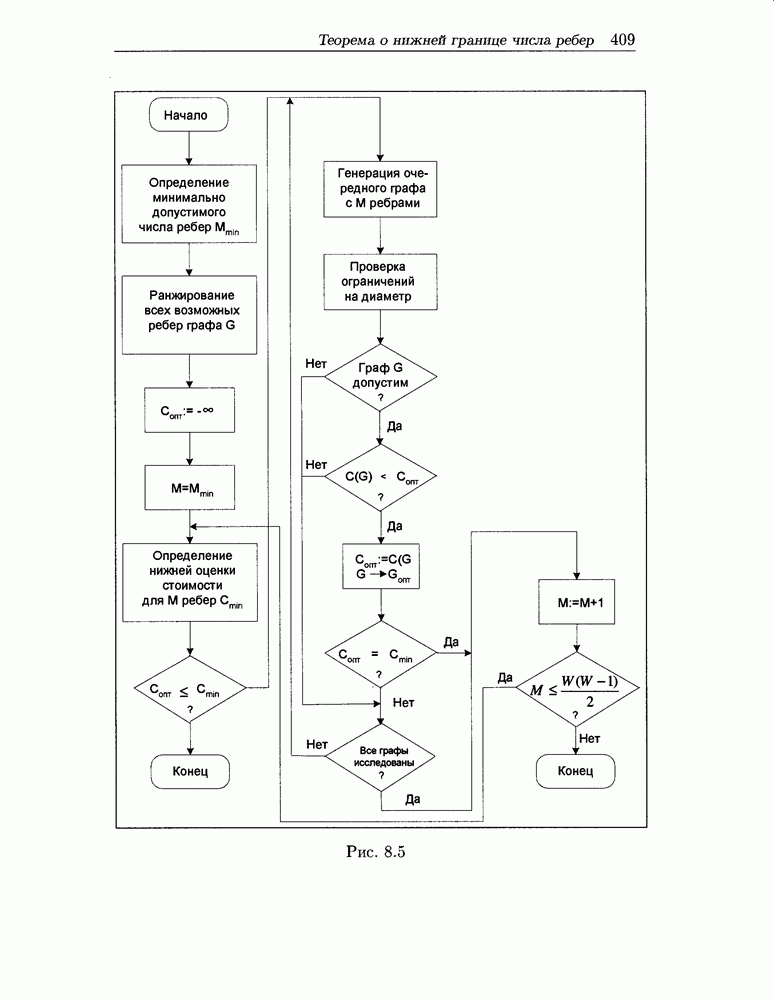
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
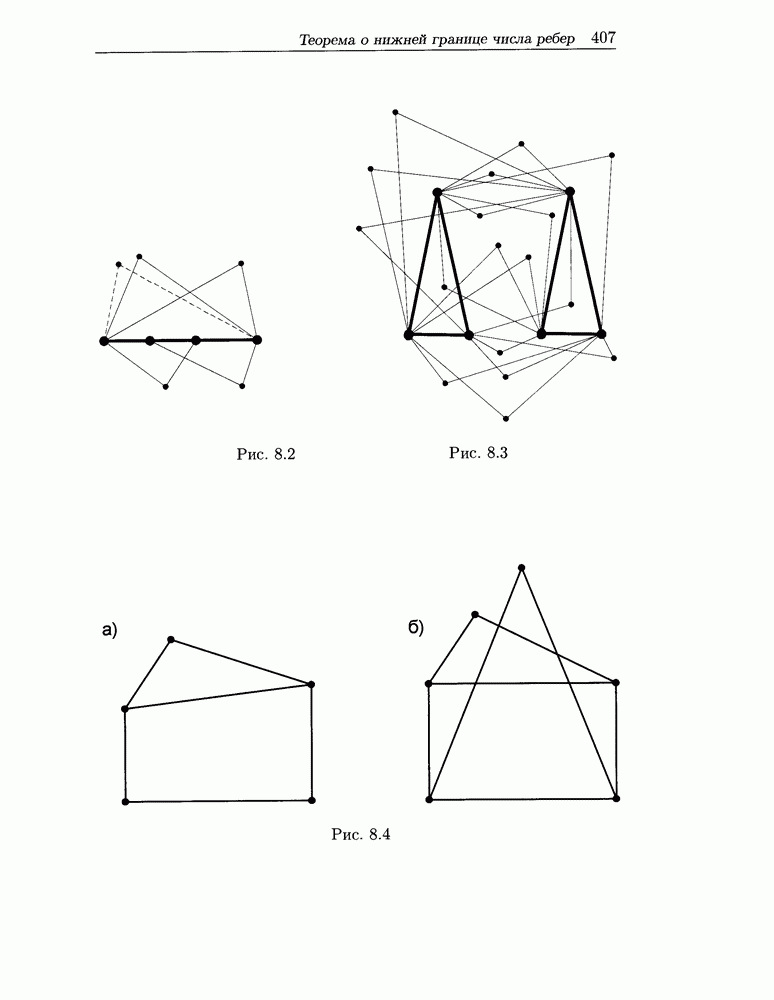
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
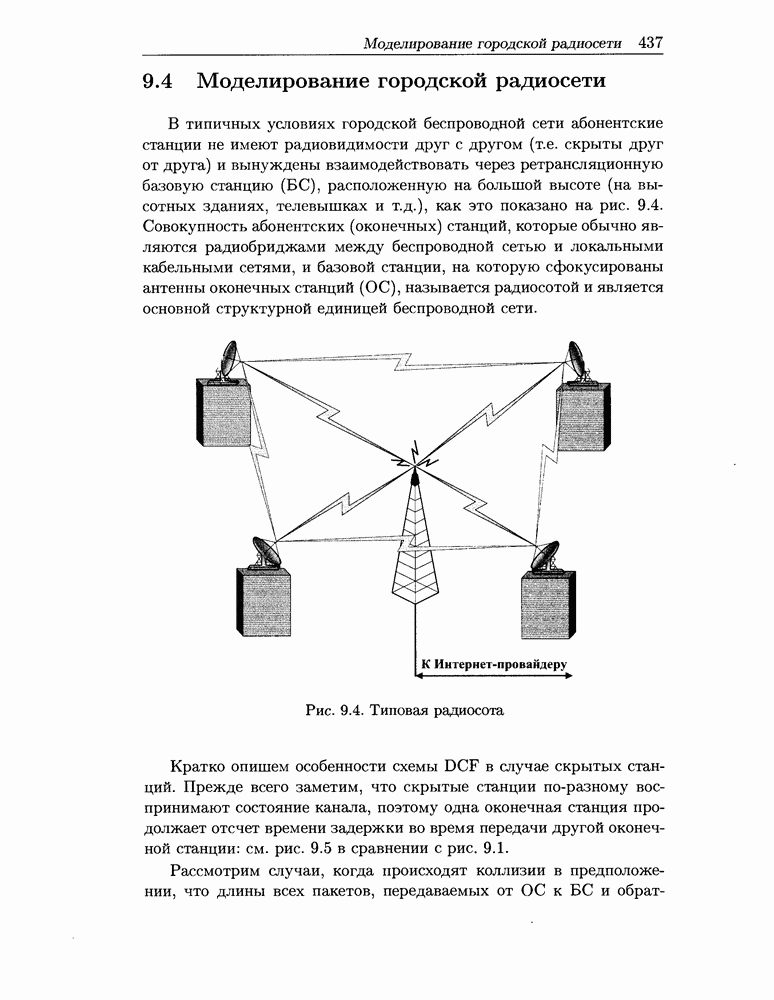
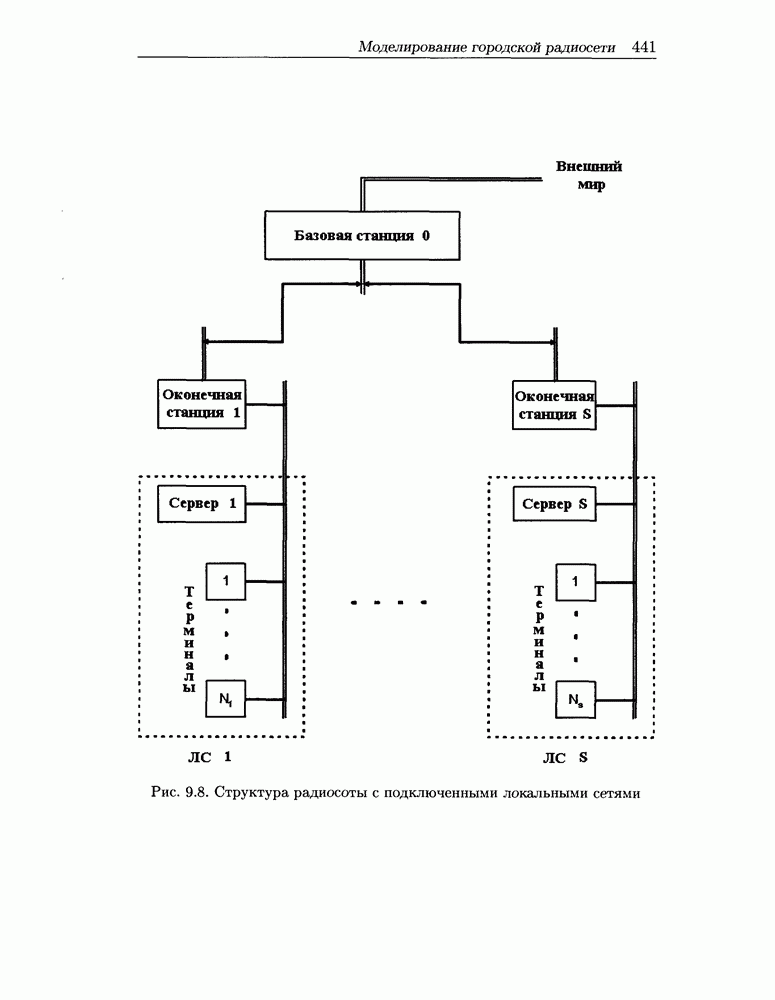
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
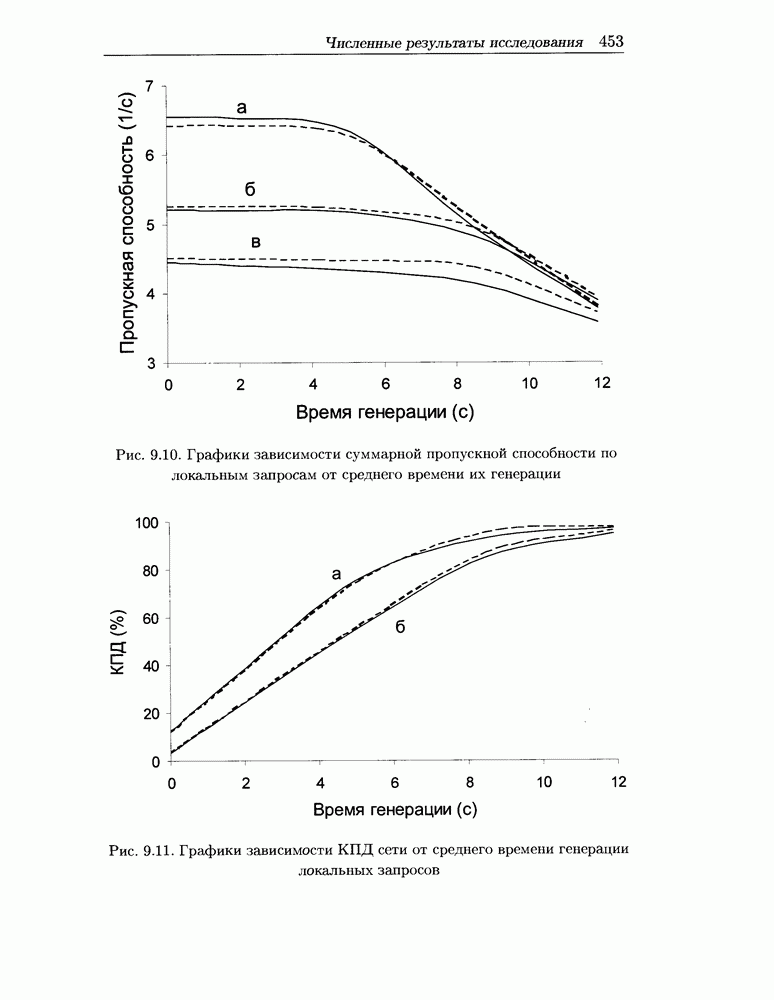
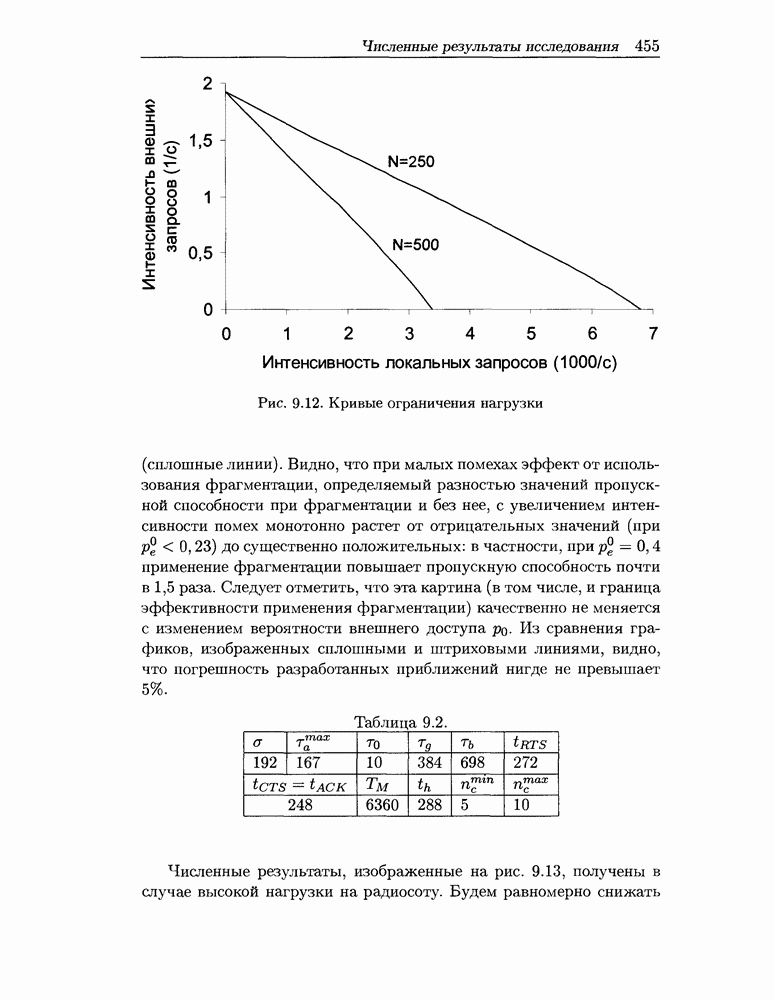
- 9.5 Численные результаты исследования городской радиосоты
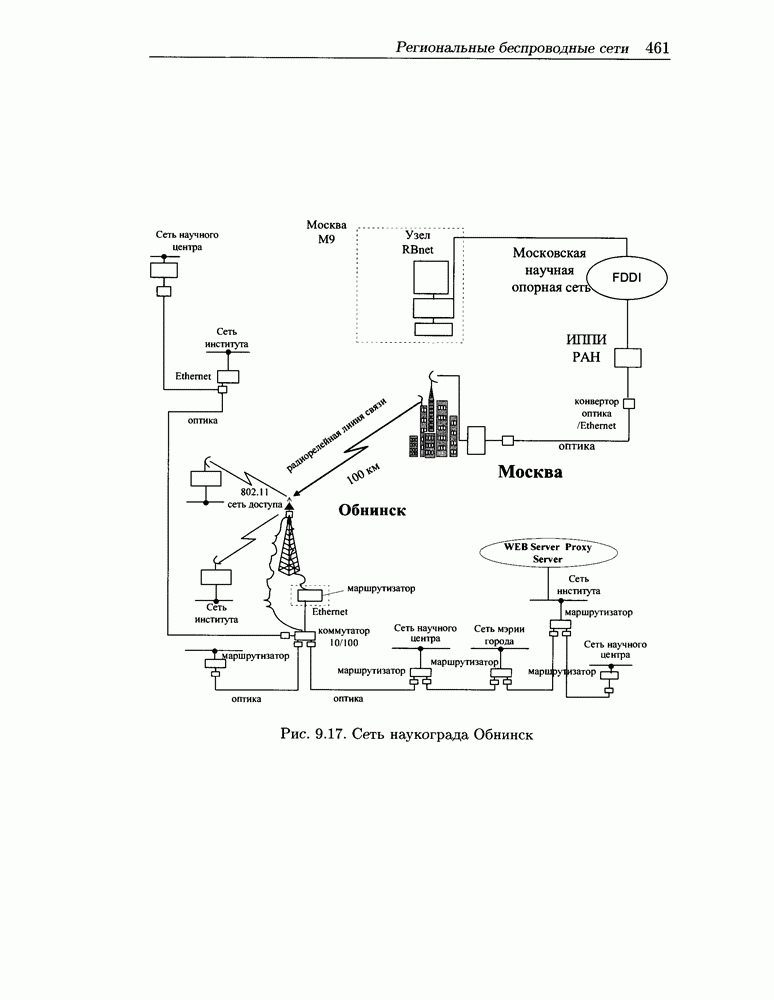
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
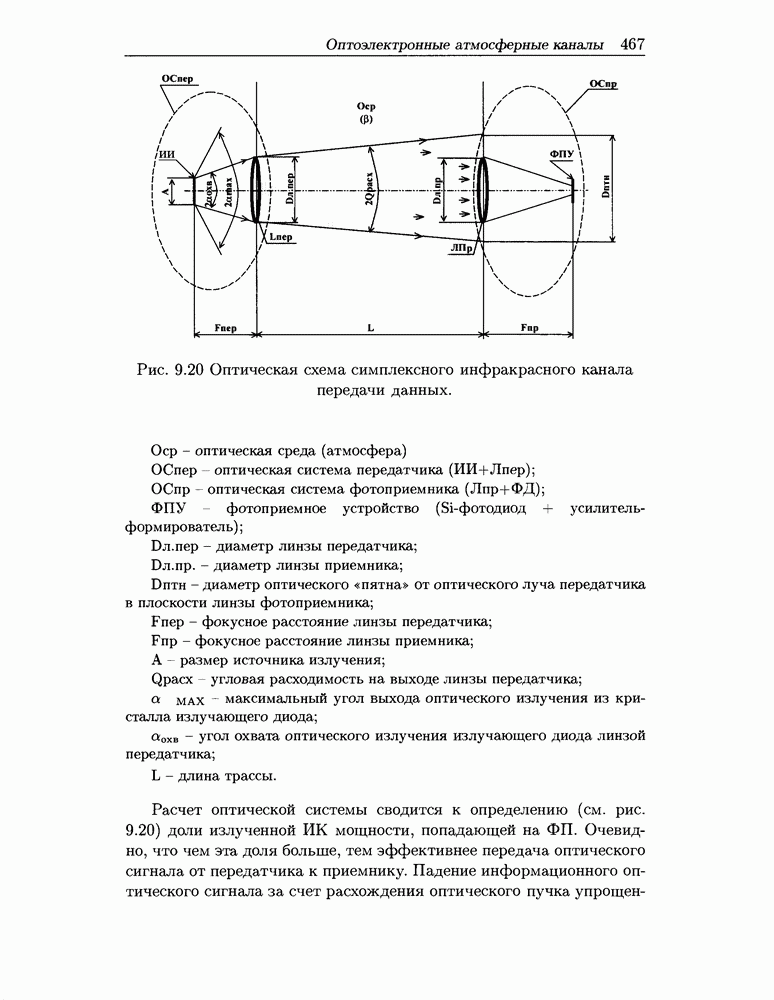
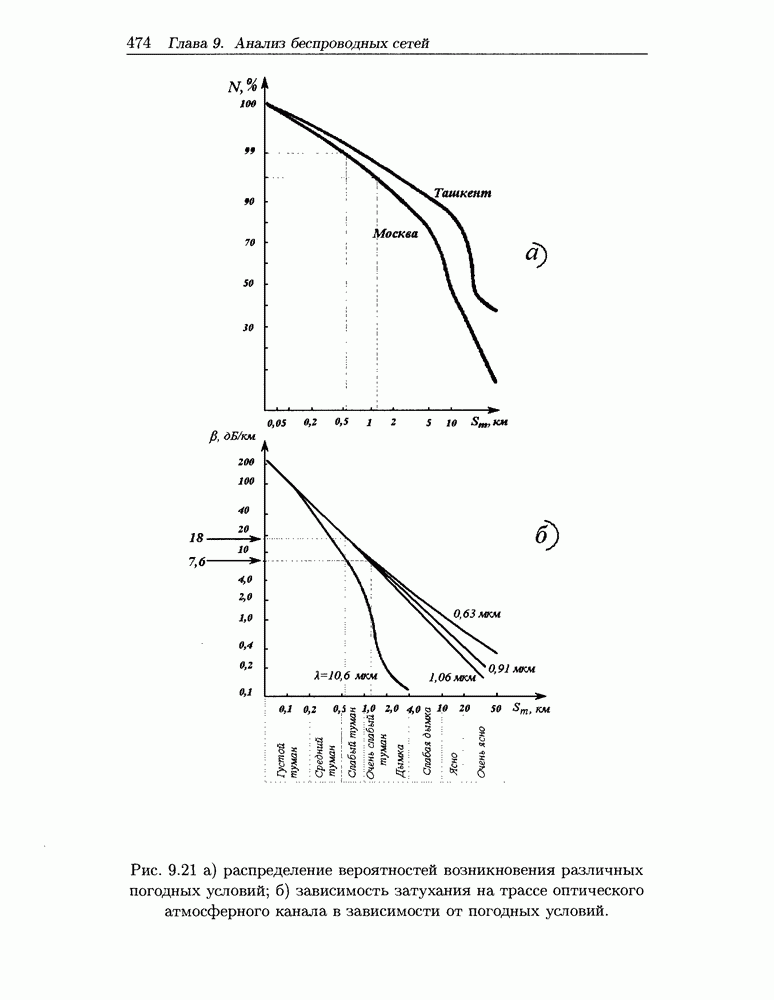
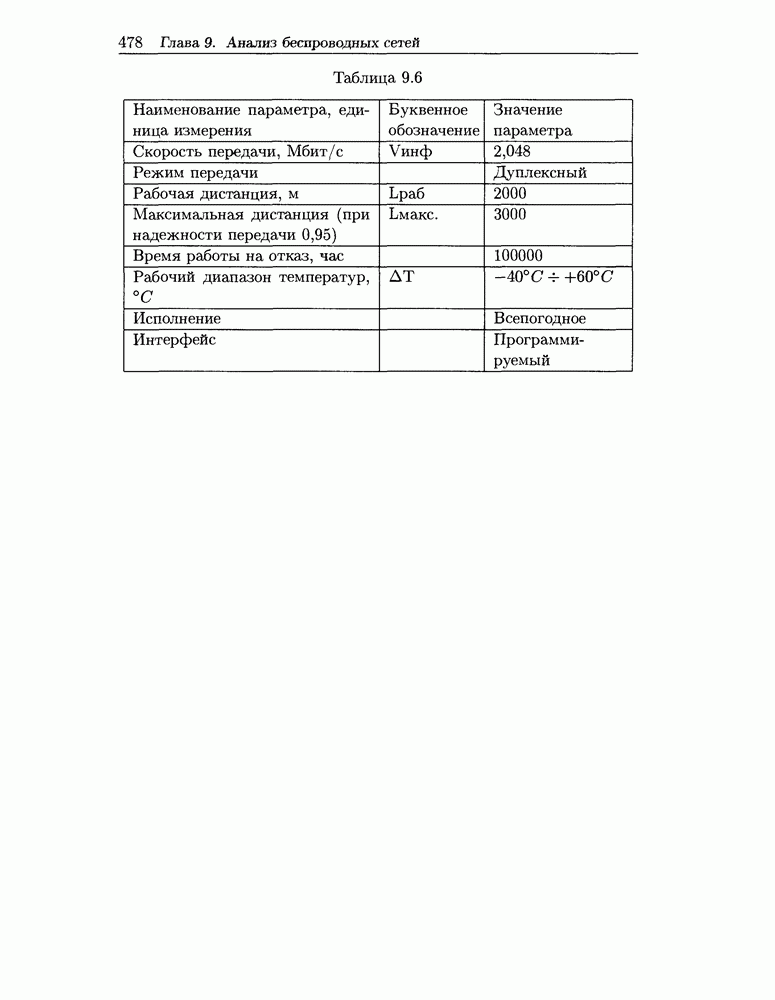
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература