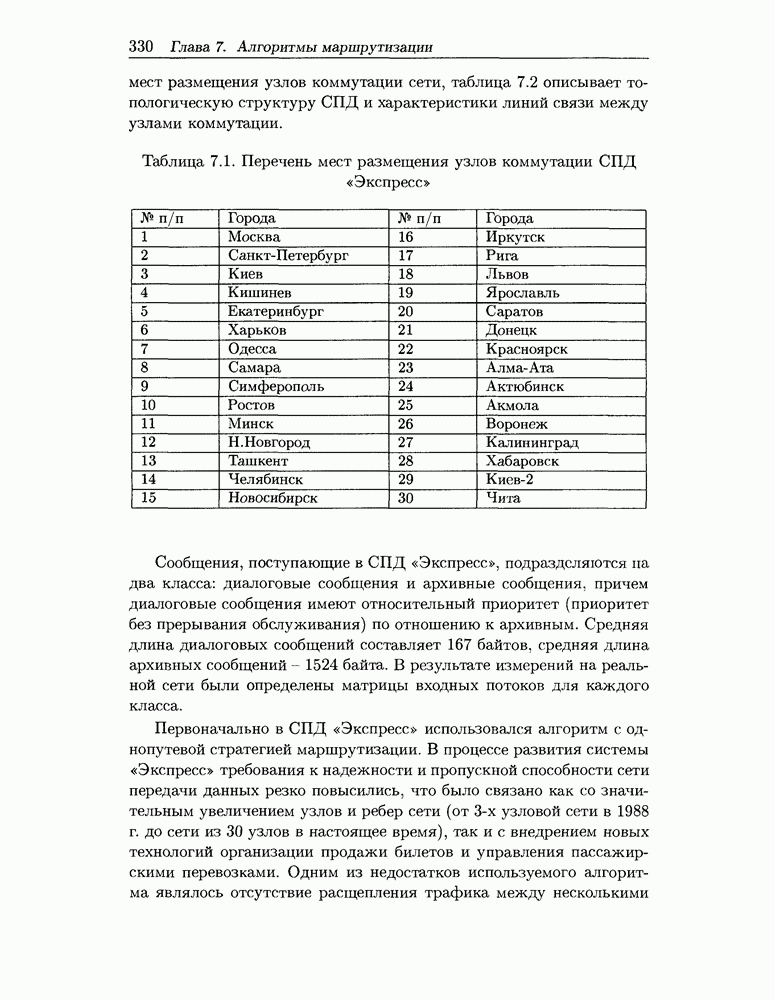
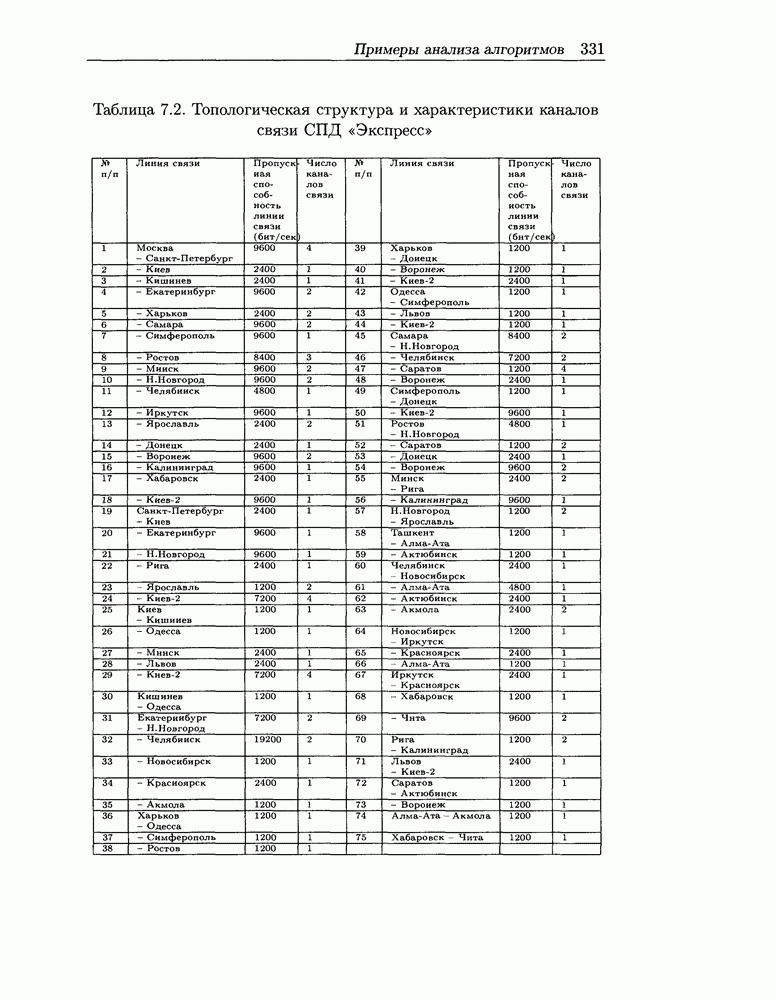
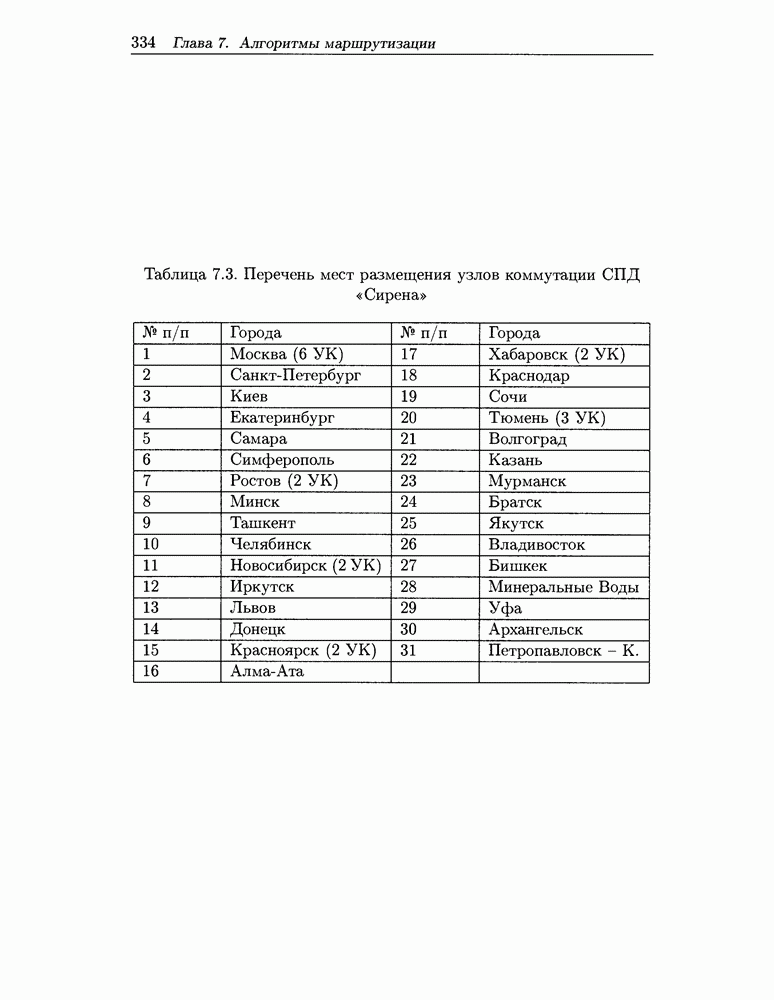
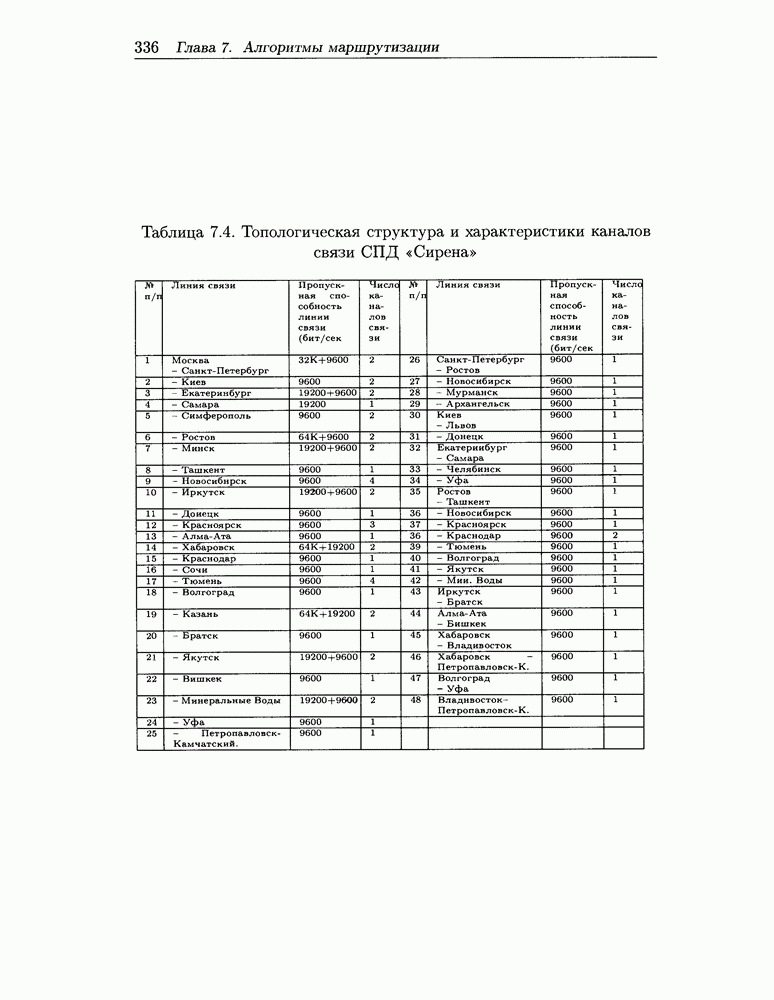
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.8 Приоритетные системы массового обслуживания
Во всех рассмотренных выше СМО предполагалось, что все запросы, поступающие в систему - однородные, то есть, они имеют один и тот же закон распределения времени обслуживания и обслуживаются в системе согласно общей дисциплины выбора из очереди. Однако, во многих реальных системах запросы, поступающие в систему, неоднородны как по распределению времени обслуживания, так и по их ценности для системы и, следовательно, праву претендовать на первоочередное обслуживание в момент освобождения прибора. Такие модели исследуются в рамках теории приоритетных СМО. Эта теория довольно хорошо развита и ее изложению посвящено немало монографий (см., например, [68], [69], [13], и т.д.). Здесь мы ограничимся кратким описанием приоритетных систем и рассмотрим одну систему.
Рассмотрим однолинейную СМО с ожиданием. На вход системы поступают  независимых простейших потоков,
независимых простейших потоков,  поток имеет интенсивность
поток имеет интенсивность  . Будем обозначать
. Будем обозначать 
Времена обслуживания запросов из  потока характеризуются функцией распределения
потока характеризуются функцией распределения  с преобразованием Лапласа - Стилтьеса
с преобразованием Лапласа - Стилтьеса  и конечными начальными моментами
и конечными начальными моментами 
Запросы из  потока назовем запросами приоритета к.
потока назовем запросами приоритета к.
Считаем, что запросы из  потока более приоритетны, чем запросы из
потока более приоритетны, чем запросы из  потока, если
потока, если  Приоритетность проявляется в том, что в момент окончания обслуживания следующим на обслуживание выбирается из очереди запрос, имеющий максимальный приоритет. Запросы, имеющие один и тот же приоритет, выбираются согласно установленной дисциплине обслуживания, например, согласно дисциплине FIFO.
Приоритетность проявляется в том, что в момент окончания обслуживания следующим на обслуживание выбирается из очереди запрос, имеющий максимальный приоритет. Запросы, имеющие один и тот же приоритет, выбираются согласно установленной дисциплине обслуживания, например, согласно дисциплине FIFO.
Рассматриваются различные варианты поведения системы в ситуации, когда во время обслуживания запроса некоторого приоритета в систему поступает запрос более высокого приоритета.
Система называется СМО с относительным приоритетом, если поступление такого запроса не прерывает обслуживание запроса. Если же такое прерывание происходит, то система называется СМО с абсолютным приоритетом. В этом случае, однако, требуется уточнить дальнейшее поведение запроса, обслуживание которого оказалось прерванным. Различают следующие варианты: прерванный запрос уходит из системы и теряется; прерванный запрос возвращается в очередь и продолжает обслуживание с места прерывания после ухода из системы всех запросов, имеющих более высокий приоритет; прерванный запрос возвращается в очередь и начинает обслуживание заново после ухода из системы всех запросов, имеющих более высокий приоритет. Прерванный запрос обслуживается прибором после ухода из системы всех запросов, имеющих более высокий приоритет, в течение времени, имеющего прежнее или некоторое другое распределение. Возможен вариант, когда требуемое время обслуживания в последующих попытках идентично времени, которое требовалось для полного обслуживания данного запроса в первой попытке.
Таким образом, имеется достаточно большое число вариантов поведения системы с приоритетом, с которыми можно ознакомиться в вышеупомянутых книгах. Общим в анализе всех систем с приоритетами является использование понятия периода занятости системы запросами приоритета к и выше. При этом основным методом исследования этих систем является метод введения дополнительного события, кратко описанный в разделе 6.
Проиллюстрируем особенности нахождения характеристик систем с приоритетами на примере системы, описанной в начале раздела. Будем считать, что это система с относительным приоритетом и найдем стационарное распределения времени  ожидания запроса приоритета
ожидания запроса приоритета  если бы он поступил в систему в момент времени t (так называемого виртуального времени ожидания), для системы с относительными приоритетами.
если бы он поступил в систему в момент времени t (так называемого виртуального времени ожидания), для системы с относительными приоритетами.
Обозначим

Условием существования этих пределов является выполнение неравенства
 (1.115)
(1.115)
где величина  вычисляется по формуле:
вычисляется по формуле: 
Обозначим также  .
.
Утверждение 21. Преобразование Лапласа - Стилтьеса  стационарного распределения виртуального времени ожидания запроса приоритета к определяется следующим образом:
стационарного распределения виртуального времени ожидания запроса приоритета к определяется следующим образом:

где функции  задаются формулой:
задаются формулой:
 (1.117)
(1.117)
а функции  находятся как решения функциональных уравнений:
находятся как решения функциональных уравнений:

Доказательство. Заметим, что функция  представляет собой преобразование Лапласа - Стилтьеса распределения длины периода занятости системы запросами приоритета I и выше (то есть, интервала времени с момента поступления в пустую систему запроса приоритета I и выше и до первого после этого момента, когда система окажется свободной от присутствия запросов приоритета I и выше). Доказательство того, что функция
представляет собой преобразование Лапласа - Стилтьеса распределения длины периода занятости системы запросами приоритета I и выше (то есть, интервала времени с момента поступления в пустую систему запроса приоритета I и выше и до первого после этого момента, когда система окажется свободной от присутствия запросов приоритета I и выше). Доказательство того, что функция  удовлетворяет уравнению (1.118), почти дословно повторяет доказательство Утверждения 13. Отметим лишь, что величина есть вероятность того, что период занятости системы запросами приоритета I и выше начинается с прихода запроса приоритета
удовлетворяет уравнению (1.118), почти дословно повторяет доказательство Утверждения 13. Отметим лишь, что величина есть вероятность того, что период занятости системы запросами приоритета I и выше начинается с прихода запроса приоритета  а величина
а величина  трактуется как вероятность ненаступления катастрофы и запросов приоритета I и выше, за периоды занятости, порожденные которыми наступает катастрофа, за время обслуживания запроса приоритета
трактуется как вероятность ненаступления катастрофы и запросов приоритета I и выше, за периоды занятости, порожденные которыми наступает катастрофа, за время обслуживания запроса приоритета  , начавшего данный период занятости.
, начавшего данный период занятости.
Сначала вместо процесса  рассмотрим существенно более простой вспомогательный процесс
рассмотрим существенно более простой вспомогательный процесс  - время, в течение которого ожидал бы начала обслуживания запрос приоритета к,
- время, в течение которого ожидал бы начала обслуживания запрос приоритета к,  если бы он поступил в систему в момент времени t и после этого в систему не поступало запросов более высокого приоритета.
если бы он поступил в систему в момент времени t и после этого в систему не поступало запросов более высокого приоритета.
Пусть  - преобразование Лапласа - Стилтьеса распределения случайной величины
- преобразование Лапласа - Стилтьеса распределения случайной величины  . Покажем, что функция
. Покажем, что функция  определяется следующим образом:
определяется следующим образом:
 (1.119)
(1.119)
где

 - вероятность того, что система пуста в момент времени
- вероятность того, что система пуста в момент времени  - вероятность того, что в интервале
- вероятность того, что в интервале  началось обслуживание запроса приоритета
началось обслуживание запроса приоритета 
Для доказательства (1.119) применим метод введения дополнительного события. Пусть независимо от работы системы поступает простейший поток катастроф интенсивности s. Каждый запрос назовем «плохим», если во время его обслуживания поступает катастрофа, и «хорошим» - в противном случае. Как следует из утверждений 5 и 6, поток плохих запросов приоритета к и выше является простейшим с интенсивностью 
Введем событие A(s,t) - за время t в систему не поступали плохие запросы приоритета к и выше. В силу утверждения 1 вероятность этого события подсчитывается как:

Подсчитаем эту вероятность иначе. Событие A(s,t) является объединением трех несовместных событий 
Событие  состоит в том, что катастрофы не поступили ни за время t, ни за время
состоит в том, что катастрофы не поступили ни за время t, ни за время  При этом, естественно, за время t в систему поступали только хорошие запросы приоритета к и выше. Вероятность события
При этом, естественно, за время t в систему поступали только хорошие запросы приоритета к и выше. Вероятность события  очевидно, равна
очевидно, равна 
Событие  состоит в том, что катастрофа поступила в интервале
состоит в том, что катастрофа поступила в интервале  , но в момент поступления система была пуста, а за время
, но в момент поступления система была пуста, а за время  не поступило плохих запросов приоритета к и выше.
не поступило плохих запросов приоритета к и выше.
Вероятность события  вычисляется как:
вычисляется как:

Событие  состоит в том, что катастрофа поступила в интервале
состоит в том, что катастрофа поступила в интервале  но в момент ее поступления в системе обслуживался запрос приоритета ниже k, который начал обслуживаться в интервале
но в момент ее поступления в системе обслуживался запрос приоритета ниже k, который начал обслуживаться в интервале  а за время t — и не поступило плохих запросов приоритета k и выше. Вероятность события
а за время t — и не поступило плохих запросов приоритета k и выше. Вероятность события  определяется следующим образом:
определяется следующим образом:

Поскольку событие  есть сумма трех несовместных событий, то его вероятность есть сумма вероятностей этих событий. Поэтому
есть сумма трех несовместных событий, то его вероятность есть сумма вероятностей этих событий. Поэтому

Приравнивая два полученных выражения для вероятности  и умножая обе части равенства на
и умножая обе части равенства на  после несложных преобразований получаем (1.119)
после несложных преобразований получаем (1.119)
Очевидно, что для того, чтобы за время  ожидания запроса, поступившего в момент t не поступило катастрофы, необходимо и достаточно, чтобы за время
ожидания запроса, поступившего в момент t не поступило катастрофы, необходимо и достаточно, чтобы за время  не поступило катастроф и запросов приоритета
не поступило катастроф и запросов приоритета  и выше, таких, что за периоды занятости (запросами приоритета
и выше, таких, что за периоды занятости (запросами приоритета  и выше), порожденные ими, наступает катастрофа. Из этих рассуждениий и вероятностной трактовки преобразования Лапласа - Стилтьеса получаем формулу, дающую связь преобразований
и выше), порожденные ими, наступает катастрофа. Из этих рассуждениий и вероятностной трактовки преобразования Лапласа - Стилтьеса получаем формулу, дающую связь преобразований  в очевидной форме:
в очевидной форме:
 (1.120)
(1.120)
Переходим в (1.120) с учетом (1.119) к пределу при 
Можно показать, что вероятность  удовлетворяет соотношению
удовлетворяет соотношению

откуда в силу свойства 4 преобразования Лапласа - Стилтьеса следует, что

Кроме того, устремляя в (1.119)  с учетом ограниченности функции
с учетом ограниченности функции  для всех действительных
для всех действительных  можно получить рекуррентную процедуру для вычисления интегралов
можно получить рекуррентную процедуру для вычисления интегралов

Из этой процедуры можно получить рекуррентные формулы и для величин

С учетом полученных выражений для величин  , в результате предельного перехода в (1.120) получаем доказываемое соотношение (1.116). Утверждение 21 доказано.
, в результате предельного перехода в (1.120) получаем доказываемое соотношение (1.116). Утверждение 21 доказано.
Обозначим  математическое ожидание виртуального времени ожидания в системе запроса приоритета k.
математическое ожидание виртуального времени ожидания в системе запроса приоритета k.
Следствие. Величины  высчитываются следующим образом:
высчитываются следующим образом:

Доказательство следует из (1.116) с использованием свойства 5 преобразования Лапласа - Стилтьеса.
Отметим, что из систем с абсолютным приоритетом наиболее легко исследуется система с двумя потоками запросов и дообслуживанием прерванных запросов. В этой системе характеристики процесса обслуживания приоритетного потока совершенно не зависят от наличия второго потока и вычисляются по обычным формулам для системы MG1 при интенсивности входящего потока, равной  и распределении
и распределении  времени обслуживания запроса. В свою очередь, характеристики процесса обслуживания неприоритетного потока вычисляются по формулам для ненадежной системы MG1 при интенсивности входящего потока, равной
времени обслуживания запроса. В свою очередь, характеристики процесса обслуживания неприоритетного потока вычисляются по формулам для ненадежной системы MG1 при интенсивности входящего потока, равной  и распределении
и распределении  времени обслуживания запроса. Приход приоритетного запроса здесь трактуется как поломка прибора, а время ремонта прибора распределено как период занятости системы, обслуживающей приоритетные запросы.
времени обслуживания запроса. Приход приоритетного запроса здесь трактуется как поломка прибора, а время ремонта прибора распределено как период занятости системы, обслуживающей приоритетные запросы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
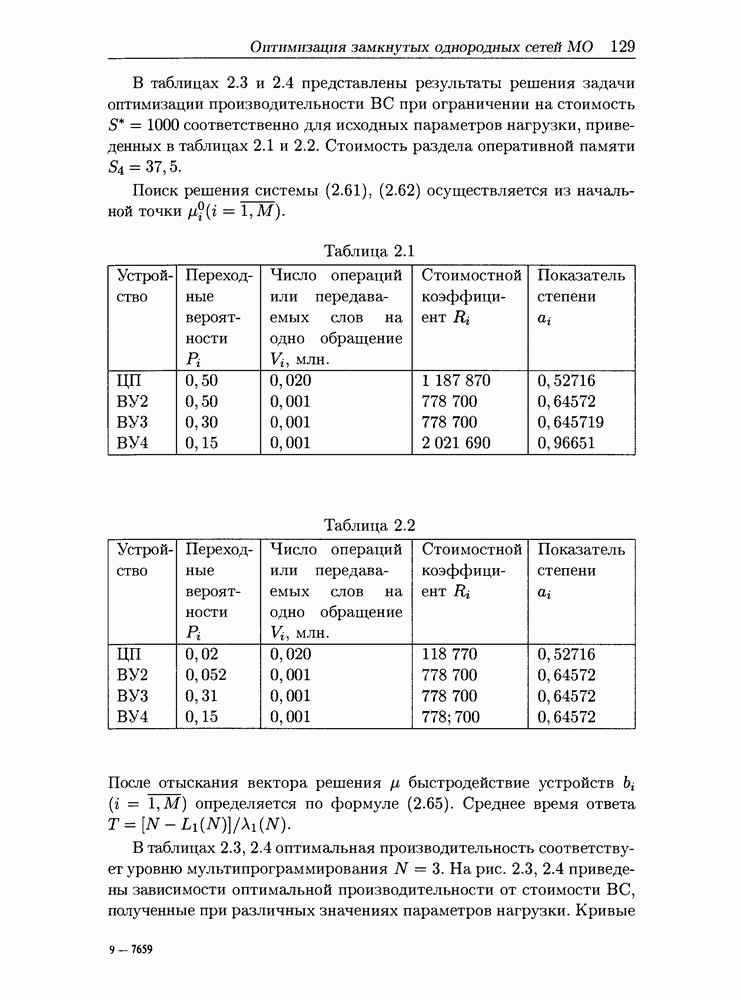
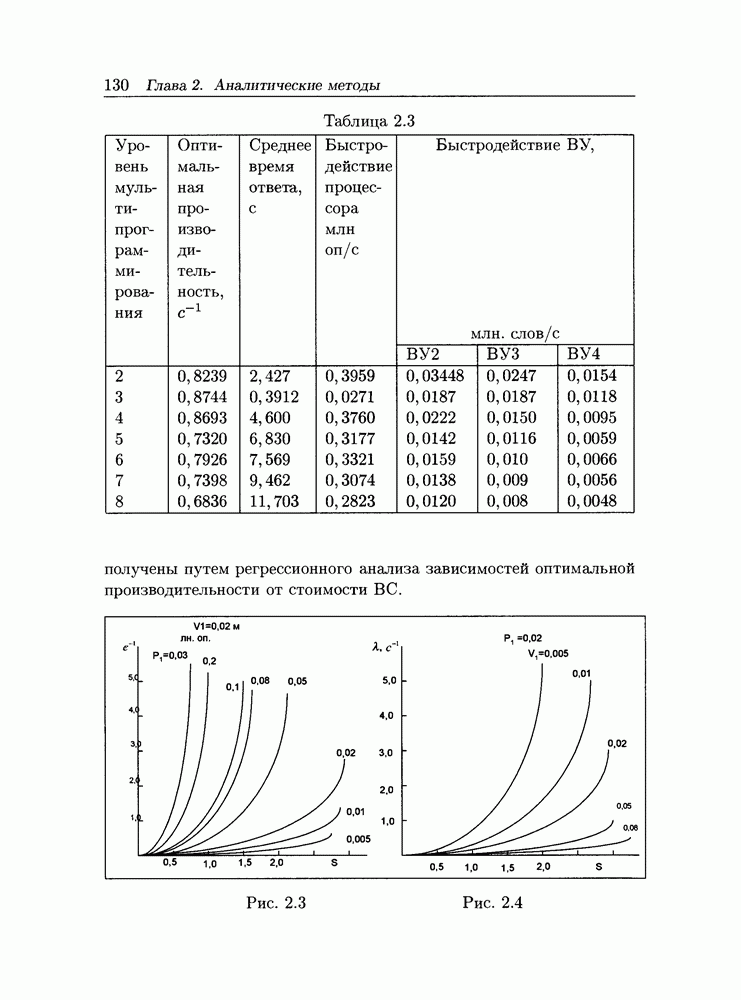
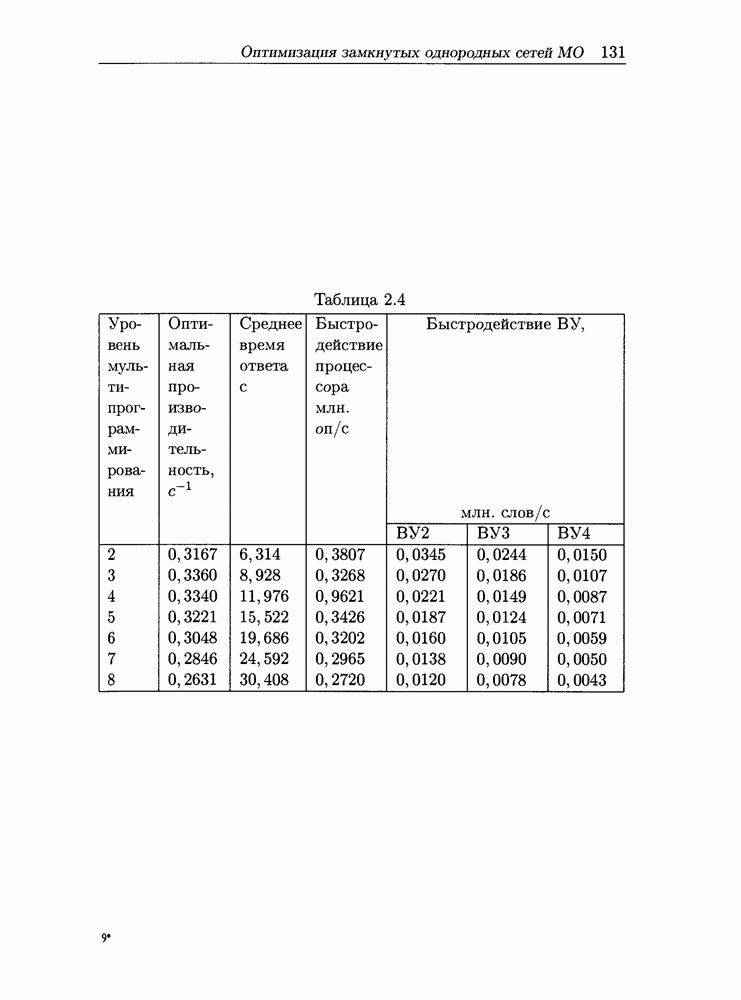
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
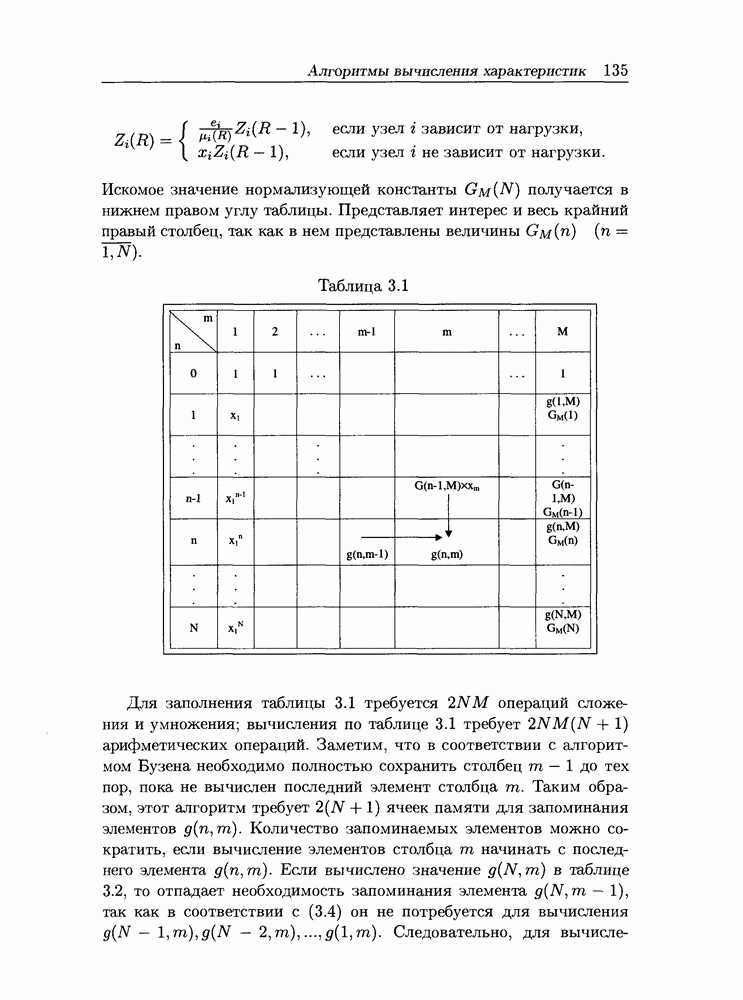
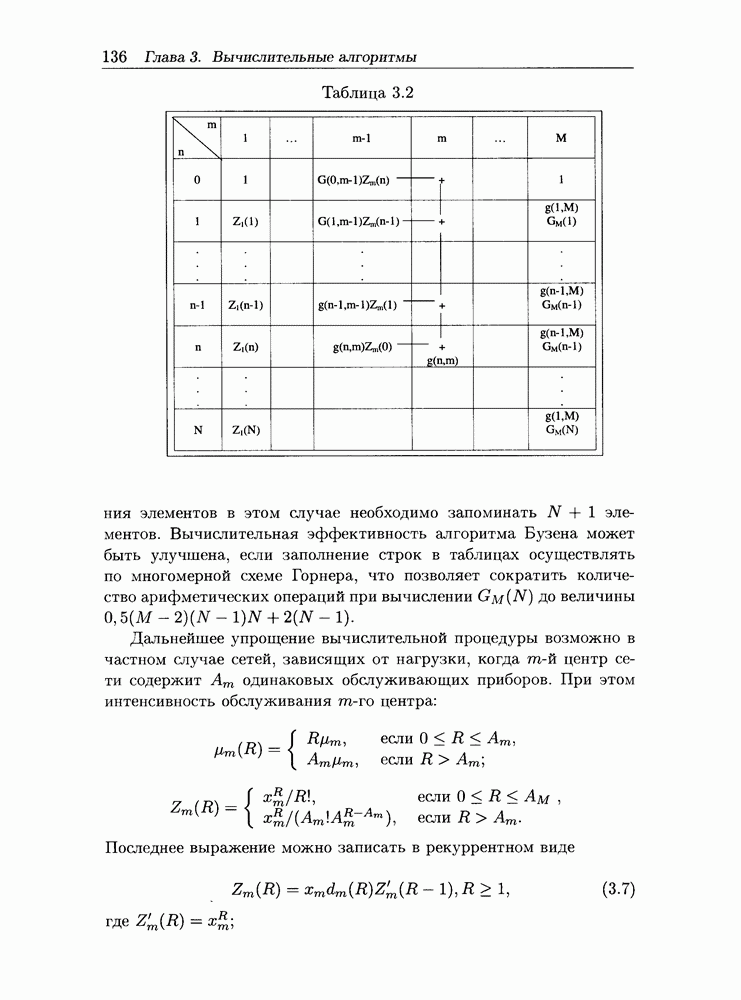
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
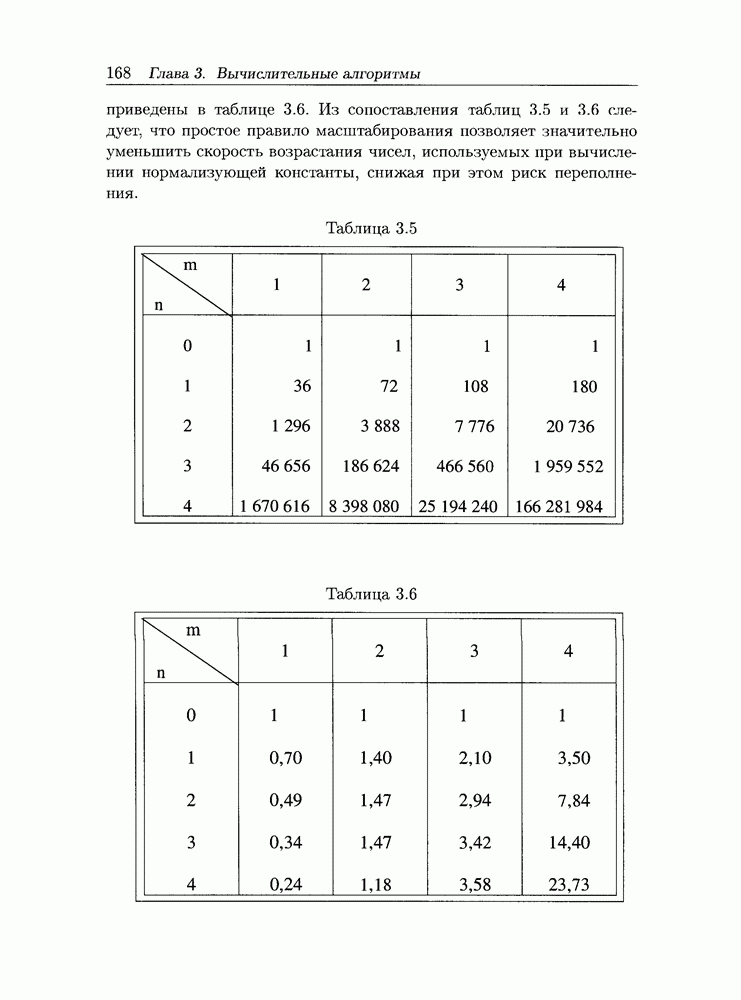
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
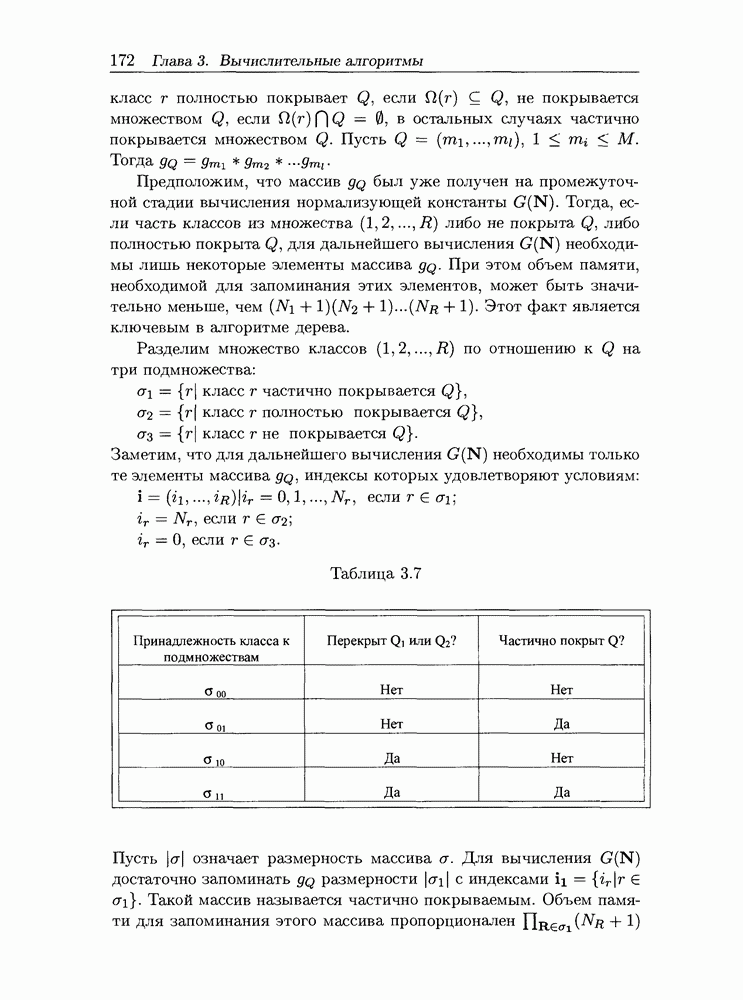
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
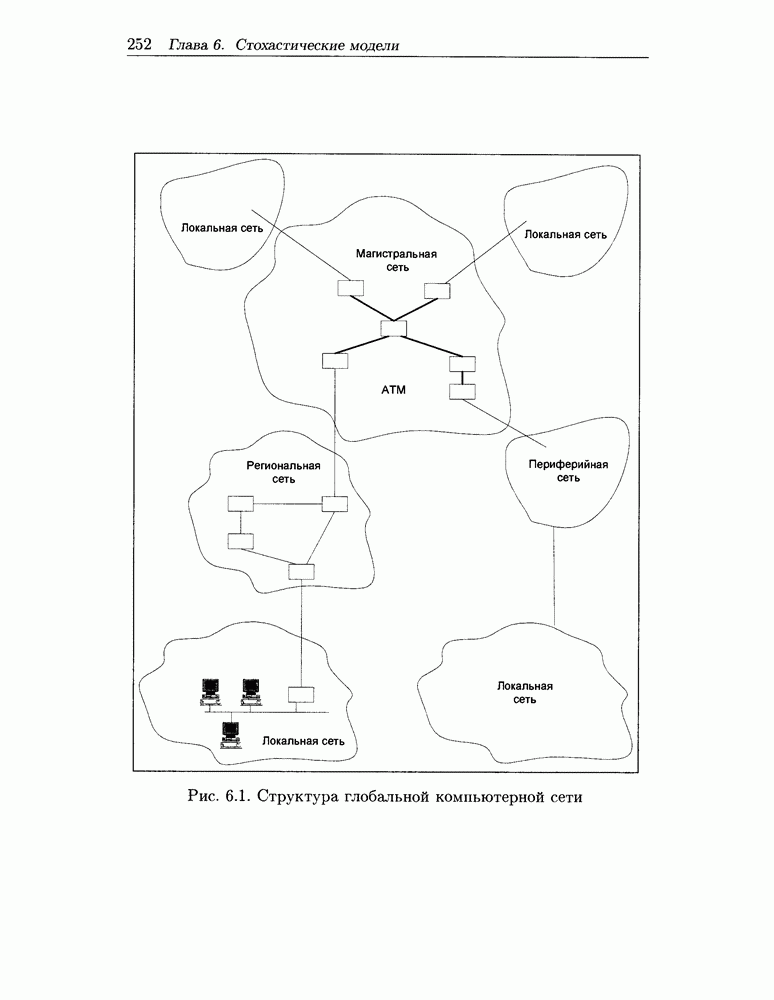
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
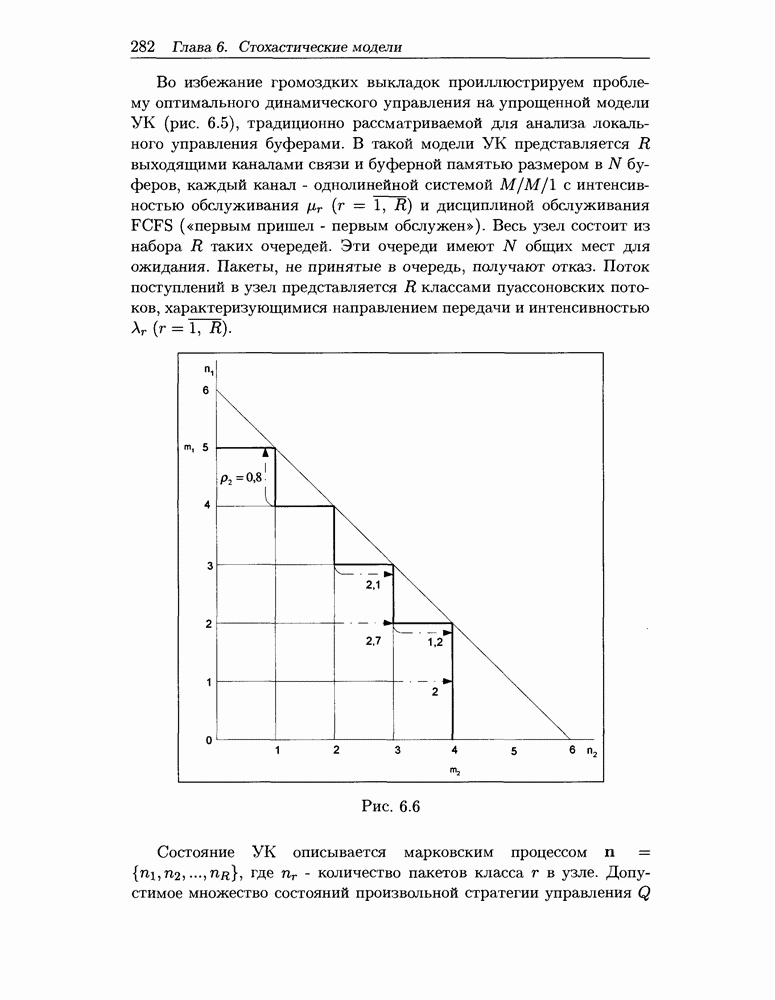
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
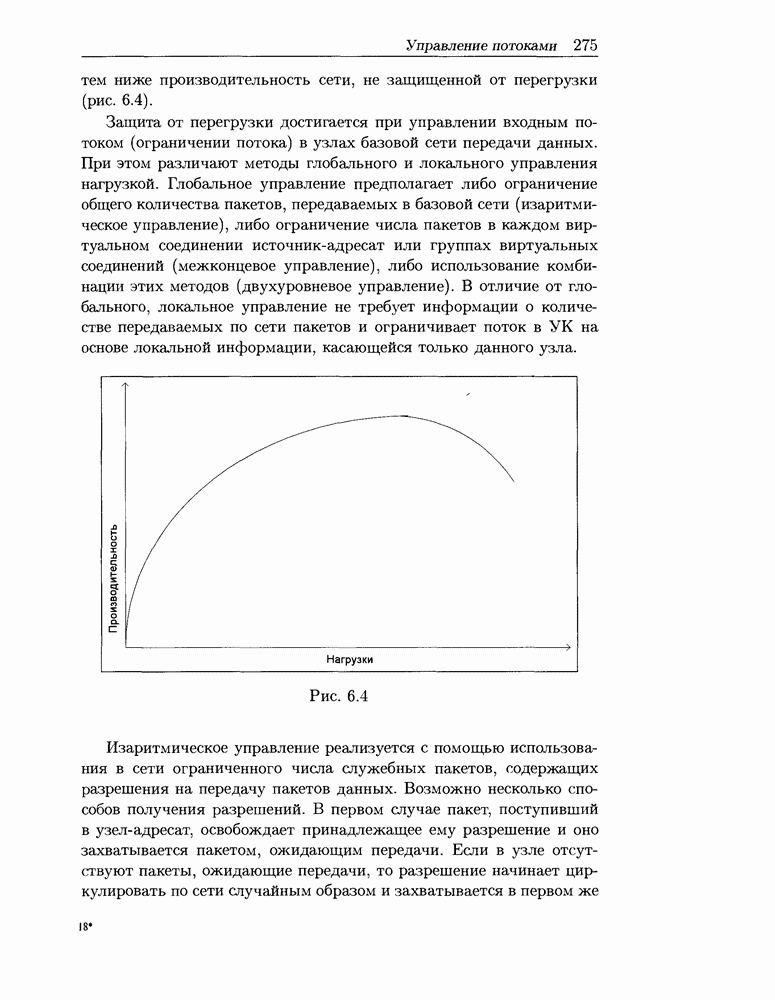
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
- 6.3.3 Локальное управление буферами
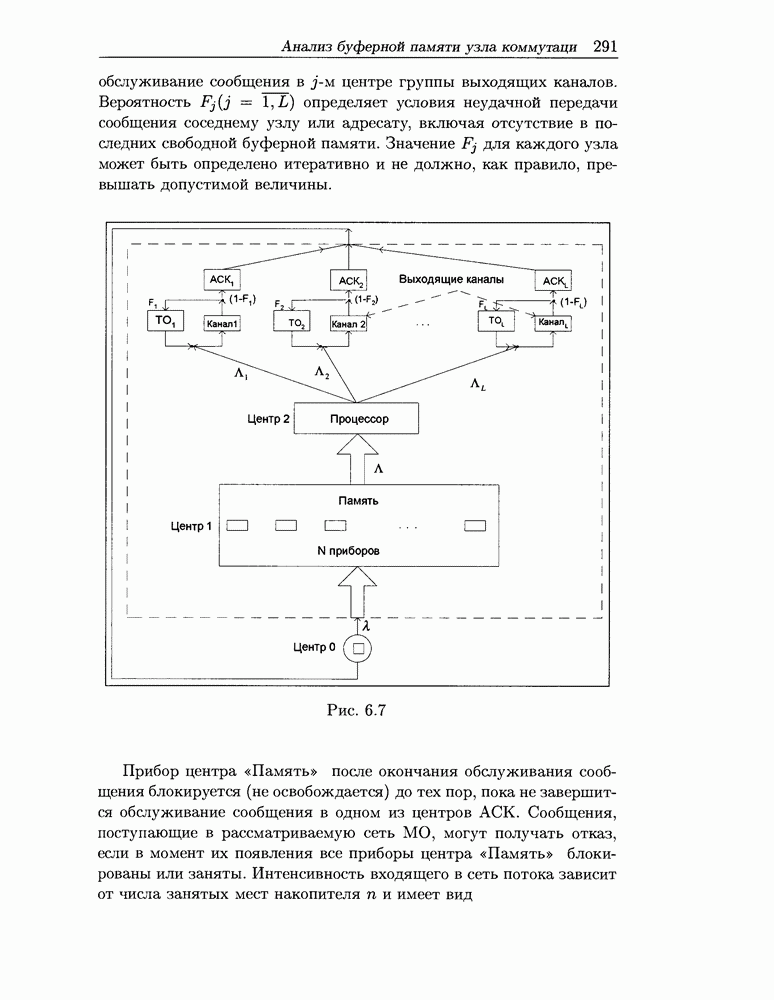
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
- 7.4.2 Анализ развития СПД «Сирена»
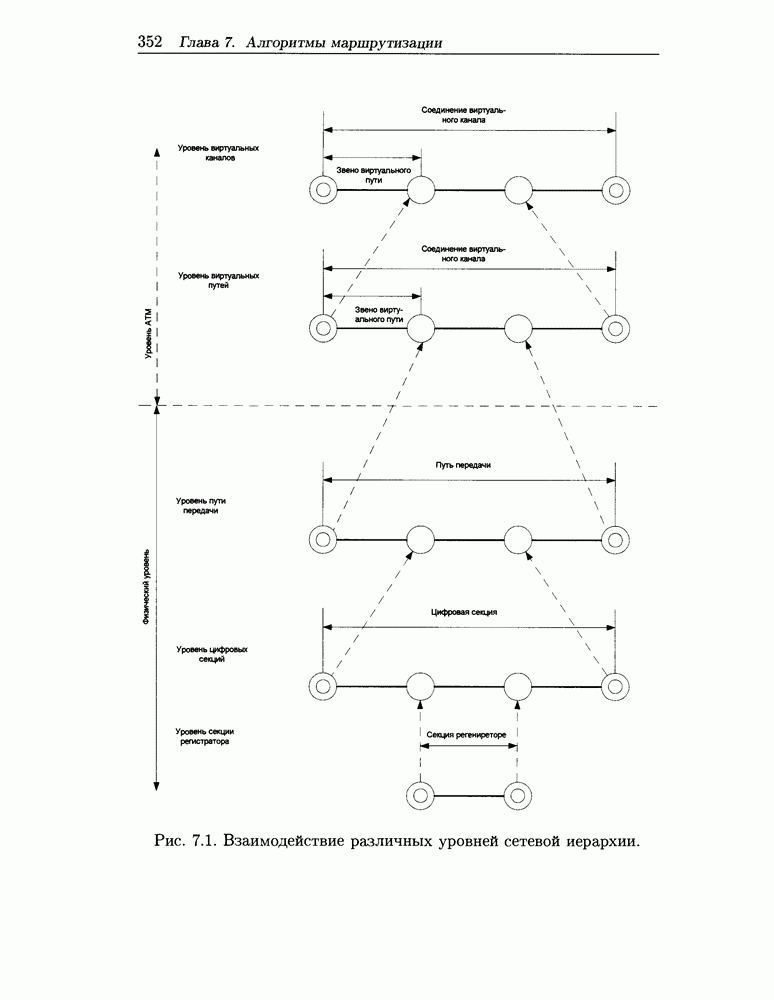
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
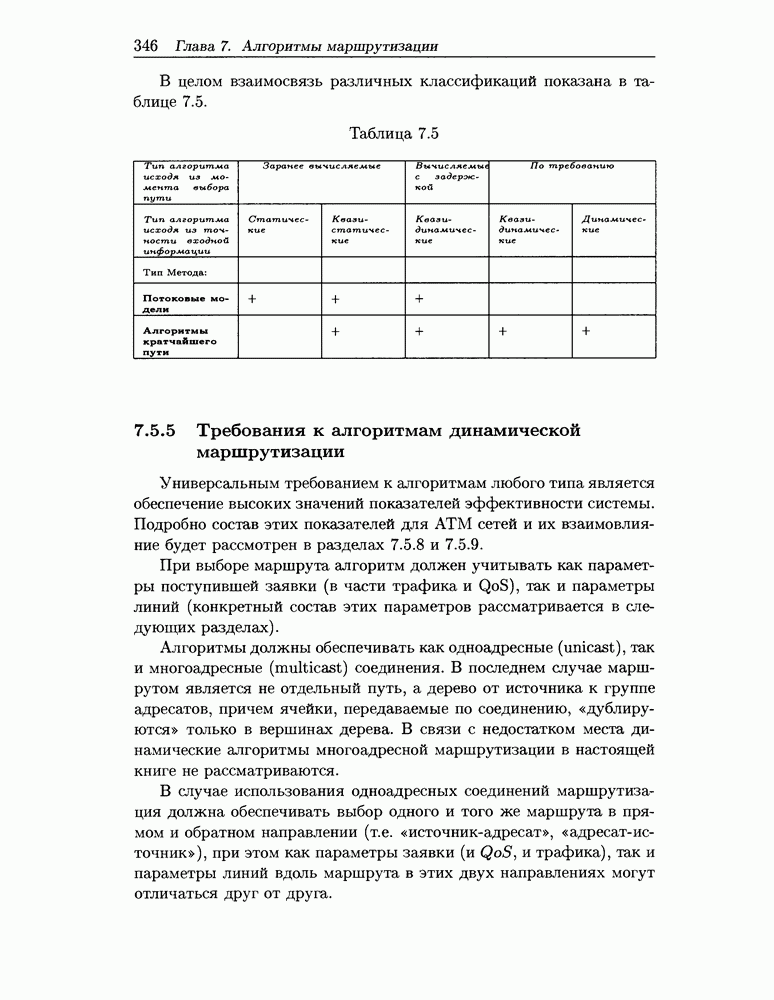
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
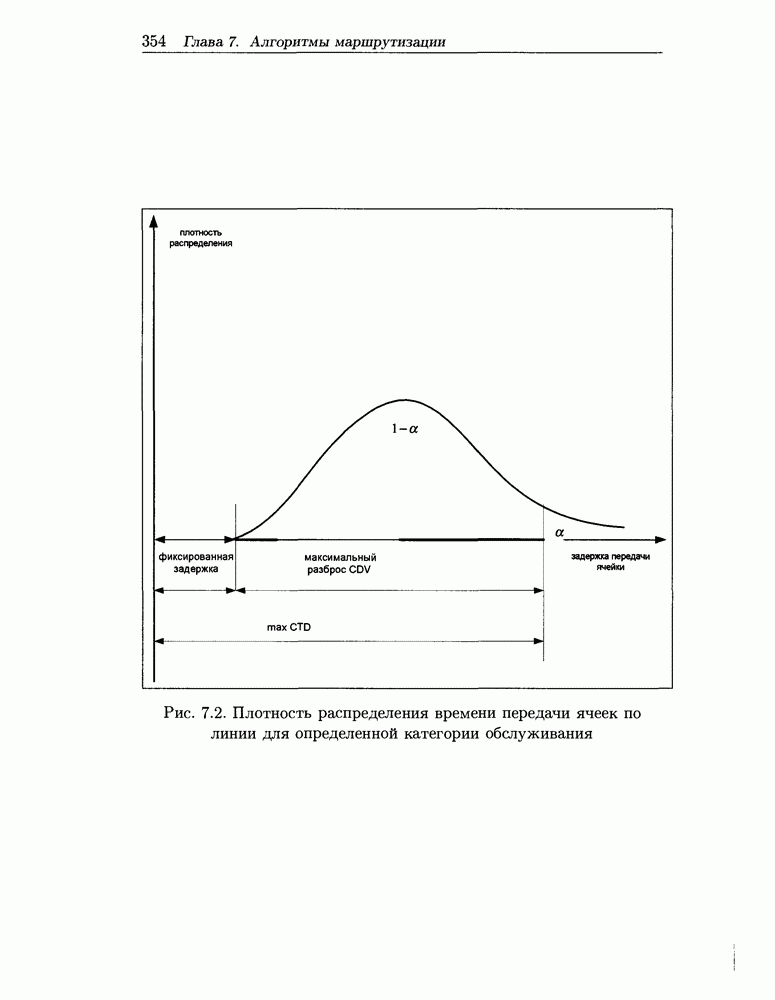
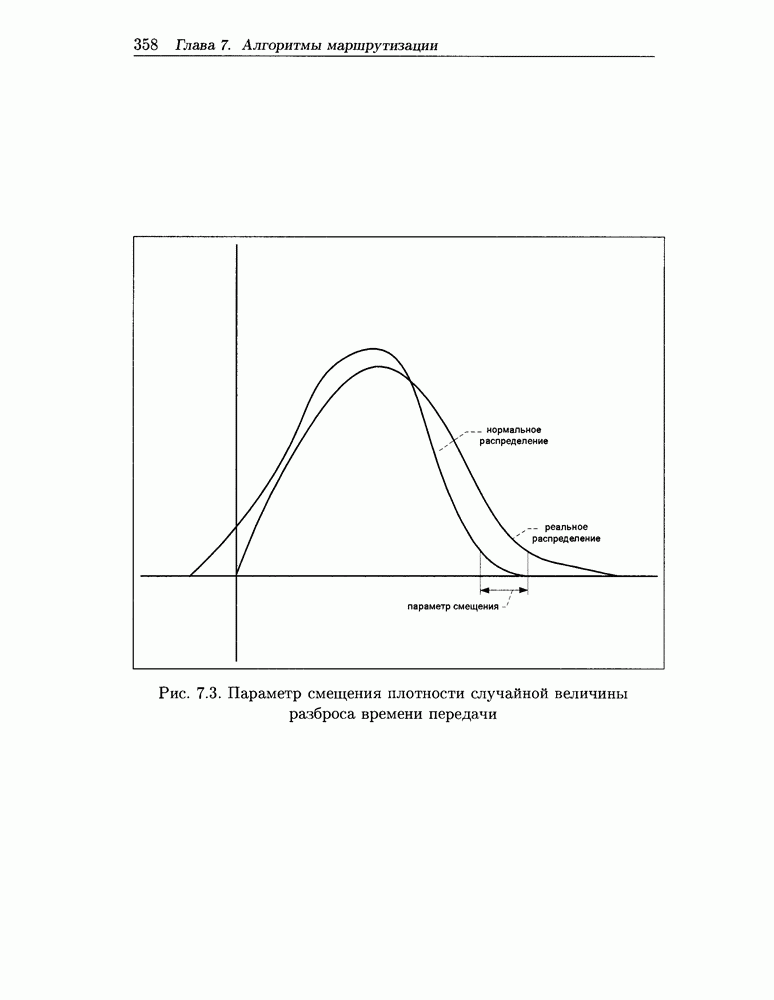
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
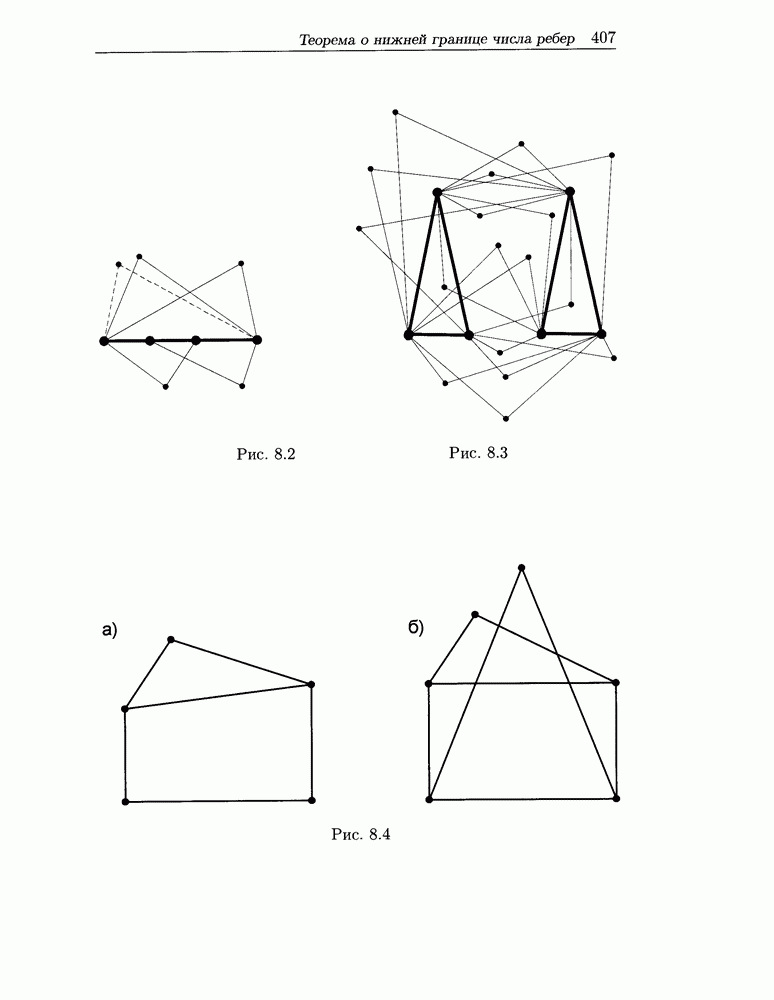
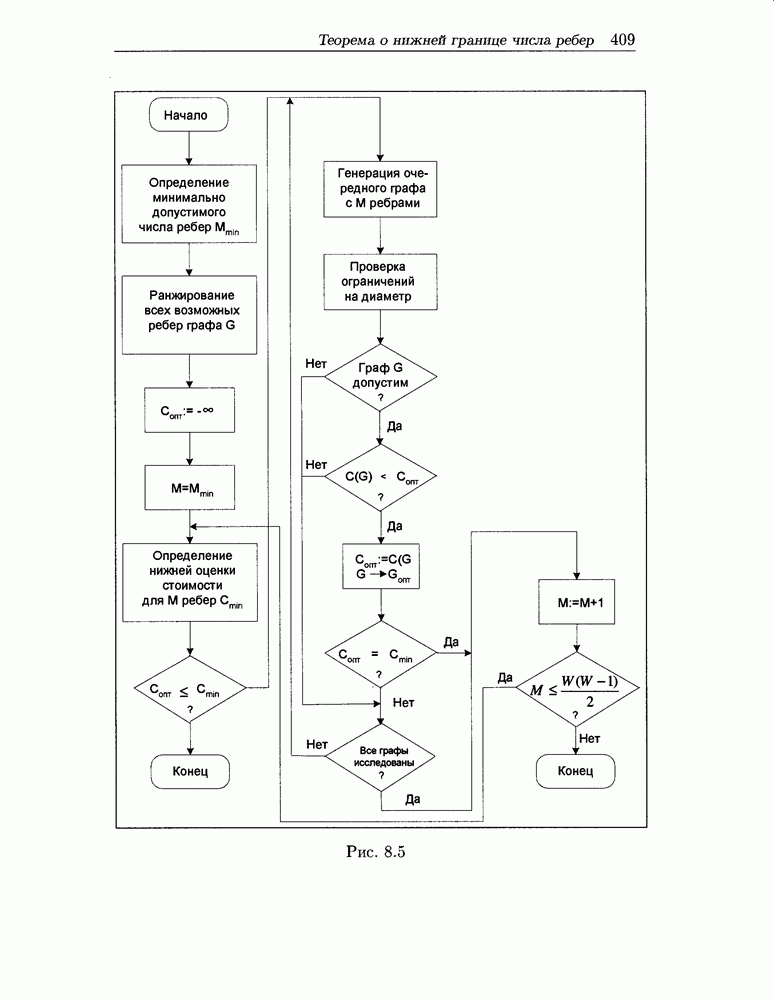
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
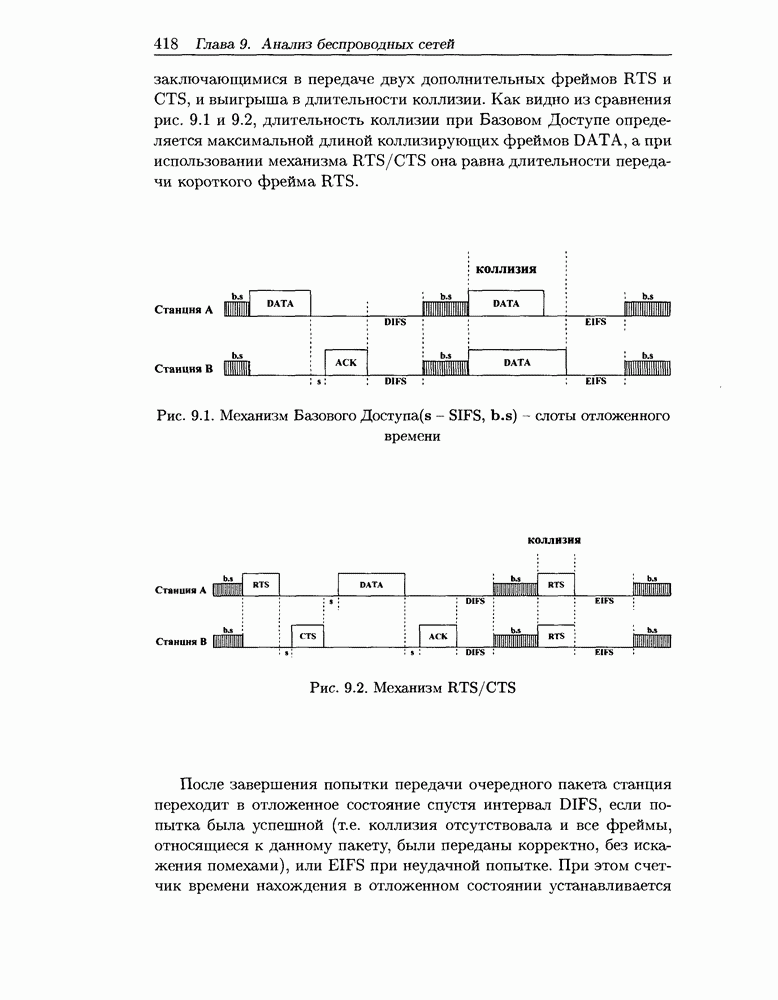
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
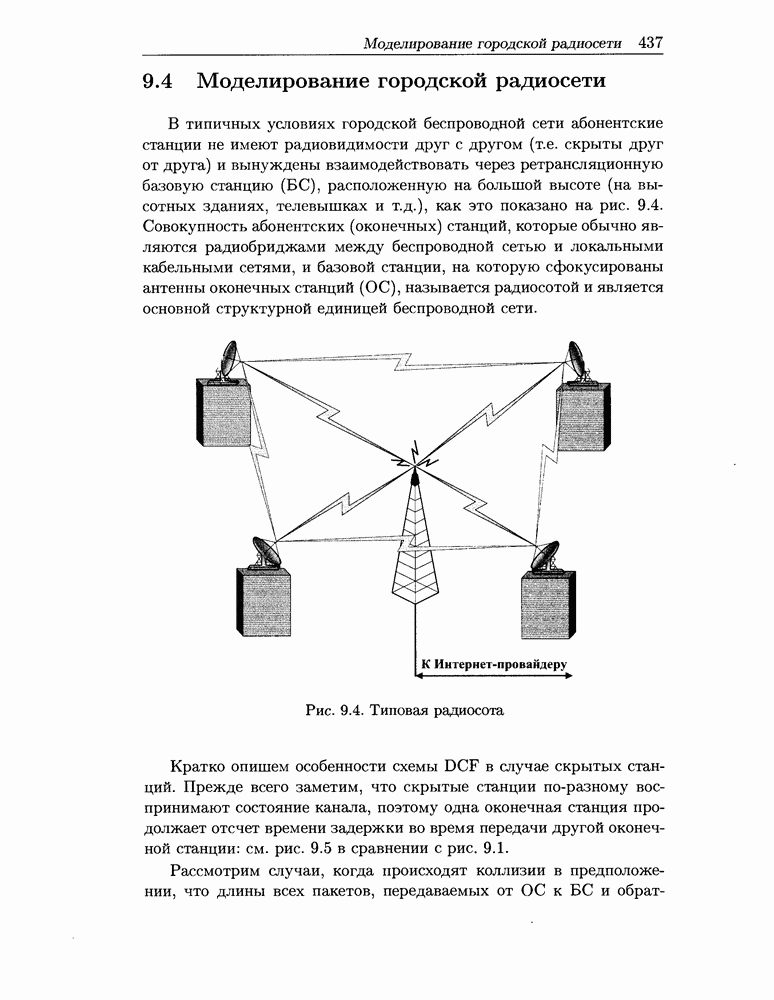
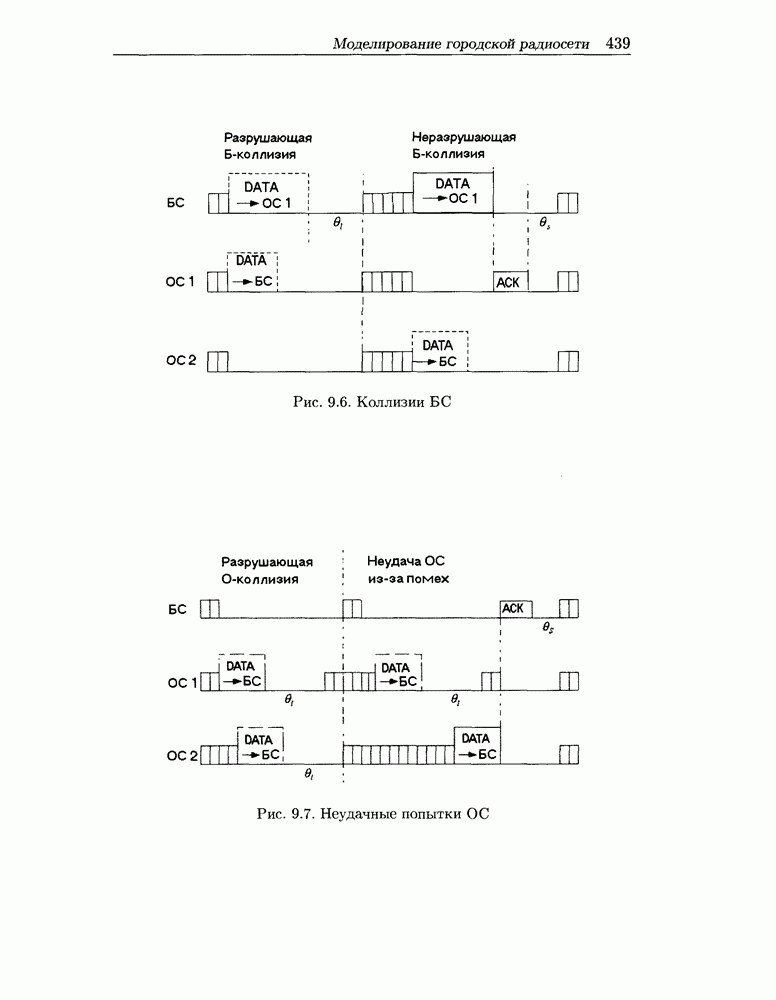
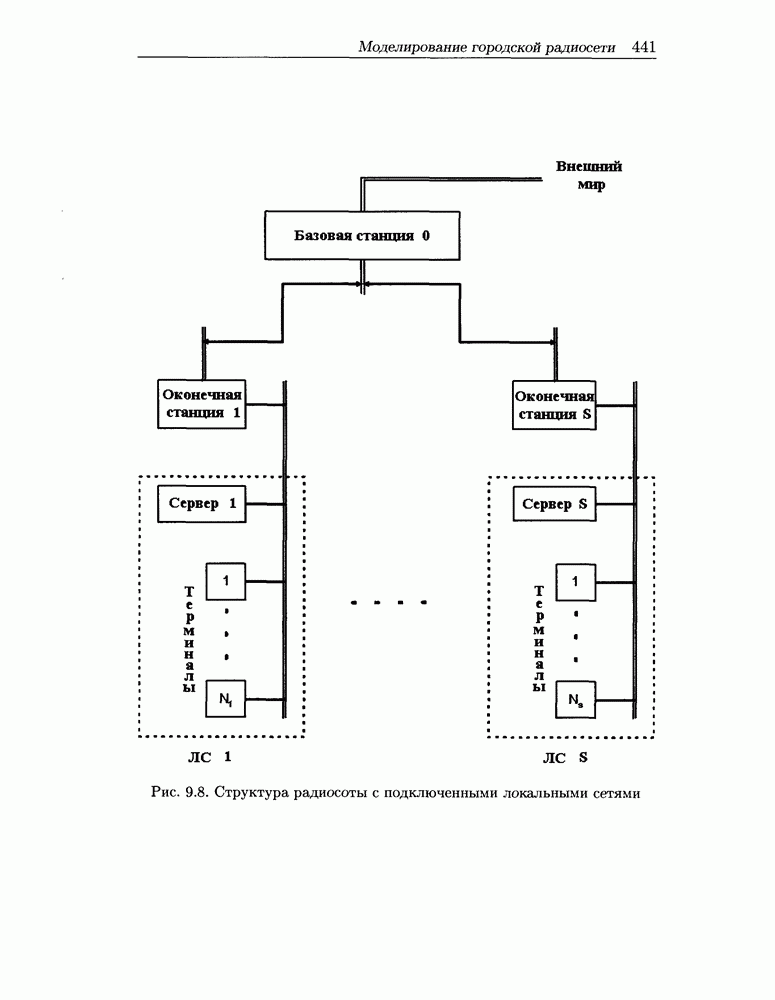
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
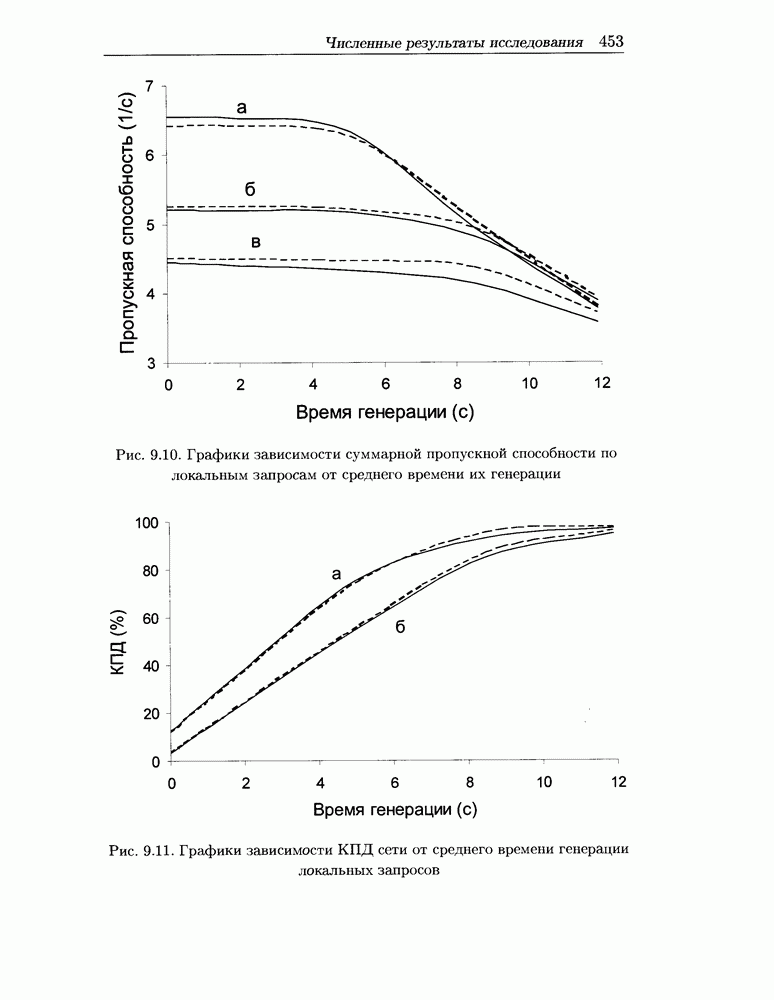
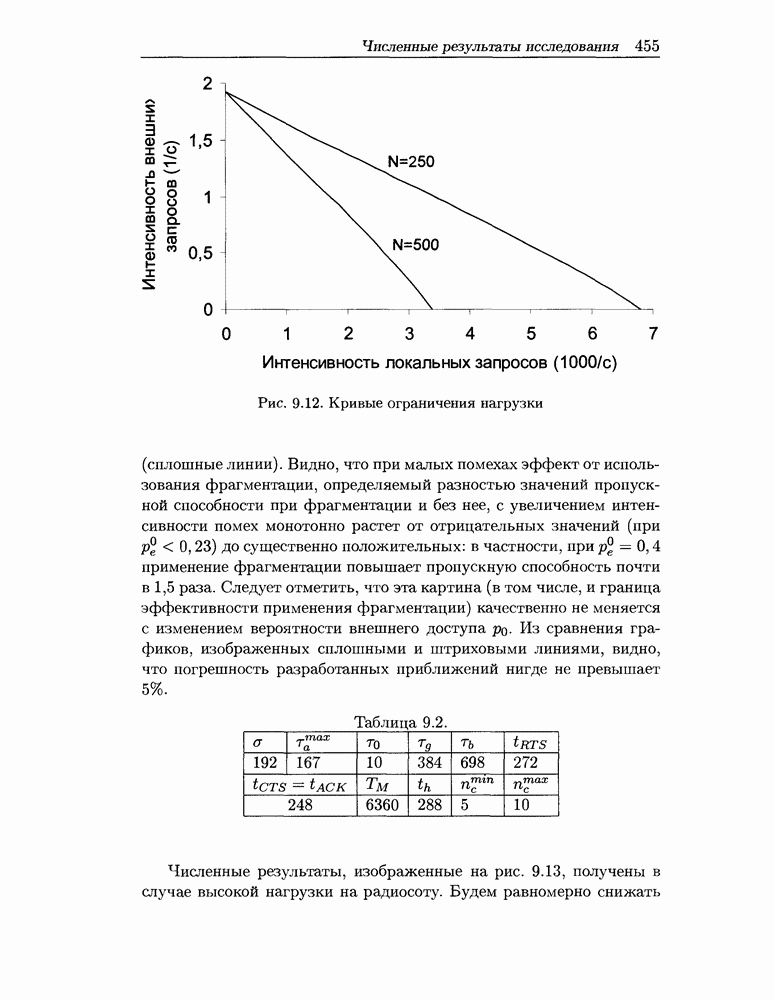
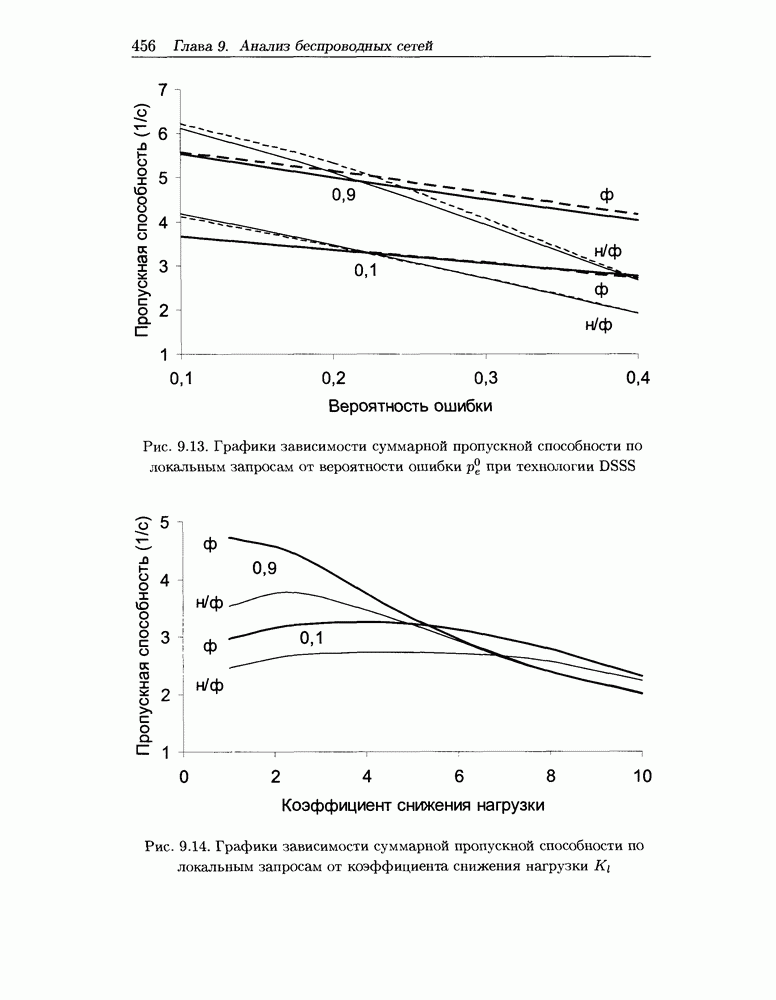
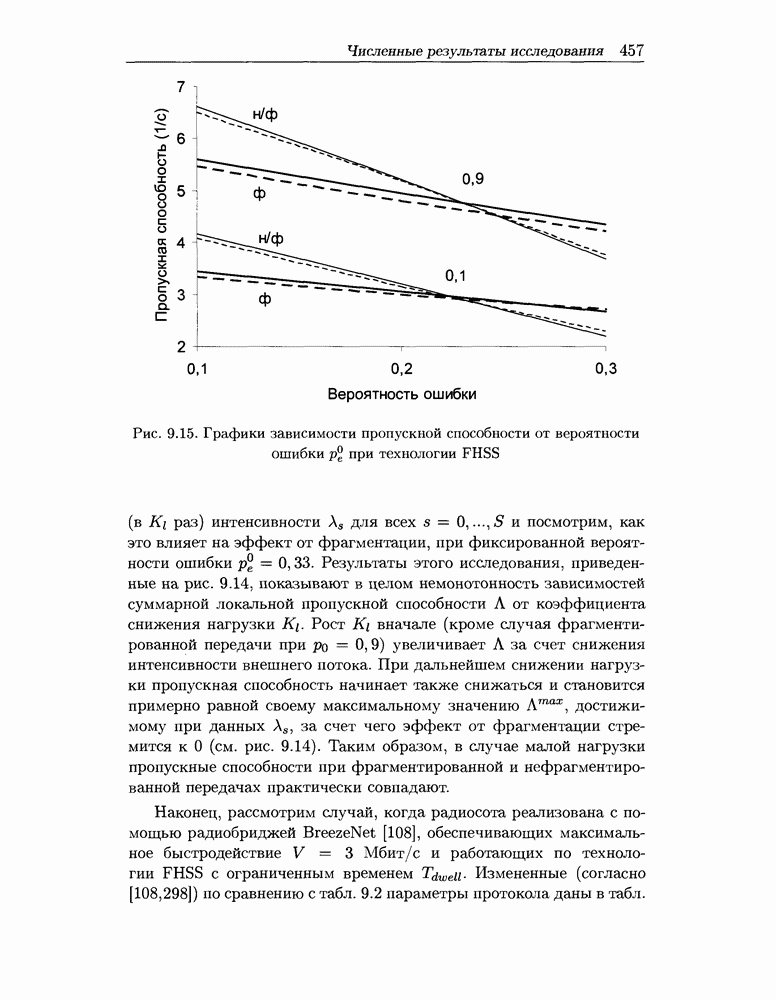
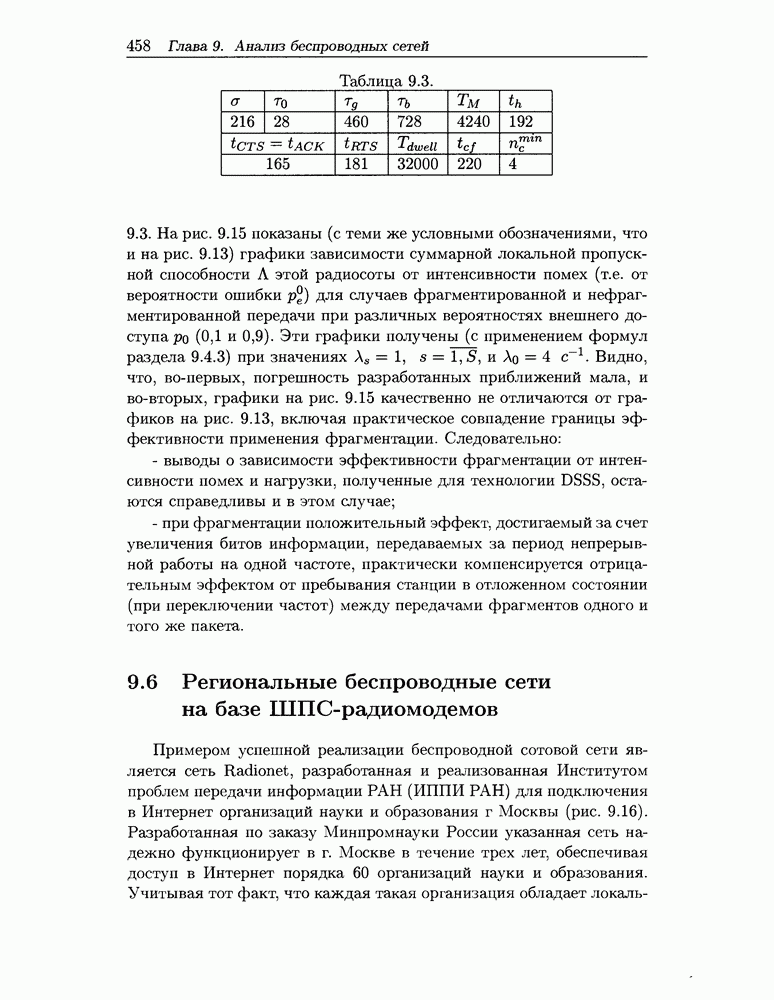
- 9.5 Численные результаты исследования городской радиосоты
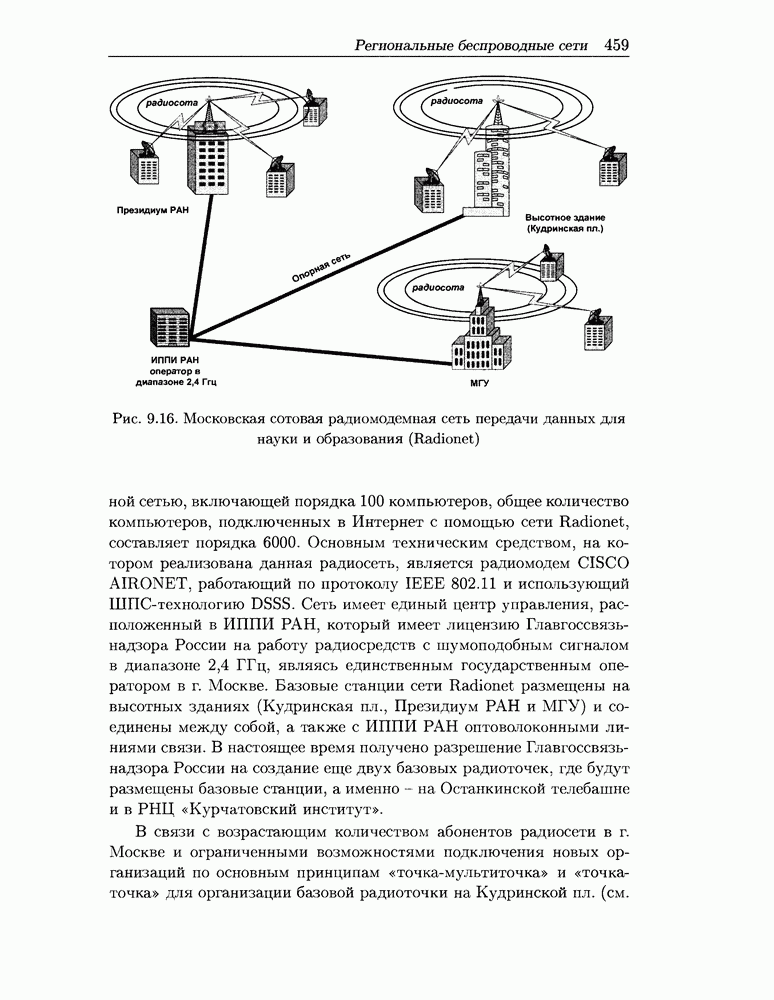
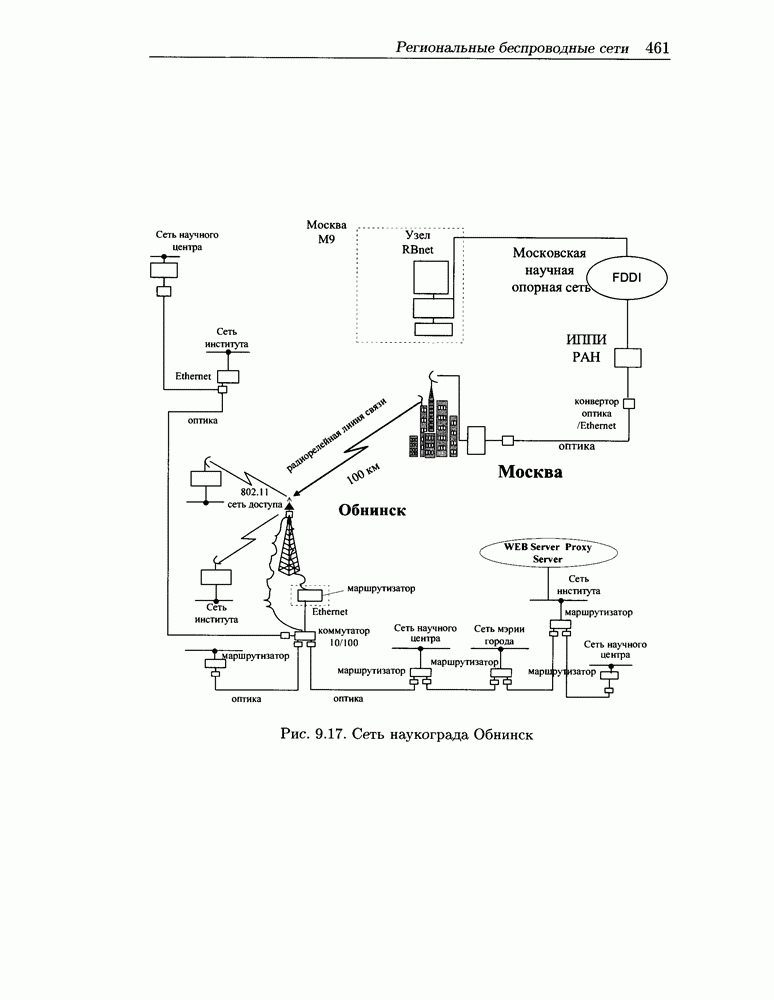
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
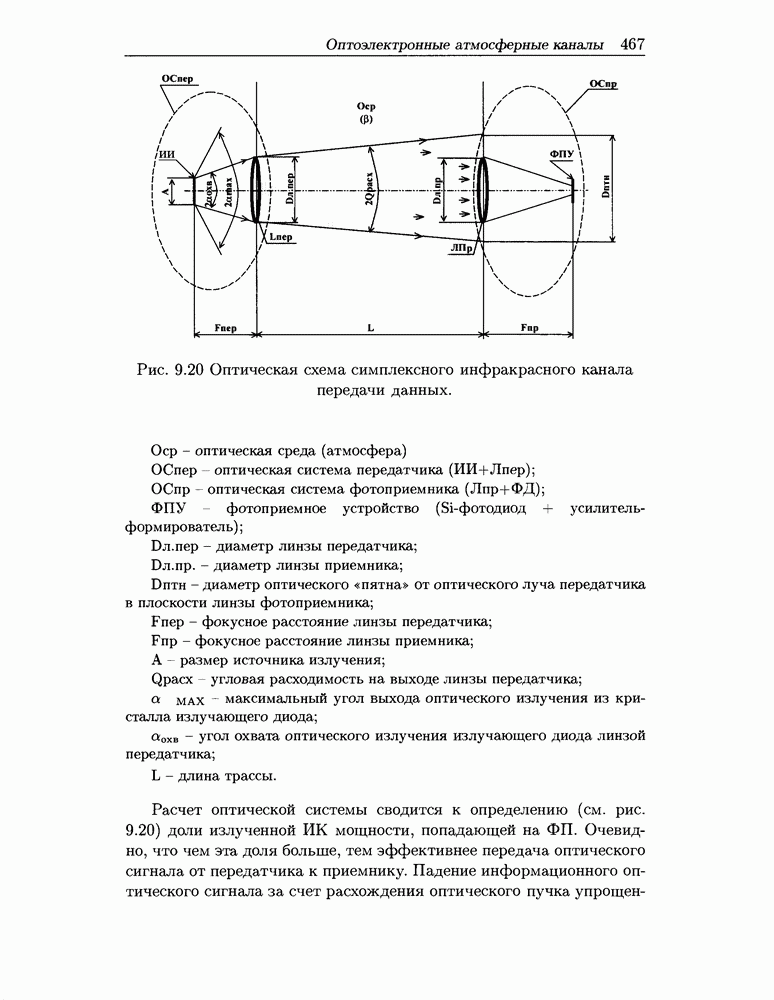
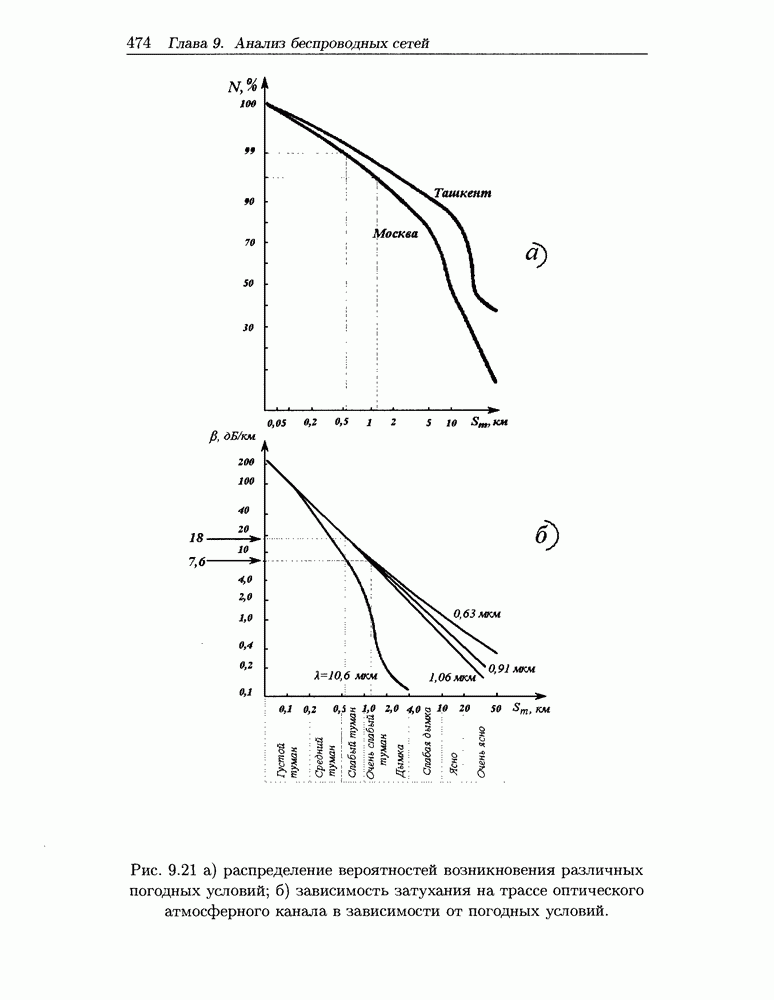
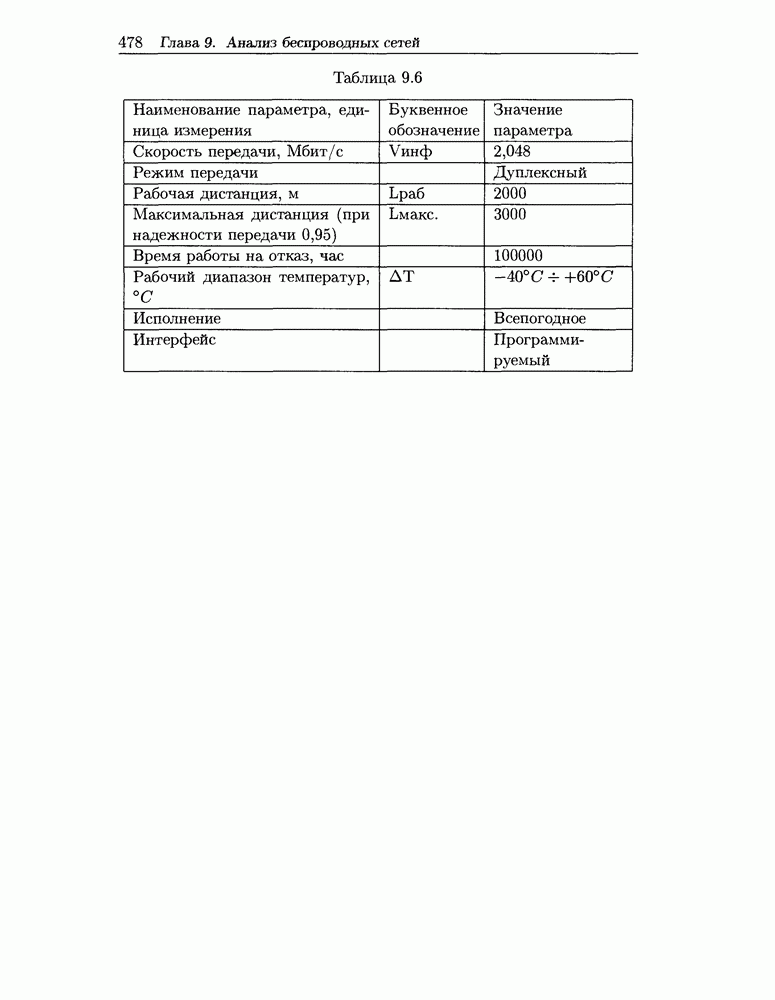
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература