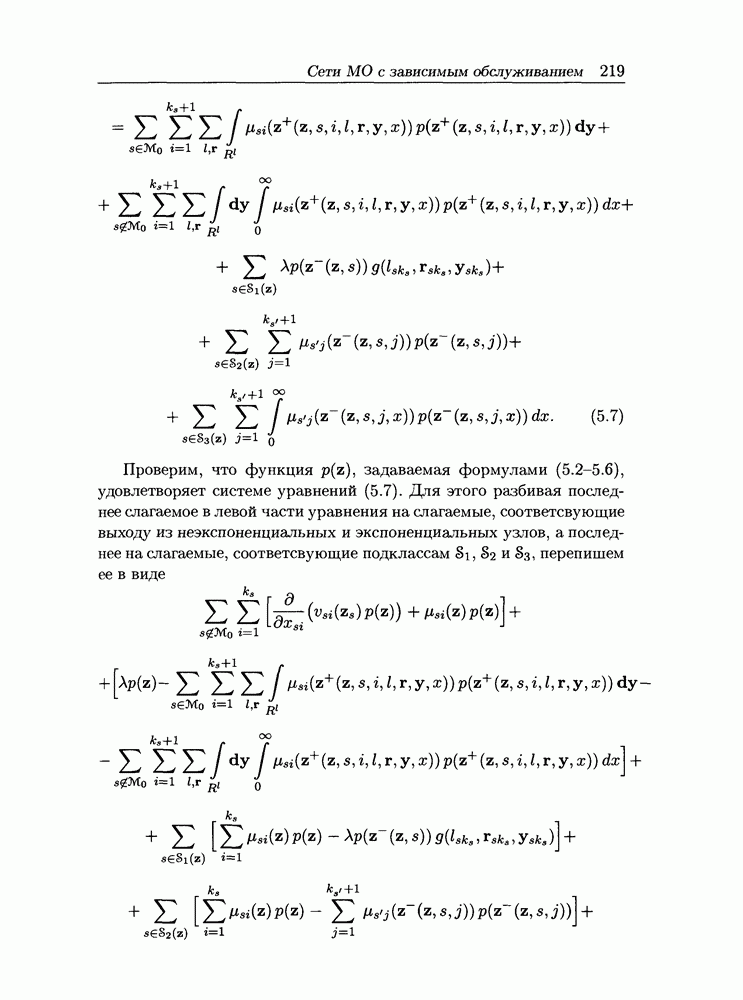| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2.4 Основная теорема о мультипликативности сети
В этом разделе доказывается теорема о мультипликативном представлении стационарных вероятностей состояний для рассматриваемой сети.
Стационарную плотность распределения вероятностей состояний процесса  будем обозначать
будем обозначать  Ниже прямым построением мы покажем существование этой плотности при естественном ограничении на загрузку сети.
Ниже прямым построением мы покажем существование этой плотности при естественном ограничении на загрузку сети.
Теорема. Если для узлов s типа  для узлов s типа
для узлов s типа  и для узлов s типов 2 и
и для узлов s типов 2 и  то существует предельное (стационарное) распределение вероятностей состояний процесса
то существует предельное (стационарное) распределение вероятностей состояний процесса  с плотностью распределения вероятностей
с плотностью распределения вероятностей

где:
для узлов s типа  при
при 

и

для узлов s типа 1

для узлов s типов 2 или 3

Доказательство. Нетрудно видеть, что марковский процесс  является неприводимым, регулярным и положительно возвратным по Харрису, так как состояние 0 является для него положительно возвратным атомом. Поэтому для доказательства теоремы достаточно показать, что функция
является неприводимым, регулярным и положительно возвратным по Харрису, так как состояние 0 является для него положительно возвратным атомом. Поэтому для доказательства теоремы достаточно показать, что функция  определяемая утверждением теоремы, удовлетворяет системе уравнений для стационарных плотностей распределения вероятностей состояний процесса, которую аналогично дискретному случаю назовем системой уравнений равновесия (СУР).
определяемая утверждением теоремы, удовлетворяет системе уравнений для стационарных плотностей распределения вероятностей состояний процесса, которую аналогично дискретному случаю назовем системой уравнений равновесия (СУР).
Для записи СУР введем следующие обозначения. Пусть  узел находится в состоянии
узел находится в состоянии  . Тогда через
. Тогда через  обозначим скорость обслуживания
обозначим скорость обслуживания  заявки, находящейся в этом узле, т.е.
заявки, находящейся в этом узле, т.е.

а через

интенсивность выхода из состояния z за счет окончания обслуживания  заявки в
заявки в  узле. Заметим, что в силу предположения
узле. Заметим, что в силу предположения  для узлов s типа 0 имеем
для узлов s типа 0 имеем 
Кроме того, для неэкспоненциальных узлов  при
при  обозначим через
обозначим через  вероятность того, что заявке, поступающей в узел s, в котором находится еще
вероятность того, что заявке, поступающей в узел s, в котором находится еще  заявок, будет присвоен номер
заявок, будет присвоен номер  . Согласно принятому правилу нумерации заявок в узлах эта вероятность имеет вид
. Согласно принятому правилу нумерации заявок в узлах эта вероятность имеет вид

Так как уравнения будут иметь различный вид для внутренних и граничных состояний множества состояний Z процесса  , то разобьем его на два подмножества - внутренних и граничных состояний. К внутренним отнесем такие состояния, для которых
, то разобьем его на два подмножества - внутренних и граничных состояний. К внутренним отнесем такие состояния, для которых  для всех тех
для всех тех  для которых они определены (т.е. для всех
для которых они определены (т.е. для всех  ). Очевидно, что внутреннее состояние - это такое состояние, в котором все заявки, находящиеся в узлах типов 1-3, уже обслуживались какое-то время. Остальные состояния будем называть граничными.
). Очевидно, что внутреннее состояние - это такое состояние, в котором все заявки, находящиеся в узлах типов 1-3, уже обслуживались какое-то время. Остальные состояния будем называть граничными.
Каждому внутреннему состоянию  . поставим в соответствие множество состояний
. поставим в соответствие множество состояний  , которые будем называть предшествующими состоянию z. Смысл введения предшествующих состояний заключается в том, что только из них возможен непосредственный переход в состояние z. В свою очередь, все состояния, предшествующие внутреннему состоянию z, разобьем на 4 класса, каждый из которых соответствовать определенному типу перехода в состояние z. Первый класс
, которые будем называть предшествующими состоянию z. Смысл введения предшествующих состояний заключается в том, что только из них возможен непосредственный переход в состояние z. В свою очередь, все состояния, предшествующие внутреннему состоянию z, разобьем на 4 класса, каждый из которых соответствовать определенному типу перехода в состояние z. Первый класс

соответствует тем состояниям сети, переход из которых в состояние z осуществляется за счет окончания обслуживания заявки в каком-либо из узлов и ухода ее из сети и состоит из состояний

имеющих вид

где

и

а  , могут принимать любые (возможные) значения.
, могут принимать любые (возможные) значения.
Остальные 3 класса предшествующих состояний не пусты только для сетей МО, в которых есть экспоненциальные узлы. Пусть  и состояние z таково, что
и состояние z таково, что  Предположим также, что
Предположим также, что 
Обозначим через  класс, содержащий все предшествующие состоянию Обозначим через
класс, содержащий все предшествующие состоянию Обозначим через  состояния, из которых возможен переход в состояние z за счет поступления новой заявки в экспоненциальный узел сети, а через
состояния, из которых возможен переход в состояние z за счет поступления новой заявки в экспоненциальный узел сети, а через  подмножество экспоненциальных узлов, в которых на последнем месте стоит заявка, только что поступившая в сеть МО. Состояния
подмножество экспоненциальных узлов, в которых на последнем месте стоит заявка, только что поступившая в сеть МО. Состояния  этого класса имеют вид
этого класса имеют вид

где

Класс  соответствует предшествующим состояниям, переход из которых в состояние z осуществляется при окончании обслуживания в одном экспоненциальном узле и поступлении ее на обслуживание в другой экспоненциальный узел (на последнее место), и состоит из непересекающихся подклассов
соответствует предшествующим состояниям, переход из которых в состояние z осуществляется при окончании обслуживания в одном экспоненциальном узле и поступлении ее на обслуживание в другой экспоненциальный узел (на последнее место), и состоит из непересекающихся подклассов  определяемых следующим образом. Пусть
определяемых следующим образом. Пусть  и состояние z таково, что
и состояние z таково, что  Предположим также, что
Предположим также, что  Тогда
Тогда

причем каждое состояние  имеет вид
имеет вид

где

Множество узлов s, для которых подклассы  не пусты, обозначим через
не пусты, обозначим через 
Наконец, класс  аналогичен классу
аналогичен классу  за исключением того, что переход в состояние z осуществляется при окончании обслуживания в неэкспоненциальном узле. Непересекающиеся подклассы
за исключением того, что переход в состояние z осуществляется при окончании обслуживания в неэкспоненциальном узле. Непересекающиеся подклассы  образующие класс
образующие класс  определяются так. Пусть
определяются так. Пусть  и состояние z таково, что
и состояние z таково, что  . Предположим также, что
. Предположим также, что  . Тогда
. Тогда

причем каждое состояние  имеет вид
имеет вид

где


Множество узлов s, для которых не пусты подклассы  обозначим через
обозначим через 
Отметим еще раз, что каждый из классов  может быть пустым. В частности, для состояния
может быть пустым. В частности, для состояния  пустыми являются все классы
пустыми являются все классы 
Выпишем уравнения глобального баланса для внутреннего состояния z. Для этого вычислим потоки вероятностей, входящие и выходящие из состояния 
Поток, выходящий из состояния z, состоит из двух частей. Во-первых, выход из состояния z осуществляется при поступлении новой заявки в сеть МО (с интенсивностью  ). Выходящий из состояния z поток вероятностей, связанный с поступлением новых заявок, равен
). Выходящий из состояния z поток вероятностей, связанный с поступлением новых заявок, равен  .
.
Во-вторых, выход из состояния z происходит и при окончании обслуживания  заявки в
заявки в  узле (с интенсивностью
узле (с интенсивностью  ). Общий выходящий из состояния z поток вероятностей, связанный с окончанием обслуживания заявок во всех узлах, равен
). Общий выходящий из состояния z поток вероятностей, связанный с окончанием обслуживания заявок во всех узлах, равен

Вход во внутреннее состояние z может произойти при окончании обслуживания  заявки в
заявки в  узле из состояния
узле из состояния  . Поскольку интенсивность окончания обслуживания
. Поскольку интенсивность окончания обслуживания  заявки в
заявки в  узле равна
узле равна  , то суммарный входящий в состояние z поток вероятностей, связанный с окончанием обслуживания заявок в узлах, равен
, то суммарный входящий в состояние z поток вероятностей, связанный с окончанием обслуживания заявок в узлах, равен

Кроме того, в состояние z можно попасть в случае поступления заявки в экспоненциальный узел с номером  т.е. из состояний классов
т.е. из состояний классов 
При этом поступающая в узел s заявка может либо впервые появиться в сети, либо перейти из другого экспоненциального узла, либо перейти из неэкспоненциального узла.
Первый случай возможен при  . Поскольку интенсивность перехода из состояния
. Поскольку интенсивность перехода из состояния  в состояние z равна
в состояние z равна  то суммарный входящий в состояние z поток вероятностей, связанный с поступлением новых заявок, равен
то суммарный входящий в состояние z поток вероятностей, связанный с поступлением новых заявок, равен

Второй случай возможен при  . Интенсивность перехода из состояния
. Интенсивность перехода из состояния  в состояние z равна
в состояние z равна  и суммарный входящий в состояние z поток вероятностей, связанный с переходом заявок из экспоненциального узла в экспоненциальный, равен
и суммарный входящий в состояние z поток вероятностей, связанный с переходом заявок из экспоненциального узла в экспоненциальный, равен

Аналогично, в третьем случае суммарный входящий в состояние z поток вероятностей, связанный с переходом заявок из неэкспоненциального узла в экспоненциальный, равен

Наконец, при составлении уравнений глобального баланса для внутренних состояний z необходимо учесть также слагаемое, связанное с изменением текущего времени пребывания заявок в неэкспоненциальных узлах. Это слагаемое, равное

наряду с первыми двумя должно быть записано в левой части уравнения равновесия.
Теперь мы можем выписать СУР для внутренних состояний z. Эта система имеет вид


Проверим, что функция  задаваемая формулами
задаваемая формулами  удовлетворяет системе уравнений (5.7). Для этого разбивая последнее слагаемое в левой части уравнения на слагаемые, соответсвующие выходу из неэкспоненциальных и экспоненциальных узлов, а последнее на слагаемые, соответсвующие подклассам
удовлетворяет системе уравнений (5.7). Для этого разбивая последнее слагаемое в левой части уравнения на слагаемые, соответсвующие выходу из неэкспоненциальных и экспоненциальных узлов, а последнее на слагаемые, соответсвующие подклассам  перепишем ее в виде
перепишем ее в виде


Следующая далее лемма 1 выявляет определенные соотношения во внутренних точках z для функции  задаваемой формулами (5.2-5.6) и показывает, что каждое из выражений, заключенных в квадратных скобках, равно нулю, и, следовательно, функция
задаваемой формулами (5.2-5.6) и показывает, что каждое из выражений, заключенных в квадратных скобках, равно нулю, и, следовательно, функция  действительно удовлетворяет СУР (5.7) во всех внутренних точках
действительно удовлетворяет СУР (5.7) во всех внутренних точках 
Лемма 1. Функция  задаваемая формулами (5.2-5.6) для всех внутренних состояний z сети удовлетворяет соотношениям 1.
задаваемая формулами (5.2-5.6) для всех внутренних состояний z сети удовлетворяет соотношениям 1.

2. Для любого узла s типов 1-3 ( ) и любого
) и любого 

3. Для любого узла 

4. Для любого узла 

5. Для любого узла 

Доказательство леммы 1 осуществляется непосредственной проверкой справедливости соответствующих соотношений для функций, определяемых формулами (5.2-5.6).
Покажем, что эти соотношения представляют собой уравнения частичного баланса для внутренних состояний сети, для чего дадим более подробный комментарий к этому результату.
Первое равенство представляет собой частичный баланс потока вероятностей, выходящего из состояния z за счет поступления в сеть МО новых заявок, и суммарного потока вероятностей, входящего в состояние z за счет окончания обслуживания заявок и ухода их из сети.
Второе равенство отражает частичный баланс скорости изменения выработанной длительности обслуживания  заявки в
заявки в  (неэкспоненциальном) узле и интенсивности выхода из состояния z за счет окончания обслуживания этой заявки.
(неэкспоненциальном) узле и интенсивности выхода из состояния z за счет окончания обслуживания этой заявки.
Наконец, третье, четвертое и пятое равенства отражают частичный баланс потока вероятностей, выходящего из  (экспоненциального) узла, и потока вероятностей, входящего в этот узел за счет поступления в сеть новой заявки (третье равенство), за счет перехода из экспоненциального узла (четвертое равенство) и за счет перехода из неэкспоненциального узла (пятое равенство).
(экспоненциального) узла, и потока вероятностей, входящего в этот узел за счет поступления в сеть новой заявки (третье равенство), за счет перехода из экспоненциального узла (четвертое равенство) и за счет перехода из неэкспоненциального узла (пятое равенство).
Перейдем теперь к граничным состояниям. При этом достаточно ограничиться такими граничными состояниями z, у которых  только для одной пары
только для одной пары  .
.
Пусть z - граничное состояние, т.е. состояние, у которого  для некоторого
для некоторого  . Каждое такое состояние отнесем к одному из 3 типов по следующему принципу.
. Каждое такое состояние отнесем к одному из 3 типов по следующему принципу.
Пусть  . Тогда состояние z отнесем к первому типу граничных состояний. Очевидно, что попадание в граничное состояние z первого типа происходит за счет поступления в сеть МО новой заявки, попадающей на
. Тогда состояние z отнесем к первому типу граничных состояний. Очевидно, что попадание в граничное состояние z первого типа происходит за счет поступления в сеть МО новой заявки, попадающей на  место в
место в  (неэкспоненциальный) узел.
(неэкспоненциальный) узел.
Если  и
и  то состояние z отнесем ко второму типу граничных состояний. Попадание в граничное состояние z второго типа происходит за счет поступления на
то состояние z отнесем ко второму типу граничных состояний. Попадание в граничное состояние z второго типа происходит за счет поступления на  место в
место в  (неэкспоненциальный) узел заявки, обслуживавшейся ранее в экспоненциальном узле.
(неэкспоненциальный) узел заявки, обслуживавшейся ранее в экспоненциальном узле.
Наконец, при  и
и  состояние z отнесем к третьему типу граничных состояний. Попадание в граничное состояние z третьего типа происходит за счет поступления на
состояние z отнесем к третьему типу граничных состояний. Попадание в граничное состояние z третьего типа происходит за счет поступления на  место в
место в  (неэкспоненциальный) узел заявки, обслуживавшейся ранее в неэкспоненциальном узле.
(неэкспоненциальный) узел заявки, обслуживавшейся ранее в неэкспоненциальном узле.
Так же, как это было сделано ранее для внутреннего состояния, для граничного состояния z определим множество  предшествующих состояний.
предшествующих состояний.
Для граничного состояния z первого типа множество  состоит всего из одного состояния
состоит всего из одного состояния

где

Для граничного состояния z второго типа множество  состоит из состояний
состоит из состояний  имеющих вид
имеющих вид

где

Для граничного состояния z третьего типа множество  состоит из состояний
состоит из состояний  имеющих вид
имеющих вид

где

Выпишем уравнения равновесия для граничного состояния z.
Поскольку переход в граничное состояние z первого типа происходит только из состояния  причем интенсивность такого перехода равна
причем интенсивность такого перехода равна  то уравнение равновесия в этом случае имеет вид
то уравнение равновесия в этом случае имеет вид

Переход в граничное состояние z второго типа происходит из состояний  с интенсивностями
с интенсивностями  откуда получаем уравнение равновесия
откуда получаем уравнение равновесия

Наконец, переход в граничное состояние z третьего типа происходит из состояний  с интенсивностями
с интенсивностями  Уравнение равновесия в этом случае имеет вид
Уравнение равновесия в этом случае имеет вид

Тот факт, что функция  определенная формулами (5.2-5.6), в граничных точках z удовлетворяет СУР (5.8-5.10) вытекает из следующей леммы 2, которая аналогично доказательству леммы 1 проверяется непосредственной подстановкой.
определенная формулами (5.2-5.6), в граничных точках z удовлетворяет СУР (5.8-5.10) вытекает из следующей леммы 2, которая аналогично доказательству леммы 1 проверяется непосредственной подстановкой.
Лемма 2. Функция  задаваемой формулами (5.2-5.6), для всех граничных состояний z сети удовлетворяет соотношениям.
задаваемой формулами (5.2-5.6), для всех граничных состояний z сети удовлетворяет соотношениям.
1. Для граничного состояния z первого типа

2. Для граничного состояния z второго типа

3. Для граничного состояния z третьего типа

Доказательство теоремы завершается тривиальной проверкой выполнения условия нормировки для функции 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
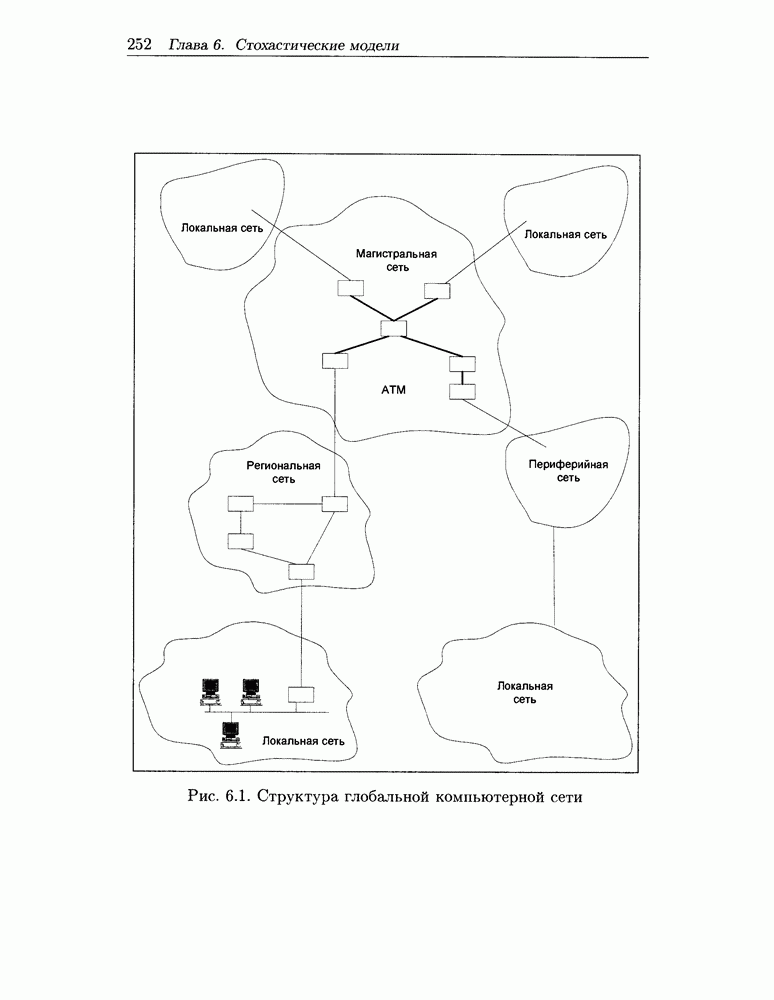
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
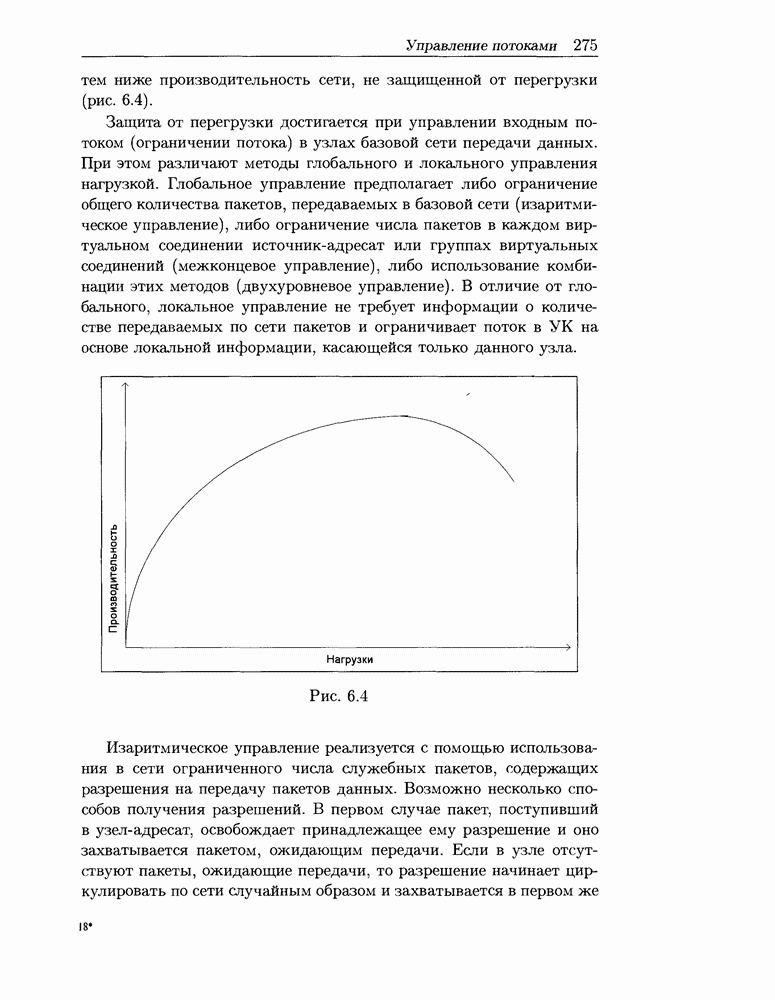
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
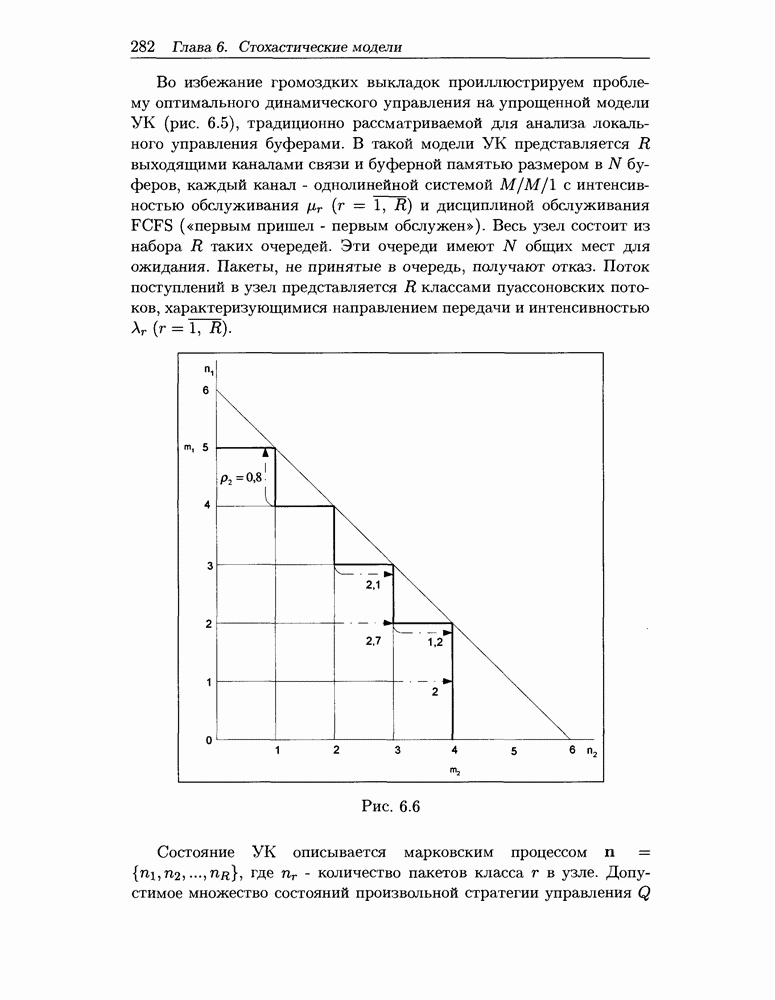
- 6.3.3 Локальное управление буферами
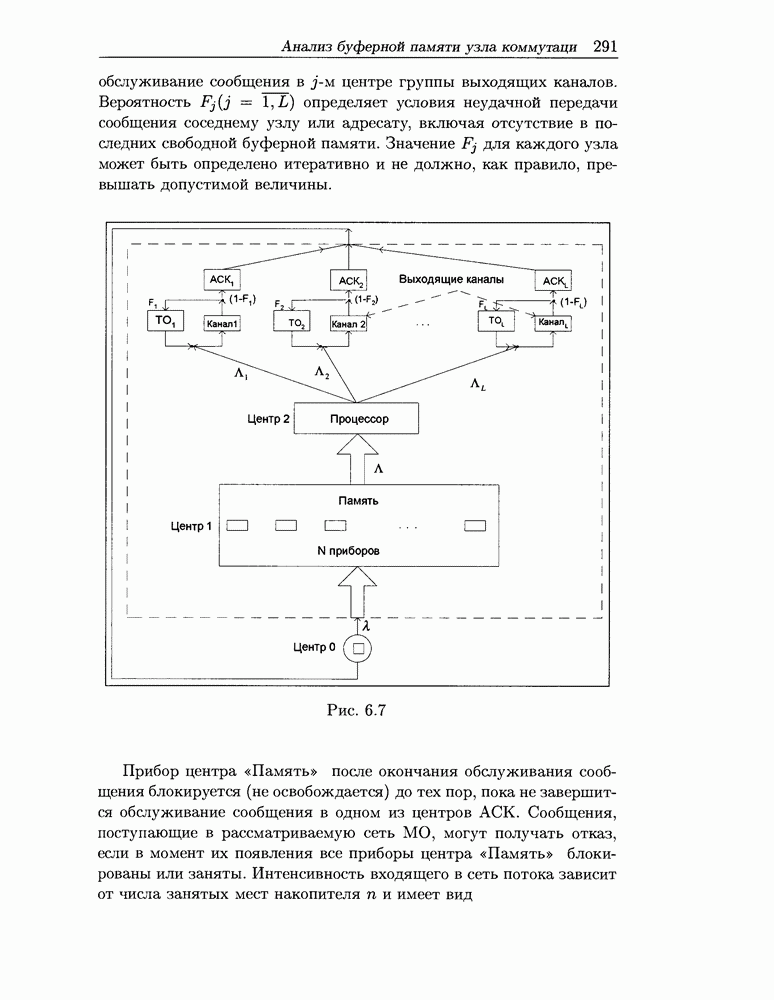
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
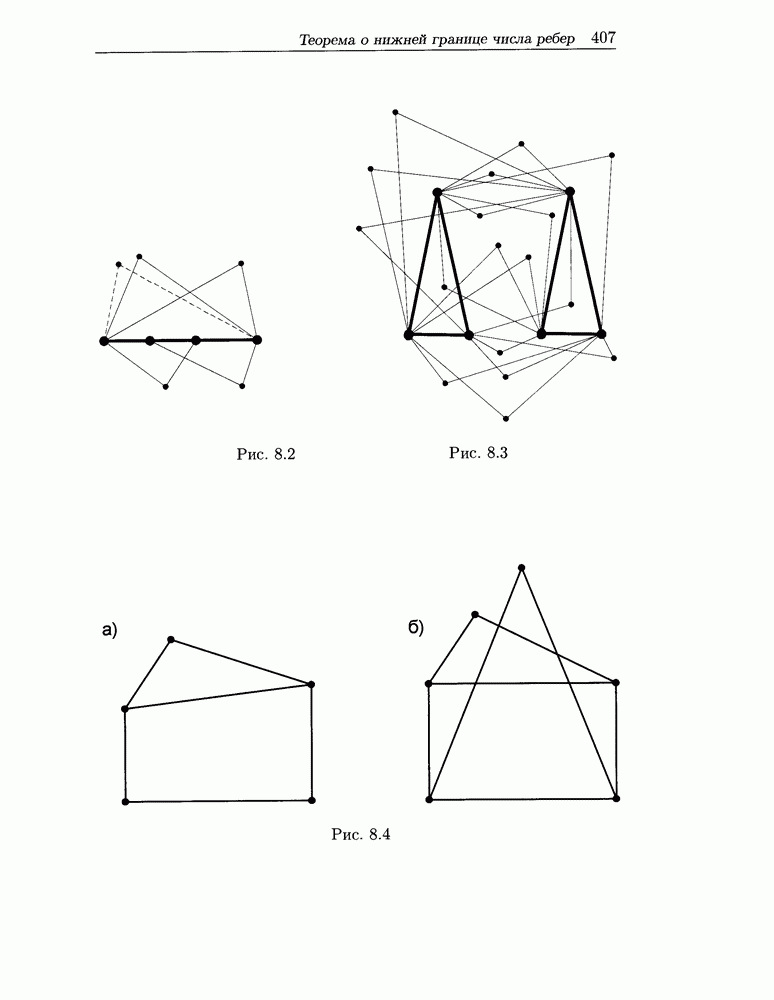
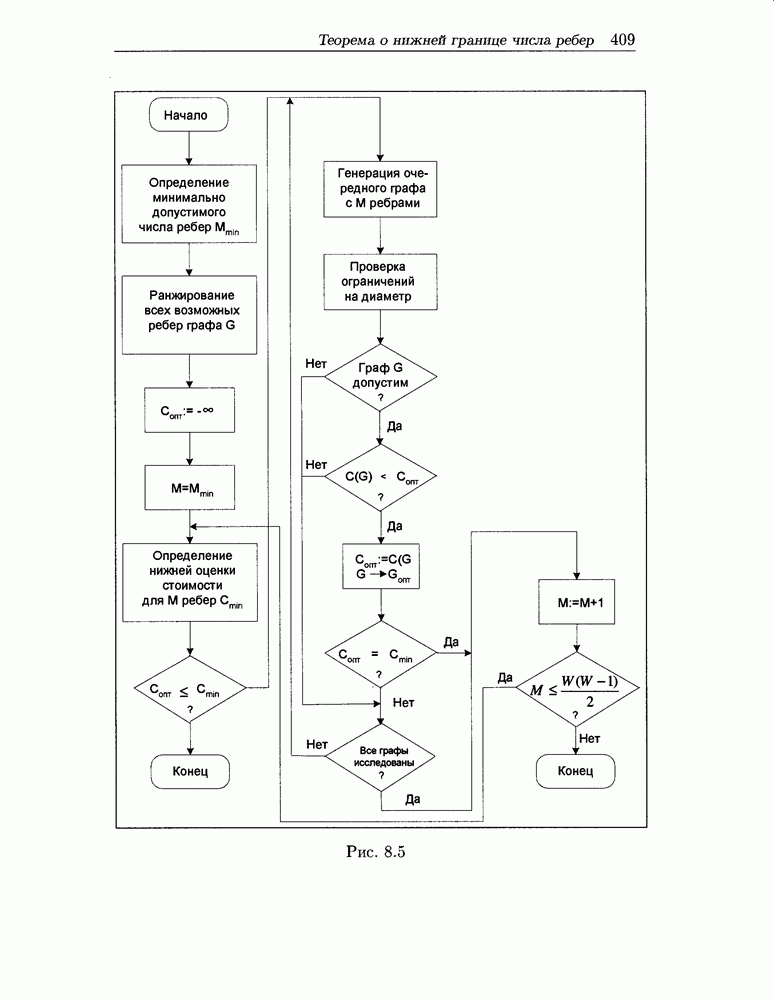
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
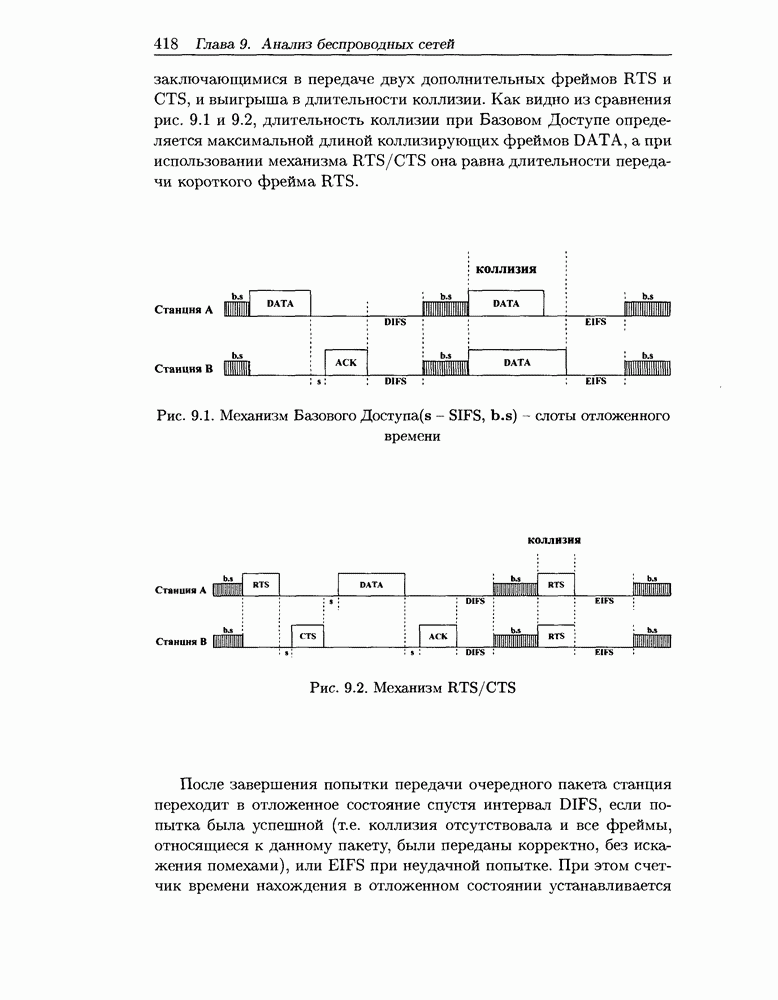
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
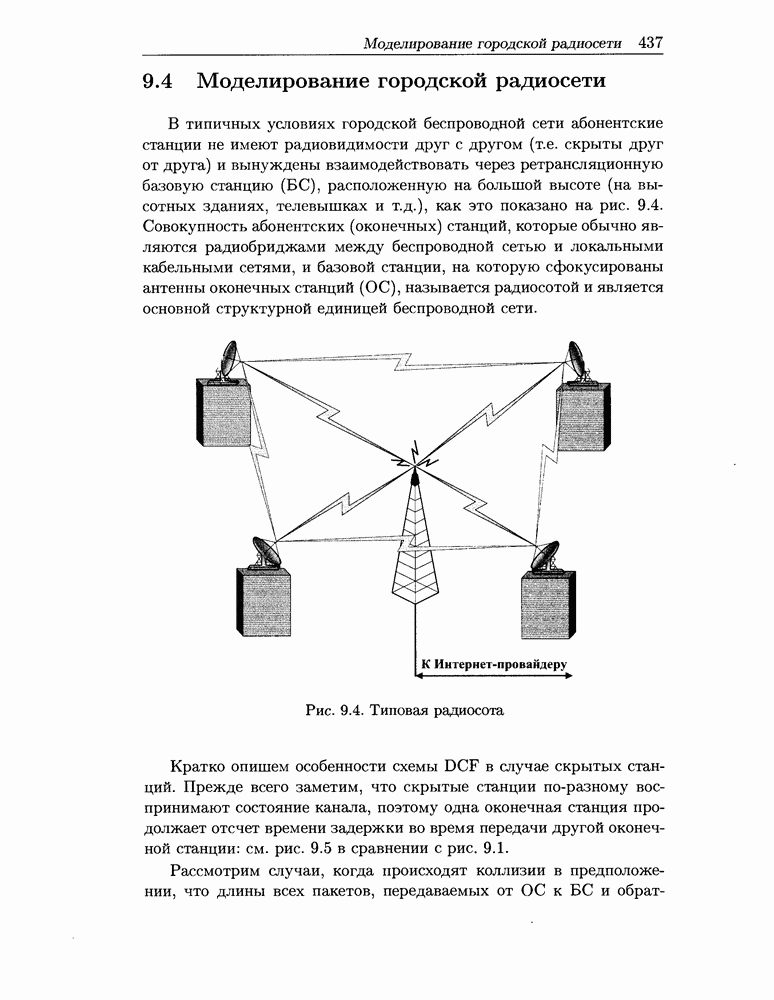
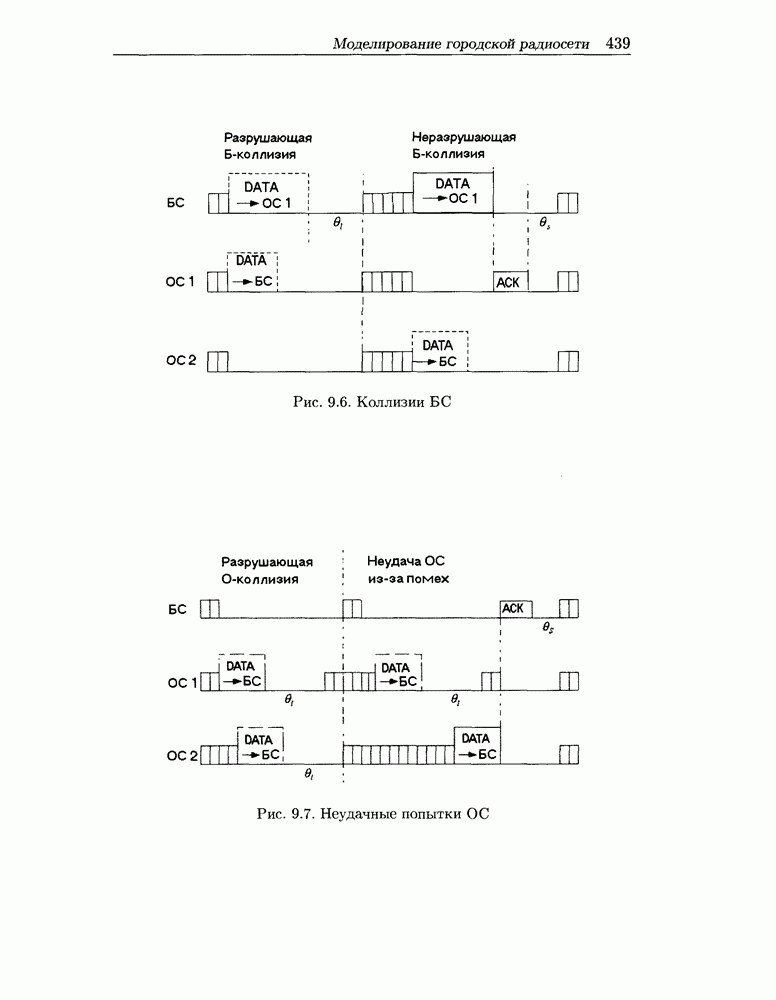
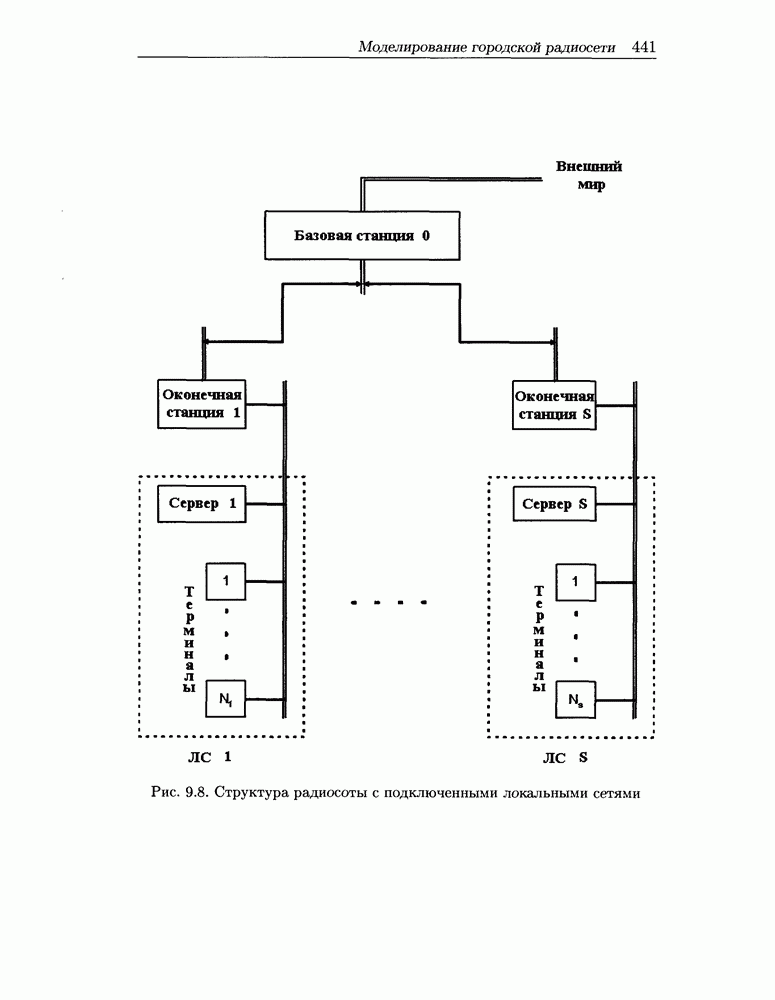
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
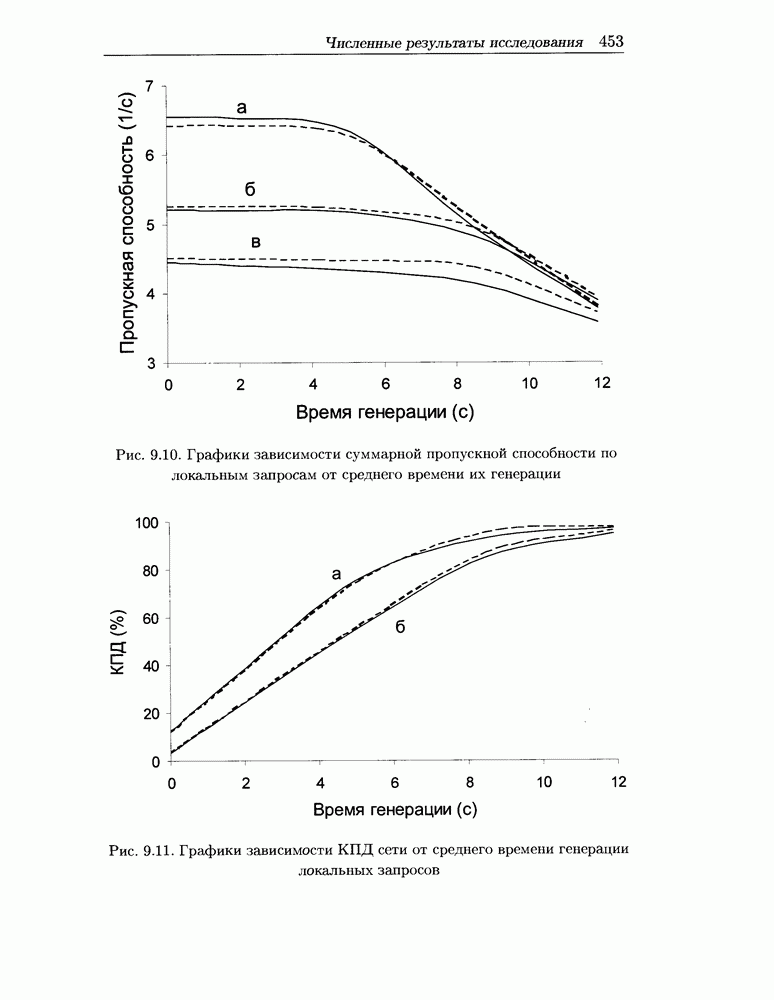
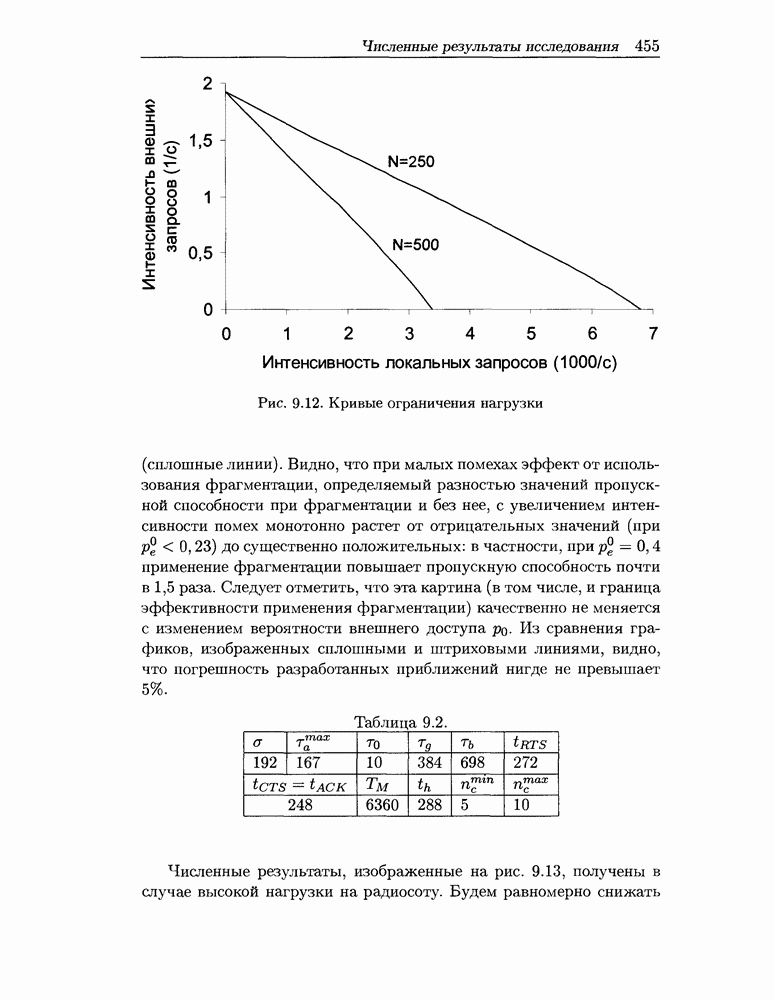
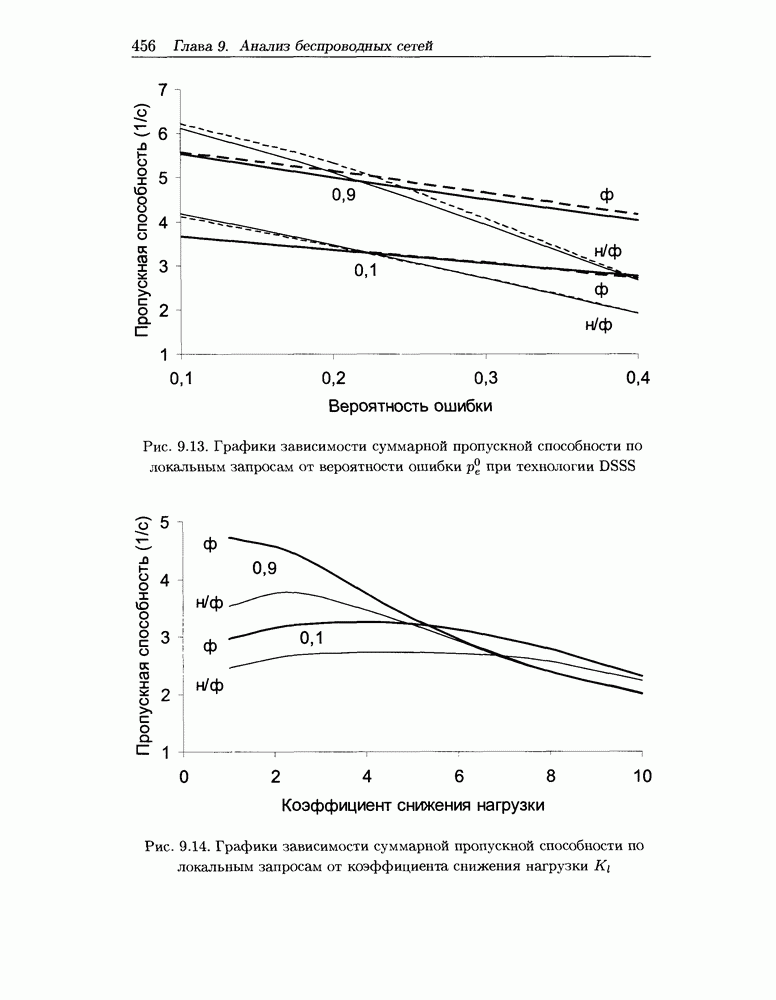
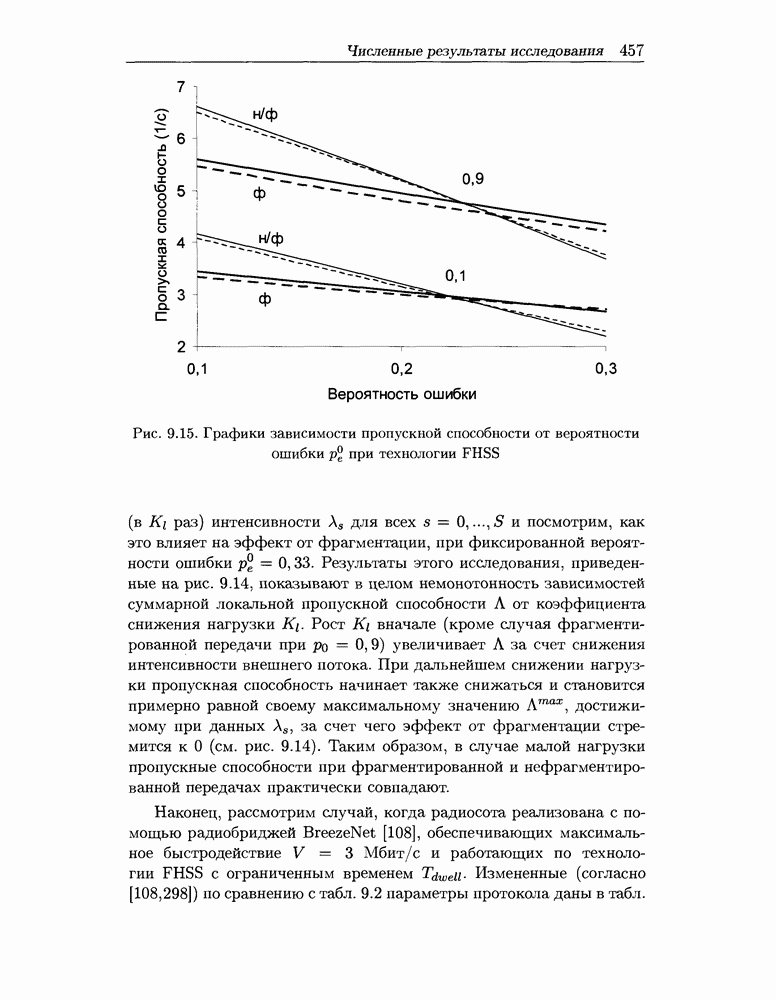
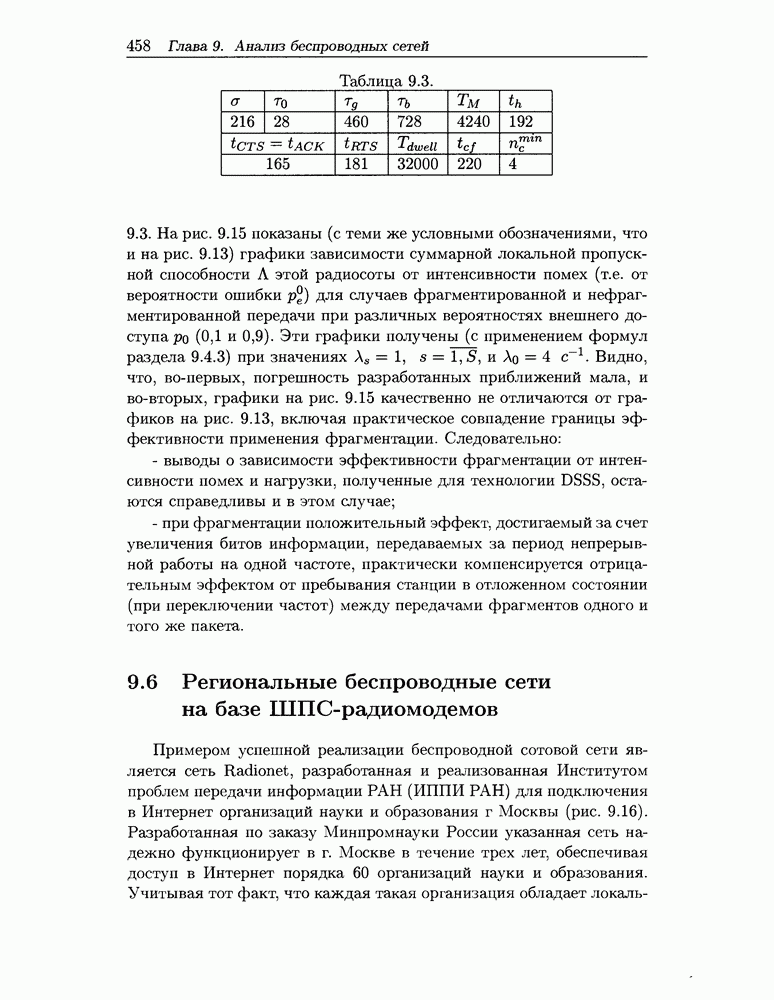
- 9.5 Численные результаты исследования городской радиосоты
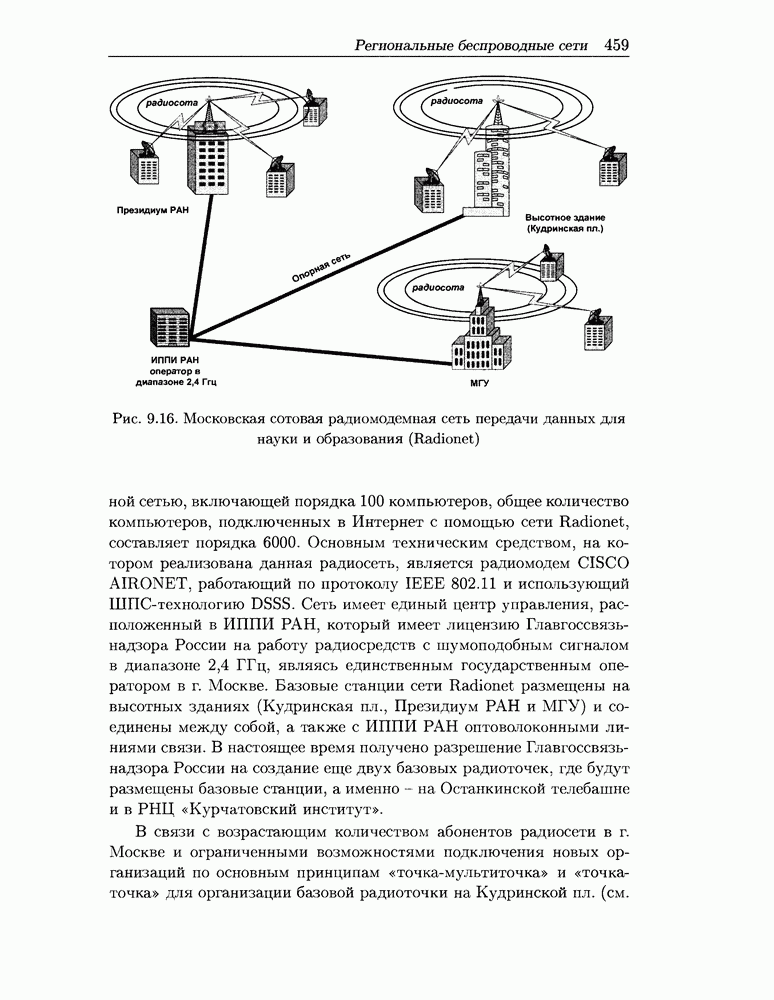
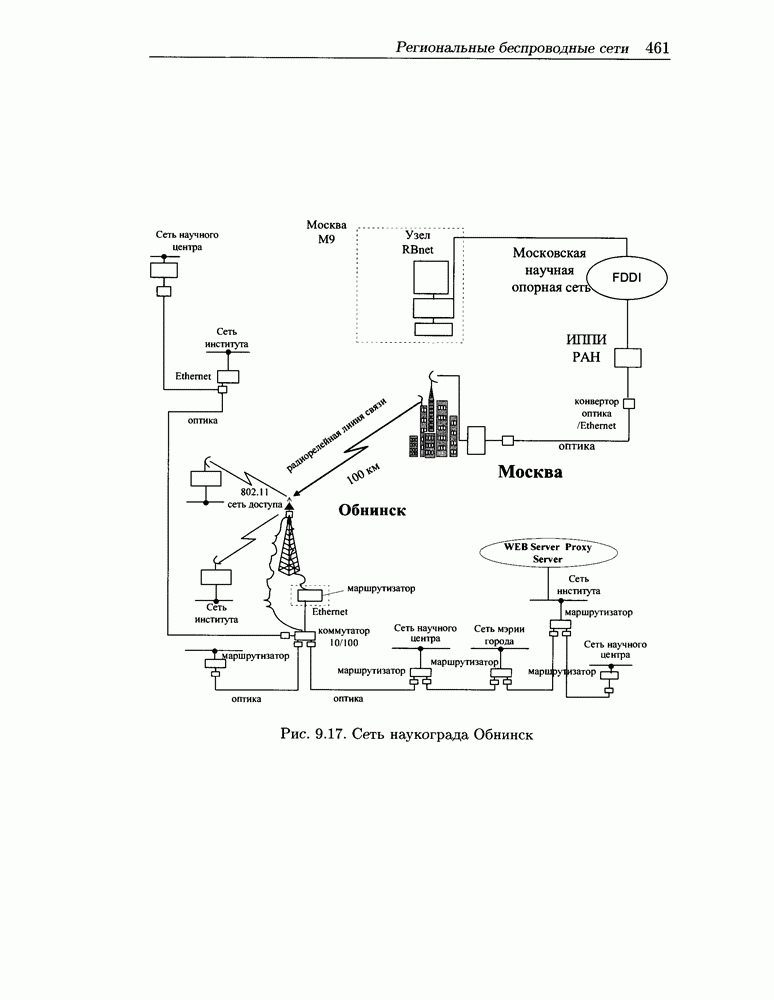
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
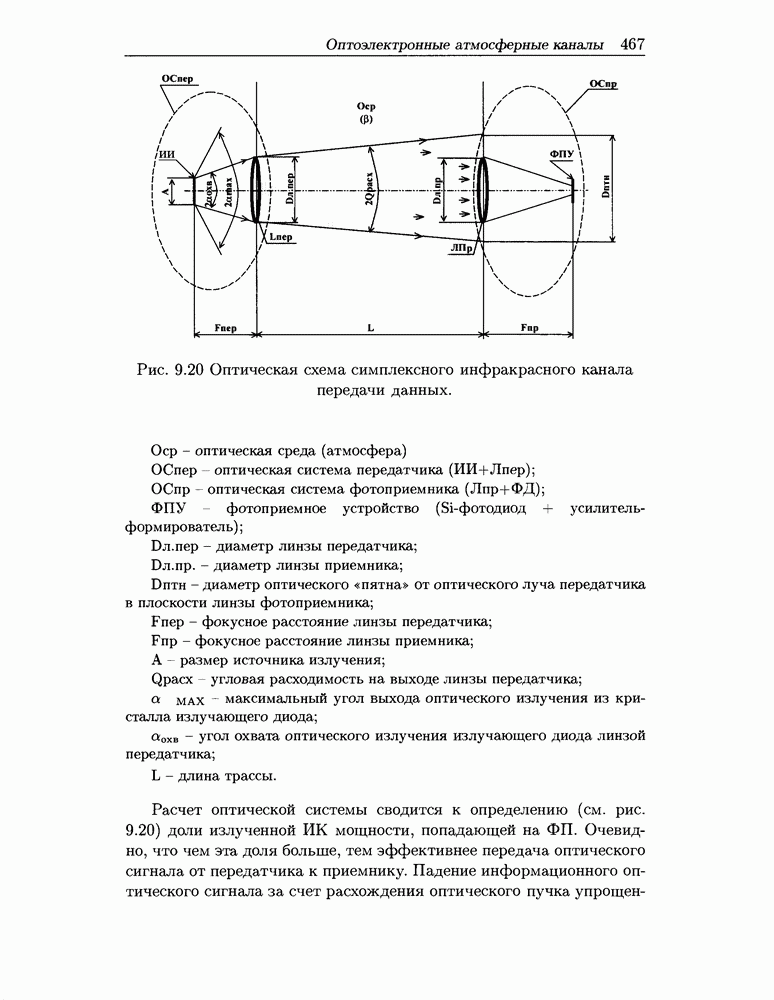
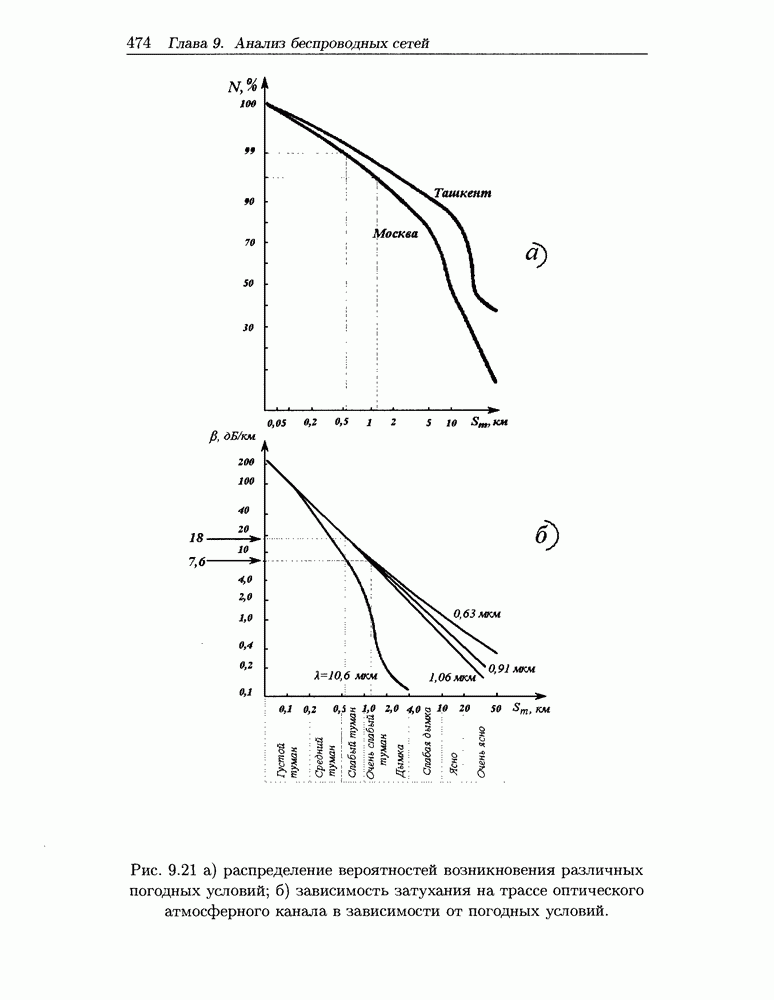
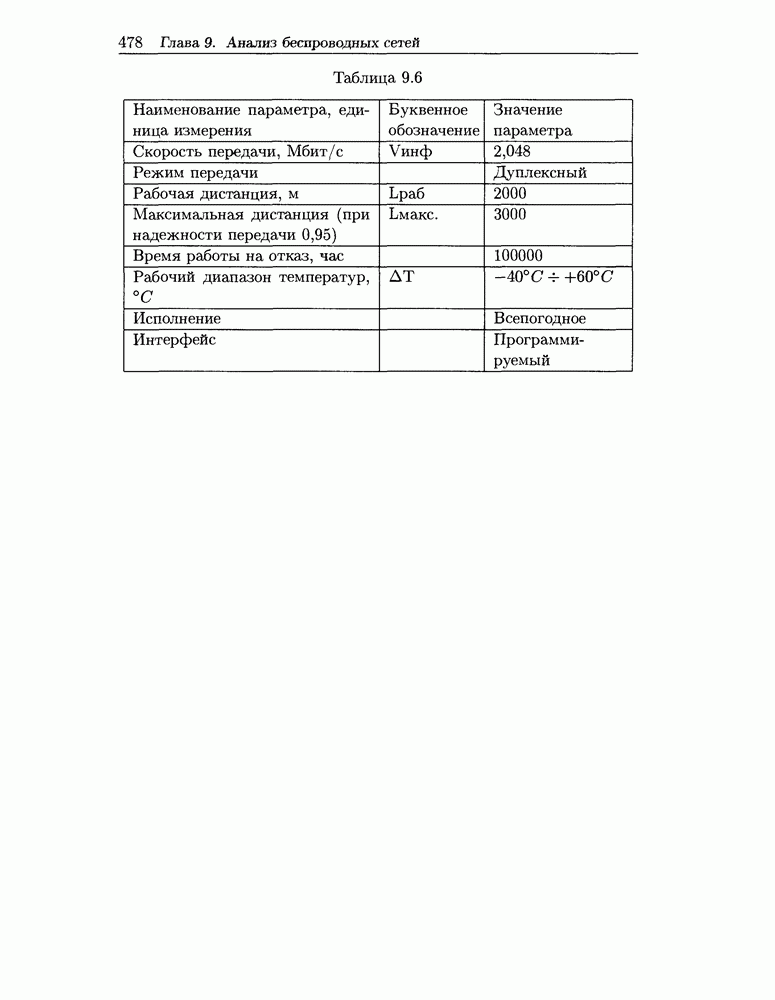
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература