| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ IV.4. ЭНТРОПИЯ. НАПРАВЛЕНИЕ И ПРЕДЕЛ ПРОТЕКАНИЯ ПРОЦЕССОВ В ИЗОЛИРОВАННЫХ СИСТЕМАХ
Самопроизвольные и несамопроизвольные процессы.
Многие процессы осуществляются самопроизвольно, т. е. без затраты работы извне. В результате их может быть получена работа против внешних сил, пропорциональная происшедшему изменению
энергии системы. Так, самопроизвольно вода стекает по наклонному желобу или теплота передается от более нагретого тела к менее нагретому. В принципе при всяком самопроизвольном процессе может совершаться полезная работа: падающая с высоты вода может вращать турбину, переданная от топлива к воде теплота может генерировать водяной пар. В ходе самопроизвольного процесса система теряет способность производить полезную работу.
Самопроизвольный процесс не может протекать в обратном направлении так же самопроизвольно, как в прямом. Так, вода не может сама по себе перетекать вверх по наклонному желобу, а теплота не может сама по себе переходить от холодного тела к горячему. Чтобы перекачать воду наверх или передать теплоту от холодной части системы к горячей, необходимо совершить работу над системой. К процессам, обратным по отношению к самопроизвольным, применяется термин «несамопроизвольные».
При изучении химических взаимодействий очень важно оценить возможность или невозможность их самопроизвольного протекания при заданных условиях, выяснить химическое сродство веществ. Должен быть критерий, с помощью которого можно было бы установить принципиальную осуществимость, направление и пределы самопроизвольного течения реакции при тех или иных температурах и давлениях. Первый закон термодинамики такого критерия не дает. Тепловой эффект реакции не определяет направления процесса: самопроизвольно могут протекать как экзотермические, так и эндотермические реакции. Так, например, самопроизвольно идет процесс растворения нитрата аммония  в воде, хотя тепловой эффект этого процесса положителен:
в воде, хотя тепловой эффект этого процесса положителен:  (процесс эндотермический), и в то же время невозможно осуществить при
(процесс эндотермический), и в то же время невозможно осуществить при  кПа синтез
кПа синтез  -гептана
-гептана  , несмотря на то, что стандартная теплота его образования отрицательна:
, несмотря на то, что стандартная теплота его образования отрицательна:  (процесс экзотермический)
(процесс экзотермический) 
Критерий самопроизвольного протекания процесса в изолированных системах дает второй закон термодинамики. Прежде чем перейти к рассмотрению этого закона, введем представление о термодинамической функции состояния системы, называемой энтропией.
Энтропия.
Для характеристики состояния некоторого количества вещества, являющегося совокупностью очень большого числа молекул, можно или указать температуру, давление и другие термодинамические параметры состояния системы, или указать мгновенные координаты каждой молекулы  и скорости перемещения по всем трем направлениям
и скорости перемещения по всем трем направлениям  . В первом случае охарактеризовывается макросостояние системы, во втором — микросостояние. Каждому макросостоянию отвечает
. В первом случае охарактеризовывается макросостояние системы, во втором — микросостояние. Каждому макросостоянию отвечает
огромное число микросостояний. Число микросостояний, с помощью которых осуществляется данное макросостояние, называют термодинамической вероятностью состояния системы и обозначают 
Термодинамическая вероятность состояния системы, состоящей всего из 10 молекул газа, примерно 1000, а ведь только в  газа содержится
газа содержится  молекул (н. у.). Чтобы перейти к более удобным для восприятия и расчетов числам, в термодинамике используют не величину
молекул (н. у.). Чтобы перейти к более удобным для восприятия и расчетов числам, в термодинамике используют не величину  а ее логарифм
а ее логарифм  . Последнему можно придать размерность
. Последнему можно придать размерность  умножив на константу Больцмана
умножив на константу Больцмана 

Величину  называют энтропией системы.
называют энтропией системы.
Энтропия — термодинамическая функция состояния системы и ее величина зависит от количества рассматриваемого вещества. Поэтому целесообразно относить величину энтропии к одному молю вещества  и выражать как
и выражать как

где  - молярная газовая постоянная;
- молярная газовая постоянная;  — постоянная Авогадро.
— постоянная Авогадро.
Из уравнения (IV. 15) следует, что энтропия системы увеличивается пропорционально логарифму термодинамической вероятности состояния  . Это соотношение лежит в основе современной статистической термодинамики.
. Это соотношение лежит в основе современной статистической термодинамики.
Представим себе один моль воды  при комнатной температуре и атмосферном давлении. Пусть
при комнатной температуре и атмосферном давлении. Пусть  — термодинамическая вероятность состояния этой системы. пР и понижении температуры до
— термодинамическая вероятность состояния этой системы. пР и понижении температуры до  вода замерзает, превращается в лед; при этом молекулы
вода замерзает, превращается в лед; при этом молекулы  как бы закрепляются в узлах кристаллической решетки и термодинамическая вероятность состояния системы уменьшается:
как бы закрепляются в узлах кристаллической решетки и термодинамическая вероятность состояния системы уменьшается:  Следовательно, падает и энтропия системы:
Следовательно, падает и энтропия системы:  Наоборот, при повышении температуры до
Наоборот, при повышении температуры до  вода закипает, превращается в пар; при этом термодинамическая вероятность состояния системы увеличивается (молекулы
вода закипает, превращается в пар; при этом термодинамическая вероятность состояния системы увеличивается (молекулы  в паре имеют большую скорость, чем в жидкой воде):
в паре имеют большую скорость, чем в жидкой воде):  Следовательно, растет и энтропия системы
Следовательно, растет и энтропия системы  Итак, при
Итак, при  энтропия является функцией температуры
энтропия является функцией температуры  причем температура замерзания и температура кипения воды — это те точки, в которых энтропия изменяется особенно резко, скачкообразно.
причем температура замерзания и температура кипения воды — это те точки, в которых энтропия изменяется особенно резко, скачкообразно.
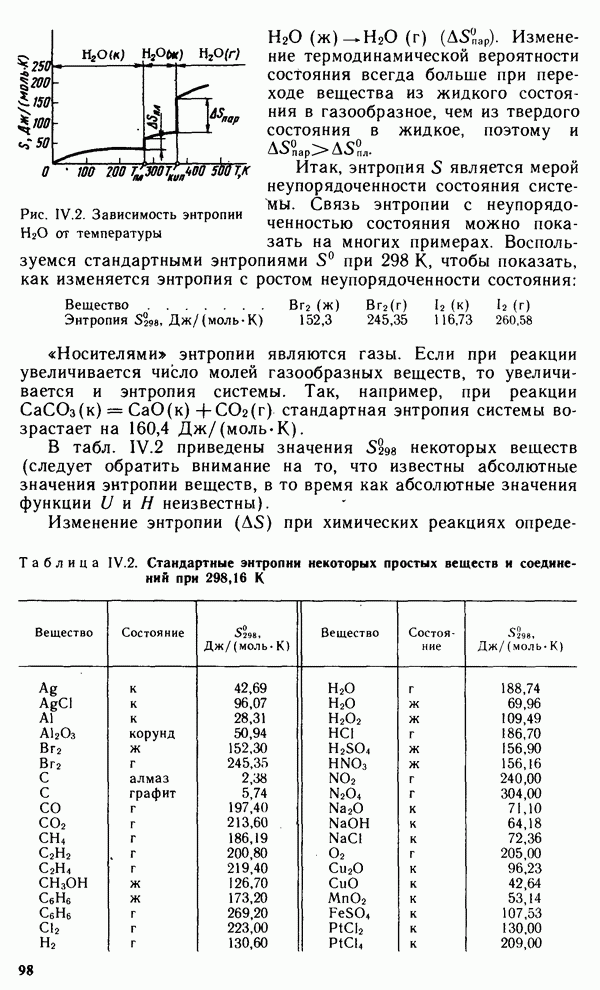
На рис. IV.2 представлена зависимость энтропии  от температуры Т при
от температуры Т при  кПа. Первый в направлении роста температуры энтропийный скачок отвечает температуре плавления льда
кПа. Первый в направлении роста температуры энтропийный скачок отвечает температуре плавления льда 
— изменение энтропии при переходе  Второй энтропийный скачок отвечает температуре кипения воды
Второй энтропийный скачок отвечает температуре кипения воды  — изменение энтропии при переходе
— изменение энтропии при переходе

Рис. IV.2. Зависимость энтропии  от температуры
от температуры
 Изменение термодинамической вероятности состояния всегда больше при переходе вещества из жидкого состояния в газообразное, чем из твердого состояния в жидкое, поэтому и
Изменение термодинамической вероятности состояния всегда больше при переходе вещества из жидкого состояния в газообразное, чем из твердого состояния в жидкое, поэтому и 
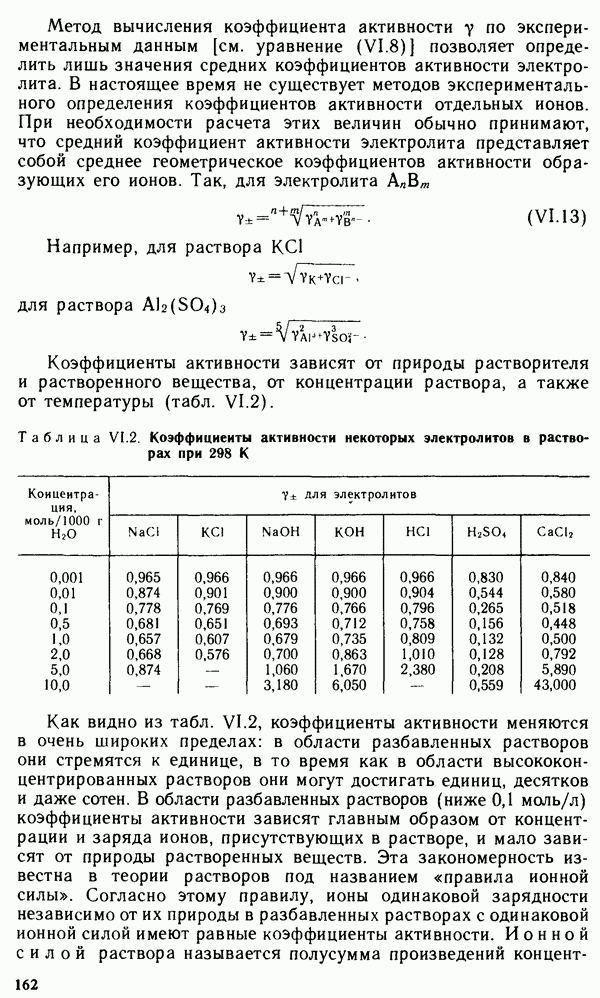
Итак, энтропия S является мерой неупорядоченности состояния системы. Связь энтропии с неупорядоченностью состояния можно показать на многих примерах. Воспользуемся стандартными энтропиями  при 298 К, чтобы показать, как изменяется энтропия с ростом неупорядоченности состояния:
при 298 К, чтобы показать, как изменяется энтропия с ростом неупорядоченности состояния:

«Носителями» энтропии являются газы. Если при реакции увеличивается число молей газообразных веществ, то увеличивается и энтропия системы. Так, например, при реакции  стандартная энтропия системы возрастает на
стандартная энтропия системы возрастает на 
В табл. IV.2 приведены значения  некоторых веществ (следует обратить внимание на то, что известны абсолютные значения энтропии веществ, в то время как абсолютные значения функции
некоторых веществ (следует обратить внимание на то, что известны абсолютные значения энтропии веществ, в то время как абсолютные значения функции  и Н неизвестны).
и Н неизвестны).
Изменение энтропии  при химических реакциях определяется
при химических реакциях определяется
Таблица IV.2. Стандартные энтропии некоторых простых веществ и соединений при 298,16 К

разностью  в которой
в которой  сумма энтропий всех продуктов реакции,
сумма энтропий всех продуктов реакции,  сумма энтропий всех исходных веществ.
сумма энтропий всех исходных веществ.
Направление и предел протекания процессов в изолированных системах.
Второй закон термодинамики. Изолированные системы не обмениваются с внешней средой ни теплотой, ни работой. На основании уравнения (IV. 12) можно утверждать, что при  величина
величина  тоже равна нулю, т. е. внутренняя энергия изолированной системы постоянна
тоже равна нулю, т. е. внутренняя энергия изолированной системы постоянна  постоянен и ее объем
постоянен и ее объем  . В изолированных системах самопроизвольно идут только те процессы, которые сопровождаются ростом энтропии системы:
. В изолированных системах самопроизвольно идут только те процессы, которые сопровождаются ростом энтропии системы:  при этом пределом самопроизвольного течения процесса является достижение максимальной для данных условий энтропии
при этом пределом самопроизвольного течения процесса является достижение максимальной для данных условий энтропии  и тем самым равенства
и тем самым равенства 
Рассмотренное положение представляет одну из формулировок второго закона термодинамики (закон имеет статистический характер, т. е. применим лишь к системам, состоящим из очень большого числа частиц). Требование постоянства внутренней энергии и объема системы исключает использование энтропии как критерия направления и предела протекания химических реакций, при которых внутренняя энергия веществ неизбежно меняется, а также совершается работа расширения против внешнего давления.
Энтропийный и энтальпийный факторы химических реакций, протекающих в изобарно-изотермических условиях.
Движущей силой процесса, протекающего в изобарно-изотермических условиях, может быть или стремление системы перейти в состояние с наименьшей энергией, т. е. выделить теплоту в окружающую среду, уменьшить энтальпию  или стремление системы перейти в состояние с наибольшей термодинамической вероятностью, т. е. увеличить энтропию
или стремление системы перейти в состояние с наибольшей термодинамической вероятностью, т. е. увеличить энтропию  Если процесс протекает так, что
Если процесс протекает так, что  то рост энтропии становится его единственной движущей силой. И наоборот, при условии
то рост энтропии становится его единственной движущей силой. И наоборот, при условии  единственной движущей силой процесса является убыль энтальпии. В связи с этим можно говорить об энтальпийном
единственной движущей силой процесса является убыль энтальпии. В связи с этим можно говорить об энтальпийном  и энтропийном
и энтропийном  факторах процесса. Наиболее устойчивое состояние системы соответствует равенству
факторах процесса. Наиболее устойчивое состояние системы соответствует равенству

Вывести систему из равновесного состояния можно только внешним воздействием (изменением температуры и т. п.).
Следует отметить, что энтропия как термодинамическая функция для обратимых

и необратимых

процессов была введена Клаузиусом в 1865 г.
Размерность энтропии совпадает с размерностью теплоемкости, однако отсюда не следует аналогия их физического смысла. Теплоемкость характеризует количество теплоты, необходимой для нагревания тела на 1 К» а энтропия — ко личество рассеянной энергии, отнесенной к 1 К.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. ПРЕДМЕТ ХИМИИ
- § 2. ЗНАЧЕНИЕ ХИМИИ В ИЗУЧЕНИИ ПРИРОДЫ И РАЗВИТИИ ТЕХНИКИ
- 1. СТРОЕНИЕ ВЕЩЕСТВА
- Глава I. СТРОЕНИЕ АТОМА И СИСТЕМАТИКА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- § 1.2. КВАНТОВО-МЕХАНИЧЕСКАЯ МОДЕЛЬ АТОМА
- § 1.3. КВАНТОВЫЕ ЧИСЛА И АТОМНЫЕ ОРБИТАЛИ
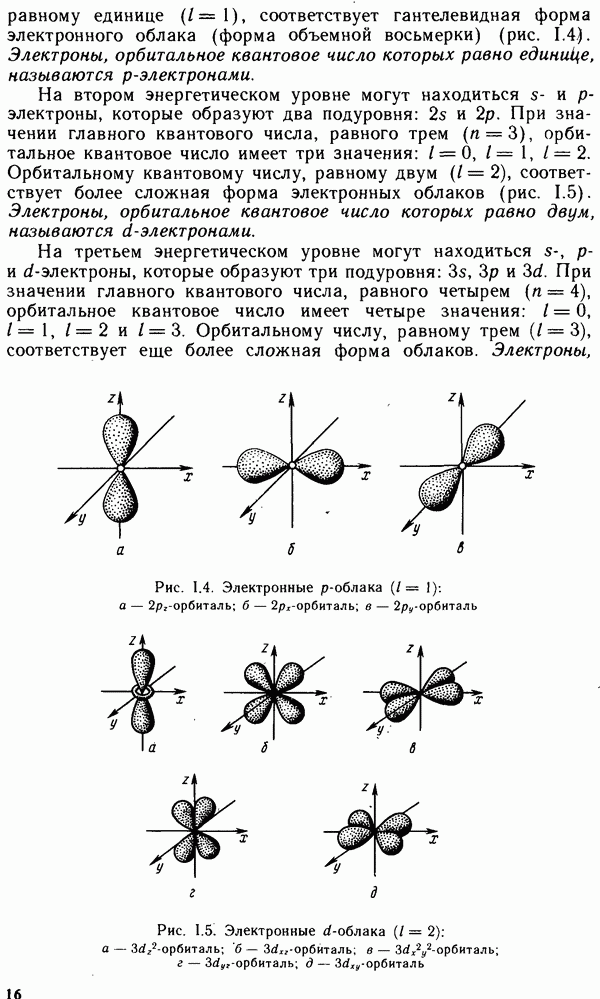
- § 1.4. МНОГОЭЛЕКТРОННЫЕ АТОМЫ
- § 1.5. ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ Д. И. МЕНДЕЛЕЕВА
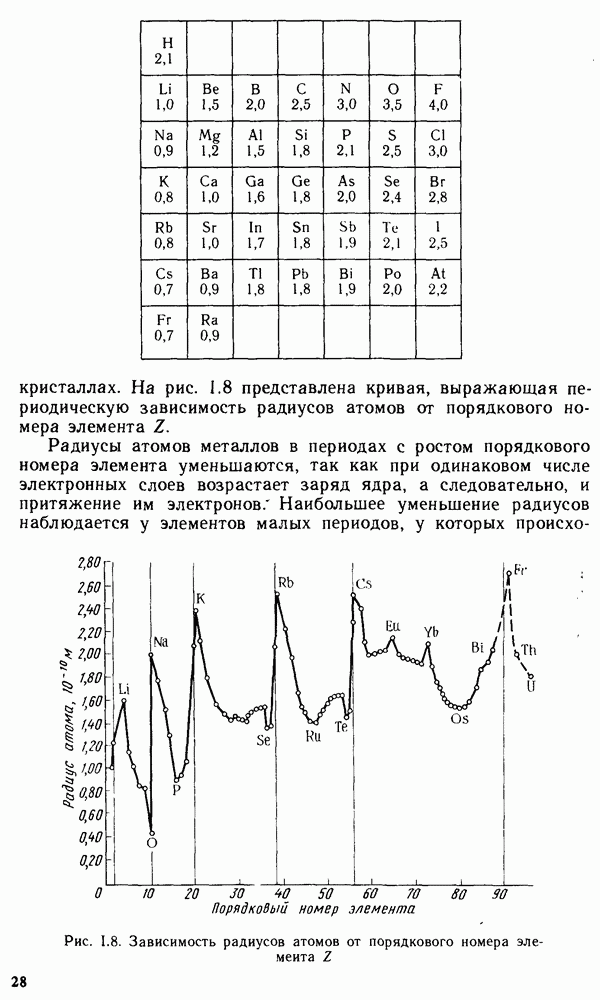
- § 1.6. ПЕРИОДИЧЕСКОЕ ИЗМЕНЕНИЕ СВОЙСТВ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- Глава II. ХИМИЧЕСКАЯ СВЯЗЬ
- § II.1. ОСНОВНЫЕ ВИДЫ И ХАРАКТЕРИСТИКИ ХИМИЧЕСКОЙ СВЯЗИ
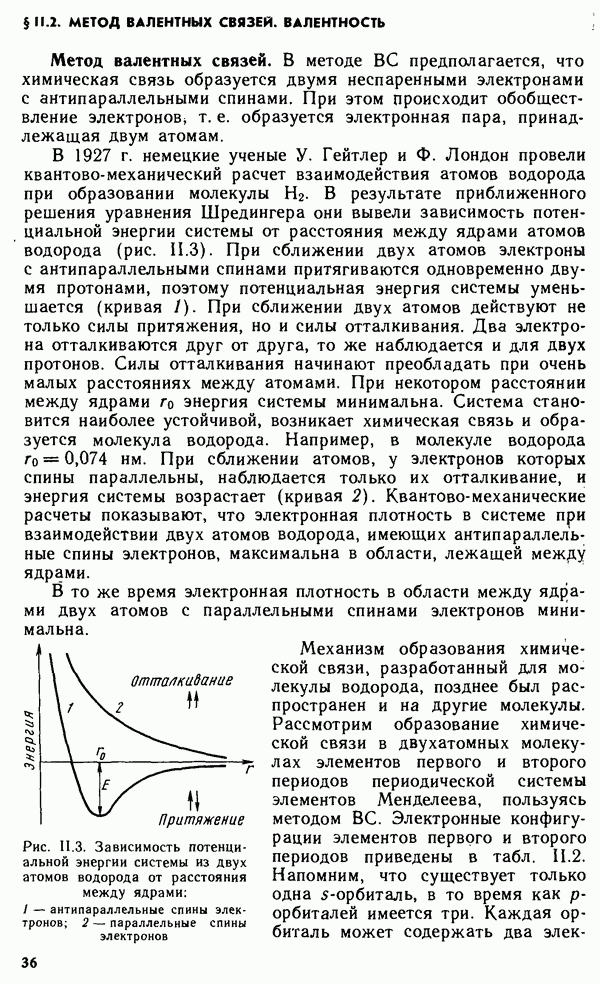
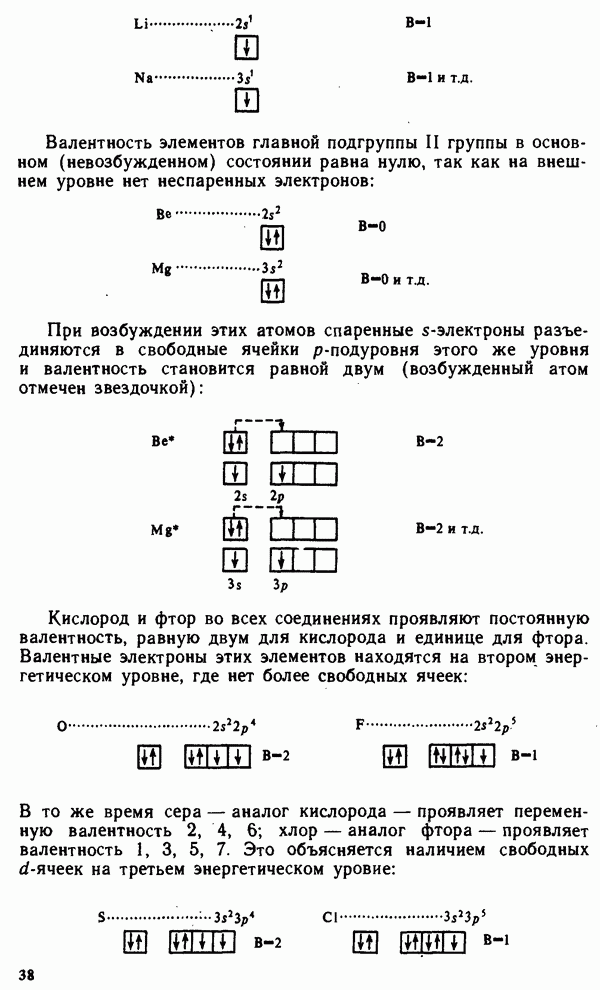
- § II.2. МЕТОД ВАЛЕНТНЫХ СВЯЗЕЙ. ВАЛЕНТНОСТЬ
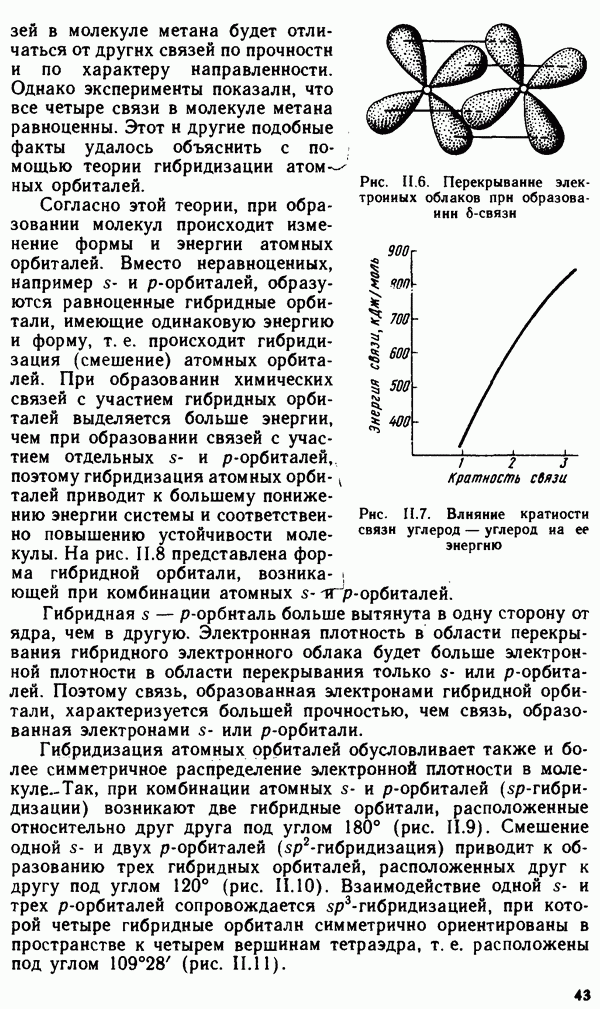
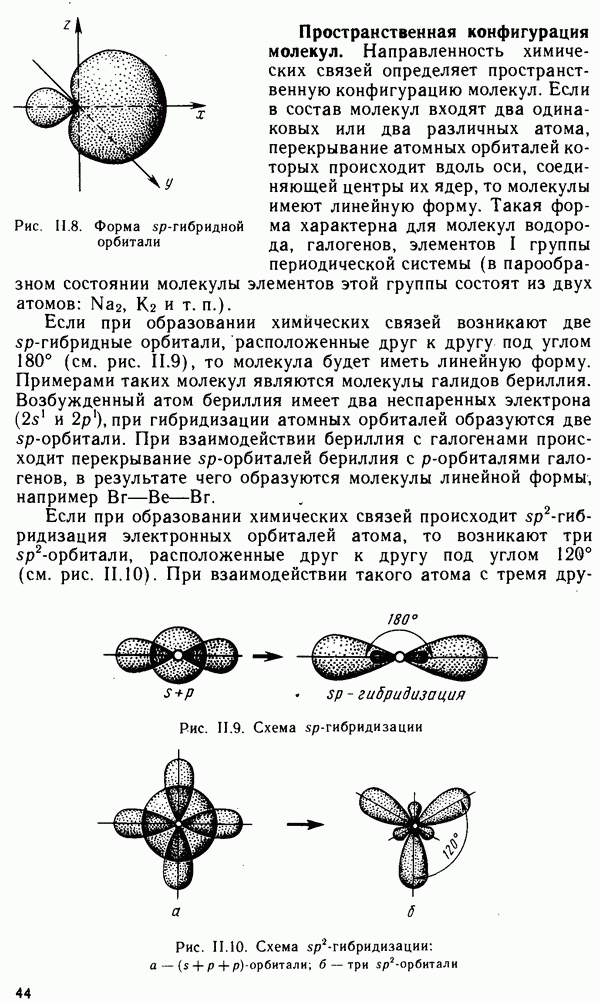
- § II.3. НАПРАВЛЕННОСТЬ КОВАЛЕНТНОЙ СВЯЗИ. ПРОСТРАНСТВЕННАЯ СТРУКТУРА МОЛЕКУЛ
- § 11.4. МЕТОД МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ
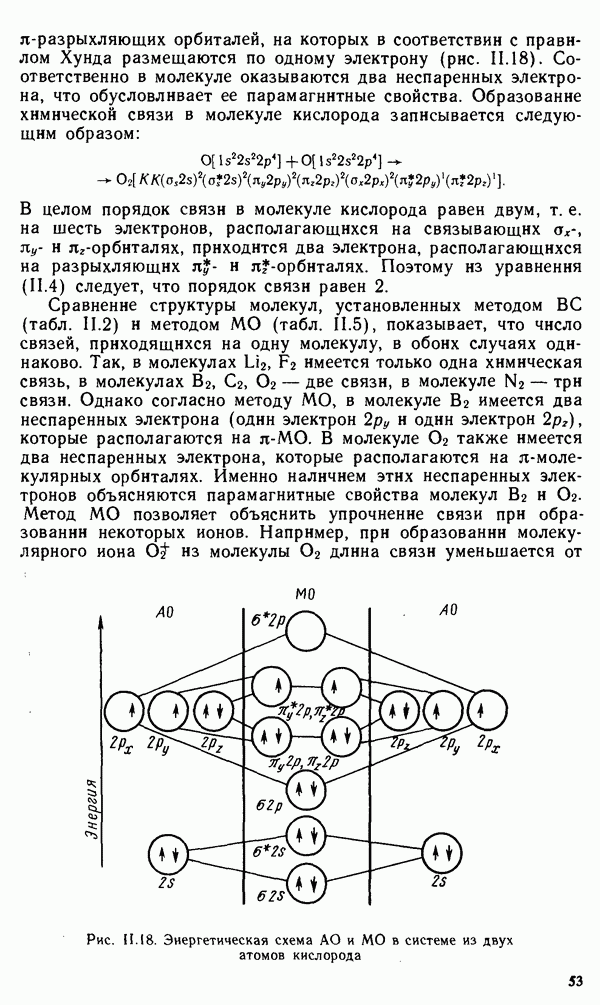
- § 11.5. ЭЛЕКТРОННАЯ СТРУКТУРА НЕКОТОРЫХ МОЛЕКУЛ
- Глава III. ТИПЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ. КОНДЕНСИРОВАННОЕ СОСТОЯНИЕ ВЕЩЕСТВА
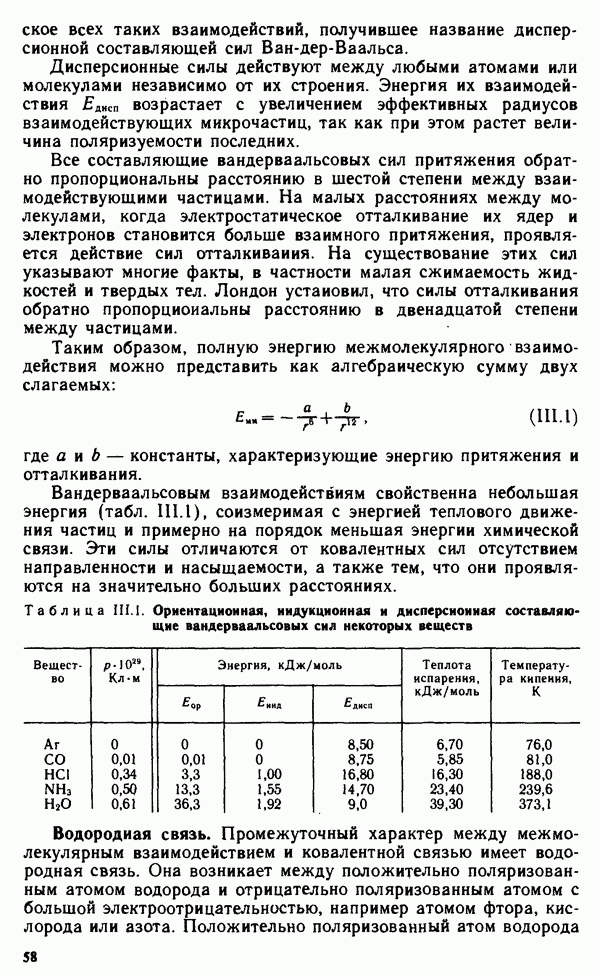
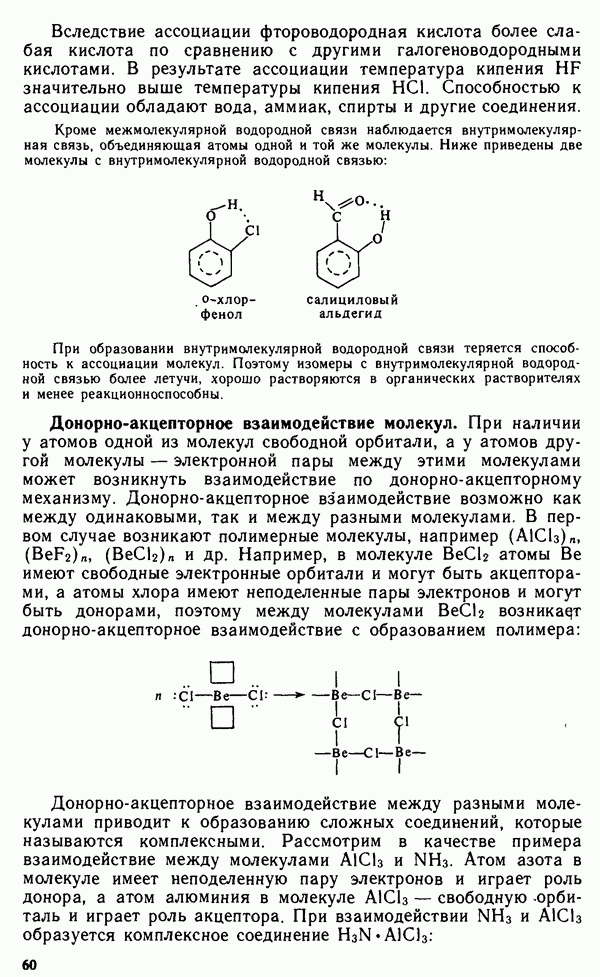
- § III.1. ВЗАИМОДЕЙСТВИЕ МЕЖДУ МОЛЕКУЛАМИ
- § III.2. СВОЙСТВА ВЕЩЕСТВ В РАЗЛИЧНЫХ СОСТОЯНИЯХ
- § III.3. СТРОЕНИЕ КРИСТАЛЛОВ. ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ТЕЛАХ
- § III.4. МЕТАЛЛЫ, ПОЛУПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § III.5. РЕАЛЬНЫЕ КРИСТАЛЛЫ
- 2. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКИХ ПРОЦЕССОВ
- Глава IV. ЭНЕРГЕТИКА ХИМИЧЕСКИХ ПРОЦЕССОВ. ХИМИЧЕСКОЕ СРОДСТВО
- § IV.2. ЭНЕРГЕТИЧЕСКИЕ ЭФФЕКТЫ ХИМИЧЕСКИХ РЕАКЦИЙ И ФАЗОВЫХ ПРЕВРАЩЕНИЙ. ТЕРМОХИМИЧЕСКИЕ ЗАКОНЫ
- § IV.3. ЭНТАЛЬПИЯ ОБРАЗОВАНИЯ ХИМИЧЕСКИХ СОЕДИНЕНИЙ. ТЕРМОХИМИЧЕСКИЕ РАСЧЕТЫ
- § IV.4. ЭНТРОПИЯ. НАПРАВЛЕНИЕ И ПРЕДЕЛ ПРОТЕКАНИЯ ПРОЦЕССОВ В ИЗОЛИРОВАННЫХ СИСТЕМАХ
- § IV.5. ЭНЕРГИЯ ГИББСА И ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА ХИМИЧЕСКОЙ РЕАКЦИИ
- Глава V. ХИМИЧЕСКАЯ КИНЕТИКА И РАВНОВЕСИЕ
- § V.2. СКОРОСТЬ ГЕТЕРОГЕННЫХ ХИМИЧЕСКИХ РЕАКЦИЙ
- § V.3. ЗАВИСИМОСТЬ СКОРОСТИ ХИМИЧЕСКОЙ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- § V.4. ФИЗИЧЕСКИЕ ВОЗДЕЙСТВИЯ НА ХИМИЧЕСКИЕ РЕАКЦИИ. ЦЕПНЫЕ РЕАКЦИИ
- § V.5. КИНЕТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ХИМИЧЕСКОМ РАВНОВЕСИИ
- § V.6. ФАЗОВЫЕ РАВНОВЕСИЯ ПРАВИЛО ФАЗ
- § V.7. АДСОРБЦИОННОЕ РАВНОВЕСИЕ
- § V.8. КАТАЛИЗ
- 3. РАСТВОРЫ ДИСПЕРСНЫЕ СИСТЕМЫ ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- VI.1. ОБЩИЕ ПОНЯТИЯ О РАСТВОРАХ
- § VI.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЖИДКИХ РАСТВОРОВ
- § VI.3. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- § VI.4. ВОДНЫЕ РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- § VI.5. ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ ВОДЫ. ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ
- § VI.6. РАВНОВЕСИЯ В ВОДНЫХ РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- § VI.7. ДИСПЕРСНЫЕ СИСТЕМЫ. КОЛЛОИДНЫЕ РАСТВОРЫ
- § VI.8. УСТОЙЧИВОСТЬ И КОАГУЛЯЦИЯ КОЛЛОИДНЫХ СИСТЕМ
- Глава VII. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ И ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- § VII.1. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ ПРОЦЕССЫ
- § VII.2. ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- § VII.3. ПОТЕНЦИАЛЫ МЕТАЛЛИЧЕСКИХ И ГАЗОВЫХ ЭЛЕКТРОДОВ
- § VII.4. ПОТЕНЦИАЛЫ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ (РЕДОКСИ-) ЭЛЕКТРОДОВ
- § VII.5. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ. ПОЛЯРИЗАЦИЯ
- § VII.6. ЭЛЕКТРОЛИЗ
- Глава VIII. КОРРОЗИЯ И ЗАЩИТА МЕТАЛЛОВ
- § VIII.1. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ КОРРОЗИОННЫХ ПРОЦЕССОВ
- § VIII.2. ХИМИЧЕСКАЯ КОРРОЗИЯ
- § VIII.3. ЭЛЕКТРОХИМИЧЕСКАЯ КОРРОЗИЯ
- § VIII.4. ЗАЩИТА МЕТАЛЛОВ ОТ КОРРОЗИИ
- 4. ОБЩАЯ ХАРАКТЕРИСТИКА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ И ИХ СОЕДИНЕНИЙ
- Глава IX. ПРОСТЫЕ ВЕЩЕСТВА И ДВОЙНЫЕ СОЕДИНЕНИЯ. КРАТКИЙ ОБЗОР ХИМИЧЕСКИХ СВОЙСТВ s- И р-ЭЛЕМЕНТОВ
- § IX.2. МЕТАЛЛЫ И СПЛАВЫ. ОСНОВЫ ФИЗИКО-ХИМИЧЕСКОГО АНАЛИЗА
- § IX.3. ДВОЙНЫЕ СОЕДИНЕНИЯ
- § IX.4. СВОЙСТВА МЕТАЛЛОВ ГЛАВНЫХ ПОДГРУПП I И II ГРУПП
- § IX.5. СВОЙСТВА р-ЭЛЕМЕНТОВ III ГРУППЫ
- § IX.6. СВОЙСТВА р-ЭЛЕМЕНТОВ IV ГРУППЫ
- § IX.7. СВОЙСТВА р-ЭЛЕМЕНТОВ V, VI И VII ГРУПП ПЕРИОДИЧЕСКОЙ СИСТЕМЫ ЭЛЕМЕНТОВ
- Глава Х. КОМПЛЕКСНЫЕ СОЕДИНЕНИЯ
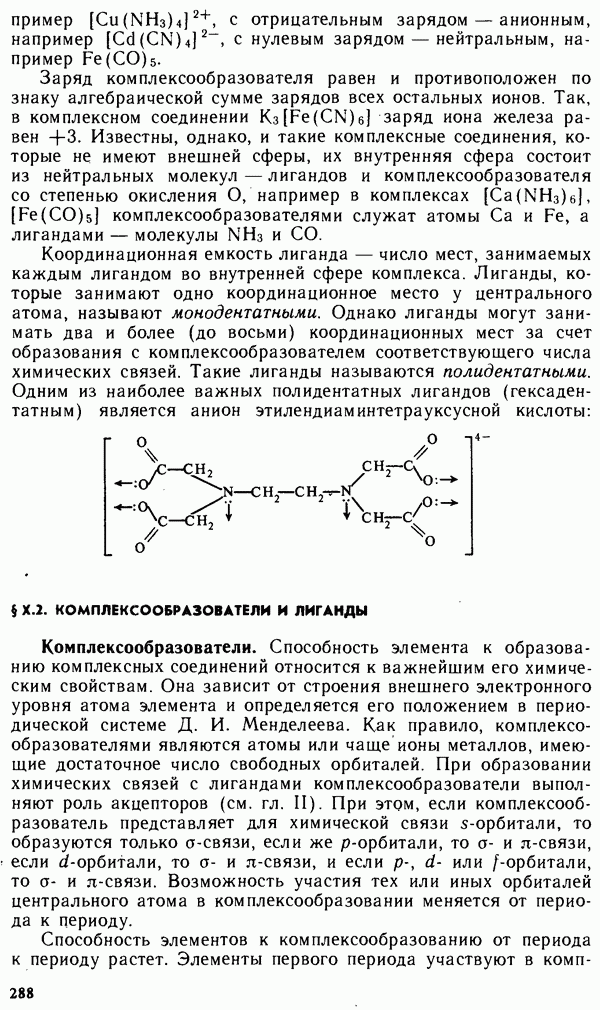
- § Х.1. СТРУКТУРА КОМПЛЕКСНЫХ СОЕДИНЕНИИ
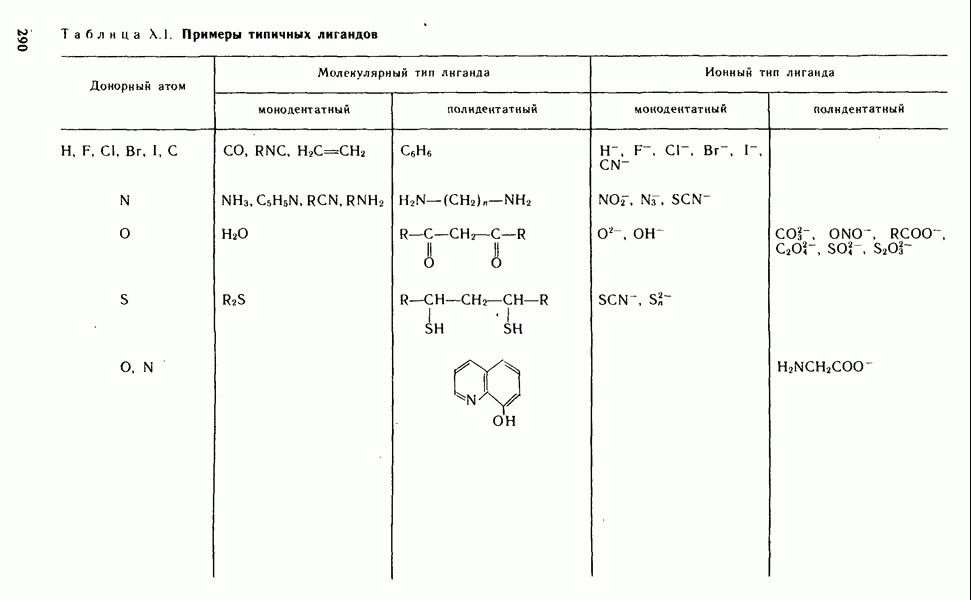
- § Х.2. КОМПЛЕКСООБРАЗОВАТЕЛИ И ЛИГАНДЫ
- § Х.3. НОМЕНКЛАТУРА И КЛАССИФИКАЦИЯ КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
- § Х.4. МЕТОДЫ РАСЧЕТА ХИМИЧЕСКИХ СВЯЗЕЙ В КОМПЛЕКСНЫХ СОЕДИНЕНИЯХ
- § Х.5. УСТОЙЧИВОСТЬ КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
- Глава XI. ОРГАНИЧЕСКИЕ СОЕДИНЕНИЯ
- § XI.1. ОСОБЕННОСТИ. ТЕОРИЯ ХИМИЧЕСКОГО СТРОЕНИЯ И КЛАССИФИКАЦИЯ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- § XI.2. УГЛЕВОДОРОДЫ
- § ХI.3. ПРОИЗВОДНЫЕ УГЛЕВОДОРОДОВ
- 5. СПЕЦИАЛЬНЫЕ ВОПРОСЫ ХИМИИ
- Глава XII. ХИМИЯ КОНСТРУКЦИОННЫХ И ЭЛЕКТРОТЕХНИЧЕСКИХ МАТЕРИАЛОВ
- § XII.2. СВОЙСТВА ПЕРЕХОДНЫХ МЕТАЛЛОВ VIII ГРУППЫ
- § ХII.3. СВОЙСТВА ЭЛЕМЕНТОВ I И II ГРУПП
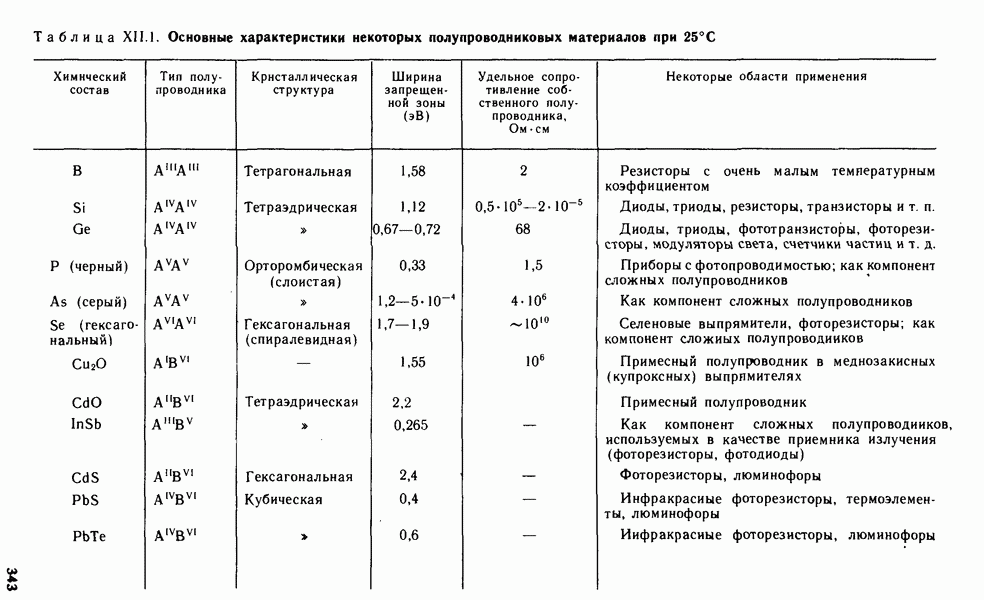
- § XII.4. ХИМИЯ ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ
- § XII.5. МЕТОДЫ ПОЛУЧЕНИЯ МАТЕРИАЛОВ ВЫСОКОЙ ЧИСТОТЫ
- Глава XIII. ПОЛИМЕРНЫЕ МАТЕРИАЛЫ И ИХ ПРИМЕНЕНИЕ В ЭНЕРГЕТИКЕ
- § XIII.1. МЕТОДЫ ПОЛУЧЕНИЯ ПОЛИМЕРОВ
- § XIII.2. СТРОЕНИЕ ПОЛИМЕРОВ
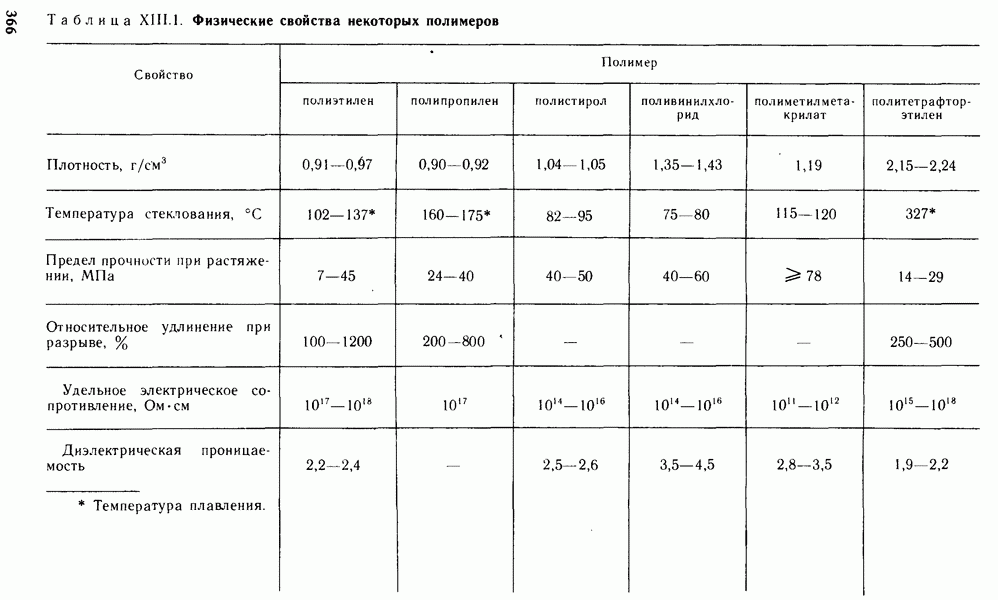
- § XIII.3. СВОЙСТВА ПОЛИМЕРОВ
- § XIII.4. ПРИМЕНЕНИЕ ПОЛИМЕРОВ
- Глава XIV. ХИМИЯ ВОДЫ И ТОПЛИВА. ХИМИЯ И ОХРАНА ОКРУЖАЮЩЕЙ СРЕДЫ
- § XIV.1. СТРОЕНИЕ И СВОЙСТВА ВОДЫ
- § XIV.2. ПРИРОДНЫЕ ВОДЫ
- § ХIV.3. ОСНОВНЫЕ МЕТОДЫ ОЧИСТКИ ВОДЫ
- § XIV.4. СОСТАВ И СВОЙСТВА ОРГАНИЧЕСКОГО ТОПЛИВА
- § XIV.5. ЭКОЛОГИЧЕСКИЕ ПРОБЛЕМЫ ОБЩЕСТВА
- § XIV.6. ОХРАНА ВОЗДУШНОГО БАССЕЙНА
- § XIV.7. ОХРАНА ВОДНОГО БАССЕЙНА
- Глава XV. ЯДЕРНАЯ ХИМИЯ И РАДИОХИМИЯ
- § XV.1. АТОМНОЕ ЯДРО. РАДИОАКТИВНОСТЬ
- § XV.2. ЯДЕРНЫЕ РЕАКЦИИ
- § XV.3. ЯДЕРНАЯ ЭНЕРГЕТИКА
- § XV.4. ХИМИЧЕСКИЕ СВОЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
- Глава XVI. ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ В ЭНЕРГЕТИКЕ, ЭЛЕКТРОНИКЕ И АВТОМАТИКЕ
- § ХVI.1. ХИМИЧЕСКИЕ ИСТОЧНИКИ ТОКА. ЭЛЕКТРОХИМИЧЕСКИЕ ЭНЕРГОУСТАНОВКИ
- § XVI.2. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ (ХЕМОТРОНЫ)
- § ХVI.3. ЭЛЕКТРОХИМИЧЕСКАЯ АНОДНАЯ ОБРАБОТКА МЕТАЛЛОВ И СПЛАВОВ
- § XVI.4. ПОЛУЧЕНИЕ И СВОЙСТВА ГАЛЬВАНОПОКРЫТИИ
- ЗАКЛЮЧЕНИЕ