| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
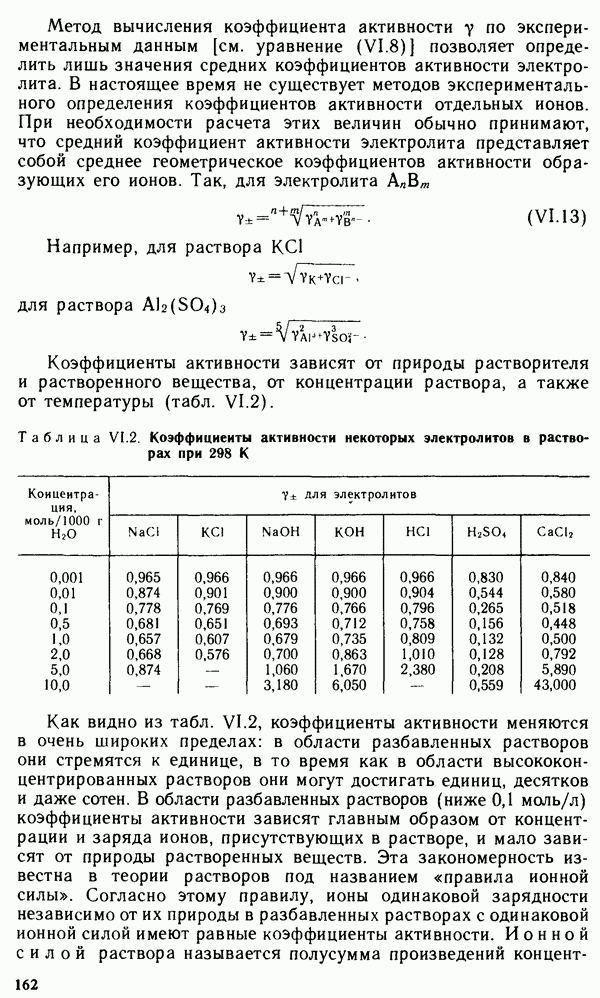
§ 1.2. КВАНТОВО-МЕХАНИЧЕСКАЯ МОДЕЛЬ АТОМА
В 1924 г. французский физик Луи де Бройль высказал идею о том, что материя обладает как волновыми, так и корпускулярными свойствами. Согласно уравнению де Бройля (одному из основных уравнений квантовой механики),

т. е. частице с массой  движущейся со скоростью
движущейся со скоростью  соответствует волна длиной X;
соответствует волна длиной X;  — постоянная Планка.
— постоянная Планка.
Длину волны такой частицы называют длиной волны де Бройля. Для любой частицы с массой  и известной скоростью
и известной скоростью  длину волны де Бройля можно рассчитать. Идея де Бройля была экспериментально подтверждена в
длину волны де Бройля можно рассчитать. Идея де Бройля была экспериментально подтверждена в  когда были обнаружены у электронов как волновые, так и корпускулярные свойства.
когда были обнаружены у электронов как волновые, так и корпускулярные свойства.
 немецким ученым В. Гейзенбергом был предложен принцип неопределенности, согласно которому для микрочастиц невозможно одновременно точно определить и координату частицы X, и составляющую
немецким ученым В. Гейзенбергом был предложен принцип неопределенности, согласно которому для микрочастиц невозможно одновременно точно определить и координату частицы X, и составляющую  импульса вдоль оси х. Математически принцип неопределенности записывают следующими уравнениями:
импульса вдоль оси х. Математически принцип неопределенности записывают следующими уравнениями:

Отсюда следует, что при точном определении координаты  микрочастицы исчезает информация о ее импульсе
микрочастицы исчезает информация о ее импульсе  так как при
так как при  величина
величина  Если удастся снизить погрешность
Если удастся снизить погрешность  будет велика погрешность
будет велика погрешность  Источник этих погрешностей заключен не в приборах, а в самой природе вещей.
Источник этих погрешностей заключен не в приборах, а в самой природе вещей.
Поскольку постоянная Планка очень мала, то ограничения, накладываемые принципом неопределенности, существенны только в масштабах атомных размеров. Согласно принципу неопределенности, невозможно утверждать, что электрон, имеющий определенную скорость, находится в данной точке пространства, здесь можно использовать лишь вероятностное описание.
Для описания свойств электрона используют волновую функцию, которую обозначают буквой  Квадрат ее модуля
Квадрат ее модуля  вычисленный для определенного момента времени и определенной точки пространства, пропорционален вероятности обнаружить частицу в этой точке в указанное время. Величину
вычисленный для определенного момента времени и определенной точки пространства, пропорционален вероятности обнаружить частицу в этой точке в указанное время. Величину  называют плотностью вероятности. Наглядное представление о распределении электронной плотности атома дает функция радиального распределения. Такая функция служит мерой вероятности нахождения электрона в сферическом слое между расстояниями
называют плотностью вероятности. Наглядное представление о распределении электронной плотности атома дает функция радиального распределения. Такая функция служит мерой вероятности нахождения электрона в сферическом слое между расстояниями  от ядра. Объем, лежащий между двумя сферами, имеющими радиусы
от ядра. Объем, лежащий между двумя сферами, имеющими радиусы  равен
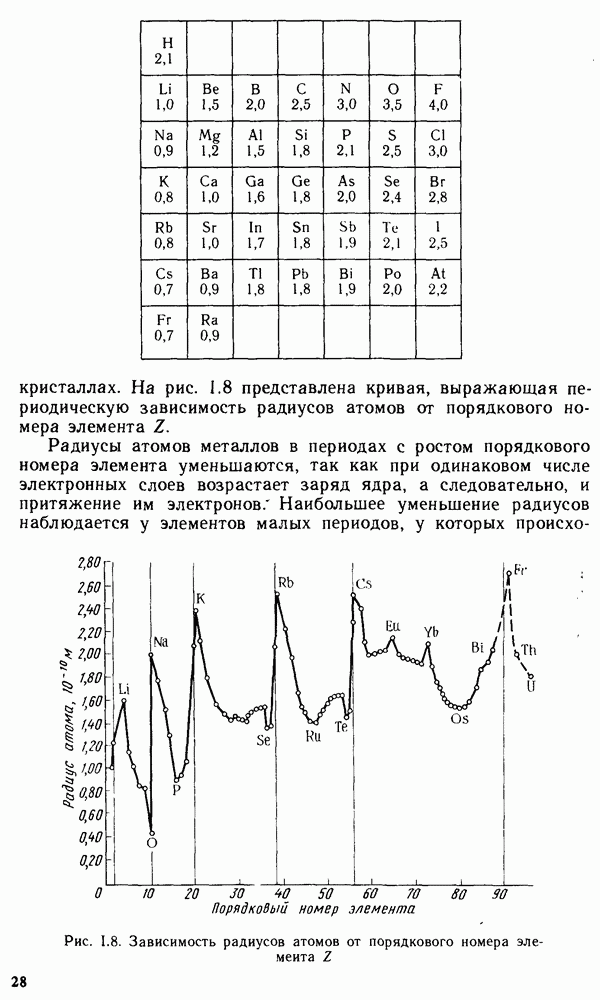
равен  а вероятность нахождения электрона в этом элементарном объеме может быть представлена графически в виде зависимостей функции радиального распределения. На рис. 1.2 представлена функция вероятности для основного энергетического состояния электрона в атоме водорода. Плотность вероятности
а вероятность нахождения электрона в этом элементарном объеме может быть представлена графически в виде зависимостей функции радиального распределения. На рис. 1.2 представлена функция вероятности для основного энергетического состояния электрона в атоме водорода. Плотность вероятности  достигает максимального значения на некотором конечном расстоянии от ядра. При этом наиболее вероятное значение
достигает максимального значения на некотором конечном расстоянии от ядра. При этом наиболее вероятное значение  для электрона атома водорода равно радиусу орбиты
для электрона атома водорода равно радиусу орбиты  соответствующей основному состоянию электрона в модели Бора. Различная плотность вероятности дает представление об электроне, как бы размазанном вокруг ядра в виде так называемого
соответствующей основному состоянию электрона в модели Бора. Различная плотность вероятности дает представление об электроне, как бы размазанном вокруг ядра в виде так называемого

Рис. 1.2. Радиальное распределение вероятности пребывания электрона для основного энергетического  стояния атома водорода
стояния атома водорода

Рис. 1.3. Электронное  -облако
-облако
электронного облака (рис. 1.3). Чем больше величина  , тем больше вероятность нахождения электрона в данной области атомного пространства.
, тем больше вероятность нахождения электрона в данной области атомного пространства.
В квантовой механике вместо термина «орбита» используют термин «орбиталь», которым называют волновую функцию электрона. Соответственно орбиталь характеризует и энергию и форму пространственного распределения электронного облака.
Расчеты в квантовой механике проводят с помощью предложенного в 1926 г. австрийским ученым Э. Шредингером уравнения, которое является математическим описанием электронного строения атома в трехмерном-пространстве.
В простейшем случае уравнение Шредингера может быть записано в виде

где  — постоянная Планка;
— постоянная Планка;  — масса частицы;
— масса частицы;  — потенциальная энергия; Е — полная энергия;
— потенциальная энергия; Е — полная энергия;  — координаты;
— координаты;  — волновая функция.
— волновая функция.
Решая уравнение Шредингера, находят волновую функцию  Решение уравнения Шредингера возможно лишь при определенных значениях полной энергии Е. Определив вероятностную функцию
Решение уравнения Шредингера возможно лишь при определенных значениях полной энергии Е. Определив вероятностную функцию  можно оценить величину
можно оценить величину  — вероятность нахождения электрона в объеме пространства
— вероятность нахождения электрона в объеме пространства  окружающего атомное ядро. Решение уравнения Шредингера представляет сложную математическую задачу.
окружающего атомное ядро. Решение уравнения Шредингера представляет сложную математическую задачу.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. ПРЕДМЕТ ХИМИИ
- § 2. ЗНАЧЕНИЕ ХИМИИ В ИЗУЧЕНИИ ПРИРОДЫ И РАЗВИТИИ ТЕХНИКИ
- 1. СТРОЕНИЕ ВЕЩЕСТВА
- Глава I. СТРОЕНИЕ АТОМА И СИСТЕМАТИКА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- § 1.2. КВАНТОВО-МЕХАНИЧЕСКАЯ МОДЕЛЬ АТОМА
- § 1.3. КВАНТОВЫЕ ЧИСЛА И АТОМНЫЕ ОРБИТАЛИ
- § 1.4. МНОГОЭЛЕКТРОННЫЕ АТОМЫ
- § 1.5. ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ Д. И. МЕНДЕЛЕЕВА
- § 1.6. ПЕРИОДИЧЕСКОЕ ИЗМЕНЕНИЕ СВОЙСТВ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- Глава II. ХИМИЧЕСКАЯ СВЯЗЬ
- § II.1. ОСНОВНЫЕ ВИДЫ И ХАРАКТЕРИСТИКИ ХИМИЧЕСКОЙ СВЯЗИ
- § II.2. МЕТОД ВАЛЕНТНЫХ СВЯЗЕЙ. ВАЛЕНТНОСТЬ
- § II.3. НАПРАВЛЕННОСТЬ КОВАЛЕНТНОЙ СВЯЗИ. ПРОСТРАНСТВЕННАЯ СТРУКТУРА МОЛЕКУЛ
- § 11.4. МЕТОД МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ
- § 11.5. ЭЛЕКТРОННАЯ СТРУКТУРА НЕКОТОРЫХ МОЛЕКУЛ
- Глава III. ТИПЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ. КОНДЕНСИРОВАННОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- § III.1. ВЗАИМОДЕЙСТВИЕ МЕЖДУ МОЛЕКУЛАМИ
- § III.2. СВОЙСТВА ВЕЩЕСТВ В РАЗЛИЧНЫХ СОСТОЯНИЯХ
- § III.3. СТРОЕНИЕ КРИСТАЛЛОВ. ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ТЕЛАХ
- § III.4. МЕТАЛЛЫ, ПОЛУПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § III.5. РЕАЛЬНЫЕ КРИСТАЛЛЫ
- 2. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКИХ ПРОЦЕССОВ
- Глава IV. ЭНЕРГЕТИКА ХИМИЧЕСКИХ ПРОЦЕССОВ. ХИМИЧЕСКОЕ СРОДСТВО
- § IV.2. ЭНЕРГЕТИЧЕСКИЕ ЭФФЕКТЫ ХИМИЧЕСКИХ РЕАКЦИЙ И ФАЗОВЫХ ПРЕВРАЩЕНИЙ. ТЕРМОХИМИЧЕСКИЕ ЗАКОНЫ
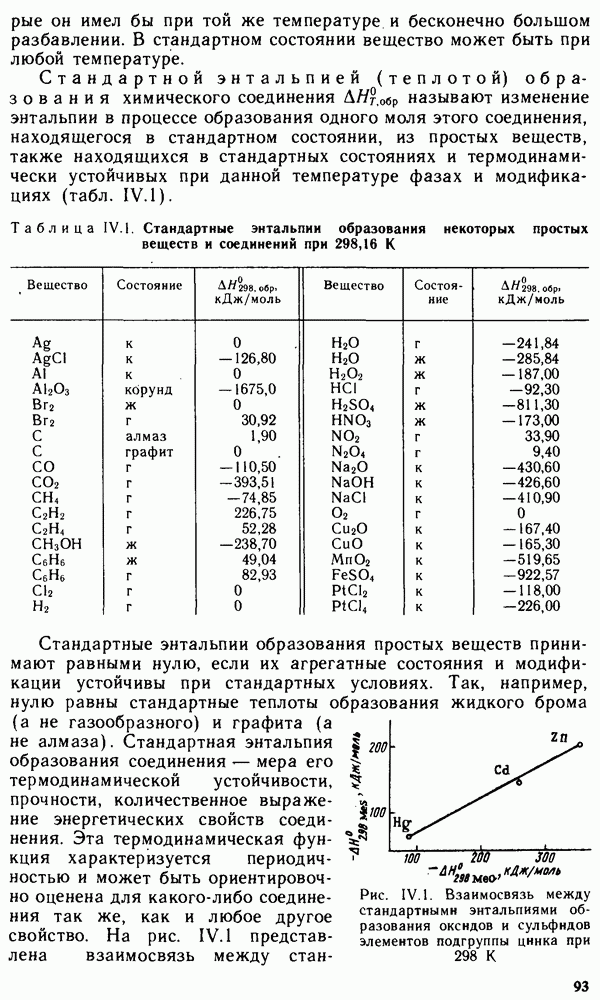
- § IV.3. ЭНТАЛЬПИЯ ОБРАЗОВАНИЯ ХИМИЧЕСКИХ СОЕДИНЕНИЙ. ТЕРМОХИМИЧЕСКИЕ РАСЧЕТЫ
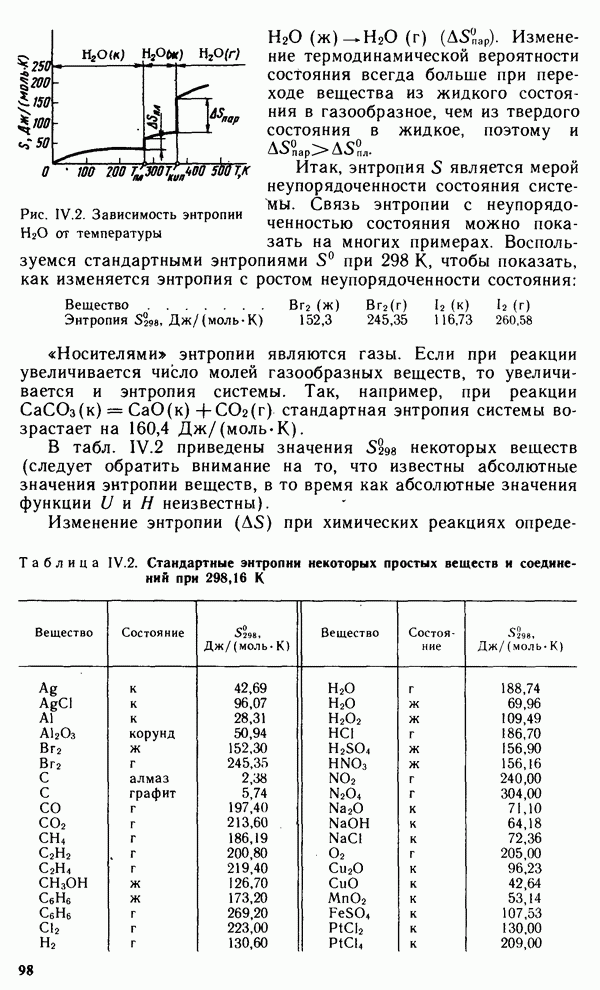
- § IV.4. ЭНТРОПИЯ. НАПРАВЛЕНИЕ И ПРЕДЕЛ ПРОТЕКАНИЯ ПРОЦЕССОВ В ИЗОЛИРОВАННЫХ СИСТЕМАХ
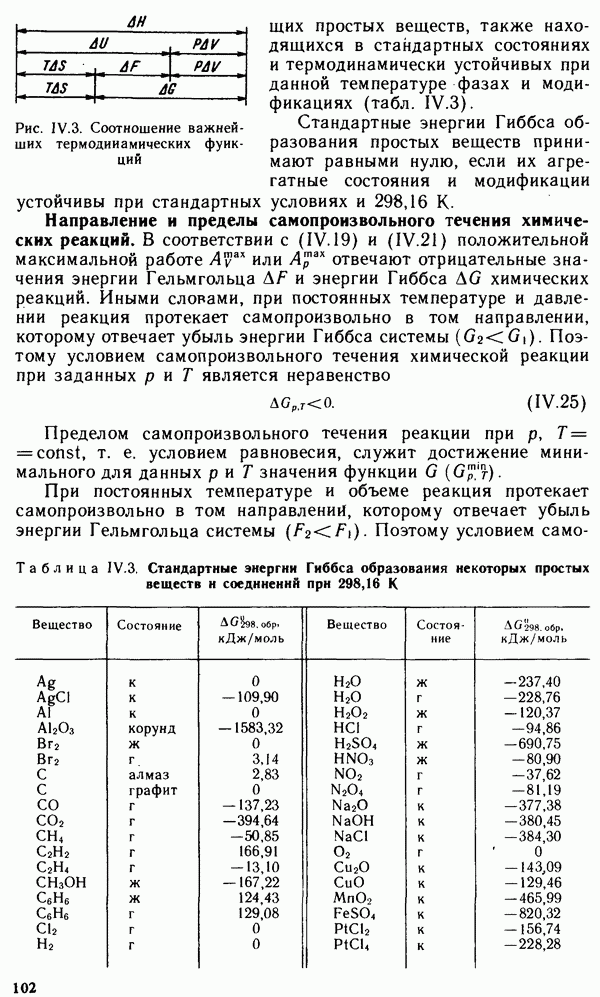
- § IV.5. ЭНЕРГИЯ ГИББСА И ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА ХИМИЧЕСКОЙ РЕАКЦИИ
- Глава V. ХИМИЧЕСКАЯ КИНЕТИКА И РАВНОВЕСИЕ
- § V.2. СКОРОСТЬ ГЕТЕРОГЕННЫХ ХИМИЧЕСКИХ РЕАКЦИЙ
- § V.3. ЗАВИСИМОСТЬ СКОРОСТИ ХИМИЧЕСКОЙ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
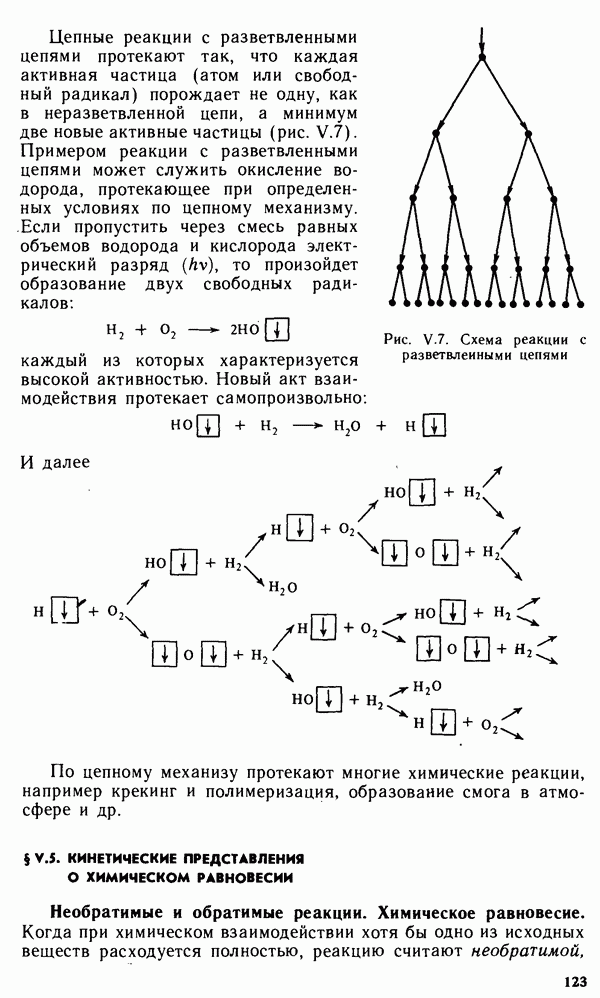
- § V.4. ФИЗИЧЕСКИЕ ВОЗДЕЙСТВИЯ НА ХИМИЧЕСКИЕ РЕАКЦИИ. ЦЕПНЫЕ РЕАКЦИИ
- § V.5. КИНЕТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ХИМИЧЕСКОМ РАВНОВЕСИИ
- § V.6. ФАЗОВЫЕ РАВНОВЕСИЯ ПРАВИЛО ФАЗ
- § V.7. АДСОРБЦИОННОЕ РАВНОВЕСИЕ
- § V.8. КАТАЛИЗ
- 3. РАСТВОРЫ ДИСПЕРСНЫЕ СИСТЕМЫ ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- VI.1. ОБЩИЕ ПОНЯТИЯ О РАСТВОРАХ
- § VI.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЖИДКИХ РАСТВОРОВ
- § VI.3. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- § VI.4. ВОДНЫЕ РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- § VI.5. ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ ВОДЫ. ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ
- § VI.6. РАВНОВЕСИЯ В ВОДНЫХ РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- § VI.7. ДИСПЕРСНЫЕ СИСТЕМЫ. КОЛЛОИДНЫЕ РАСТВОРЫ
- § VI.8. УСТОЙЧИВОСТЬ И КОАГУЛЯЦИЯ КОЛЛОИДНЫХ СИСТЕМ
- Глава VII. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ И ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- § VII.1. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ ПРОЦЕССЫ
- § VII.2. ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- § VII.3. ПОТЕНЦИАЛЫ МЕТАЛЛИЧЕСКИХ И ГАЗОВЫХ ЭЛЕКТРОДОВ
- § VII.4. ПОТЕНЦИАЛЫ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ (РЕДОКСИ-) ЭЛЕКТРОДОВ
- § VII.5. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ. ПОЛЯРИЗАЦИЯ
- § VII.6. ЭЛЕКТРОЛИЗ
- Глава VIII. КОРРОЗИЯ И ЗАЩИТА МЕТАЛЛОВ
- § VIII.1. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ КОРРОЗИОННЫХ ПРОЦЕССОВ
- § VIII.2. ХИМИЧЕСКАЯ КОРРОЗИЯ
- § VIII.3. ЭЛЕКТРОХИМИЧЕСКАЯ КОРРОЗИЯ
- § VIII.4. ЗАЩИТА МЕТАЛЛОВ ОТ КОРРОЗИИ
- 4. ОБЩАЯ ХАРАКТЕРИСТИКА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ И ИХ СОЕДИНЕНИЙ
- Глава IX. ПРОСТЫЕ ВЕЩЕСТВА И ДВОЙНЫЕ СОЕДИНЕНИЯ. КРАТКИЙ ОБЗОР ХИМИЧЕСКИХ СВОЙСТВ s- И р-ЭЛЕМЕНТОВ
- § IX.2. МЕТАЛЛЫ И СПЛАВЫ. ОСНОВЫ ФИЗИКО-ХИМИЧЕСКОГО АНАЛИЗА
- § IX.3. ДВОЙНЫЕ СОЕДИНЕНИЯ
- § IX.4. СВОЙСТВА МЕТАЛЛОВ ГЛАВНЫХ ПОДГРУПП I И II ГРУПП
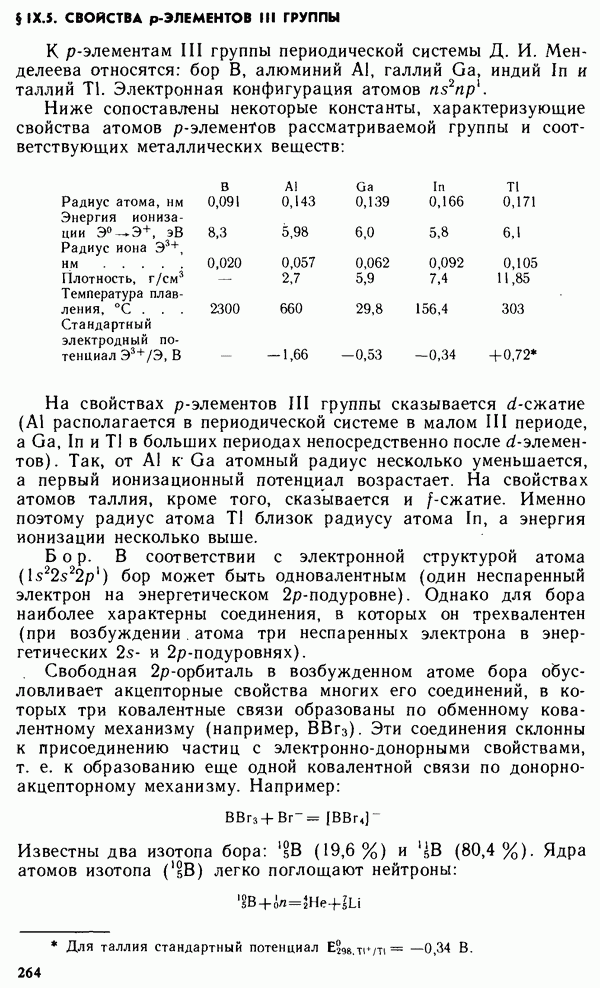
- § IX.5. СВОЙСТВА р-ЭЛЕМЕНТОВ III ГРУППЫ
- § IX.6. СВОЙСТВА р-ЭЛЕМЕНТОВ IV ГРУППЫ
- § IX.7. СВОЙСТВА р-ЭЛЕМЕНТОВ V, VI И VII ГРУПП ПЕРИОДИЧЕСКОЙ СИСТЕМЫ ЭЛЕМЕНТОВ
- Глава Х. КОМПЛЕКСНЫЕ СОЕДИНЕНИЯ
- § Х.1. СТРУКТУРА КОМПЛЕКСНЫХ СОЕДИНЕНИИ
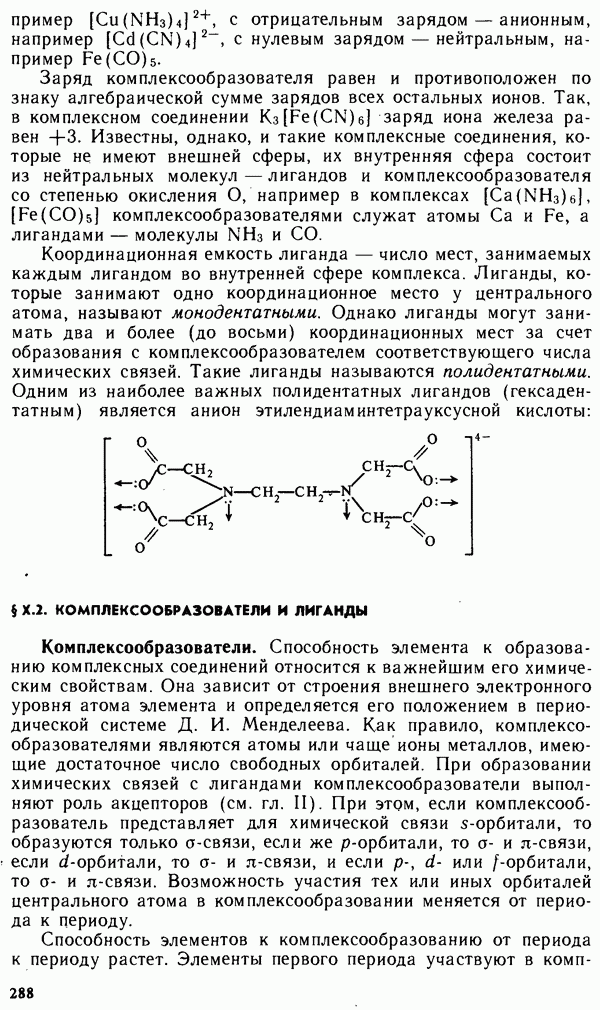
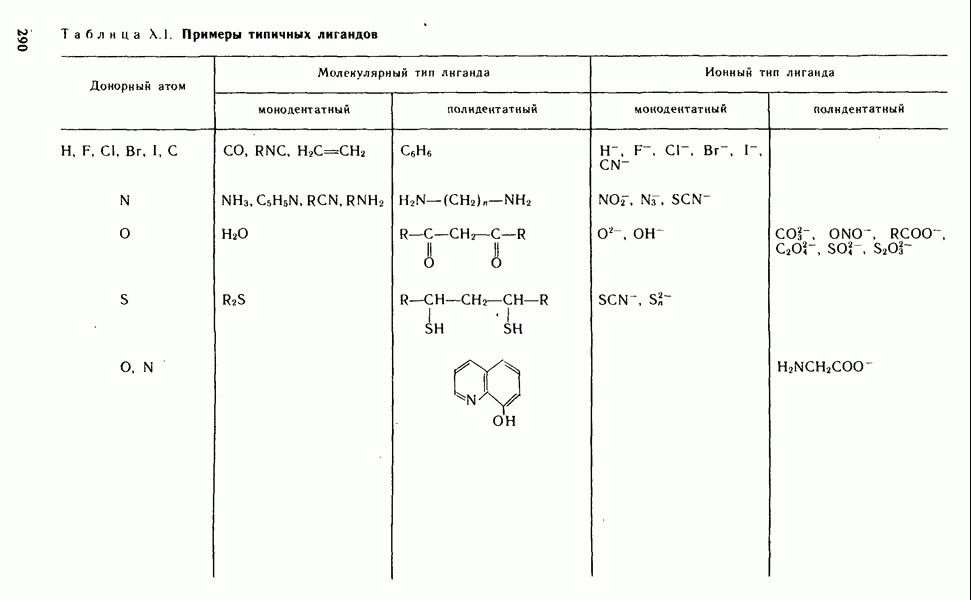
- § Х.2. КОМПЛЕКСООБРАЗОВАТЕЛИ И ЛИГАНДЫ
- § Х.3. НОМЕНКЛАТУРА И КЛАССИФИКАЦИЯ КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
- § Х.4. МЕТОДЫ РАСЧЕТА ХИМИЧЕСКИХ СВЯЗЕЙ В КОМПЛЕКСНЫХ СОЕДИНЕНИЯХ
- § Х.5. УСТОЙЧИВОСТЬ КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
- Глава XI. ОРГАНИЧЕСКИЕ СОЕДИНЕНИЯ
- § XI.1. ОСОБЕННОСТИ. ТЕОРИЯ ХИМИЧЕСКОГО СТРОЕНИЯ И КЛАССИФИКАЦИЯ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- § XI.2. УГЛЕВОДОРОДЫ
- § ХI.3. ПРОИЗВОДНЫЕ УГЛЕВОДОРОДОВ
- 5. СПЕЦИАЛЬНЫЕ ВОПРОСЫ ХИМИИ
- Глава XII. ХИМИЯ КОНСТРУКЦИОННЫХ И ЭЛЕКТРОТЕХНИЧЕСКИХ МАТЕРИАЛОВ
- § XII.2. СВОЙСТВА ПЕРЕХОДНЫХ МЕТАЛЛОВ VIII ГРУППЫ
- § ХII.3. СВОЙСТВА ЭЛЕМЕНТОВ I И II ГРУПП
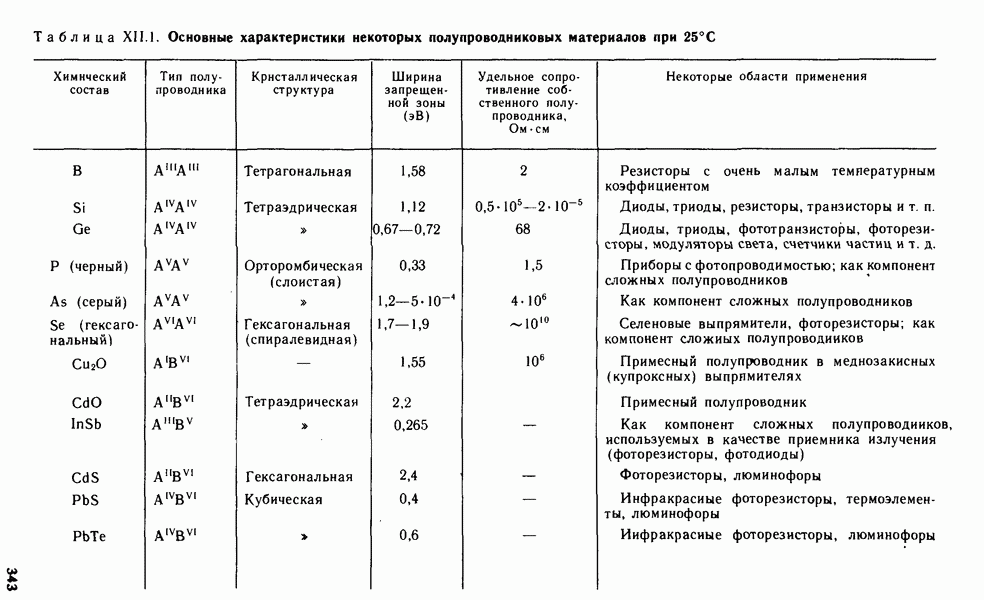
- § XII.4. ХИМИЯ ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ
- § XII.5. МЕТОДЫ ПОЛУЧЕНИЯ МАТЕРИАЛОВ ВЫСОКОЙ ЧИСТОТЫ
- Глава XIII. ПОЛИМЕРНЫЕ МАТЕРИАЛЫ И ИХ ПРИМЕНЕНИЕ В ЭНЕРГЕТИКЕ
- § XIII.1. МЕТОДЫ ПОЛУЧЕНИЯ ПОЛИМЕРОВ
- § XIII.2. СТРОЕНИЕ ПОЛИМЕРОВ
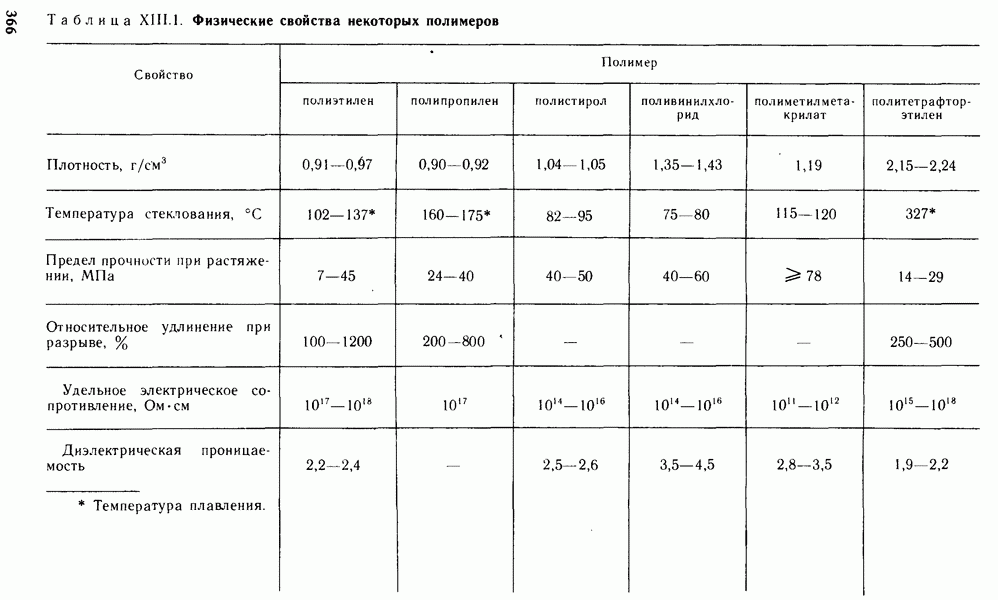
- § XIII.3. СВОЙСТВА ПОЛИМЕРОВ
- § XIII.4. ПРИМЕНЕНИЕ ПОЛИМЕРОВ
- Глава XIV. ХИМИЯ ВОДЫ И ТОПЛИВА. ХИМИЯ И ОХРАНА ОКРУЖАЮЩЕЙ СРЕДЫ
- § XIV.1. СТРОЕНИЕ И СВОЙСТВА ВОДЫ
- § XIV.2. ПРИРОДНЫЕ ВОДЫ
- § ХIV.3. ОСНОВНЫЕ МЕТОДЫ ОЧИСТКИ ВОДЫ
- § XIV.4. СОСТАВ И СВОЙСТВА ОРГАНИЧЕСКОГО ТОПЛИВА
- § XIV.5. ЭКОЛОГИЧЕСКИЕ ПРОБЛЕМЫ ОБЩЕСТВА
- § XIV.6. ОХРАНА ВОЗДУШНОГО БАССЕЙНА
- § XIV.7. ОХРАНА ВОДНОГО БАССЕЙНА
- Глава XV. ЯДЕРНАЯ ХИМИЯ И РАДИОХИМИЯ
- § XV.1. АТОМНОЕ ЯДРО. РАДИОАКТИВНОСТЬ
- § XV.2. ЯДЕРНЫЕ РЕАКЦИИ
- § XV.3. ЯДЕРНАЯ ЭНЕРГЕТИКА
- § XV.4. ХИМИЧЕСКИЕ СВОЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
- Глава XVI. ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ В ЭНЕРГЕТИКЕ, ЭЛЕКТРОНИКЕ И АВТОМАТИКЕ
- § ХVI.1. ХИМИЧЕСКИЕ ИСТОЧНИКИ ТОКА. ЭЛЕКТРОХИМИЧЕСКИЕ ЭНЕРГОУСТАНОВКИ
- § XVI.2. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ (ХЕМОТРОНЫ)
- § ХVI.3. ЭЛЕКТРОХИМИЧЕСКАЯ АНОДНАЯ ОБРАБОТКА МЕТАЛЛОВ И СПЛАВОВ
- § XVI.4. ПОЛУЧЕНИЕ И СВОЙСТВА ГАЛЬВАНОПОКРЫТИИ
- ЗАКЛЮЧЕНИЕ