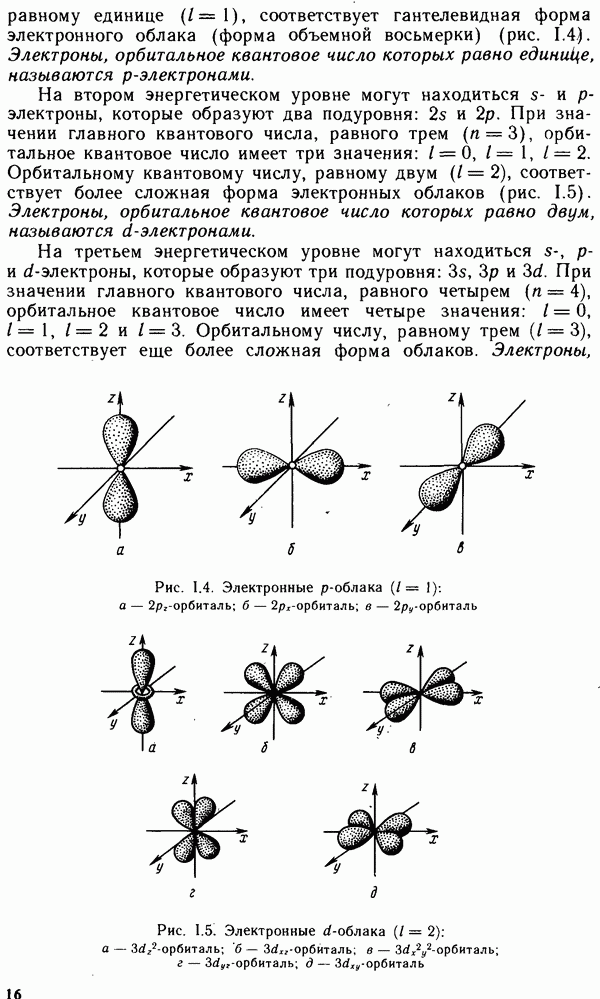
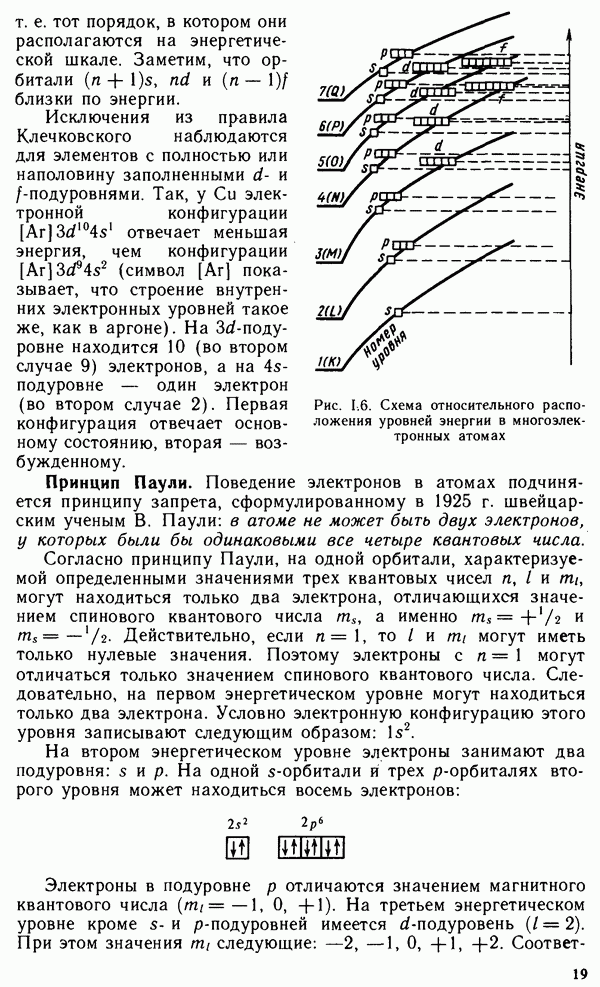
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ V.6. ФАЗОВЫЕ РАВНОВЕСИЯ ПРАВИЛО ФАЗ
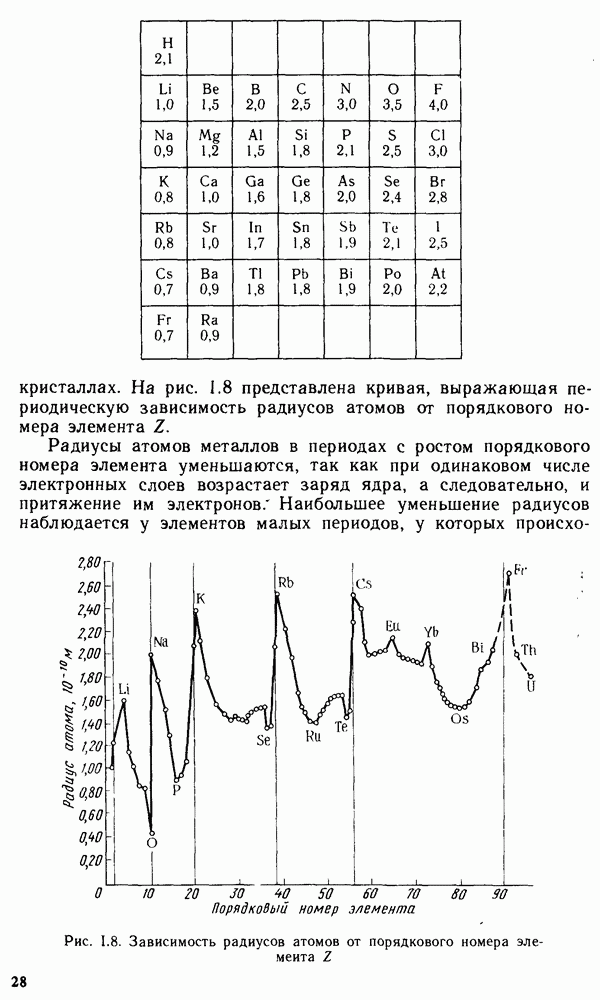
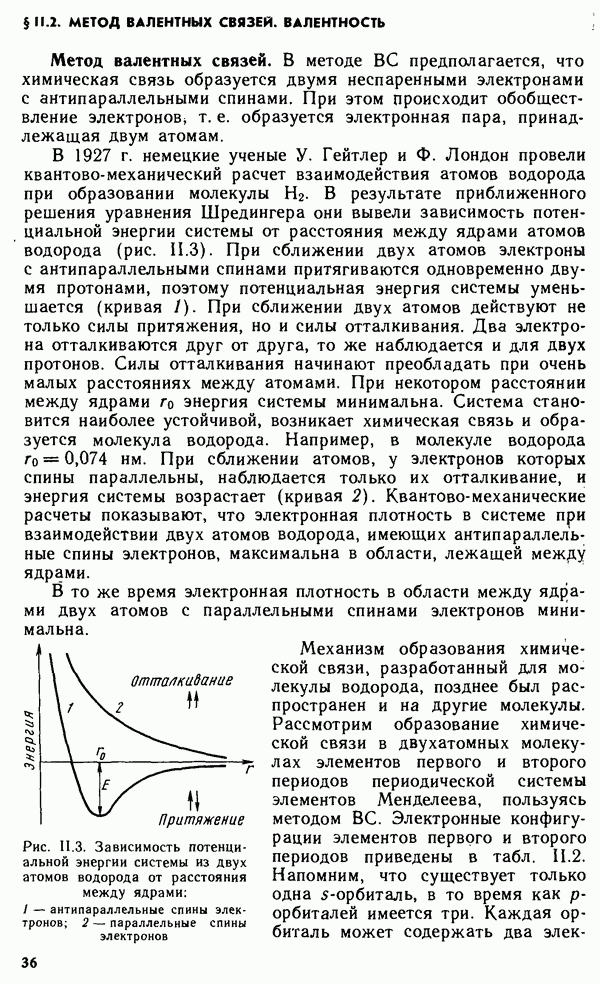
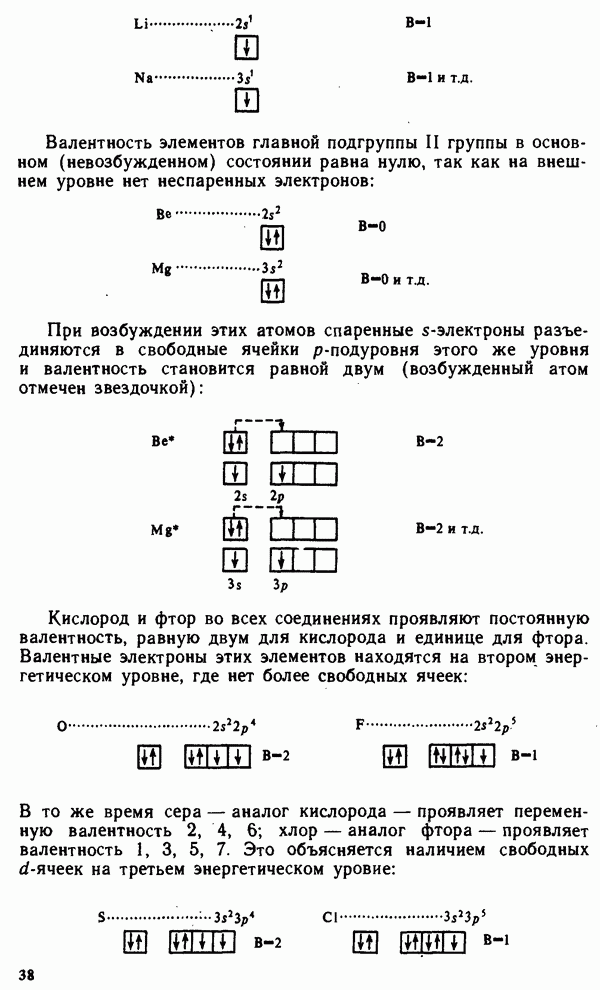
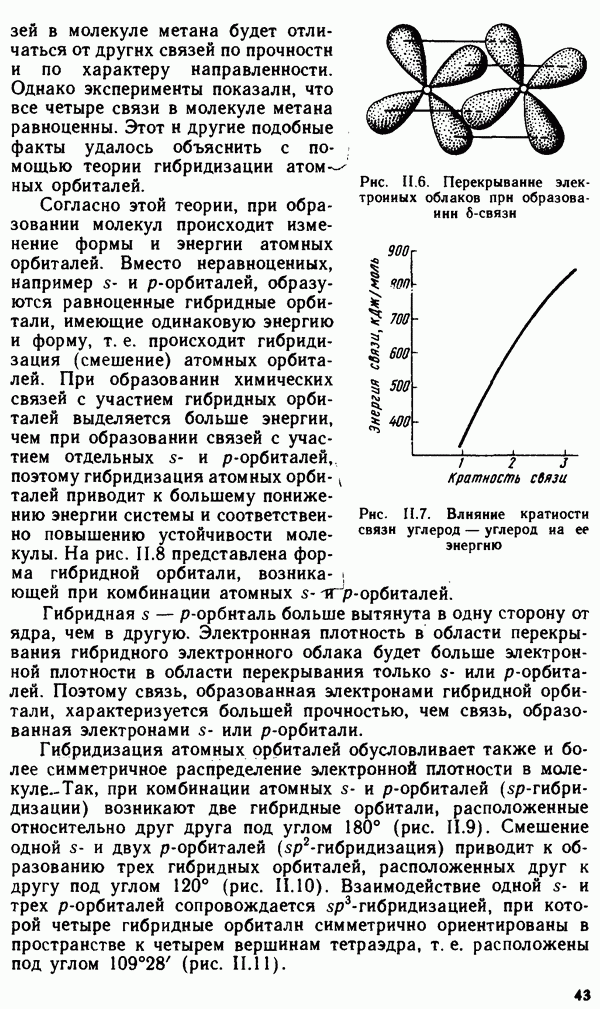
Гетерогенные равновесия, связанные с переходом вещества из одной фазы в другую без изменения химического состава, называются фазовыми. К их числу можно отнести равновесия в процессах
испарения, плавления, конденсации и т. п. Фазовые равновесия, так же как химические, характеризуются минимальным значением энергии Гиббса системы и равенством скоростей прямого и обратного процессов. Так, например, равновесие в системе лед — вода:  характеризуется равенством скоростей плавления льда и кристаллизации воды.
характеризуется равенством скоростей плавления льда и кристаллизации воды.
Для фазовых равновесий справедлив принцип Ле Шателье. В системе лед — вода равновесие можно сместить в правую сторону (в сторону плавления льда), повышая температуру, так как переход  сопровождается поглощением энергии
сопровождается поглощением энергии  , а в системе пар — вода:
, а в системе пар — вода:  при повышении температуры равновесие смещается в левую сторону (в сторону испарения воды), так как поглощением энергии сопровождается процесс
при повышении температуры равновесие смещается в левую сторону (в сторону испарения воды), так как поглощением энергии сопровождается процесс 
Одним из наиболее общих законов гетерогенных (в том числе и фазовых) равновесий является правило фаз. Согласно этому правилу, в равновесной системе число фаз Ф, число независимых компонентов К и число степеней свободы С связаны соотно-: шением

где  — число внешних факторов, влияющих на равновесие системы.
— число внешних факторов, влияющих на равновесие системы.
До сих пор понятие «компонент» использовалось для обозначения какого-либо вещества, являющегося составной частью системы. Например, в водном растворе сульфата меди компонентами являются  Теперь введем понятие «независимый компонент». Число независимых компонентов К в системе — наименьшее число ее компонентов, достаточное для образования всех фаз данной системы. При рассмотрении фазовых равновесий, когда в системе не происходит химических превращений, понятия «компонент» и «независимый компонент» совпадают. Но если в системе протекает химическая реакция, эти понятия различаются. При химическом равновесии относительные количества всех веществ в системе взаимно связаны. Так, в системе
Теперь введем понятие «независимый компонент». Число независимых компонентов К в системе — наименьшее число ее компонентов, достаточное для образования всех фаз данной системы. При рассмотрении фазовых равновесий, когда в системе не происходит химических превращений, понятия «компонент» и «независимый компонент» совпадают. Но если в системе протекает химическая реакция, эти понятия различаются. При химическом равновесии относительные количества всех веществ в системе взаимно связаны. Так, в системе  три компонента, но независимыми являются только два
три компонента, но независимыми являются только два  так как при равновесии содержание любого из трех компонентов однозначно определяется содержанием двух других:
так как при равновесии содержание любого из трех компонентов однозначно определяется содержанием двух других:

где  — константа равновесия.
— константа равновесия.
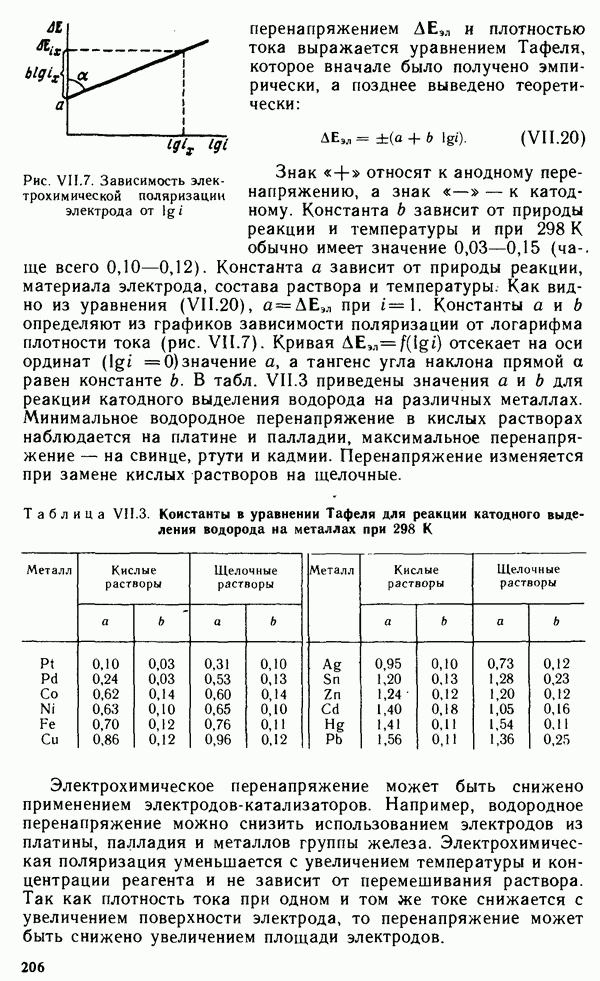
В общем случае число независимых компонентов К равно

Рис. V.10. Диаграмма состояния 
общему числу компонентов за вычетом числа уравнений независимых реакций, связывающих эти компоненты.
Внешними факторами, влияющими на равновесие системы, чаще всего бывают температура и давление. Тогда  и уравнение (V.35) принимает вид
и уравнение (V.35) принимает вид

Число степеней свободы (точнее термодинамических степеней свободы) С равно числу условий (температура, давление, концентрация), произвольное изменение которых в известных пределах не меняет числа и вида фаз системы. По числу степеней свободы системы делят на инвариантные  моновариантные
моновариантные  бивариантные
бивариантные  и поливариантные
и поливариантные 
Рассмотрим однокомпонентную систему  Согласно уравнению (V.36), при
Согласно уравнению (V.36), при  Поскольку число степеней свободы не может быть отрицательным, число фаз однокомпонентной системы, находящихся в равновесии между собой, не может быть больше трех. Однокомпонентные системы могут быть однофазными, двухфазными и трехфазными.
Поскольку число степеней свободы не может быть отрицательным, число фаз однокомпонентной системы, находящихся в равновесии между собой, не может быть больше трех. Однокомпонентные системы могут быть однофазными, двухфазными и трехфазными.
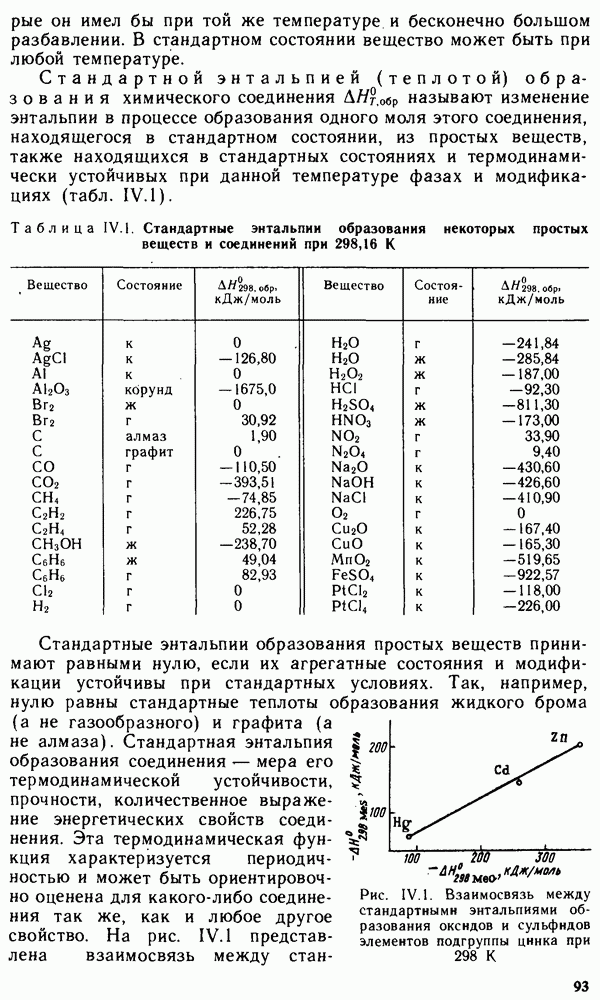
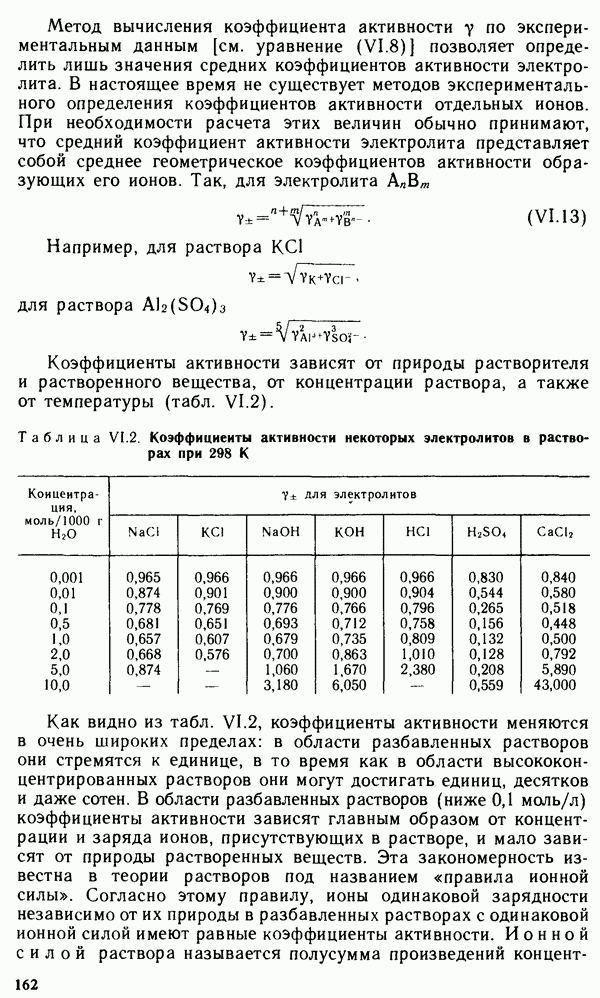
При изучении фазовых равновесий широко применяется графический метод — метод построения диаграмм состояния. Диаграмма состояния может быть построена на основании опытных данных для любого вещества; она позволяет судить об устойчивости какой-либо одной фазы системы и об устойчивости равновесия между двумя или тремя фазами при заданных условиях. На рис. V.10 представлена диаграмма состояния иодида серебра  имеющего три кристаллические модификации: А, Б и В. Каждой модификации, т. е. каждой фазе, отвечает определенная область диаграммы, отделенная от других областей линиями, характеризующими равновесия между двумя отдельными фазами. Так, например, линия
имеющего три кристаллические модификации: А, Б и В. Каждой модификации, т. е. каждой фазе, отвечает определенная область диаграммы, отделенная от других областей линиями, характеризующими равновесия между двумя отдельными фазами. Так, например, линия  характеризует равновесие между кристаллическими модификациями А и Б.
характеризует равновесие между кристаллическими модификациями А и Б.
В пределах каждой области диаграммы (А, Б и В) система однофазна  и число степеней свободы
и число степеней свободы  равно двум. Это значит, что в определенных пределах можно менять и температуру, и давление без каких-либо изменений числа или вида фаз. Так, при любом давлении в пределах
равно двум. Это значит, что в определенных пределах можно менять и температуру, и давление без каких-либо изменений числа или вида фаз. Так, при любом давлении в пределах  и любой температуре в интервале
и любой температуре в интервале  устойчива кристаллическая модификация А, а в условиях
устойчива кристаллическая модификация А, а в условиях  — модификация В.
— модификация В.
Каждая кривая на диаграмме  относится к двухфазной системе
относится к двухфазной системе  Число степеней свободы, отвечающее равновесию двух фаз, равно единице
Число степеней свободы, отвечающее равновесию двух фаз, равно единице  Это значит,
Это значит,
что произвольно можно менять только температуру (или только давление). Система моновариантна. Например, кристаллические формы иодида серебра А и Б могут находиться в равновесии при различных температурах и давлениях (кривая 1), но при этом каждому давлению соответствует строго определенная температура и, наоборот, каждой температуре — строго определенное давление. Так, равновесию А при  отвечает
отвечает 
Точка  на диаграмме состояния
на диаграмме состояния  называется тройной точкой. В ней пересекаются все три кривые. Эта точка отвечает равновесию между тремя фазами: А, Б и В. Число степеней свободы равновесной трехфазной системы равно нулю
называется тройной точкой. В ней пересекаются все три кривые. Эта точка отвечает равновесию между тремя фазами: А, Б и В. Число степеней свободы равновесной трехфазной системы равно нулю  Система инвариантна. Условия равновесия (температура и давление) строго определены, и ни одно из них не может изменяться.
Система инвариантна. Условия равновесия (температура и давление) строго определены, и ни одно из них не может изменяться.
Часто в однокомпонентных системах отдельные фазы представляют собой одно и то же вещество в различных агрегатных состояниях — твердом, жидком и газообразном. Каждому агрегатному состоянию, т. е. каждой фазе, отвечает определенная область диаграммы состояния вещества. Пограничные линии характеризуют равновесия: а) между газообразной и жидкой фазами, б) между жидкой и твердой фазами, в) между твердой и газообразной фазами. Тройная точка показывает значения температуры и давления, при которых сосуществуют все три фазы, т. е. вещество во всех трех агрегатных состояниях.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. ПРЕДМЕТ ХИМИИ
- § 2. ЗНАЧЕНИЕ ХИМИИ В ИЗУЧЕНИИ ПРИРОДЫ И РАЗВИТИИ ТЕХНИКИ
- 1. СТРОЕНИЕ ВЕЩЕСТВА
- Глава I. СТРОЕНИЕ АТОМА И СИСТЕМАТИКА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- § 1.2. КВАНТОВО-МЕХАНИЧЕСКАЯ МОДЕЛЬ АТОМА
- § 1.3. КВАНТОВЫЕ ЧИСЛА И АТОМНЫЕ ОРБИТАЛИ
- § 1.4. МНОГОЭЛЕКТРОННЫЕ АТОМЫ
- § 1.5. ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ Д. И. МЕНДЕЛЕЕВА
- § 1.6. ПЕРИОДИЧЕСКОЕ ИЗМЕНЕНИЕ СВОЙСТВ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- Глава II. ХИМИЧЕСКАЯ СВЯЗЬ
- § II.1. ОСНОВНЫЕ ВИДЫ И ХАРАКТЕРИСТИКИ ХИМИЧЕСКОЙ СВЯЗИ
- § II.2. МЕТОД ВАЛЕНТНЫХ СВЯЗЕЙ. ВАЛЕНТНОСТЬ
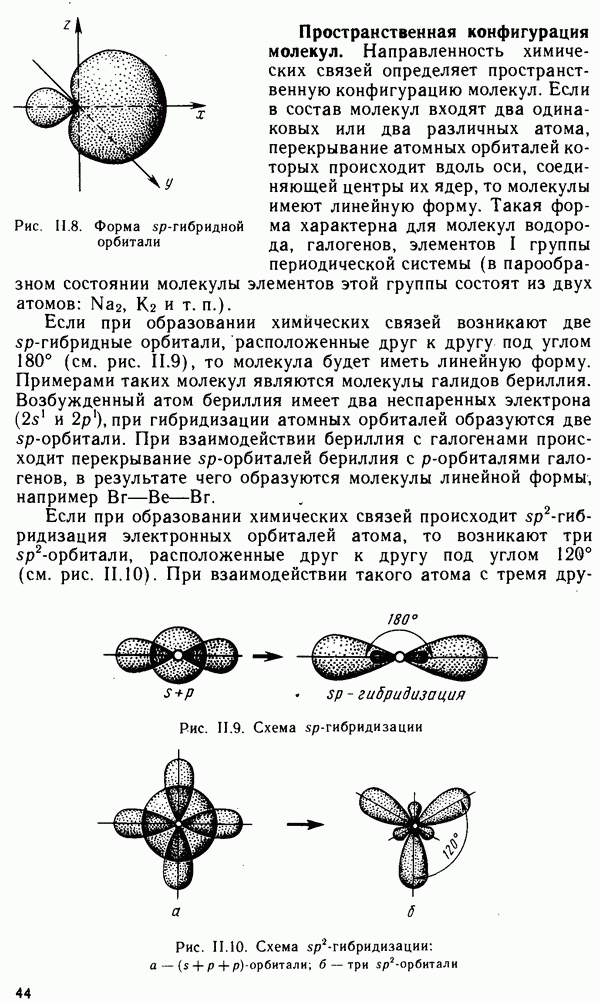
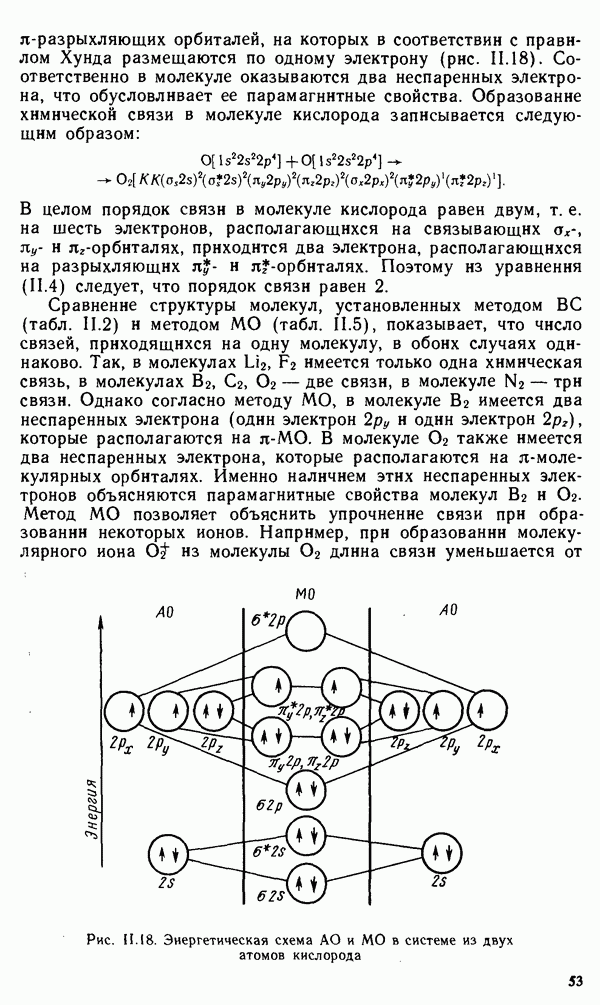
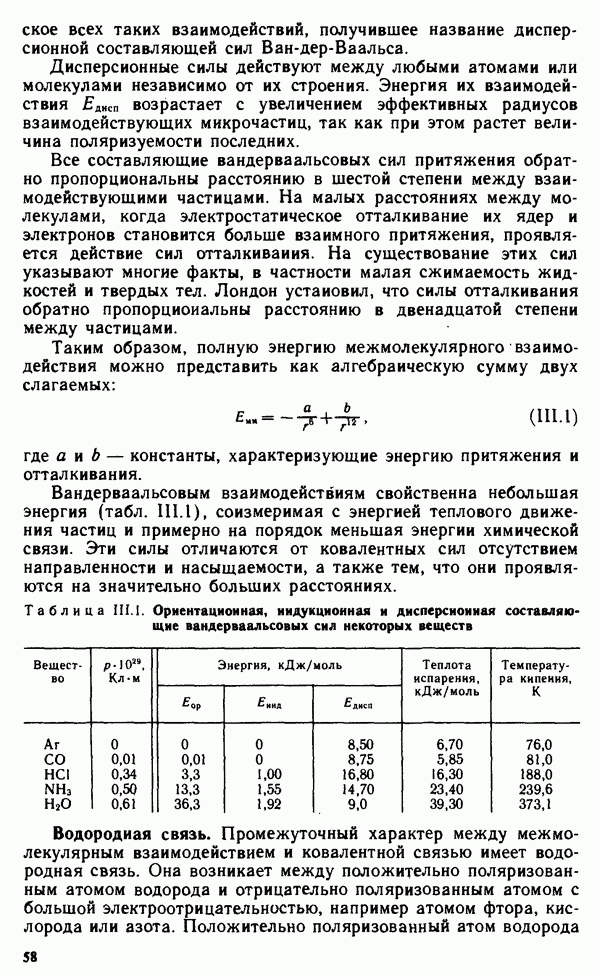
- § II.3. НАПРАВЛЕННОСТЬ КОВАЛЕНТНОЙ СВЯЗИ. ПРОСТРАНСТВЕННАЯ СТРУКТУРА МОЛЕКУЛ
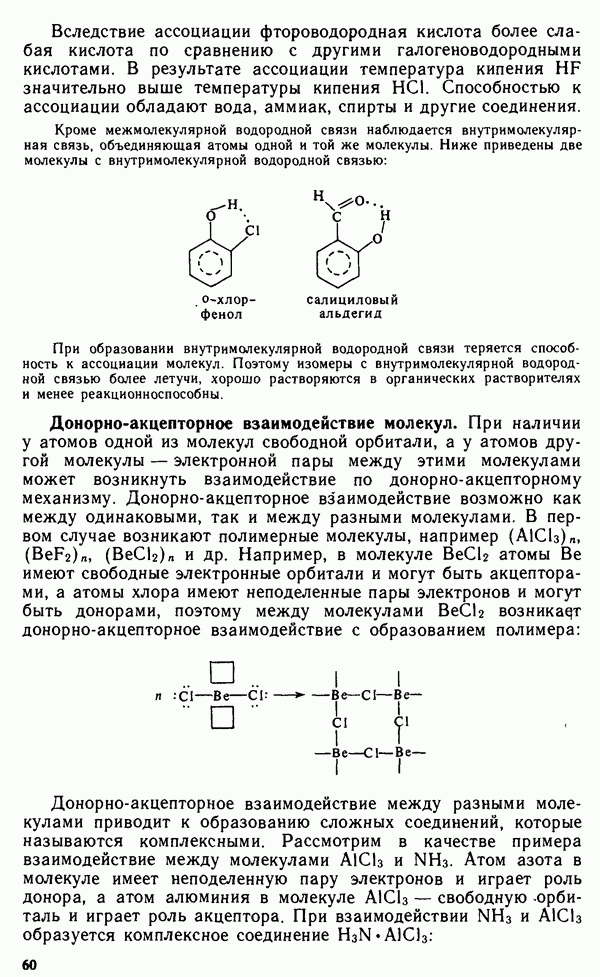
- § 11.4. МЕТОД МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ
- § 11.5. ЭЛЕКТРОННАЯ СТРУКТУРА НЕКОТОРЫХ МОЛЕКУЛ
- Глава III. ТИПЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ. КОНДЕНСИРОВАННОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- § III.1. ВЗАИМОДЕЙСТВИЕ МЕЖДУ МОЛЕКУЛАМИ
- § III.2. СВОЙСТВА ВЕЩЕСТВ В РАЗЛИЧНЫХ СОСТОЯНИЯХ
- § III.3. СТРОЕНИЕ КРИСТАЛЛОВ. ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ТЕЛАХ
- § III.4. МЕТАЛЛЫ, ПОЛУПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § III.5. РЕАЛЬНЫЕ КРИСТАЛЛЫ
- 2. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКИХ ПРОЦЕССОВ
- Глава IV. ЭНЕРГЕТИКА ХИМИЧЕСКИХ ПРОЦЕССОВ. ХИМИЧЕСКОЕ СРОДСТВО
- § IV.2. ЭНЕРГЕТИЧЕСКИЕ ЭФФЕКТЫ ХИМИЧЕСКИХ РЕАКЦИЙ И ФАЗОВЫХ ПРЕВРАЩЕНИЙ. ТЕРМОХИМИЧЕСКИЕ ЗАКОНЫ
- § IV.3. ЭНТАЛЬПИЯ ОБРАЗОВАНИЯ ХИМИЧЕСКИХ СОЕДИНЕНИЙ. ТЕРМОХИМИЧЕСКИЕ РАСЧЕТЫ
- § IV.4. ЭНТРОПИЯ. НАПРАВЛЕНИЕ И ПРЕДЕЛ ПРОТЕКАНИЯ ПРОЦЕССОВ В ИЗОЛИРОВАННЫХ СИСТЕМАХ
- § IV.5. ЭНЕРГИЯ ГИББСА И ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА ХИМИЧЕСКОЙ РЕАКЦИИ
- Глава V. ХИМИЧЕСКАЯ КИНЕТИКА И РАВНОВЕСИЕ
- § V.2. СКОРОСТЬ ГЕТЕРОГЕННЫХ ХИМИЧЕСКИХ РЕАКЦИЙ
- § V.3. ЗАВИСИМОСТЬ СКОРОСТИ ХИМИЧЕСКОЙ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
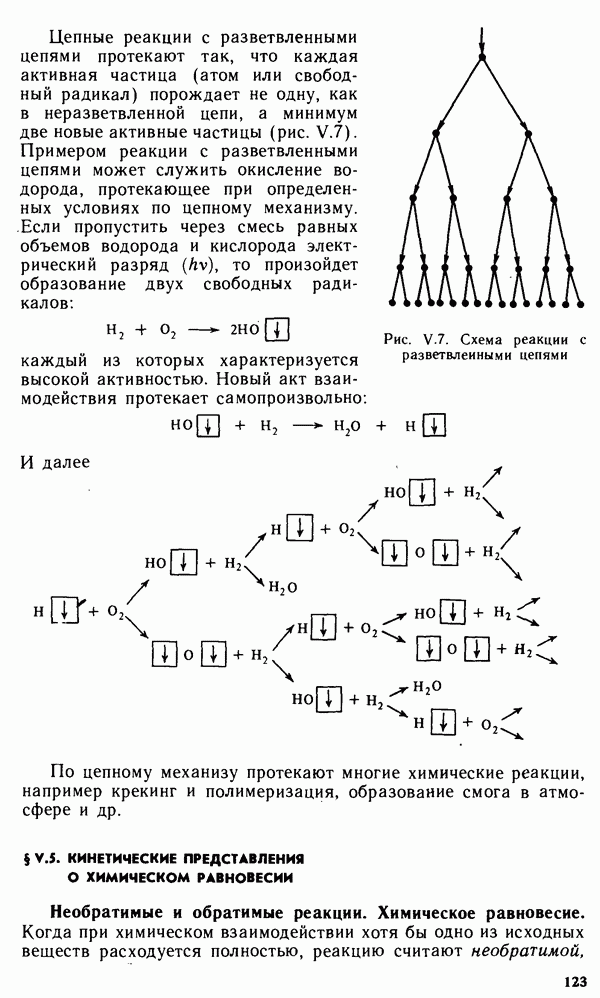
- § V.4. ФИЗИЧЕСКИЕ ВОЗДЕЙСТВИЯ НА ХИМИЧЕСКИЕ РЕАКЦИИ. ЦЕПНЫЕ РЕАКЦИИ
- § V.5. КИНЕТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ХИМИЧЕСКОМ РАВНОВЕСИИ
- § V.6. ФАЗОВЫЕ РАВНОВЕСИЯ ПРАВИЛО ФАЗ
- § V.7. АДСОРБЦИОННОЕ РАВНОВЕСИЕ
- § V.8. КАТАЛИЗ
- 3. РАСТВОРЫ ДИСПЕРСНЫЕ СИСТЕМЫ ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- VI.1. ОБЩИЕ ПОНЯТИЯ О РАСТВОРАХ
- § VI.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЖИДКИХ РАСТВОРОВ
- § VI.3. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РАСТВОРАХ
- § VI.4. ВОДНЫЕ РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- § VI.5. ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ ВОДЫ. ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ
- § VI.6. РАВНОВЕСИЯ В ВОДНЫХ РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- § VI.7. ДИСПЕРСНЫЕ СИСТЕМЫ. КОЛЛОИДНЫЕ РАСТВОРЫ
- § VI.8. УСТОЙЧИВОСТЬ И КОАГУЛЯЦИЯ КОЛЛОИДНЫХ СИСТЕМ
- Глава VII. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ И ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- § VII.1. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ ПРОЦЕССЫ
- § VII.2. ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ
- § VII.3. ПОТЕНЦИАЛЫ МЕТАЛЛИЧЕСКИХ И ГАЗОВЫХ ЭЛЕКТРОДОВ
- § VII.4. ПОТЕНЦИАЛЫ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ (РЕДОКСИ-) ЭЛЕКТРОДОВ
- § VII.5. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ. ПОЛЯРИЗАЦИЯ
- § VII.6. ЭЛЕКТРОЛИЗ
- Глава VIII. КОРРОЗИЯ И ЗАЩИТА МЕТАЛЛОВ
- § VIII.1. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ КОРРОЗИОННЫХ ПРОЦЕССОВ
- § VIII.2. ХИМИЧЕСКАЯ КОРРОЗИЯ
- § VIII.3. ЭЛЕКТРОХИМИЧЕСКАЯ КОРРОЗИЯ
- § VIII.4. ЗАЩИТА МЕТАЛЛОВ ОТ КОРРОЗИИ
- 4. ОБЩАЯ ХАРАКТЕРИСТИКА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ И ИХ СОЕДИНЕНИЙ
- Глава IX. ПРОСТЫЕ ВЕЩЕСТВА И ДВОЙНЫЕ СОЕДИНЕНИЯ. КРАТКИЙ ОБЗОР ХИМИЧЕСКИХ СВОЙСТВ s- И р-ЭЛЕМЕНТОВ
- § IX.2. МЕТАЛЛЫ И СПЛАВЫ. ОСНОВЫ ФИЗИКО-ХИМИЧЕСКОГО АНАЛИЗА
- § IX.3. ДВОЙНЫЕ СОЕДИНЕНИЯ
- § IX.4. СВОЙСТВА МЕТАЛЛОВ ГЛАВНЫХ ПОДГРУПП I И II ГРУПП
- § IX.5. СВОЙСТВА р-ЭЛЕМЕНТОВ III ГРУППЫ
- § IX.6. СВОЙСТВА р-ЭЛЕМЕНТОВ IV ГРУППЫ
- § IX.7. СВОЙСТВА р-ЭЛЕМЕНТОВ V, VI И VII ГРУПП ПЕРИОДИЧЕСКОЙ СИСТЕМЫ ЭЛЕМЕНТОВ
- Глава Х. КОМПЛЕКСНЫЕ СОЕДИНЕНИЯ
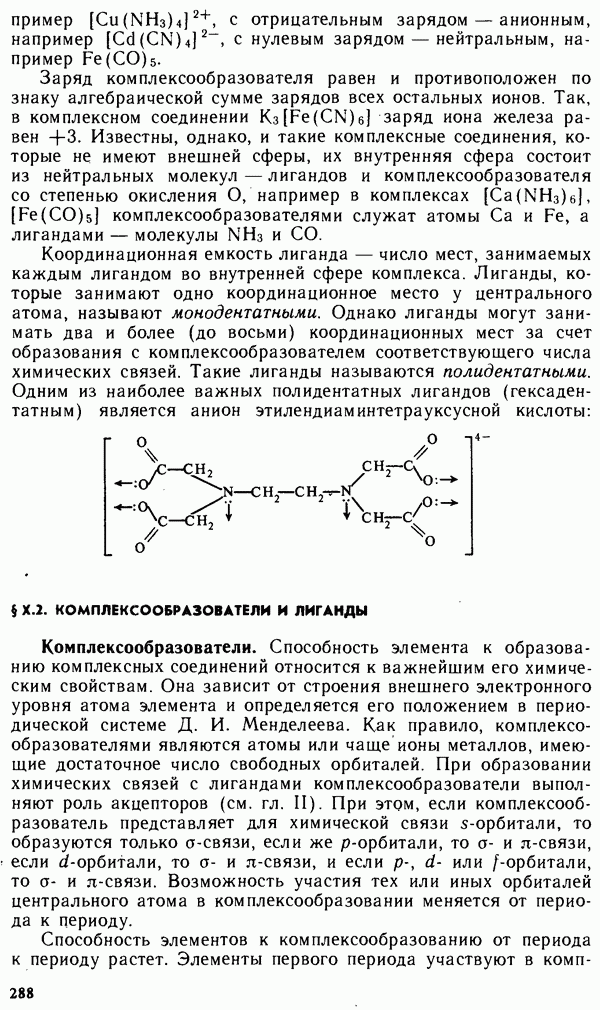
- § Х.1. СТРУКТУРА КОМПЛЕКСНЫХ СОЕДИНЕНИИ
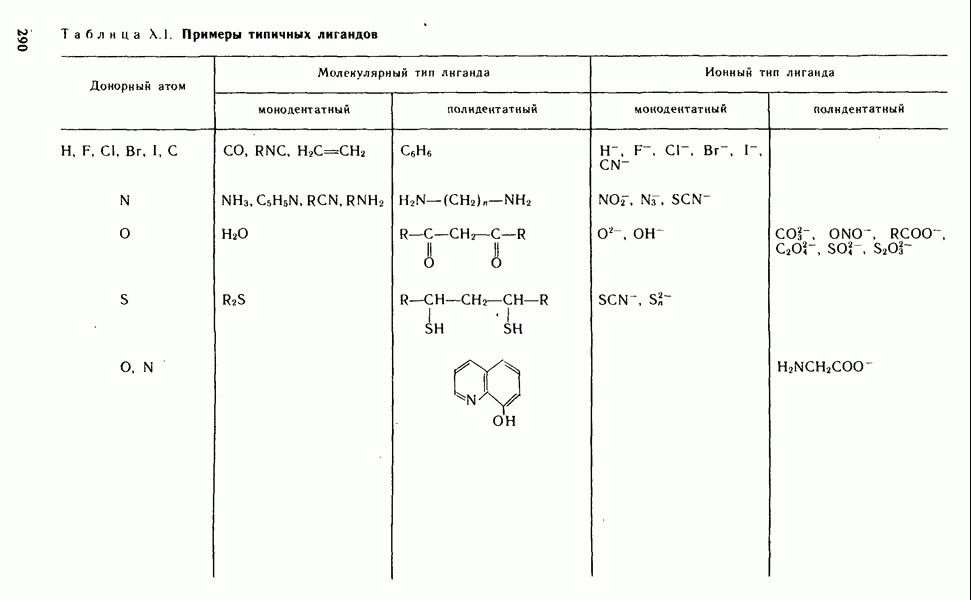
- § Х.2. КОМПЛЕКСООБРАЗОВАТЕЛИ И ЛИГАНДЫ
- § Х.3. НОМЕНКЛАТУРА И КЛАССИФИКАЦИЯ КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
- § Х.4. МЕТОДЫ РАСЧЕТА ХИМИЧЕСКИХ СВЯЗЕЙ В КОМПЛЕКСНЫХ СОЕДИНЕНИЯХ
- § Х.5. УСТОЙЧИВОСТЬ КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
- Глава XI. ОРГАНИЧЕСКИЕ СОЕДИНЕНИЯ
- § XI.1. ОСОБЕННОСТИ. ТЕОРИЯ ХИМИЧЕСКОГО СТРОЕНИЯ И КЛАССИФИКАЦИЯ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- § XI.2. УГЛЕВОДОРОДЫ
- § ХI.3. ПРОИЗВОДНЫЕ УГЛЕВОДОРОДОВ
- 5. СПЕЦИАЛЬНЫЕ ВОПРОСЫ ХИМИИ
- Глава XII. ХИМИЯ КОНСТРУКЦИОННЫХ И ЭЛЕКТРОТЕХНИЧЕСКИХ МАТЕРИАЛОВ
- § XII.2. СВОЙСТВА ПЕРЕХОДНЫХ МЕТАЛЛОВ VIII ГРУППЫ
- § ХII.3. СВОЙСТВА ЭЛЕМЕНТОВ I И II ГРУПП
- § XII.4. ХИМИЯ ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ
- § XII.5. МЕТОДЫ ПОЛУЧЕНИЯ МАТЕРИАЛОВ ВЫСОКОЙ ЧИСТОТЫ
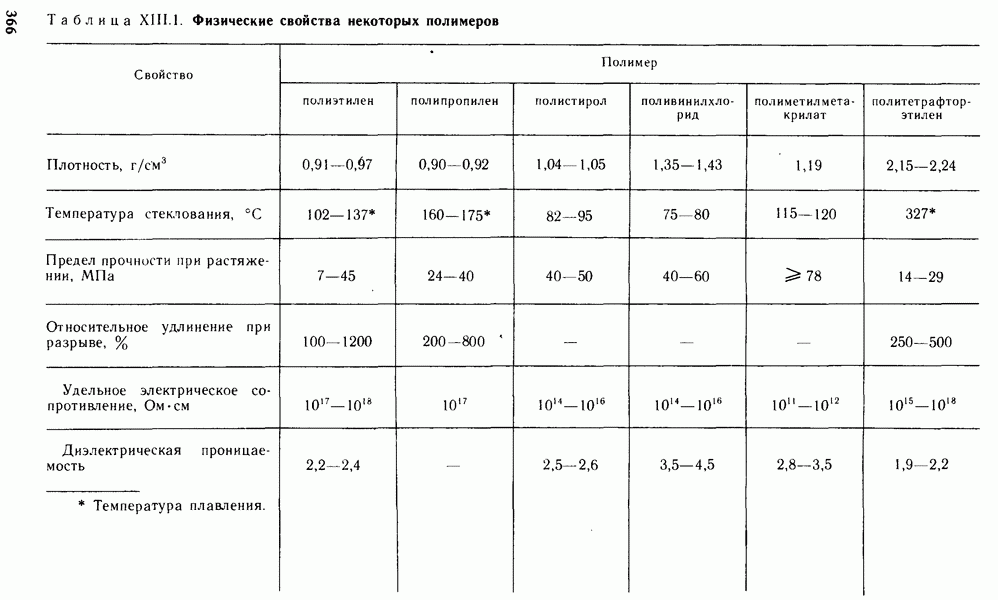
- Глава XIII. ПОЛИМЕРНЫЕ МАТЕРИАЛЫ И ИХ ПРИМЕНЕНИЕ В ЭНЕРГЕТИКЕ
- § XIII.1. МЕТОДЫ ПОЛУЧЕНИЯ ПОЛИМЕРОВ
- § XIII.2. СТРОЕНИЕ ПОЛИМЕРОВ
- § XIII.3. СВОЙСТВА ПОЛИМЕРОВ
- § XIII.4. ПРИМЕНЕНИЕ ПОЛИМЕРОВ
- Глава XIV. ХИМИЯ ВОДЫ И ТОПЛИВА. ХИМИЯ И ОХРАНА ОКРУЖАЮЩЕЙ СРЕДЫ
- § XIV.1. СТРОЕНИЕ И СВОЙСТВА ВОДЫ
- § XIV.2. ПРИРОДНЫЕ ВОДЫ
- § ХIV.3. ОСНОВНЫЕ МЕТОДЫ ОЧИСТКИ ВОДЫ
- § XIV.4. СОСТАВ И СВОЙСТВА ОРГАНИЧЕСКОГО ТОПЛИВА
- § XIV.5. ЭКОЛОГИЧЕСКИЕ ПРОБЛЕМЫ ОБЩЕСТВА
- § XIV.6. ОХРАНА ВОЗДУШНОГО БАССЕЙНА
- § XIV.7. ОХРАНА ВОДНОГО БАССЕЙНА
- Глава XV. ЯДЕРНАЯ ХИМИЯ И РАДИОХИМИЯ
- § XV.1. АТОМНОЕ ЯДРО. РАДИОАКТИВНОСТЬ
- § XV.2. ЯДЕРНЫЕ РЕАКЦИИ
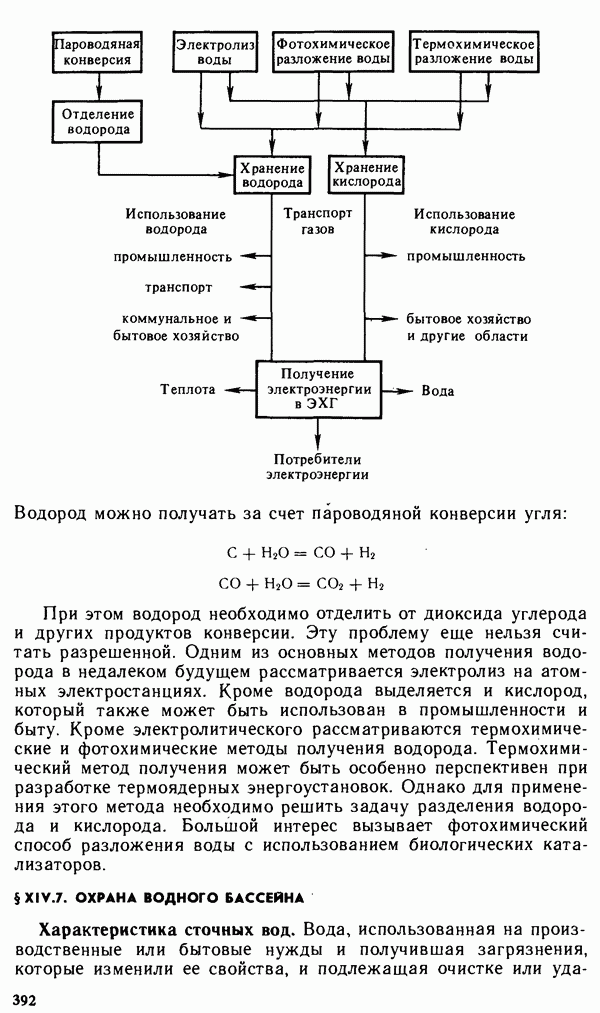
- § XV.3. ЯДЕРНАЯ ЭНЕРГЕТИКА
- § XV.4. ХИМИЧЕСКИЕ СВОЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
- Глава XVI. ЭЛЕКТРОХИМИЧЕСКИЕ ПРОЦЕССЫ В ЭНЕРГЕТИКЕ, ЭЛЕКТРОНИКЕ И АВТОМАТИКЕ
- § ХVI.1. ХИМИЧЕСКИЕ ИСТОЧНИКИ ТОКА. ЭЛЕКТРОХИМИЧЕСКИЕ ЭНЕРГОУСТАНОВКИ
- § XVI.2. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ (ХЕМОТРОНЫ)
- § ХVI.3. ЭЛЕКТРОХИМИЧЕСКАЯ АНОДНАЯ ОБРАБОТКА МЕТАЛЛОВ И СПЛАВОВ
- § XVI.4. ПОЛУЧЕНИЕ И СВОЙСТВА ГАЛЬВАНОПОКРЫТИИ
- ЗАКЛЮЧЕНИЕ