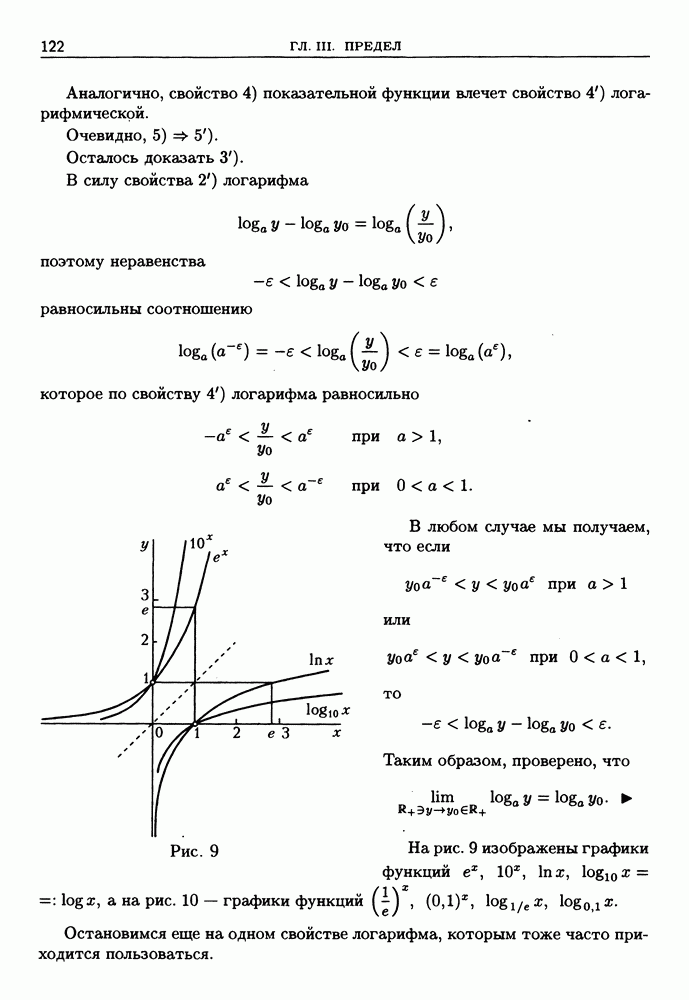
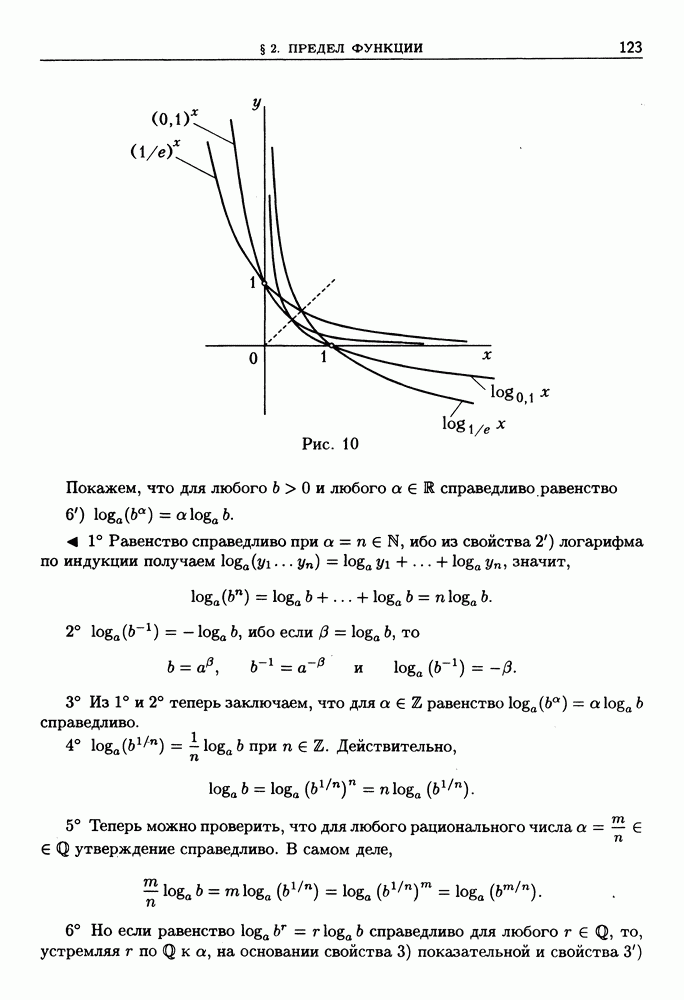
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Формула Тейлора.
Из той части дифференциального исчисления, которая уже изложена к настоящему моменту, могло возникнуть верное представление о том, что чем больше производных (включая производную нулевого порядка) совпадает у двух функций в некоторой точке, тем лучше эти функции аппроксимируют друг друга в окрестности этой точки. Мы в основном интересовались и сейчас будем интересоваться приближением функции в окрестности некоторой точки с помощью многочлена  Нам известно (см. пример 25 из § 2, п. 6), что алгебраический полином можно представить в виде
Нам известно (см. пример 25 из § 2, п. 6), что алгебраический полином можно представить в виде

 В этом легко убедиться непосредственно.
В этом легко убедиться непосредственно.
Таким образом, если нам будет дана функция  имеющая в точке
имеющая в точке  все производные до порядка
все производные до порядка  включительно, то мы можем немедленно выписать полином
включительно, то мы можем немедленно выписать полином

производные которого до порядка  включительно в точке
включительно в точке  совпадают с производными соответствующего порядка функции
совпадают с производными соответствующего порядка функции  в точке
в точке 
Определение 5. Алгебраический полином, заданный соотношением (5), называется полиномом Тейлора порядка  функции
функции  в точке
в точке 
Нас будет интересовать величина

уклонения полинома  от функции
от функции  называемая часто остатком, точнее,
называемая часто остатком, точнее,  остатком или
остатком или  остаточным членом формулы Тейлора:
остаточным членом формулы Тейлора:

Само по себе равенство (7), конечно, не представляет интереса, если о функции  не известно ничего, кроме ее определения (6).
не известно ничего, кроме ее определения (6).
Сейчас мы воспользуемся довольно искусственным приемом для получения информации об остаточном члене. Более естественный путь к этому даст интегральное исчисление.
Теорема 2. Если на отрезке с концами  функция
функция  непрерывна вместе с первыми
непрерывна вместе с первыми  своими производными, а во внутренних точках этого отрезка она имеет производную порядка
своими производными, а во внутренних точках этого отрезка она имеет производную порядка  то при любой функции (
то при любой функции ( , непрерывной на этом отрезке и имеющей отличную от нуля производную в его внутренних точках, найдется точка
, непрерывной на этом отрезке и имеющей отличную от нуля производную в его внутренних точках, найдется точка  , лежащая между
, лежащая между  такая, что
такая, что

На отрезке I с концами  рассмотрим вспомогательную функцию
рассмотрим вспомогательную функцию

от аргумента  Запишем определение
Запишем определение  подробнее:
подробнее:

Из определения функции  и условий теоремы видно, что
и условий теоремы видно, что  непрерывна на отрезке I и дифференцируема в его внутренних точках, причем
непрерывна на отрезке I и дифференцируема в его внутренних точках, причем

Применяя к паре функций  на отрезке I теорему Коши (см. соотношение (4)), находим точку
на отрезке I теорему Коши (см. соотношение (4)), находим точку  между
между  в которой
в которой

Подставляя сюда выражение для  и замечая из сопоставления формул (6), (9) и (10), что
и замечая из сопоставления формул (6), (9) и (10), что  получаем формулу (8).
получаем формулу (8).
Полагая в  получаем Следствие 1 (формула Коши остаточного члена).
получаем Следствие 1 (формула Коши остаточного члена).

Особенно изящная формула получается, если положить в соотношении 
Следствие 2 (формула Лагранжа остаточного члена).

Отметим, что формулу (7) Тейлора при  часто называют формулой Маклорена
часто называют формулой Маклорена
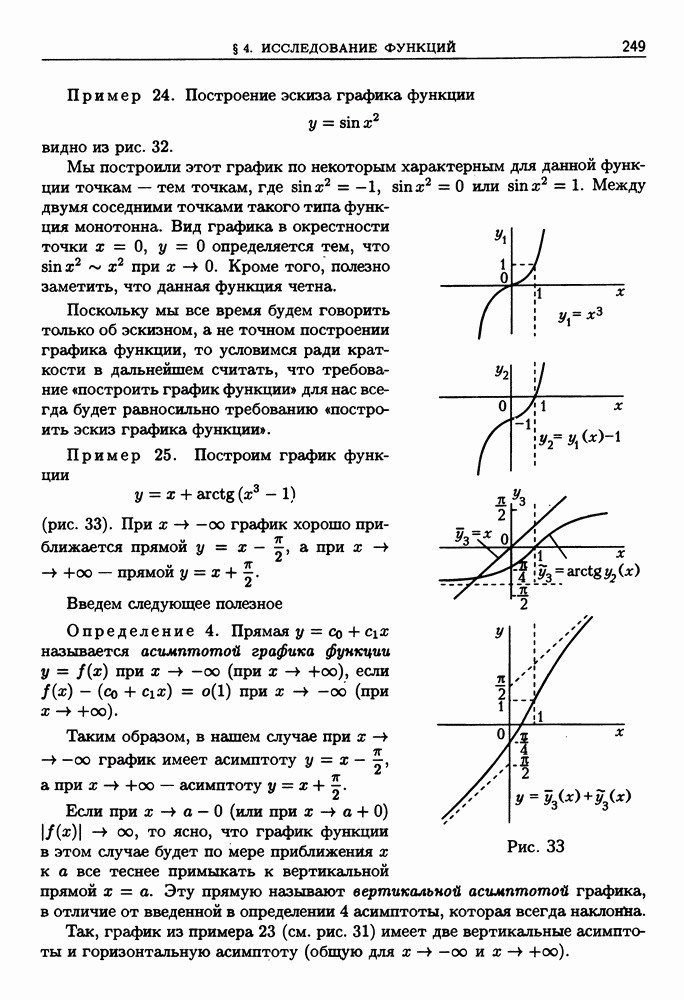
Рассмотрим примеры.
Пример 3. Для функции  при
при  формула Тейлора имеет вид
формула Тейлора имеет вид

и на основании равенства (12) можно считать, что

где 
Таким образом,

Но при любом фиксированном  если
если  величина
величина  как нам известно (см. пример 12 из гл.
как нам известно (см. пример 12 из гл.  стремится к нулю. Значит, из
стремится к нулю. Значит, из
оценки (14) и определения суммы ряда вытекает, что для 

Пример 4. Аналогично получаем разложение функции  для любого
для любого 

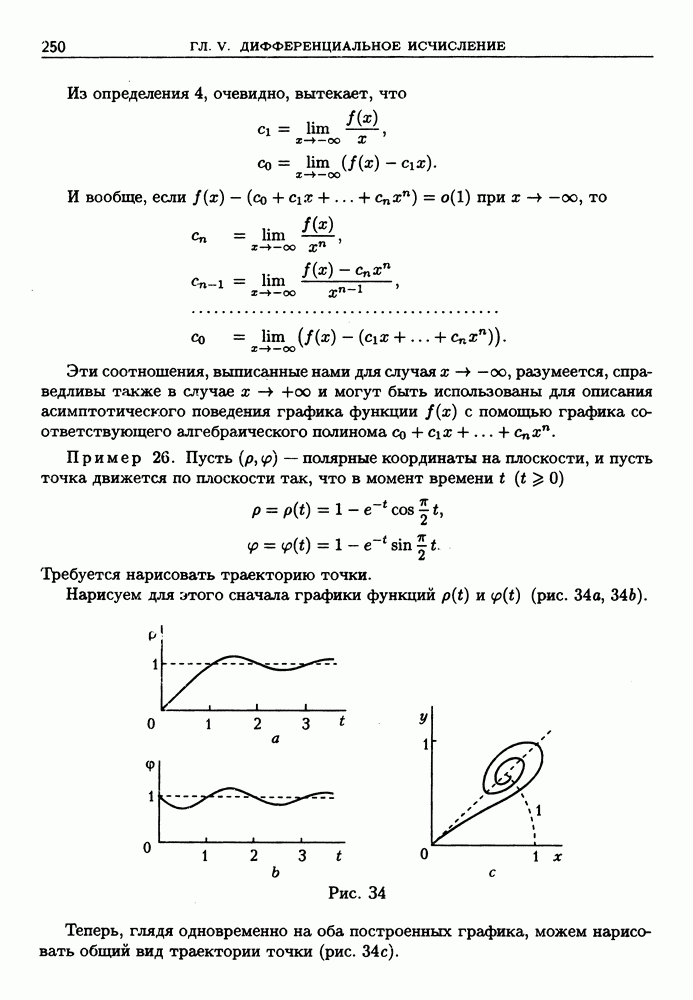
Пример 5. Пусть  Нам известно (см. пример 18 из § 2, п. 6), что
Нам известно (см. пример 18 из § 2, п. 6), что  поэтому из формулы (12) Лагранжа при
поэтому из формулы (12) Лагранжа при  и любом
и любом  находим
находим

откуда следует, что для любого фиксированного значения  величина
величина  стремится к нулю при
стремится к нулю при  Таким образом, при любом
Таким образом, при любом  справедливо разложение
справедливо разложение

Пример 6. Аналогично, для функции  получаем
получаем

и

Пример 7. Поскольку  для функции
для функции  при
при  из формулы (12) получаем
из формулы (12) получаем

где  если
если  четно, и
четно, и  если
если  нечетно. В любом случае
нечетно. В любом случае  ибо
ибо  Значит, для любого фиксированного значения
Значит, для любого фиксированного значения  выполняется
выполняется  при
при  и мы получаем разложение
и мы получаем разложение

справедливое для любого 
Пример 8. Аналогично получаем разложение

справедливое для любого значения 
Пример 9. Для функции  имеем
имеем  поэтому формула Тейлора (7) при
поэтому формула Тейлора (7) при  для этой функции имеет вид
для этой функции имеет вид

На сей раз представим  по формуле Коши (11):
по формуле Коши (11):

или

где точка  лежит между 0 и
лежит между 0 и  .
.
Если  то из условия, что
то из условия, что  лежит между 0 и х, следует, что
лежит между 0 и х, следует, что

Таким образом, при 

и, следовательно, при  справедливо разложение
справедливо разложение

Заметим, что вне отрезка  ряд, стоящий справа в (26), всюду расходится, так как его общий член не стремится к нулю, если
ряд, стоящий справа в (26), всюду расходится, так как его общий член не стремится к нулю, если 
Пример 10. Если  где а
где а  то
то  поэтому формула Тейлора (7) при
поэтому формула Тейлора (7) при  для этой функции имеет вид
для этой функции имеет вид

Используя формулу Коши (11), находим

где  лежит между 0 и х.
лежит между 0 и х.
Если  то, используя оценку (24), имеем
то, используя оценку (24), имеем

При увеличении  на единицу правая часть неравенства (29) умножается на
на единицу правая часть неравенства (29) умножается на  поскольку
поскольку  то при достаточно больших значениях
то при достаточно больших значениях  независимо от значения а, будем иметь
независимо от значения а, будем иметь  если
если 
Отсюда следует, что при любом а  и любом х из интервала
и любом х из интервала  выполнено
выполнено  когда
когда  поэтому на интервале
поэтому на интервале  справедливо полученное Ньютоном разложение (бином Ньютона)
справедливо полученное Ньютоном разложение (бином Ньютона)

Заметим, что, как следует из признака Даламбера (см. гл.  при
при  ряд (30) вообще расходится, если только а
ряд (30) вообще расходится, если только а 
Рассмотрим теперь особо случай, когда 
В этом случае функция  является полиномом степени
является полиномом степени  и поэтому все ее производные порядка выше чем
и поэтому все ее производные порядка выше чем  равны нулю. Таким образом, формула Тейлора (7) и, например, формула Лагранжа (12) позволяют записать следующее равенство:
равны нулю. Таким образом, формула Тейлора (7) и, например, формула Лагранжа (12) позволяют записать следующее равенство:

представляющее собой известную из школы формулу бинома Ньютона для натурального показателя:

Итак, мы определили формулу Тейлора (7) и получили вид (8), (11), (12) остаточного члена формулы Тейлора. Мы получили соотношения (14), (16), (18), (25), (29), позволяющие оценивать погрешность вычисления важных элементарных функций по формуле Тейлора. Наконец, мы получили разложения этих функций в степенные ряды.
Определение 6. Если функция  имеет в точке
имеет в точке  производные любого порядка
производные любого порядка  то ряд
то ряд

называется рядом Тейлора функции  в точке
в точке 
Не следует думать, что ряд Тейлора каждой бесконечно дифференцируй емой функции сходится в некоторой окрестности точки  ибо для любой последовательности
ибо для любой последовательности  чисел можно построить (это не совсем просто) функцию
чисел можно построить (это не совсем просто) функцию  такую, что
такую, что 
Не следует также думать, что если ряд Тейлора сходится, то он обязательно сходится к породившей его функции. Сходимость ряда Тейлора к породившей его функции имеет место только для так называемых аналитических функций.
Вот пример Коши неаналитической функции:

Исходя из определения производной и того, что  при
при  независимо от значения к (см. пример 30 из § 2 гл. III), можно проверить, что
независимо от значения к (см. пример 30 из § 2 гл. III), можно проверить, что  для
для  Таким образом, ряд Тейлора в данном случае состоит только из нулевых членов и его сумма тождественно равна нулю, в то время как
Таким образом, ряд Тейлора в данном случае состоит только из нулевых членов и его сумма тождественно равна нулю, в то время как  при
при  .
.
В заключение остановимся на локальном варианте формулы Тейлора.
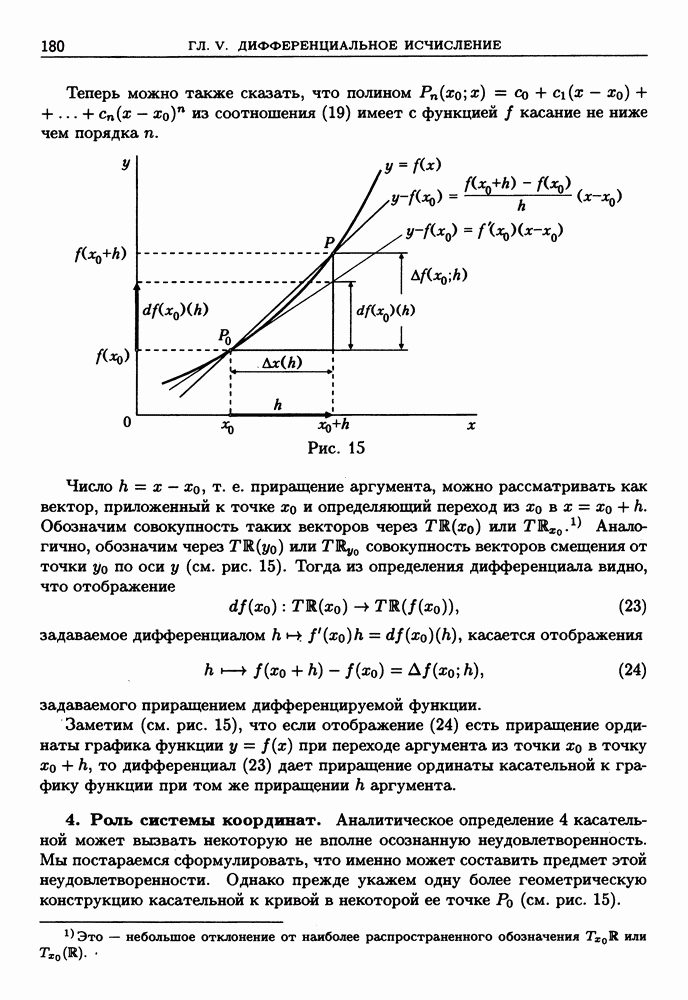
Вернемся снова к задаче о локальном приближении функции  полиномом, которую мы начали обсуждать в § 1, п. 3. Мы хотим подобрать полином
полиномом, которую мы начали обсуждать в § 1, п. 3. Мы хотим подобрать полином  так, чтобы иметь
так, чтобы иметь

или, подробнее,

Сформулируем в явном виде по существу уже доказанное
Утверждение 3. Если полином  удовлетворяющий условию (32), существует, то он единственный.
удовлетворяющий условию (32), существует, то он единственный.
Действительно, из условия (32) последовательно и вполне однозначно (в силу единственности предела) находятся коэффициенты полинома

Докажем теперь следующее
Утверждение 4 (локальная формула Тейлора). Пусть Е — отрезок с концом  . Если функция
. Если функция  имеет в точке
имеет в точке  все производные
все производные  до порядка
до порядка  включительно, то справедливо следующее представление:
включительно, то справедливо следующее представление:

Таким образом, задачу локального приближения дифференцируемой функции решает полином Тейлора соответствующего порядка.
Поскольку полином Тейлора  строится из условия совпадения всех его производных до порядка
строится из условия совпадения всех его производных до порядка  включительно с производными соответствующего порядка функции
включительно с производными соответствующего порядка функции  в точке
в точке  то
то  и справедливость формулы (33) устанавливает следующая
и справедливость формулы (33) устанавливает следующая
Лемма 2. Если функция  определенная на отрезке Е с концом
определенная на отрезке Е с концом  такова, что она имеет в точке
такова, что она имеет в точке  все производные
все производные  до порядка
до порядка  включительно и
включительно и  то
то  при
при  .
.
При  утверждение вытекает из определения дифференцируемости функции
утверждение вытекает из определения дифференцируемости функции  в точке
в точке  в силу которого
в силу которого

и, поскольку  имеем
имеем

Предположим, что утверждение доказано для порядков  Покажем, что тогда оно справедливо также для порядка
Покажем, что тогда оно справедливо также для порядка 
Заметим предварительно, что поскольку

то существование  предполагает, что функция
предполагает, что функция  определена на Е хотя бы вблизи точки
определена на Е хотя бы вблизи точки  Уменьшая, если нужно, отрезок Е, можно заранее считать, что функции
Уменьшая, если нужно, отрезок Е, можно заранее считать, что функции  где
где  , определены на всем отрезке Е с концом
, определены на всем отрезке Е с концом  Поскольку
Поскольку  , то функция
, то функция  имеет на
имеет на  производную
производную  и по условию
и по условию

Таким образом, по предположению индукции

Тогда, используя теорему Лагранжа, получаем

где  — точка, лежащая между
— точка, лежащая между  при
при  . Значит, при
. Значит, при  одновременно будем иметь
одновременно будем иметь  , и поскольку
, и поскольку

то проверено, что

Таким образом, утверждение леммы 2 проверено принципом математической индукции.
Соотношение (33) называется локальной формулой Тейлора, поскольку указанный в нем вид остаточного члена (так называемая форма Пеано)

позволяет делать заключения только об асимптотическом характере связи полинома Тейлора и функции при  .
.
Формула (33) удобна, таким образом, при вычислении пределов и описании асимптотики функции при  , но она не может служить для приближенного вычисления значений функции до тех пор, пока нет фактической оценки величины
, но она не может служить для приближенного вычисления значений функции до тех пор, пока нет фактической оценки величины 
Подведем итоги. Мы определили полином Тейлора

написали формулу Тейлора

и получили следующие ее важнейшие конкретизации:
Если  имеет производную порядка
имеет производную порядка  интервале с концами
интервале с концами  то
то

где  — точка, лежащая между
— точка, лежащая между 
Если  имеет в точке
имеет в точке  все производные до порядка
все производные до порядка  включительно, то
включительно, то

Соотношение (35), называемое формулой Тейлора с остаточным членом в форме Лагранжа, очевидно, является обобщением теоремы Лагранжа, в которую оно превращается при 
Соотношение (36), называемое формулой Тейлора с остаточным членом в форме Пеано, очевидно, является обобщением определения дифференцируемости функции в точке, в которое оно переходит при 
Заметим, что формула (35) практически всегда более содержательна, ибо, с одной стороны, как мы видели, она позволяет оценивать абсолютную величину остаточного члена, а с другой, например, при ограниченности  в окрестности
в окрестности  из нее вытекает также асимптотическая формула
из нее вытекает также асимптотическая формула

Так что для бесконечно дифференцируемых функций, с которыми в подавляющем большинстве случаев имеет дело классический анализ, формула (35) содержит в себе локальную формулу (36).
В частности, на основании формулы (37) и разобранных выше примеров 3—10 можно теперь выписать следующую таблицу асимптотических формул при  :
:

Рассмотрим теперь еще некоторые примеры использования формулы Тейлора.
Пример 11. Напишем полином, позволяющий вычислять значения функции  на отрезке
на отрезке  с абсолютной погрешностью, не превышающей
с абсолютной погрешностью, не превышающей 
В качестве такого многочлена можно взять тейлоровский многочлен подходящей степени, получаемый разложением функции  в окрестности точки
в окрестности точки  Поскольку
Поскольку

где по формуле Лагранжа

то при 

Но  при
при  Таким образом, с нужной точностью на отрезке
Таким образом, с нужной точностью на отрезке  имеем
имеем 
Пример 12. Покажем, что  при
при  Имеем
Имеем

Таким образом,  и написанное соотношение следует из локальной формулы Тейлора.
и написанное соотношение следует из локальной формулы Тейлора.
Пример 13. Пусть  Исследуем сходимость ряда
Исследуем сходимость ряда 
При  когда
когда  Оценим порядок члена ряда
Оценим порядок члена ряда

Таким образом, мы имеем знакопостоянный ряд, члены которого эквивалентны членам ряда Поскольку последний ряд сходится только при  в указанной области
в указанной области  исходный ряд сходится лишь при
исходный ряд сходится лишь при  (см. задачу 16b).
(см. задачу 16b).
Пример 14. Покажем, что 
На сей раз, вместо того чтобы вычислять подряд шесть производите, мы воспользуемся уже известными разложениями  при
при  при и
при и 

Пример 15. Найдем значения первых шести производных функции  при
при 
Имеем  потому ясно, что в нуле данная функция имеет производные любого порядка, ибо
потому ясно, что в нуле данная функция имеет производные любого порядка, ибо  Мы не станем искать функциональные выражения этих производных, а воспользуемся единственностью полинома Тейлора и результатом предыдущего примера.
Мы не станем искать функциональные выражения этих производных, а воспользуемся единственностью полинома Тейлора и результатом предыдущего примера.
Если

то

Таким образом, в нашем случае получаем

Пример 16. Пусть  — бесконечно дифференцируемая в точке
— бесконечно дифференцируемая в точке  функция, и пусть известно разложение
функция, и пусть известно разложение

ее производной в окрестности нуля. Тогда из единственности тейлоровского разложения имеем

поэтому  Таким образом, для самой функции
Таким образом, для самой функции  имеем разложение
имеем разложение

или, после упрощений,

Пример 17. Найдем тейлоровское разложение функции  в нуле.
в нуле.
Поскольку  то по соображениям, изложенным в предыдущем примере,
то по соображениям, изложенным в предыдущем примере,

т. е.

Пример 18. Аналогично, раскладывая функцию  по формуле Тейлора в окрестности нуля, последовательно находим
по формуле Тейлора в окрестности нуля, последовательно находим

или, после элементарных преобразований,

Здесь 
Пример 19. Воспользуемся результатами примеров 5,12,17,18 и найдем

Задачи и упражнения
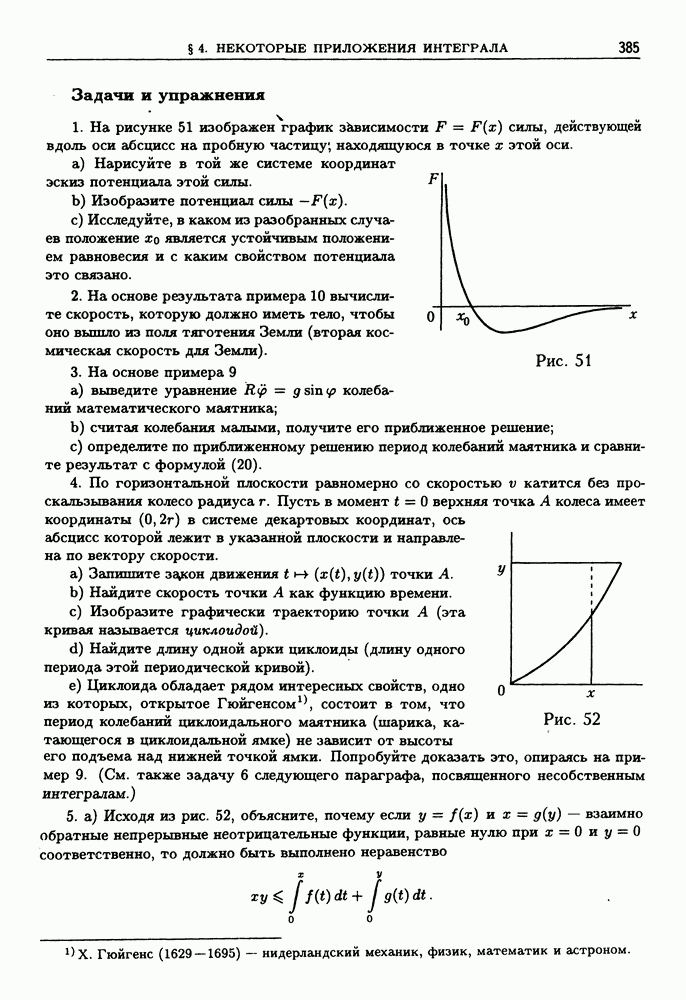
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- § 1. Логическая символика
- § 2. Множество и элементарные операции над множествами
- 2. Отношение включения.
- 3. Простейшие операции над множествами.
- Упражнения
- § 3. Функция
- 2. Простейшая классификация отображений.
- 3. Композиция функций и взаимно обратные отображения.
- 4. Функция как отношение. График функции.
- § 4. Некоторые дополнения
- 2. Об аксиоматике теории множеств.
- 3. Замечания о структуре математических высказываний и записи их на языке теории множеств.
- Упражнения
- ГЛАВА II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
- § 1. Аксиоматика и некоторые общие свойства множества действительных чисел
- 2. Некоторые общие алгебраические свойства действительных чисел.
- 3. Аксиома полноты и существование верхней (нижней) грани числового множества
- § 2. Важнейшие классы действительных чисел и вычислительные аспекты операций с действительными числами
- 2. Рациональные и иррациональные числа
- 3. Принцип Архимеда.
- 4. Геометрическая интерпретация множества действительных чисел и вычислительные аспекты операций с действительными числами
- Задачи и упражнения
- § 3. Основные леммы, связанные с полнотой множества действительных чисел
- 2. Лемма о конечном покрытии (принцип Бореля — Лебега)
- 3. Лемма о предельной точке (принцип Больцано—Вейерштрасса).
- Задачи и упражнения
- § 4. Счетные и несчетные множества
- 2. Мощность континуума
- Задачи и упражнения
- ГЛАВА III. ПРЕДЕЛ
- 2. Свойства предела последовательности
- 3. Вопросы существования предела последовательности
- 4. Начальные сведения о рядах
- § 2. Предел функции
- 2. Свойства предела функции.
- 3. Общее определение предела функции (предел по базе).
- 4. Вопросы существования предела функции
- ГЛАВА IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
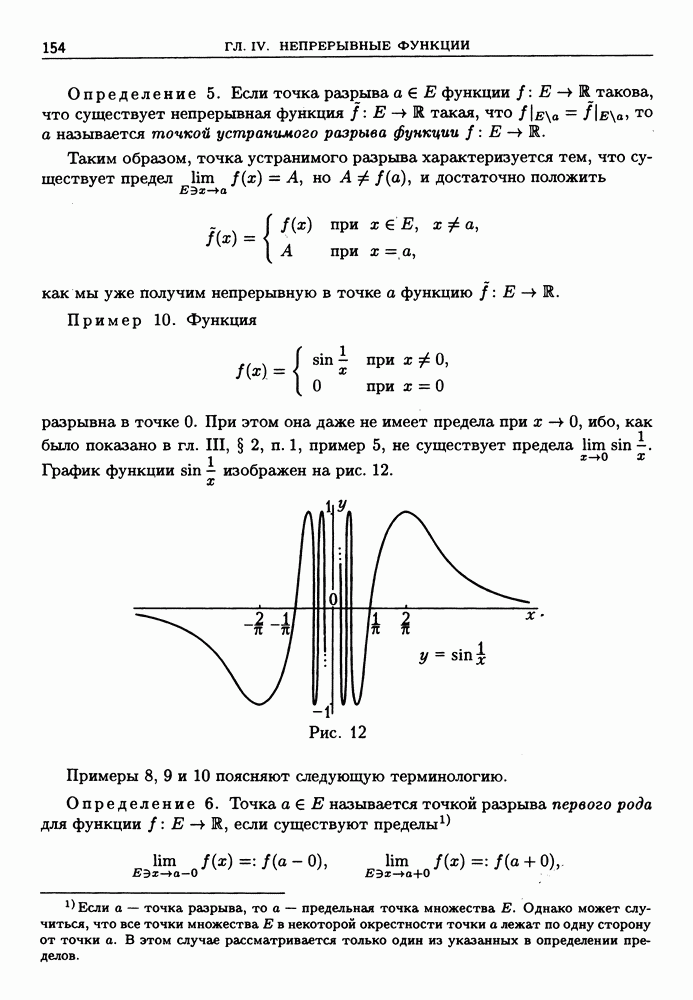
- 2. Точки разрыва.
- § 2. Свойства непрерывных функций
- 2. Глобальные свойства непрерывных функций.
- ГЛАВА V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- 2. Функция, дифференцируемая в точке.
- 3. Касательная; геометрический смысл производной и дифференциала.
- 4. Роль системы координат.
- 5. Некоторые примеры
- Задачи и упражнения
- § 2. Основные правила дифференцирования
- 2. Дифференцирование композиции функций
- 3. Дифференцирование обратной функции
- 4. Таблица производных основных элементарных функций.
- 5. Дифференцирование простейшей неявно заданной функции.
- 6. Производные высших порядков.
- § 3. Основные теоремы дифференциального исчисления
- 2. Теоремы Лагранжа и Коши о конечном приращении.
- 3. Формула Тейлора.
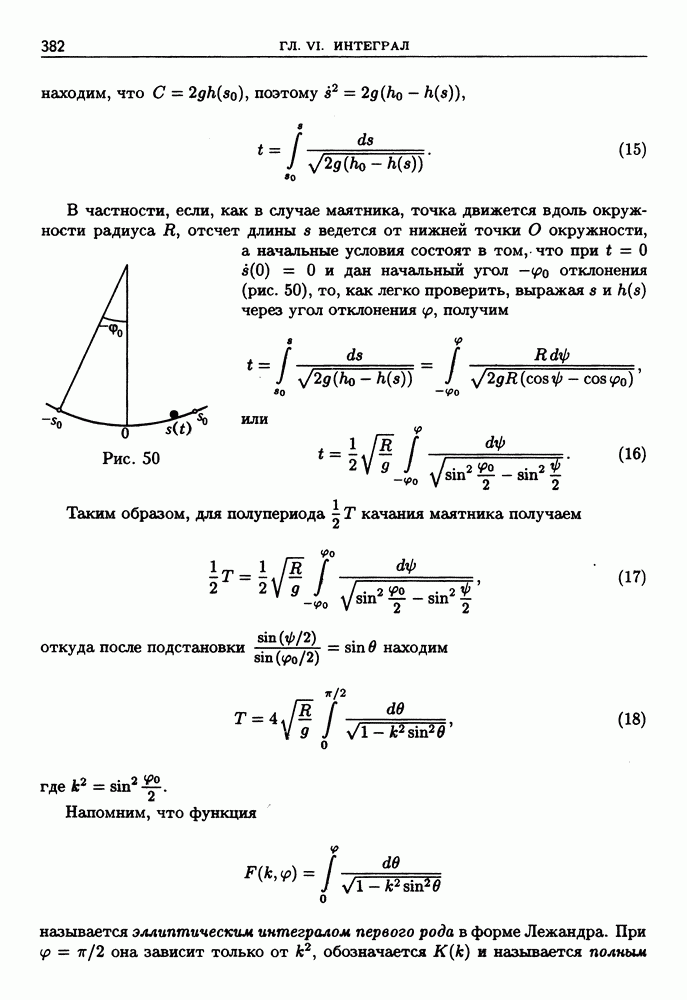
- § 4. Исследование функций методами дифференциального исчисления
- 2. Условия внутреннего экстремума функции.
- 3. Условия выпуклости функции
- 4. Правило Лопиталя.
- 5. Построение графика функции.
- § 5. Комплексные числа и взаимосвязь элементарных функций
- 2. Сходимость в С и ряды с комплексными членами.
- 3. Формула Эйлера и взаимосвязь элементарных функций.
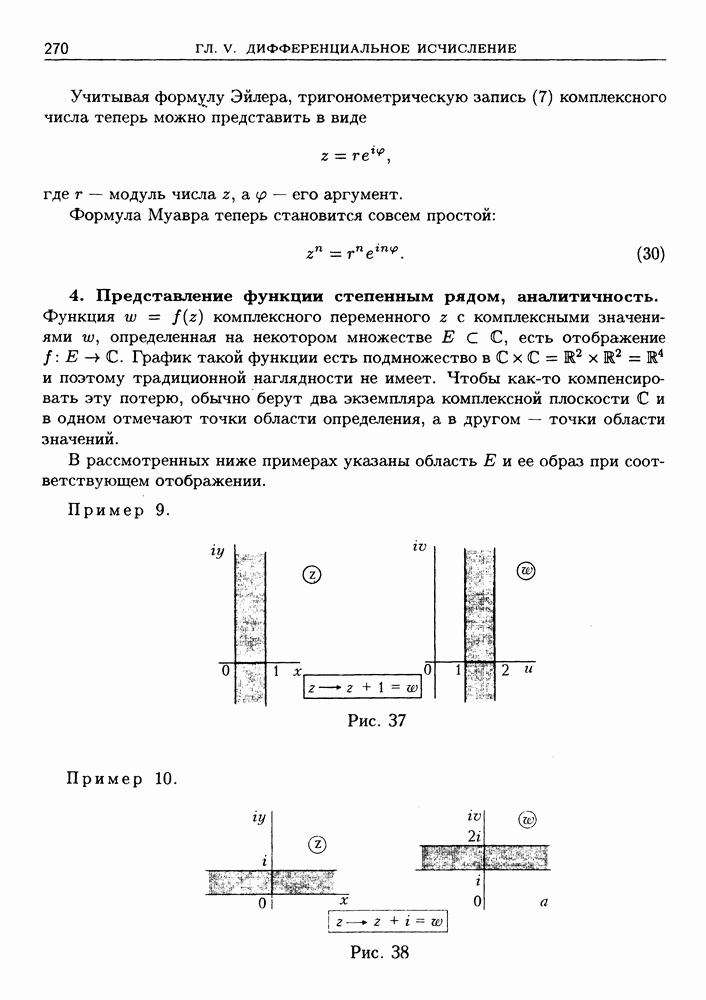
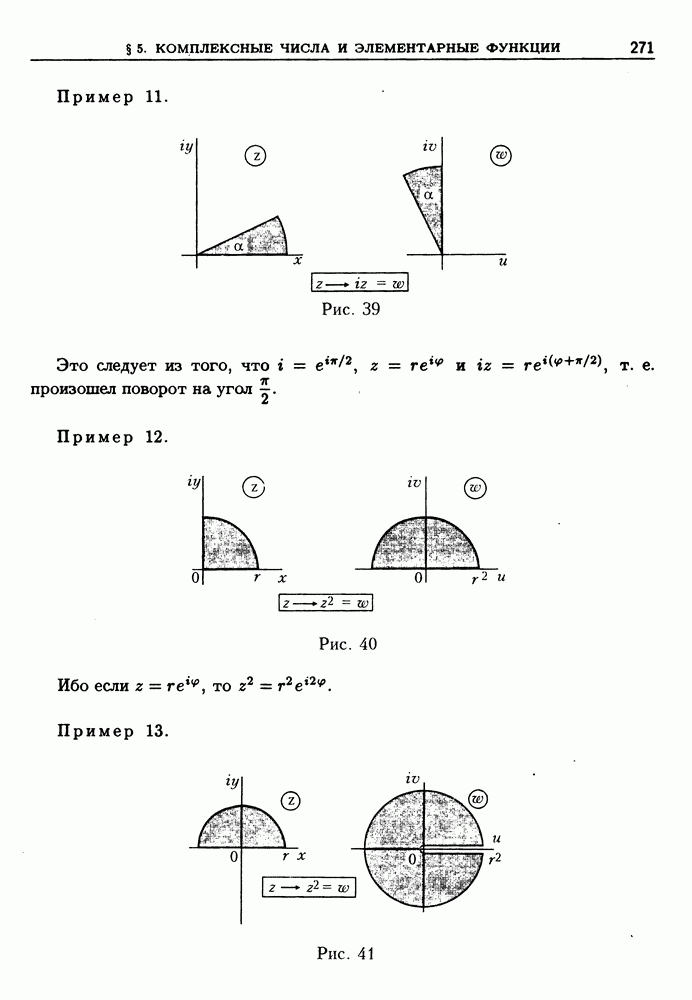
- 4. Представление функции степенным рядом, аналитичность.
- 5. Алгебраическая замкнутость поля С комплексных чисел.
- § 6. Некоторые примеры использования дифференциального исчисления в задачах естествознания
- 2. Барометрическая формула.
- 3. Радиоактивный распад, цепная реакция и атомный котел.
- 4. Падение тел в атмосфере.
- 5. Еще раз о числе e и функции exp(x).
- 6. Колебания.
- § 7. Первообразная
- 2. Основные общие приемы отыскания первообразной.
- 3. Первообразные рациональных функций.
- 4. Первообразные вида …
- 5. Первообразные вида …
- ГЛАВА VI. ИНТЕГРАЛ
- § 1. Определение интеграла и описание множества интегрируемых функций
- 2. Определение интеграла Римана
- 3. Множество интегрируемых функций.
- § 2. Линейность, аддитивность и монотонность интеграла
- 2. Интеграл как аддитивная функция отрезка интегрирования.
- 3. Оценка интеграла, монотонность интеграла, теоремы о среднем
- § 3. Интеграл и производная
- 2. Формула Ньютона—Лейбница
- 3. Интегрирование по частям в определенном интеграле и формула Тейлора
- 4. Замена переменной в интеграле.
- 5. Некоторые примеры.
- § 4. Некоторые приложения интеграла
- 2. Длина пути.
- 3. Площадь криволинейной трапеции.
- 4. Объем тела вращения.
- 5. Работа и энергия.
- § 5. Несобственный интеграл
- 2. Исследование сходимости несобственного интеграла
- 3. Несобственные интегралы с несколькими особенностями.
- ГЛАВА VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
- 2. Открытые и замкнутые множества в R^m
- 3. Компакты в R^m
- § 2. Предел и непрерывность функции многих переменных
- 2. Непрерывность функции многих переменных и свойства непрерывных функций.
- ГЛАВА VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 2. Линейные отображения L : R^m -> R^n.
- 3. Норма в R^m.
- 4. Евклидова структура в R^m.
- § 2. Дифференциал функции многих переменных
- 2. Дифференциал и частные производные вещественнозначной функции.
- 3. Координатное представление дифференциала отображения. Матрица Якоби.
- 4. Непрерывность, частные производные и дифференцируемость функции в точке.
- § 3. Основные законы дифференцирования
- 2. Дифференцирование композиции отображений
- 3. Дифференцирование обратного отображения
- § 4. Основные факты дифференциального исчисления вещественнозначных функций многих переменных
- 2. Достаточное условие дифференцируемости функции многих переменных
- 4. Формула Тейлора
- 5. Экстремумы функций многих переменных.
- 6. Некоторые геометрические образы, связанные с функциями многих переменных
- § 5. Теорема о неявной функции
- 2. Простейший вариант теоремы о неявной функции.
- 3. Переход к случаю зависимости
- 4. Теорема о неявной функции.
- § 6. Некоторые следствия теоремы о неявной функции
- 2. Локальное приведение гладкого отображения к каноническому виду.
- 3. Зависимость функций
- 4. Локальное разложение диффеоморфизма в композицию простейших.
- 5. Лемма Морса.
- § 7. Поверхность в R^n и теория условного экстремума
- 2. Касательное пространство.
- 3. Условный экстремум
- НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
- ВОПРОСЫ К ЭКЗАМЕНУ
- ЛИТЕРАТУРА