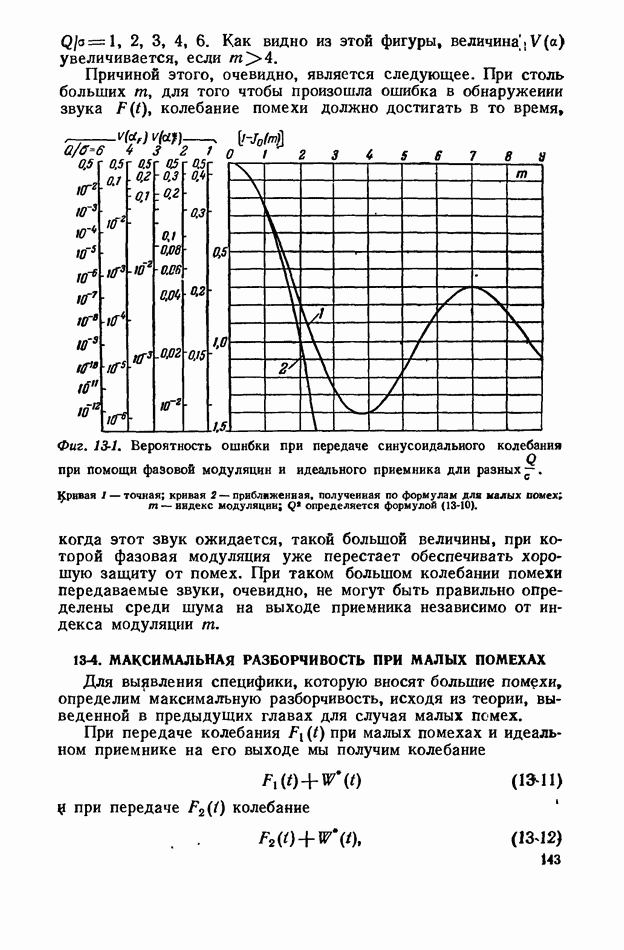
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава пятая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СИГНАЛАХ СО МНОГИМИ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
5-1. РЕШЕНИЕ ЗАДАЧИ В ОБЩЕМ ВИДЕ
В предыдущей главе мы рассмотрели помехоустойчивость в случае, когда сигнал мог принимать только два значения.
В этой главе мы. займемся аналогичным вопросом, но для более общего случая, когда сообщения и, значит, сигналы могут иметь  дискретных значений. Пусть эти значения сигналов будут:
дискретных значений. Пусть эти значения сигналов будут:

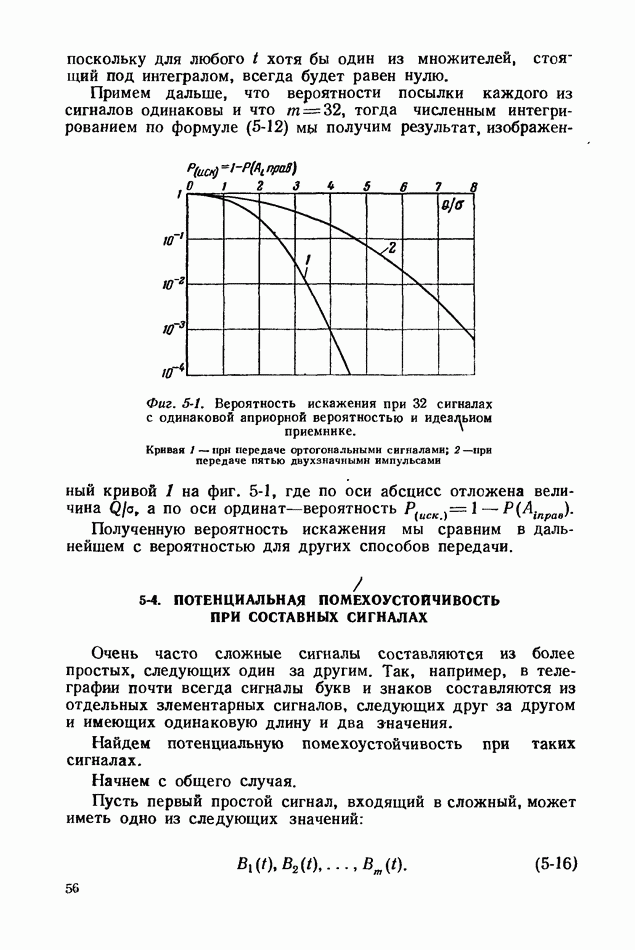
Найдем вероятность искажения при приеме таких сигналов на идеальный приемник, рассмотренный в гл. 3. Эта
вероятность., очевидно, будет характеризовать потенциальную помехоустойчивость.
Пусть передавался сигнал  тогда действующее на приемник колебание будет:
тогда действующее на приемник колебание будет:

Очевидно идеальный приемник при этом воспроизведет сообщение, соответствующее передававшемуся сигналу  если в соответствии с § 3-2 мы будем иметь:
если в соответствии с § 3-2 мы будем иметь:

Если хотя бы одно из неравенств  не будет удовлетворяться, произойдет искажение.
не будет удовлетворяться, произойдет искажение.
Подставляя в уравнение  значение
значение  из
из  мы после преобразования получим:
мы после преобразования получим:

Вероятность выполнения системы этих неравенств равна вероятности правильного приема сигнала  на идеальный приемник. Аналогичные выражения будем иметь и для других сигналов. В общем случае селичина этой вероятности выражается интегралами, которые не берутся.
на идеальный приемник. Аналогичные выражения будем иметь и для других сигналов. В общем случае селичина этой вероятности выражается интегралами, которые не берутся.
Поэтому в дальнейшем будут рассмотрены лишь наиболее интересные частные случаи.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ 1. ВСПОМОГАТЕЛЬНЫЙ МАТЕРИАЛ
- 1-2. КЛАССИФИКАЦИЯ ПОМЕХ
- 1-3. СООБЩЕНИЯ И СИГНАЛЫ
- 1-4. СОДЕРЖАНИЕ ДАННОЙ РАБОТЫ
- Глава вторая. ВСПОМОГАТЕЛЬНЫЙ МАТЕМАТИЧЕСКИЙ МАТЕРИАЛ
- 2-2. ЛИНЕЙНОЕ ВЫРАЖЕНИЕ ФУНКЦИЯ ПРИ ПОМОЩИ ЕДИНИЧНЫХ ОРТОГОНАЛЬНЫХ ФУНКЦИЯ
- 2-3. НОРМАЛЬНО ФЛЮКТУАЦИОННОЕ КОЛЕБАНИЕ
- 2-4. ВЫРАЖЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ РЯДОМ ФУРЬЕ
- 2-5. ЛИНЕЙНЫЕ ФУНКЦИИ НЕЗАВИСИМЫХ НОРМАЛЬНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 2-6. ВЕРОЯТНОСТЬ ПОПАДАНИЯ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ В ДАННУЮ ОБЛАСТЬ
- 2-7. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ ПОЛУЧЕННЫХ СООТНОШЕНИЙ
- ЧАСТЬ II. ПЕРЕДАЧА ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3-1. ДИСКРЕТНЫЕ СООБЩЕНИЯ И СИГНАЛЫ
- 3-2. ИДЕАЛЬНЫЙ ПРИЕМНИК
- 3-3. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 3
- Глава четвертая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СИГНАЛАХ С ДВУМЯ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 4-1. ВЕРОЯТНОСТЬ ИСКАЖЕНИЯ ПРИ ИДЕАЛЬНОМ ПРИЕМНИКЕ
- 4-2. ВЛИЯНИЕ ОТНОШЕНИЯ …
- 4-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ С ПАССИВНОЙ ПАУЗОЙ
- 4-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ
- 4-5. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ И ПРИЕМЕ С СИНХРОННЫМ ДЕТЕКТОРОМ
- 4-6. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ И ПРИЕМЕ С ОБЫЧНЫМ ДЕТЕКТОРОМ
- 4-7. ВЫВОДЫ ОТНОСИТЕЛЬНО ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ С ПАССИВНОЙ ПАУЗОЙ
- 4-8. ОПТИМАЛЬНАЯ СИСТЕМА ПЕРЕДАЧИ С АКТИВНОЙ ПАУЗОЙ
- 4-9. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНОЙ МАНИПУЛЯЦИИ
- 4-10. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ НОРМАЛЬНО ФЛЮКТУАЦИОННОИ ПОМЕХЕ С ИНТЕНСИВНОСТЬЮ, ЗАВИСЯЩЕЙ ОТ ЧАСТОТЫ
- 4-11. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 4
- Глава пятая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СИГНАЛАХ СО МНОГИМИ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 5-2. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ОРТОГОНАЛЬНЫХ РАВНОВЕРОЯТНЫХ СИГНАЛАХ, ИМЕЮЩИХ ОДИНАКОВУЮ ЭНЕРГИЮ
- 5-3. ПРИМЕР ТЕЛЕГРАФНОЙ ПЕРЕДАЧИ С 32 ОРТОГОНАЛЬНЫМИ СИГНАЛАМИ
- 5-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СОСТАВНЫХ СИГНАЛАХ
- 5-5. ПРИМЕР ПЯТИЗНАЧНОГО КОДА
- 5-6. ОПТИМАЛЬНАЯ СИСТЕМА ПРИ СИГНАЛАХ СО МНОГИМИ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 5-7. ПРИБЛИЖЕННАЯ ОЦЕНКА ПОТЕНЦИАЛЬНОЙ ПОМЕХОУСТОЙЧИВОСТИ
- 5-8. ПРИМЕР ПЕРЕДАЧИ ЦИФР КОДОМ МОРЗЕ
- ЧАСТЬ III. ПЕРЕДАЧА ОТДЕЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Глава шестая. ОБЩАЯ ТЕОРИЯ ВЛИЯНИЯ ПОМЕХ НА ПЕРЕДАЧУ ОТДЕЛЬНЫХ ЗНАЧЕНИИ ПАРАМЕТРОВ
- 6-2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ ПЕРЕДАВАВШЕГОСЯ ПАРАМЕТРА
- 6-3. ФУНКЦИЯ … ВБЛИЗИ НАИВЕРОЯТНЕЙШЕГО ЗНАЧЕНИЯ …
- 6-4. ОШИБКИ И ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 6-5. ВТОРОЙ МЕТОД ОПРЕДЕЛЕНИЯ ОШИБОК И ПОТЕНЦИАЛЬНОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 6-6. ИТОГИ ГЛ. 6
- 6-7. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 6
- Глава седьмая. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ РАЗНЫХ СИСТЕМАХ ПЕРЕДАЧИ ОТДЕЛЬНЫХ ЗНАЧЕНИИ ПАРАМЕТРОВ И ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 7-1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 7-2. ЛИНЕЙНАЯ МОДУЛЯЦИЯ
- 7-3. ОБЩИЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- 7-4. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ)
- 7-5. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРВОМ МЕТОДЕ ПРИЕМА)
- 7-6. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ВТОРОМ МЕТОДЕ ПРИЕМА)
- 7-7. ЧАСТОТНАЯ МОДУЛЯЦИЯ (ОБЩИЙ СЛУЧАЙ)
- 7-8. ЧАСТОТНАЯ МОДУЛЯЦИЯ (ЧАСТНЫЙ СЛУЧАЙ)
- 7-9. ПОВЫШЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ БЕЗ УВЕЛИЧЕНИЯ ЭНЕРГИИ, ДЛИТЕЛЬНОСТИ И ШИРИНЫ СПЕКТРА СИГНАЛА
- Глава восьмая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ ОТДЕЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ПРИ БОЛЬШИХ ПОМЕХАХ
- 8-1. ВЫВОД ОБЩЕЙ ФОРМУЛЫ ДЛЯ ОЦЕНКИ ВЛИЯНИЯ ПОМЕХИ БОЛЬШОЙ ИНТЕНСИВНОСТИ
- 8-2. СРАВНЕНИЕ ФОРМУЛ ДЛЯ МАЛЫХ И БОЛЬШИХ ПОМЕХ
- 8-3. ВРЕМЯ-ИМПУЛЬСНАЯ МОДУЛЯЦИЯ
- 8-4. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 8-5. СИСТЕМА ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ БЕЗ УВЕЛИЧЕНИЯ ЭНЕРГИИ, ДЛИТЕЛЬНОСТИ И ШИРИНЫ СПЕКТРА СИГНАЛА
- 8-6. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ РЕЗУЛЬТАТОВ ГЛ. 8
- ЧАСТЬ IV. ПЕРЕДАЧА КОЛЕБАНИЙ
- Глава девятая. ОБЩАЯ ТЕОРИЯ ВЛИЯНИЯ МАЛЫХ ПОМЕХ НА ПЕРЕДАЧУ КОЛЕБАНИЙ
- 9-2. ВЛИЯНИЕ МАЛЫХ ПОМЕХ НА ПЕРЕДАВАЕМЫЕ КОЛЕБАНИЯ
- 9-3. УСЛОВИЯ ИДЕАЛЬНОГО ПРИЕМНИКА
- 9-4. СПОСОБ ОСУЩЕСТВЛЕНИЯ ИДЕАЛЬНОГО ПРИЕМНИКА
- 9-5. ИСКАЖЕНИЯ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- Глава десятая. ПРЯМЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 10-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНОЙ И ЛИНЕЙНОЙ МОДУЛЯЦИИ
- 10-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ
- 10-5. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ И ОБЫЧНОМ ПРИЕМЕ
- 10-6. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ И ОБЫЧНОМ ПРИЕМЕ
- 10-7. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ ОДНОЙ БОКОВОЙ ПОЛОСОЙ
- Глава одиннадцатая. ИМПУЛЬСНЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 11-2. ПРИМЕР ОСУЩЕСТВЛЕНИЯ ИМПУЛЬСНОЙ СИСТЕМЫ МОДУЛЯЦИИ
- 11-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ИМПУЛЬСНОЙ СИСТЕМЕ МОДУЛЯЦИИ
- 11-4. ПОМЕХОУСТОЙЧИВОСТЬ ПРИЕМНИКА, РАЗОБРАННОГО В § 11-2
- 11-5. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- 11-6. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ВРЕМЯ-ИМПУЛЬСНОИ МОДУЛЯЦИИ
- 11-7. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- Глава двенадцатая. ИНТЕГРАЛЬНЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 12-2. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ИНТЕГРАЛЬНЫХ СИСТЕМАХ МОДУЛЯЦИИ
- 12-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- Глава тринадцатая. ОЦЕНКА ВЛИЯНИЯ БОЛЬШИХ ПОМЕХ НА ПЕРЕДАЧУ КОЛЕБАНИЙ
- 13-3. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ
- 13-4. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ МАЛЫХ ПОМЕХАХ
- 13-5. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ МАЛЫХ ПОМЕХАХ И ФАЗОВОЙ МОДУЛЯЦИИ
- Приложение А. УДЕЛЬНАЯ ЭНЕРГИЯ ВЫСОКОЧАСТОТНЫХ КОЛЕБАНИЙ
- Приложение В. ВЫРАЖЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ ДВУМЯ АМПЛИТУДНО-МОДУЛИРОВАННЫМИ КОЛЕБАНИЯМИ
- Приложение С. МГНОВЕННОЕ ЗНАЧЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ
- Приложение D. НОРМАЛЬНО ФЛЮКТУАЦИОННОЕ КОЛЕБАНИЕ ИЗ ПРОИЗВОЛЬНЫХ ИМПУЛЬСОВ