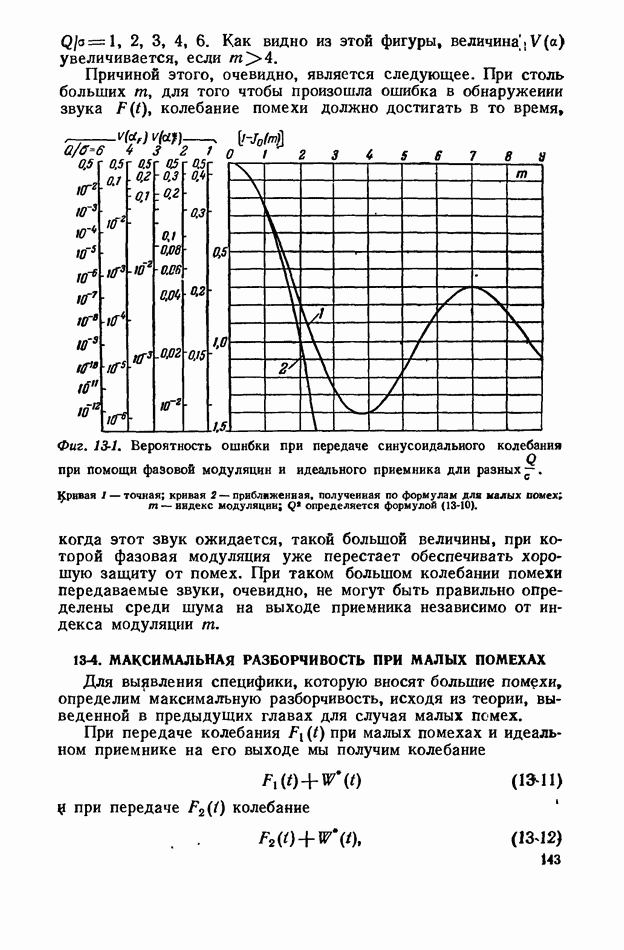
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
9-2. ВЛИЯНИЕ МАЛЫХ ПОМЕХ НА ПЕРЕДАВАЕМЫЕ КОЛЕБАНИЯ
Как мы установили, передаваемое колебание определяется полностью параметрами  Очевидно, приемник, воспроизводя функцию
Очевидно, приемник, воспроизводя функцию  этим самым будет воспроизводить данные параметры.
этим самым будет воспроизводить данные параметры.
Представим колебание  так:
так:

где  представляют некоторую систему единичных ортогональных функций.
представляют некоторую систему единичных ортогональных функций.
Очевидно, воспроизводимые приемником параметры А, будут некоторыми функциями величин  которые характеризуют приходящее колебание
которые характеризуют приходящее колебание  Таким образом, можно записать:
Таким образом, можно записать:

где 
Вид этих функций зависит от системы модуляции и приемника.
Если приходящее колебание получит некоторое приращение

то, очевидно, параметры  получат приращения
получат приращения

где обозначено:

Предположим, что приемник при отсутствии помех правильно воспроизводит передававшееся колебание.
Пусть это колебание изменится так, что  получит приращение
получит приращение  При этом сигнал и, значит (поскольку помехи отсутствуют) колебания
При этом сигнал и, значит (поскольку помехи отсутствуют) колебания  должны получить приращение
должны получить приращение

где мы обозначили:

Исходя из  и учитывая, что приемник должен воспроизвести переданное колебание без искажений, должно быть справедливо следующее равенство:
и учитывая, что приемник должен воспроизвести переданное колебание без искажений, должно быть справедливо следующее равенство:

или

Остальные воспроизводимые параметры при этом не должны меняться и, значит,

откуда

если 
Таким образом, для любого приемника, правильно воспроизводящего передаваемые колебания в отсутствие помех, должны удовлетворяться уравнения (9-11) и (9-12), в  любое целое число от до
любое целое число от до 
Пусть теперь передано некоторое колебание, которое характеризуется параметрами  Пусть на сигнал, передающий это колебание, наложилась помеха
Пусть на сигнал, передающий это колебание, наложилась помеха  достаточно малая по величине. Тогда под действием этой помехи пришедшее колебание получит приращение
достаточно малая по величине. Тогда под действием этой помехи пришедшее колебание получит приращение

вследствие чего параметры воспроизведенного приемником колебания получат приращения

и будут равны 
Таким образом, приращения  получаемые от действия помехи, будут случайными величинами, подчиняющимися закону Гаусса. Чем меньше
получаемые от действия помехи, будут случайными величинами, подчиняющимися закону Гаусса. Чем меньше

тем меньше будут эти приращения и, значит, ошибки, даваемые приемником.
Если мы выберем  такими, чтобы они удовлетворяли уравнениям (9-12) и (9-11) и в то же время значения (9-14) имели наименьшие возможные величины, то приемник, характеризующийся такими
такими, чтобы они удовлетворяли уравнениям (9-12) и (9-11) и в то же время значения (9-14) имели наименьшие возможные величины, то приемник, характеризующийся такими  будет давать наименьшие погрешности воспроизведения при достаточно малых помехах. В следующем параграфе мы найдем эти оптимальные значения
будет давать наименьшие погрешности воспроизведения при достаточно малых помехах. В следующем параграфе мы найдем эти оптимальные значения  и далее покажем, что приемник, обладающий такими
и далее покажем, что приемник, обладающий такими  по крайней мере принципиально, осуществим.
по крайней мере принципиально, осуществим.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ 1. ВСПОМОГАТЕЛЬНЫЙ МАТЕРИАЛ
- 1-2. КЛАССИФИКАЦИЯ ПОМЕХ
- 1-3. СООБЩЕНИЯ И СИГНАЛЫ
- 1-4. СОДЕРЖАНИЕ ДАННОЙ РАБОТЫ
- Глава вторая. ВСПОМОГАТЕЛЬНЫЙ МАТЕМАТИЧЕСКИЙ МАТЕРИАЛ
- 2-2. ЛИНЕЙНОЕ ВЫРАЖЕНИЕ ФУНКЦИЯ ПРИ ПОМОЩИ ЕДИНИЧНЫХ ОРТОГОНАЛЬНЫХ ФУНКЦИЯ
- 2-3. НОРМАЛЬНО ФЛЮКТУАЦИОННОЕ КОЛЕБАНИЕ
- 2-4. ВЫРАЖЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ РЯДОМ ФУРЬЕ
- 2-5. ЛИНЕЙНЫЕ ФУНКЦИИ НЕЗАВИСИМЫХ НОРМАЛЬНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 2-6. ВЕРОЯТНОСТЬ ПОПАДАНИЯ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ В ДАННУЮ ОБЛАСТЬ
- 2-7. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ ПОЛУЧЕННЫХ СООТНОШЕНИЙ
- ЧАСТЬ II. ПЕРЕДАЧА ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3-1. ДИСКРЕТНЫЕ СООБЩЕНИЯ И СИГНАЛЫ
- 3-2. ИДЕАЛЬНЫЙ ПРИЕМНИК
- 3-3. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 3
- Глава четвертая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СИГНАЛАХ С ДВУМЯ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 4-1. ВЕРОЯТНОСТЬ ИСКАЖЕНИЯ ПРИ ИДЕАЛЬНОМ ПРИЕМНИКЕ
- 4-2. ВЛИЯНИЕ ОТНОШЕНИЯ …
- 4-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ С ПАССИВНОЙ ПАУЗОЙ
- 4-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ
- 4-5. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ И ПРИЕМЕ С СИНХРОННЫМ ДЕТЕКТОРОМ
- 4-6. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ И ПРИЕМЕ С ОБЫЧНЫМ ДЕТЕКТОРОМ
- 4-7. ВЫВОДЫ ОТНОСИТЕЛЬНО ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ С ПАССИВНОЙ ПАУЗОЙ
- 4-8. ОПТИМАЛЬНАЯ СИСТЕМА ПЕРЕДАЧИ С АКТИВНОЙ ПАУЗОЙ
- 4-9. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНОЙ МАНИПУЛЯЦИИ
- 4-10. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ НОРМАЛЬНО ФЛЮКТУАЦИОННОИ ПОМЕХЕ С ИНТЕНСИВНОСТЬЮ, ЗАВИСЯЩЕЙ ОТ ЧАСТОТЫ
- 4-11. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 4
- Глава пятая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СИГНАЛАХ СО МНОГИМИ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 5-2. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ОРТОГОНАЛЬНЫХ РАВНОВЕРОЯТНЫХ СИГНАЛАХ, ИМЕЮЩИХ ОДИНАКОВУЮ ЭНЕРГИЮ
- 5-3. ПРИМЕР ТЕЛЕГРАФНОЙ ПЕРЕДАЧИ С 32 ОРТОГОНАЛЬНЫМИ СИГНАЛАМИ
- 5-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СОСТАВНЫХ СИГНАЛАХ
- 5-5. ПРИМЕР ПЯТИЗНАЧНОГО КОДА
- 5-6. ОПТИМАЛЬНАЯ СИСТЕМА ПРИ СИГНАЛАХ СО МНОГИМИ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 5-7. ПРИБЛИЖЕННАЯ ОЦЕНКА ПОТЕНЦИАЛЬНОЙ ПОМЕХОУСТОЙЧИВОСТИ
- 5-8. ПРИМЕР ПЕРЕДАЧИ ЦИФР КОДОМ МОРЗЕ
- ЧАСТЬ III. ПЕРЕДАЧА ОТДЕЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Глава шестая. ОБЩАЯ ТЕОРИЯ ВЛИЯНИЯ ПОМЕХ НА ПЕРЕДАЧУ ОТДЕЛЬНЫХ ЗНАЧЕНИИ ПАРАМЕТРОВ
- 6-2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ ПЕРЕДАВАВШЕГОСЯ ПАРАМЕТРА
- 6-3. ФУНКЦИЯ … ВБЛИЗИ НАИВЕРОЯТНЕЙШЕГО ЗНАЧЕНИЯ …
- 6-4. ОШИБКИ И ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 6-5. ВТОРОЙ МЕТОД ОПРЕДЕЛЕНИЯ ОШИБОК И ПОТЕНЦИАЛЬНОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 6-6. ИТОГИ ГЛ. 6
- 6-7. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 6
- Глава седьмая. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ РАЗНЫХ СИСТЕМАХ ПЕРЕДАЧИ ОТДЕЛЬНЫХ ЗНАЧЕНИИ ПАРАМЕТРОВ И ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 7-1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 7-2. ЛИНЕЙНАЯ МОДУЛЯЦИЯ
- 7-3. ОБЩИЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- 7-4. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ)
- 7-5. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРВОМ МЕТОДЕ ПРИЕМА)
- 7-6. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ВТОРОМ МЕТОДЕ ПРИЕМА)
- 7-7. ЧАСТОТНАЯ МОДУЛЯЦИЯ (ОБЩИЙ СЛУЧАЙ)
- 7-8. ЧАСТОТНАЯ МОДУЛЯЦИЯ (ЧАСТНЫЙ СЛУЧАЙ)
- 7-9. ПОВЫШЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ БЕЗ УВЕЛИЧЕНИЯ ЭНЕРГИИ, ДЛИТЕЛЬНОСТИ И ШИРИНЫ СПЕКТРА СИГНАЛА
- Глава восьмая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ ОТДЕЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ПРИ БОЛЬШИХ ПОМЕХАХ
- 8-1. ВЫВОД ОБЩЕЙ ФОРМУЛЫ ДЛЯ ОЦЕНКИ ВЛИЯНИЯ ПОМЕХИ БОЛЬШОЙ ИНТЕНСИВНОСТИ
- 8-2. СРАВНЕНИЕ ФОРМУЛ ДЛЯ МАЛЫХ И БОЛЬШИХ ПОМЕХ
- 8-3. ВРЕМЯ-ИМПУЛЬСНАЯ МОДУЛЯЦИЯ
- 8-4. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 8-5. СИСТЕМА ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ БЕЗ УВЕЛИЧЕНИЯ ЭНЕРГИИ, ДЛИТЕЛЬНОСТИ И ШИРИНЫ СПЕКТРА СИГНАЛА
- 8-6. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ РЕЗУЛЬТАТОВ ГЛ. 8
- ЧАСТЬ IV. ПЕРЕДАЧА КОЛЕБАНИЙ
- Глава девятая. ОБЩАЯ ТЕОРИЯ ВЛИЯНИЯ МАЛЫХ ПОМЕХ НА ПЕРЕДАЧУ КОЛЕБАНИЙ
- 9-2. ВЛИЯНИЕ МАЛЫХ ПОМЕХ НА ПЕРЕДАВАЕМЫЕ КОЛЕБАНИЯ
- 9-3. УСЛОВИЯ ИДЕАЛЬНОГО ПРИЕМНИКА
- 9-4. СПОСОБ ОСУЩЕСТВЛЕНИЯ ИДЕАЛЬНОГО ПРИЕМНИКА
- 9-5. ИСКАЖЕНИЯ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- Глава десятая. ПРЯМЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 10-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНОЙ И ЛИНЕЙНОЙ МОДУЛЯЦИИ
- 10-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ
- 10-5. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ И ОБЫЧНОМ ПРИЕМЕ
- 10-6. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ И ОБЫЧНОМ ПРИЕМЕ
- 10-7. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ ОДНОЙ БОКОВОЙ ПОЛОСОЙ
- Глава одиннадцатая. ИМПУЛЬСНЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 11-2. ПРИМЕР ОСУЩЕСТВЛЕНИЯ ИМПУЛЬСНОЙ СИСТЕМЫ МОДУЛЯЦИИ
- 11-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ИМПУЛЬСНОЙ СИСТЕМЕ МОДУЛЯЦИИ
- 11-4. ПОМЕХОУСТОЙЧИВОСТЬ ПРИЕМНИКА, РАЗОБРАННОГО В § 11-2
- 11-5. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- 11-6. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ВРЕМЯ-ИМПУЛЬСНОИ МОДУЛЯЦИИ
- 11-7. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- Глава двенадцатая. ИНТЕГРАЛЬНЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 12-2. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ИНТЕГРАЛЬНЫХ СИСТЕМАХ МОДУЛЯЦИИ
- 12-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- Глава тринадцатая. ОЦЕНКА ВЛИЯНИЯ БОЛЬШИХ ПОМЕХ НА ПЕРЕДАЧУ КОЛЕБАНИЙ
- 13-3. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ
- 13-4. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ МАЛЫХ ПОМЕХАХ
- 13-5. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ МАЛЫХ ПОМЕХАХ И ФАЗОВОЙ МОДУЛЯЦИИ
- Приложение А. УДЕЛЬНАЯ ЭНЕРГИЯ ВЫСОКОЧАСТОТНЫХ КОЛЕБАНИЙ
- Приложение В. ВЫРАЖЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ ДВУМЯ АМПЛИТУДНО-МОДУЛИРОВАННЫМИ КОЛЕБАНИЯМИ
- Приложение С. МГНОВЕННОЕ ЗНАЧЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ
- Приложение D. НОРМАЛЬНО ФЛЮКТУАЦИОННОЕ КОЛЕБАНИЕ ИЗ ПРОИЗВОЛЬНЫХ ИМПУЛЬСОВ