7-9. ПОВЫШЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ БЕЗ УВЕЛИЧЕНИЯ ЭНЕРГИИ, ДЛИТЕЛЬНОСТИ И ШИРИНЫ СПЕКТРА СИГНАЛА

В этом параграфе мы рассмотрим системы, при которых можно теоретически беспредельно увеличивать потенциальную помехоустойчивость при помехах с достаточно малой интенсивностью, не увеличивая при этом ни энергии сигнала, ни времени, ни полосы частот, им занимаемых.

Пусть передаваемый сигнал определяется выражением:

Таким образом, этот сигнал отличается от разобранного ранее в случае частотной модуляции тем, что в нем фаза также меняется в зависимости от передаваемой величины. Для этого сигнала получим:

при

откуда

Второй интеграл при увеличении будет стремиться к нулю, и поэтому им при достаточно большом значении можно пренебречь. Мы получим:

откуда минимальная средняя квадратическая ошибка, характеризующая потенциальную помехоустойчивость при данных сигналах, будет

Как видно из этой формулы, с увеличением а ошибку можно сделать сколь угодно малой. В то же время значение а не вызывает изменения ни энергии сигнала, ни полосы частот, ни времени, занимаемых сигналом.

Аналогичный результат получается, если менять фазу высокочастотного колебания пропорционально передаваемому параметру у сигнала с время-импульсной модуляцией, разобранной в § 7-3.

Получаемую в этих системах потенциальную помехоустойчивость на практике реализовать довольно трудно, так как для этого требуется приемник, реагирующий на начальную фазу высокочастотного колебания сигнала. Однако можно предложить системы модуляции, в которых большую помехоустойчивость практически реализовать будет легче. К таким "истемам относится, например, система с сигналом:

Этот сигнал имеет то преимущество перед сигналами, рассмотренными выше, что в нем меняется фаза низкочастотного колебания, а не высокочастотного. Эта фаза будет меньше искажена при распространении сигнала и легче улавливается приемником.

Рассмотренные примеры далеко не исчерпывают всех возможных вариантов систем модуляции, помехоустойчивость которых при малых помехах может быть беспредельно увеличена.

Такие системы модуляции могут быть построены, например, на следующем общем принципе. Следует в зависимости от передаваемой величины Я менять в сигнале некоторый параметр, например некоторую фазу, беспредельное изменение которого не увеличивает отводимое сигналу место во времени и в частотном спектре, а также его энергию. Таким образом, этот параметр можно менять на сколь угодно большую величину и этим сколь угодно удлинять линию сигнала и понижать помехоустойчивость при малых помехах. Однако изменением одного этого параметра обычно ограничиться нельзя, так как он вызывает периодические изменения в сигнале и, таким образом, нескольким различным значениям параметра будет соответствовать один и тот же сигнал. Для ликвидации этой многозначности необходимо менять одновременно еще какой-либо другой параметр, например: частоту колебания, его амплитуду, положение импульса сигнала во времени и т. п. Это изменение приходится осуществлять в ограниченных пределах, поскольку оно обычно вызывает либо увеличение энергии сигнала, либо места, отводимого сигналу во времени или по частоте.

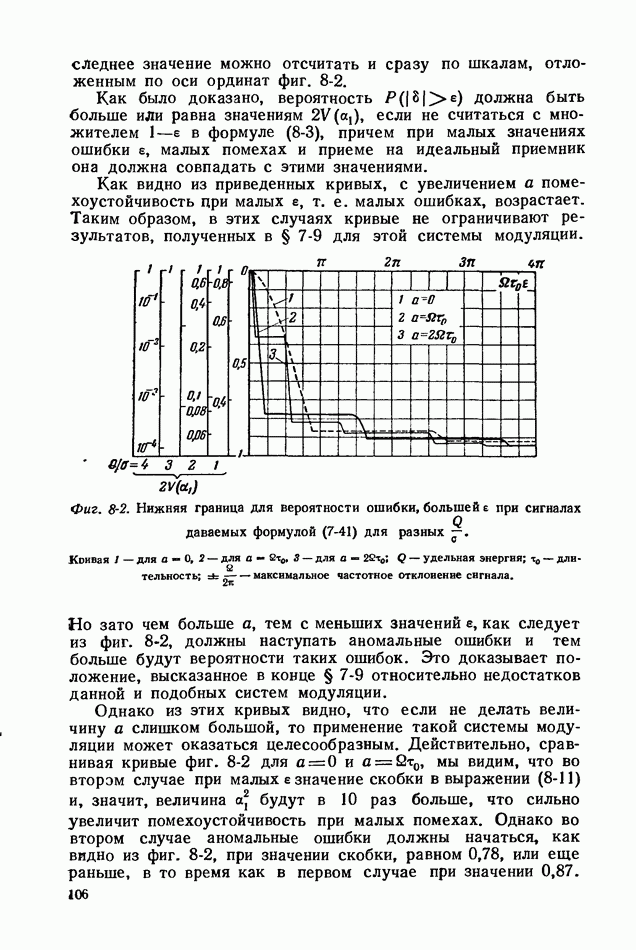
Недостаток рассмотренных в этом параграфе систем обнаруживается, если провести исследование их помехоустойчивости при помехах большой интенсивности, чему "посвящена следующая глава. При этом окаеываетоя, что чем больше мы повышаем помехоустойчивость методами, изложенными в этом параграфе, тем при меньшей интенсивности помехи наступает граница между «большой» и «малой» помехой. При «большой» же помехе выведенные формулы становятся неверными. В пределе изложенные тут способы позволяют свести погрешность, получаемую от воздействия «малых» помех, к нулю, но при этом «малыми» помехами должны будут считаться помехи, интенсивность которых также равна нулю. Таким образом, этими способами совершенно уничтожить действие помех, как и следовало ожидать, не удается, — можно лишь получить уменьшение их влияния. Такое уменьшение бывает целесообразно в случае помех с достаточно малой интенсивностью и необходимости иметь очень малые ошибки при передаче.