| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2-7. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ ПОЛУЧЕННЫХ СООТНОШЕНИЙ
Полученные в этой главе соотношения, а также соотношения, которые мы получим в дальнейшем, допускают толкование при помощи геометрии многомерного пространства.
Хотя непосредственно образы многомерного пространства не очень наглядны, но все же такое толкование дает ряд удобств, в особенности для тех, кто имеет склонность к геометрическому мышлению.
Дело в том, что соотношения, справедливые для любого многомерного пространства, справедливы и для частных случаев — пространств трехмерного и двумерного. Это позволяет предугадывать и проверять общие свойства пространств со многими измерениями на наглядных образах обычной геометрии.
Кроме того, применение терминологии и образов, вэятых из геометрий трехмерного пространства, позволяет легче запоминать полученные соотношения.
Мы условились, что будем рассматривать функции в интервале  и с частотами, лежащими в некоторых пределах. В этом случае рассматриваемые функции могут быть представлены в виде:
и с частотами, лежащими в некоторых пределах. В этом случае рассматриваемые функции могут быть представлены в виде:

где  вполне определенные функции, даваемые равенствами (2-14).
вполне определенные функции, даваемые равенствами (2-14).
Таким образом, любая рассматриваемая функция будет полностью определяться  величинами
величинами 
Мы можем эту функцию условно представлять некоторым радиусом-вектором  -мерного пространства, конец которого имеет координаты
-мерного пространства, конец которого имеет координаты  или точкой конца этого вектора. Такой вектор мы будем называть вектором, соответствующим функции
или точкой конца этого вектора. Такой вектор мы будем называть вектором, соответствующим функции  или кратко вектором функции
или кратко вектором функции  . В случае
. В случае  такое представление особо наглядно.
такое представление особо наглядно.
Функция  будет иметь все координаты, равные нулю, кроме координаты с номером I, которая будет равна единице. Таким образом, радиус-вектор, соответствующий функции
будет иметь все координаты, равные нулю, кроме координаты с номером I, которая будет равна единице. Таким образом, радиус-вектор, соответствующий функции  будет лежать на оси с номером
будет лежать на оси с номером  и иметь длину, равную единице.
и иметь длину, равную единице.
Нетрудно видеть, что вектор суммы нескольких функций будет равен сумме векторов слагаемых функций. Вектор разности функций — разности векторов этих функций.
При принятых в § 2-1 определениях скалярное произведение функций равно скалярному произведению соответствующих им векторов, как это следует из формулы (2-22).
Таким образом, сложение, вычитание и скалярное умножение функций можно заменить сложением, вычитанием и скалярным умножением их векторов.
Далее ортогональным функциям будут соответствовать ортогональные векторы. Функциям, совпадающим по направлению, — векторы, совпадающие по направлению.
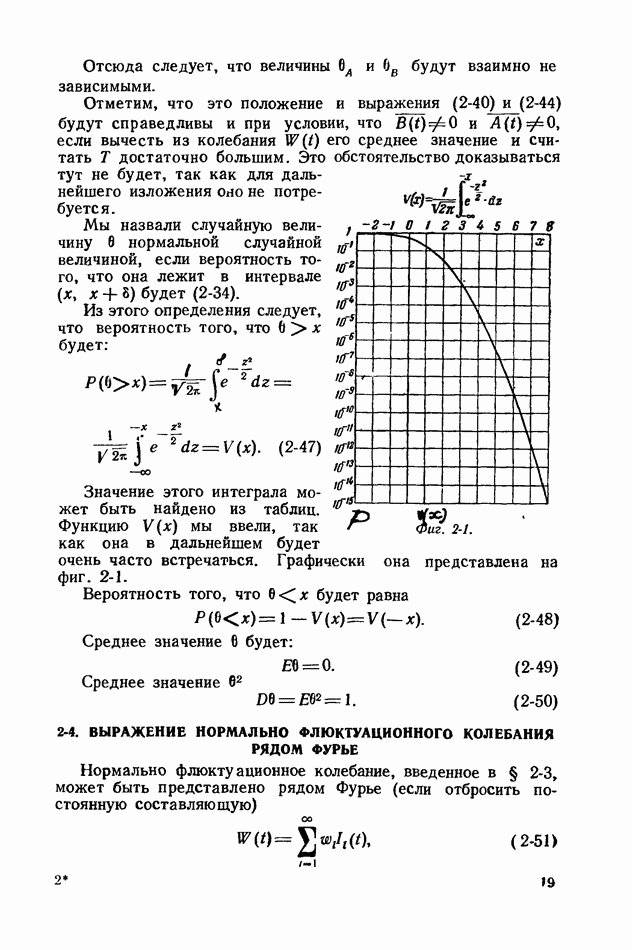
Величина эффективного значения функции, квадрат которого дается выражением (2-23), равна длине вектора, соответствующего этой функции. В соответствии с этим квадрат расстояния между точками, соответствующими функциям  будет равен:
будет равен:

Единичной функции соответствует единичный вектор.
Системе единичных ортогональных функций соответствует система единичных ортогональных векторов.
Введенное в § 2-6 формулой (2-82) понятие объема области соответствует объему в пространстве, в котором мы строим векторы.
Случайной функции  определенной уравнением (2-66), соответствует случайный радиус-вектор. Вероятность того, что конец этого вектора попадет в тот или иной малый объем
определенной уравнением (2-66), соответствует случайный радиус-вектор. Вероятность того, что конец этого вектора попадет в тот или иной малый объем  определяется формулой (2-85). Как видно из этой формулы, эта вероятность пропорциональна объему
определяется формулой (2-85). Как видно из этой формулы, эта вероятность пропорциональна объему  и зависит еще от расстояния этого объема от начала координат. Это расстояние равно величине
и зависит еще от расстояния этого объема от начала координат. Это расстояние равно величине 
Из формулы (2-68) следует, что проекция вектора, соответствующего  на любое направление, равная скалярному произведению единичного вектора, совпадающего с данным направлением, на вектор, соответствующий
на любое направление, равная скалярному произведению единичного вектора, совпадающего с данным направлением, на вектор, соответствующий  всегда равна нормальной случайной величине. Проекции вектора, соответствующего
всегда равна нормальной случайной величине. Проекции вектора, соответствующего  на ортогональные направления будут независимые между собой нормальные случайные величины.
на ортогональные направления будут независимые между собой нормальные случайные величины.
Все, что говорилось здесь о векторе, соответствующем случайному колебанию  может быть перенесено на вектор, соответствующий колебанию помехи
может быть перенесено на вектор, соответствующий колебанию помехи  поскольку эти колебания отличаются лишь постоянным множителем.
поскольку эти колебания отличаются лишь постоянным множителем.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ 1. ВСПОМОГАТЕЛЬНЫЙ МАТЕРИАЛ
- 1-2. КЛАССИФИКАЦИЯ ПОМЕХ
- 1-3. СООБЩЕНИЯ И СИГНАЛЫ
- 1-4. СОДЕРЖАНИЕ ДАННОЙ РАБОТЫ
- Глава вторая. ВСПОМОГАТЕЛЬНЫЙ МАТЕМАТИЧЕСКИЙ МАТЕРИАЛ
- 2-2. ЛИНЕЙНОЕ ВЫРАЖЕНИЕ ФУНКЦИЯ ПРИ ПОМОЩИ ЕДИНИЧНЫХ ОРТОГОНАЛЬНЫХ ФУНКЦИЯ
- 2-3. НОРМАЛЬНО ФЛЮКТУАЦИОННОЕ КОЛЕБАНИЕ
- 2-4. ВЫРАЖЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ РЯДОМ ФУРЬЕ
- 2-5. ЛИНЕЙНЫЕ ФУНКЦИИ НЕЗАВИСИМЫХ НОРМАЛЬНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- 2-6. ВЕРОЯТНОСТЬ ПОПАДАНИЯ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ В ДАННУЮ ОБЛАСТЬ
- 2-7. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ ПОЛУЧЕННЫХ СООТНОШЕНИЙ
- ЧАСТЬ II. ПЕРЕДАЧА ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3-1. ДИСКРЕТНЫЕ СООБЩЕНИЯ И СИГНАЛЫ
- 3-2. ИДЕАЛЬНЫЙ ПРИЕМНИК
- 3-3. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 3
- Глава четвертая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СИГНАЛАХ С ДВУМЯ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 4-1. ВЕРОЯТНОСТЬ ИСКАЖЕНИЯ ПРИ ИДЕАЛЬНОМ ПРИЕМНИКЕ
- 4-2. ВЛИЯНИЕ ОТНОШЕНИЯ …
- 4-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ С ПАССИВНОЙ ПАУЗОЙ
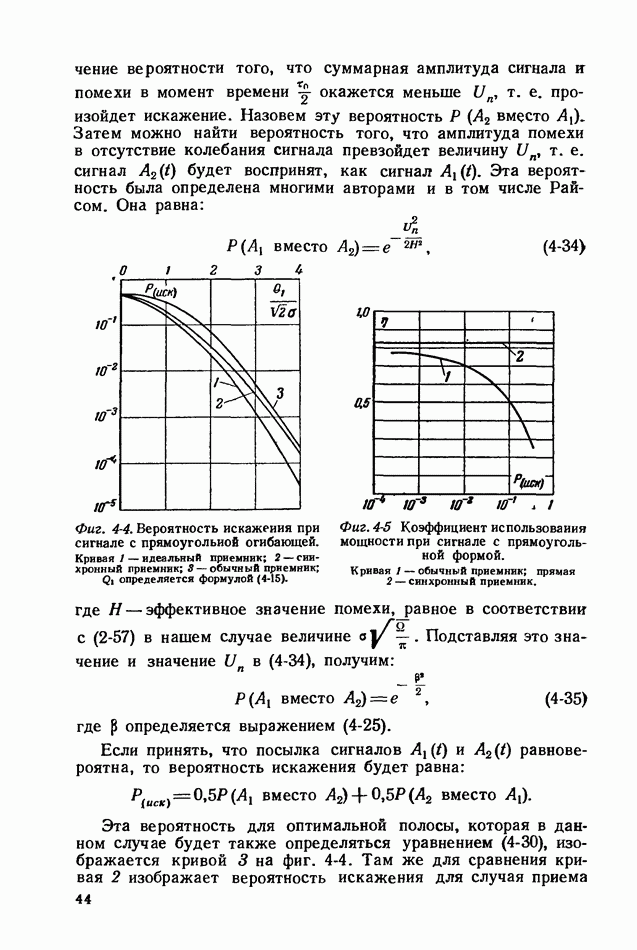
- 4-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ
- 4-5. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ И ПРИЕМЕ С СИНХРОННЫМ ДЕТЕКТОРОМ
- 4-6. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ КЛАССИЧЕСКОМ ТЕЛЕГРАФНОМ СИГНАЛЕ И ПРИЕМЕ С ОБЫЧНЫМ ДЕТЕКТОРОМ
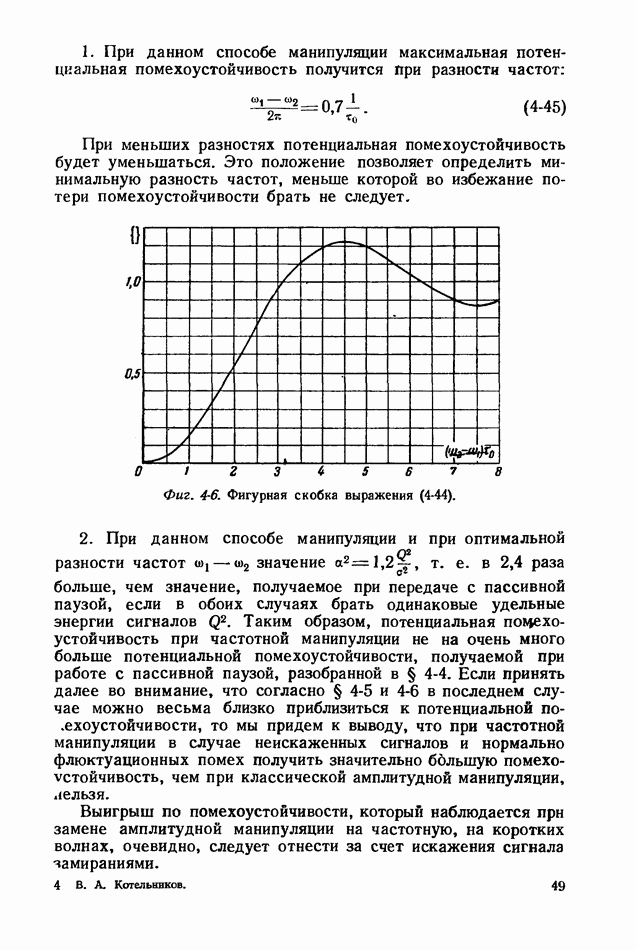
- 4-7. ВЫВОДЫ ОТНОСИТЕЛЬНО ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ С ПАССИВНОЙ ПАУЗОЙ
- 4-8. ОПТИМАЛЬНАЯ СИСТЕМА ПЕРЕДАЧИ С АКТИВНОЙ ПАУЗОЙ
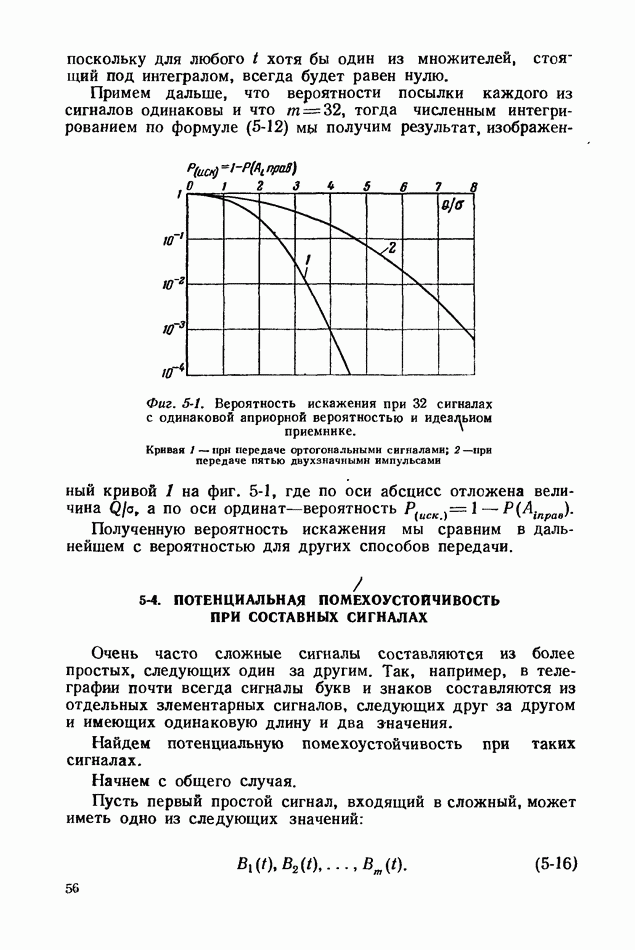
- 4-9. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНОЙ МАНИПУЛЯЦИИ
- 4-10. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ НОРМАЛЬНО ФЛЮКТУАЦИОННОИ ПОМЕХЕ С ИНТЕНСИВНОСТЬЮ, ЗАВИСЯЩЕЙ ОТ ЧАСТОТЫ
- 4-11. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 4
- Глава пятая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СИГНАЛАХ СО МНОГИМИ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 5-2. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ОРТОГОНАЛЬНЫХ РАВНОВЕРОЯТНЫХ СИГНАЛАХ, ИМЕЮЩИХ ОДИНАКОВУЮ ЭНЕРГИЮ
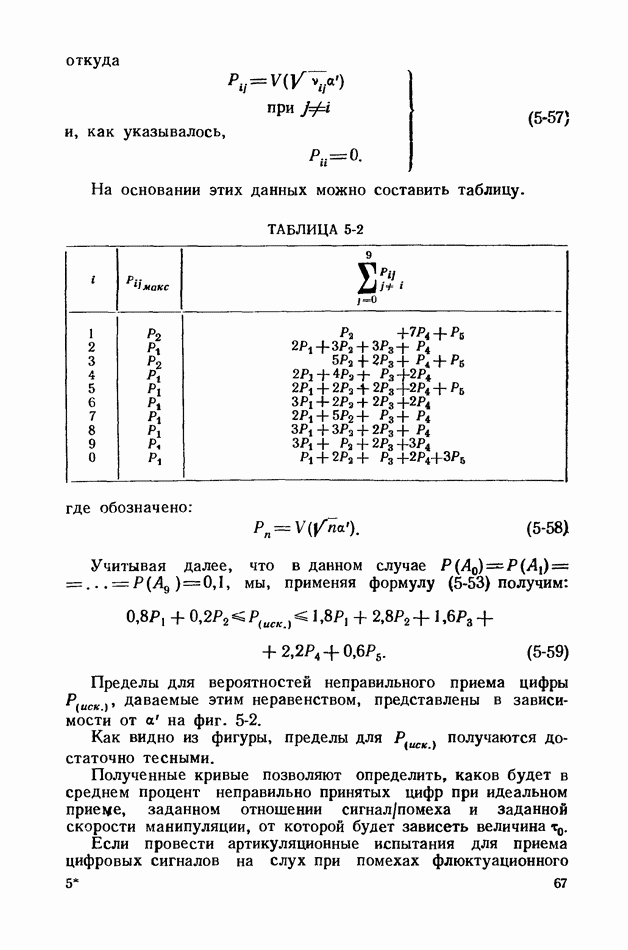
- 5-3. ПРИМЕР ТЕЛЕГРАФНОЙ ПЕРЕДАЧИ С 32 ОРТОГОНАЛЬНЫМИ СИГНАЛАМИ
- 5-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ СОСТАВНЫХ СИГНАЛАХ
- 5-5. ПРИМЕР ПЯТИЗНАЧНОГО КОДА
- 5-6. ОПТИМАЛЬНАЯ СИСТЕМА ПРИ СИГНАЛАХ СО МНОГИМИ ДИСКРЕТНЫМИ ЗНАЧЕНИЯМИ
- 5-7. ПРИБЛИЖЕННАЯ ОЦЕНКА ПОТЕНЦИАЛЬНОЙ ПОМЕХОУСТОЙЧИВОСТИ
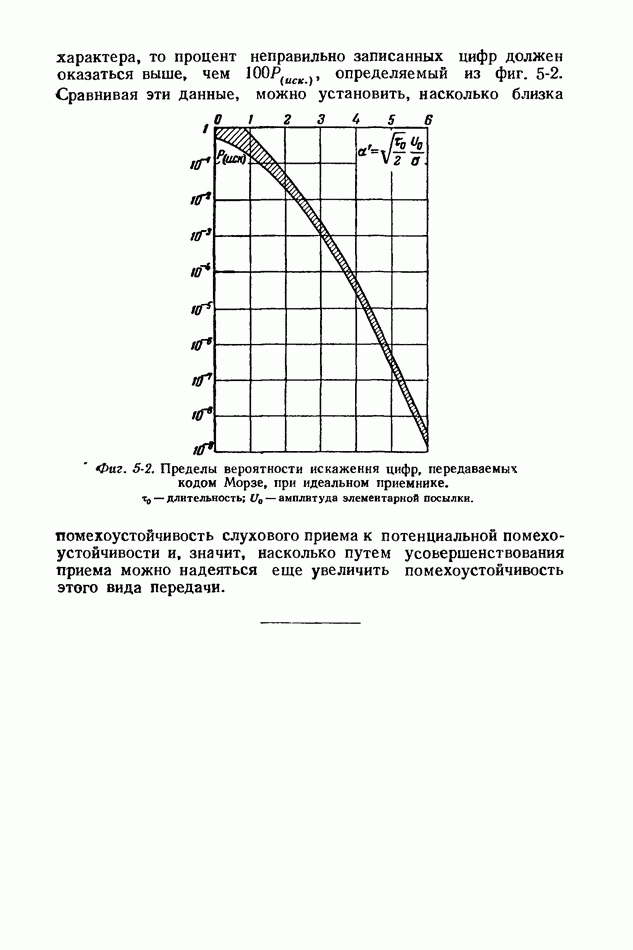
- 5-8. ПРИМЕР ПЕРЕДАЧИ ЦИФР КОДОМ МОРЗЕ
- ЧАСТЬ III. ПЕРЕДАЧА ОТДЕЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Глава шестая. ОБЩАЯ ТЕОРИЯ ВЛИЯНИЯ ПОМЕХ НА ПЕРЕДАЧУ ОТДЕЛЬНЫХ ЗНАЧЕНИИ ПАРАМЕТРОВ
- 6-2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ ПЕРЕДАВАВШЕГОСЯ ПАРАМЕТРА
- 6-3. ФУНКЦИЯ … ВБЛИЗИ НАИВЕРОЯТНЕЙШЕГО ЗНАЧЕНИЯ …
- 6-4. ОШИБКИ И ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 6-5. ВТОРОЙ МЕТОД ОПРЕДЕЛЕНИЯ ОШИБОК И ПОТЕНЦИАЛЬНОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 6-6. ИТОГИ ГЛ. 6
- 6-7. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ МАТЕРИАЛА ГЛ. 6
- Глава седьмая. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ РАЗНЫХ СИСТЕМАХ ПЕРЕДАЧИ ОТДЕЛЬНЫХ ЗНАЧЕНИИ ПАРАМЕТРОВ И ПОМЕХЕ МАЛОЙ ИНТЕНСИВНОСТИ
- 7-1. АМПЛИТУДНАЯ МОДУЛЯЦИЯ
- 7-2. ЛИНЕЙНАЯ МОДУЛЯЦИЯ
- 7-3. ОБЩИЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- 7-4. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ)
- 7-5. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРВОМ МЕТОДЕ ПРИЕМА)
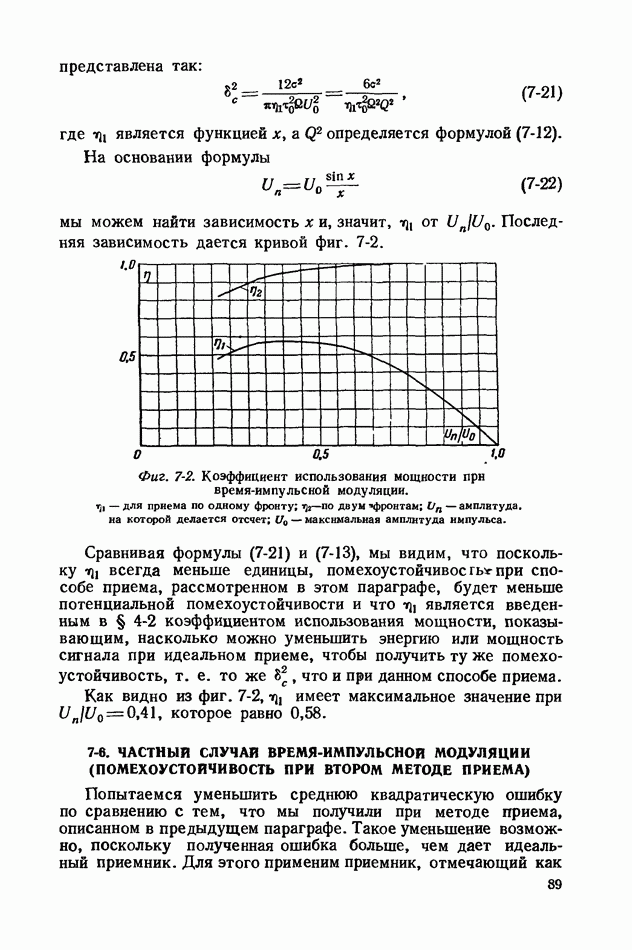
- 7-6. ЧАСТНЫЙ СЛУЧАЙ ВРЕМЯ-ИМПУЛЬСНОЙ МОДУЛЯЦИИ (ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ВТОРОМ МЕТОДЕ ПРИЕМА)
- 7-7. ЧАСТОТНАЯ МОДУЛЯЦИЯ (ОБЩИЙ СЛУЧАЙ)
- 7-8. ЧАСТОТНАЯ МОДУЛЯЦИЯ (ЧАСТНЫЙ СЛУЧАЙ)
- 7-9. ПОВЫШЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ БЕЗ УВЕЛИЧЕНИЯ ЭНЕРГИИ, ДЛИТЕЛЬНОСТИ И ШИРИНЫ СПЕКТРА СИГНАЛА
- Глава восьмая. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ ОТДЕЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ПРИ БОЛЬШИХ ПОМЕХАХ
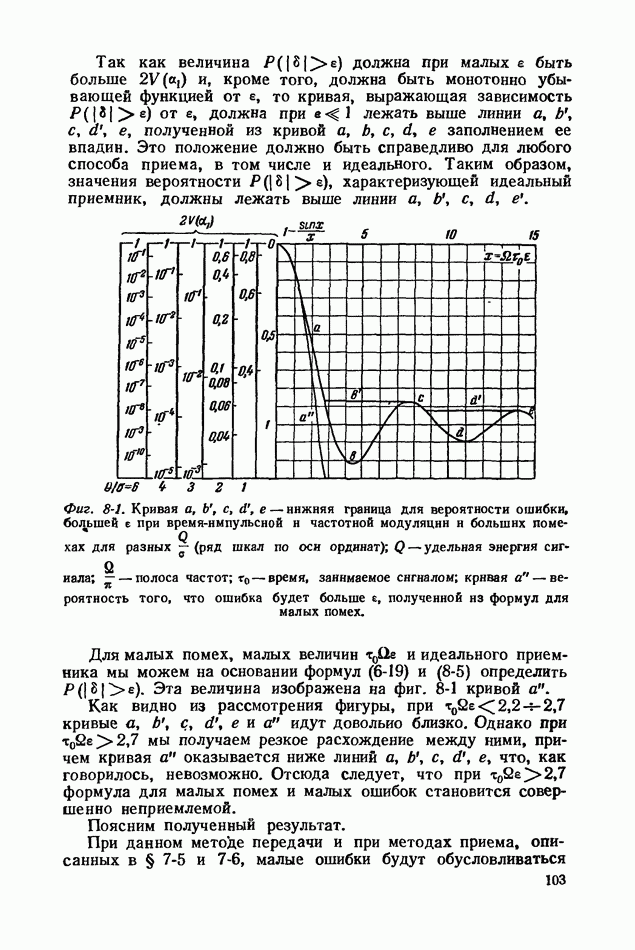
- 8-1. ВЫВОД ОБЩЕЙ ФОРМУЛЫ ДЛЯ ОЦЕНКИ ВЛИЯНИЯ ПОМЕХИ БОЛЬШОЙ ИНТЕНСИВНОСТИ
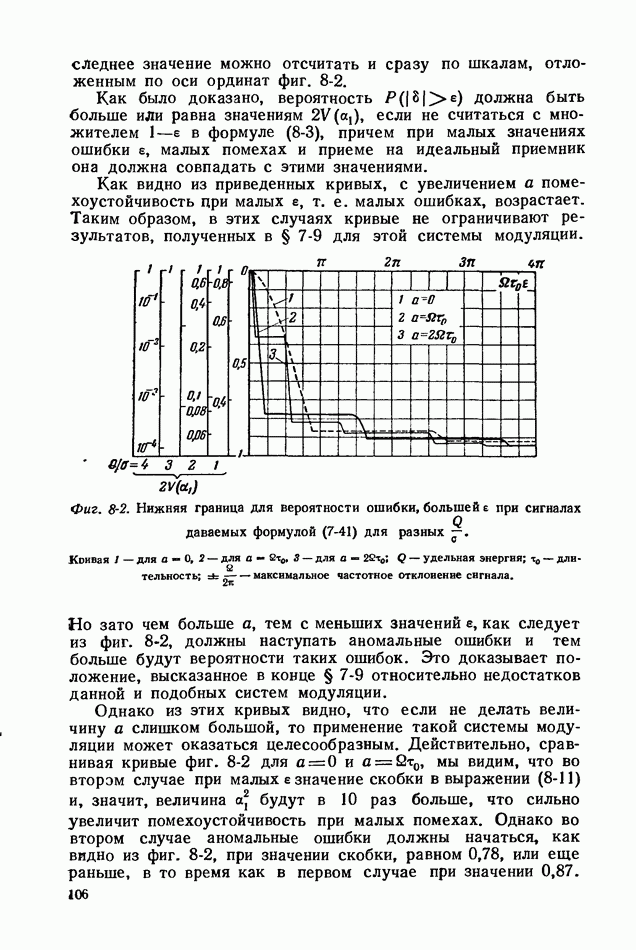
- 8-2. СРАВНЕНИЕ ФОРМУЛ ДЛЯ МАЛЫХ И БОЛЬШИХ ПОМЕХ
- 8-3. ВРЕМЯ-ИМПУЛЬСНАЯ МОДУЛЯЦИЯ
- 8-4. ЧАСТОТНАЯ МОДУЛЯЦИЯ
- 8-5. СИСТЕМА ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ БЕЗ УВЕЛИЧЕНИЯ ЭНЕРГИИ, ДЛИТЕЛЬНОСТИ И ШИРИНЫ СПЕКТРА СИГНАЛА
- 8-6. ГЕОМЕТРИЧЕСКОЕ ТОЛКОВАНИЕ РЕЗУЛЬТАТОВ ГЛ. 8
- ЧАСТЬ IV. ПЕРЕДАЧА КОЛЕБАНИЙ
- Глава девятая. ОБЩАЯ ТЕОРИЯ ВЛИЯНИЯ МАЛЫХ ПОМЕХ НА ПЕРЕДАЧУ КОЛЕБАНИЙ
- 9-2. ВЛИЯНИЕ МАЛЫХ ПОМЕХ НА ПЕРЕДАВАЕМЫЕ КОЛЕБАНИЯ
- 9-3. УСЛОВИЯ ИДЕАЛЬНОГО ПРИЕМНИКА
- 9-4. СПОСОБ ОСУЩЕСТВЛЕНИЯ ИДЕАЛЬНОГО ПРИЕМНИКА
- 9-5. ИСКАЖЕНИЯ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- Глава десятая. ПРЯМЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 10-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНОЙ И ЛИНЕЙНОЙ МОДУЛЯЦИИ
- 10-4. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ
- 10-5. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНОЙ МОДУЛЯЦИИ И ОБЫЧНОМ ПРИЕМЕ
- 10-6. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ И ОБЫЧНОМ ПРИЕМЕ
- 10-7. ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ПЕРЕДАЧЕ ОДНОЙ БОКОВОЙ ПОЛОСОЙ
- Глава одиннадцатая. ИМПУЛЬСНЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 11-2. ПРИМЕР ОСУЩЕСТВЛЕНИЯ ИМПУЛЬСНОЙ СИСТЕМЫ МОДУЛЯЦИИ
- 11-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ИМПУЛЬСНОЙ СИСТЕМЕ МОДУЛЯЦИИ
- 11-4. ПОМЕХОУСТОЙЧИВОСТЬ ПРИЕМНИКА, РАЗОБРАННОГО В § 11-2
- 11-5. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ АМПЛИТУДНО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- 11-6. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ВРЕМЯ-ИМПУЛЬСНОИ МОДУЛЯЦИИ
- 11-7. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНО-ИМПУЛЬСНОЙ МОДУЛЯЦИИ
- Глава двенадцатая. ИНТЕГРАЛЬНЫЕ СИСТЕМЫ МОДУЛЯЦИИ
- 12-2. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ИНТЕГРАЛЬНЫХ СИСТЕМАХ МОДУЛЯЦИИ
- 12-3. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ ПРИ ЧАСТОТНОЙ МОДУЛЯЦИИ
- Глава тринадцатая. ОЦЕНКА ВЛИЯНИЯ БОЛЬШИХ ПОМЕХ НА ПЕРЕДАЧУ КОЛЕБАНИЙ
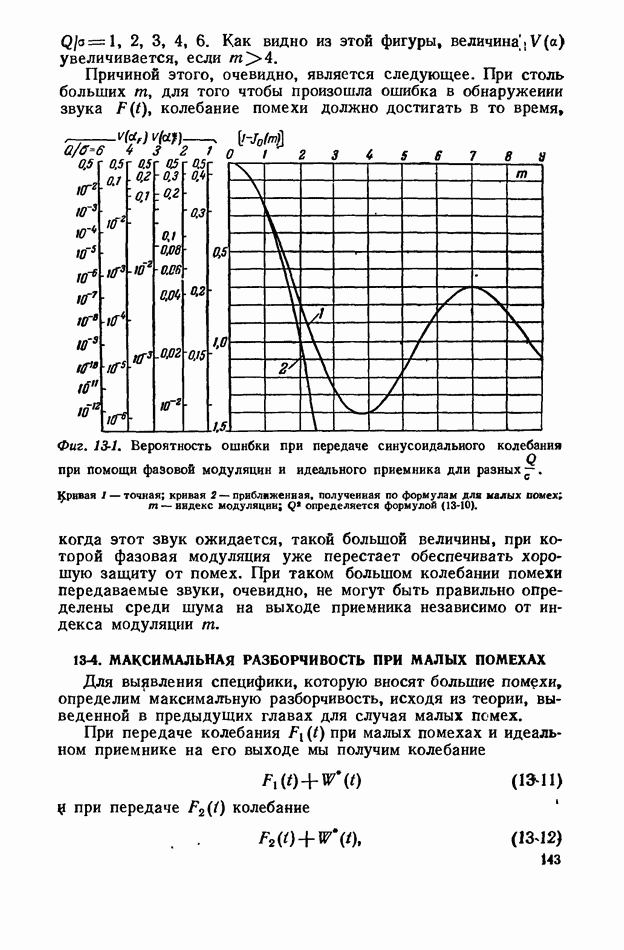
- 13-3. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ ФАЗОВОЙ МОДУЛЯЦИИ
- 13-4. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ МАЛЫХ ПОМЕХАХ
- 13-5. МАКСИМАЛЬНАЯ РАЗБОРЧИВОСТЬ ПРИ МАЛЫХ ПОМЕХАХ И ФАЗОВОЙ МОДУЛЯЦИИ
- Приложение А. УДЕЛЬНАЯ ЭНЕРГИЯ ВЫСОКОЧАСТОТНЫХ КОЛЕБАНИЙ
- Приложение В. ВЫРАЖЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ ДВУМЯ АМПЛИТУДНО-МОДУЛИРОВАННЫМИ КОЛЕБАНИЯМИ
- Приложение С. МГНОВЕННОЕ ЗНАЧЕНИЕ НОРМАЛЬНО ФЛЮКТУАЦИОННОГО КОЛЕБАНИЯ
- Приложение D. НОРМАЛЬНО ФЛЮКТУАЦИОННОЕ КОЛЕБАНИЕ ИЗ ПРОИЗВОЛЬНЫХ ИМПУЛЬСОВ