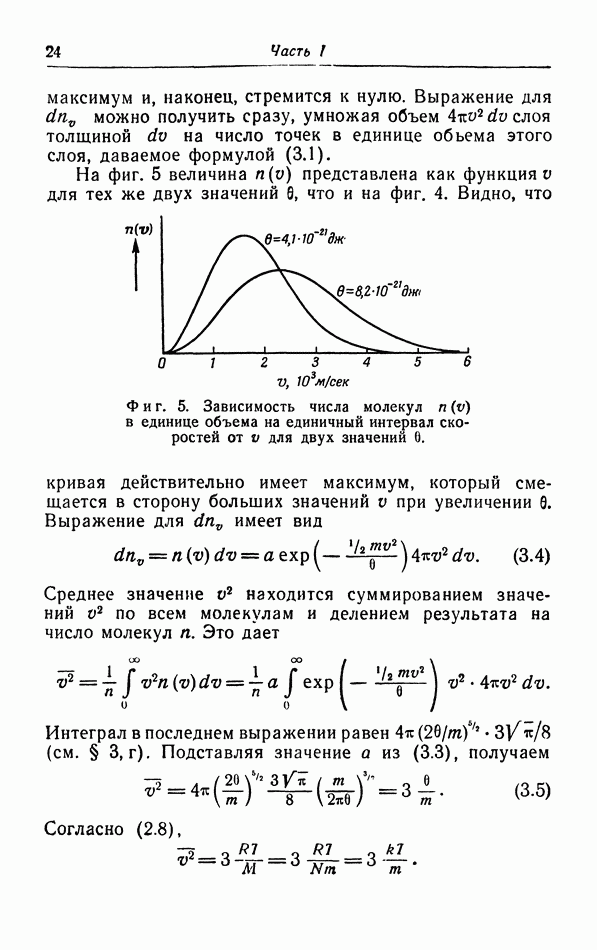
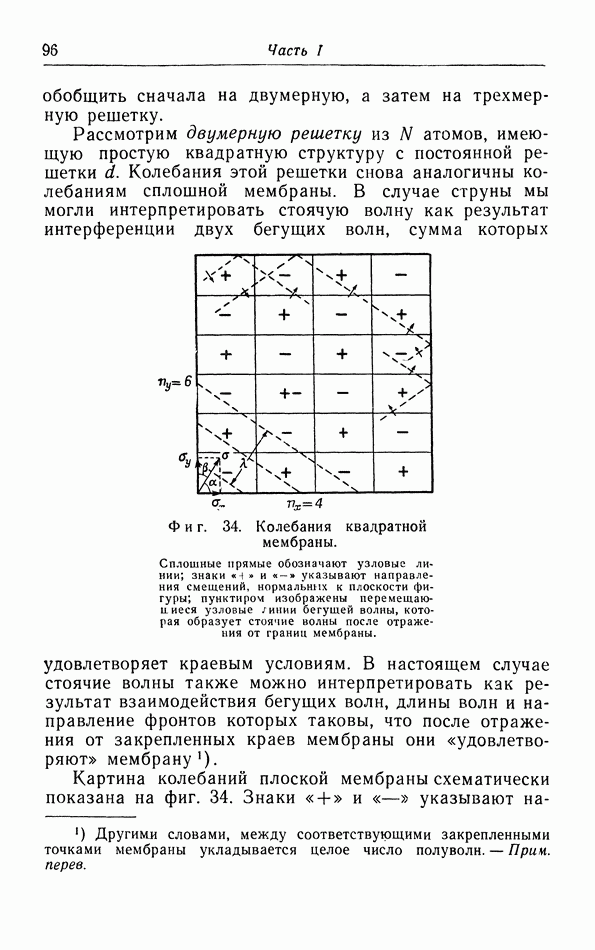
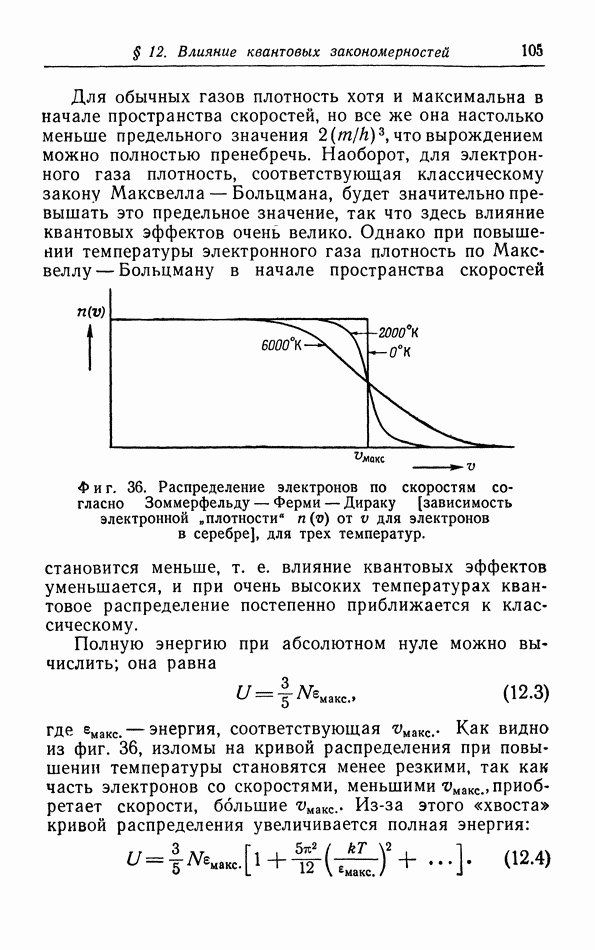
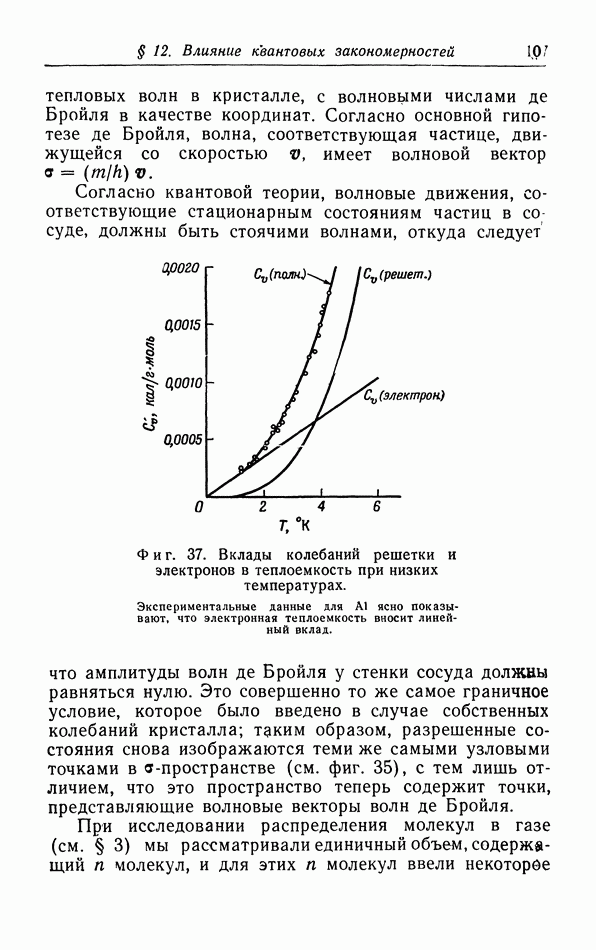
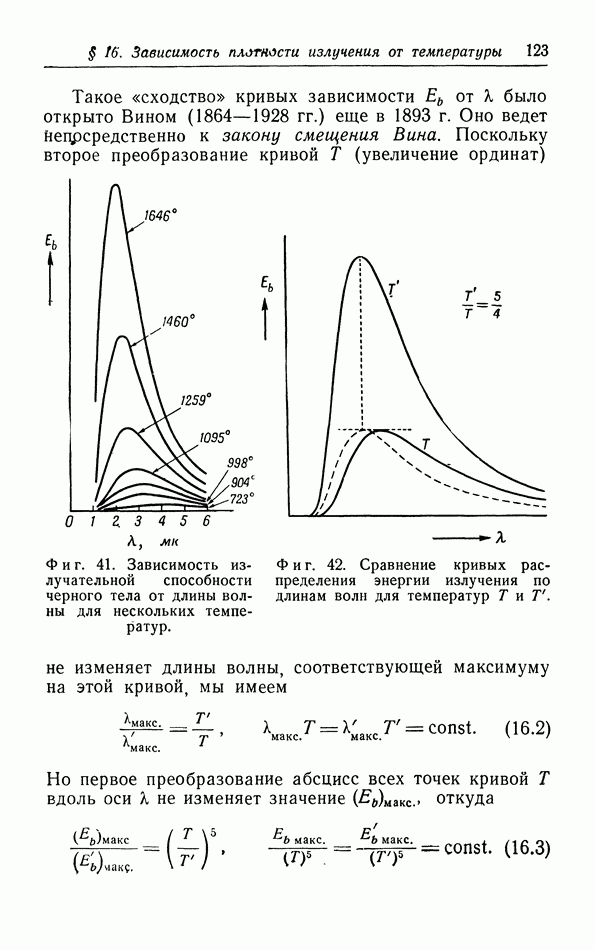
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
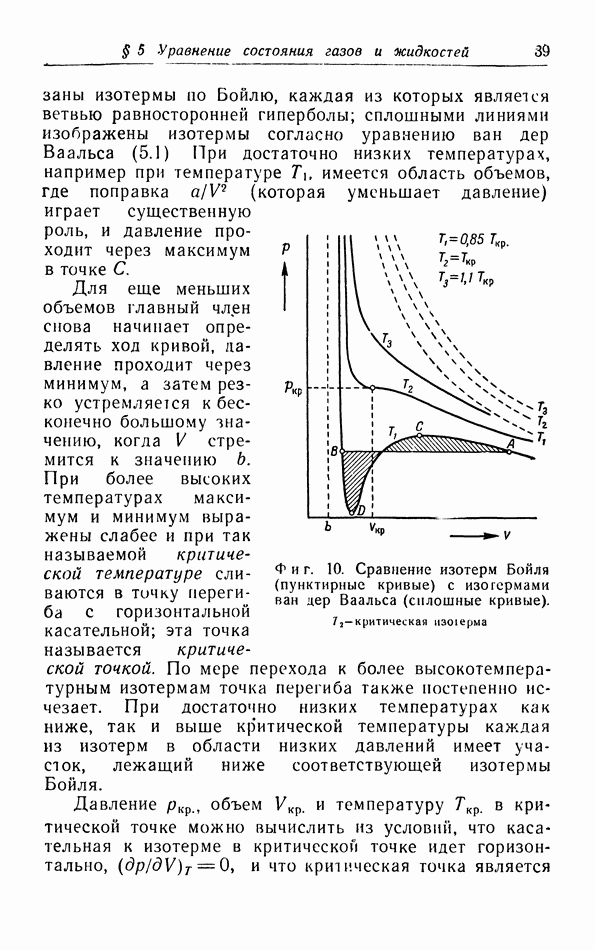
§ 5. Уравнение состояния газов и жидкостей
а. Уравнение ван дер Ваальса.
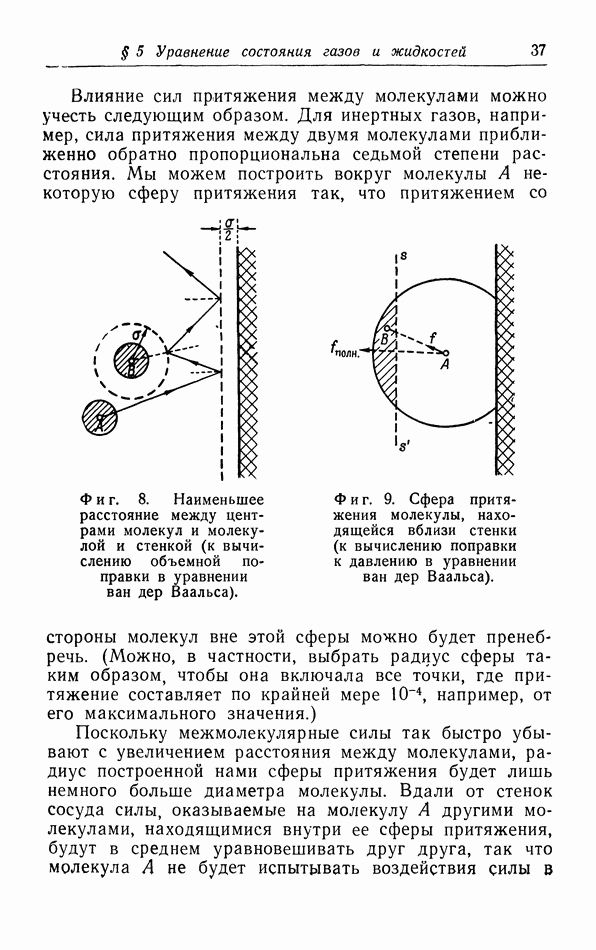
В начале предыдущего пункта мы указывали, что для объяснения явления конденсации газов и паров в жидкости необходимо учитывать взаимодействие молекул Теперь мы исследуем влияние этого взаимодействия, следуя прежде всего методу, указанному ван дер Ваальсом (1837-1923 гг.) примерно в 1870 г. Для упрощения будем считать, что молекулы являются твердыми шариками диаметром а, между которыми действуют силы притяжения, причем последние быстро возрастают при уменьшении расстояния между молекулами.
При перемещении в сосуде центр молекулы А не может подойти на расстояние, меньшее  к стенке или на расстояние, меньшее а, к центрам других молекул В, как это видно из фиг. 8). Таким образом, доступный для свободного движения молекулы А объем меньше объема сосуда V: из объема V надо вычесть некоторый объем
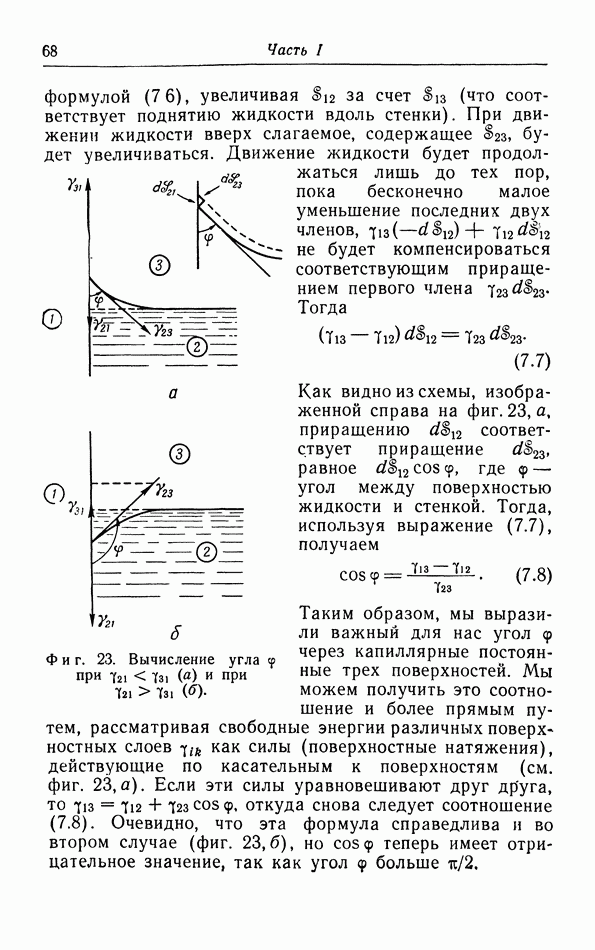
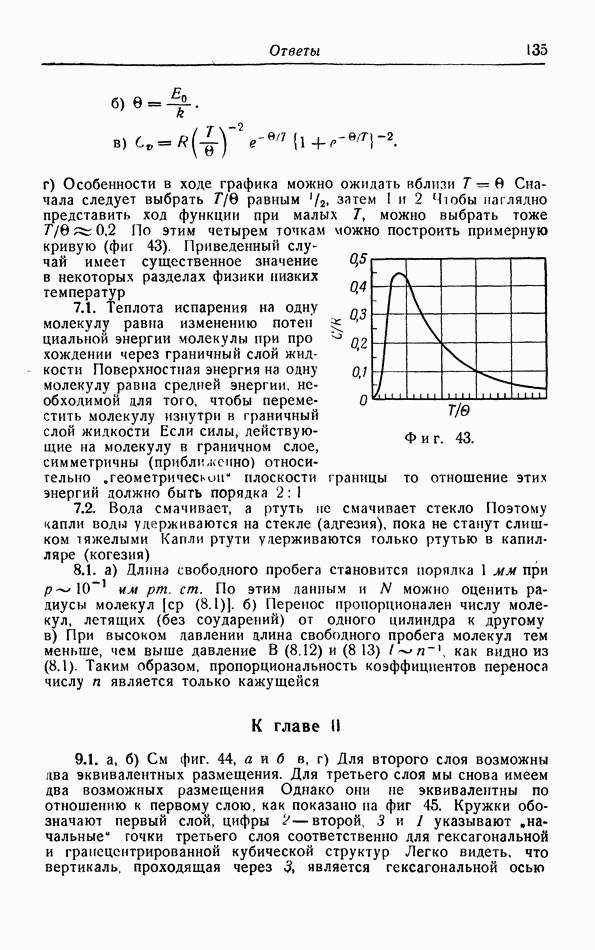
к стенке или на расстояние, меньшее а, к центрам других молекул В, как это видно из фиг. 8). Таким образом, доступный для свободного движения молекулы А объем меньше объема сосуда V: из объема V надо вычесть некоторый объем  . В соответствии с этим число ударов о стенку в единицу времени, а следовательно, и давление увеличиваются в отношении
. В соответствии с этим число ударов о стенку в единицу времени, а следовательно, и давление увеличиваются в отношении  т. е.
т. е.

Влияние сил притяжения между молекулами можно учесть следующим образом. Для инертных газов, например, сила притяжения между двумя молекулами приближенно обратно пропорциональна седьмой степени расстояния.

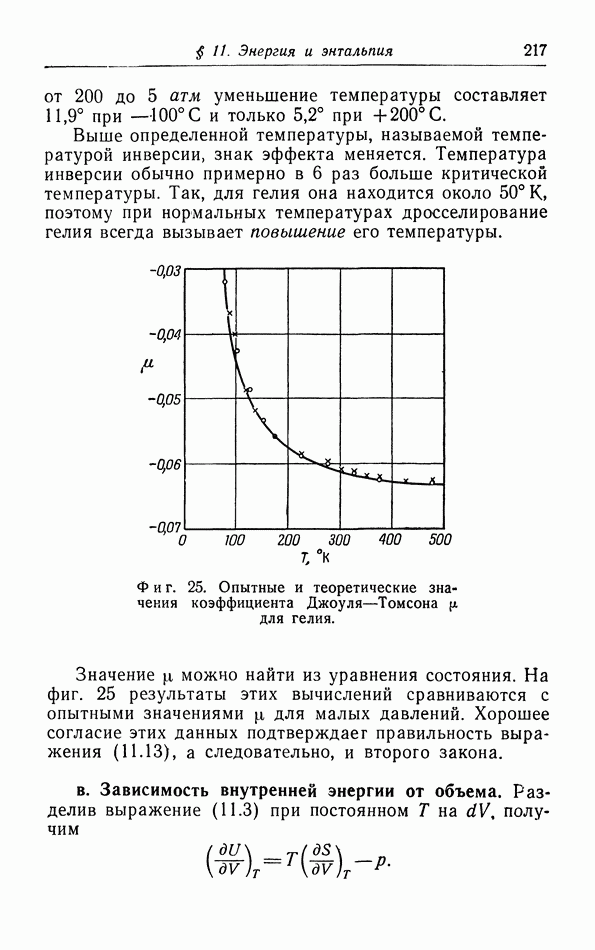
Фиг. 8. Наименьшее расстояние между центрами молекул и молекулой и стенкой (к вычислению объемной поправки в уравнении ван дер Ваальса).

Фиг. 9. Сфера притяжения молекулы, находящейся вблизи стенки (к вычислению поправки к давлению в уравнении ван дер Ваальса).
Мы можем построить вокруг молекулы А некоторую сферу притяжения так, что притяжением со стороны молекул вне этой сферы можно будет пренебречь. (Можно, в частности, выбрать радиус сферы таким образом, чтобы она включала все точки, где притяжение составляет по крайней мере  например, от его максимального значения.)
например, от его максимального значения.)
Поскольку межмолекулярные силы так быстро убывают с увеличением расстояния между молекулами, радиус построенной нами сферы притяжения будет лишь немного больше диаметра молекулы. Вдали от стенок сосуда силы, оказываемые на молекулу А другими молекулами, находяпхимися внутри ее сферы притяжения, будут в среднем уравновешивать друг друга, так что молекула А не будет испытывать воздействия силы в
определенном направлении. Если же сфера притяжения А обрезается стенкой, как показано на фиг. 9, то на молекулу А будет действовать сила в направлении от стенки, так как силы  действующие на А со стороны молекул из области левее
действующие на А со стороны молекул из области левее  не уравновешиваются аналогичными силами справа. Результирующая сила приблизительно пропорциональна объему заштрихованного сегмента на фиг. 9 и числу молекул в единице объема этого сегмента.
не уравновешиваются аналогичными силами справа. Результирующая сила приблизительно пропорциональна объему заштрихованного сегмента на фиг. 9 и числу молекул в единице объема этого сегмента.
Следовательно, на все молекулы, лежащие в так называемом поверхностном слое, имеющем толщину порядка радиуса сферы притяжения, действует некоторая сила  направленная от стенки к газу. В первом приближении можно считать, что число молекул в единице объема сегмента равно числу молекул
направленная от стенки к газу. В первом приближении можно считать, что число молекул в единице объема сегмента равно числу молекул  в единице объема
в единице объема  Тогда средняя сила, действующая на молекулу в поверхностном слое, пропорциональна
Тогда средняя сила, действующая на молекулу в поверхностном слое, пропорциональна  Эта сила притяжения направлена внутрь газа и уменьшает давление, оказываемое молекулами на стенку. Чтобы рассчитать поправку к давлению, нужно определить общую силу, действующую на все молекулы поверхностного слоя, прилегающие к единице площади стенки. В первом приближении эта величина также пропорциональна числу молекул в единице объема.
Эта сила притяжения направлена внутрь газа и уменьшает давление, оказываемое молекулами на стенку. Чтобы рассчитать поправку к давлению, нужно определить общую силу, действующую на все молекулы поверхностного слоя, прилегающие к единице площади стенки. В первом приближении эта величина также пропорциональна числу молекул в единице объема.
Поскольку число молекул в поверхностном слое пропорционально  а приложенная к каждой из молекул сила также пропорциональна
а приложенная к каждой из молекул сила также пропорциональна  поправка к давлению, т. е. сила на единицу площади поверхностного слоя, пропорциональна или обратно пропорциональна квадрату объема газа. Для одной килограмм-молекулы газа
поправка к давлению, т. е. сила на единицу площади поверхностного слоя, пропорциональна или обратно пропорциональна квадрату объема газа. Для одной килограмм-молекулы газа  где
где  число Авогадро; следовательно, поправку можно записать в виде
число Авогадро; следовательно, поправку можно записать в виде  Отсюда получаем уравнение ван дер Ваальса
Отсюда получаем уравнение ван дер Ваальса

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
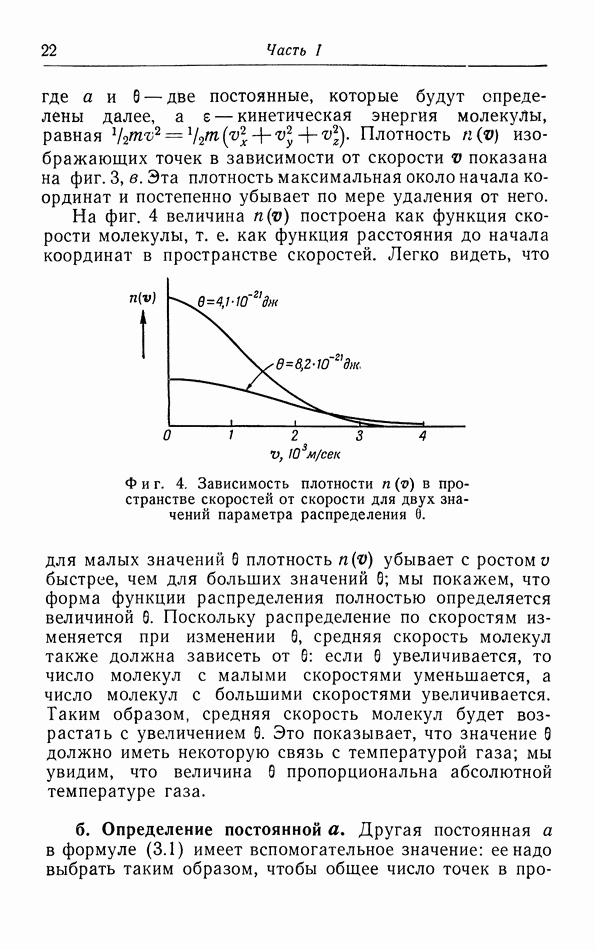
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
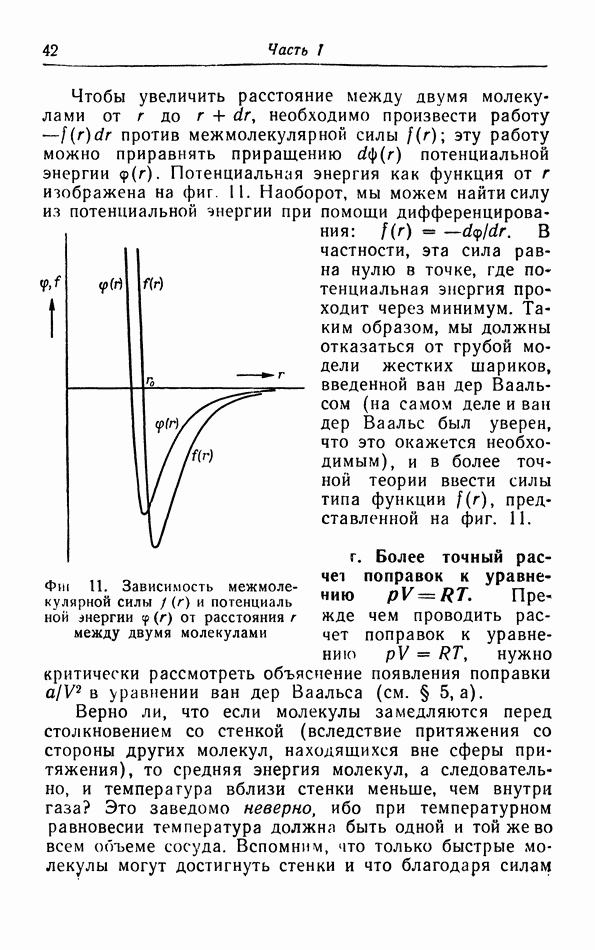
- в. Взаимодействие молекул.
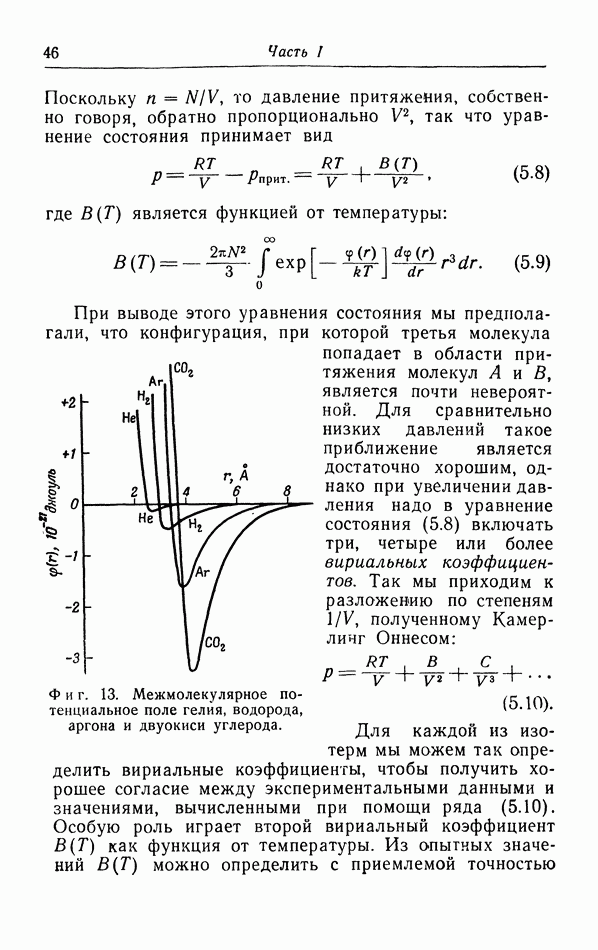
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
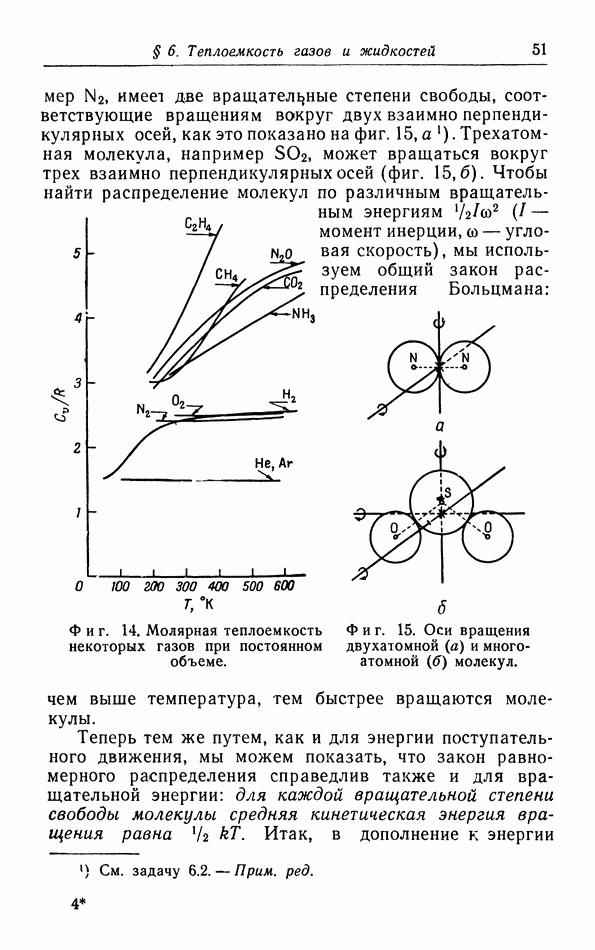
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
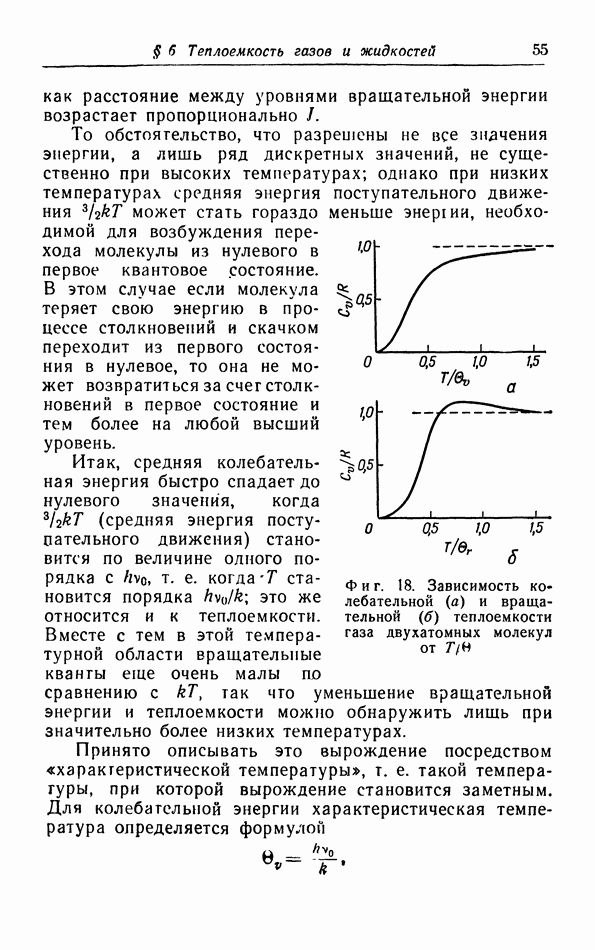
- г. Расчет колебательной теплоемкости двухатомной молекулы.
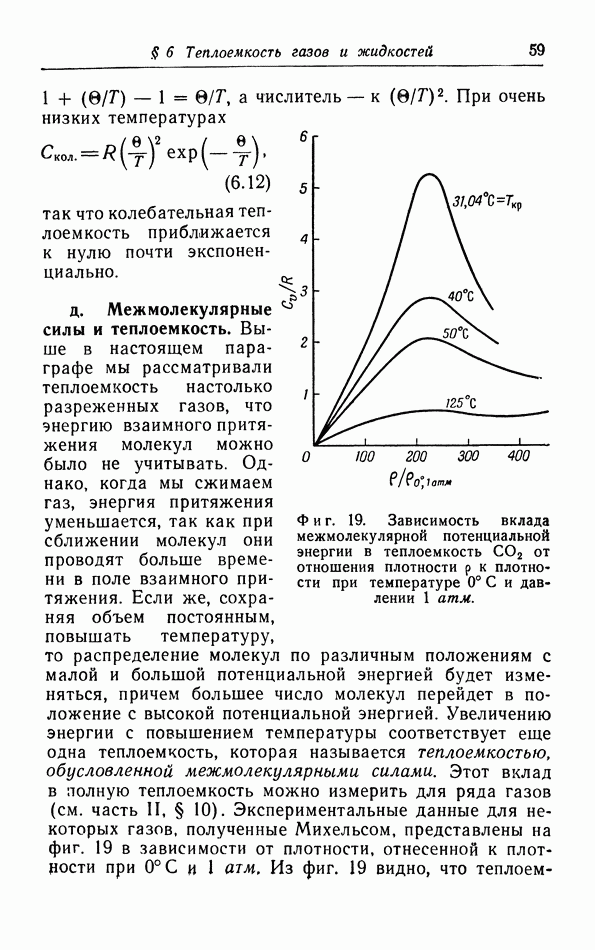
- д. Межмолекулярные силы и теплоемкость.
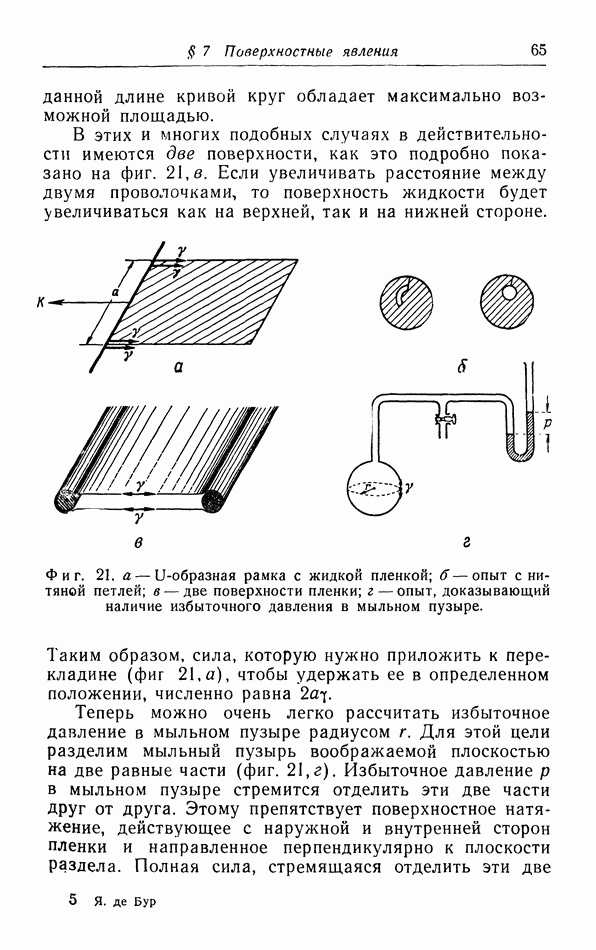
- § 7. Поверхностные явления
- б. Жидкие пленки.
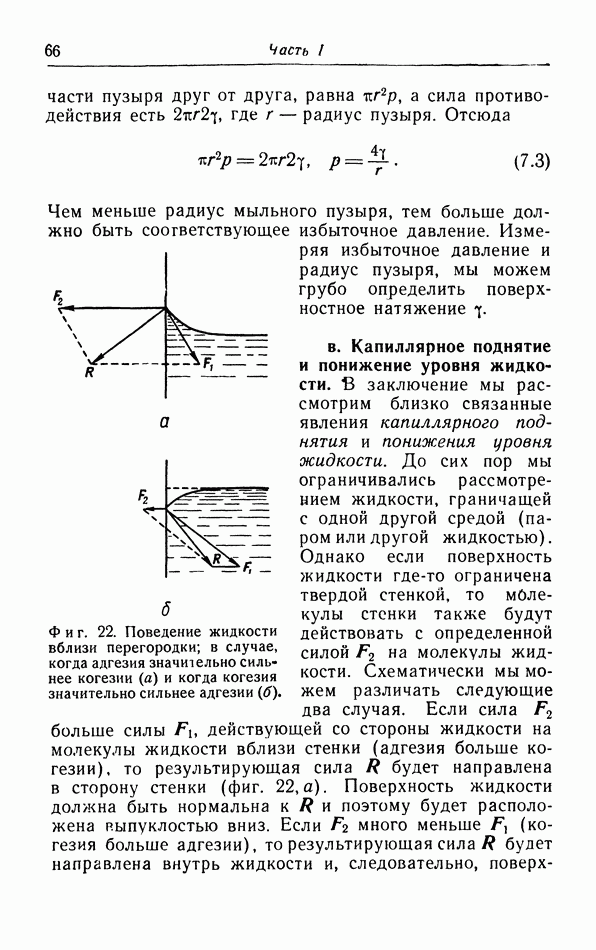
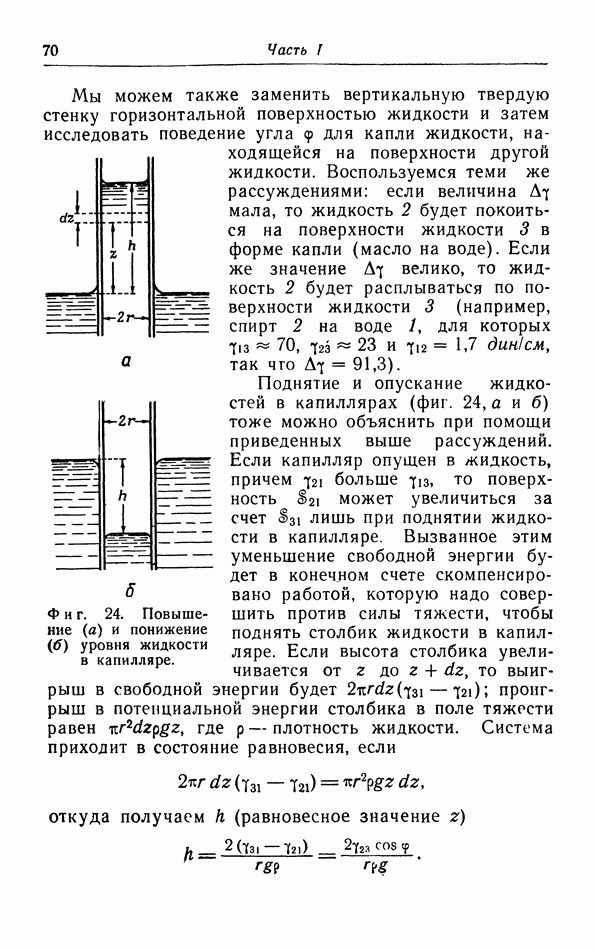
- в. Капиллярное поднятие и понижение уровня жидкости.
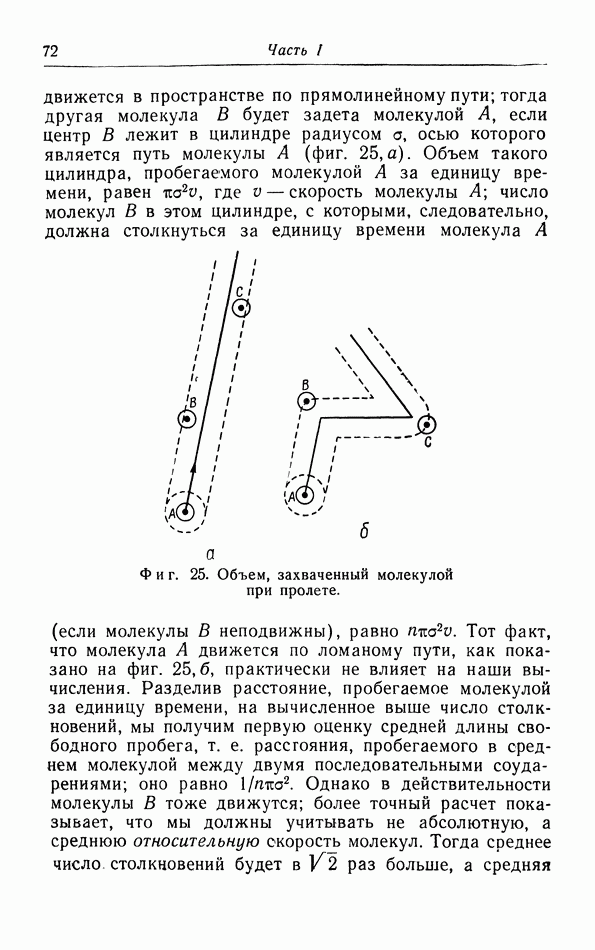
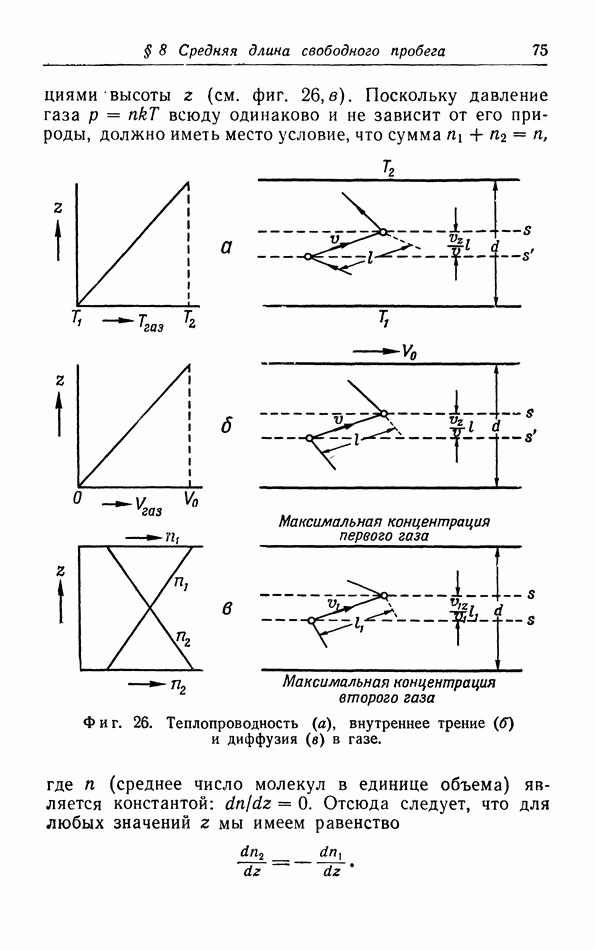
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
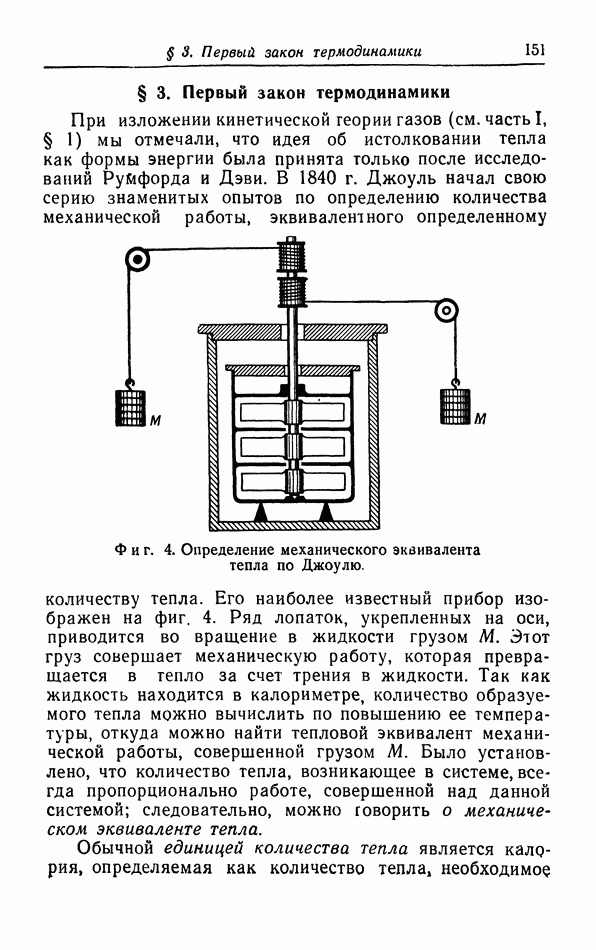
- § 3. Первый закон термодинамики
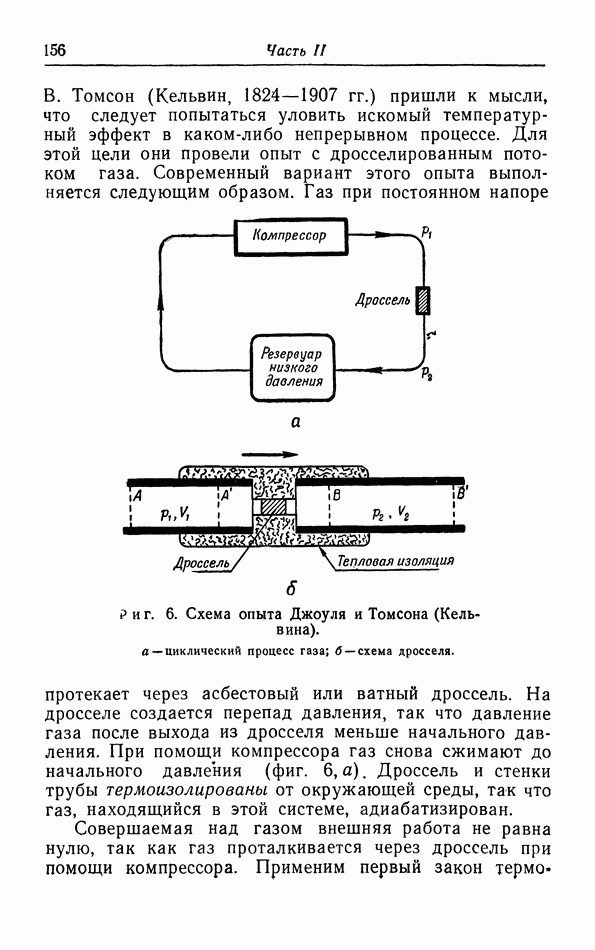
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
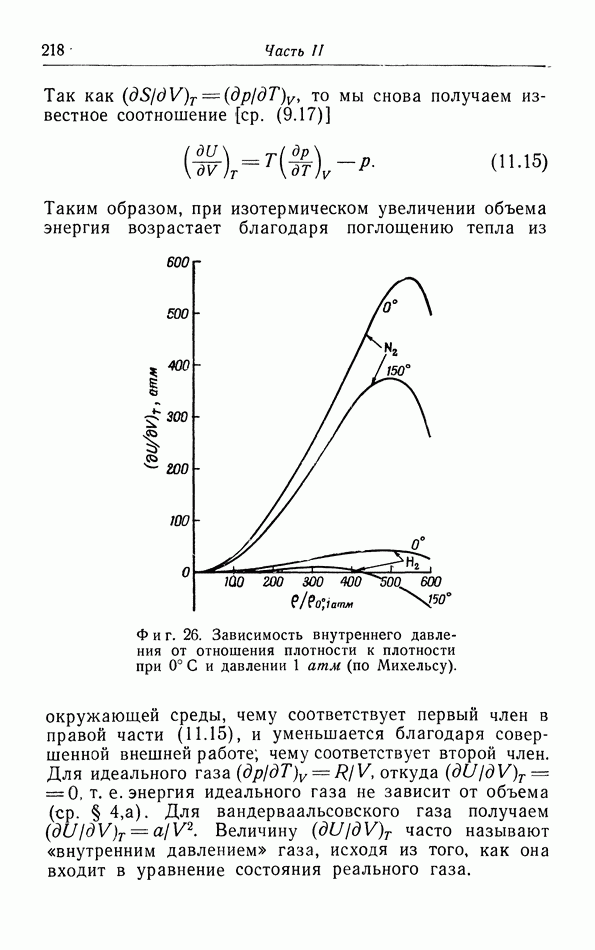
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
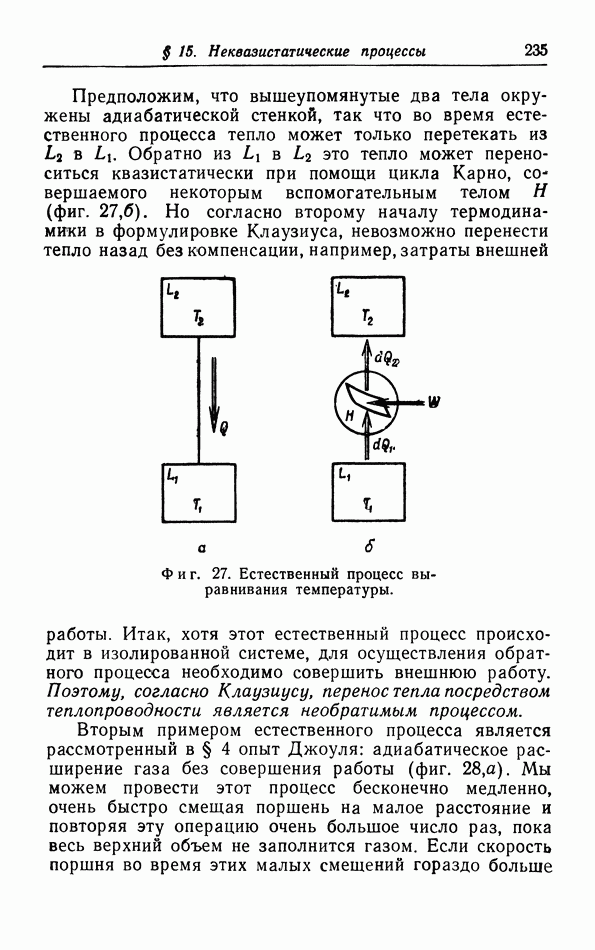
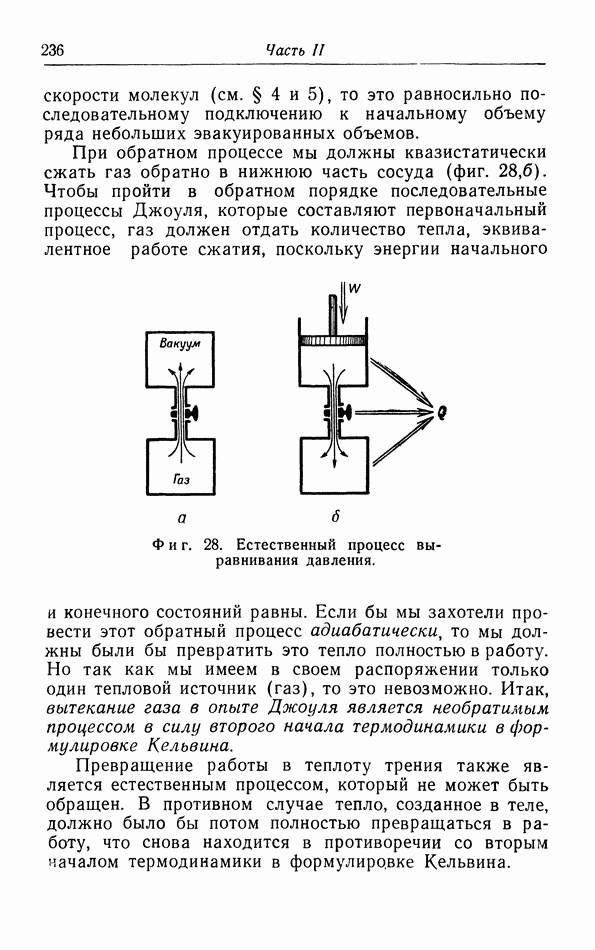
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
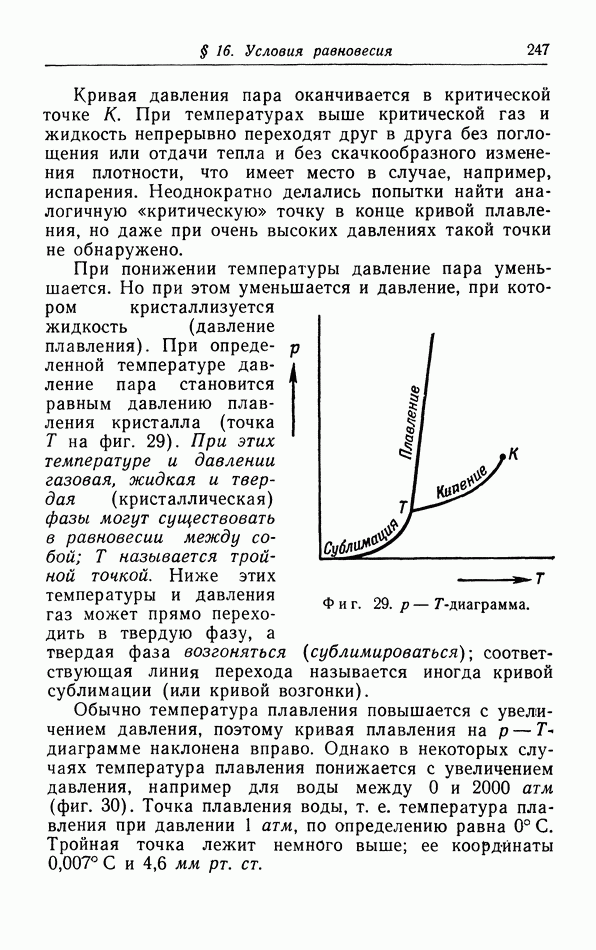
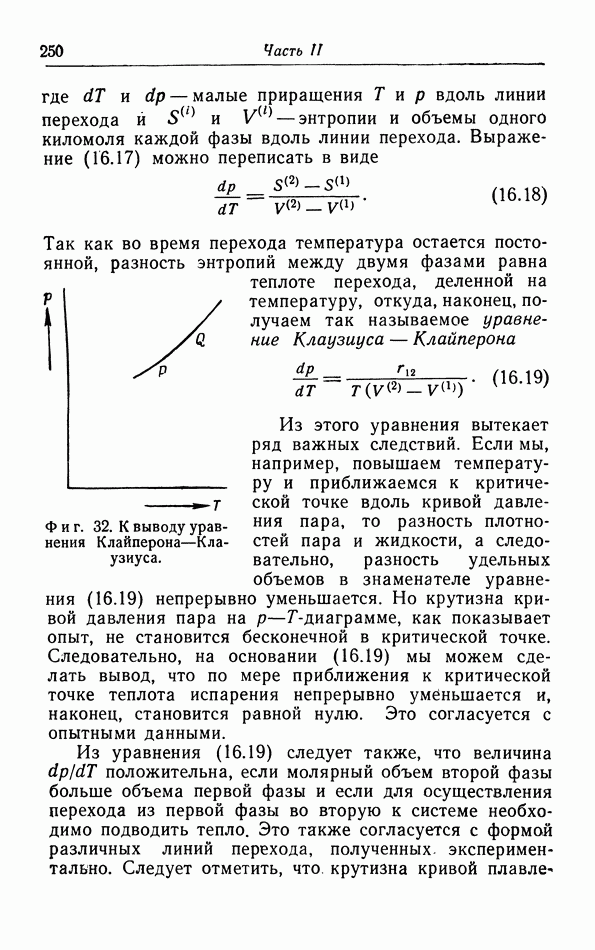
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
- д. p-T-диаграмма.
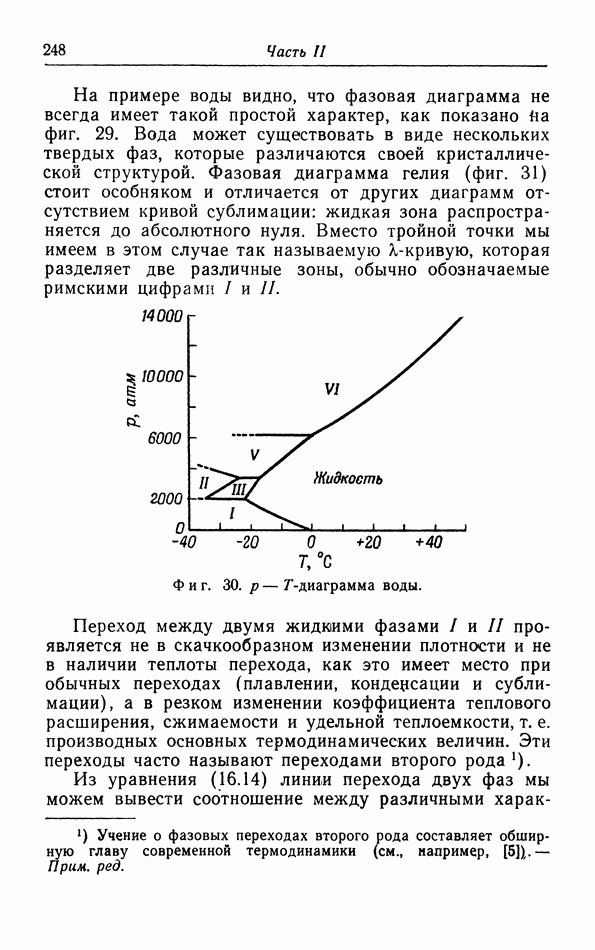
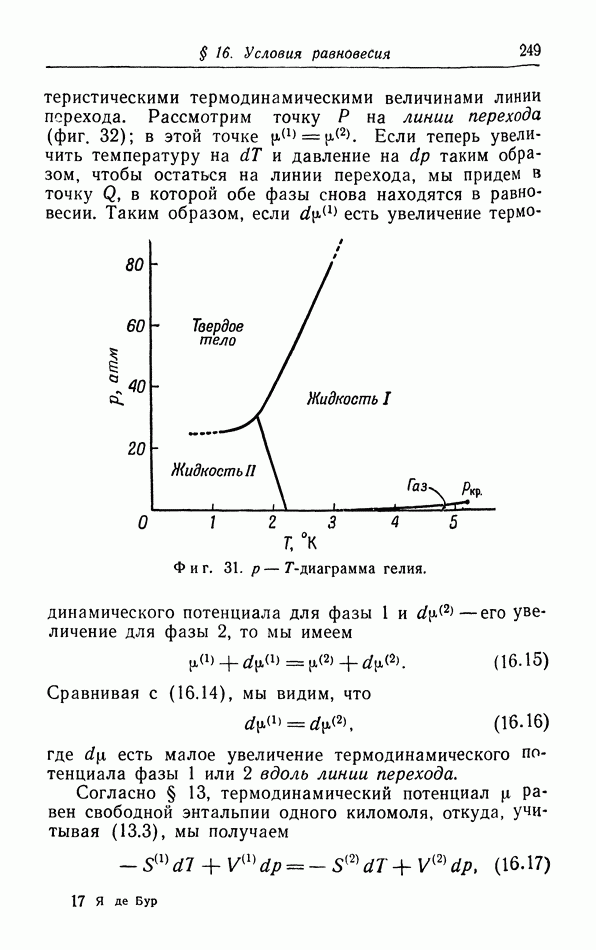
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
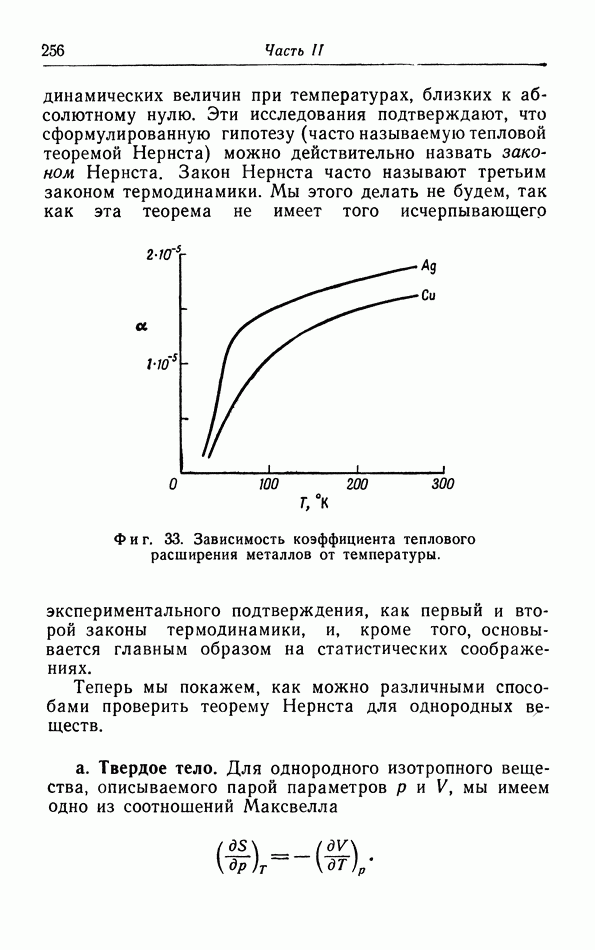
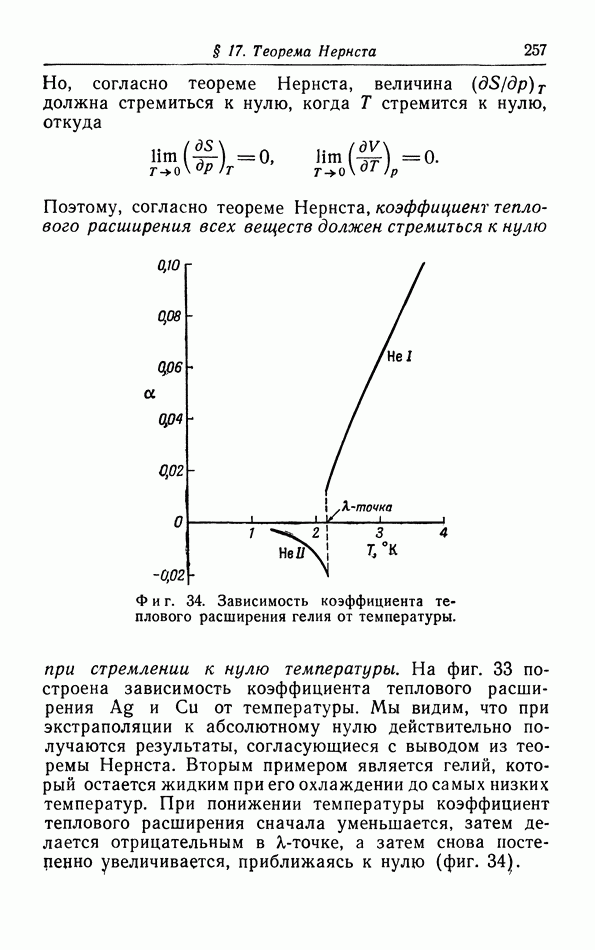
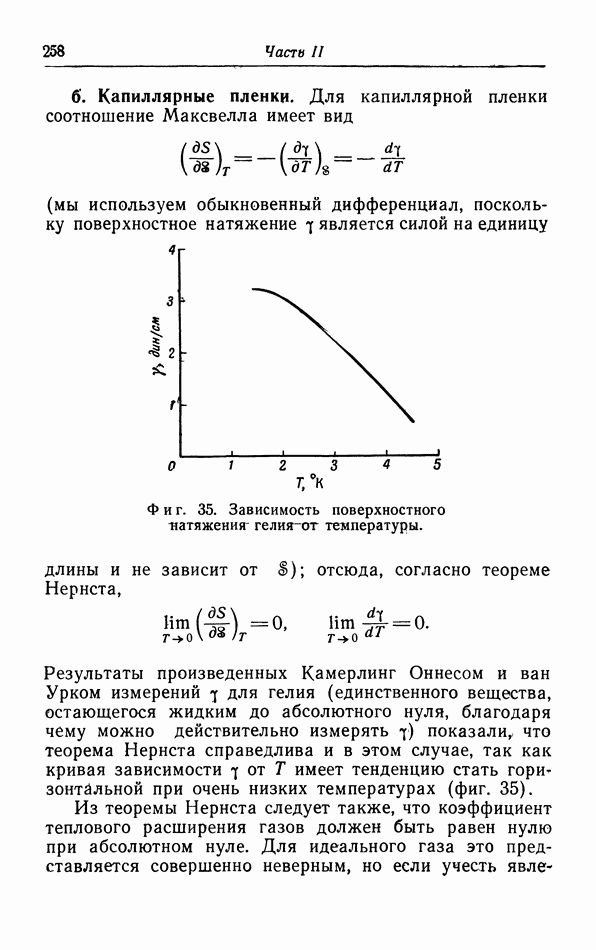
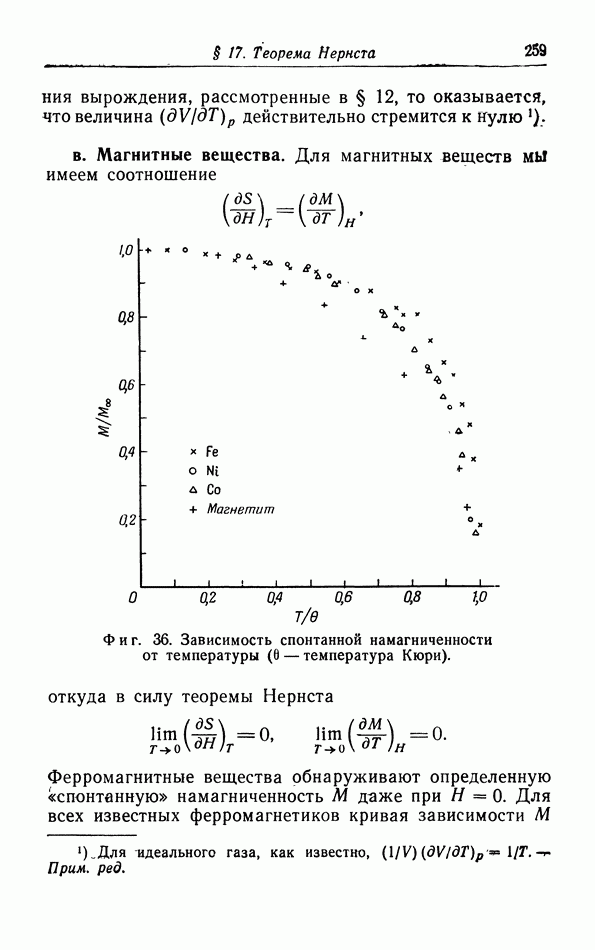
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам