| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 14. Соотношения Максвелла
Результаты § 11 — 13 можно кратко сформулировать следующим образом: имеются четыре характеристические функции:

определяемые следующими четырьмя дифференциальными выражениями:

Из (14.5), например, следует, что

Дифференцируя второй раз, получаем

сравнивая два последних выражения, находим

Таким же образом получаем из (14.6)

Из (14.7)

и, наконец, из (14.8)

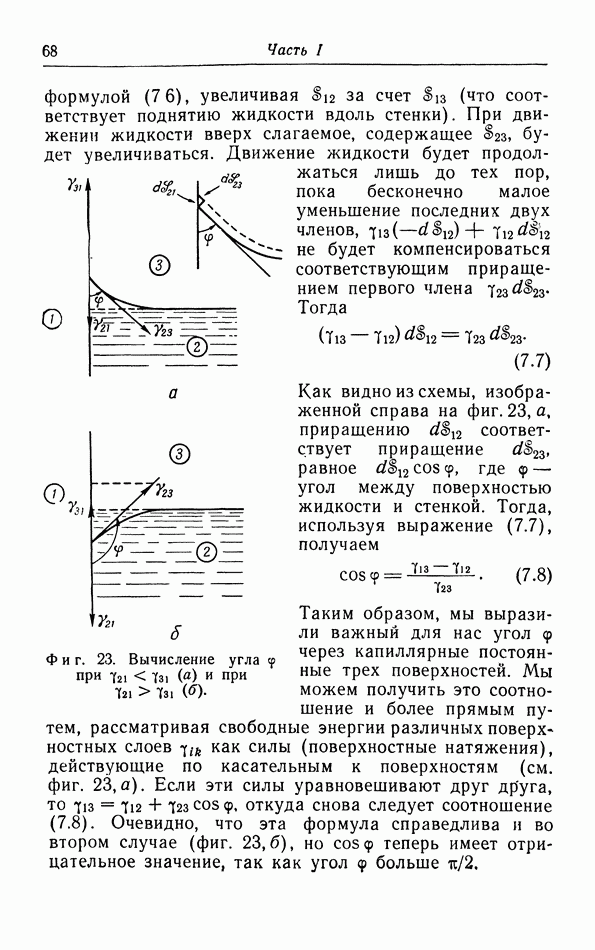
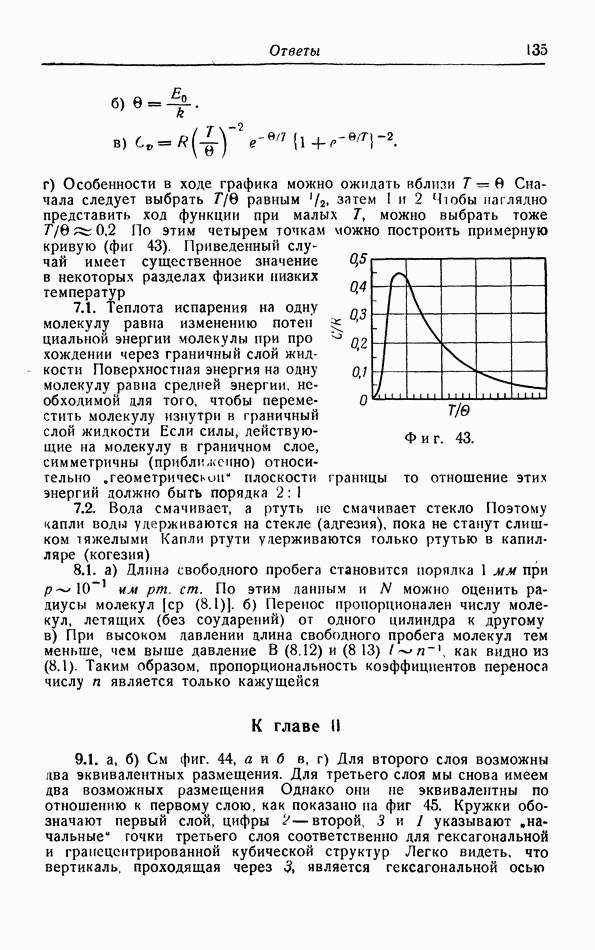
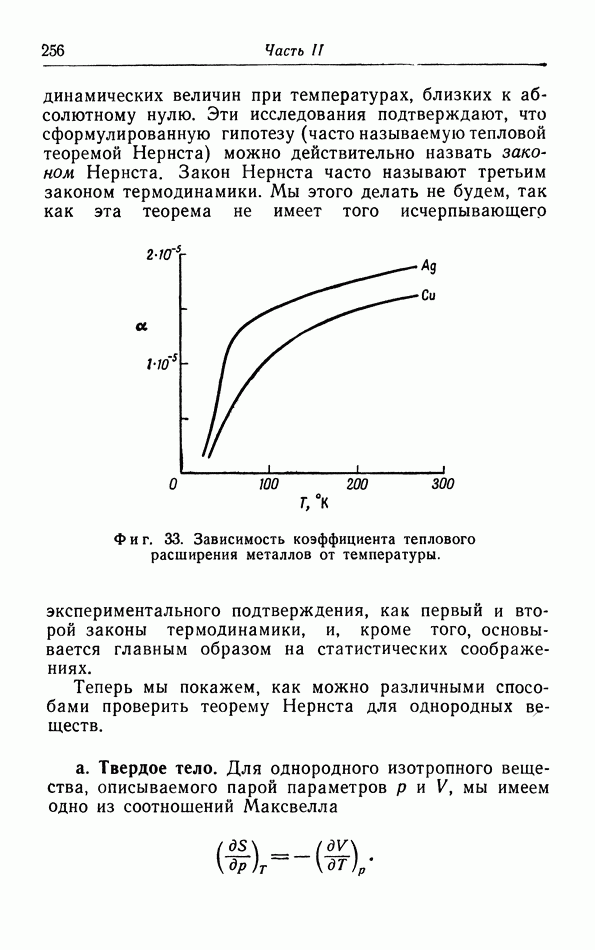
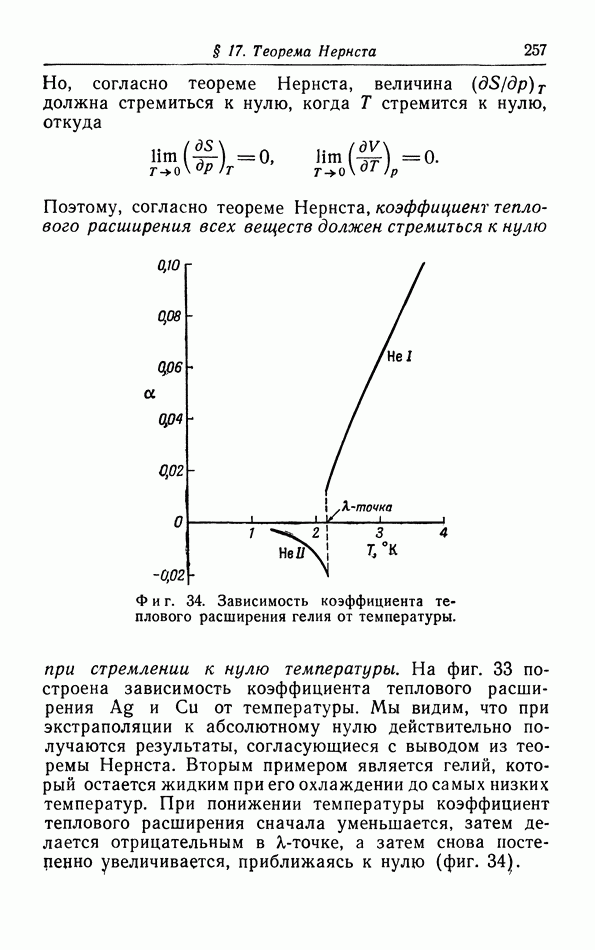
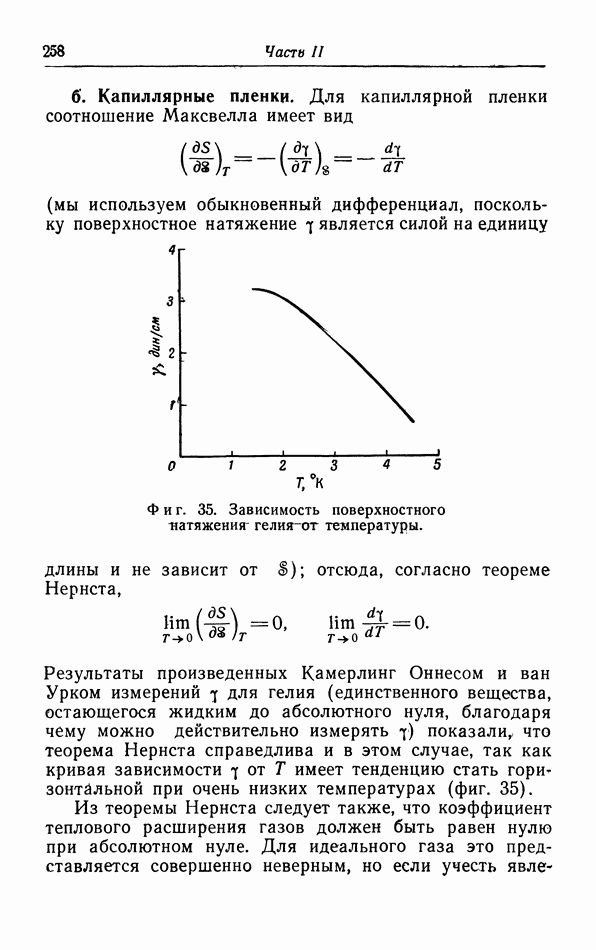
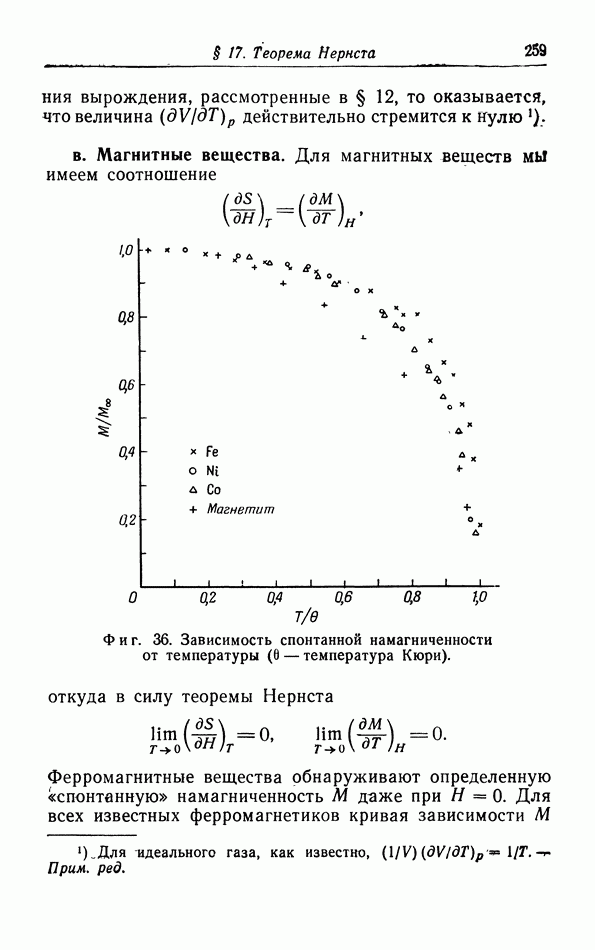
Мы получили четыре соотношения Максвелла. Последние два выведены и использованы в § 9 и 10; они выражают зависимость энтропии от  при постоянной температуре. Мы еще не встречались с первыми двумя соотношениями; они мало используются, так как они содержат дифференцирование по энтропии. Поэтому лучше записать их в обращенной форме:
при постоянной температуре. Мы еще не встречались с первыми двумя соотношениями; они мало используются, так как они содержат дифференцирование по энтропии. Поэтому лучше записать их в обращенной форме:

Эти соотношения выражают зависимость энтропии от  соответственно при постоянных V или
соответственно при постоянных V или  и совершенно аналогичны соотношениям (14.11) и (14.12).
и совершенно аналогичны соотношениям (14.11) и (14.12).
Продифференцируем (14.11) и (14.12) по  замечая, что
замечая, что

тогда получим

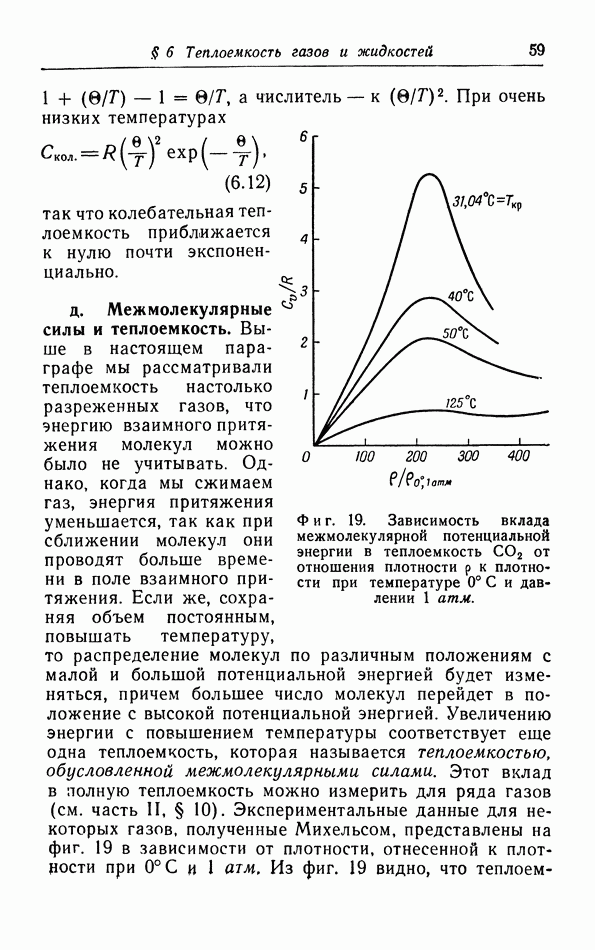
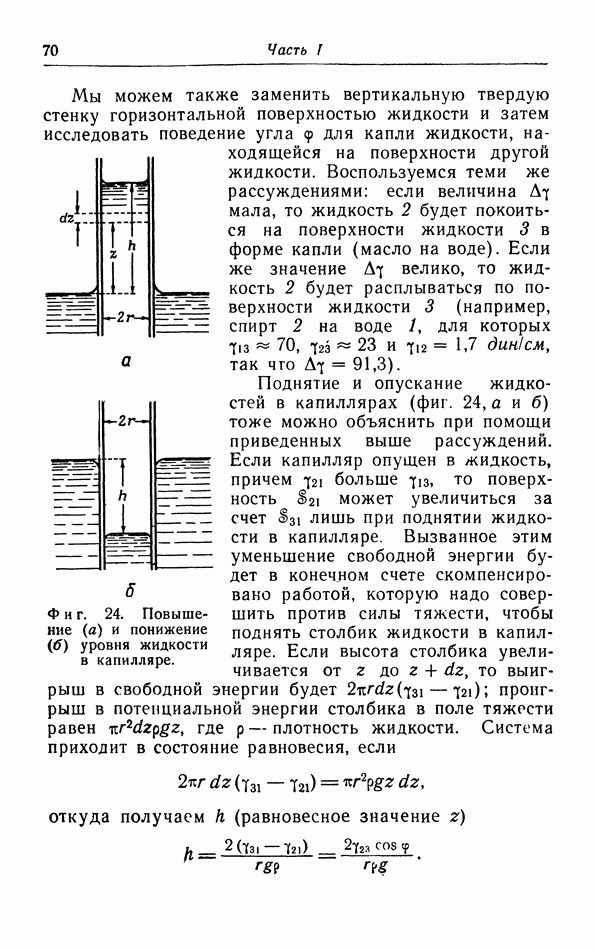
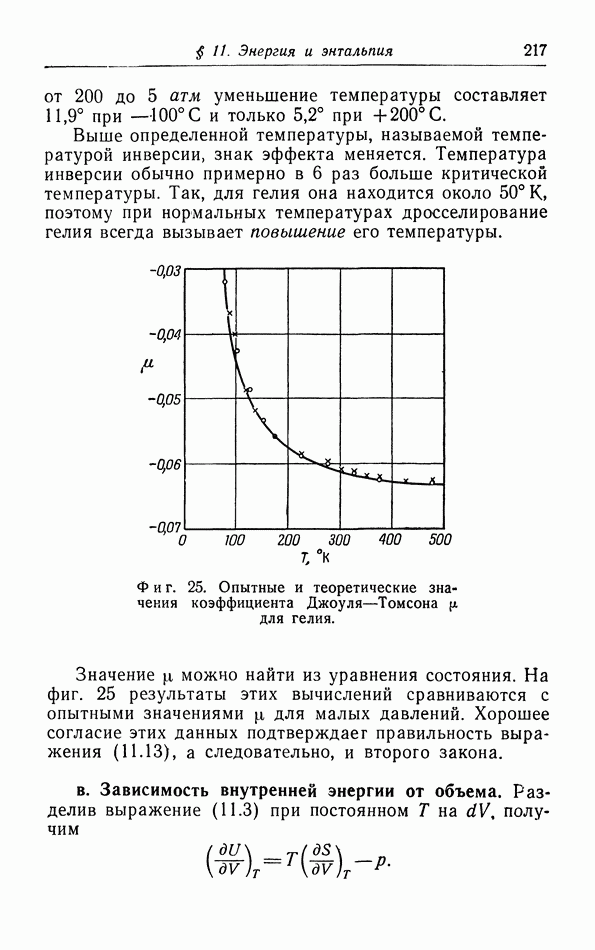
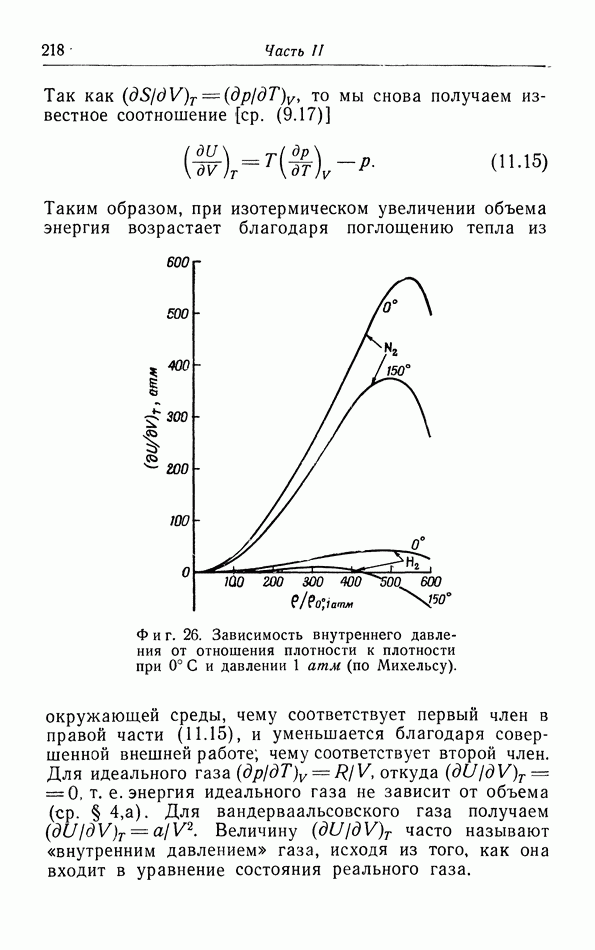
При помощи этих двух выражений можно, измеряя изотермы газа, найти изменение его удельной теплоемкости при сжатии. Таким путем [а именно интегрируя выражения (14.13)] Михельс вычислил вклад, вносимый межмолекулярной энергией в теплоемкость (см. часть I, § 6). Между прочим, термодинамическое рассмотрение показывает, что уравнение  Ваальса с постоянными a и b не позволяет найти вклад, вносимый межмолекулярной энергией в теплоемкость. Действительно, согласно этому уравнению,
Ваальса с постоянными a и b не позволяет найти вклад, вносимый межмолекулярной энергией в теплоемкость. Действительно, согласно этому уравнению,  является линейной функцией от
является линейной функцией от  следовательно, теплоемкость не зависит от объема. Чтобы объяснить изменение
следовательно, теплоемкость не зависит от объема. Чтобы объяснить изменение  мы должны учитывать зависимость а от температуры, что было неявно сделано в конце § 6 части
мы должны учитывать зависимость а от температуры, что было неявно сделано в конце § 6 части 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
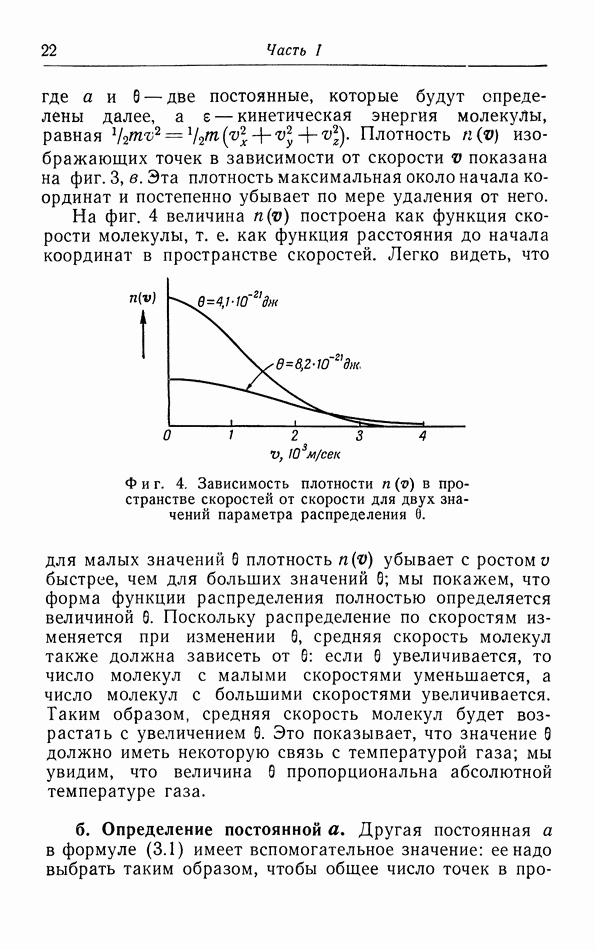
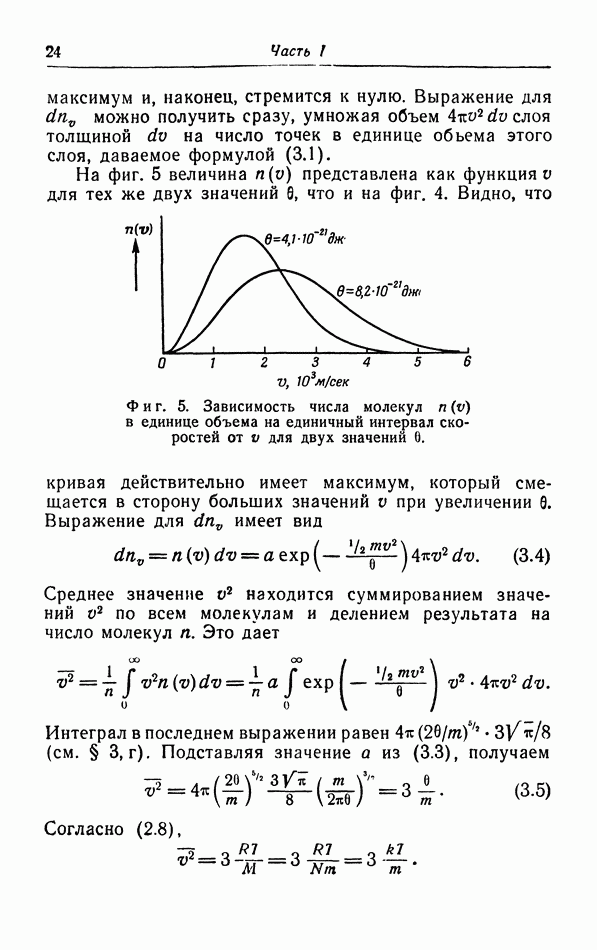
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
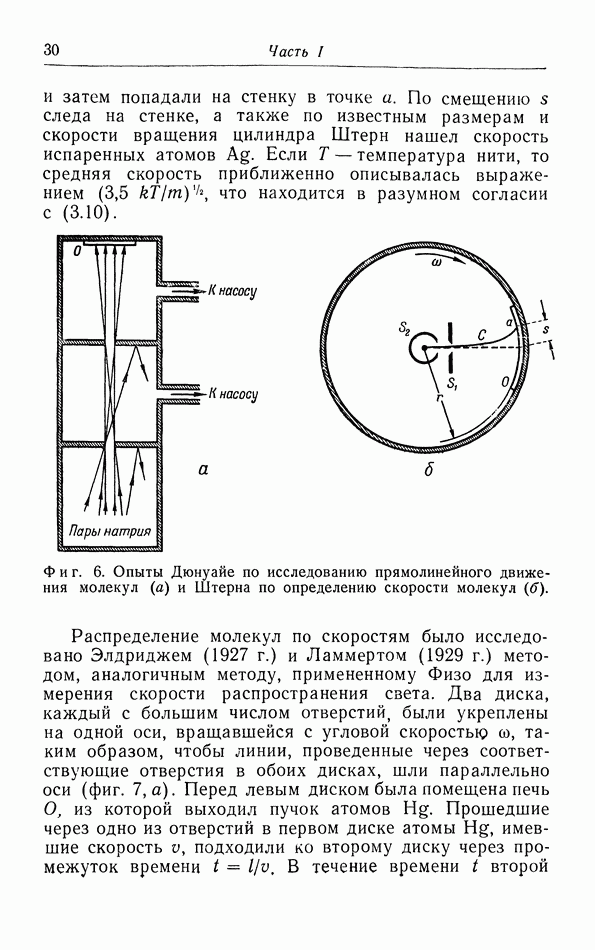
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
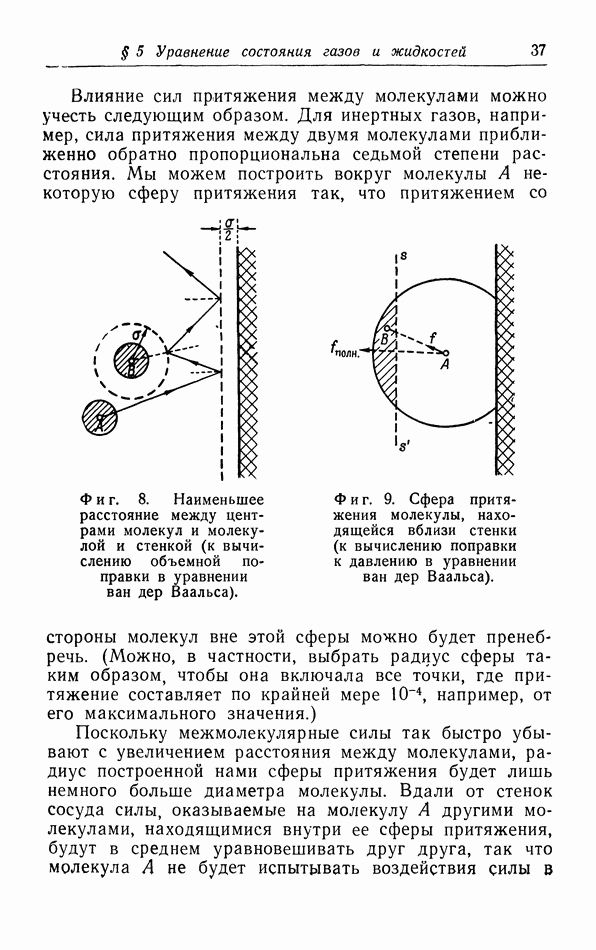
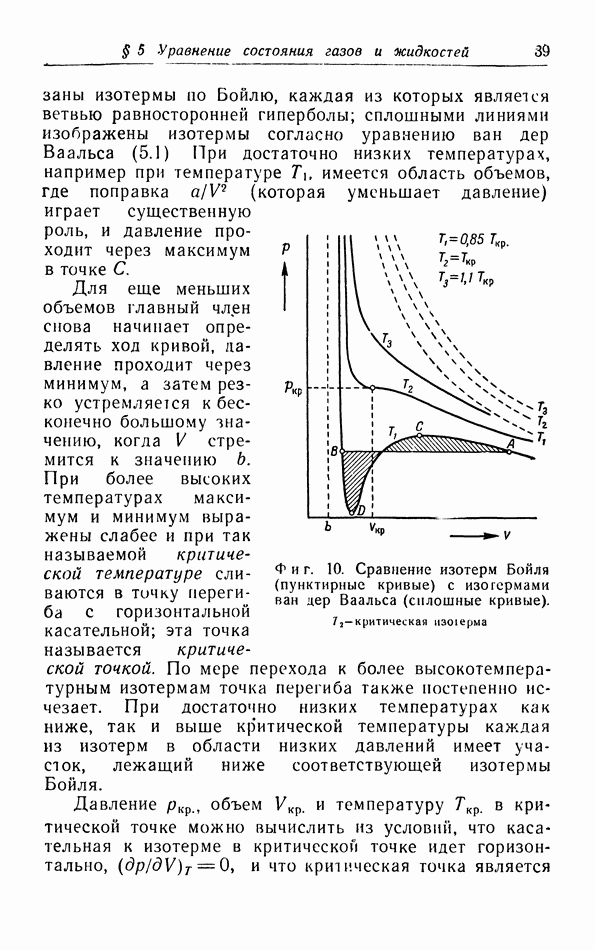
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
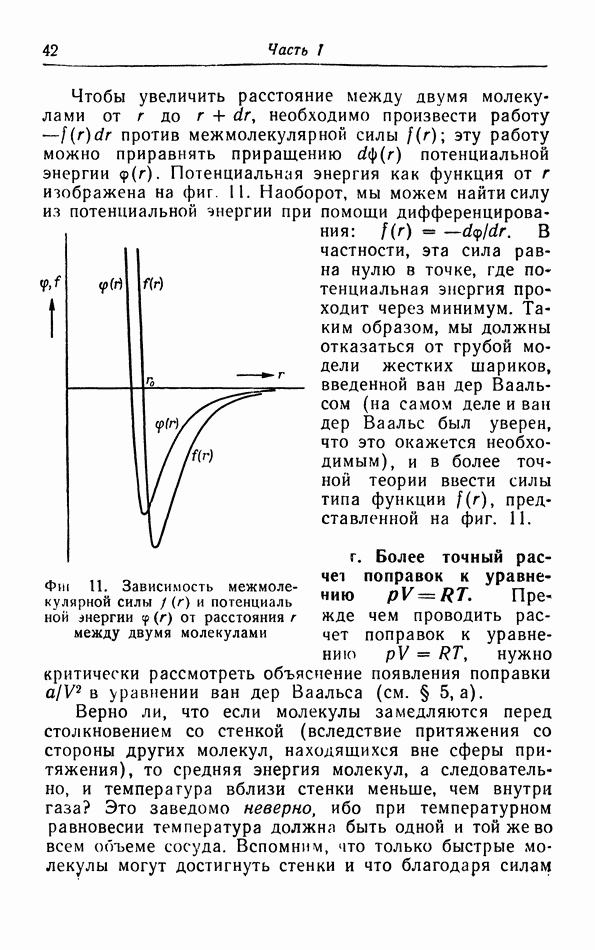
- в. Взаимодействие молекул.
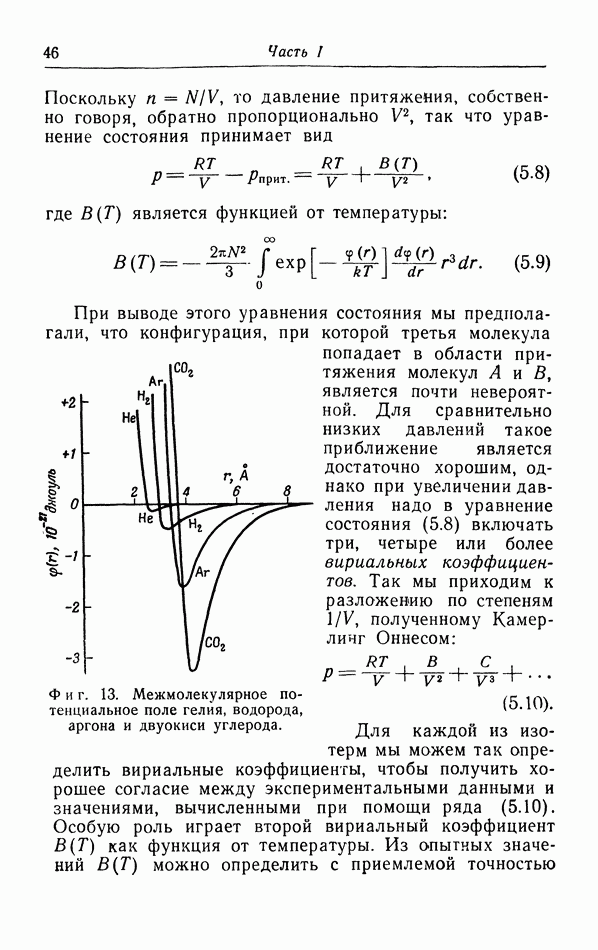
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
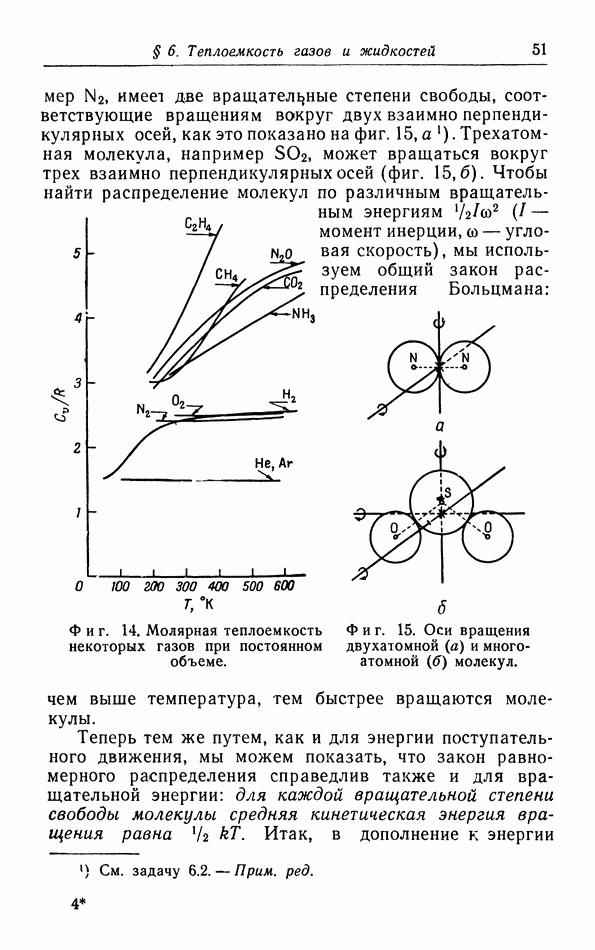
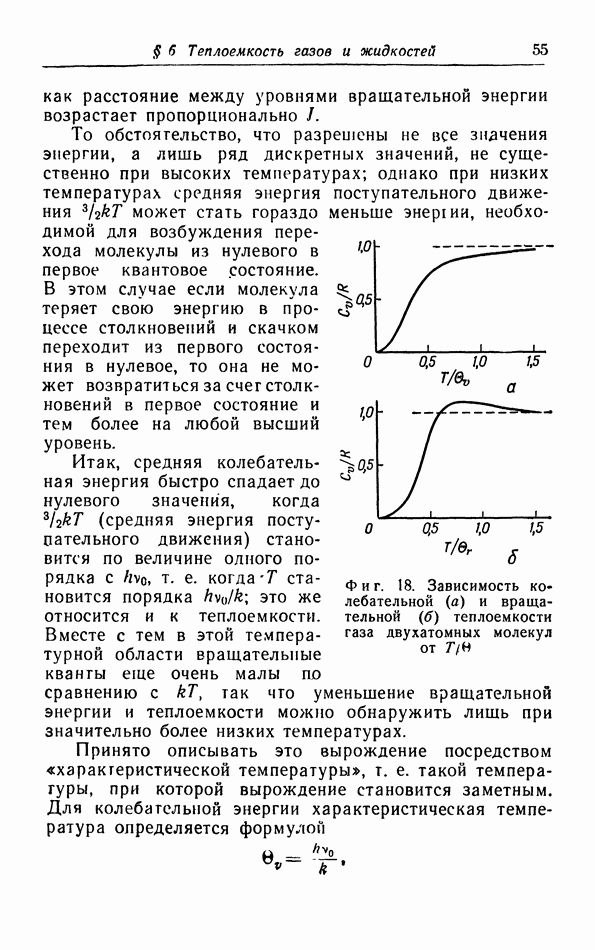
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
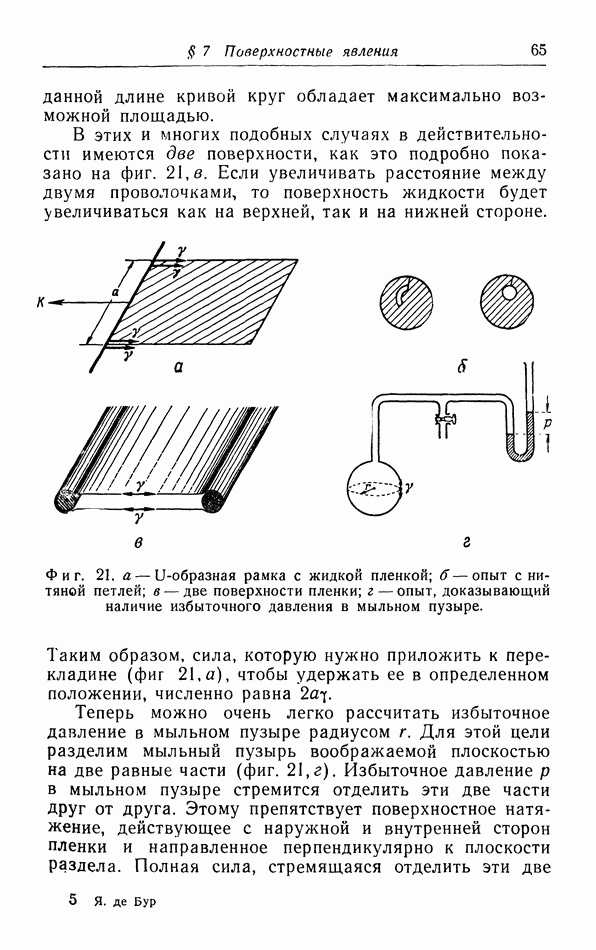
- § 7. Поверхностные явления
- б. Жидкие пленки.
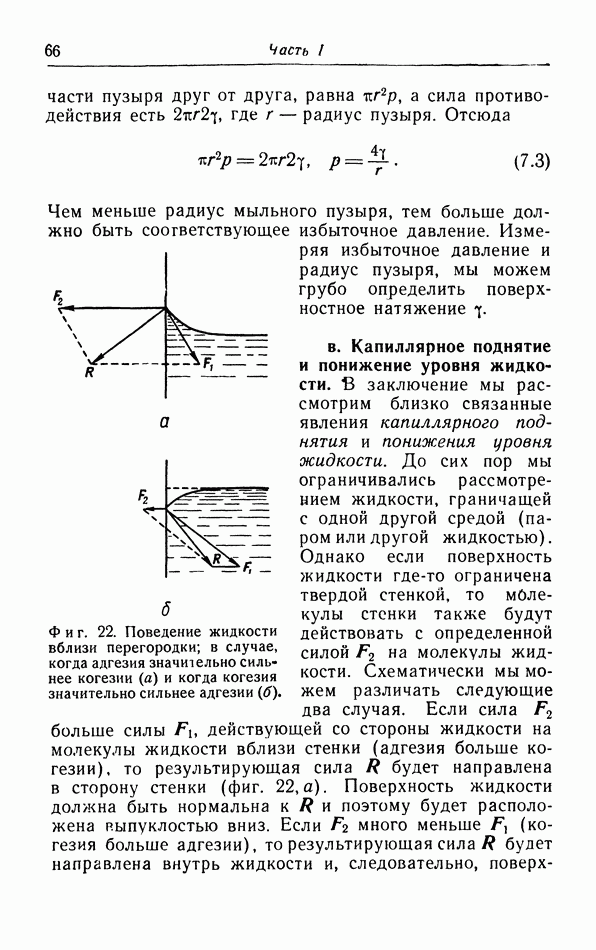
- в. Капиллярное поднятие и понижение уровня жидкости.
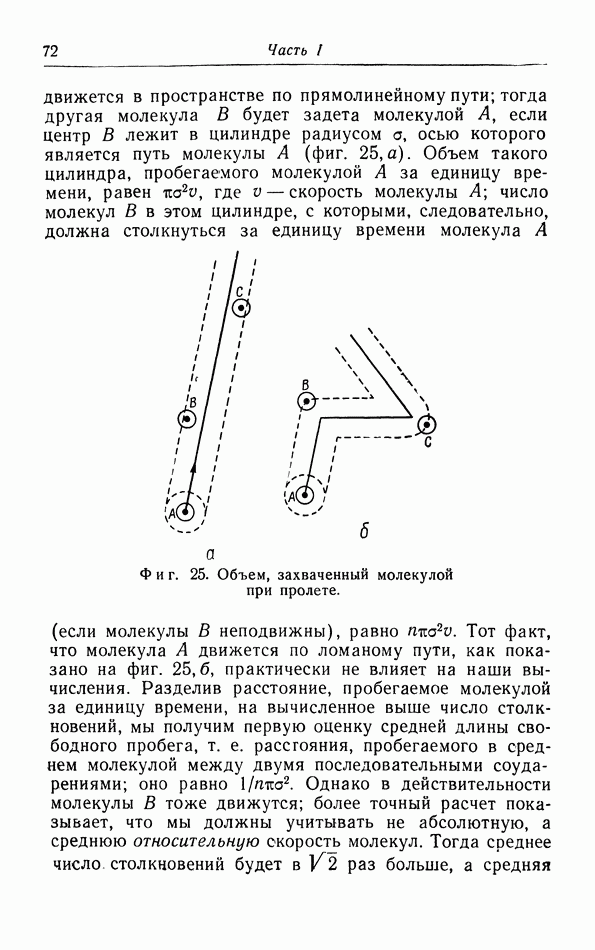
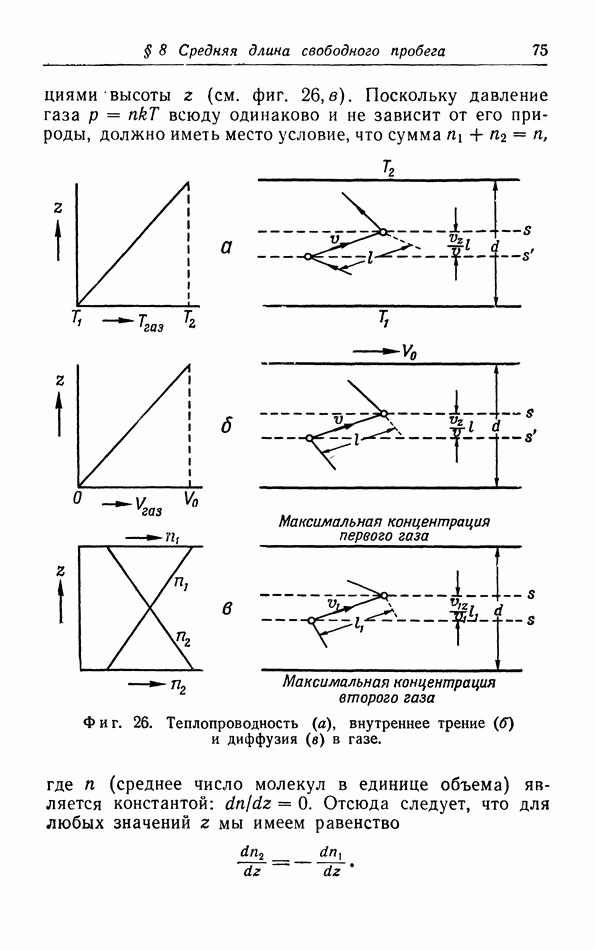
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
- § 3. Первый закон термодинамики
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
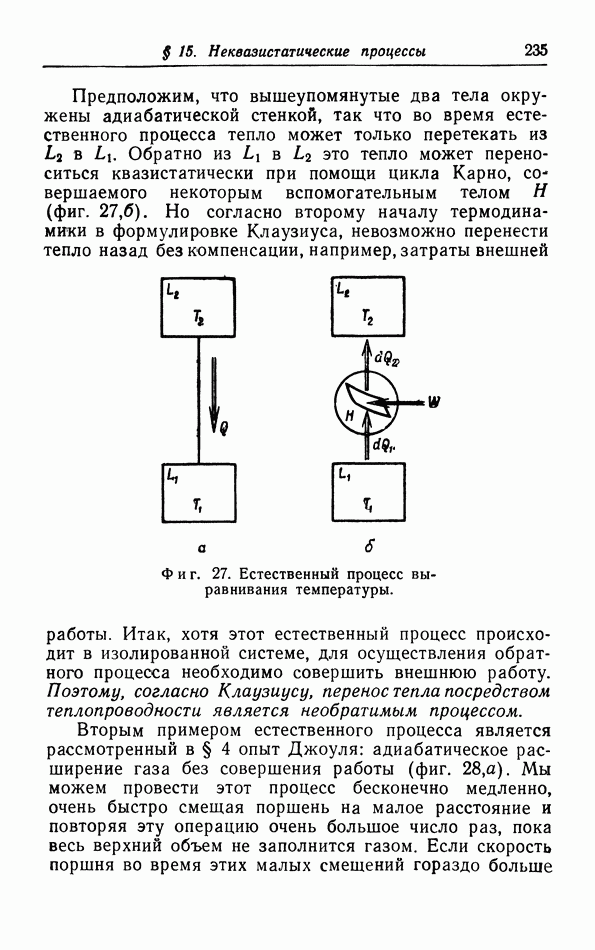
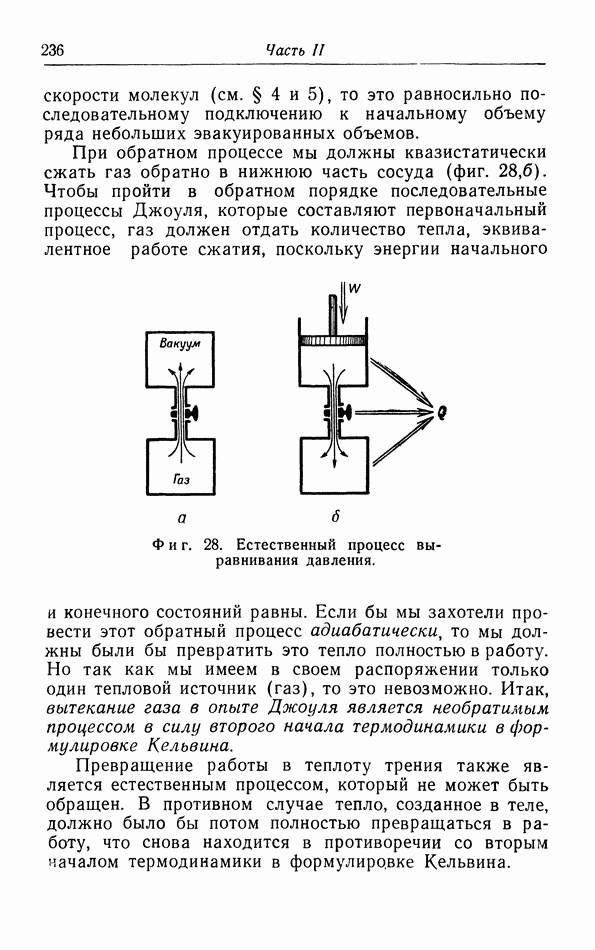
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
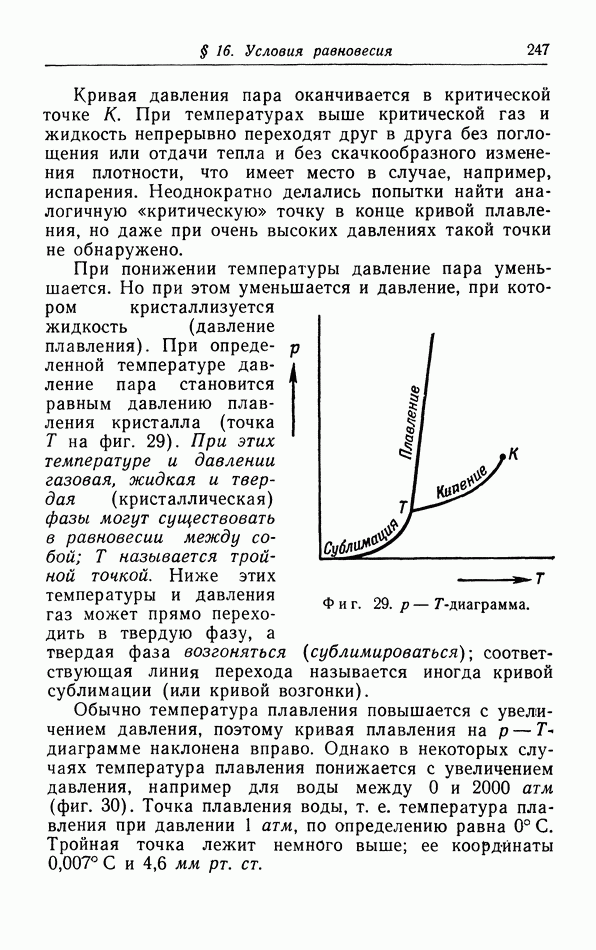
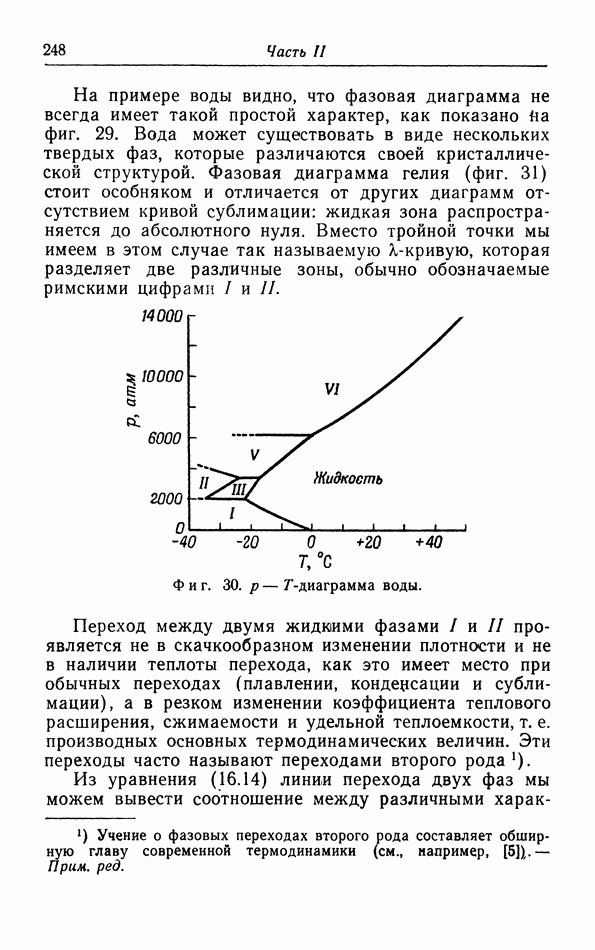
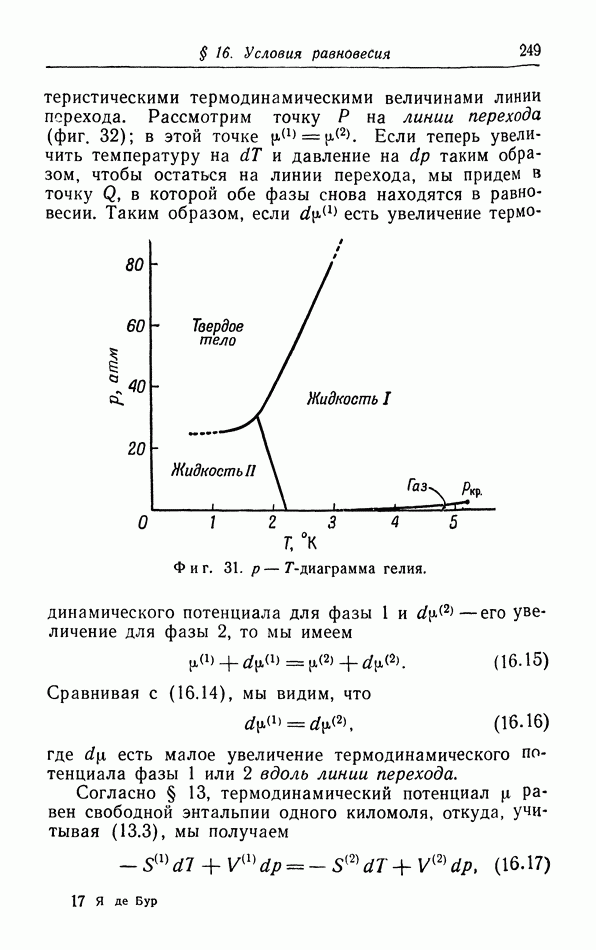
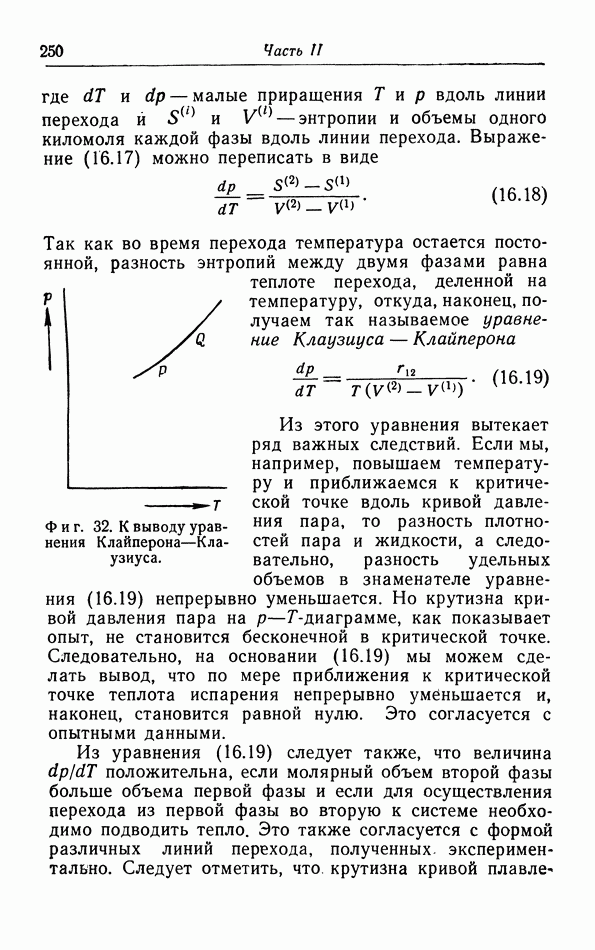
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам