| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
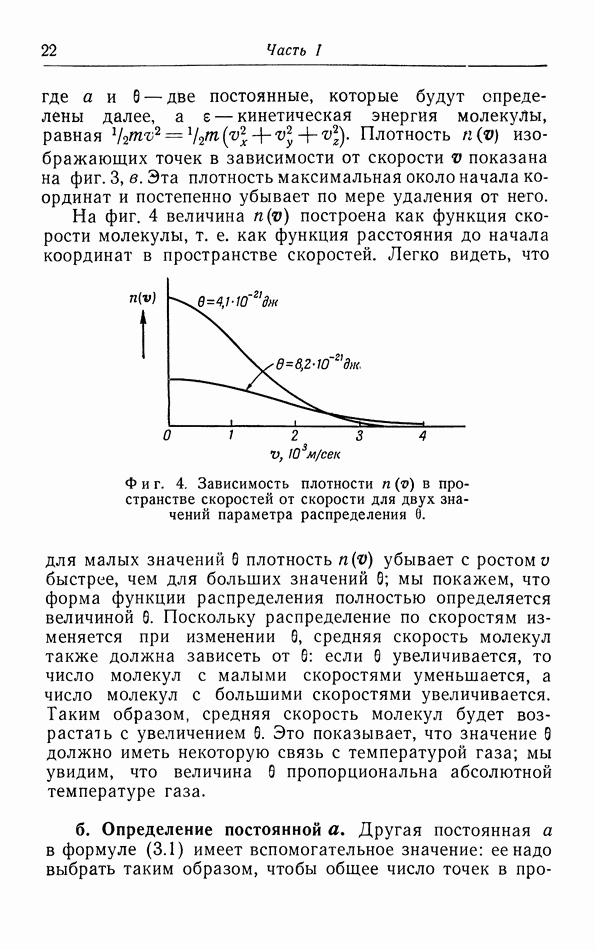
§ 9. Энтропия и второй закон термодинамики
а. Выражение второго закона термодинамики через энтропию.
В § 2 и 3 мы уже указывали, что при переходе системы из состояния 1 в состояние 2 общее количество совершенной работы и общее количество подведенного тепла, т. е. величины

зависят от пути перехода между 1 и 2. Однако, согласно первому закону, величина

где  не зависит от пути перехода между
не зависит от пути перехода между  Согласно первому закону,
Согласно первому закону,  в отличие от
в отличие от  есть полный дифференциал энергии
есть полный дифференциал энергии  которая является функцией состояния системы в данный момент времени.
которая является функцией состояния системы в данный момент времени.
Для однородной изотропной системы, описываемой двумя параметрами  , квазистатическая работа равна
, квазистатическая работа равна  откуда
откуда

Разделив  на
на  мы преобразовали
мы преобразовали  в дифференциальное выражение, которое описывает увеличение параметра состояния, а именно объема V, Следовательно, интеграл от
в дифференциальное выражение, которое описывает увеличение параметра состояния, а именно объема V, Следовательно, интеграл от  не зависит от пути перехода.
не зависит от пути перехода.
Мы можем доказать, что для тепла, обратимо подведенного к произвольной системе, также существует такой делитель, который преобразует  в полный дифференциал некоторой функции состояния Можно показать, что таким делителем является температура
в полный дифференциал некоторой функции состояния Можно показать, что таким делителем является температура  откуда
откуда

где энтропия  пока неизвестная функция состояния.
пока неизвестная функция состояния.
Чтобы доказать это, нам нужно убедиться, что интеграл от  для любого квазистатического процесса не зависит от пути перехода. Пусть процесс совершается системой
для любого квазистатического процесса не зависит от пути перехода. Пусть процесс совершается системой  а тепло, которое нужно подводить к системе
а тепло, которое нужно подводить к системе  на различных ступенях процесса, извлекается из бесконечно большого теплового резервуара
на различных ступенях процесса, извлекается из бесконечно большого теплового резервуара  при температуре
при температуре  (фиг. 17). Так как постоянная температура
(фиг. 17). Так как постоянная температура  будет в общем случае не равна переменной температуре
будет в общем случае не равна переменной температуре  системы
системы  к которой должно подводиться тепло, мы воспользуемся вспомогательной системой
к которой должно подводиться тепло, мы воспользуемся вспомогательной системой  для квазистатического (обратимого) переноса тепла от
для квазистатического (обратимого) переноса тепла от 

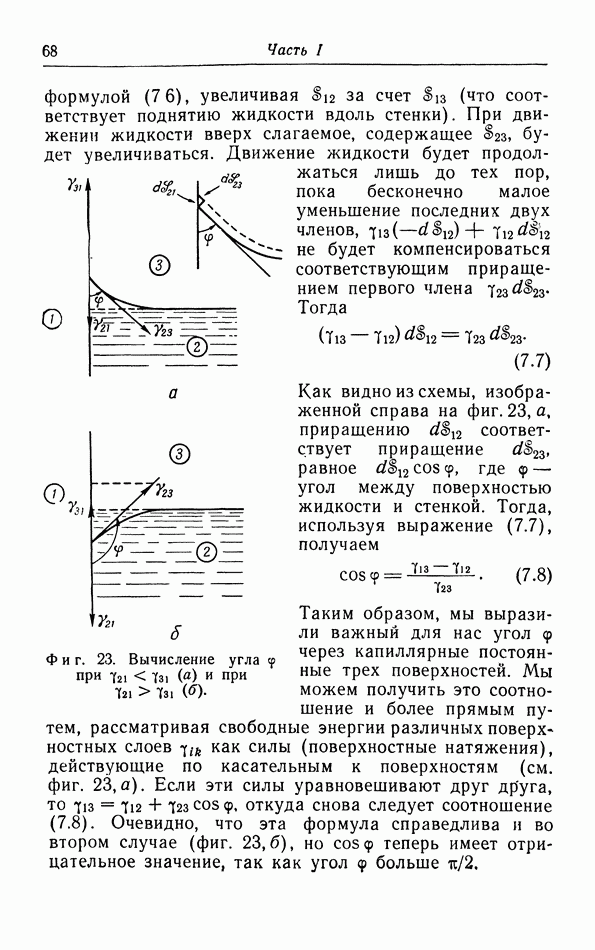
Фиг. 17. Процессы, используемые для доказательства того, что величина  одинакова для двух произвольных квазистатических процессов, проведенных с системой между ее состояниями 1 и 2.
одинакова для двух произвольных квазистатических процессов, проведенных с системой между ее состояниями 1 и 2.
Для этой цели мы заставим вспомогательную систему совершать нужные циклы Карно между  и
и  так что тепло можно, по желанию, обратимо подводить
так что тепло можно, по желанию, обратимо подводить  системе
системе  или отбирать у нее. Пусть
или отбирать у нее. Пусть  означает разность между температурой
означает разность между температурой  системы
системы  и температурой То резервуара
и температурой То резервуара  а малое количество работы, необходимое для переноса количества гепла
а малое количество работы, необходимое для переноса количества гепла  от
от  при помощи цикла, совершаемого вспомогательной системой
при помощи цикла, совершаемого вспомогательной системой  Тогда, согласно § 8,
Тогда, согласно § 8,

или

Но  есть количество тепла, переданного системе
есть количество тепла, переданного системе  в течение цикла системы
в течение цикла системы  откуда
откуда

Итак, общее количество тепла, извлеченного из резервуара  при помощи небольших циклов, совершенных системой
при помощи небольших циклов, совершенных системой  во время исследуемого произвольного вазистатического процесса, осуществляемого системой
во время исследуемого произвольного вазистатического процесса, осуществляемого системой  равно
равно

так как температура  постоянна. Индекс
постоянна. Индекс  указывает, что система
указывает, что система  переходила из состояния 1 в состояние 2 по определенному пути
переходила из состояния 1 в состояние 2 по определенному пути  Если переход системы
Если переход системы  из состояния 1 в состояние 2 происходит по другому пути
из состояния 1 в состояние 2 происходит по другому пути  то мы таким же образом найдем
то мы таким же образом найдем

Теперь мы докажем, что общие количества тепла  извлеченные из резервуара
извлеченные из резервуара  при совершении системой
при совершении системой  обоих процессов, равны В самом деле, если бы величина
обоих процессов, равны В самом деле, если бы величина  была меньше
была меньше  то мы могли бы обратить процесс
то мы могли бы обратить процесс  так как этот процесс обратимый. Тогда тепло
так как этот процесс обратимый. Тогда тепло  было бы подведено к
было бы подведено к  а не отобрано от
а не отобрано от  Следовательно, общее количество извлеченного из
Следовательно, общее количество извлеченного из  тепла было бы равно
тепла было бы равно  согласно первому закону, это тепло могло бы быть превращено в работу. Однако в этом случае система
согласно первому закону, это тепло могло бы быть превращено в работу. Однако в этом случае система  произвела бы циклический процесс
произвела бы циклический процесс  с совершением работы; поэтому величина
с совершением работы; поэтому величина  не может быть меньше
не может быть меньше  Действительно, согласно второму началу термодинамики в формулировке Кельвина, при помощи циклического процесса невозможно извлечь тепло из едудственного теплового резервуара
Действительно, согласно второму началу термодинамики в формулировке Кельвина, при помощи циклического процесса невозможно извлечь тепло из едудственного теплового резервуара  и превратить это тепло в работу.
и превратить это тепло в работу.
Обращая процесс  мы можем таким же образом показать, что величина
мы можем таким же образом показать, что величина  не может быть меньше
не может быть меньше  Следовательно, общие количества тепла, извлеченного вспомогательной системой
Следовательно, общие количества тепла, извлеченного вспомогательной системой  из резервуара
из резервуара  одинаковы для процессов I и II. Итак, выражения (9.6) и (9.7) равны, и
одинаковы для процессов I и II. Итак, выражения (9.6) и (9.7) равны, и

Интеграл от количества квазистатически подведенного тепла, деленного на соответствующую температуру, не зависит от пути перехода и является функцией
только начального и конечного состояний системы, откуда

Если количество тепла, деленное на температуру, при которой оно подводится, назвать «приведенным» теплом, то можно сказать, что для малого квазистатического изменения состояния системы приведенное количество подведенного тепла равно прирашению функции состояния системы, называемой энтропией (второй закон термодинамики) 1):

Для циклического процесса второй закон принимает форму

Для квазистатического циклического процесса интеграл от приведенного количества тепла равен нулю. Как говорилось выше (см. § 3), контурный интеграл от самого количества тепла равен, согласно первому закону, внешней работе, совершенной в течение циклического процесса.
Чтобы исследовать свойства этой новой функции состояния — энтропии, выразим прежде всего энтропию однородного изотропного вещества через параметры этой системы.
б. Выражение первого закона через T и V.
Попытаемся сначала, используя уравнение (9.10), выразить  через малые приращения
через малые приращения  Из первого закона имеем
Из первого закона имеем

В дальнейшем мы будем опускатьиндекс  так как мы будем иметь дело только с квазистатическими процессами.
так как мы будем иметь дело только с квазистатическими процессами.
Теперь нужно выразить  через
через  Мы считаем
Мы считаем  функцией от
функцией от 
Итак, энергия может увеличиваться в результате изменения  или V, или обоих параметров вместе. Если
или V, или обоих параметров вместе. Если  возрастает на
возрастает на  при неизменном объеме У, то соответствующее увеличение
при неизменном объеме У, то соответствующее увеличение  будет
будет

где мы берем частную производную по  при постоянном объеме
при постоянном объеме  Если температура
Если температура  остается постоянной, а объем V увеличивается на
остается постоянной, а объем V увеличивается на  то
то

Если же  увеличиваются одновременно на
увеличиваются одновременно на  то, согласно правилам дифференциального исчисления, полное увеличение
то, согласно правилам дифференциального исчисления, полное увеличение  в первом приближении равно сумме частных увеличений
в первом приближении равно сумме частных увеличений

Подставляя  в выражение для
в выражение для  получаем
получаем

В частном случае, когда тепло подводится при постоянном объеме  мы имеем [см. (5.5)]
мы имеем [см. (5.5)]

откуда

Подставляя в (9.12), получаем в общем случае

Это есть первый закон, выраженный через параметры  Как мы видим,
Как мы видим,  выражается через экспериментально определяемые величины
выражается через экспериментально определяемые величины  а также через
а также через  которую мы пока не можем связать с
которую мы пока не можем связать с
непосредственно измеряемыми величинами. В случае идеального газа, как вытекает из результатов опыта Джоуля,  Однако в общем случае это не имеет места.
Однако в общем случае это не имеет места.
в. Выражение второго закона через T и V
Выражение для  в зависимости от
в зависимости от  следует из (9.13):
следует из (9.13):

Если рассматривать  как функцию
как функцию  то аналогично (9.12) можно записать
то аналогично (9.12) можно записать

Сравнивая (9.14) и (9.15), находим

Теплоемкость  всегда положительна; таким образом, мы непосредственно видим, что при повыилении температуры при постоянном объеме энтропия всегда возрастает. Чтобы вывести аналогичное заключение для зависимости энтропии от объема, мы должны сначала попытаться исключить мешающую величину
всегда положительна; таким образом, мы непосредственно видим, что при повыилении температуры при постоянном объеме энтропия всегда возрастает. Чтобы вывести аналогичное заключение для зависимости энтропии от объема, мы должны сначала попытаться исключить мешающую величину  Для этого продифференцируем соотношения (9.16) соответственно по
Для этого продифференцируем соотношения (9.16) соответственно по  :
:

Поскольку  приравнивая (9.16а) и, (9.166) и умножая результат на
приравнивая (9.16а) и, (9.166) и умножая результат на  получаем
получаем

Таким образом, использовав второй закон, мы выразили  через измеряемые на опыте величины (дальнейшее обсуждение см. в § 11, в).
через измеряемые на опыте величины (дальнейшее обсуждение см. в § 11, в).
Возвранхаясь к вычислению энтропии, мы, подставляя (9.17) в (9.16), находим

Обычно если температура повышается при постоянном объеме, то давление увеличивается, так как вещество расширяется, и для сохранения постоянного объема требуется приложить давление. Однако, если коэффициент теплового расширения отрицателен, например, для воды между 0 и 4° С и для особой жидкой фазы II гелия ниже 2,19° К, величина  также отрицательна. Итак, выражение (9.18) показывает, что в том случае, когда объем увеличивается при постоянной температуре, энтропия всегда возрастает, кроме тех случаев, когда коэффициент теплового расилирения отрицателен.
также отрицательна. Итак, выражение (9.18) показывает, что в том случае, когда объем увеличивается при постоянной температуре, энтропия всегда возрастает, кроме тех случаев, когда коэффициент теплового расилирения отрицателен.
Подставляя (9.17) в (9.14), мы получаем дифференциальную форму второго закона, выраженную через  :
:

В термодинамических расчетах мы будем часто исходить из этого уравнения.
г. Энтропия.
Саму энтропию, или, вернее, разность энтропий для двух состояний 1 и 2, можно вычислить, интегрируя формулу (9.19):

Результат этого интегрирования не должен зависеть от пути перехода, так как, согласно второму закону,  есть функция состояния. Подставив в (9.20) экспериментальные значения
есть функция состояния. Подставив в (9.20) экспериментальные значения  мы в общем случае должны численно или графически вычислить интегралы как функции от
мы в общем случае должны численно или графически вычислить интегралы как функции от  и получить таким путем зависимость
и получить таким путем зависимость
энтропии от  Прежде чем обсуждать результаты этих вычислений, заметим, что интегрирование выполняется особенно просто для идеального газа, для которого
Прежде чем обсуждать результаты этих вычислений, заметим, что интегрирование выполняется особенно просто для идеального газа, для которого  не зависит от объема. Для простоты предположим, что
не зависит от объема. Для простоты предположим, что  не зависит также
не зависит также  это допустимо для большинства газов в большом интервале температур. Учитывая, что
это допустимо для большинства газов в большом интервале температур. Учитывая, что

получаем

Таким образом, энтропия на 1 кмоль равна

где  обозначает некоторую постоянную, не зависящую от
обозначает некоторую постоянную, не зависящую от  Подставляя
Подставляя  из (9.21) получаем
из (9.21) получаем

где  постоянное слагаемое
постоянное слагаемое  включено в константу. Наконец, мы можем записать 5 в третьей форме
включено в константу. Наконец, мы можем записать 5 в третьей форме

При помощи этих трех выражений энтропию идеального газа можно, по желанию, выразить через  или
или  или
или  .
.
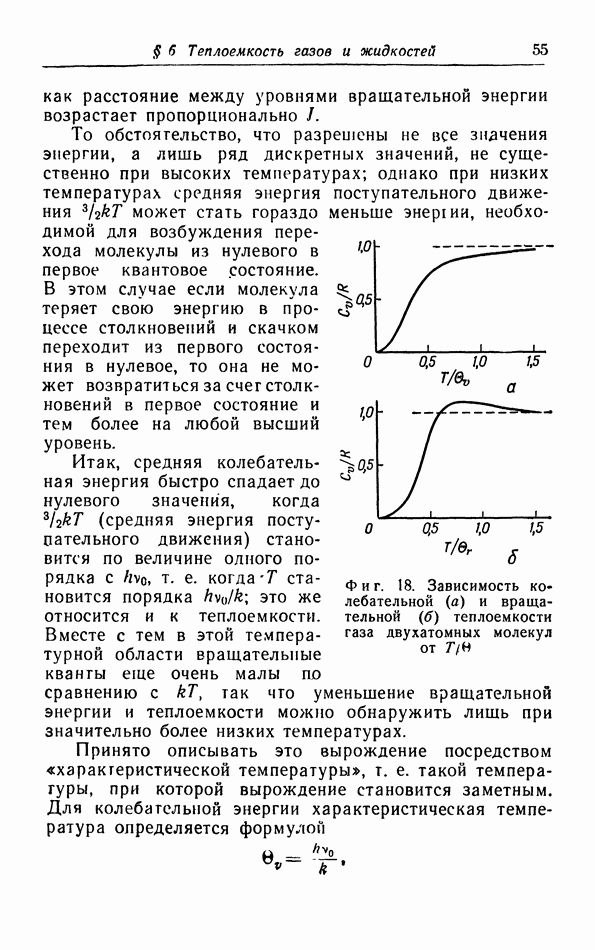
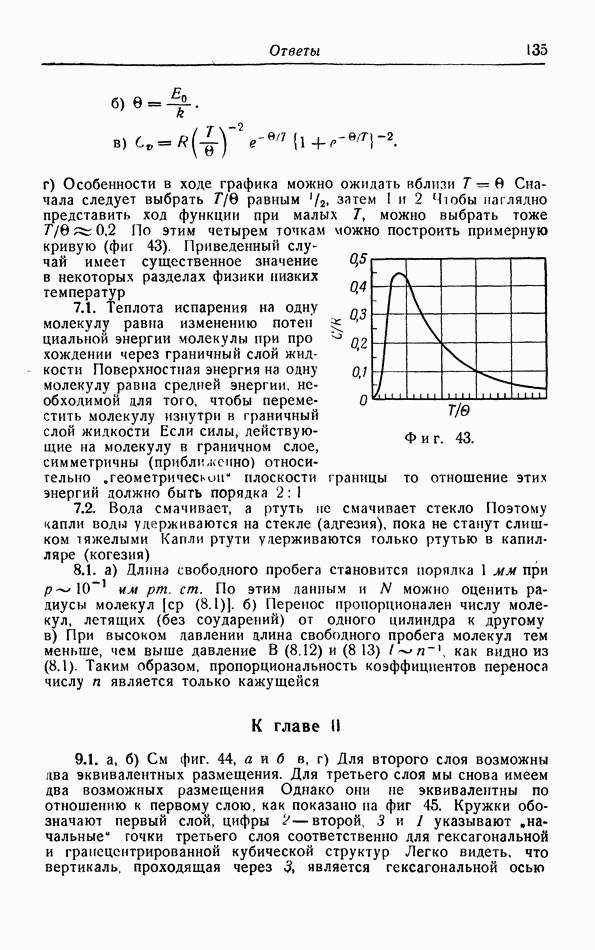
На фиг. 18, а при помощи выражения (9.22), на  -диаграмме построены линии постоянной энтропии, или изэнтропы для идеального газа; здесь же приведены изотермы. Как мы видим, изэнтропы всюду спадают круче изотерм. Приведенные на фигуре числа соответствуют значениям
-диаграмме построены линии постоянной энтропии, или изэнтропы для идеального газа; здесь же приведены изотермы. Как мы видим, изэнтропы всюду спадают круче изотерм. Приведенные на фигуре числа соответствуют значениям  рассчитанным при помощи (9.22) при константе, произвольно положенной равной нулю. На фиг. 18,б построены кривые для
рассчитанным при помощи (9.22) при константе, произвольно положенной равной нулю. На фиг. 18,б построены кривые для  в функции от
в функции от 
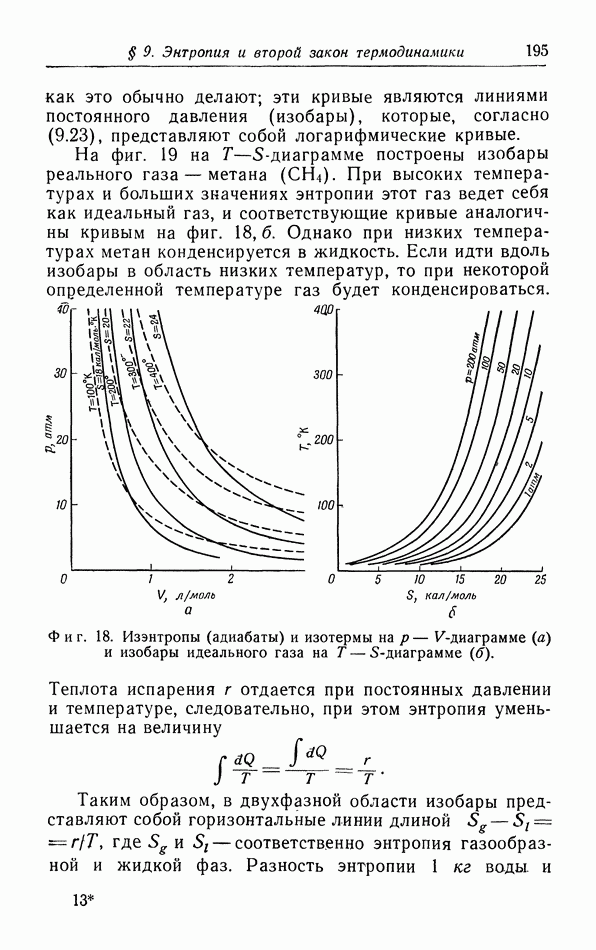
как это обычно делают; эти кривые являются линиями постоянного давления (изобары), которые, согласно (9.23), представляют собой логарифмические кривые.
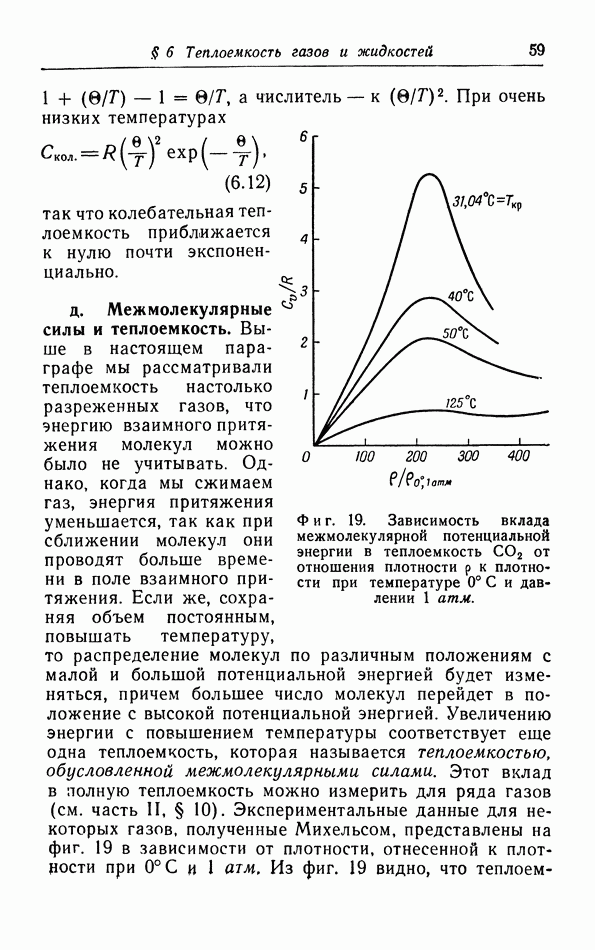
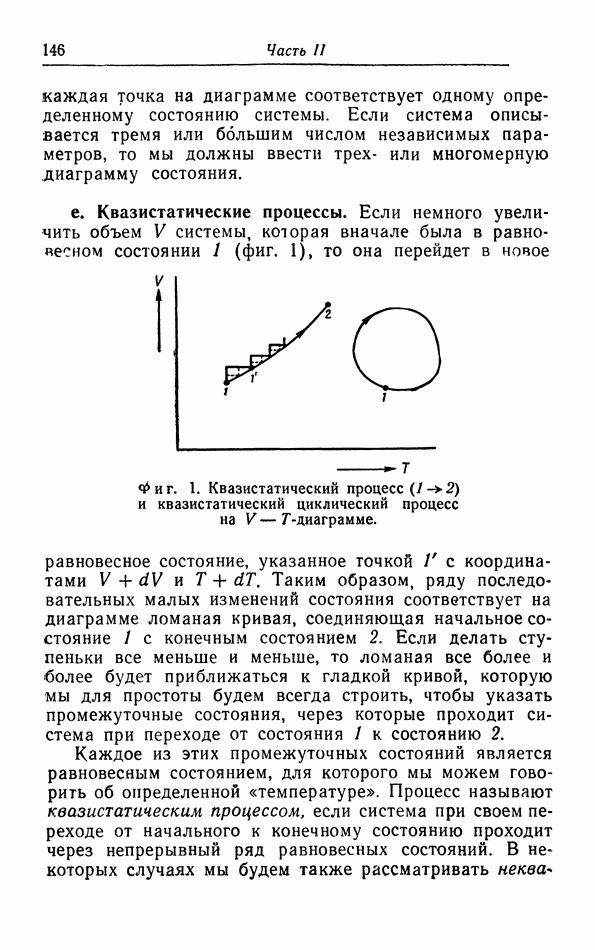
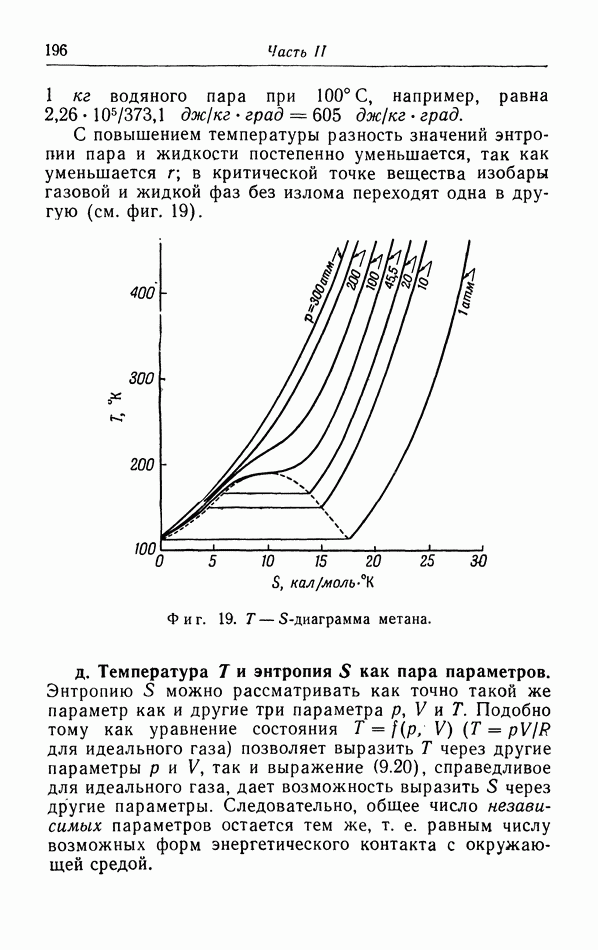
На фиг. 19 на  -диаграмме построены изобары реального газа — метана
-диаграмме построены изобары реального газа — метана  При высоких температурах и больших значениях энтропии этот газ ведет себя как идеальный газ, и соответствуюихие кривые аналогичны кривым на фиг. 18,б. Однако при низких температурах метан конденсируется в жидкость. Если идти вдоль изобары в область низких температур, то при некоторой определенной температуре газ будет конденсироваться.
При высоких температурах и больших значениях энтропии этот газ ведет себя как идеальный газ, и соответствуюихие кривые аналогичны кривым на фиг. 18,б. Однако при низких температурах метан конденсируется в жидкость. Если идти вдоль изобары в область низких температур, то при некоторой определенной температуре газ будет конденсироваться.

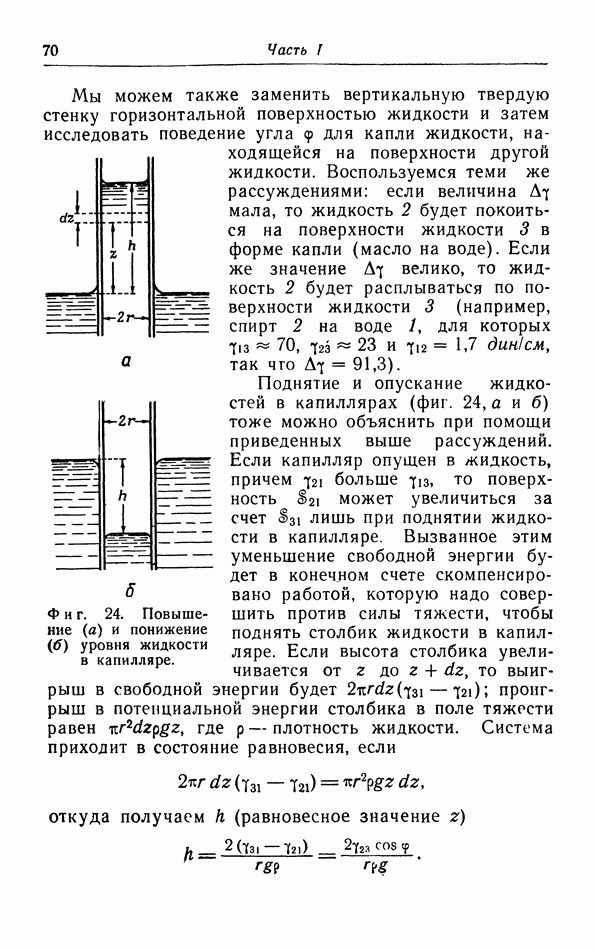
Фиг. 18. Изэнтропы (адиабаты) и изотермы на  -диаграмме
-диаграмме  и изобары идеального газа на
и изобары идеального газа на  -диаграмме
-диаграмме 
Теплота испарения  отдается при постоянных давлении и температуре, следовательно, при этом энтропия уменьшается на величину
отдается при постоянных давлении и температуре, следовательно, при этом энтропия уменьшается на величину

Таким образом, в двухфазной области изобары представляют собой горизонтальные линии длиной  где и
где и  соответственно энтропия газообразной и жидкой фаз. Разность энтропии
соответственно энтропия газообразной и жидкой фаз. Разность энтропии  воды и
воды и
 водяного пара при 100° С, например, равна
водяного пара при 100° С, например, равна  град
град  град,
град,
С повышением температуры разность значений энтропии пара и жидкости постепенно уменьшается, так как уменьшается  в критической точке вещества изобары газовой и жидкой фаз без излома переходят одна в другую (см. фиг. 19).
в критической точке вещества изобары газовой и жидкой фаз без излома переходят одна в другую (см. фиг. 19).

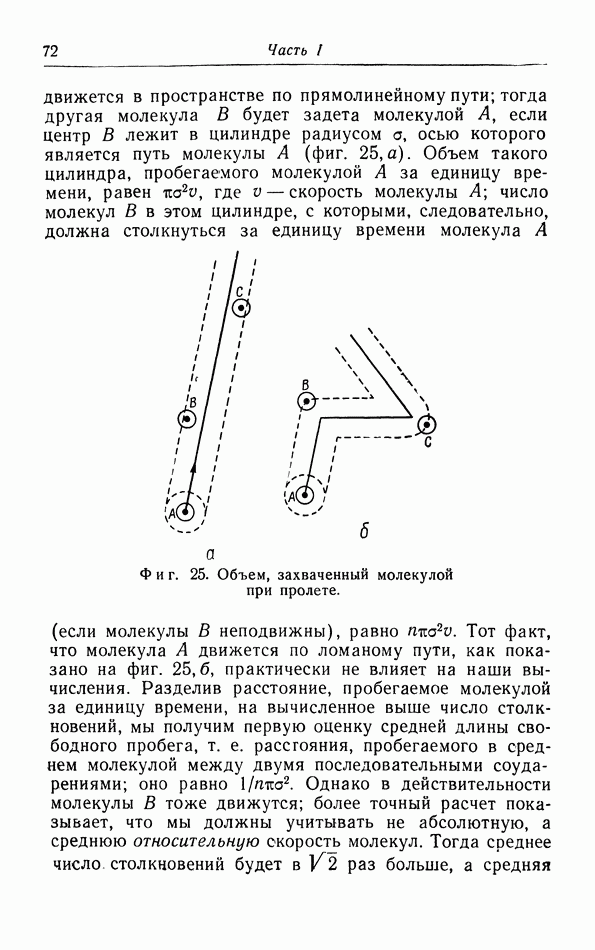
Фиг. 19.  -диаграмма метана.
-диаграмма метана.
д. Температура T и энтропия S как пара параметров.
Энтропию  можно рассматривать как точно такой же параметр как и другие три параметра
можно рассматривать как точно такой же параметр как и другие три параметра  Подобно тому как уравнение состояния
Подобно тому как уравнение состояния  для идеального газа) позволяет выразить
для идеального газа) позволяет выразить  через другие параметры
через другие параметры  так и выражение (9.20), справедливое для идеального газа, дает возможность выразить
так и выражение (9.20), справедливое для идеального газа, дает возможность выразить  через другие параметры. Следовательно, общее число независимых параметров остается тем же, т. е. равным числу возможных форм энергетического контакта с окружающей средой.
через другие параметры. Следовательно, общее число независимых параметров остается тем же, т. е. равным числу возможных форм энергетического контакта с окружающей средой.
в § 2 мы показали, что каждой форме нетеплового энергетического контакта соответствует пара параметров, а именно:  и V для контакта через давление,
и V для контакта через давление,  для магнитного контакта и т. д. Однако для теплового контакта мы смогли тогда найти единственный параметр — температуру. Теперь мы можем сказать, что температура и энтропия образуют пару параметров, в чем легко убедиться, сравнивая два выражения:
для магнитного контакта и т. д. Однако для теплового контакта мы смогли тогда найти единственный параметр — температуру. Теперь мы можем сказать, что температура и энтропия образуют пару параметров, в чем легко убедиться, сравнивая два выражения:

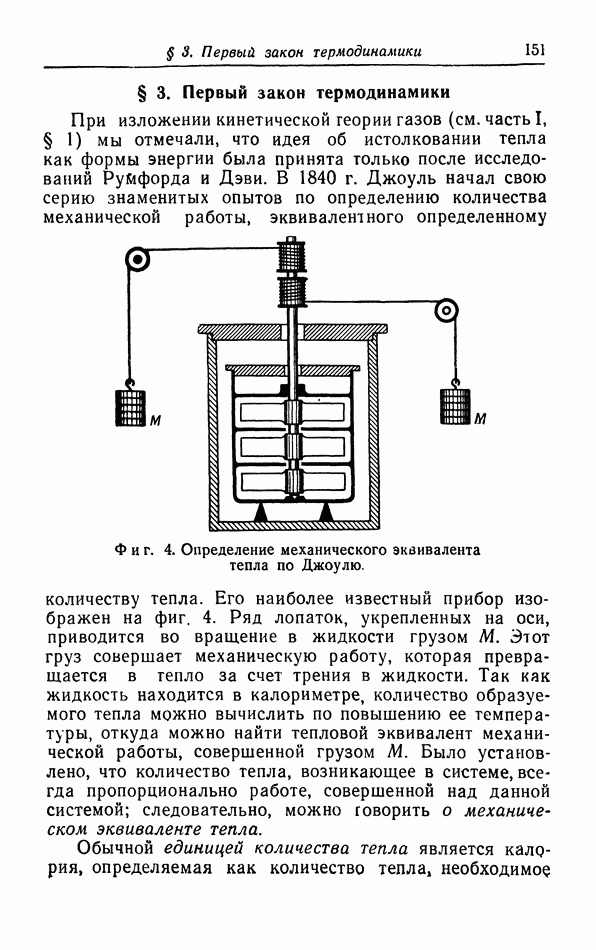
Поскольку теплообмен пропорционален увеличению энтропии и значению температуры, мы должны рассматривать энтропию как экстенсивный параметр, а температуру как соответствующий интенсивный параметр (см. § 2).

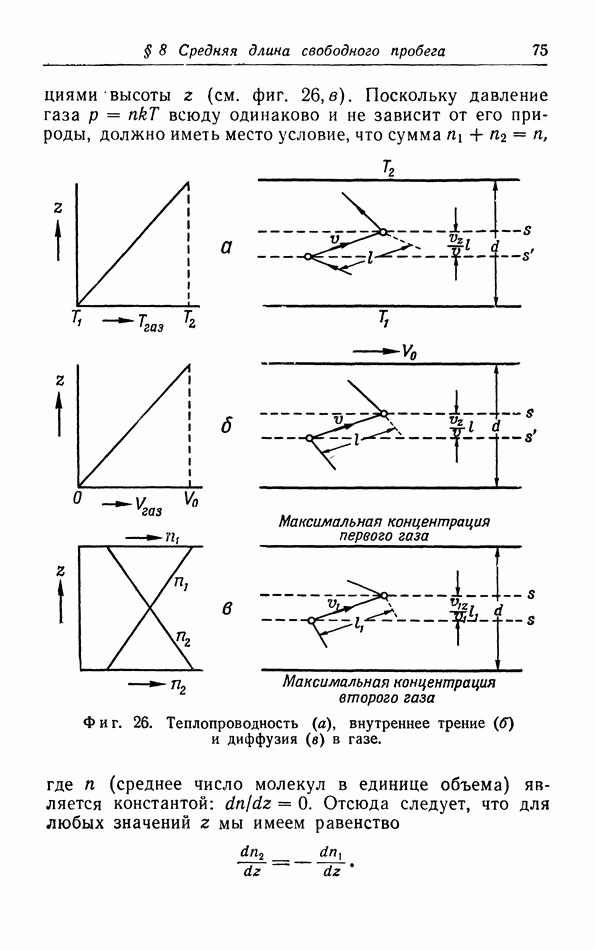
Фиг. 20.  -диаграмма, на которой указано количество тепла, подреденного во время квазистатического процесса
-диаграмма, на которой указано количество тепла, подреденного во время квазистатического процесса  и во время циклического процесса.
и во время циклического процесса.
Действительно, энтропия вещества пропорциональна количеству этого вещества; это следует непосредственно из ее определения. По этой причине мы строили на  -диаграмме (фиг. 20)
-диаграмме (фиг. 20)  как функцию от
как функцию от  а не наоборот. Подводимое в течение процесса количество тепла численно равно площади, расположенной под представляющей процесс кривой (аналогично определяется величина внешней работы на
а не наоборот. Подводимое в течение процесса количество тепла численно равно площади, расположенной под представляющей процесс кривой (аналогично определяется величина внешней работы на  -диаграмме). В частности, площадь, ограниченная
-диаграмме). В частности, площадь, ограниченная  -кривой, соответствующей квазистатическому циклическому процессу, численно равна общему количеству тепла, подведенного при этом процессе.
-кривой, соответствующей квазистатическому циклическому процессу, численно равна общему количеству тепла, подведенного при этом процессе.
е. Физический смысл энтропии.
Единственная причина, из-за которой нам кажется несколько стрщнмц рассматривать энтропию как независимый параметр, добывающий состояние системы, состоит в том, что мы не имеем
измерительного прибора (такого, как термометр, манометр и т. п.), при помощи которого можно было бы непосредственно измерять энтропию. Мы можем лишь косвенно вычислять значение энтропии (с точностью до некоторой постоянной) по теплоемкости и термическому коэффициенту давления.
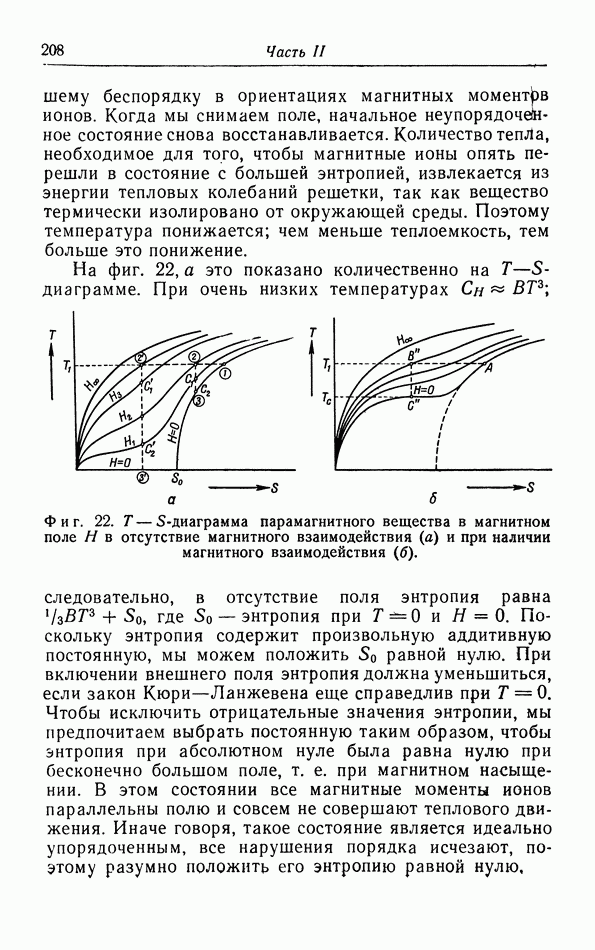
С кинетической точки зрения энтропию лучше всего определить как меру неупорядоченности системы. Когда мы охлаждаем систему при постоянном объеме, мы непрерывно извлекаем из нее тепло, а следовательно, и энтропию; при этом упорядоченность системы повышается. Когда газ конденсируется в жидкость, молекулы занимают более определенные положения друг относительно друга, в отличие от их поведения в газовой фазе, причем скачкообразное уменьшение беспорядка соответствует скачкообразному уменьшению энтропии. При дальнейшем понижении температуры жидкости тепловое движение, которое создает неупорядоченность, становится все менее интенсивным, и происходит дальнейшее постепенное уменьшение энтропии.
Когда жидкость отвердевает, молекулы в кристалле занимают вполне определенные положения одна относительно другой, так что неупорядоченность скачком становится значительно меньше. Соответственно при отвердевании выделяется тепло и энтропия также убывает скачком.
При абсолютном нуле тепловое движение полностью исчезает; следовательно, мы можем сказать, что при абсолютном нуле неупорядоченность равна нулю. В связи с этим выводом имеет смысл положить энтропию всех веществ при абсолютном нуле температуры равной нулю. Но это не является законом термодинамики, а есть лишь утверждение, основанное на рассмотренной нами кинетической картине энтропии
Представление об энтропии как мере неупорядоченности хорошо описывает ее зависимость не только от
температуры, но и от объема. Прежде всего, когда мы уменьшаем объем газа, его молекулы вынуждены занимать все более и более определенные положения одна относительно другой: при температуре ниже критической мы можем сконденсировать пар только посредством сжатия, а выше критической температуры сжатие приводит к появлению напоминающей жидкость однофазной структуры с постепенно растущей упорядоченностью.
Таким образом, кинетическая интерпретация энтропии как меры неупорядоченности дает по крайней мере качественно правильную картину поведения энтропии при изменении переменных параметров состояния системы. В кинетической теории газов проводится более строгое рассмотрение и доказывается, что энтропия  связана с вероятностью
связана с вероятностью  состояния:
состояния:

причем дается метод точного вычисления  Более подробное рассмотрение показывает, что эта вероятность тесно связана с «неупорядоченностью», введенной ранее только на основании качественных рассуждений.
Более подробное рассмотрение показывает, что эта вероятность тесно связана с «неупорядоченностью», введенной ранее только на основании качественных рассуждений.
Следует заметить, что изложенная интерпретация энтропии и, в частности, выражение (9.25) не относятся, строго говоря, к чистой термодинамике. В термодинамике эта интерпретация даже не нужна: энтропия, введенная здесь термодинамически, может быть с успехом использована как параметр и применяться в вычислениях независимо от изложенной выше интерпретации.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
- б. Жидкие пленки.
- в. Капиллярное поднятие и понижение уровня жидкости.
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
- § 3. Первый закон термодинамики
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
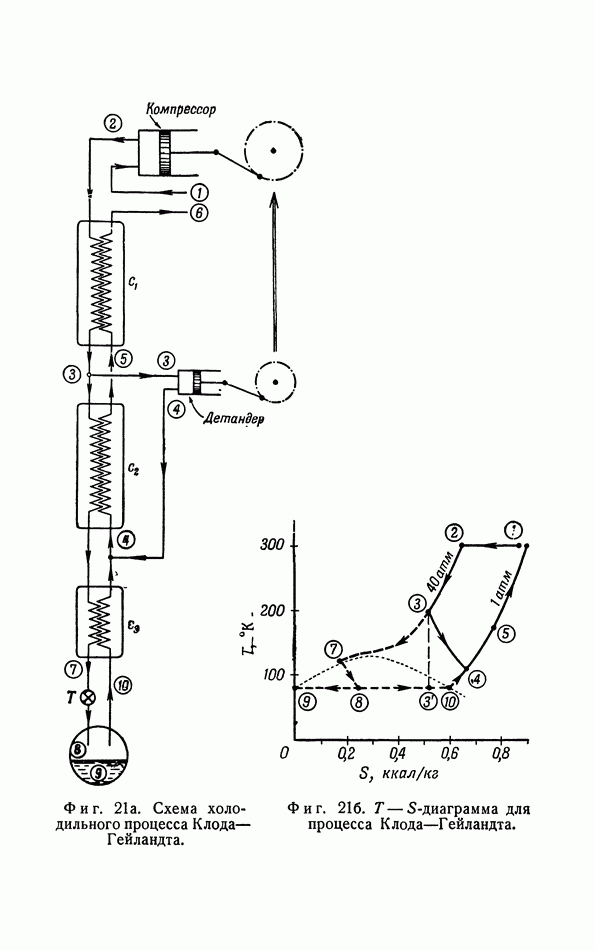
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
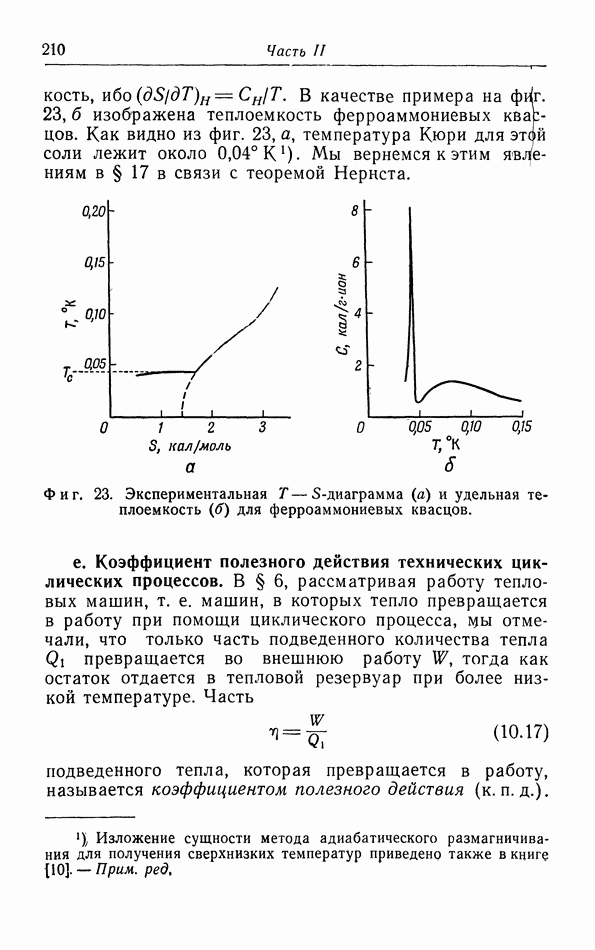
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам