| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
в. Работа при адиабатических процессах.
При помощи первого закона мы также можем связать работу, совершаемую при адиабатических процессах, с изменениями энергии и энтальпии. Так как при адиабатическом процессе тепло не подводится, мы имеем 2

Внешняя работа, совершаемая системой во время адиабатического процесса, равна уменьшению внутренней энергии данной системы. Когда система совершает внешнюю работу без притока тепла, уменьшение ее внутренней энергии равно произведенной внешней работе.
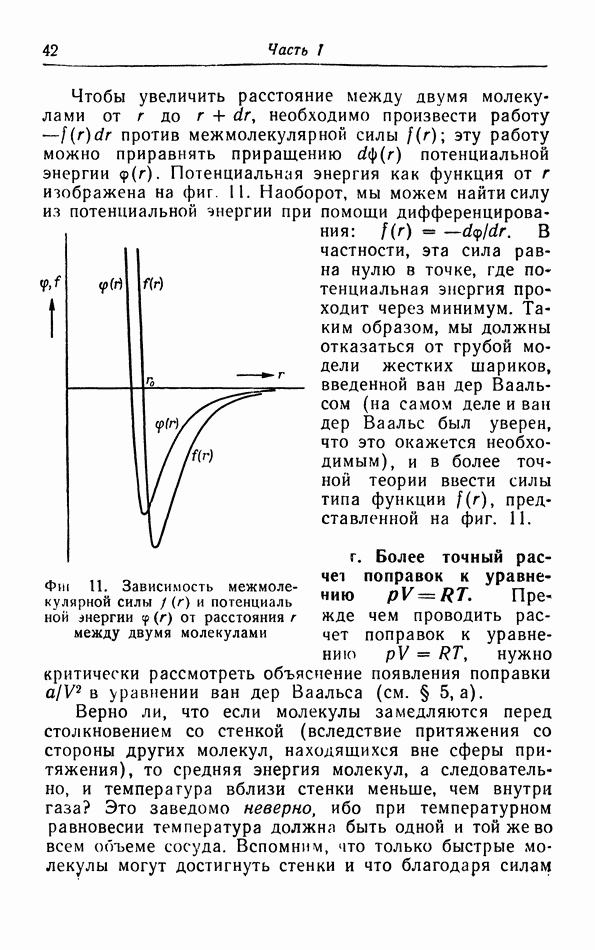
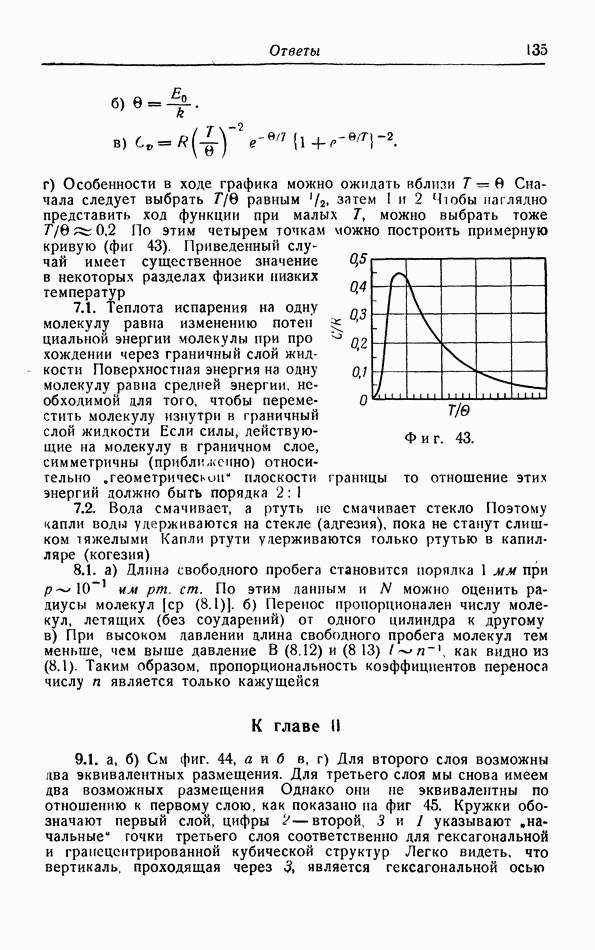
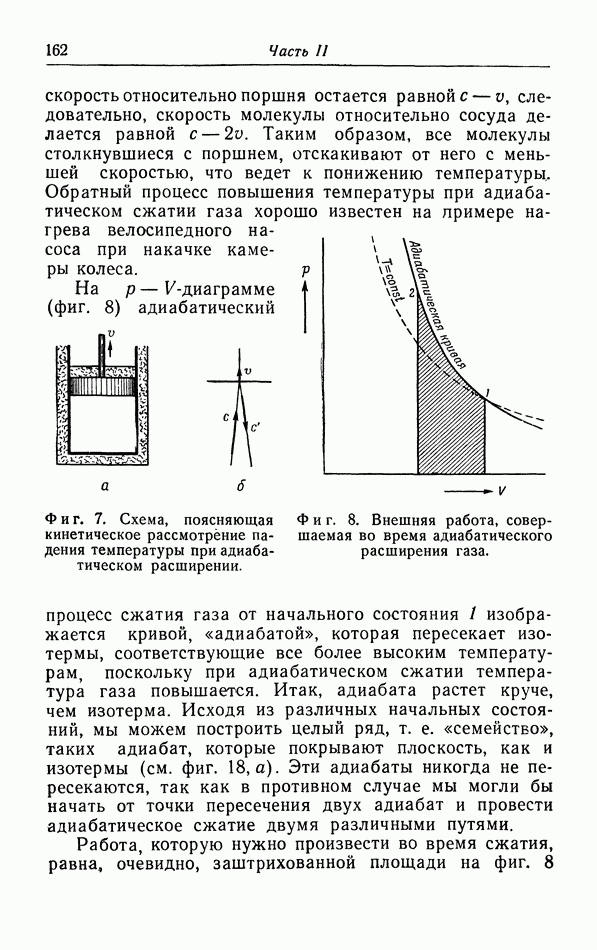
Внутренняя энергия идеального газа определяется исключительно кинетической энергией молекул  часть I, формула (2.11)]. Когда идеальный газ расширяется адиабатически, кинетическая энергия его молекул, а следовательно, и температура газа уменьшаются. Чтобы объяснить это понижение температуры на основе кинетических представлений, рассмотрим соударения молекул с поршнем (фиг. 7): молекула, движущаяся нормально к поршню со скоростью с, имеет относительно поршня скорость с — у, где
часть I, формула (2.11)]. Когда идеальный газ расширяется адиабатически, кинетическая энергия его молекул, а следовательно, и температура газа уменьшаются. Чтобы объяснить это понижение температуры на основе кинетических представлений, рассмотрим соударения молекул с поршнем (фиг. 7): молекула, движущаяся нормально к поршню со скоростью с, имеет относительно поршня скорость с — у, где  скорость движения поршня при расширении. После соударения с поршнем
скорость движения поршня при расширении. После соударения с поршнем
скорость относительно поршня остается равной с — у, следовательно, скорость молекулы относительно сосуда делается равной  Таким образом, все молекулы столкнувшиеся с поршнем, отскакивают от него с меньшей скоростью, что ведет к понижению температуры. Обратный процесс повышения температуры при адиабатическом сжатии газа хорошо известен на примере нагрева велосипедного насоса при накачке камеры колеса.
Таким образом, все молекулы столкнувшиеся с поршнем, отскакивают от него с меньшей скоростью, что ведет к понижению температуры. Обратный процесс повышения температуры при адиабатическом сжатии газа хорошо известен на примере нагрева велосипедного насоса при накачке камеры колеса.

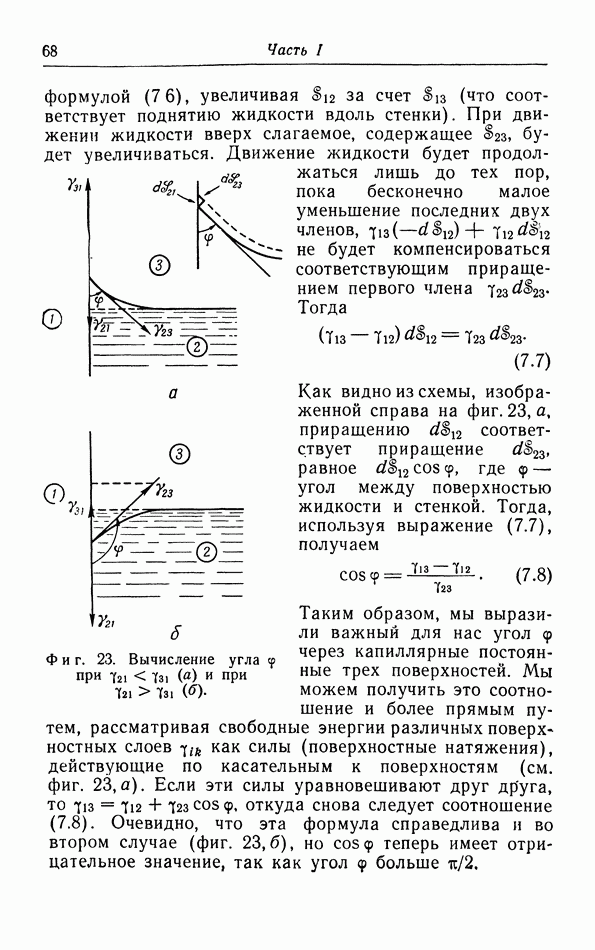
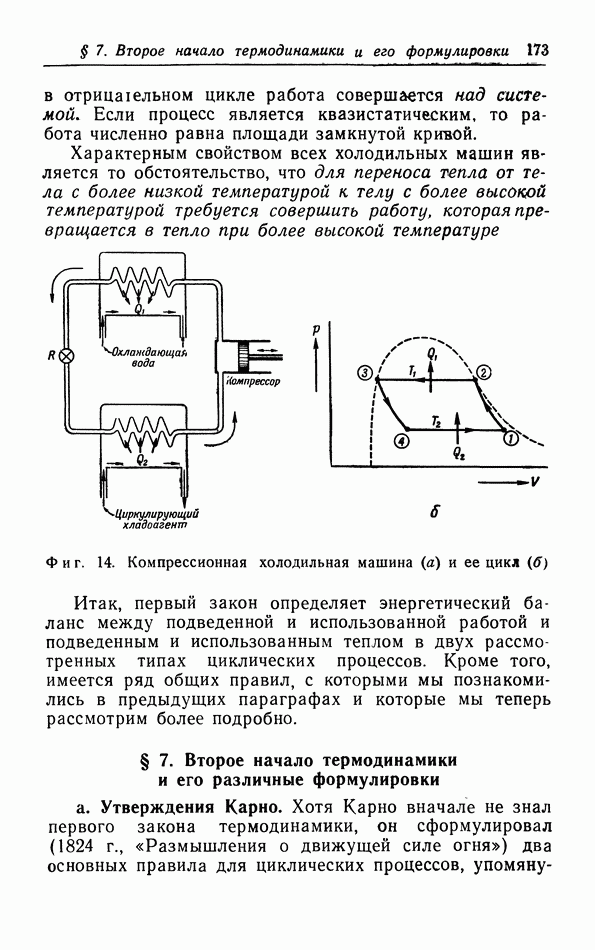
Фиг. 8. Внешняя работа, совершаемая во время адиабатического расширения газа.

Фиг. 7. Схема, поясняющая кинетическое рассмотрение падения температуры при адиабатическом расширении.
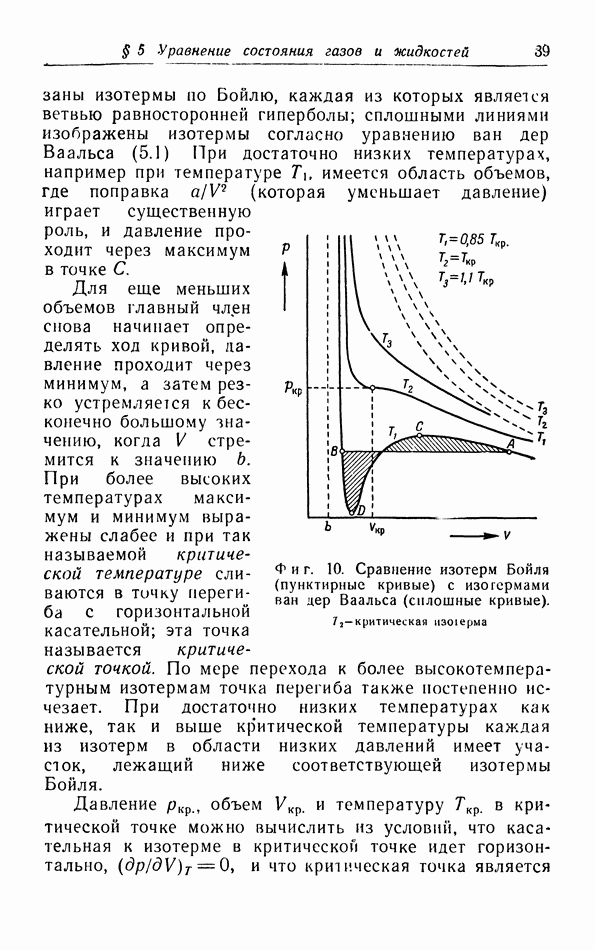
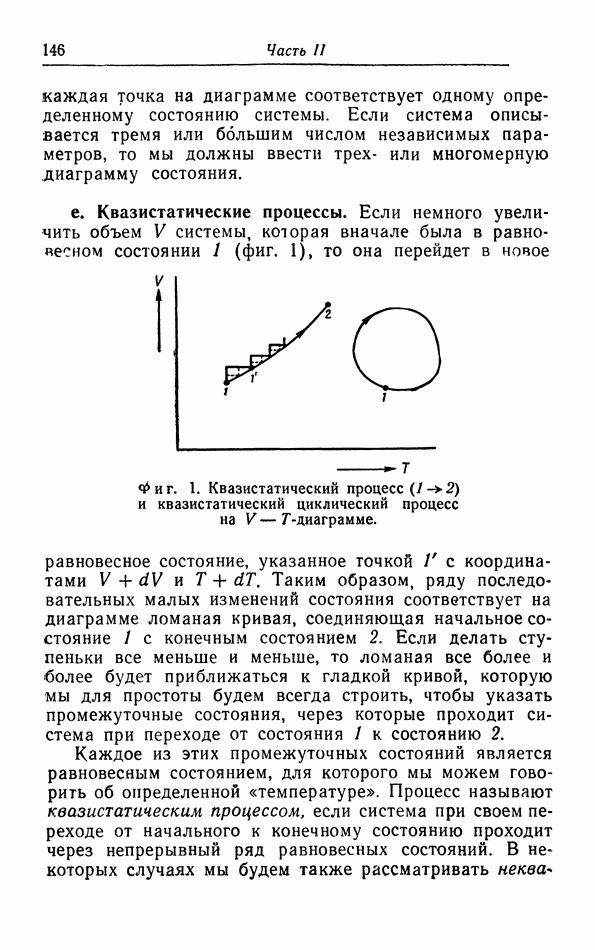
На  -диаграмме (фиг. 8) адиабатический процесс сжатия газа от начального состояния 1 изображается кривой, «адиабатой», которая пересекает изотермы, соответствующие все более высоким температурам, поскольку при адиабатическом сжатии температура газа повышается. Итак, адиабата растет круче, чем изотерма. Исходя из различных начальных состояний, мы можем построить целый ряд, т. е. «семейство», таких адиабат, которые покрывают плоскость, как и изотермы (см. фиг. 18, а). Эти адиабаты никогда не пересекаются, так как в противном случае мы могли бы начать от точки пересечения двух адиабат и провести адиабатическое сжатие двумя различными путями.
-диаграмме (фиг. 8) адиабатический процесс сжатия газа от начального состояния 1 изображается кривой, «адиабатой», которая пересекает изотермы, соответствующие все более высоким температурам, поскольку при адиабатическом сжатии температура газа повышается. Итак, адиабата растет круче, чем изотерма. Исходя из различных начальных состояний, мы можем построить целый ряд, т. е. «семейство», таких адиабат, которые покрывают плоскость, как и изотермы (см. фиг. 18, а). Эти адиабаты никогда не пересекаются, так как в противном случае мы могли бы начать от точки пересечения двух адиабат и провести адиабатическое сжатие двумя различными путями.
Работа, которую нужно произвести во время сжатия, равна, очевидно, заштрихованной плопдади на фиг. 8
(см. § 2). Когда газ сжимают, эту работу надо считать отрицательной, так как в этом случае совершаемая системой работа отрицательна.
Температура газа, который расширяется адиабатически, совершая внешнюю работу, понижается. В отличие от процесса Джоуля — Томсона этот процесс дает квазистатический обратимый метод получения низких Температур (см. § 10).
Вычитая  из обеих частей уравнения (5.9), получаем, поскольку
из обеих частей уравнения (5.9), получаем, поскольку 

Если мы рассматриваем однородную изотропную систему, описываемую двумя параметрами  и V, то совершенная при адиабатическом изобарическом процессе работа равна
и V, то совершенная при адиабатическом изобарическом процессе работа равна  откуда следует, что при адиабатическом изобарическом процессе энтальпия остается постоянной.
откуда следует, что при адиабатическом изобарическом процессе энтальпия остается постоянной.

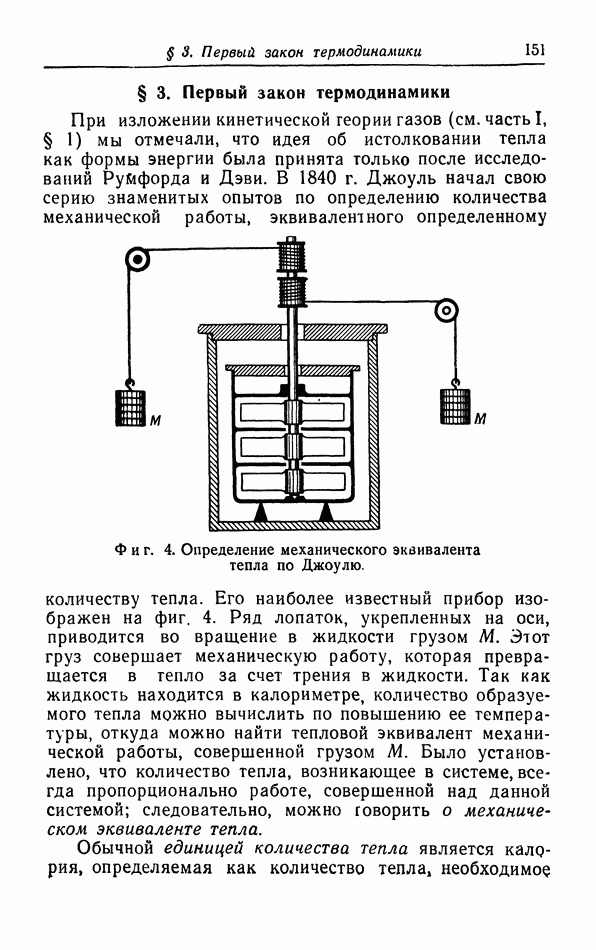
Фиг. 9. Схема, поясняющая работу газового компрессора.
Если система находится во внешнем электрическом или магнитном поле, то наряду с механической работой  приобретает также значение электрическая или магнитная работа. Тогда из уравнения (5.10) следует: работа, совершенная системой при адиабатическом изобарическом процессе, минус механическая работа равна уменьшению энтальпии.
приобретает также значение электрическая или магнитная работа. Тогда из уравнения (5.10) следует: работа, совершенная системой при адиабатическом изобарическом процессе, минус механическая работа равна уменьшению энтальпии.
В технических приложениях наряду с истинной работой сжатия, для которой также справедливо уравнение (5.9), поскольку сжатие происходит практически адиабатически, существенную роль играют и другие величины. Газовый компрессор не только сжимает газ от начального давления  до конечного давления
до конечного давления  но и
но и
засасывает газ  цилиндр через клапан 1 и выталкивает этот газ через клапан 2 (фиг. 9). Когда поршень идет вверх, клапан 1 открывается и газ заполняет цилиндр до начального объема
цилиндр через клапан 1 и выталкивает этот газ через клапан 2 (фиг. 9). Когда поршень идет вверх, клапан 1 открывается и газ заполняет цилиндр до начального объема  так что выполненная поршнем работа равна
так что выполненная поршнем работа равна  Затем газ сжимается до объема
Затем газ сжимается до объема  соответствующего давлению
соответствующего давлению  (работа сжатия
(работа сжатия  клапан 2 открывается и газ выталкивается из остающегося объема
клапан 2 открывается и газ выталкивается из остающегося объема  цилиндра при постоянном давлении
цилиндра при постоянном давлении  таким образом, поршень совершает работу
таким образом, поршень совершает работу  Произведенная над газом работа при возвратно-поступательном движении поршня равна
Произведенная над газом работа при возвратно-поступательном движении поршня равна

Рассматривая площади  на
на  -диаграмме, мы видим, что левая часть этого уравнения равна
-диаграмме, мы видим, что левая часть этого уравнения равна  откуда
откуда

Величина  называется «технической работой»; таким образом, уравнение (5.11) показывает, что техническая работа, совершенная газом, равна уменьшению энтальпии. Вот почему энтальпия имеет столь важное значение в компрессорной технике. Приведем следующий пример: для адиабатического сжатия азота от 100 до 200 атм при 20° С требуется совершить работу сжатия, равную 224 кал/моль в то время как техническая работа составляет 384 кал/моль.
называется «технической работой»; таким образом, уравнение (5.11) показывает, что техническая работа, совершенная газом, равна уменьшению энтальпии. Вот почему энтальпия имеет столь важное значение в компрессорной технике. Приведем следующий пример: для адиабатического сжатия азота от 100 до 200 атм при 20° С требуется совершить работу сжатия, равную 224 кал/моль в то время как техническая работа составляет 384 кал/моль.
г. Магнитные системы.
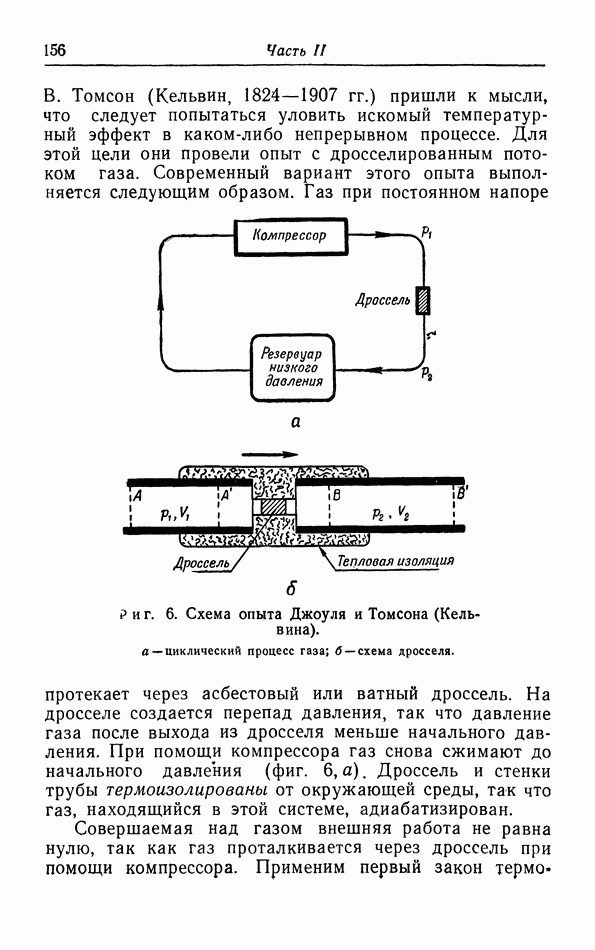
Теперь остановимся более подробно на приложениях первого закона к магнитным системам. Рассмотрим некоторое количество вещества объемом  помещенное в поле кольцевого соленоида (фиг. 10). Мы можем вызвать небольшое изменсг
помещенное в поле кольцевого соленоида (фиг. 10). Мы можем вызвать небольшое изменсг
ние состояния той системы, слегка увеличив ток  в соленоиде. При этом изменении намагниченность
в соленоиде. При этом изменении намагниченность  вещества внутри соленоида немного увеличится, что приведет к возникновению электродвижущей силы равной скорости изменения магнитного потока через соленоид:
вещества внутри соленоида немного увеличится, что приведет к возникновению электродвижущей силы равной скорости изменения магнитного потока через соленоид:  Эта
Эта  должна быть преодолена батареей; таким образом, совершенная за время
должна быть преодолена батареей; таким образом, совершенная за время  работа над системой (соленоид + магнитный материал) равна
работа над системой (соленоид + магнитный материал) равна  . К этому нужно прибавить некоторое количество тепла
. К этому нужно прибавить некоторое количество тепла  вследствие чего первый закон примет вид
вследствие чего первый закон примет вид

Левая часть этого уравнения представляет увеличение энергии системы (соленоид  магнитный материал). Эта энергия складывается из 1) суммы и энергии магнитного материала и энергии взаимодействия материала с полем соленоида, 2) энергии поля
магнитный материал). Эта энергия складывается из 1) суммы и энергии магнитного материала и энергии взаимодействия материала с полем соленоида, 2) энергии поля  которая имеется и в том случае, когда тот же ток
которая имеется и в том случае, когда тот же ток  протекает через соленоид в отсутствие магнитного материала. [В уравнении (5.12) мы пренебрегаем подводимой электрической энергией
протекает через соленоид в отсутствие магнитного материала. [В уравнении (5.12) мы пренебрегаем подводимой электрической энергией  которая полностью превращается в джоулево тепло, так как предполагаем, что это тепло непрерывно удаляется из системы и, следовательно, его не нужно учитывать.]
которая полностью превращается в джоулево тепло, так как предполагаем, что это тепло непрерывно удаляется из системы и, следовательно, его не нужно учитывать.]
Если  площадь поперечного сечения соленоида длиной
площадь поперечного сечения соленоида длиной  полное число его витков, то увеличение магнитного потока
полное число его витков, то увеличение магнитного потока  которое ответственно за наведенную
которое ответственно за наведенную  равно
равно  где В — магнитная индукция, так что
где В — магнитная индукция, так что

Далее, намагничивающее поле  или
или  откуда для изотропного вещества
откуда для изотропного вещества


Фиг. 10. Магнитное вещество в поле соленоида.
Первое слагаемое в правой части уравнения (5.13) есть увеличение энергии поля соленоида  равно
равно  Подставляя (5.13) в первый закон, записанный в виде (5.12), получаем следующую форму этого закона:
Подставляя (5.13) в первый закон, записанный в виде (5.12), получаем следующую форму этого закона:

Уравнение (5.14) относится к единице объема, что обычно молчаливо предполагается. Сравнивая уравнение (5.14) с первым законом для однородной изотропной системы

мы увидим, что для магнитной системы  играет роль интенсивного,
играет роль интенсивного,  экстенсивного параметра.
экстенсивного параметра.

Фиг. 11. Магнитное вещество в поле постоянного магнита.
Этот выбор не свободен от неоднозначности, в чем легко убедиться, если вместо магнитного материала в кольцевом соленоиде мы рассмотрим небольшое количество вещества в поле постоянного магнита (фиг. 11). Мы можем несколько увеличить намагниченность вещества, сместив его в направлении к магниту. Так как вещество подвергается действию силы  в направлении градиента
в направлении градиента  поля в месте нахождения вещества, совершенное при этом смещении (отрицательное) количество работы равно
поля в месте нахождения вещества, совершенное при этом смещении (отрицательное) количество работы равно  Если энергию системы (вещество
Если энергию системы (вещество  постоянный магнит) обозначить через то первый закон запишется в виде
постоянный магнит) обозначить через то первый закон запишется в виде

откуда видно, что  обменялись своими ролями интенсивного и экстенсивного параметра.
обменялись своими ролями интенсивного и экстенсивного параметра.
Различи между  и (5.15) нужно, конечно, отнести за счет различного смысла величин
и (5.15) нужно, конечно, отнести за счет различного смысла величин  т. е.
т. е.
связано с тем, какую из них мы считаем описывающей нашу «систему».
Это можно пояснить при помощи следующего мысленного опыта, предложенного Беккером: мы могли бы устранить взаимодействие с окружающими приборами, если бы сумели зафиксировать значение намагниченности после ее изменения. Тогда мы смогли бы удалить соленоид или магнит, не нарушая намагниченности вещества. Представим себе, например, что мы имеем возможность «заморозить» магнитное состояние системы, например, посредством фиксирования элементарных магнитиков в тех положениях, которые они займут при намагничивании.
Рассмотрим первый пример. Когда мы увеличиваем поле внутри соленоида от 0 до  на каждую единицу объема приходится работа, равная, согласно уравнению (5.13),
на каждую единицу объема приходится работа, равная, согласно уравнению (5.13),

Теперь заморозим намагниченность и будем уменьшать ток до нуля. Наведенная при этой операции э. д. с. равна

так как намагниченность  является постоянной. Таким образом мы выигрываем работу в количестве
является постоянной. Таким образом мы выигрываем работу в количестве  окончательная работа намагничивания будет составлять
окончательная работа намагничивания будет составлять

Теперь рассмотрим второй пример. При перемещении некоторого количества вещества из бесконечности в точку, где поле магнита равно  мы совершаем работу
мы совершаем работу

Заморозим снова намагниченность вещества и будем удалять магнит в бесконечность. Потенциальная энергия вещества в поле магнита равна  следовательно, при удалении магнита будет произведена работа
следовательно, при удалении магнита будет произведена работа  Таким образом, полное количество совершенной работы равно
Таким образом, полное количество совершенной работы равно

Таким образом мы получили одинаковые выражения (5.16) и (5.17) для работы  . В термодинамике первый закон обычно записывается в форме (5.12).
. В термодинамике первый закон обычно записывается в форме (5.12).
Очевидно, что мы можем ввести магнитную энтальпию, определенную выражением

Знак минус появился здесь потому, что парой параметров являются  Теперь мы можем преобразовать выражения (5.14) и (5.15) одно в другое при помощи определения (5.18).
Теперь мы можем преобразовать выражения (5.14) и (5.15) одно в другое при помощи определения (5.18).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
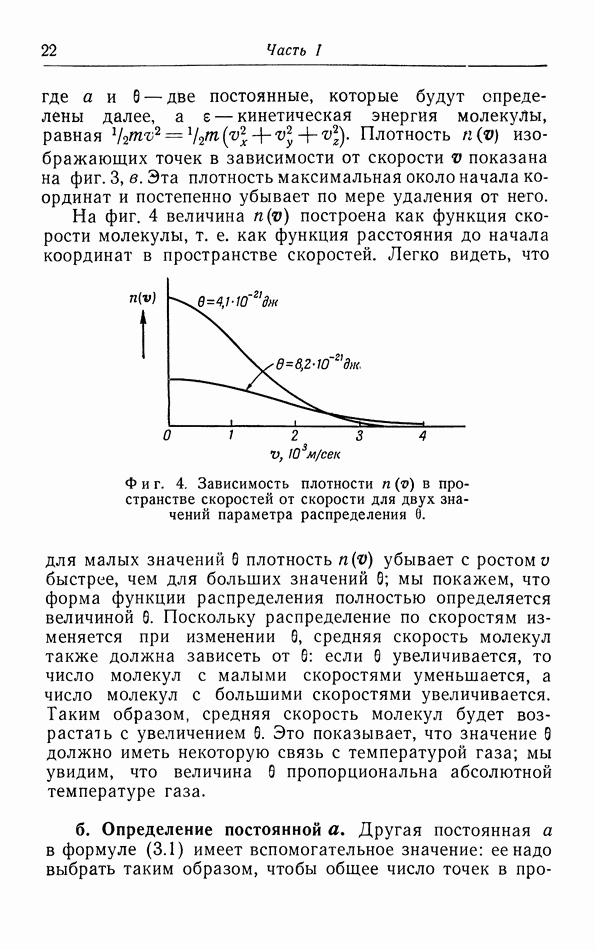
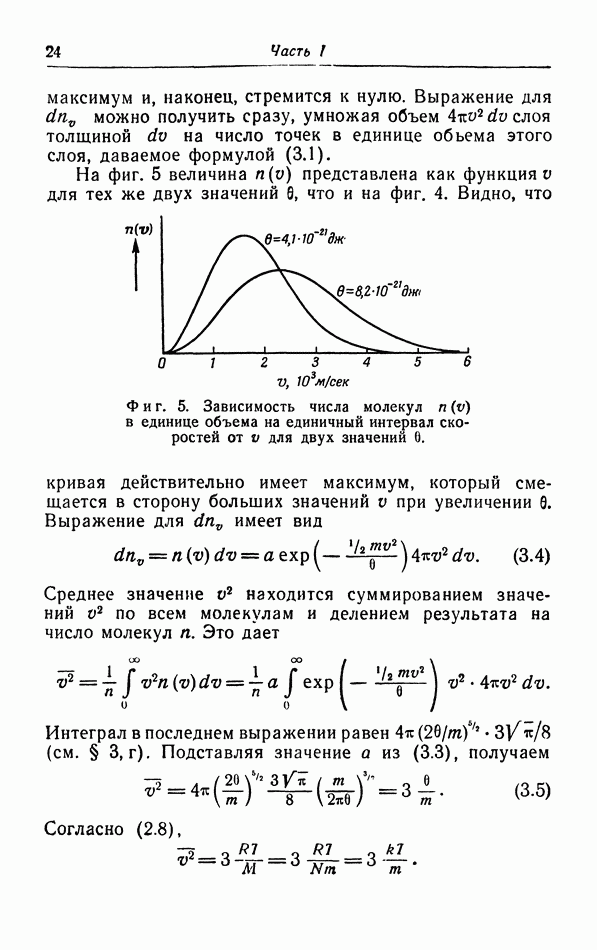
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
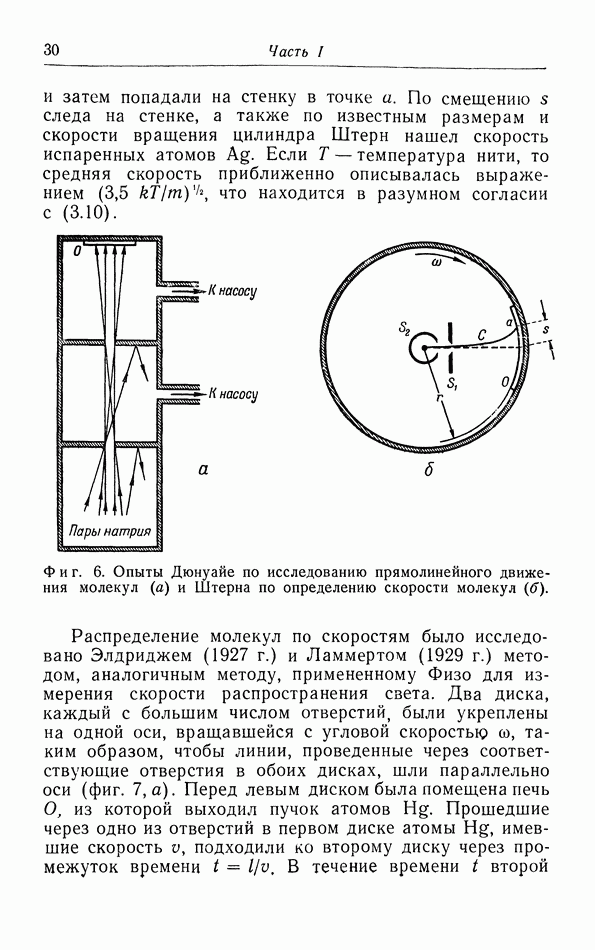
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
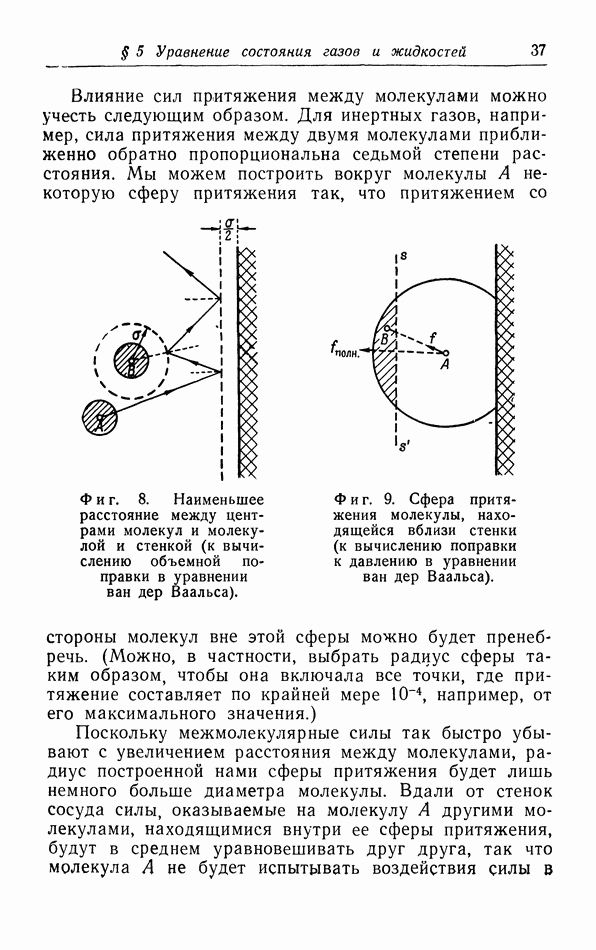
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
- б. Жидкие пленки.
- в. Капиллярное поднятие и понижение уровня жидкости.
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
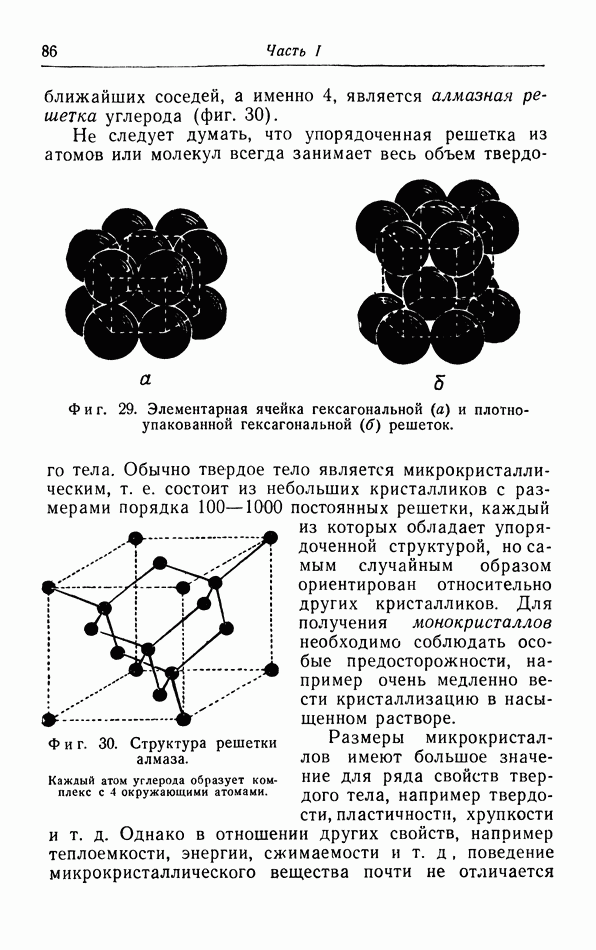
- § 9. Структура твердых тел
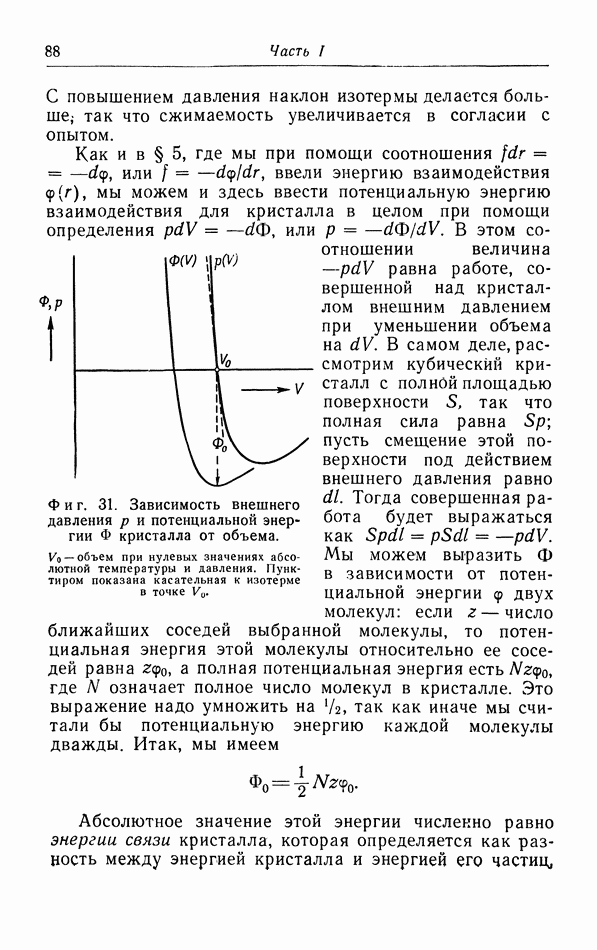
- § 10. Уравнение состояния твердых тел
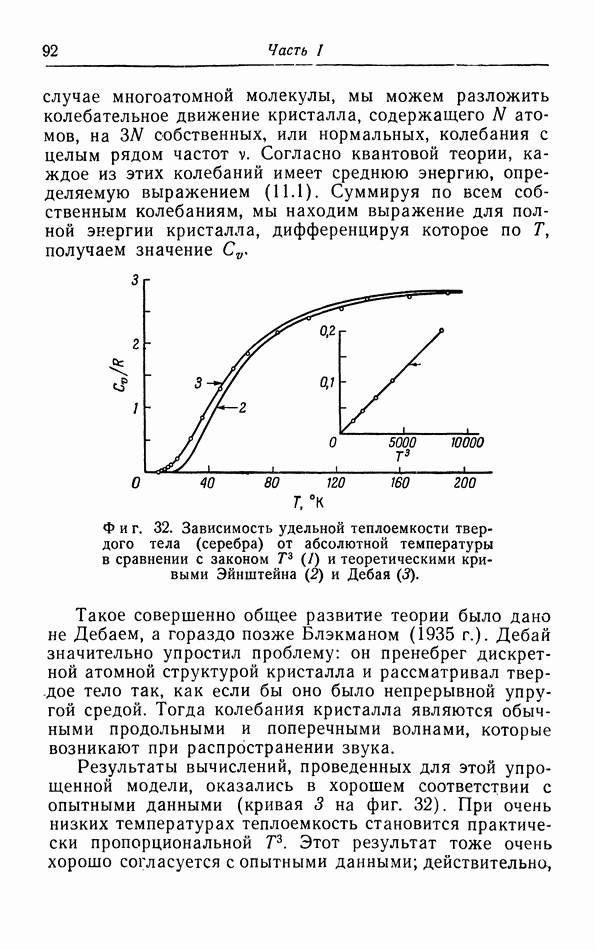
- § 11. Теплоемкость твердых тел
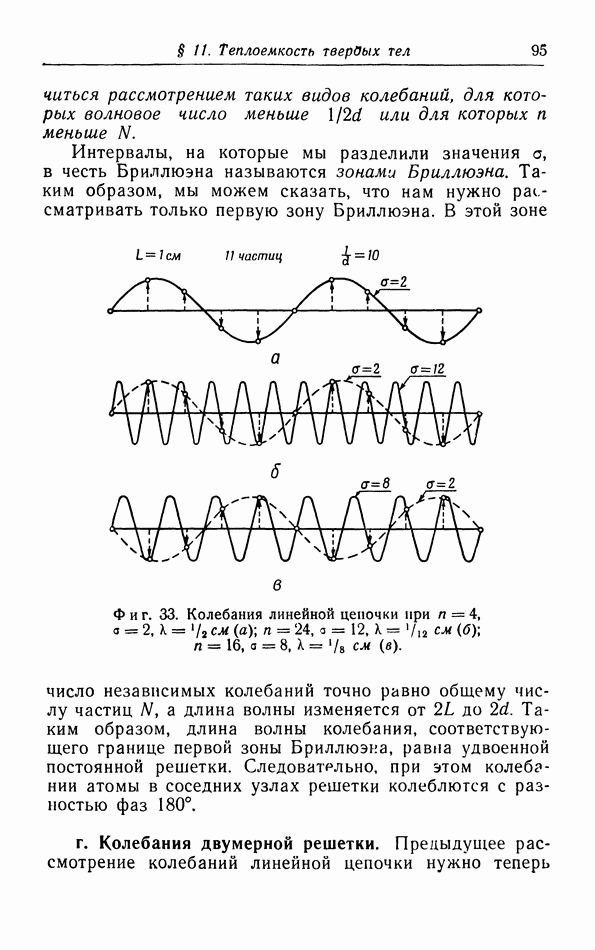
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
- § 3. Первый закон термодинамики
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
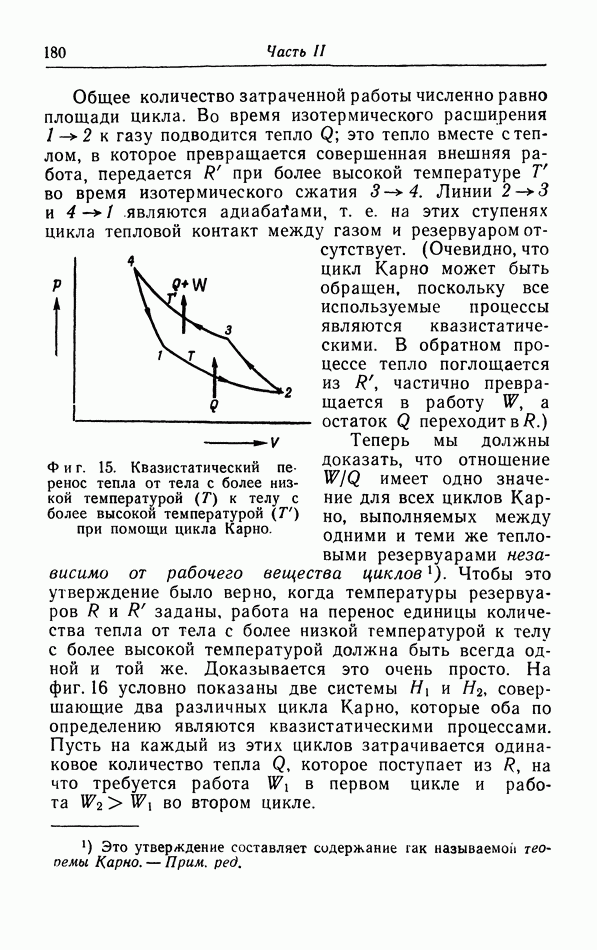
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
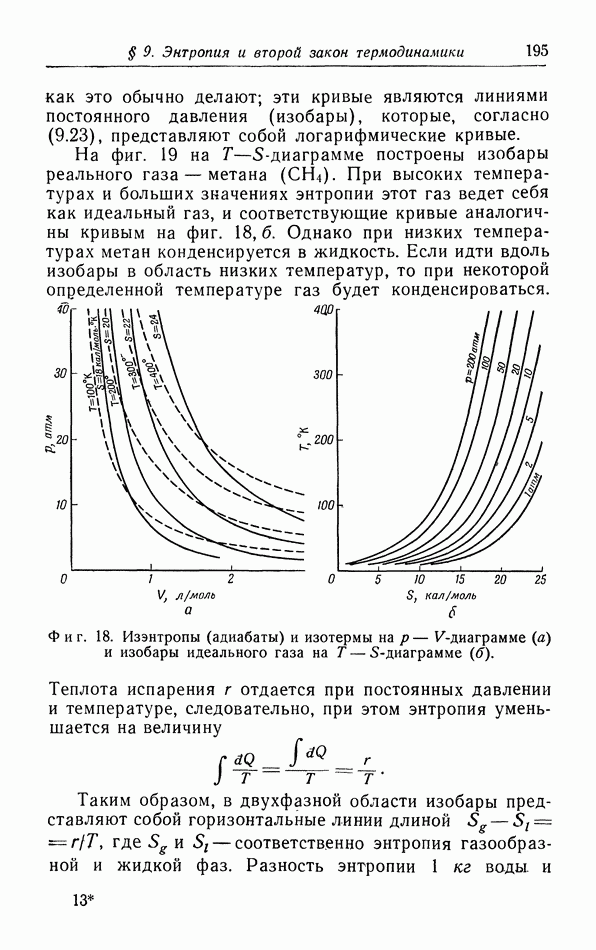
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
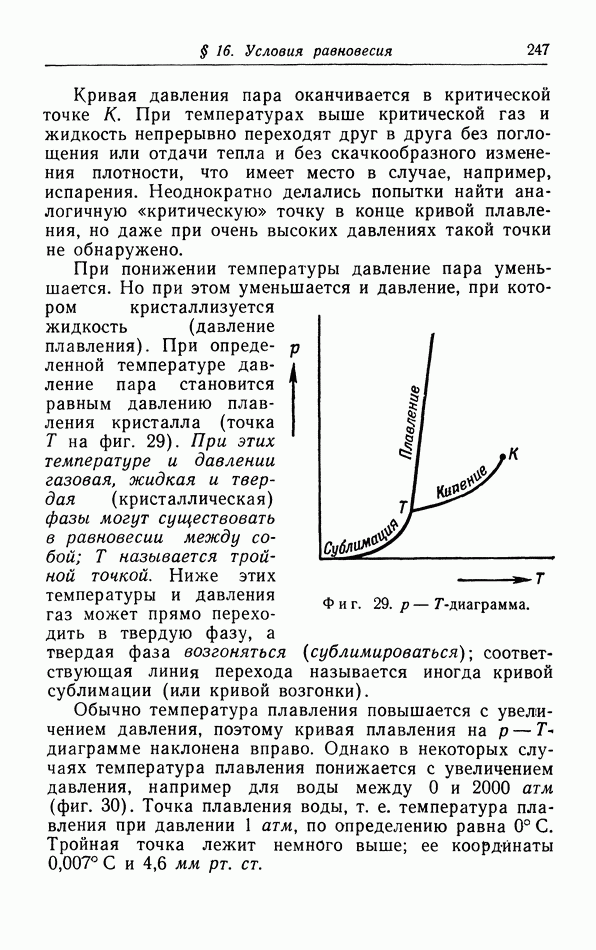
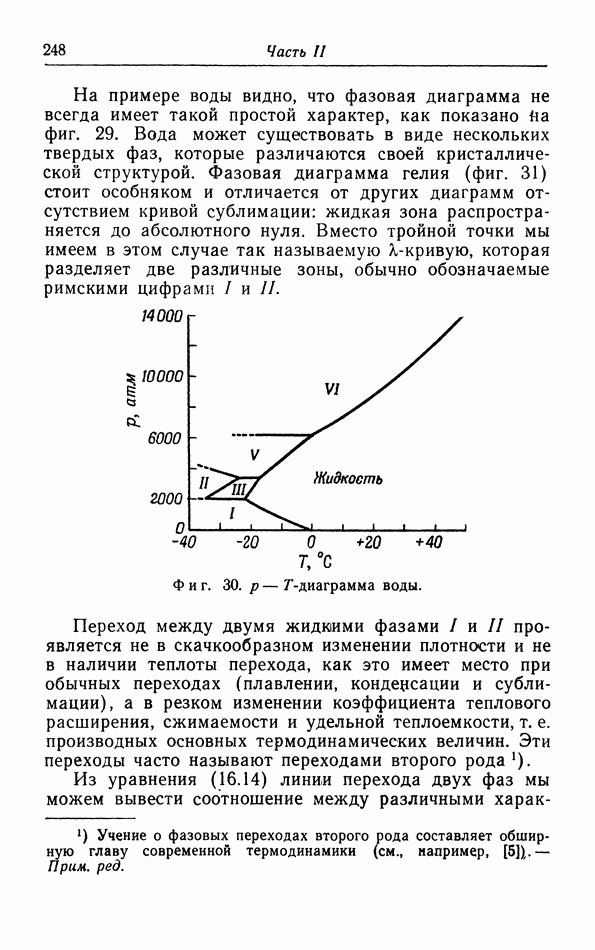
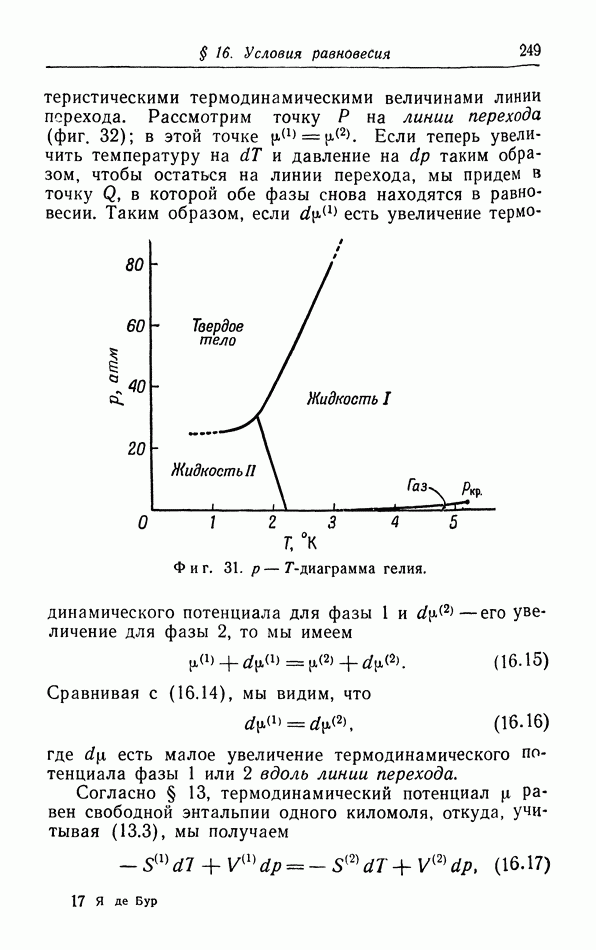
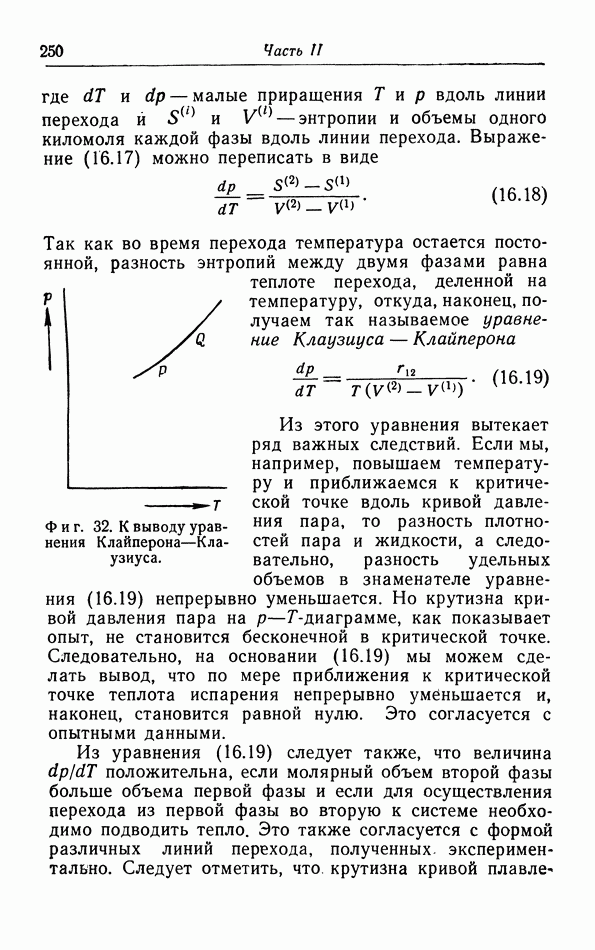
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам