| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Дальнейшие приложения первого закона
а. Подвод тепла при постоянном объеме или постоянном давлении газа.
Теперь выведем из первого закона ряд общих закономерностей и в процессе этого получим более ясное представление о свойствах новой функции, которую мы назвали энтальпией.
Когда тепло подводится к системе при постоянном объеме, внешняя работа равна нулю, откуда, согласно первому закону [см. (3.2) ],

Количество тепла, подведенное к системе при постоянном объеме, равно увеличению внутренней энергии данной системы.
Если же тепло подводится при постоянном давлении (изобарический процесс), то внешняя работа, совершаемая системой при увеличении объема от  до
до  равна
равна  откуда, согласно первому закону,
откуда, согласно первому закону,

Количество тепла, подведенное к системе при постоянном давлении, равно увеличению энтальпии данной системы. Изменение энтальпии в этом случае связано с тем, что теперь при подводе тепла система совершает внешнюю работу, в отличие от случая (5.1). Поскольку при выводе уравнений (5.1) и (5.2) не учитывалась природа процесса, оба результата справедливы как для квазистатических, так и для неквазистатических процессов.
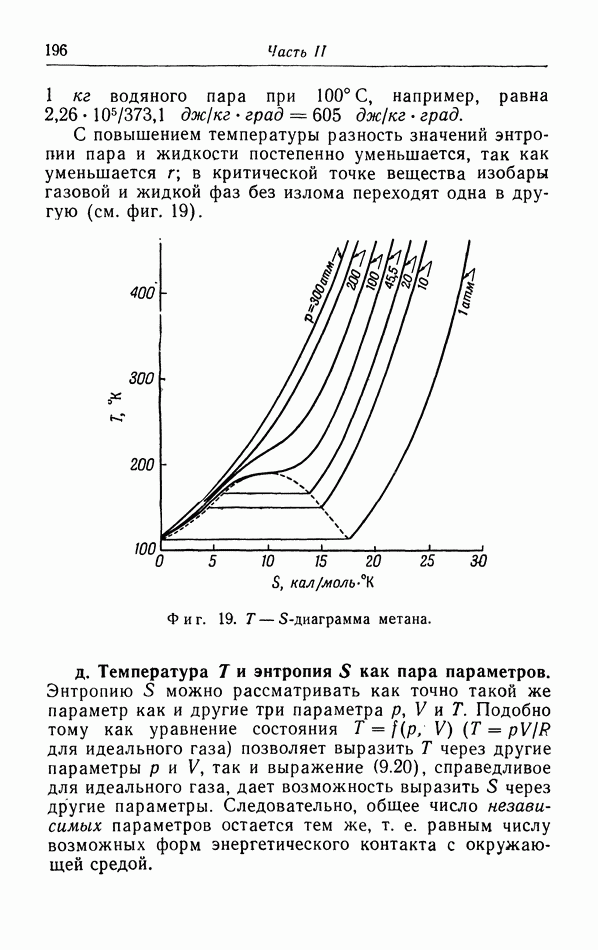
Пусть при испарении жидкости мы подводим тепло, причем над жидкостью все время остается насыщенный пар, давление которого определяется температурой жидкости.
Следовательно, теплота испарения, т. е. количество тепла, необходимое для испарения, скажем  равна разности энтальпий
равна разности энтальпий  жидкости и
жидкости и  пара. Для воды при 100° С теплота испарения составляет
пара. Для воды при 100° С теплота испарения составляет  Внешняя работа, совершаемая при этом испарении, будет
Внешняя работа, совершаемая при этом испарении, будет  следовательно, разность энергий жидкого и газового состояний равна
следовательно, разность энергий жидкого и газового состояний равна  . В процессе плавления увеличение объема, а значит и внешняя работа настолько малы, что теплота плавления, которая равна разности энтальпий жидкого и твердого состояний, практически оказывается равной разности энергий этих двух фаз.
. В процессе плавления увеличение объема, а значит и внешняя работа настолько малы, что теплота плавления, которая равна разности энтальпий жидкого и твердого состояний, практически оказывается равной разности энергий этих двух фаз.
Уравнения (5.1) и (5.2) находят важные применения в химии для определения теплового эффекта химических реакций. Еще в 1840 г. Гесс сформулировал следующий закон: полный тепловой эффект химической реакции не зависит от промежуточных состояний, через которые проходит система. Однако, это справедливо лишь в том случае, когда все реакции происходят или при постоянном давлении, или при постоянном объеме. Следовательно, на основании (5.1) и (5.2) мы можем утверждать, что в процессе перехода от вещества А к веществу  при котором имеется большое число промежуточных продуктов, алгебраическая сумма всех тепловых эффектов должна быть равна разности энергий или энтальпий веществ
при котором имеется большое число промежуточных продуктов, алгебраическая сумма всех тепловых эффектов должна быть равна разности энергий или энтальпий веществ  . В этом частном случае разность энтальпий зависит только от
. В этом частном случае разность энтальпий зависит только от  и не зависит от пути перехода между
и не зависит от пути перехода между 
Итак, мы видим, какое интересное применение получил здесь тот факт, что количество тепла, подводимое во время процессов, протекающих при постоянном давлении или при постоянном объеме, не зависит от пути перехода.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
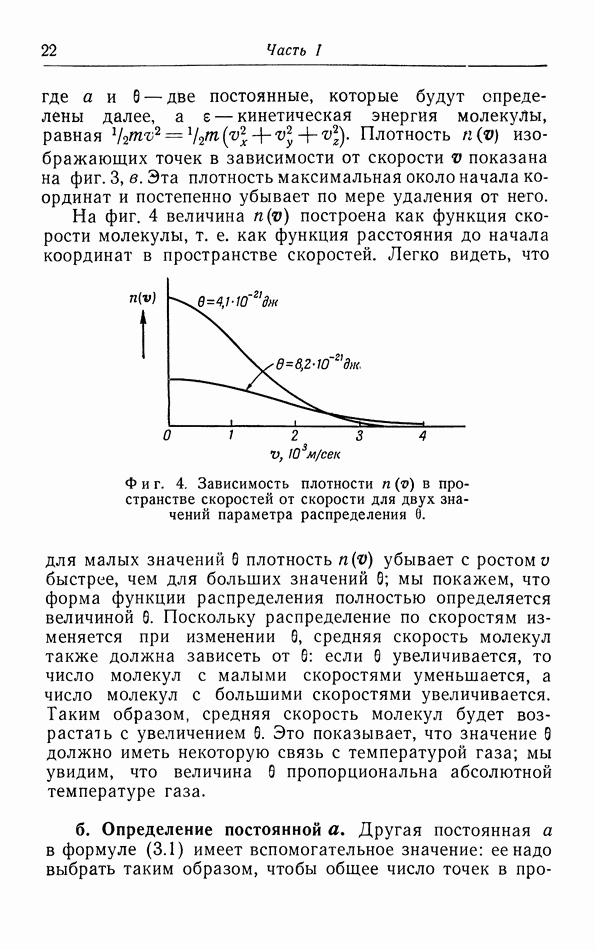
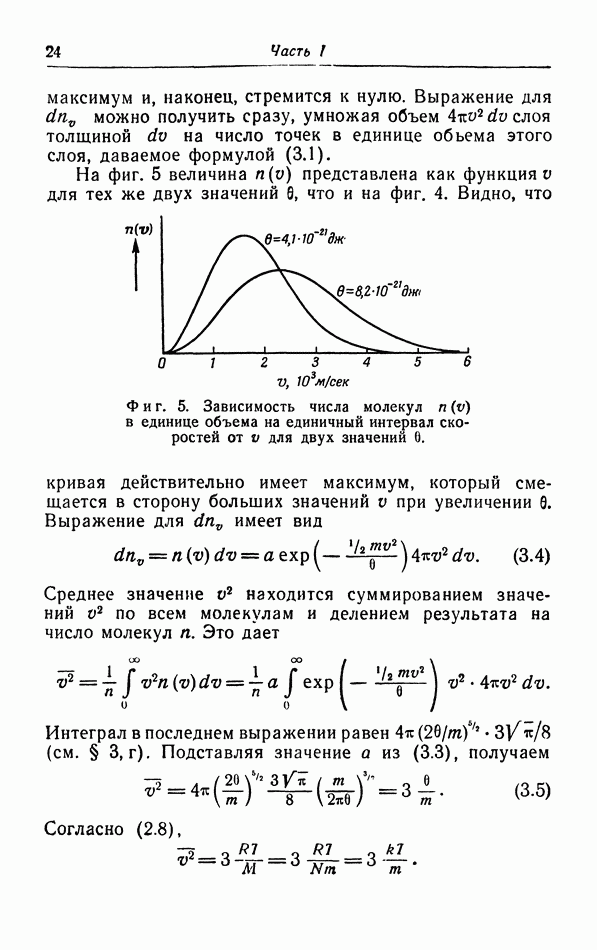
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
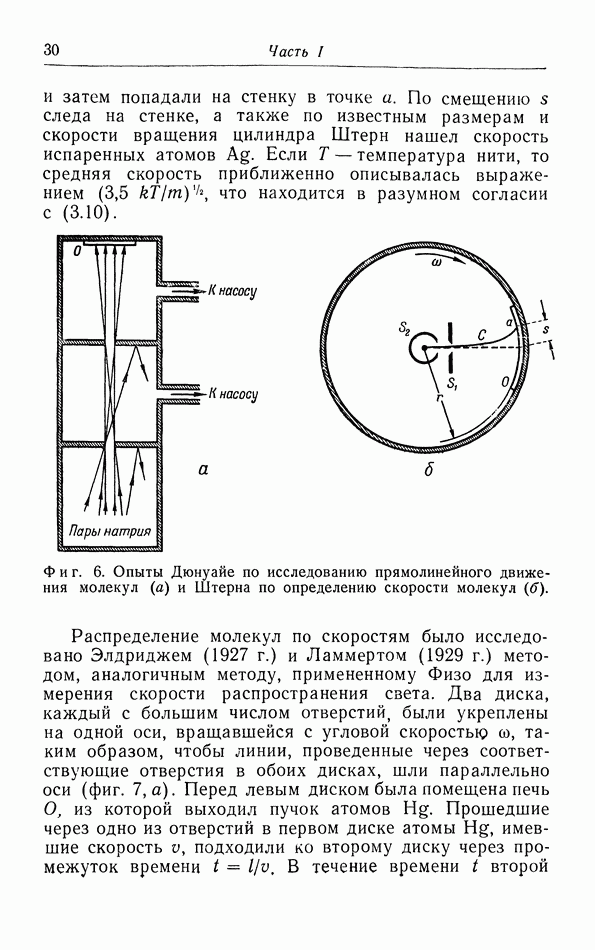
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
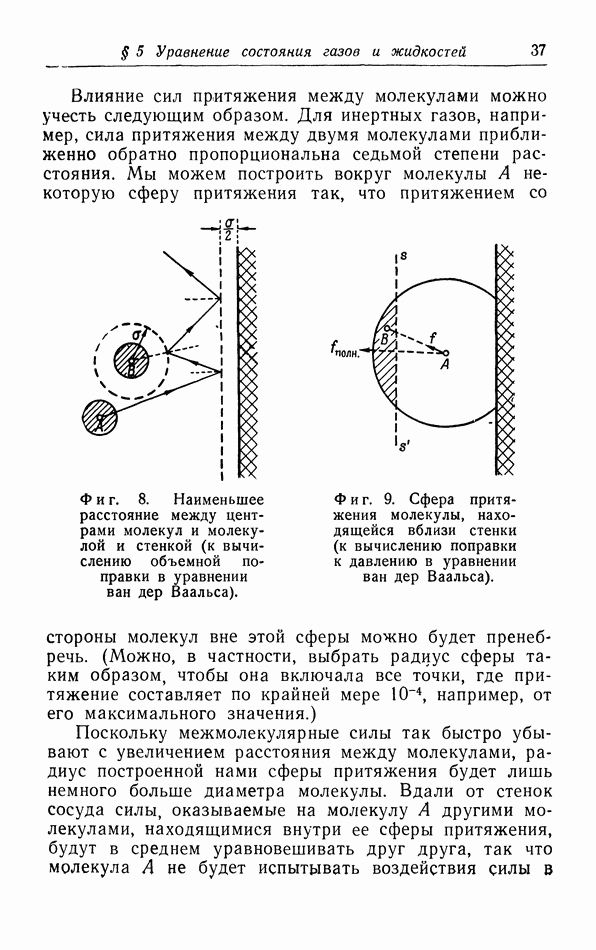
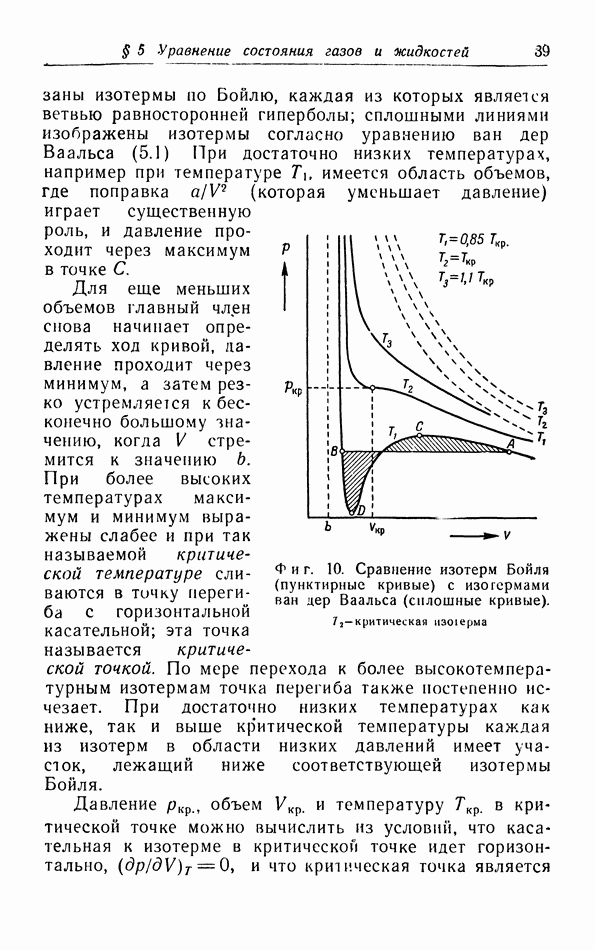
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
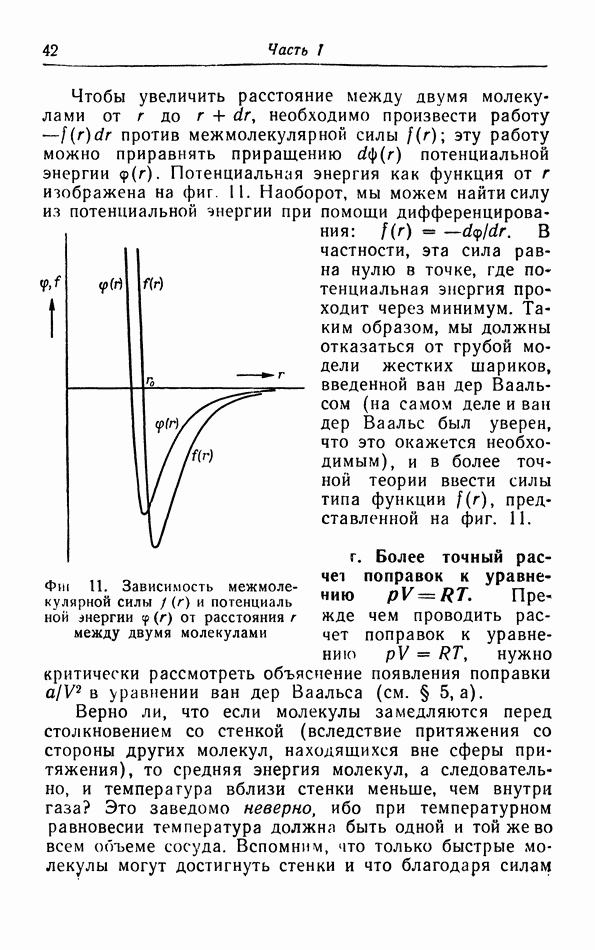
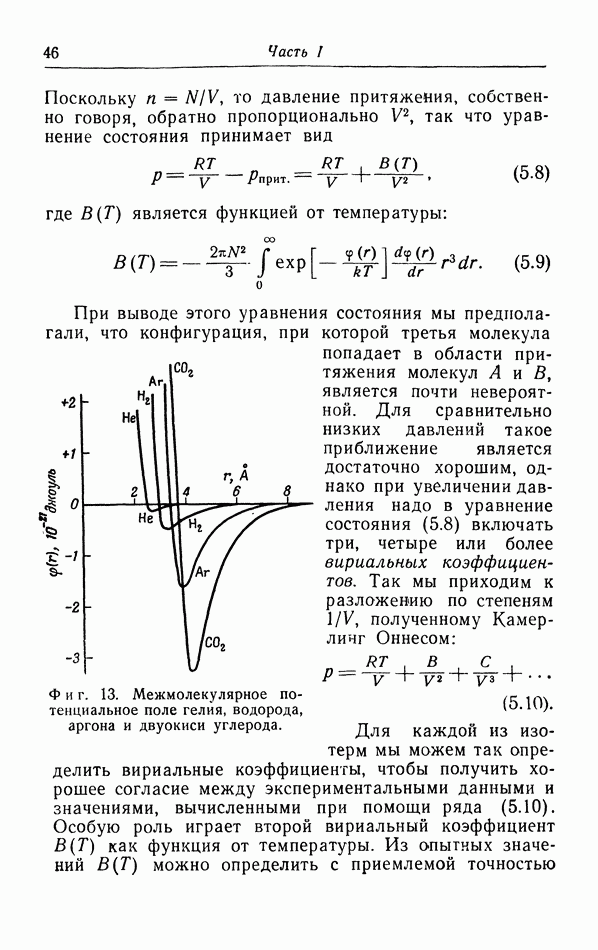
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
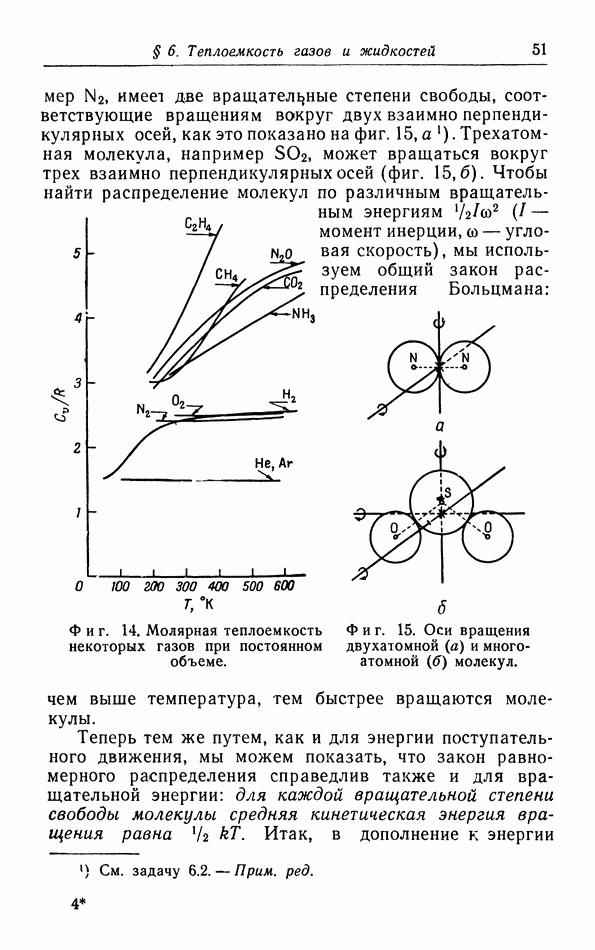
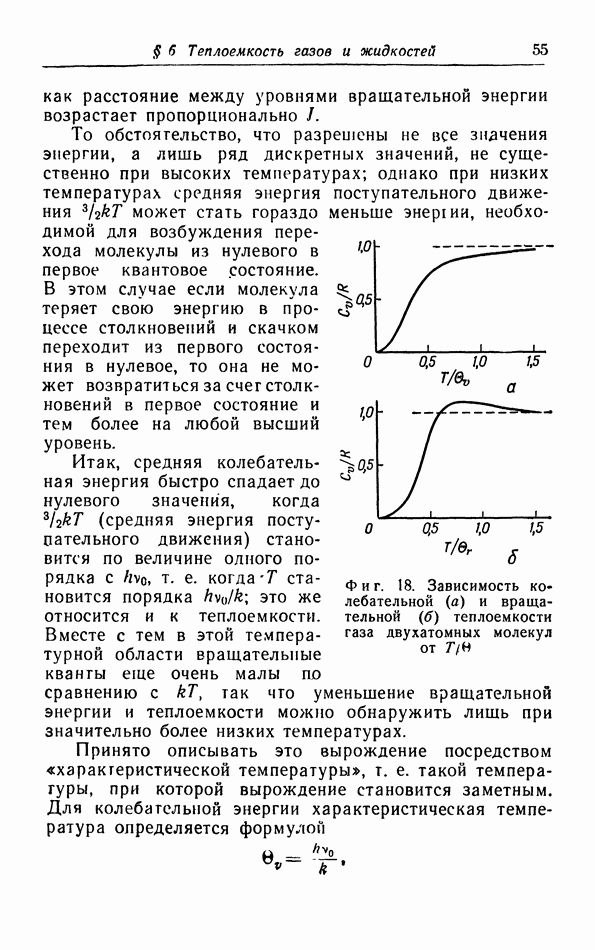
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
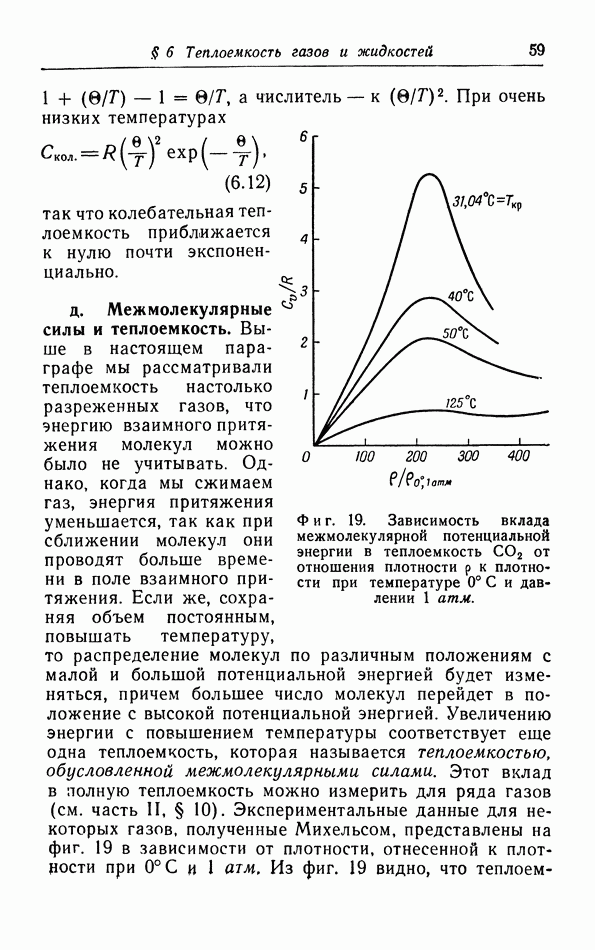
- д. Межмолекулярные силы и теплоемкость.
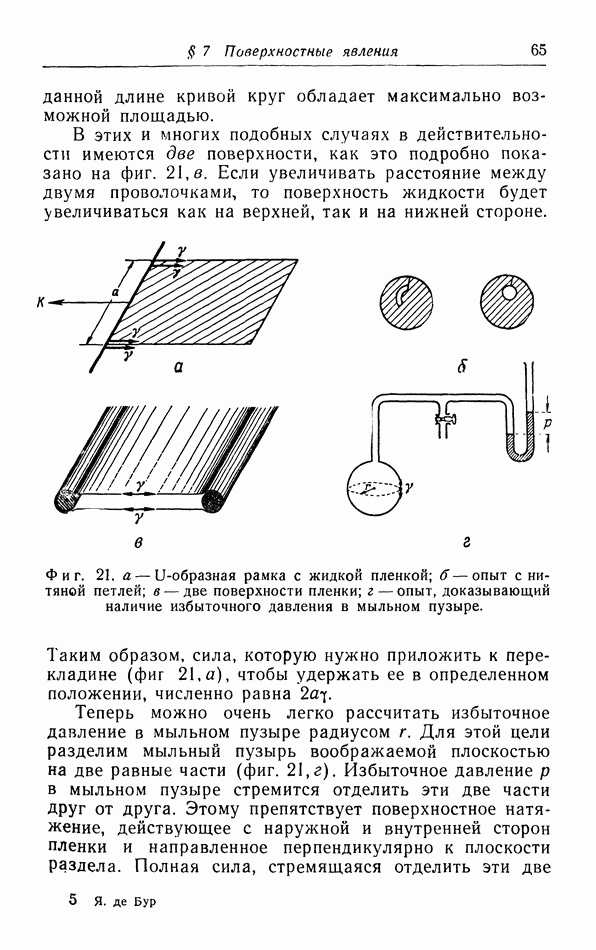
- § 7. Поверхностные явления
- б. Жидкие пленки.
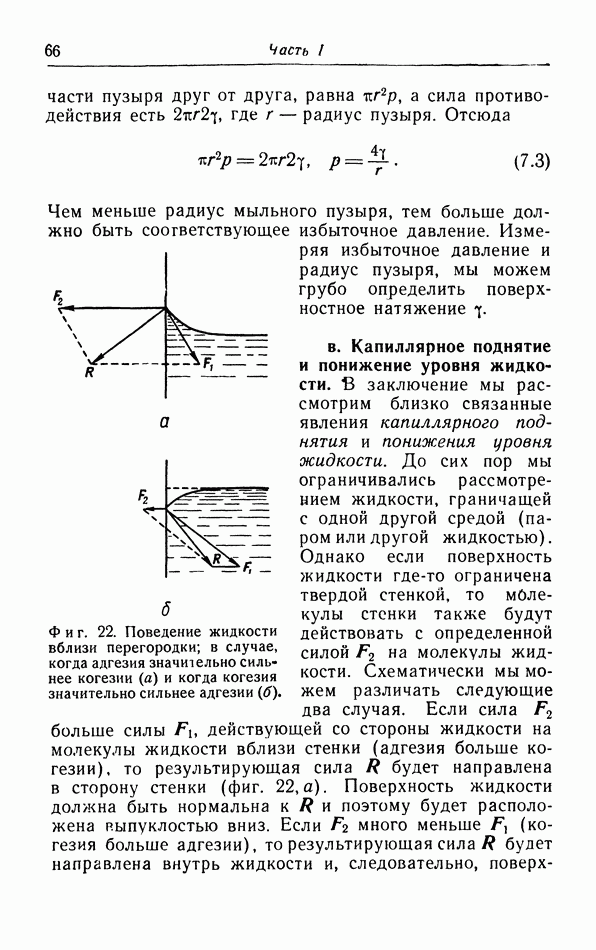
- в. Капиллярное поднятие и понижение уровня жидкости.
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
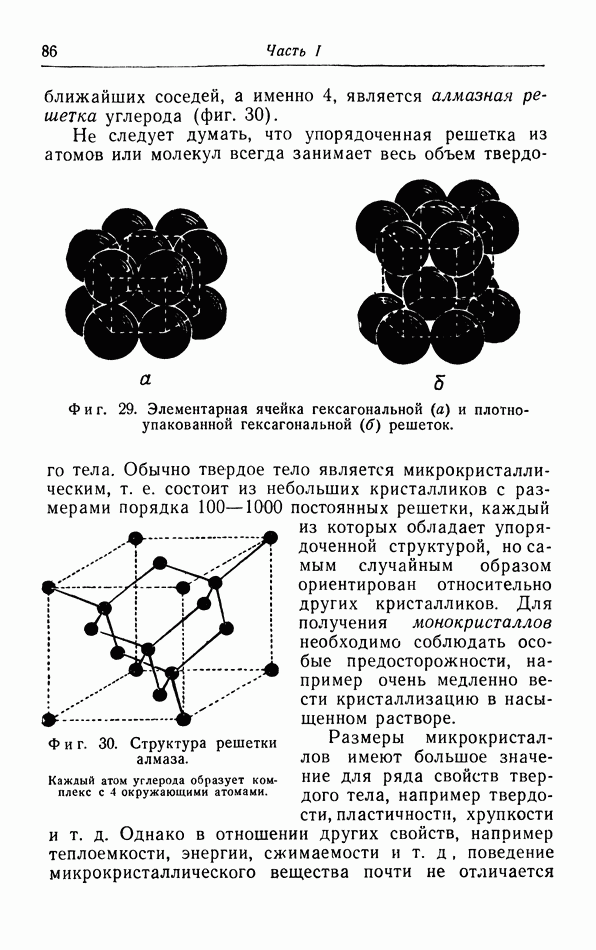
- § 9. Структура твердых тел
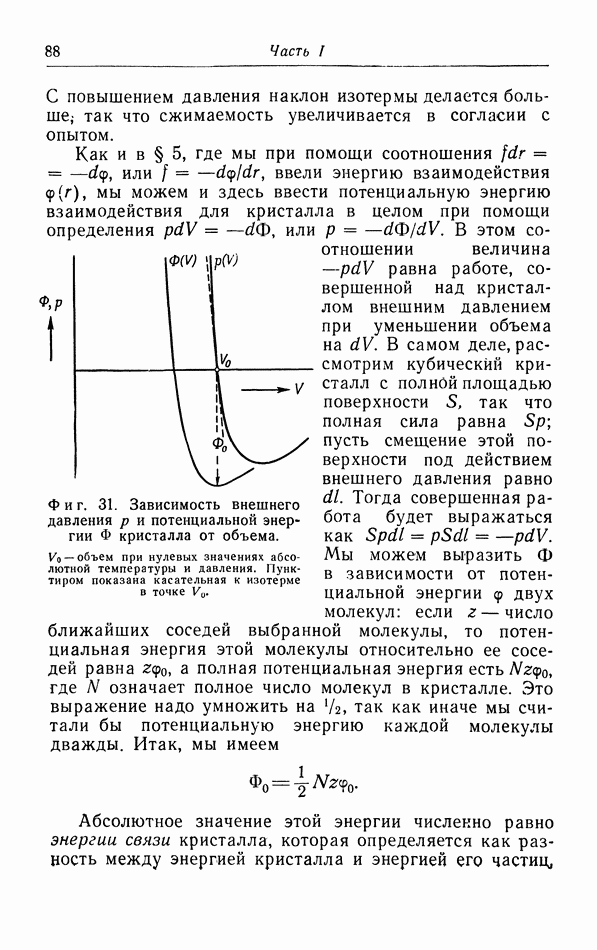
- § 10. Уравнение состояния твердых тел
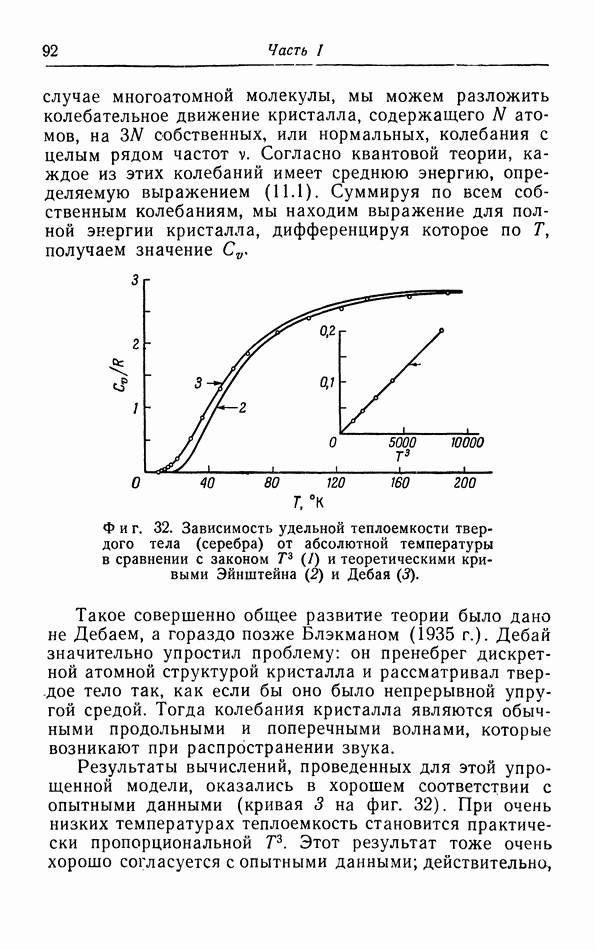
- § 11. Теплоемкость твердых тел
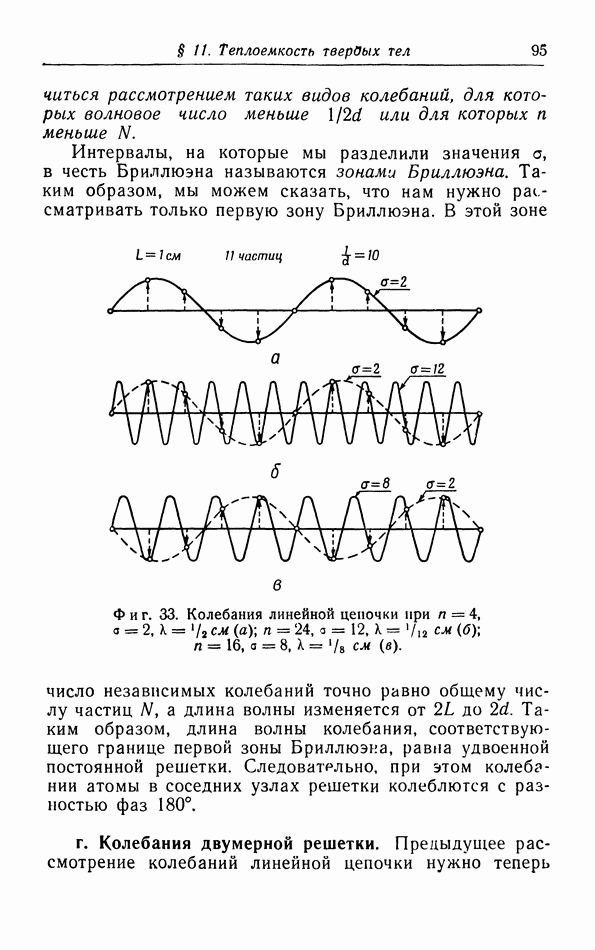
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
- § 3. Первый закон термодинамики
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
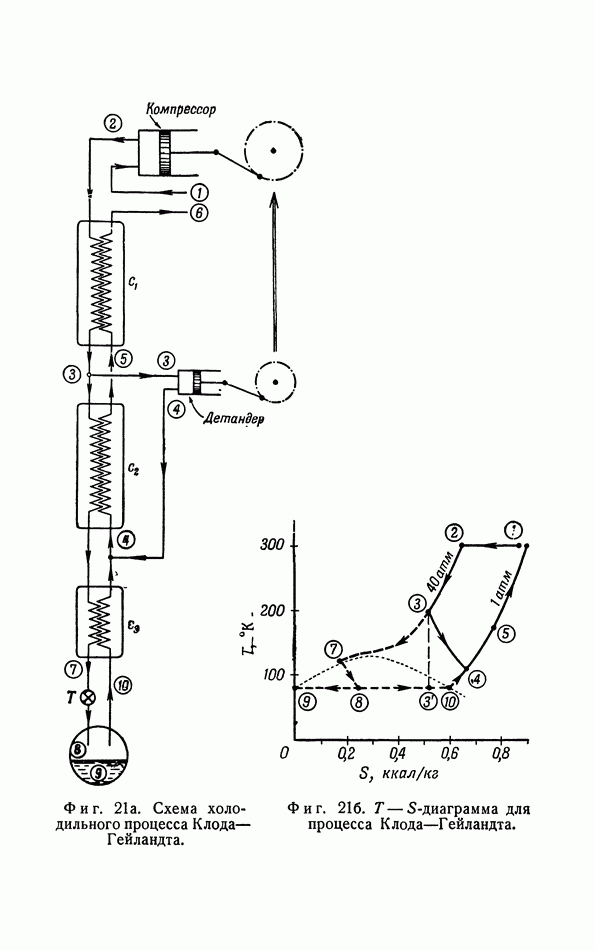
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
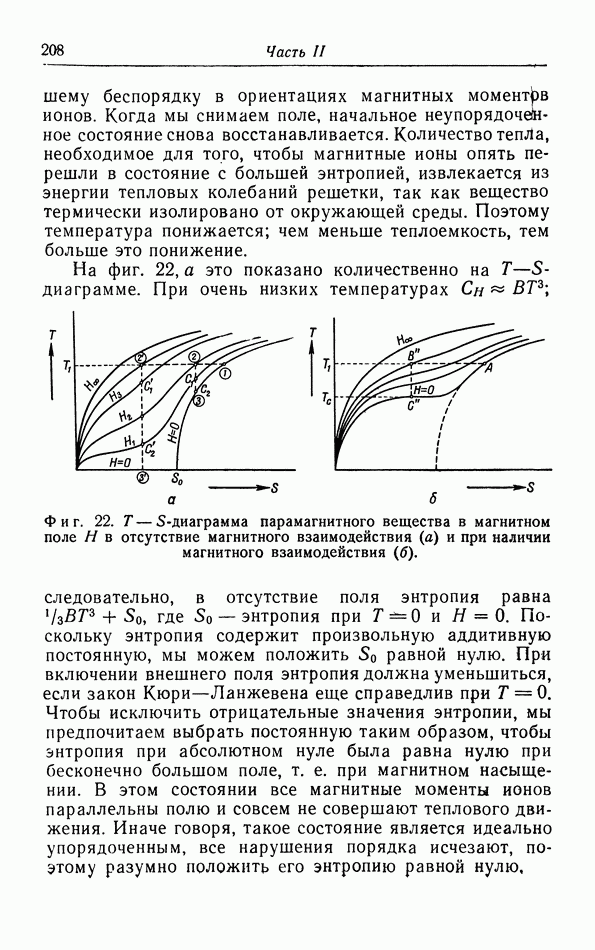
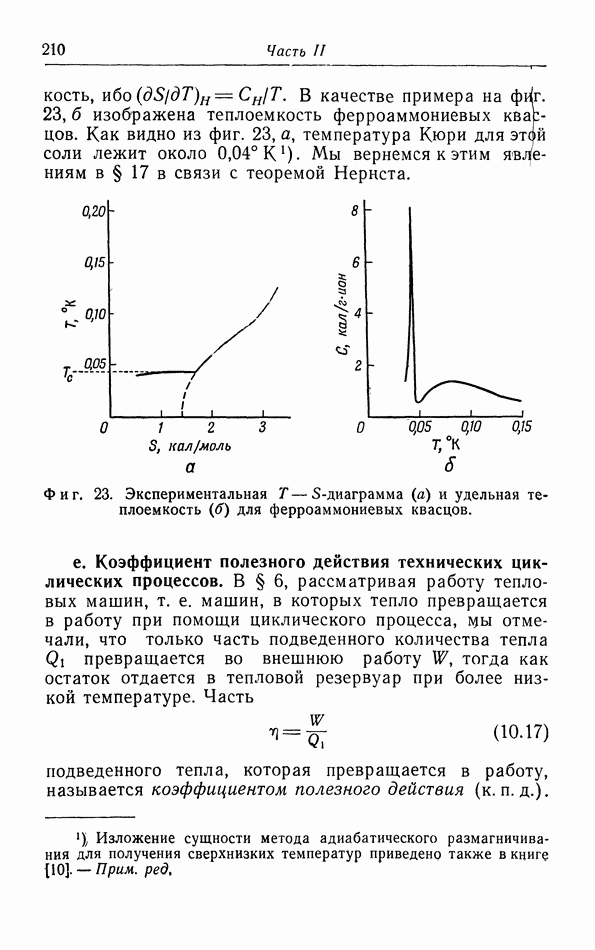
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
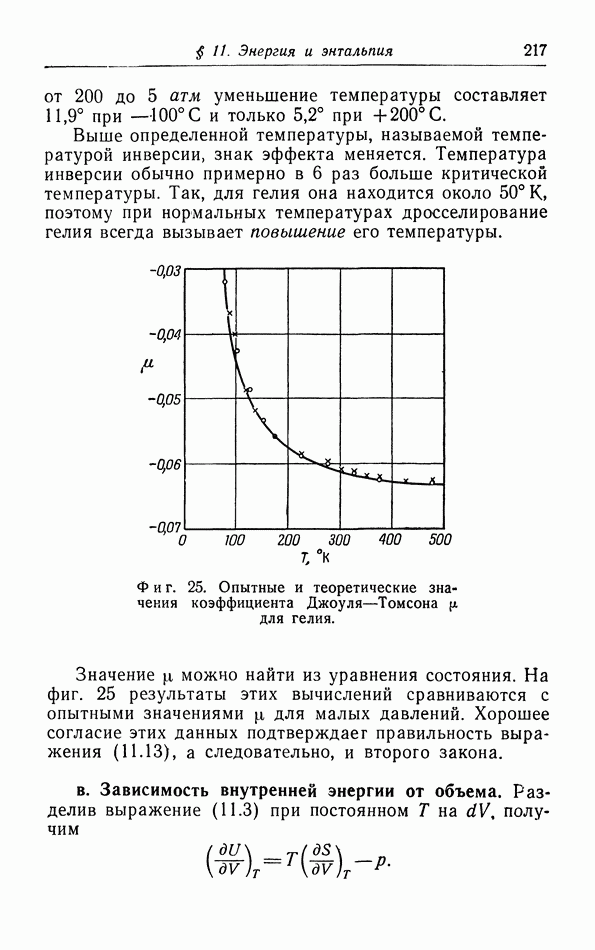
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
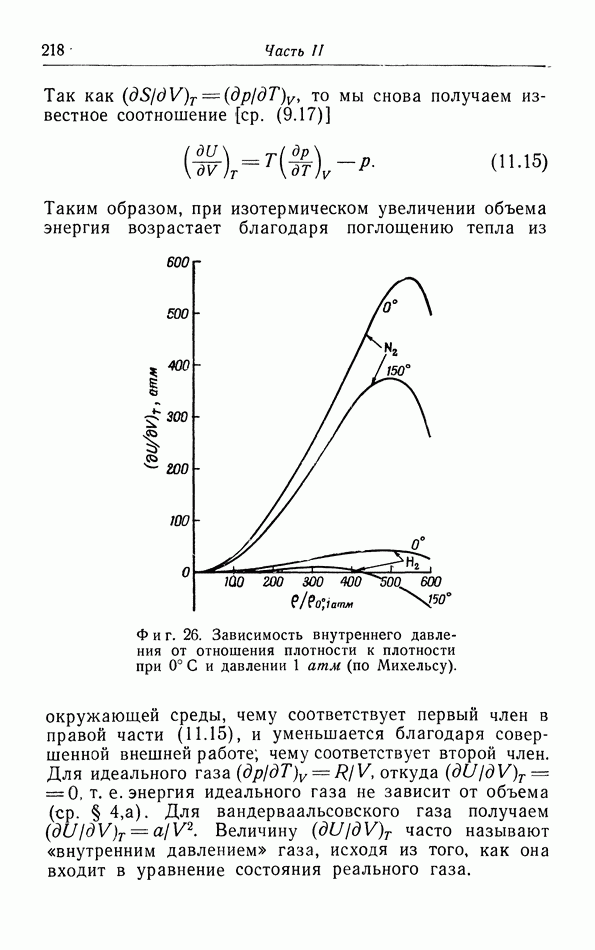
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
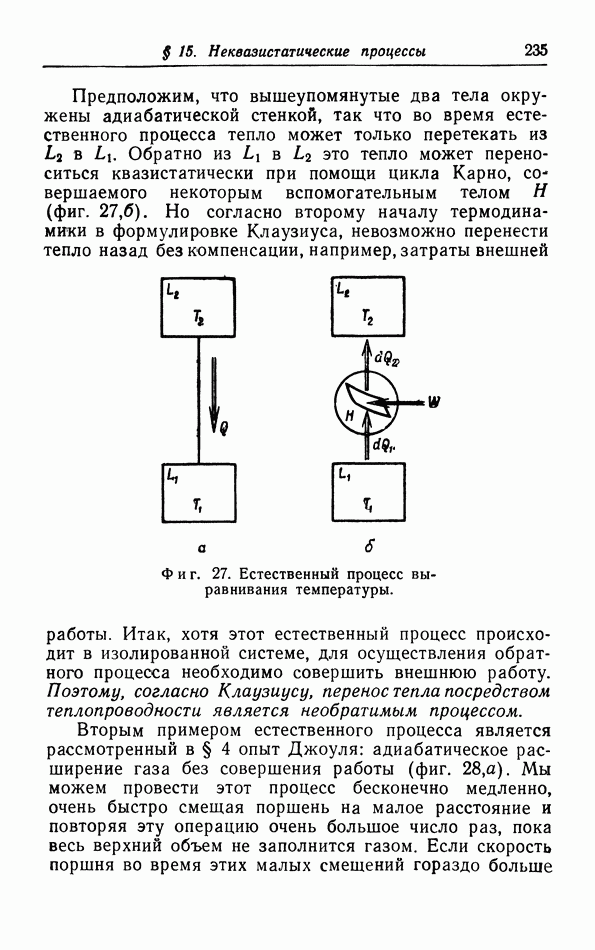
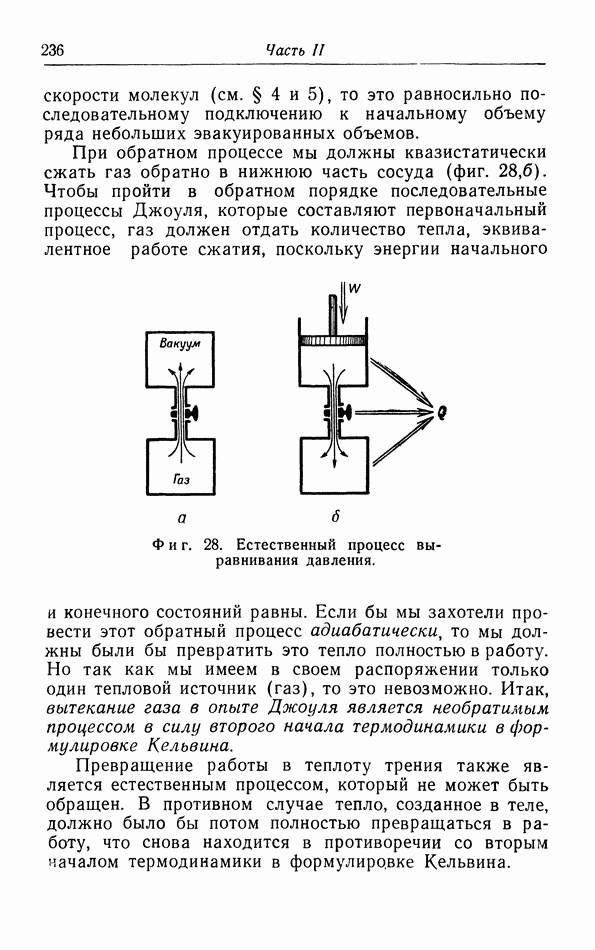
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
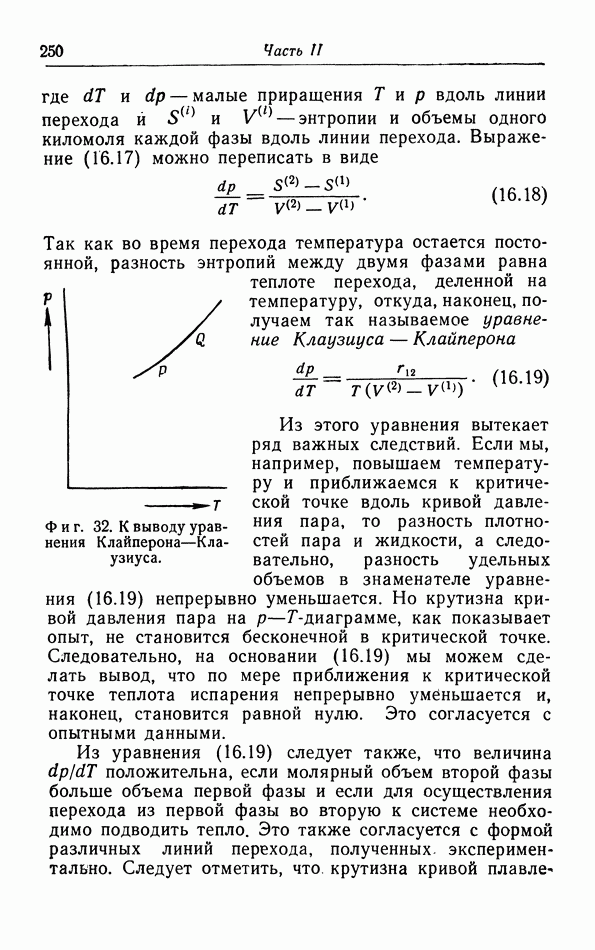
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
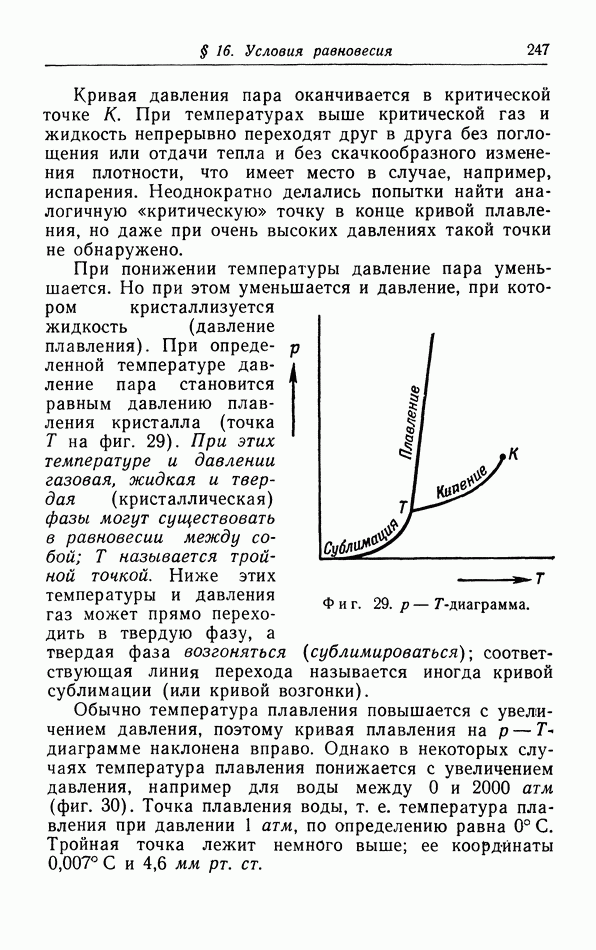
- д. p-T-диаграмма.
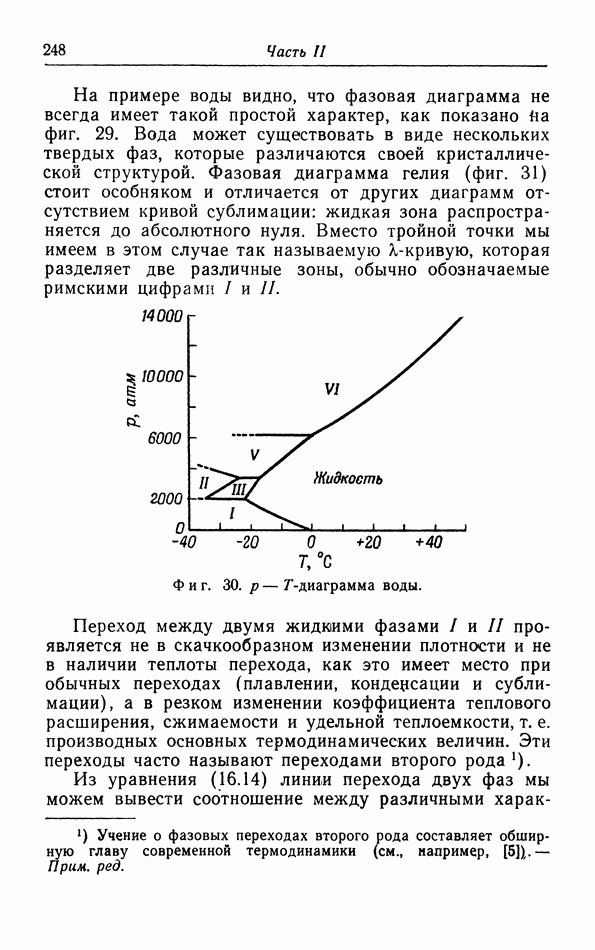
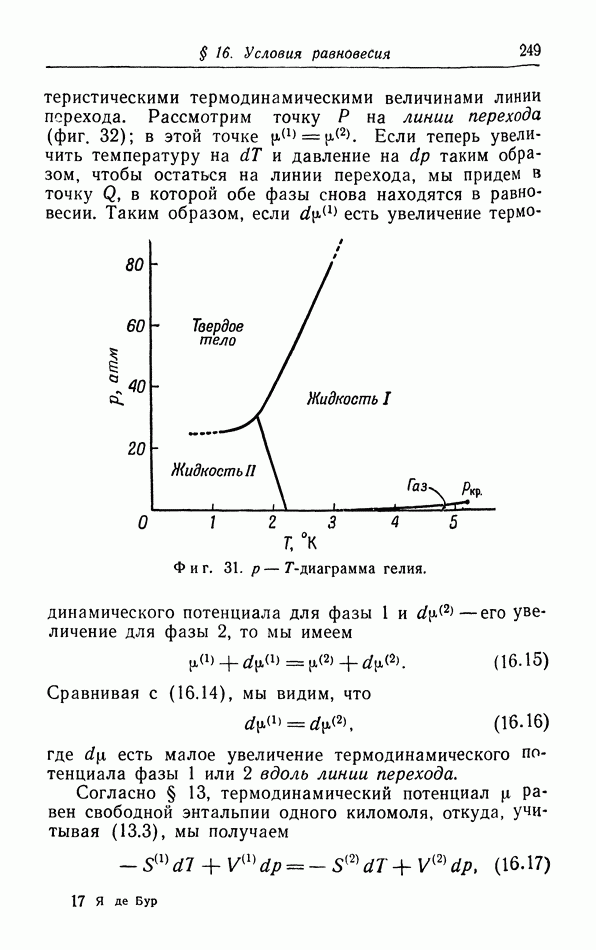
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
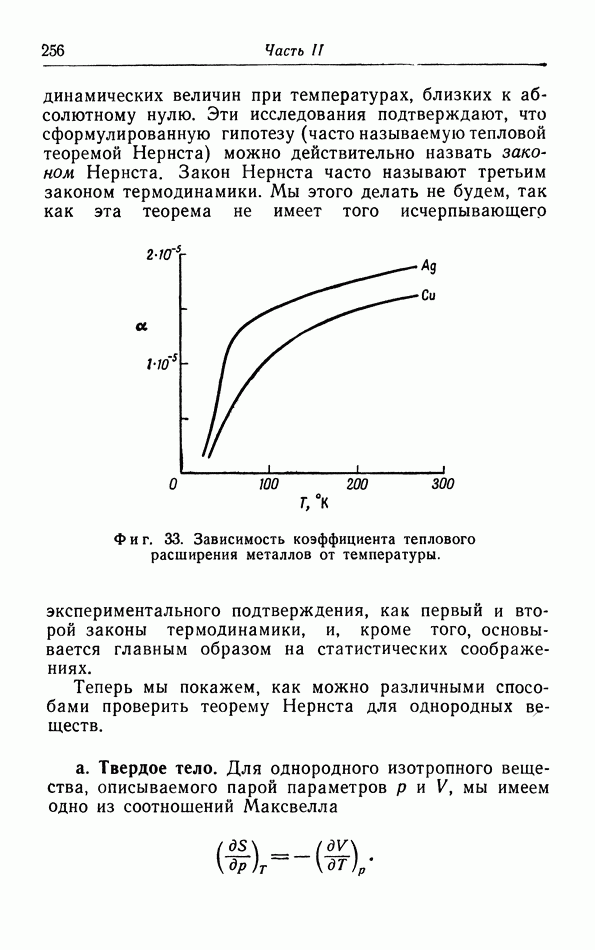
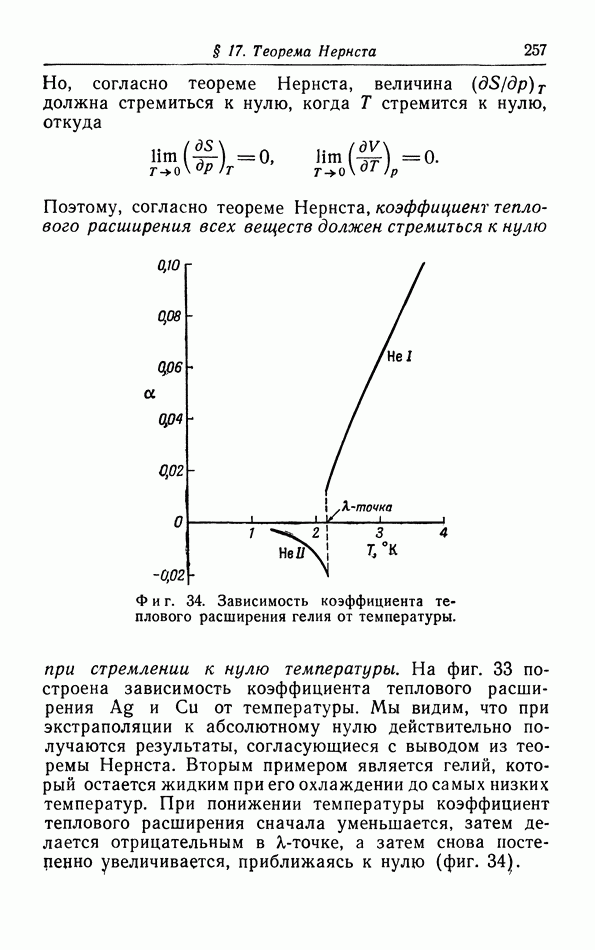
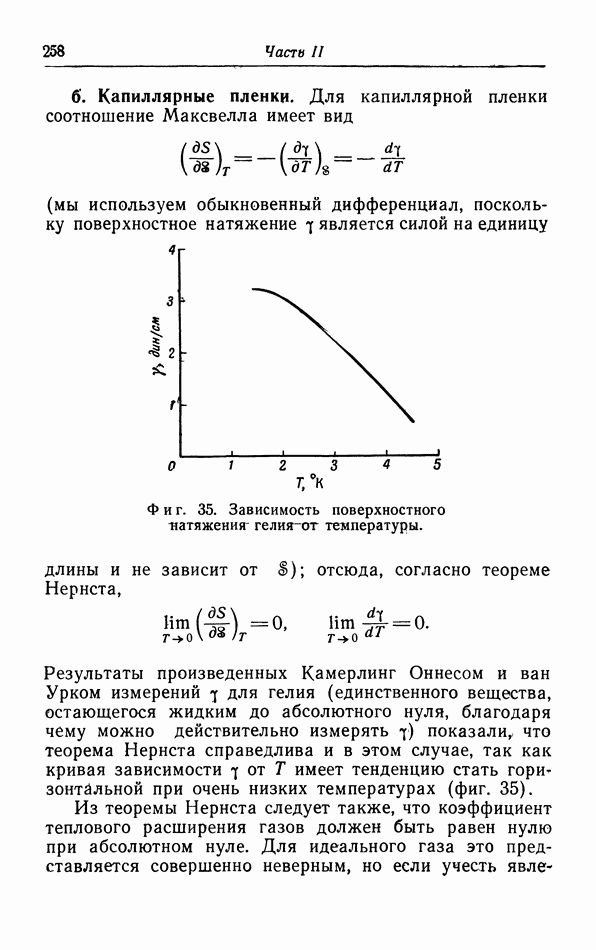
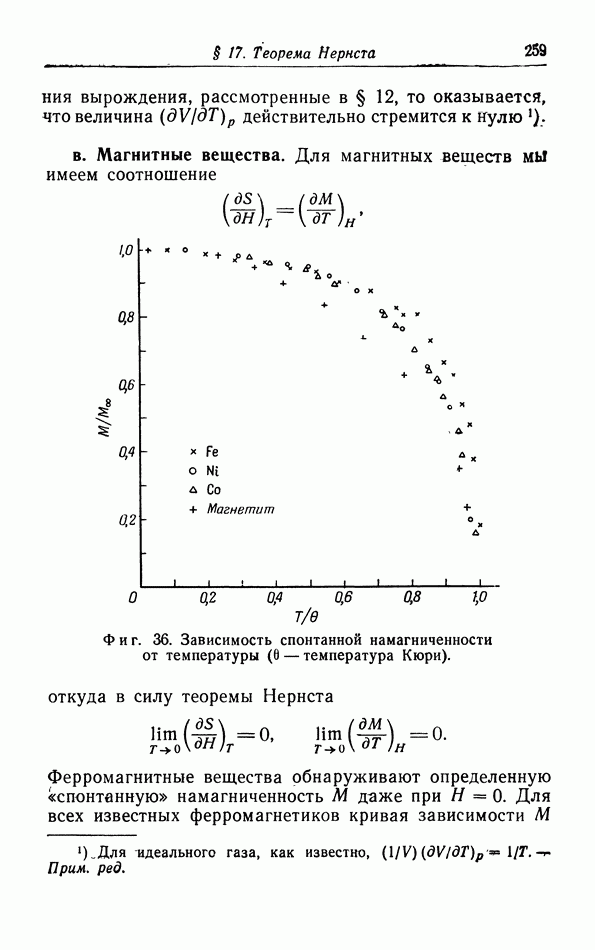
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам