| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
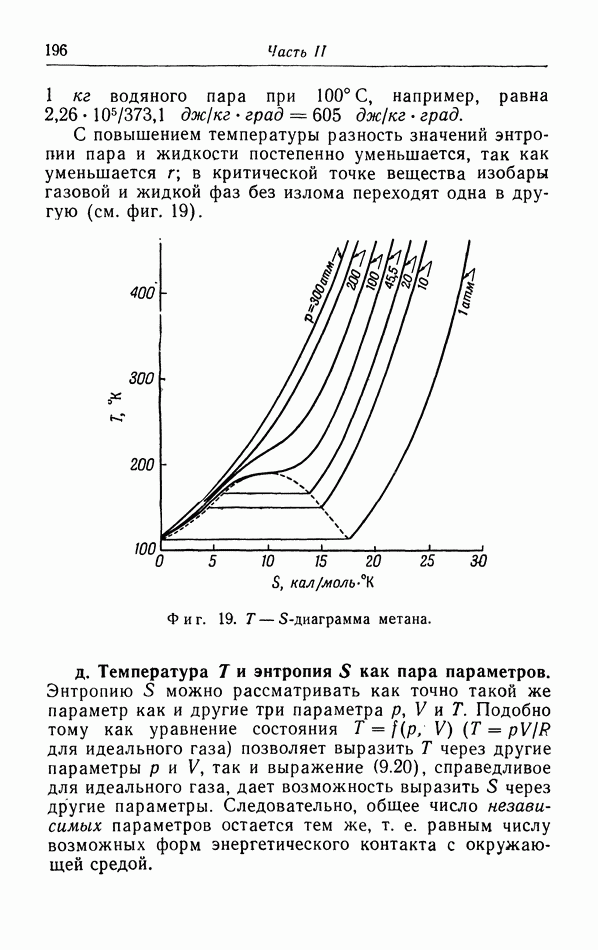
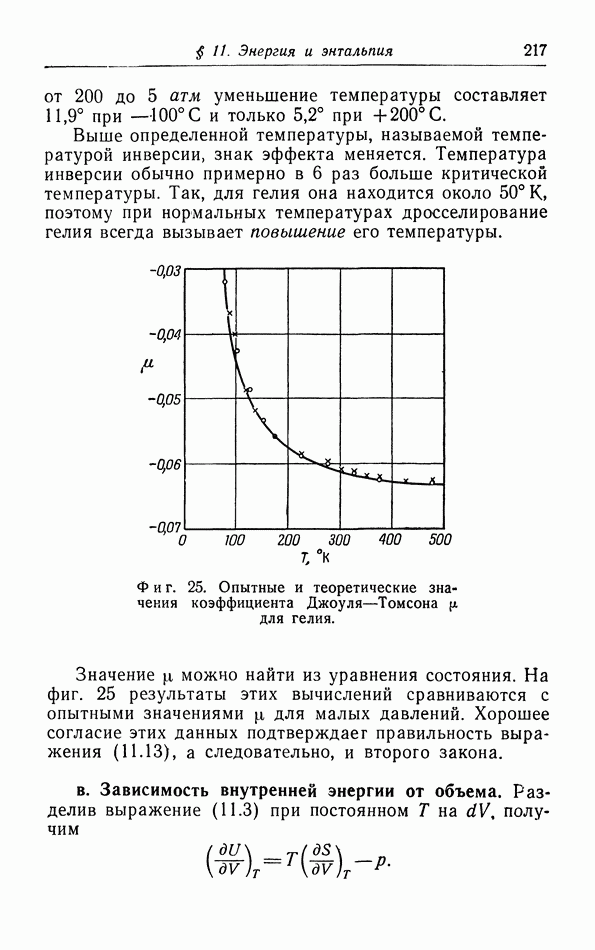
§ 11. Теплоемкость твердых тел
а. Классическая теория теплоемкости.
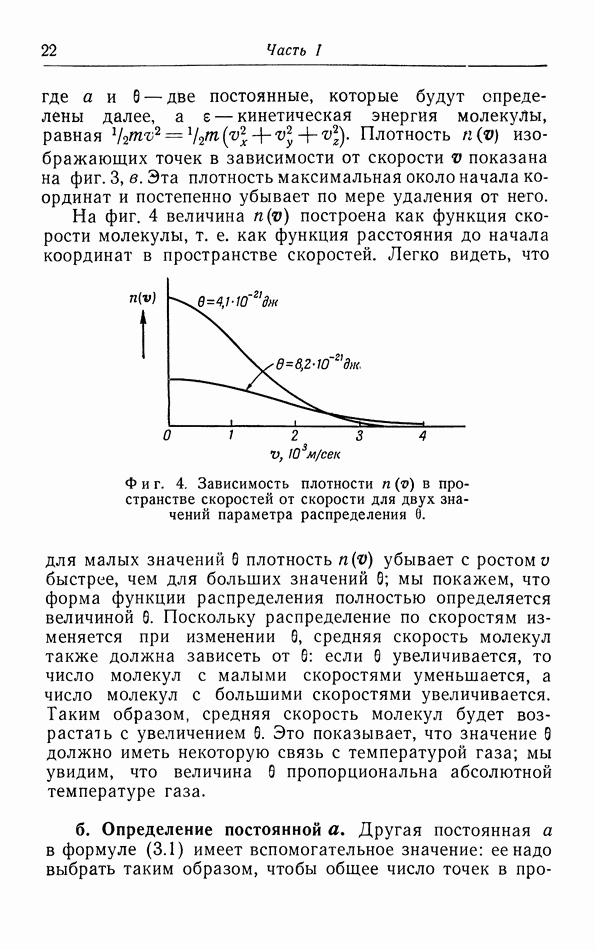
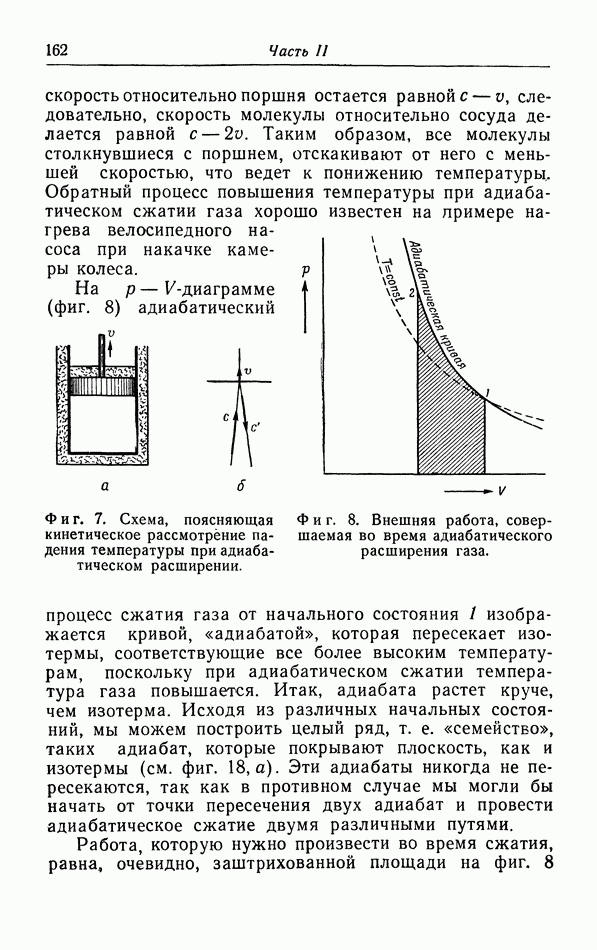
Молекулы в твердом теле колеблются около своих положений равновесия с амплитудой, которая увеличивается с повышением температуры. Мы будем для простоты рассматривать лишь такие твердые тела, в которых образующие их частицы являются атомами, как в металлах и отвердевших инертных газах, так что внутренних колебаний и вращения не происходит. В случае небольших смещений от положений равновесия восстанавливающая сила пропорциональна смещению, т. е. каждый атом совершает гармонические колебания с частотой, пропорциональной квадратному корню из отношения возмущающей силы (на единицу смещения) к массе.
Среднюю кинетическую энергию каждого из атомов можно вычислить с помощью закона равномерного распределения, который сохраняет свою силу и в этом случае. Это колебательное движение имеет три степени свободы, поскольку оно является суперпозицией колебаний в трех взаимно перпейдикулярных направлениях. Таким образом, средняя кинетическая энергия атома численно
равна  Однако, как известно из теории колебаний, в случае гармонического вибратора средняя по времени от кинетической энергии равна средней по времени от потенциальной энергии, так что последняя тоже равна
Однако, как известно из теории колебаний, в случае гармонического вибратора средняя по времени от кинетической энергии равна средней по времени от потенциальной энергии, так что последняя тоже равна 
Если вещество состоит из одноатомных молекул, то найденная энергия вибраторов  и потенциальная энергия
и потенциальная энергия  молекул друг относительно друга и составляют энергию кристалла, так что полная энергия одной килограмм-молекулы равна
молекул друг относительно друга и составляют энергию кристалла, так что полная энергия одной килограмм-молекулы равна  Если объем кристалла остается постоянным, то потенциальная энергия
Если объем кристалла остается постоянным, то потенциальная энергия  не зависит от температуры кристалла; следовательно, теплоемкость одной килограмм-молекулы при постоянном объеме будет
не зависит от температуры кристалла; следовательно, теплоемкость одной килограмм-молекулы при постоянном объеме будет  Еще до создания изложенной теории Дюлонг и
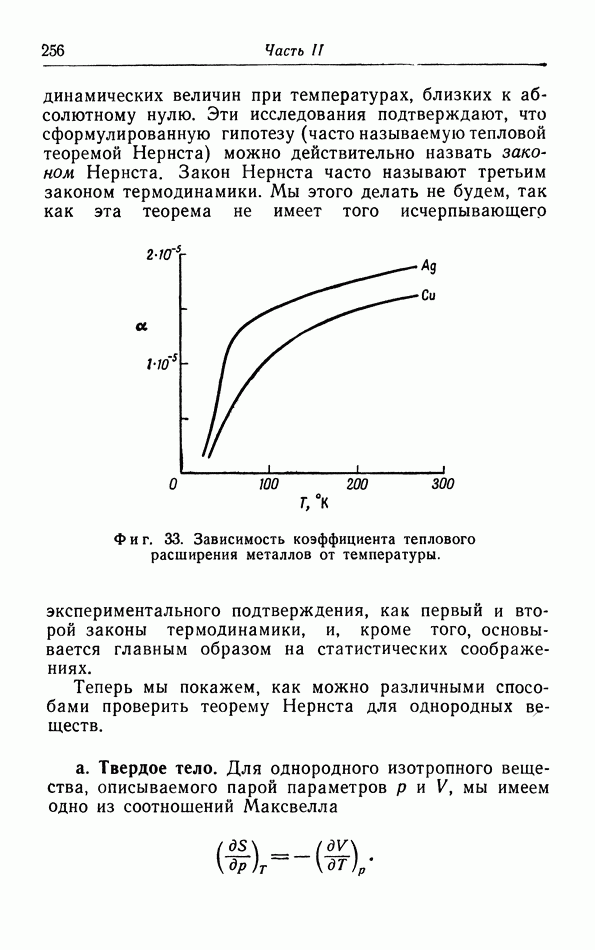
Еще до создания изложенной теории Дюлонг и  показали (1818 г.), что для большого числа металлов теплоемкость одной килограмм-молекулы приближенно равна 6 ккал, что находится в хорошем согласии с нашим теоретическим значением
показали (1818 г.), что для большого числа металлов теплоемкость одной килограмм-молекулы приближенно равна 6 ккал, что находится в хорошем согласии с нашим теоретическим значением  кал/моль). При постоянном давлении кристалл немного расширяется, так что необходимо подвести небольшое количество тепла для того, чтобы увеличить
кал/моль). При постоянном давлении кристалл немного расширяется, так что необходимо подвести небольшое количество тепла для того, чтобы увеличить  и совершить очень малую внешнюю работу. В соответствии с этим теплоемкость при постоянном давлении
и совершить очень малую внешнюю работу. В соответствии с этим теплоемкость при постоянном давлении  обычно больше теплоемкости при постоянном объеме примерно на 0,5 кал/моль.
обычно больше теплоемкости при постоянном объеме примерно на 0,5 кал/моль.
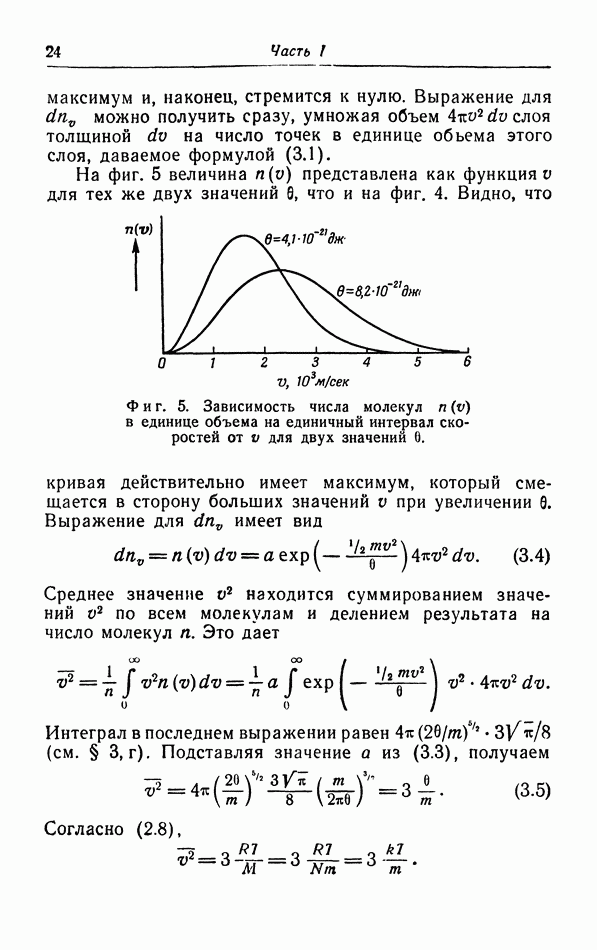
б. Квантовая теория теплоемкости.
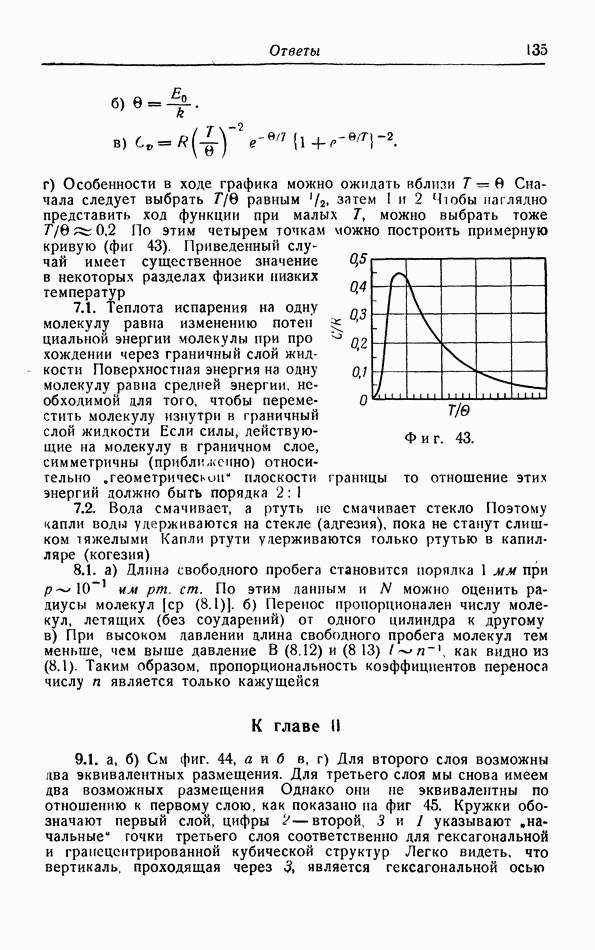
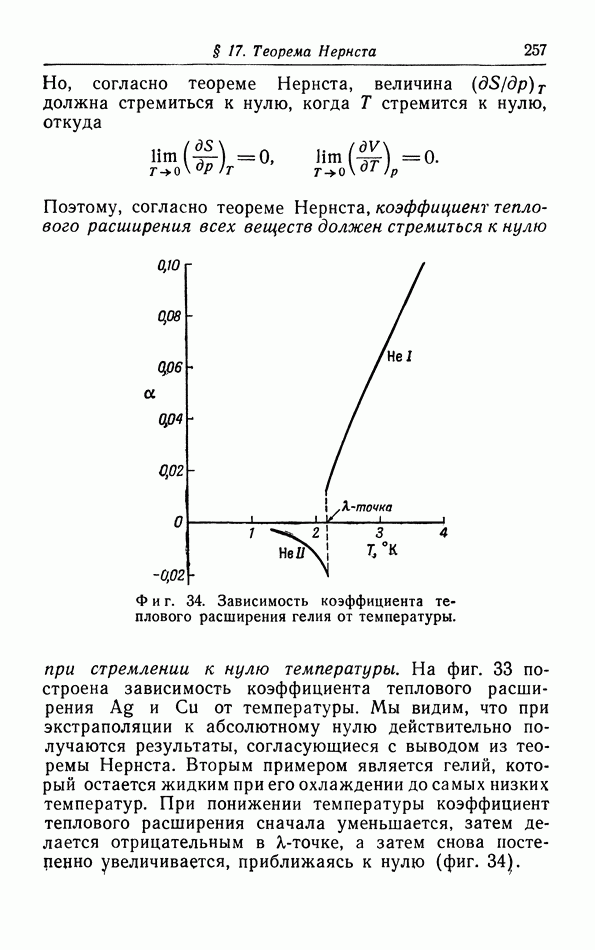
Отклонения от классической теории проявляются при низких температурах: С становится меньше теоретического значения  и при очень низких температурах стремится к нулю.
и при очень низких температурах стремится к нулю.
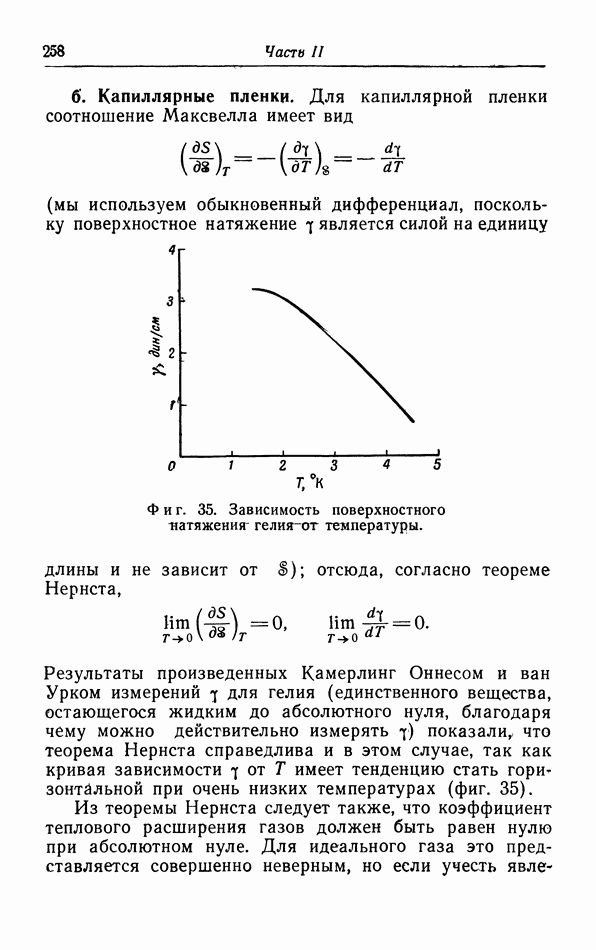
Объяснение этого уменьшения теплоемкости при низких температурах дал в 1905 г. Эйнштейн ( который указал, что колебания атомов в твердом теле, аналогично колебаниям атомов в молекуле, нужно рассматривать с квантовомеханической точки зрения. Согласно формуле (6.9), средняя энергия вибратора с частотой
который указал, что колебания атомов в твердом теле, аналогично колебаниям атомов в молекуле, нужно рассматривать с квантовомеханической точки зрения. Согласно формуле (6.9), средняя энергия вибратора с частотой  при температуре
при температуре  без учета нулевой энергии
без учета нулевой энергии  равна
равна

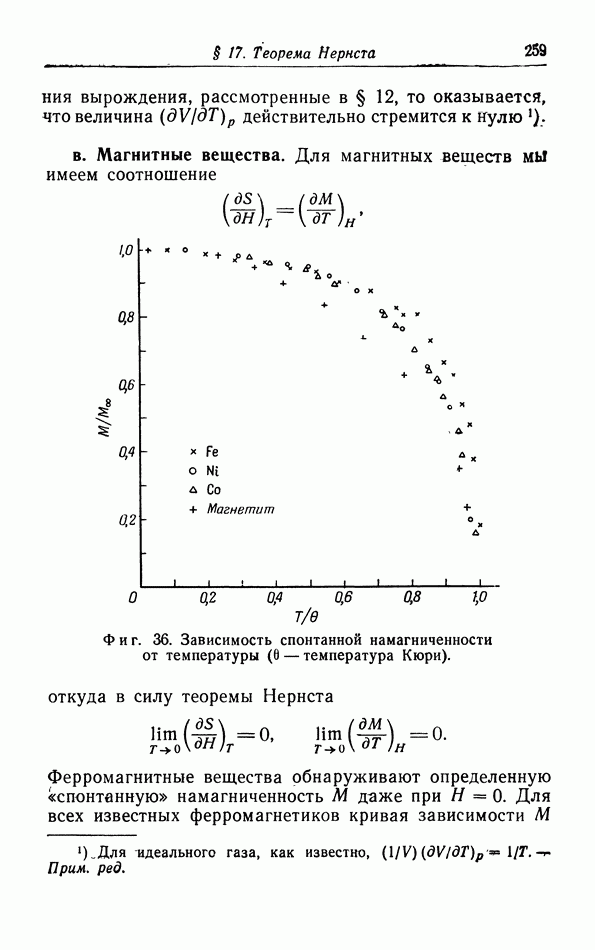
Но каждый из атомов имеет три степени свободы, а на каждую степень свободы приходится средняя энергия (11.1). Отсюда следует, что полная энергия тепловых колебаний одной килограмм-молекулы кристалла за вычетом полной нулевой энергии равна

где  характеристическая температура твердого тела. При высоких температурах выражение
характеристическая температура твердого тела. При высоких температурах выражение  приводится к
приводится к  тогда как при низких температурах и —
тогда как при низких температурах и —  стремится к нулю. Теплоемкость равна производной от и по температуре
стремится к нулю. Теплоемкость равна производной от и по температуре

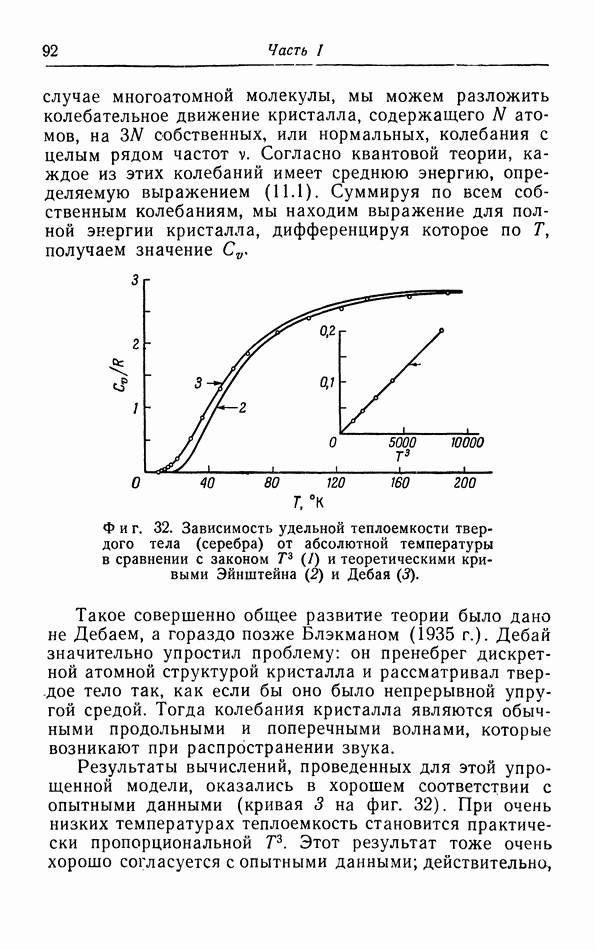
На фиг. 32 полученная Эйнштейном теоретическая кривая хода теплоемкости (2) сравнивается с опытными данными для серебра. Легко видеть, что если значение  выбрано таким образом, что теоретическая кривая хорошо согласуется с опытными данными при высоких температурах, то при низких температурах она спадает гораздо быстрее, чем экспериментальная кривая.
выбрано таким образом, что теоретическая кривая хорошо согласуется с опытными данными при высоких температурах, то при низких температурах она спадает гораздо быстрее, чем экспериментальная кривая.
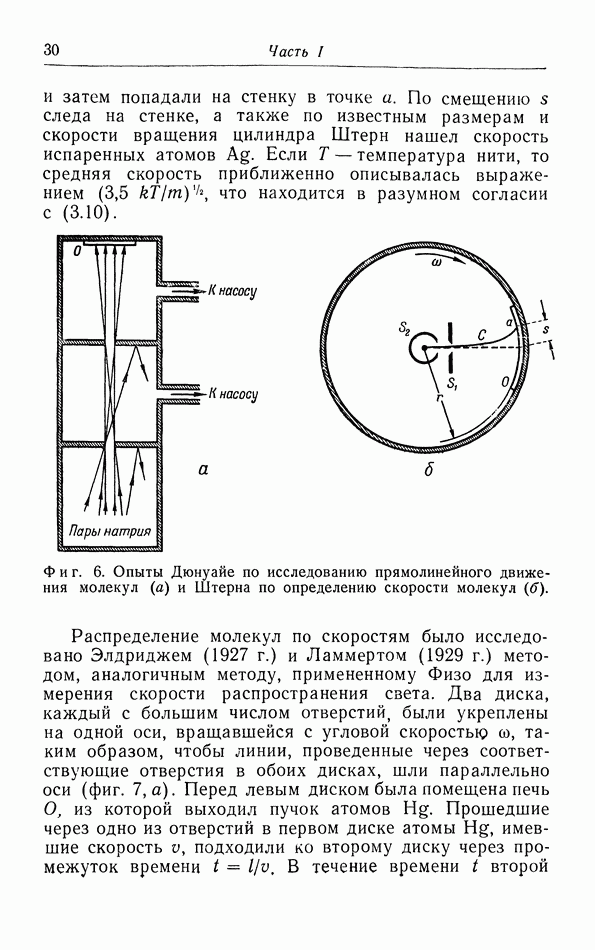
Это расхождение было устранено Дебаем в 1912 г. Он указал, что гипотеза о независимости колебаний атомов от движения соседних атомов верна лишь в том случае, когда положения равновесия не зависят от этого движения. Однако положения равновесия сильно зависят от положений соседних атомов, так как сфера действия межмолекулярных сил сравнительно мала. Если некоторый атом смещается из своего положения равновесия, то это же самое произойдет и с соседними атомами. Поэтому точка, в которую возвращается атом, тоже сместится, так что восстанавливающая сила будет меньше, чем мы могли бы ожидать с первого взгляда.
Итак, вместо индивидуальных колебаний каждого атома мы должны рассматривать коллективные колебания всех атомов кристалла вместе. Так же как и в
случае многоатомной молекулы, мы можем разложить колебательное движение кристалла, содержащего  атомов, на
атомов, на  собственных, или нормальных, колебания с целым рядом частот
собственных, или нормальных, колебания с целым рядом частот  Согласно квантовой теории, каждое из этих колебаний имеет среднюю энергию, определяемую выражением (11.1). Суммируя по всем собственным колебаниям, мы находим выражение для полной энергии кристалла, дифференцируя которое по
Согласно квантовой теории, каждое из этих колебаний имеет среднюю энергию, определяемую выражением (11.1). Суммируя по всем собственным колебаниям, мы находим выражение для полной энергии кристалла, дифференцируя которое по  получаем значение С,
получаем значение С,

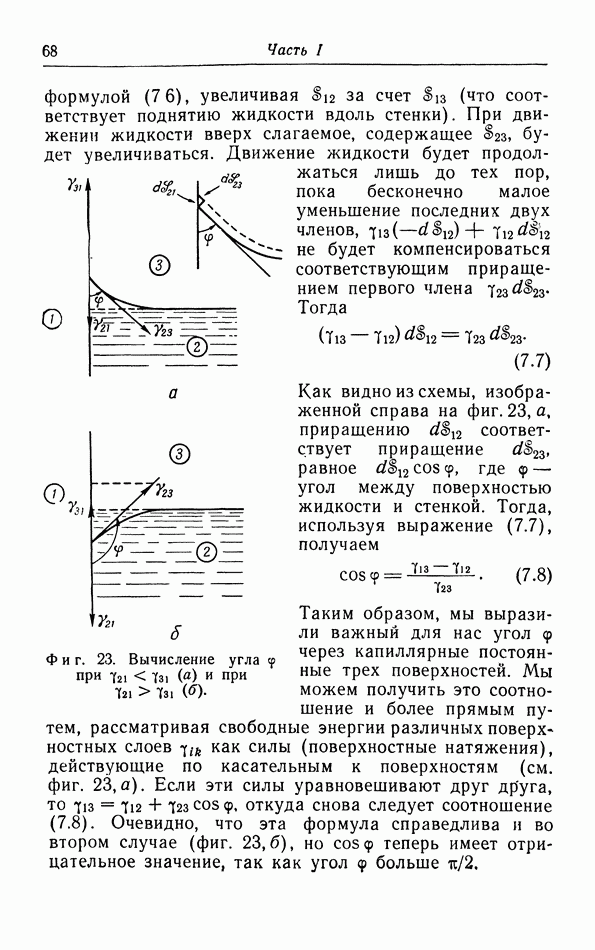
Фиг. 32. Зависимость удельной теплоемкости твердого тела (серебра) от абсолютной температуры в сравнении с законом  и теоретическими кривыми Эйнштейна (2) и Дебая (5).
и теоретическими кривыми Эйнштейна (2) и Дебая (5).
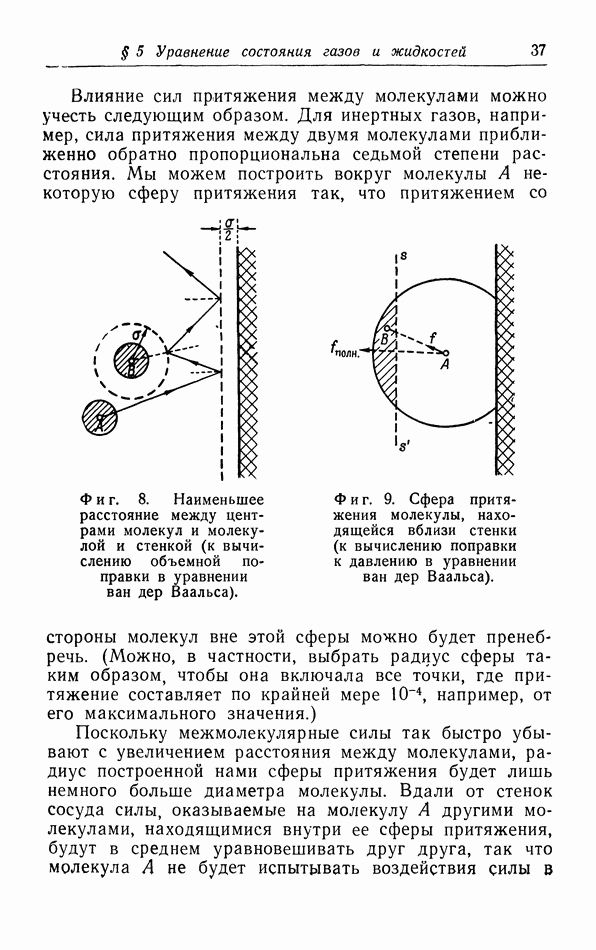
Такое совершенно общее развитие теории было дано не Дебаем, а гораздо позже Блэкманом (1935 г.). Дебай значительно упростил проблему: он пренебрег дискретной атомной структурой кристалла и рассматривал твердое тело так, как если бы оно было непрерывной упругой средой. Тогда колебания кристалла являются обычными продольными и поперечными волнами, которые возникают при распространении звука.
Результаты вычислений, проведенных для этой упрощенной модели, оказались в хорошем соответствии с опытными данными (кривая 3 на фиг. 32). При очень низких температурах теплоемкость становится практически пропорциональной  Этот результат тоже очень хорошо согласуется с опытными данными; действительно,
Этот результат тоже очень хорошо согласуется с опытными данными; действительно,
на фиг. 32 зависимость теплоемкости от  представляет собой прямую линию 1.
представляет собой прямую линию 1.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
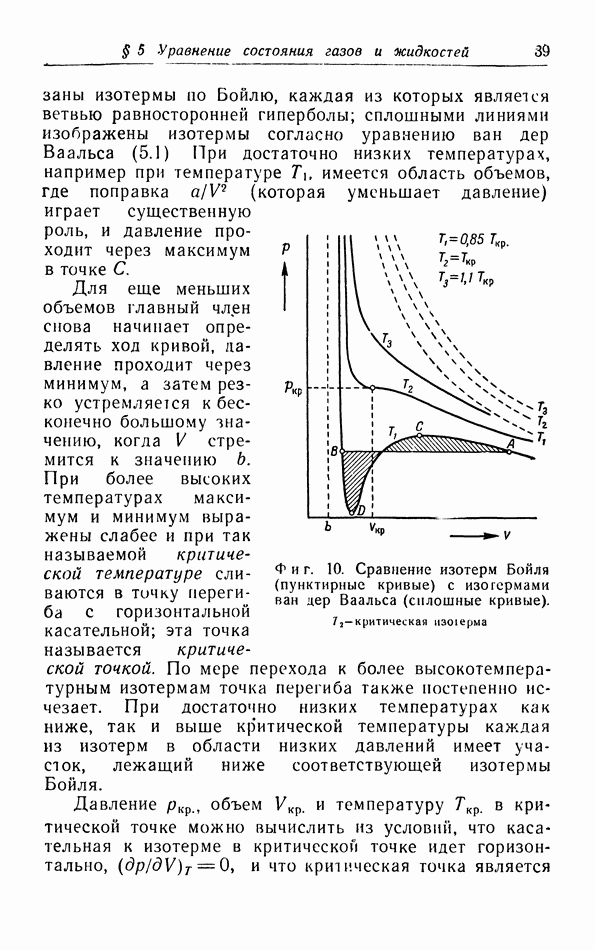
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
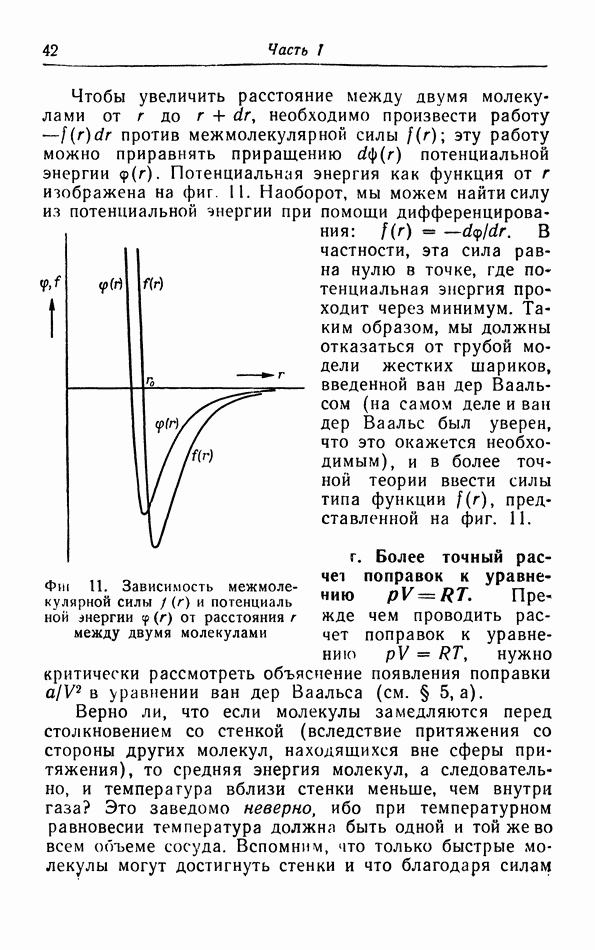
- в. Взаимодействие молекул.
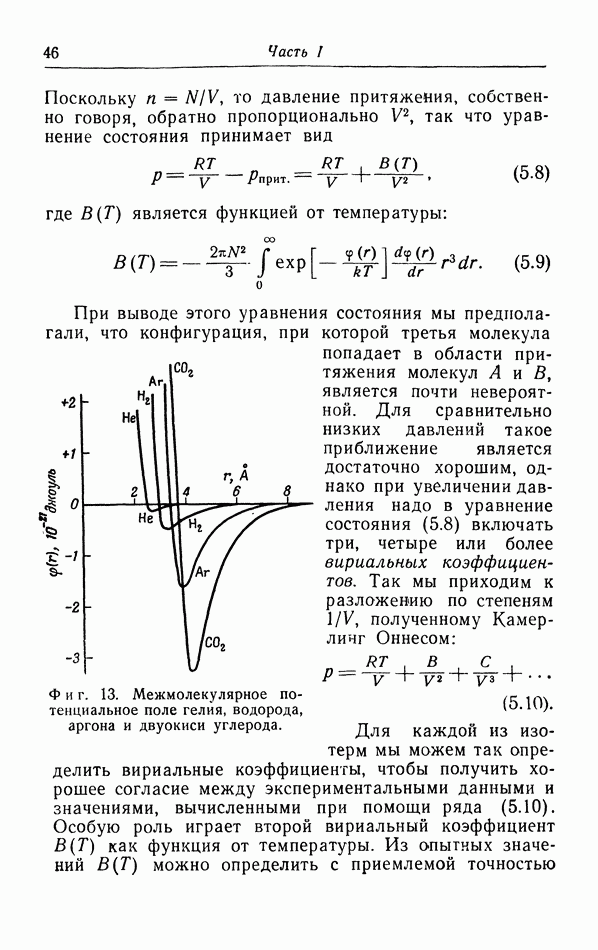
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
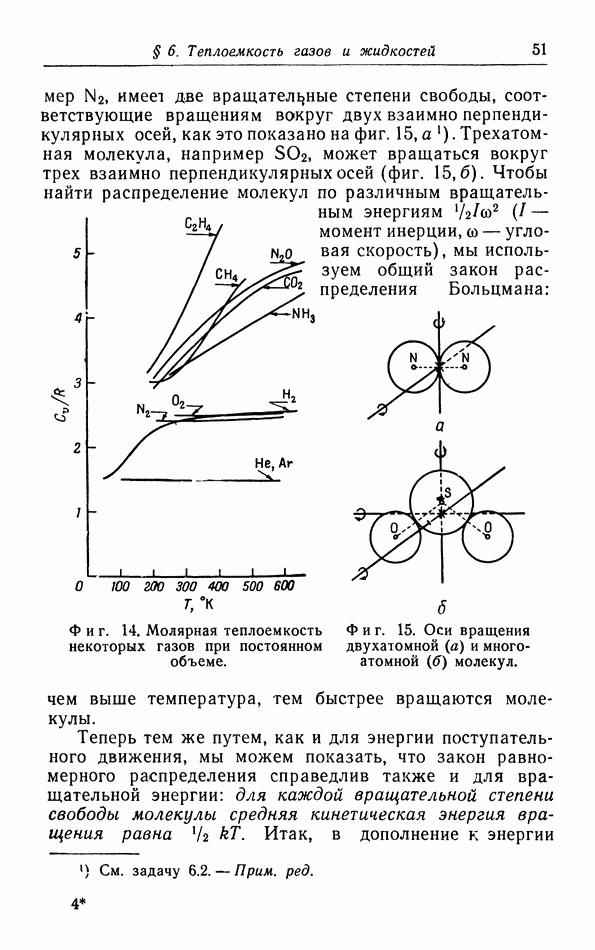
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
- б. Жидкие пленки.
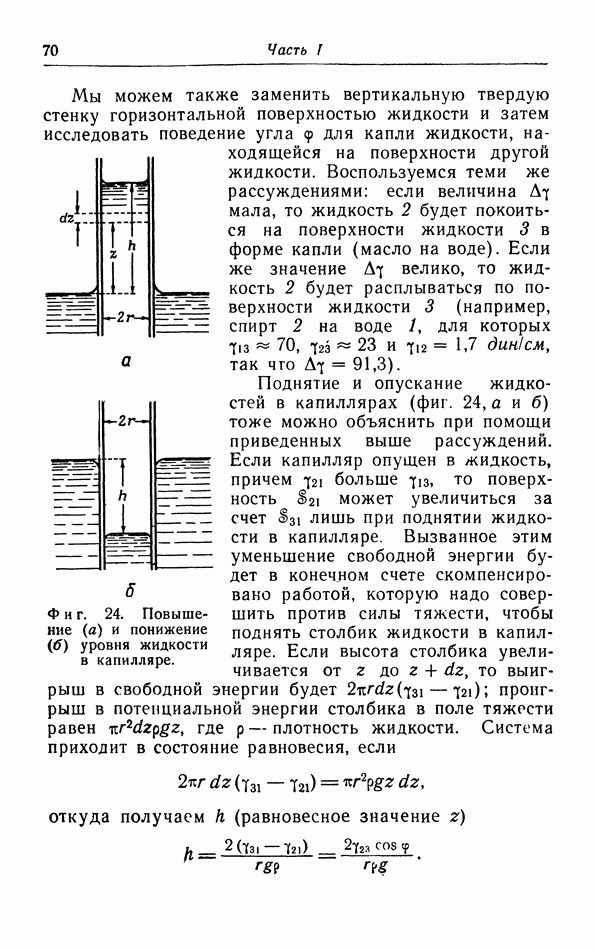
- в. Капиллярное поднятие и понижение уровня жидкости.
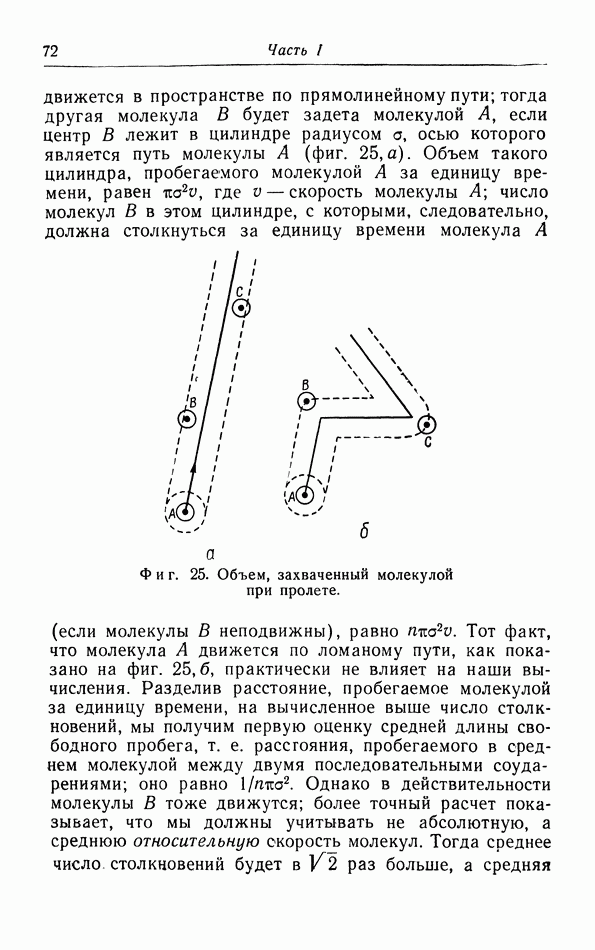
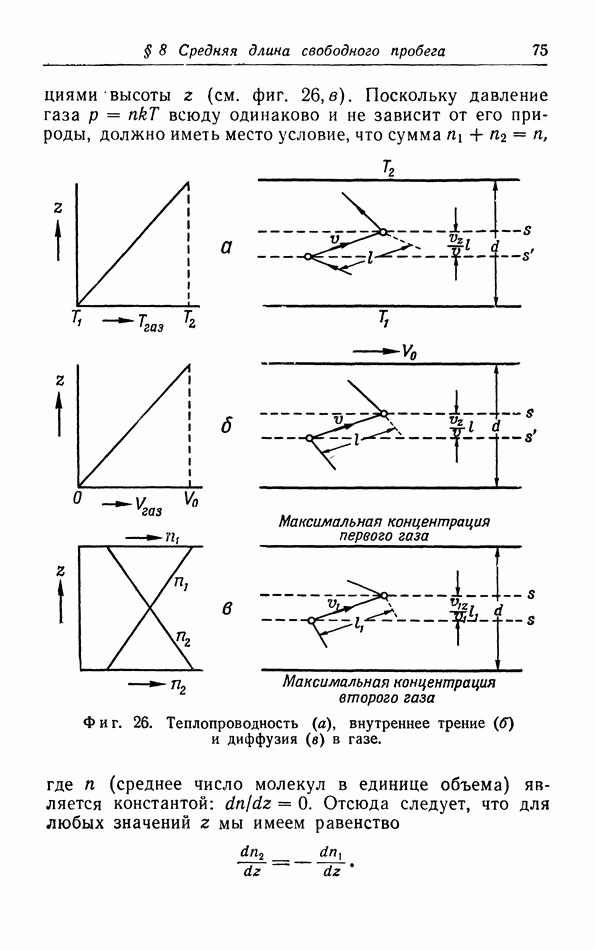
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
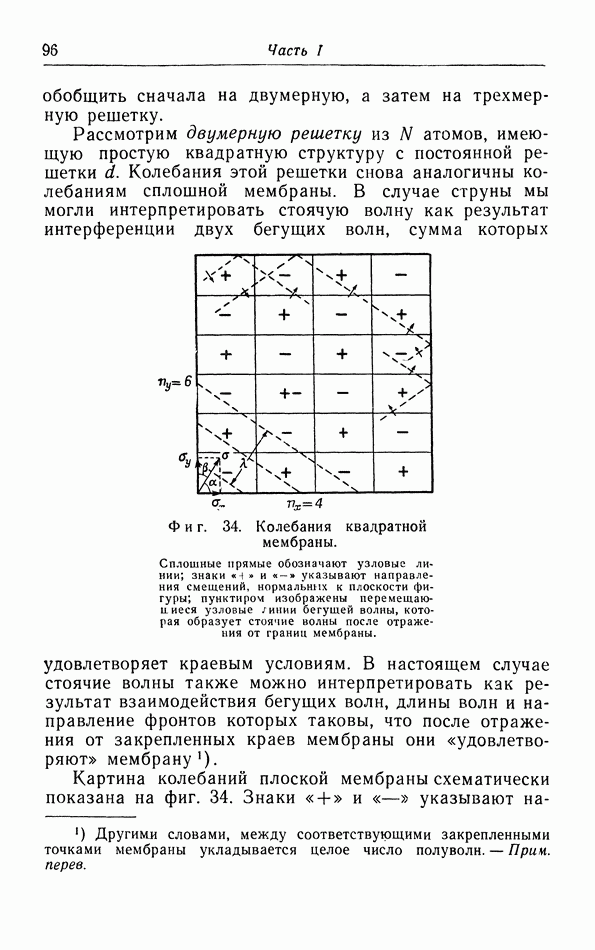
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
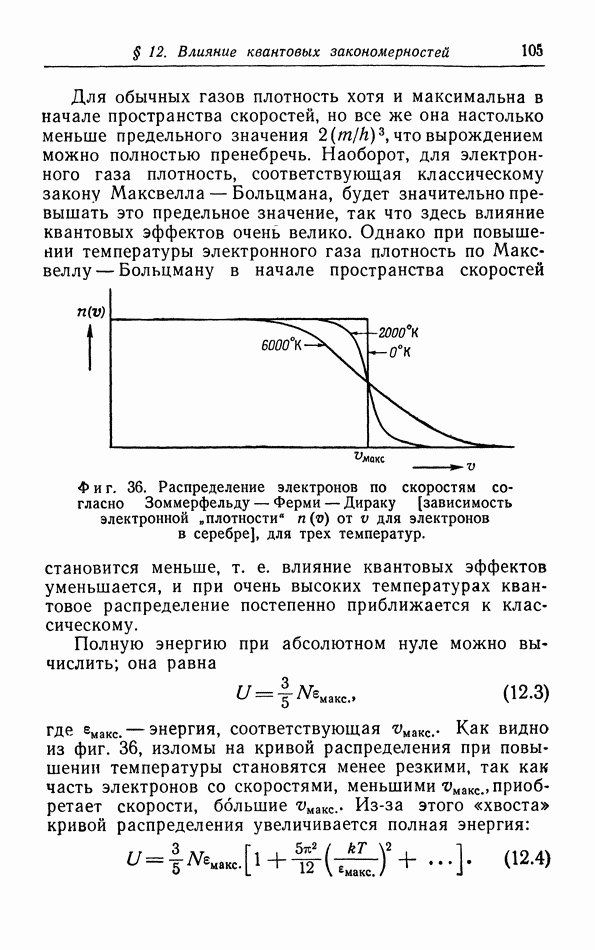
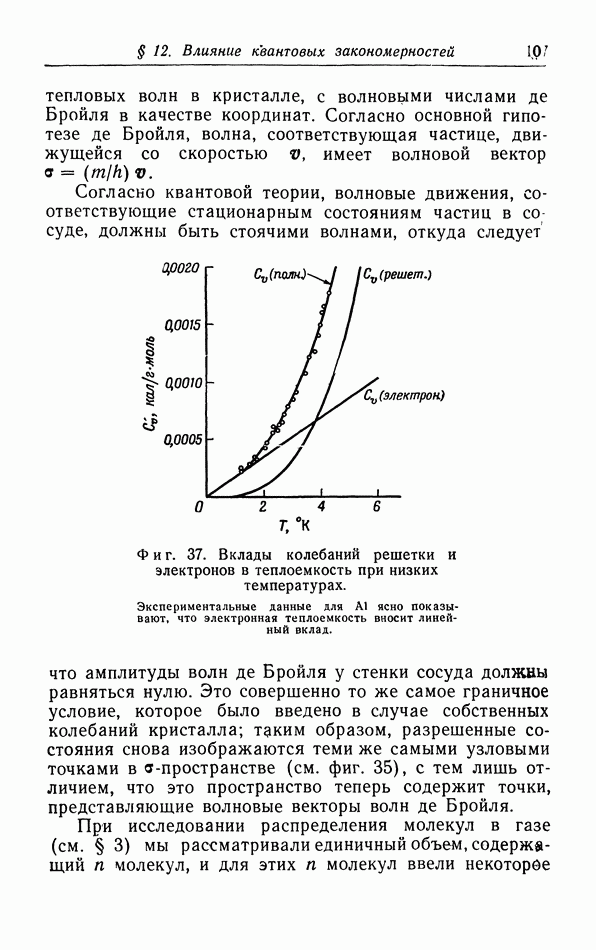
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
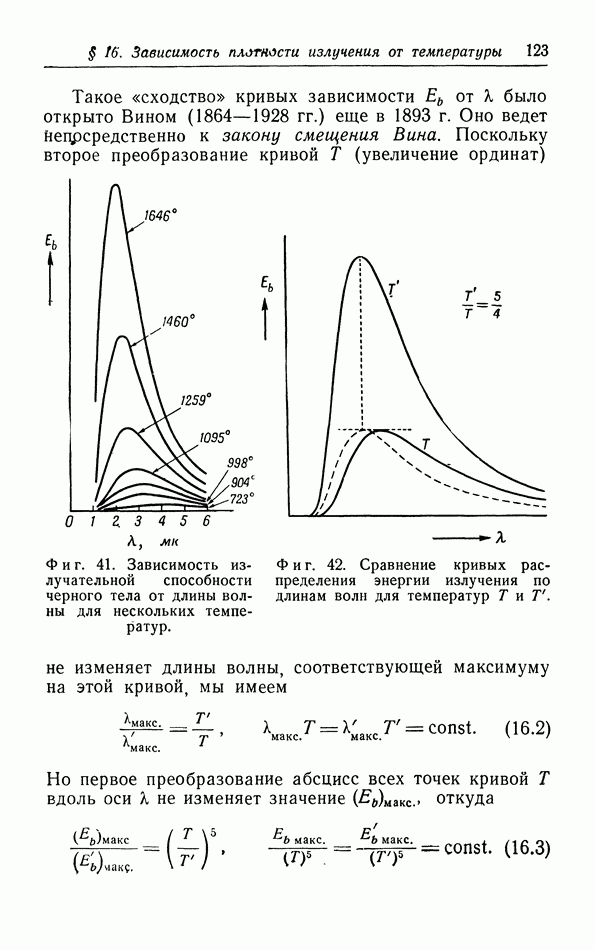
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
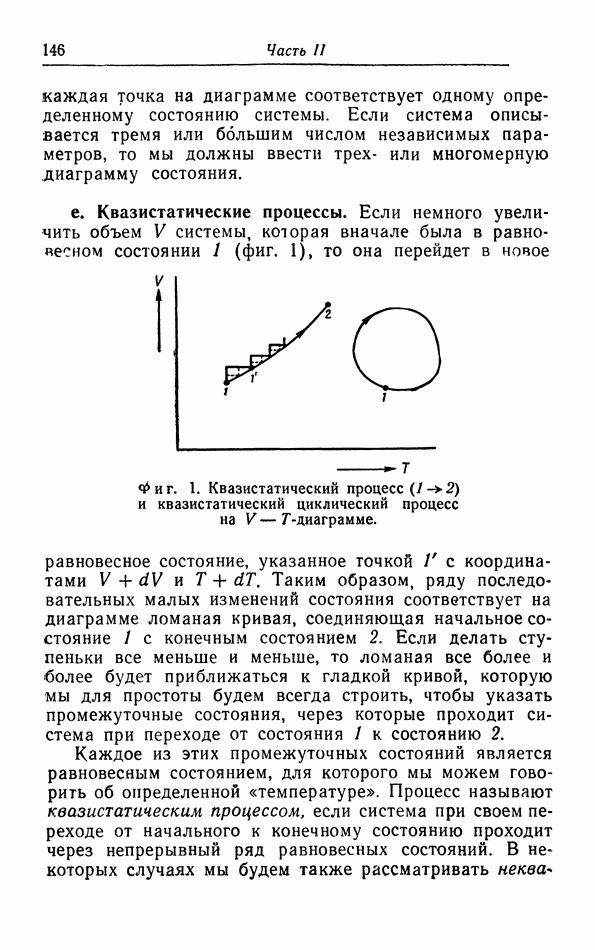
- § 2. Работа при квазистатических процессах
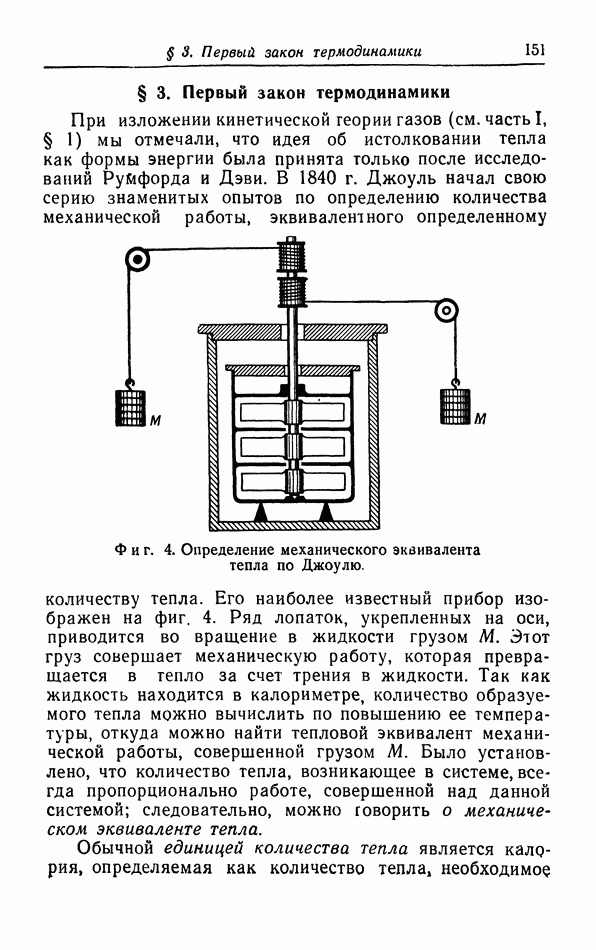
- § 3. Первый закон термодинамики
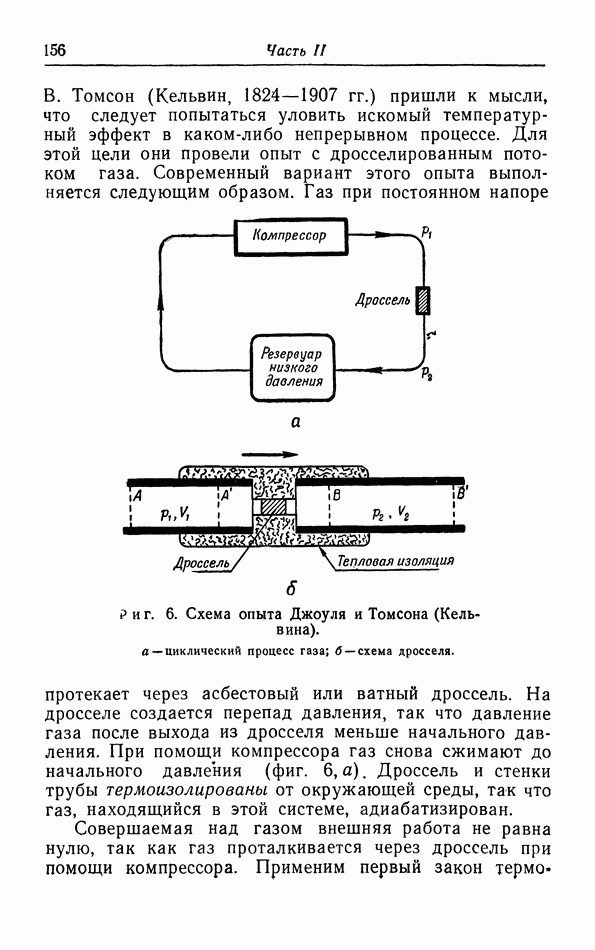
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
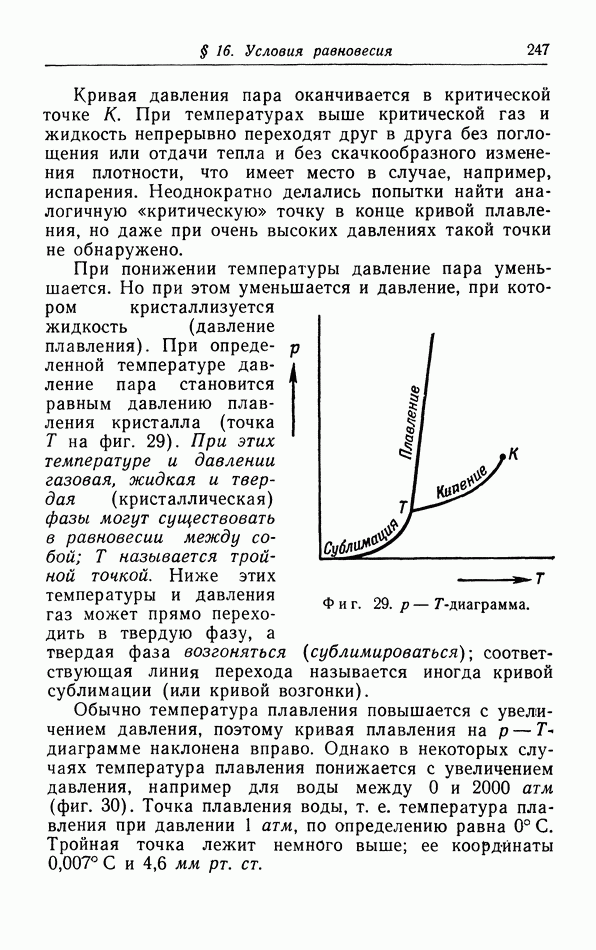
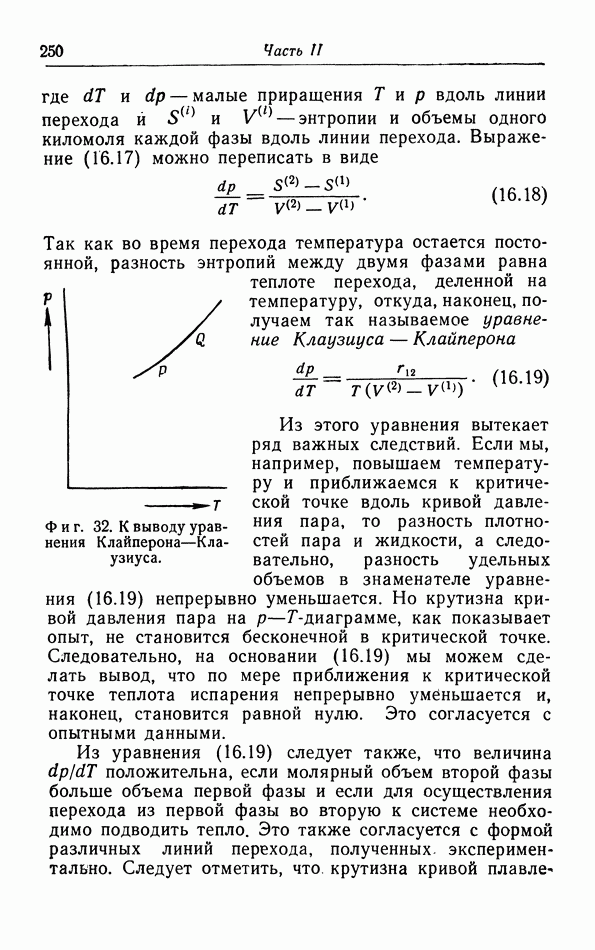
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
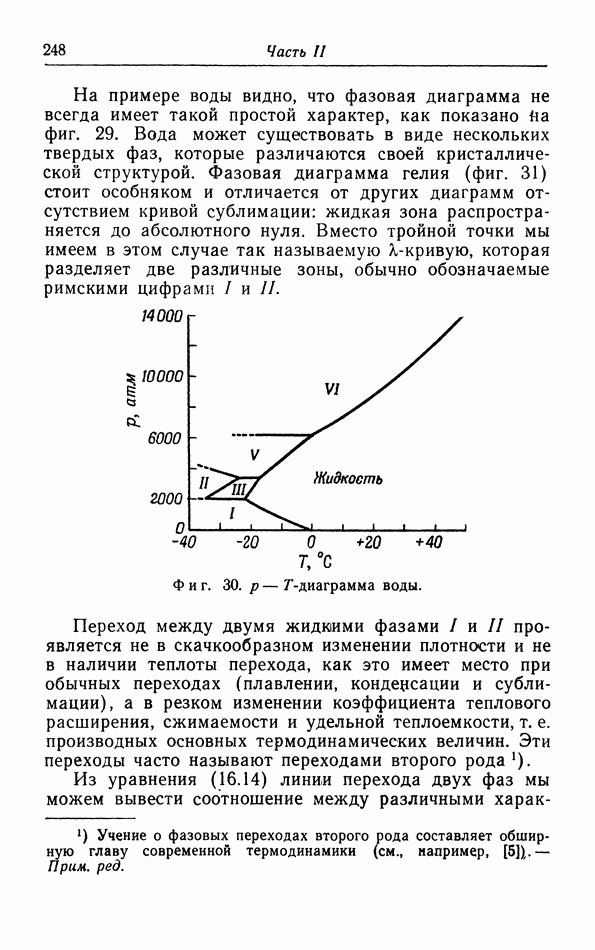
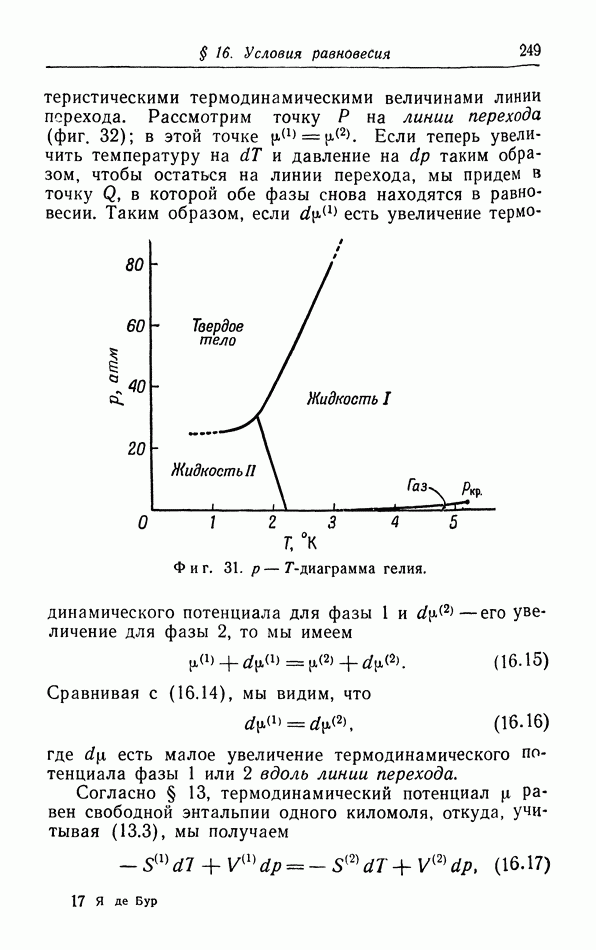
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам