| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
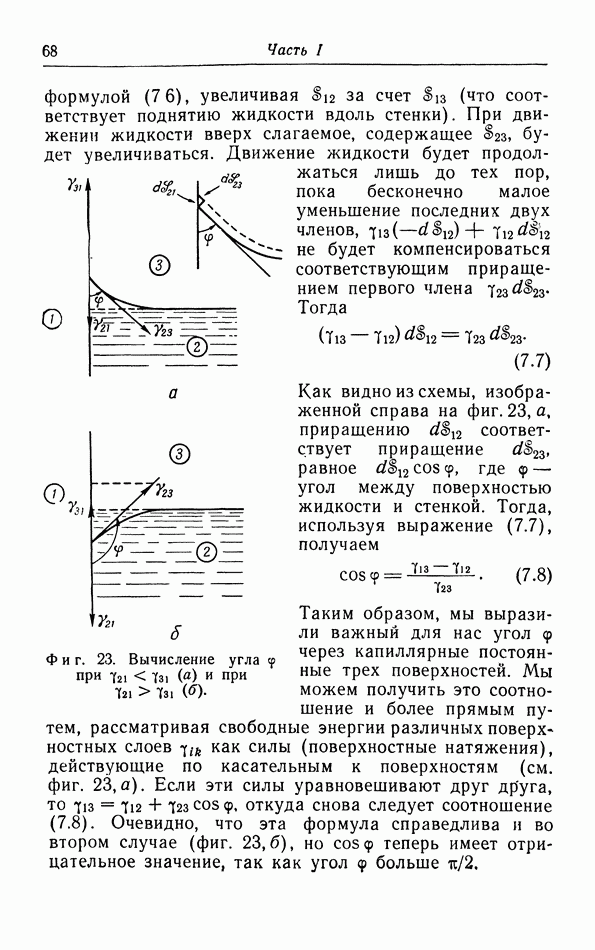
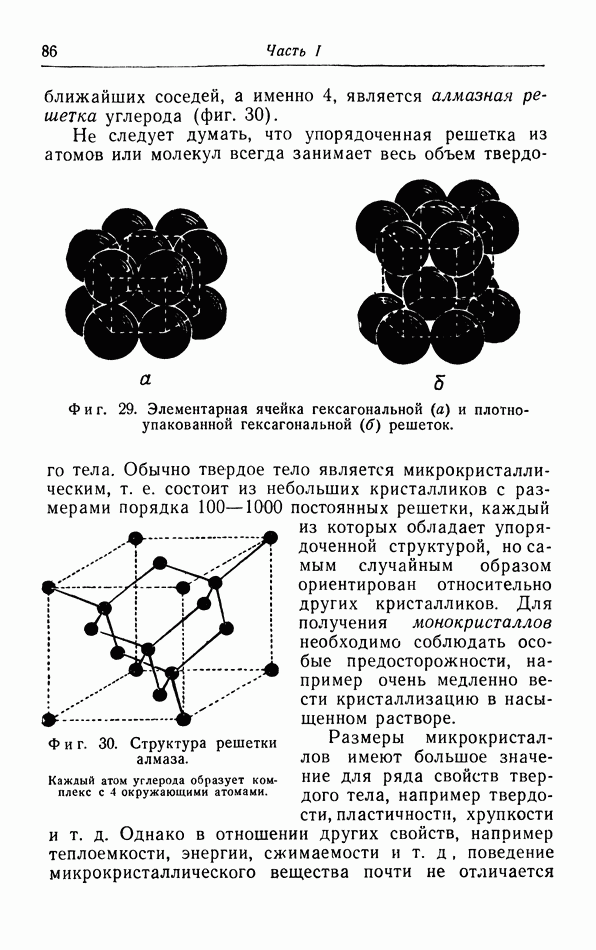
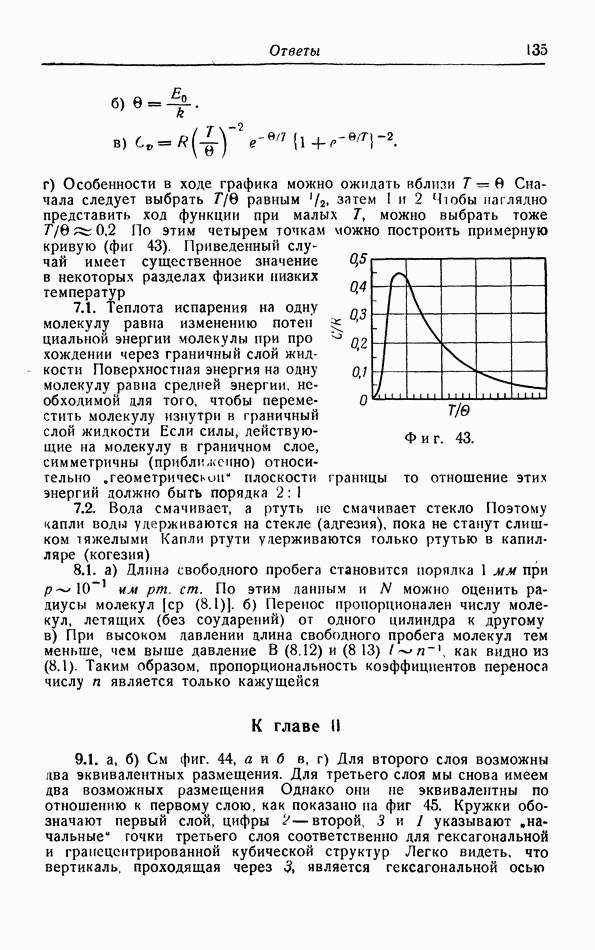
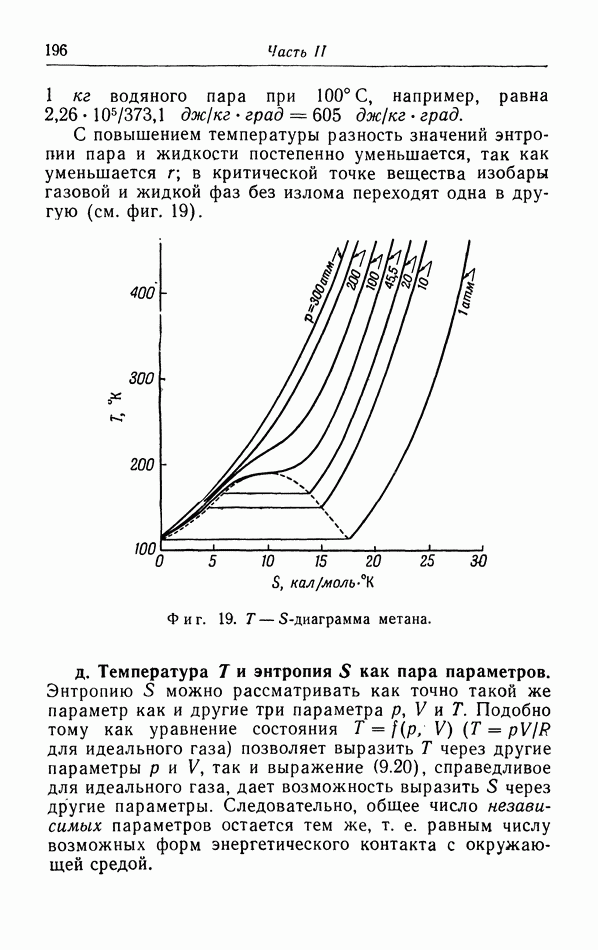
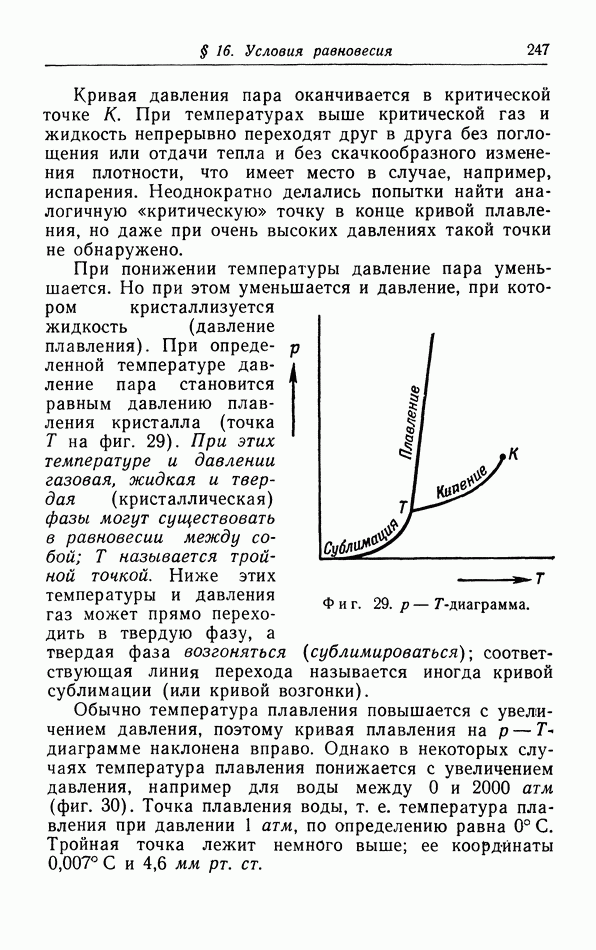
§ 7. Поверхностные явления
а. Поверхностное натяжение и поверхностная энергия.
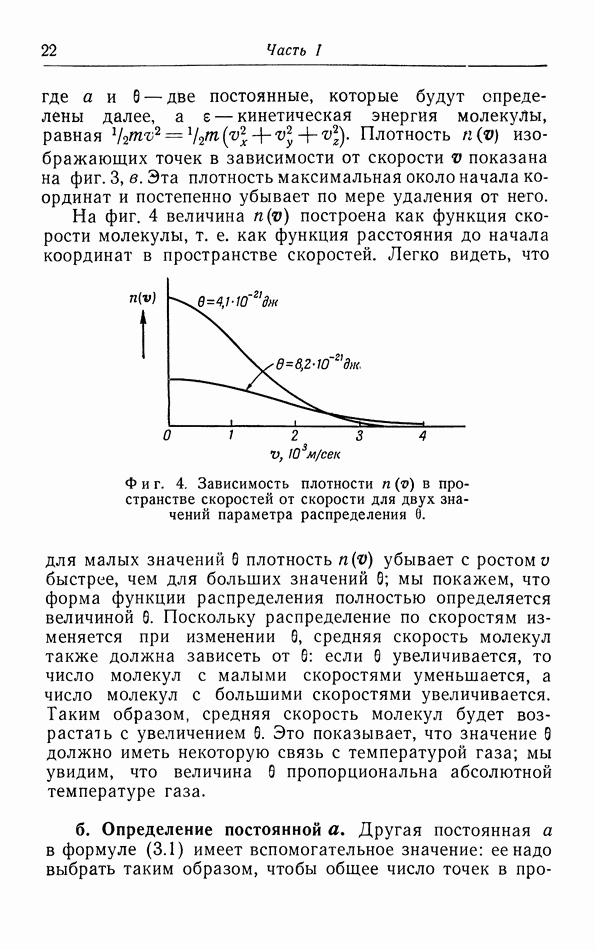
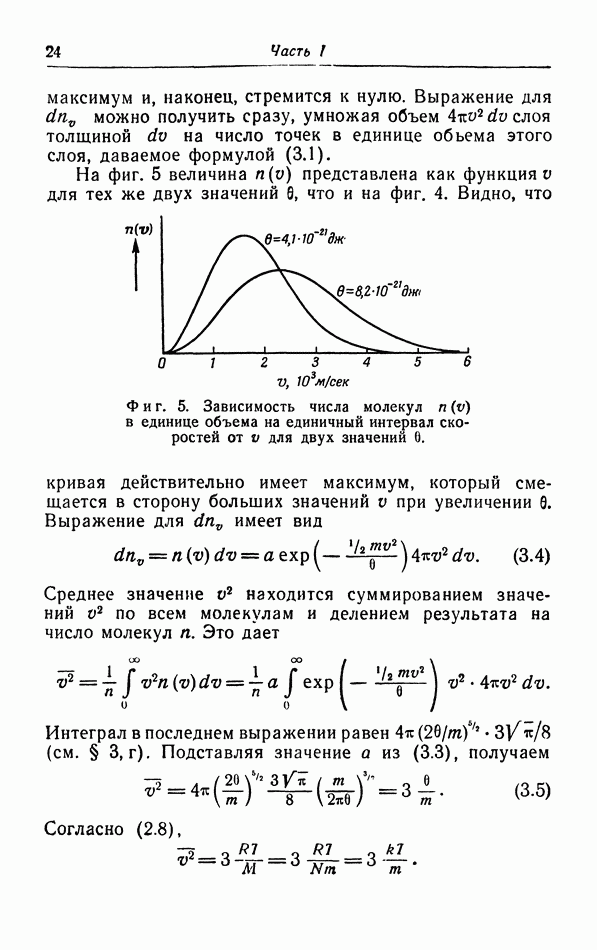
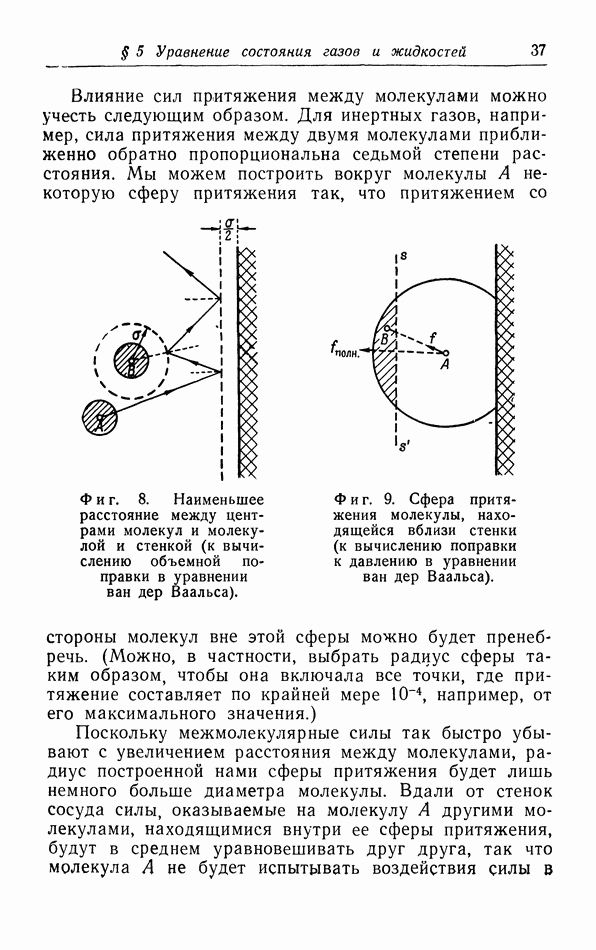
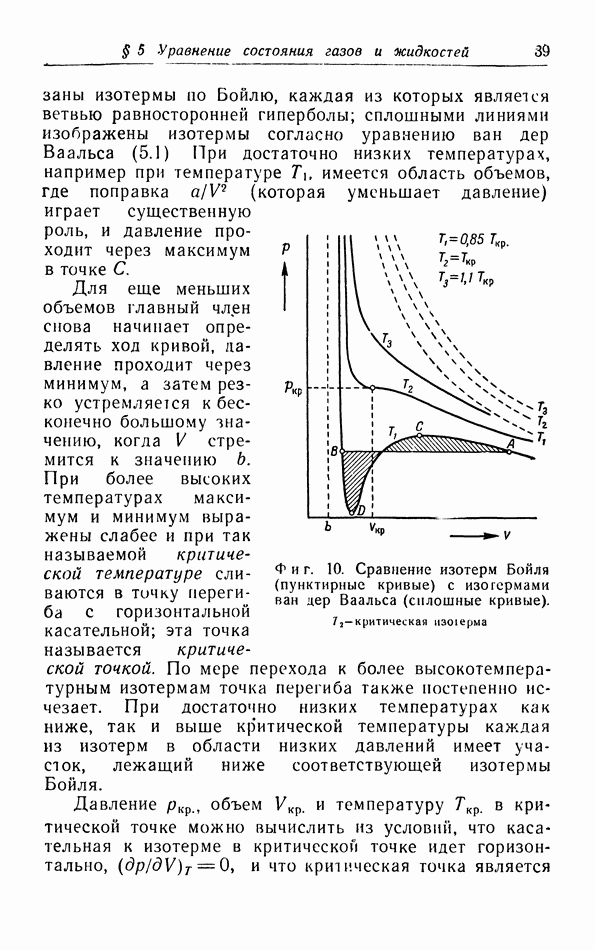
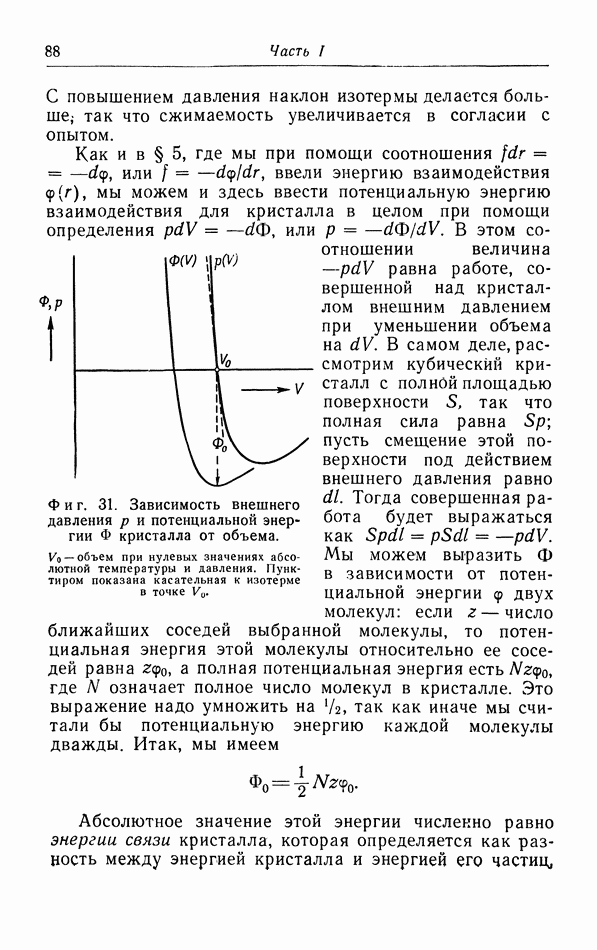
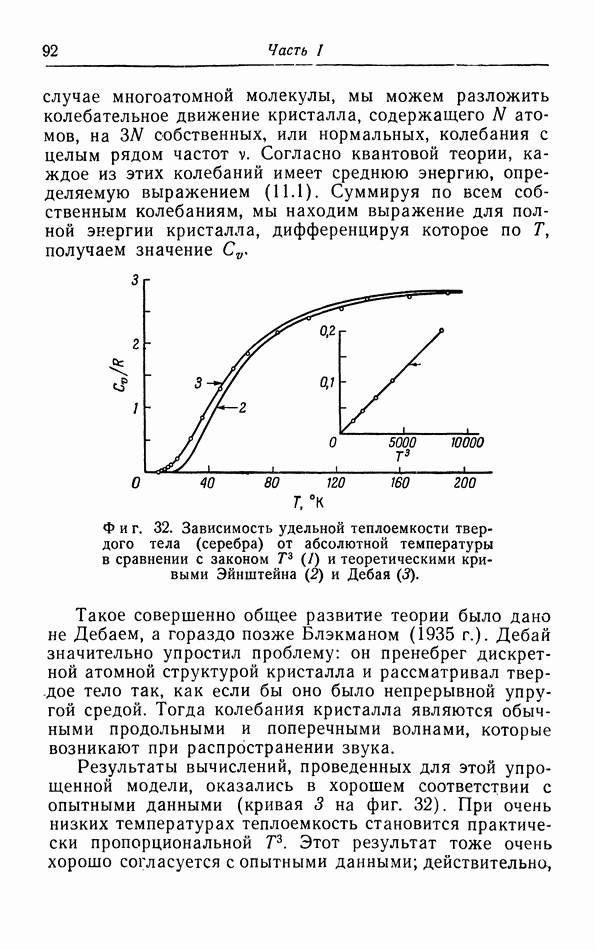
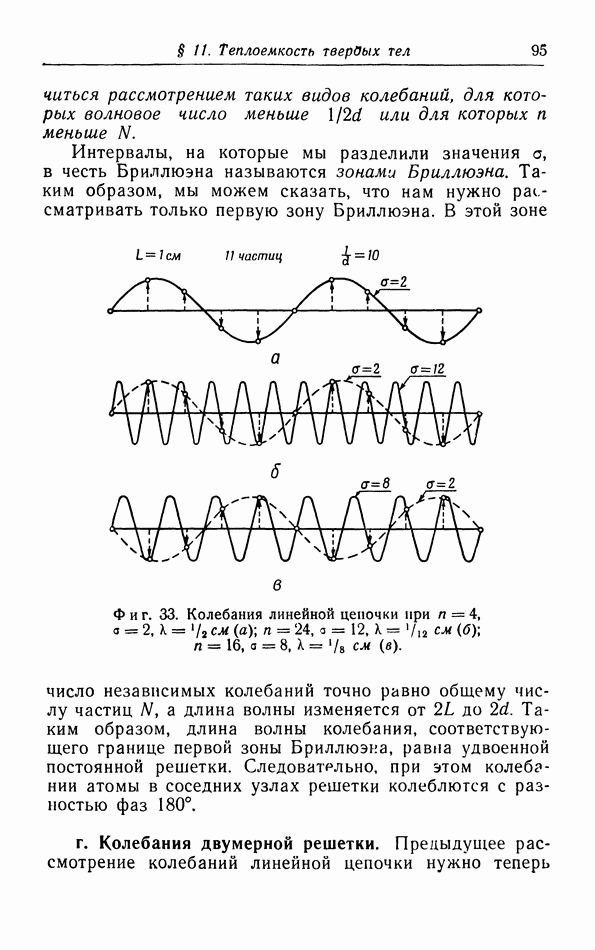
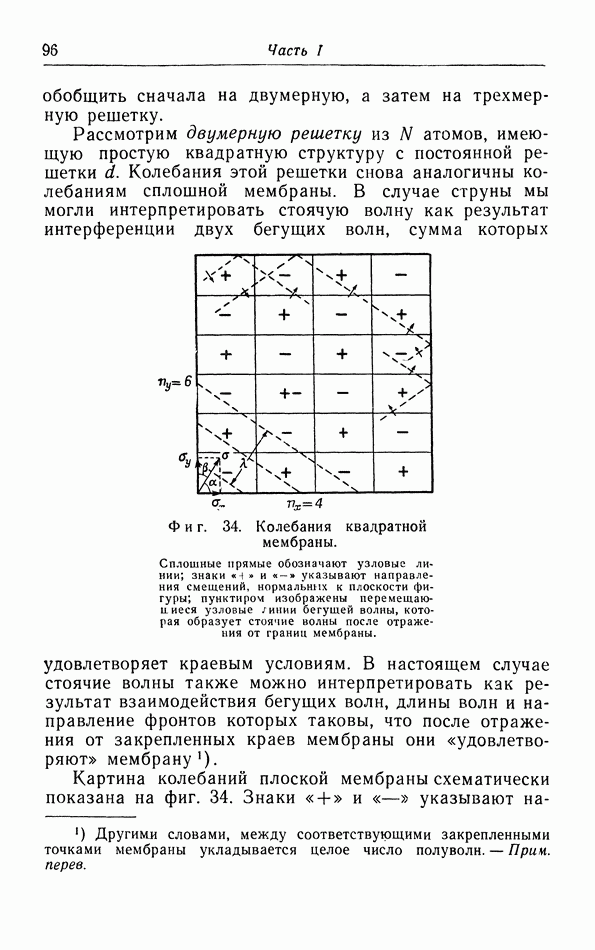
При обсуждении в § 5 уравнения состояния газов и жидкостей мы, чтобы объяснить появление в законе ван дер Ваальса поправки на давление притяжения  показали, что в поверхностном слое молекулы подвергаются действию силы, направленной внутрь газа или жидкости. Чтобы переместить молекулу из объема жидкости в некоторую точку вне этой жидкости, необходимо совершить работу против сил притяжения; следовательно, потенциальная энергия молекулы возрастет. Таким образом, молекулы в поверхностном слое жидкости обладают определенной потенциальной энергией. Для увеличения площади поверхности жидкости необходимо вывести на поверхность дополнительное число молекул;
показали, что в поверхностном слое молекулы подвергаются действию силы, направленной внутрь газа или жидкости. Чтобы переместить молекулу из объема жидкости в некоторую точку вне этой жидкости, необходимо совершить работу против сил притяжения; следовательно, потенциальная энергия молекулы возрастет. Таким образом, молекулы в поверхностном слое жидкости обладают определенной потенциальной энергией. Для увеличения площади поверхности жидкости необходимо вывести на поверхность дополнительное число молекул;
соответствующий прирост потенциальной энергии должен быть обеспечен затратой эквивалентного количества работы. Итак, мы можем сказать, что увеличение энергии, запасенной в поверхностном слое, равно количеству работы, необходимой для создания этого увеличения.
В процессе приближения к равновесному состоянию система всегда стремится к минимальной потенциальной энергии; следовательно, должна быть сила, стремящаяся уменьшить площадь поверхности. Эта сила, приложенная к единице длины по касательной к поверхности, представляет собой поверхностное натяжение  .
.

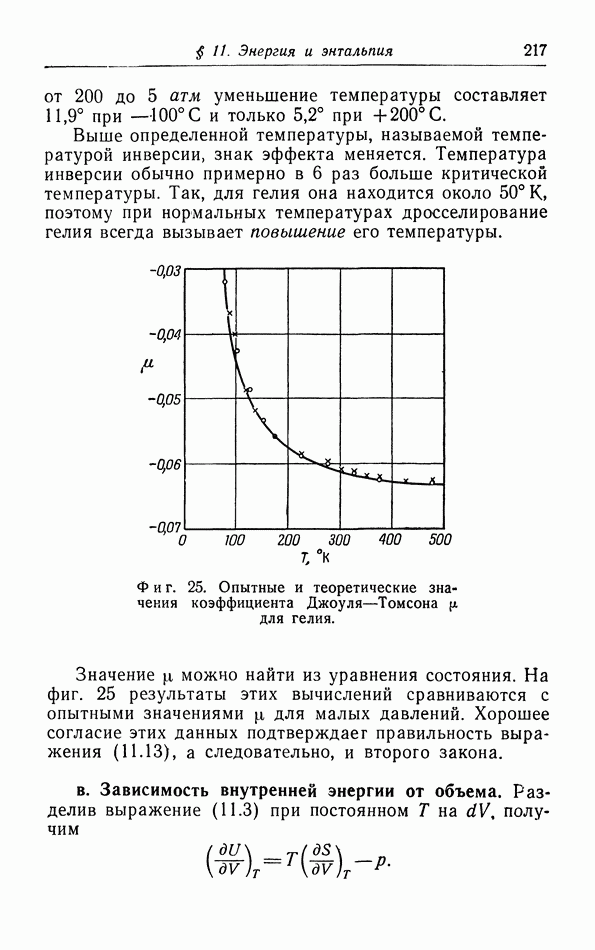
Фиг. 20. Опыт Плато и прибор для измерений поверхностного натяжения  .
.
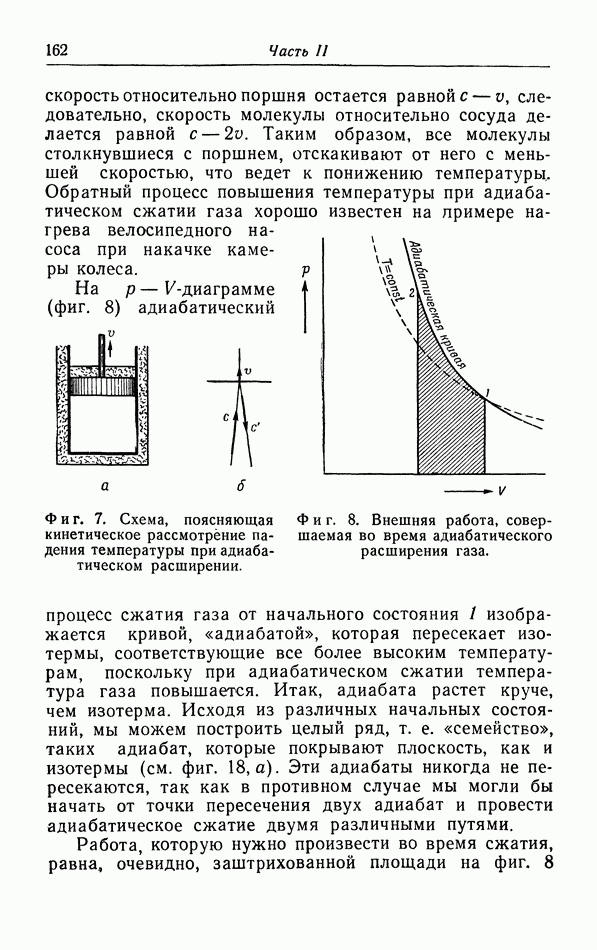
Под воздействием поверхностного натяжения жидкость всегда сокращает свою поверхность до наименьшей возможной площади. Капля жидкости, не испытывающая деформирующего действия силы тяжести, принимает форму шара. Это было хорошо показано в классическом опыте Плато (фиг. 20), который поместил каплю оливкового масла в смесь спирта с водой такой плотности, что эта капля масла находилась во взвешенном состоянии. Капля действительно приняла форму шара — пространственной фигуры, имеющей наименьшее отношение плошади поверхности к объему.
На фиг. 20 изображен также простой прибор для измерения силы поверхностного натяжения Исследуемая жидкость капает из стеклянного капилляра (радиусом  ),
),
нижний конец которого тщательно отполирован. Капли падают в маленький сосуд, помещенный на чашке весов, так что можно определить общий вес капель; зная число капель, мы можем найти среднюю массу одной капли 
Рассмотрим сначала положение непосредственно в момент перед отрывом капли от капилляра. Мы можем считать, что у края капилляра (см. фиг. 20) капля имеет очертание цилиндра. Сила  действующая со стороны висящей капли, стремится растянуть этот цилиндр, однако ей противодействует поверхностное натяжение 7, которое стремится сделать поверхность возможно меньшей. Если бы сила
действующая со стороны висящей капли, стремится растянуть этот цилиндр, однако ей противодействует поверхностное натяжение 7, которое стремится сделать поверхность возможно меньшей. Если бы сила  привела к увеличению длины цилиндра на
привела к увеличению длины цилиндра на  то была бы произведена работа
то была бы произведена работа  Соответствующее увеличение поверхностной энергии составило бы
Соответствующее увеличение поверхностной энергии составило бы  где
где  энергия на единиц площали.
энергия на единиц площали.
Из закона сохранения энергии следует, что

Поверхностная энергия, приходящаяся на единицу площади, численно равна силе, действующей на единицу длины. Эта сила называется поверхностным натяжением, или капиллярной постоянной  жидкости.
жидкости.
Однако при этом возникает некоторое затруднение, связанное с тем, что жидкость охлаждается, когда ее поверхность увеличивается за счет совершаемой извне работы. Мы можем утверждать, что произведенная работа численно равна увеличению энергии пленки только при отсутствии подвода тепла. Однако, когда мы изотермически увеличиваем поверхность жидкости, тепло поглощается из окружающей среды и поэтому приращение энергии  складывается из поглощенного тепла
складывается из поглощенного тепла  и произведенной над поверхностью работы
и произведенной над поверхностью работы  Таким образом, в этом случае превышает соответствующее количество работы
Таким образом, в этом случае превышает соответствующее количество работы  Однако если мы вычтем из
Однако если мы вычтем из  поглощенное тепло
поглощенное тепло  то мы получим величину
то мы получим величину  называемую «свободной энергией», увеличение которой при всех обстоятельствах равно работе, совершенной над поверхностью. Таким образом, согласно более точной формулировке, поверхностное натяжение
называемую «свободной энергией», увеличение которой при всех обстоятельствах равно работе, совершенной над поверхностью. Таким образом, согласно более точной формулировке, поверхностное натяжение 
численно равно свободной энергии  приходящейся на единицу площади
приходящейся на единицу площади
Теперь рассмотрим, как можно измерить поверхностное натяжение при помощи описанного ранее прибора. Капля будет удерживаться на конце капилляра до тех пор, пока ее вес меньше  Однако, как только капля станет настолько тяжелой, что ее вес будет удовлетворять равенству
Однако, как только капля станет настолько тяжелой, что ее вес будет удовлетворять равенству

она оторвется. По известным значениям  можно вычислить поверхностное натяжение
можно вычислить поверхностное натяжение
Укажем значения  для некоторых веществ:
для некоторых веществ:

Чтобы выразить приведенные значения в системе  в ньютонах на метр, нужно разделить их на 1000; например, 76 дин/см
в ньютонах на метр, нужно разделить их на 1000; например, 76 дин/см 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
- б. Жидкие пленки.
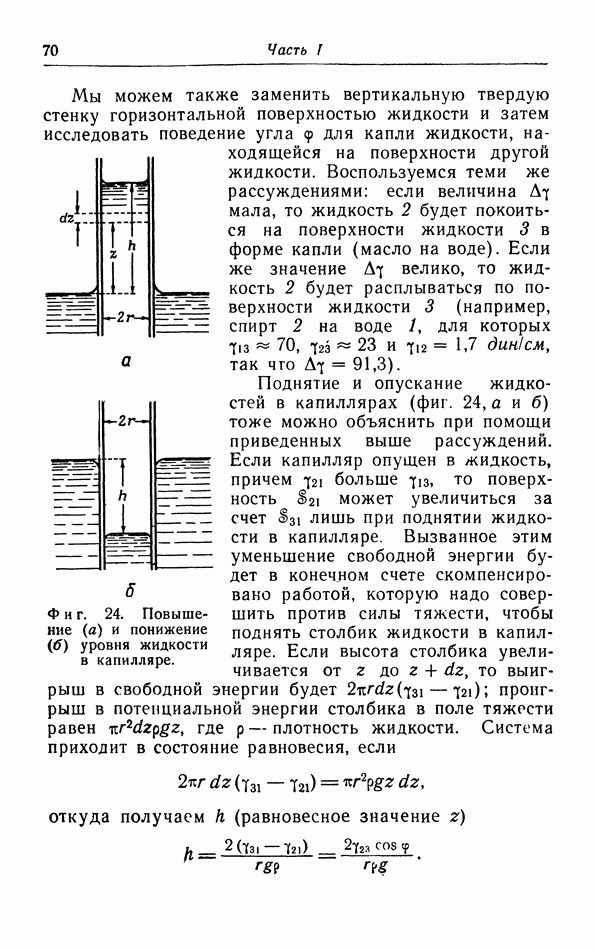
- в. Капиллярное поднятие и понижение уровня жидкости.
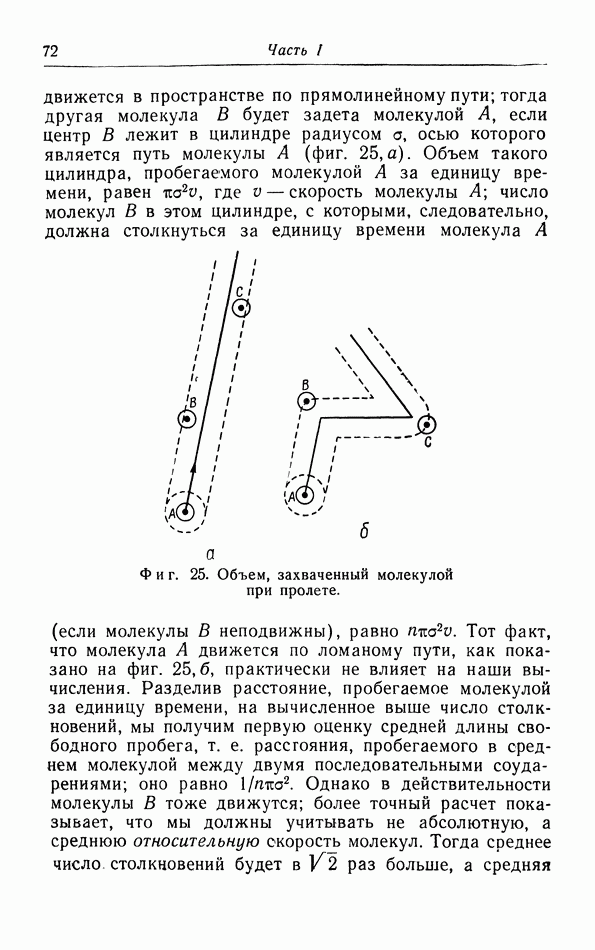
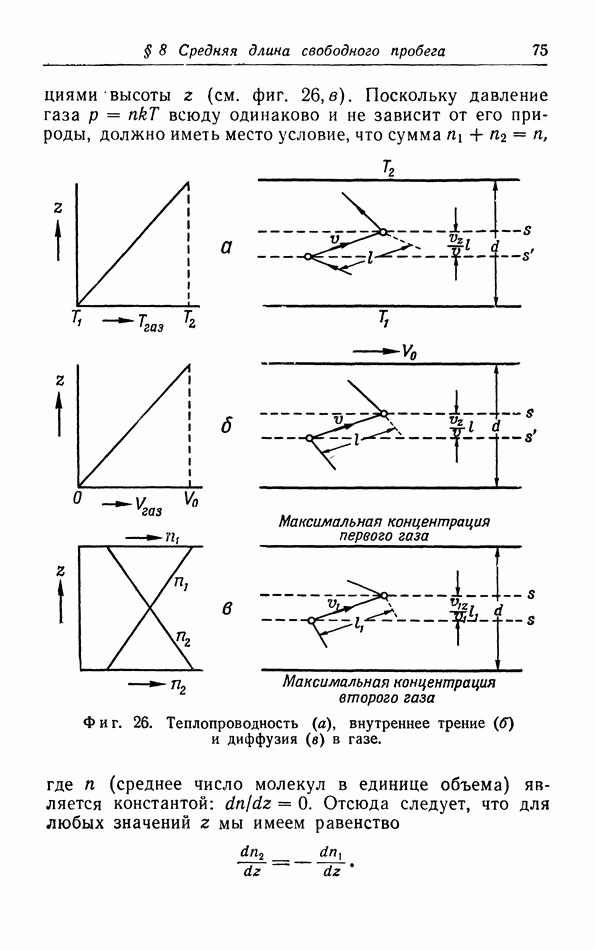
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
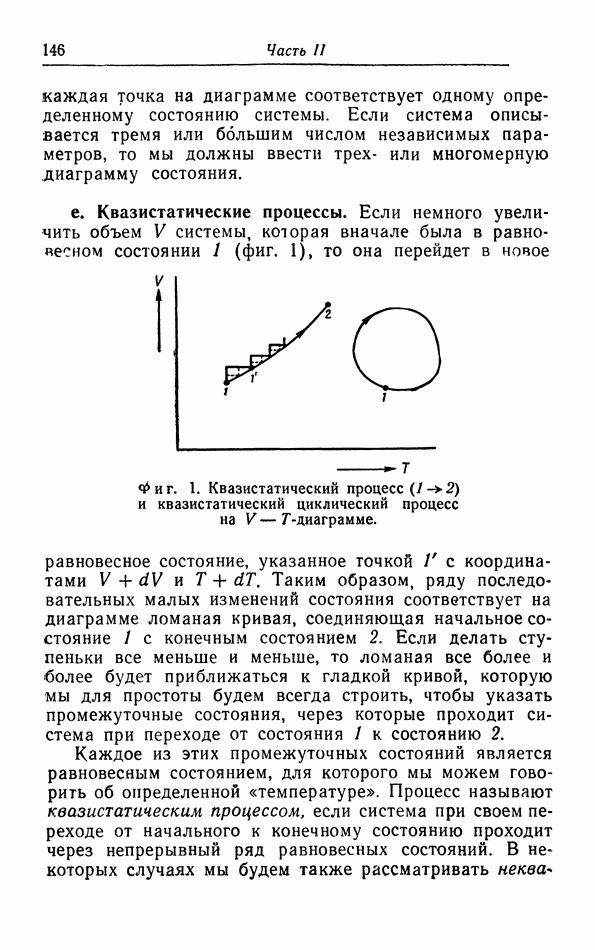
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
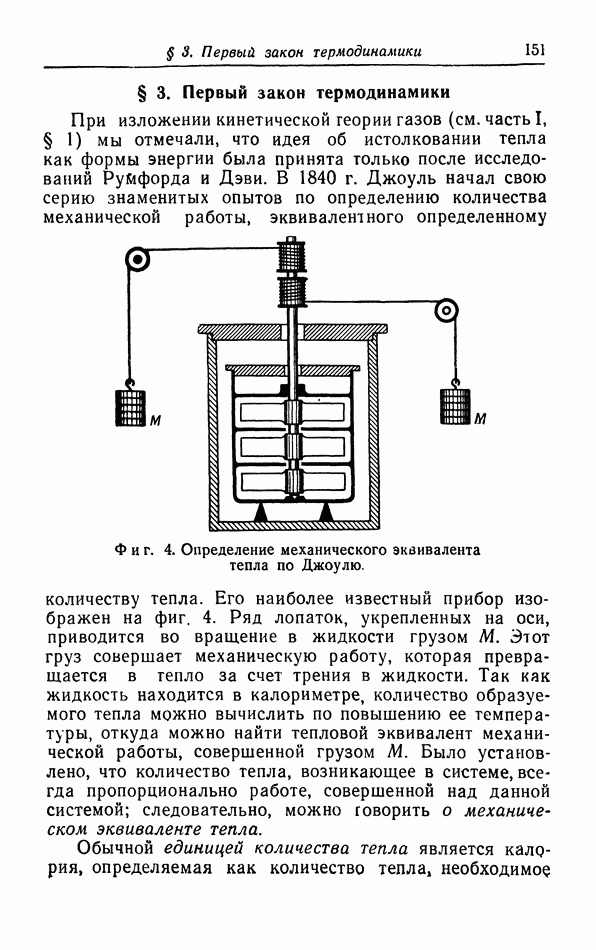
- § 3. Первый закон термодинамики
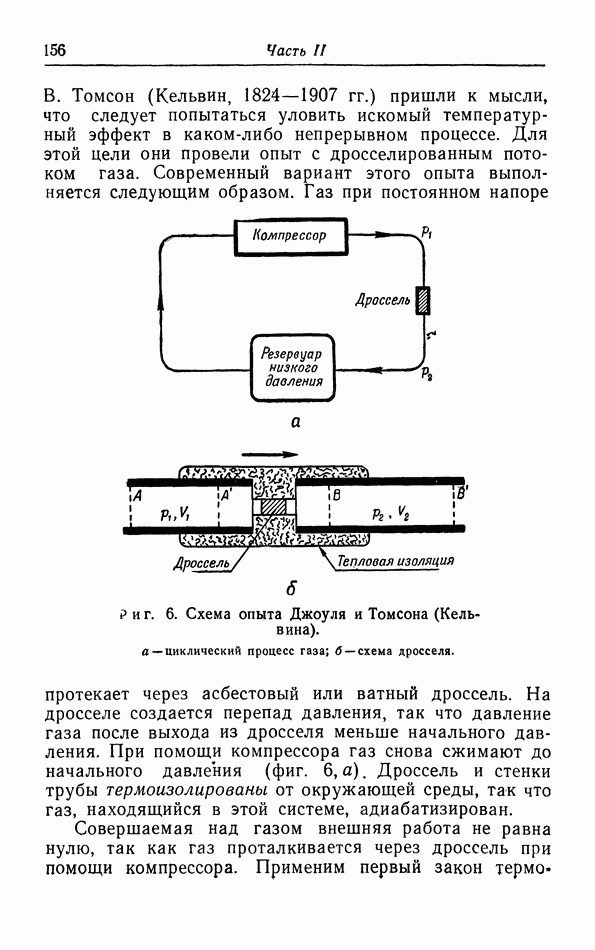
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам