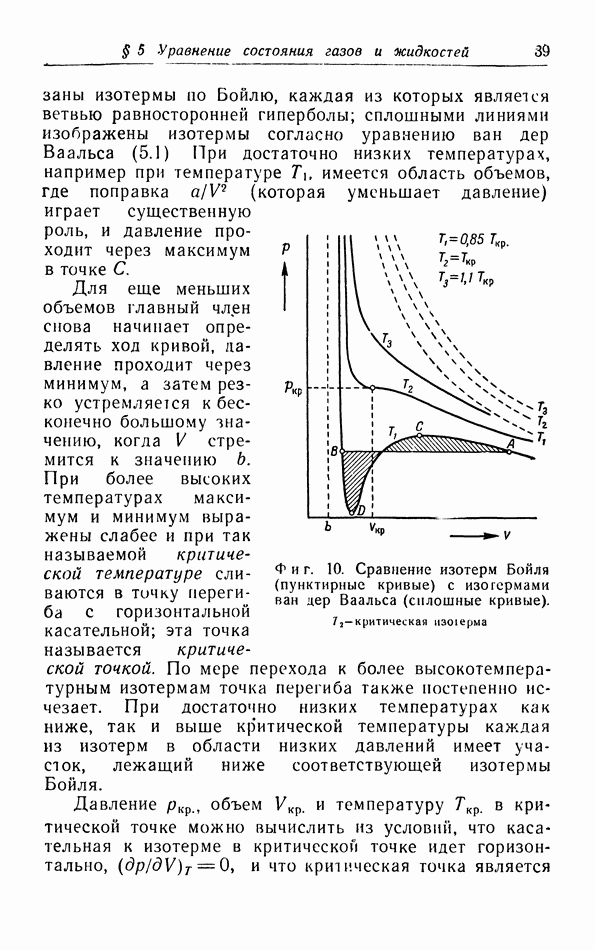
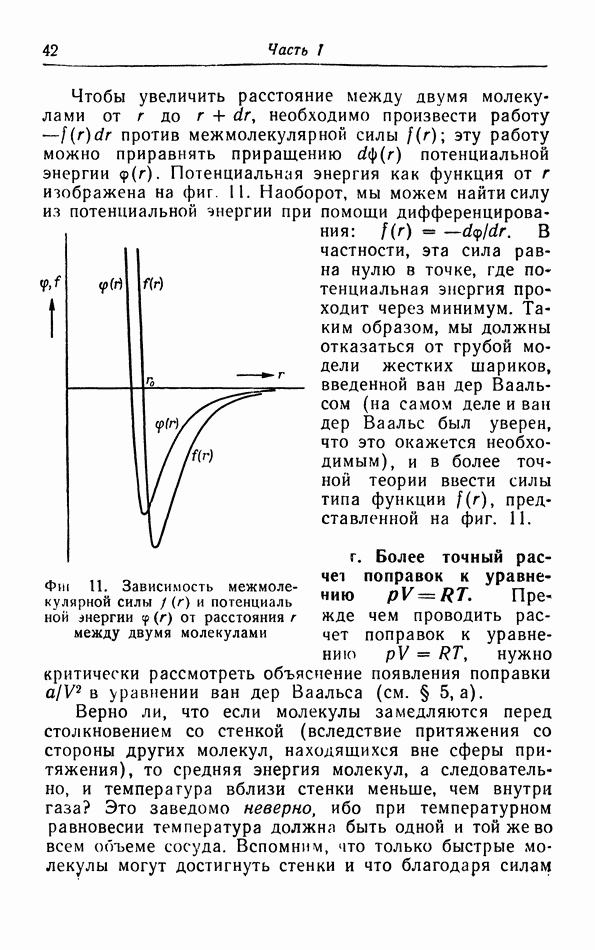
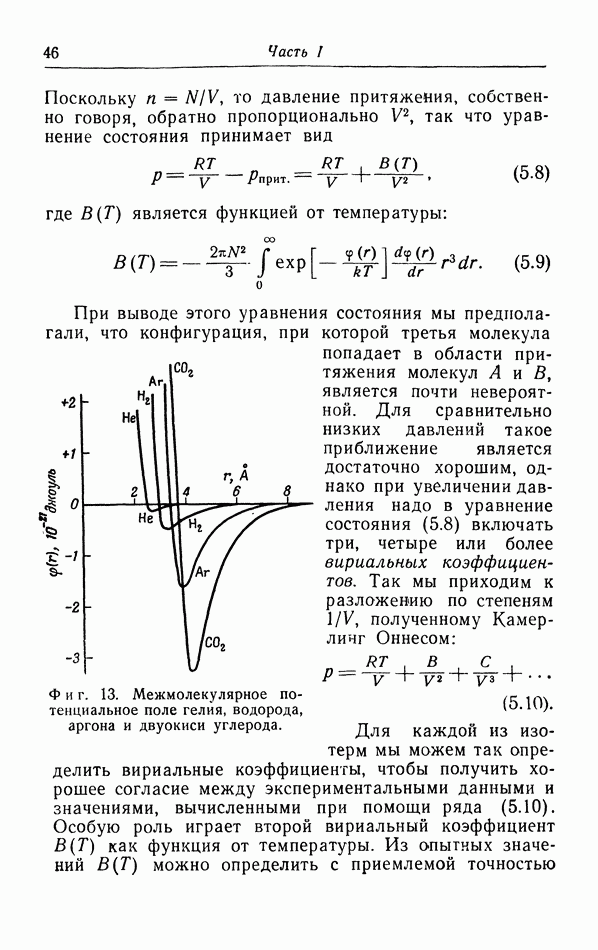
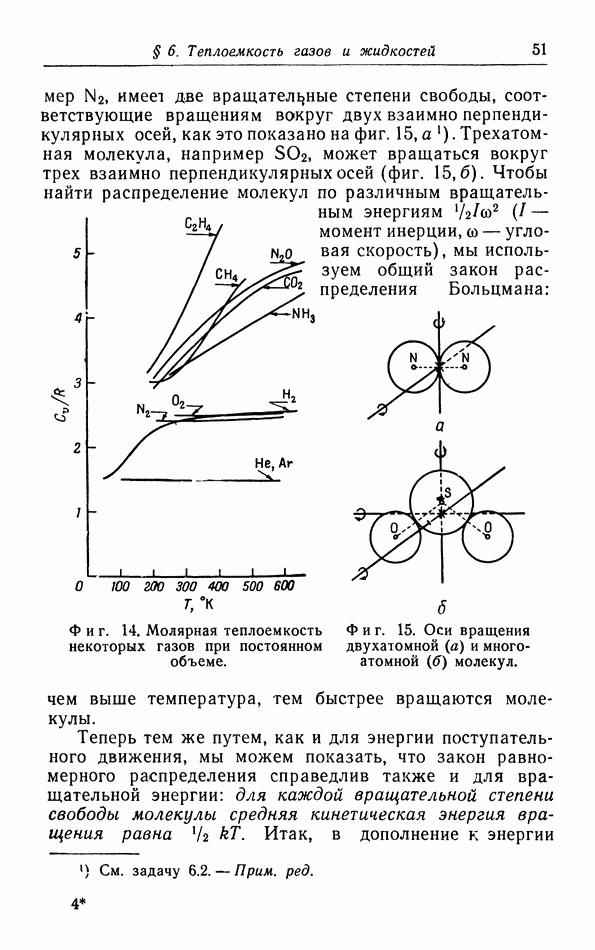
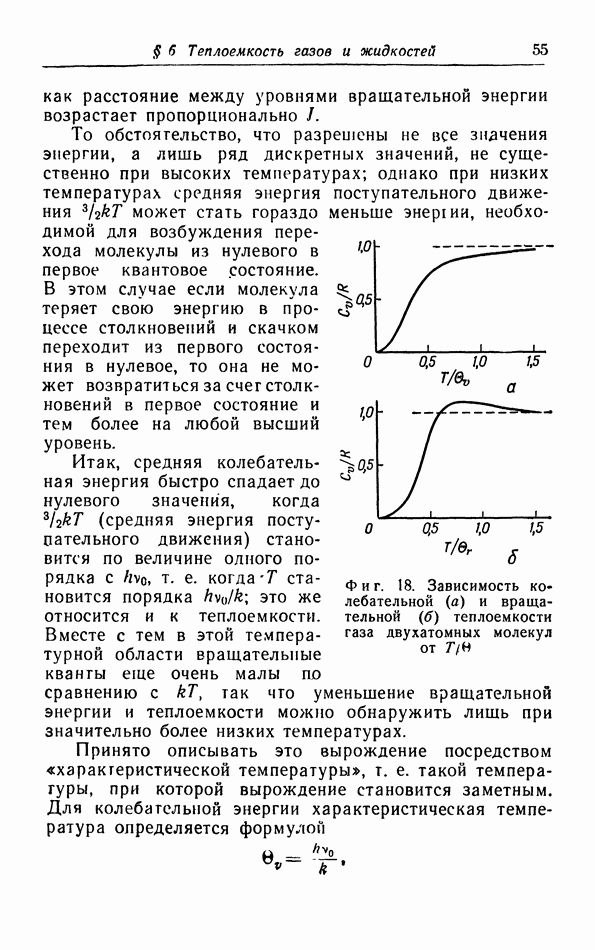
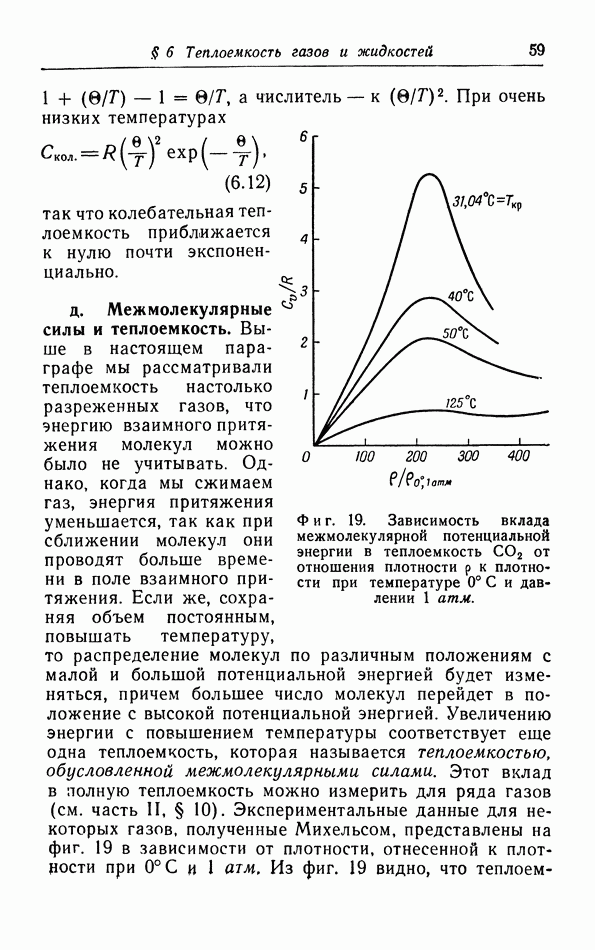
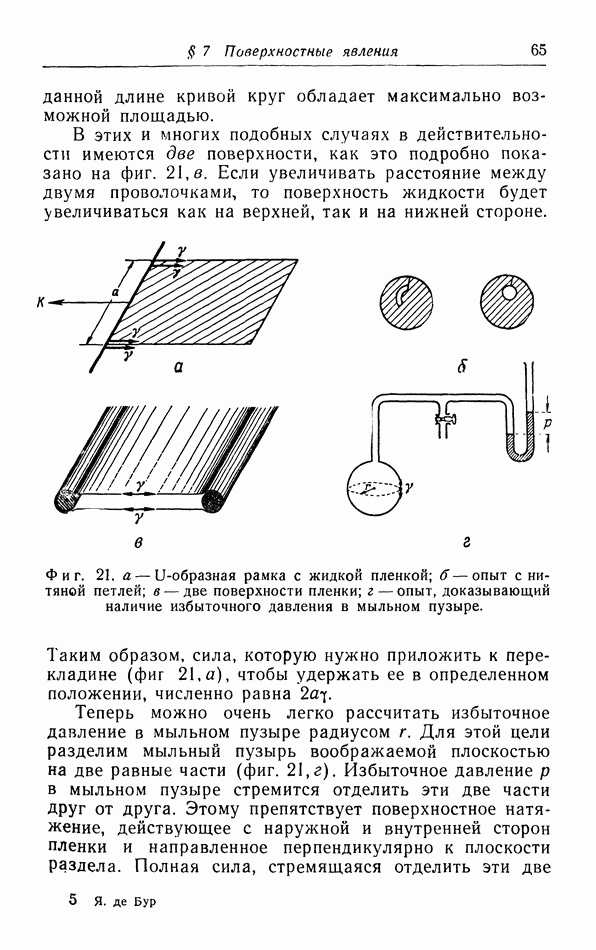
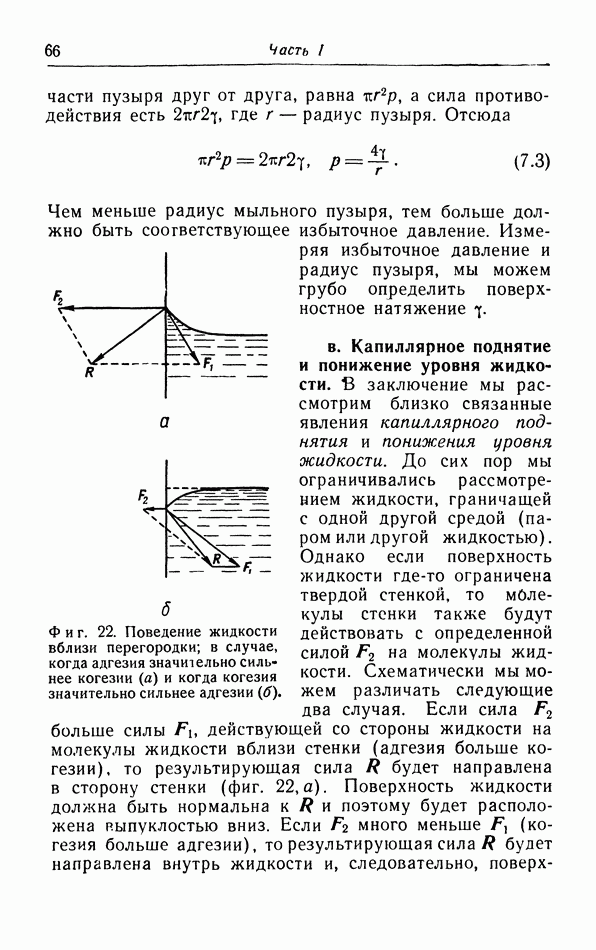
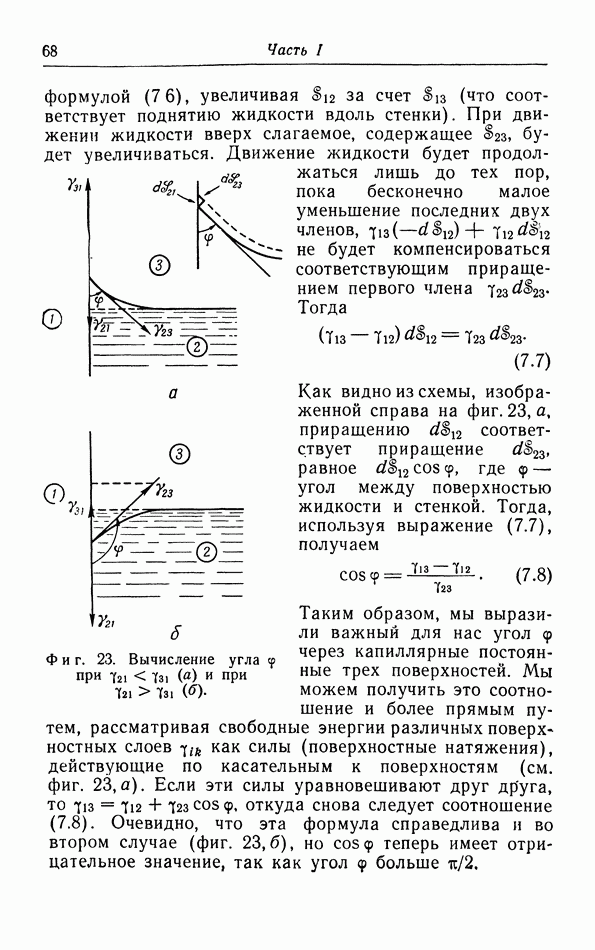
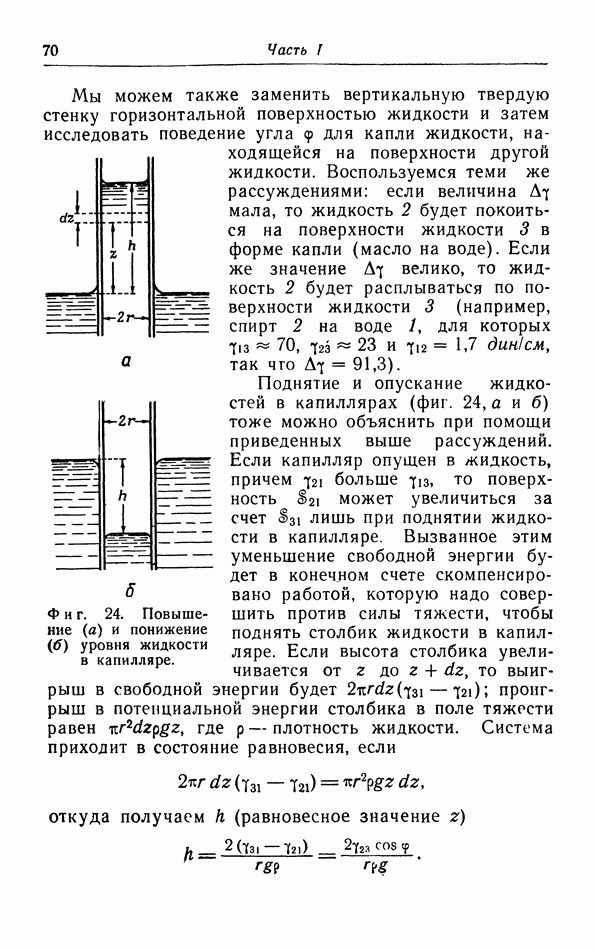
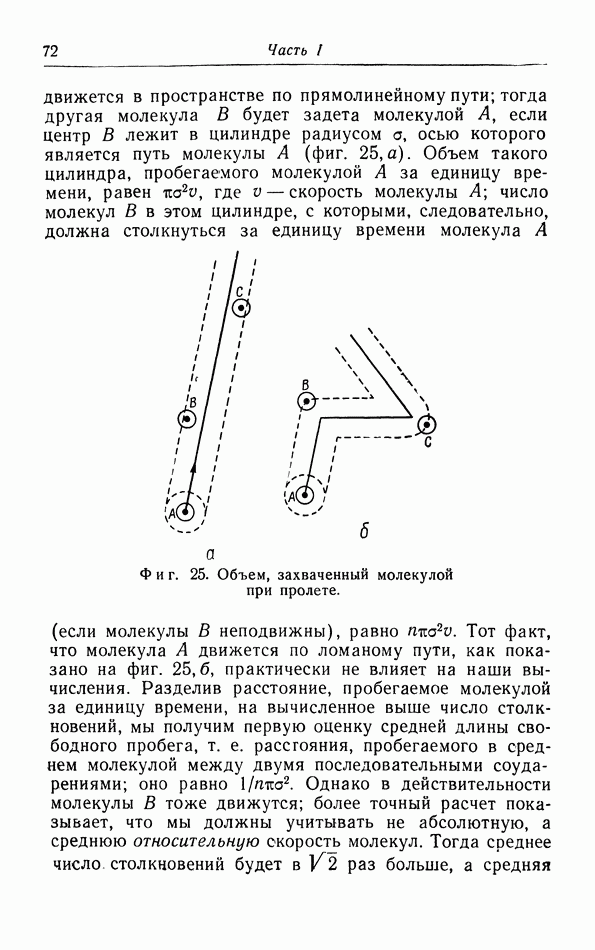
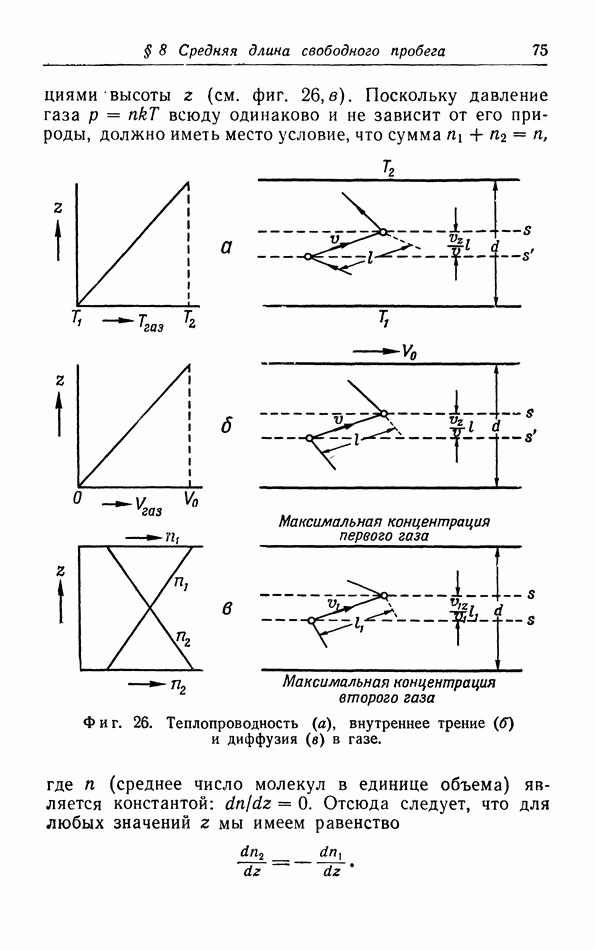
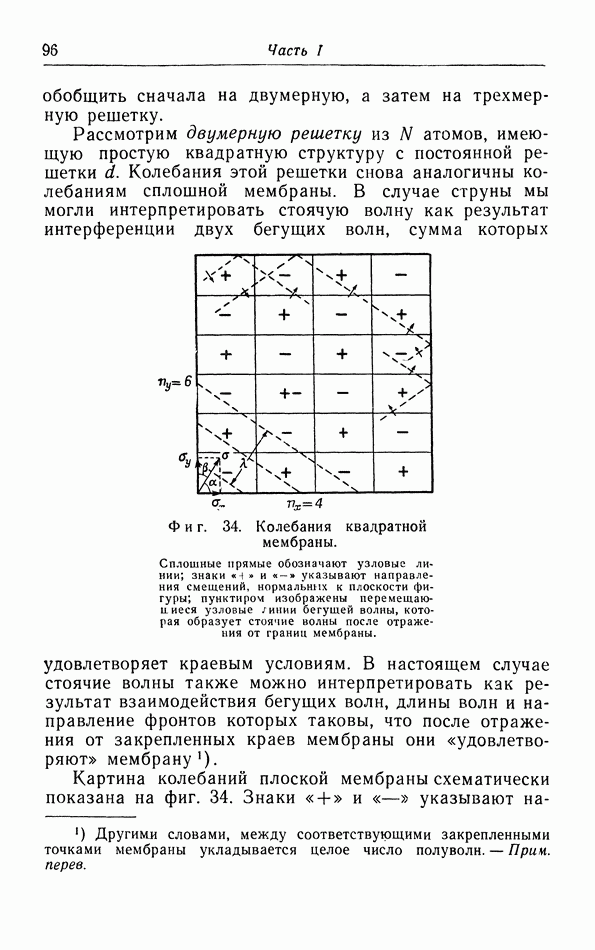
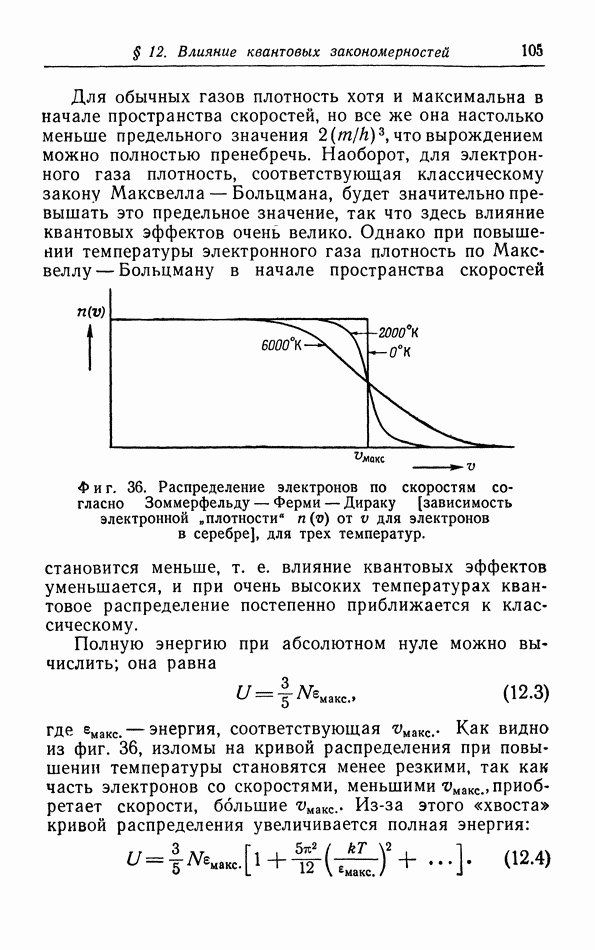
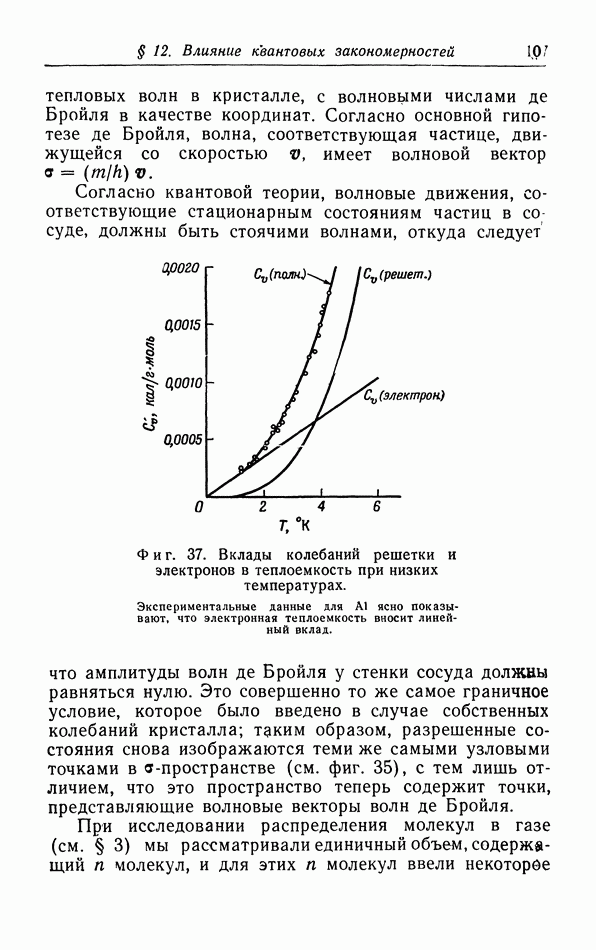
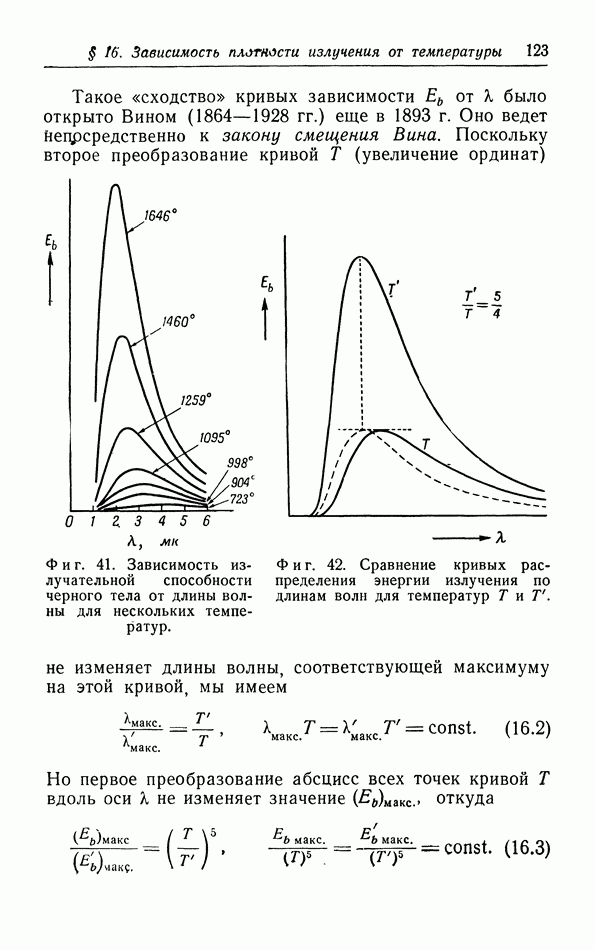
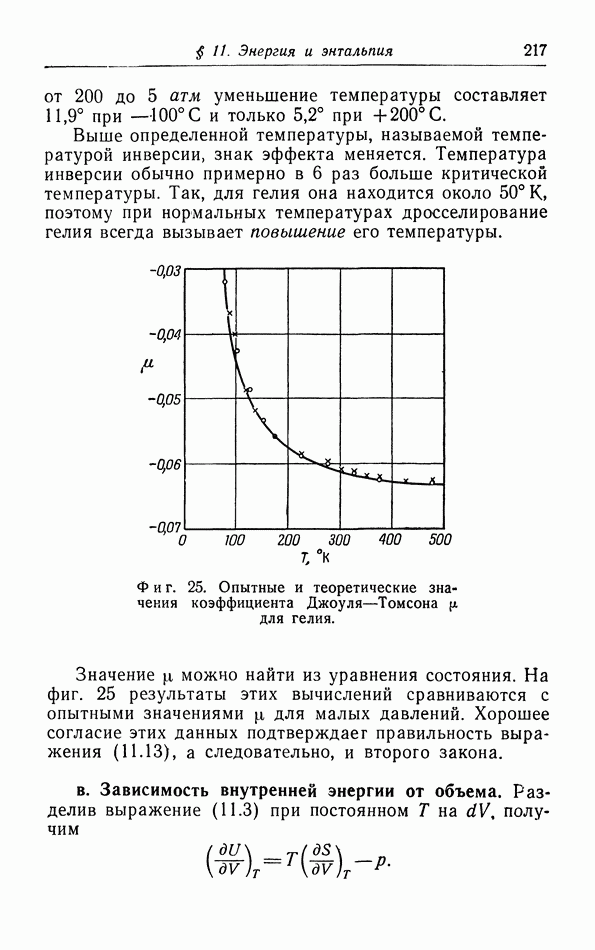
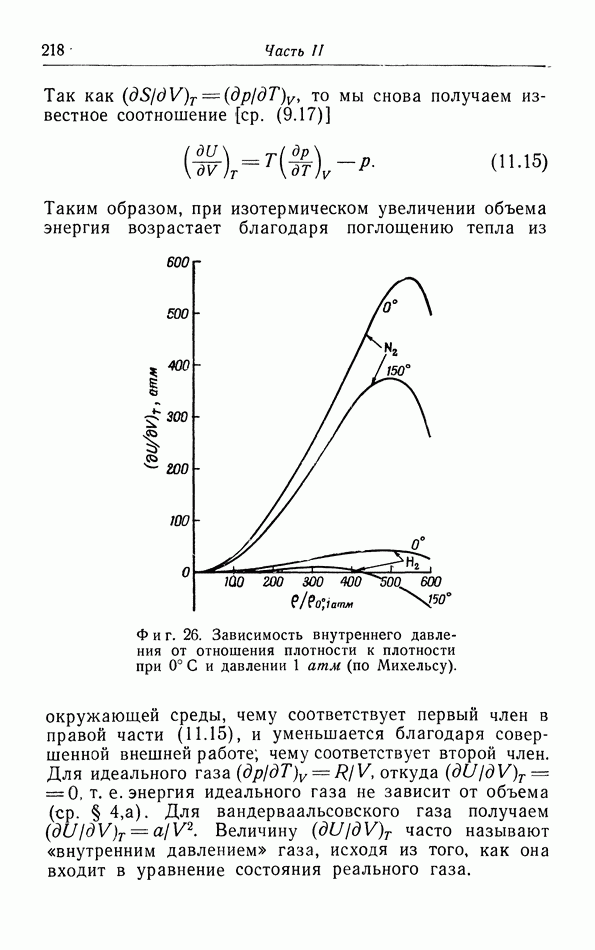
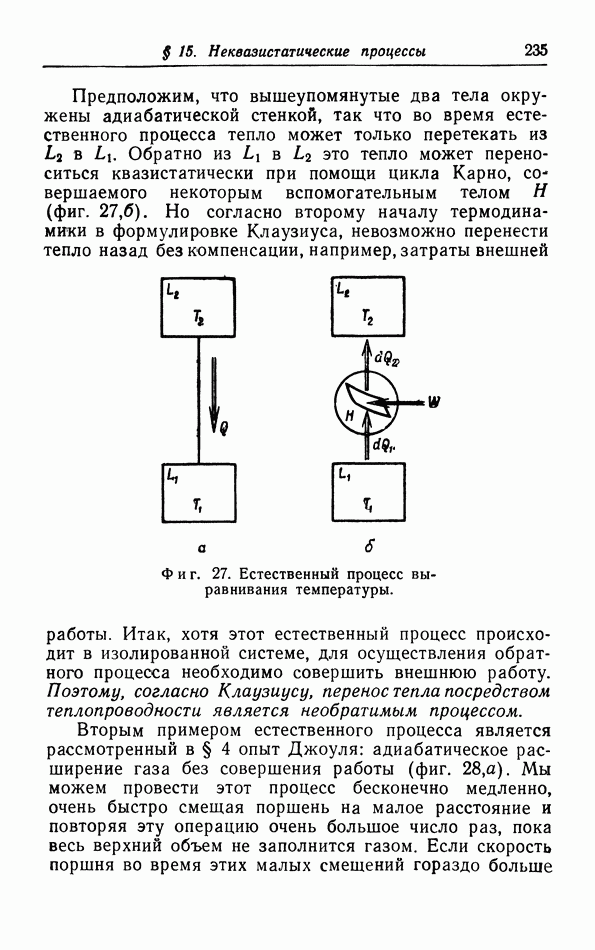
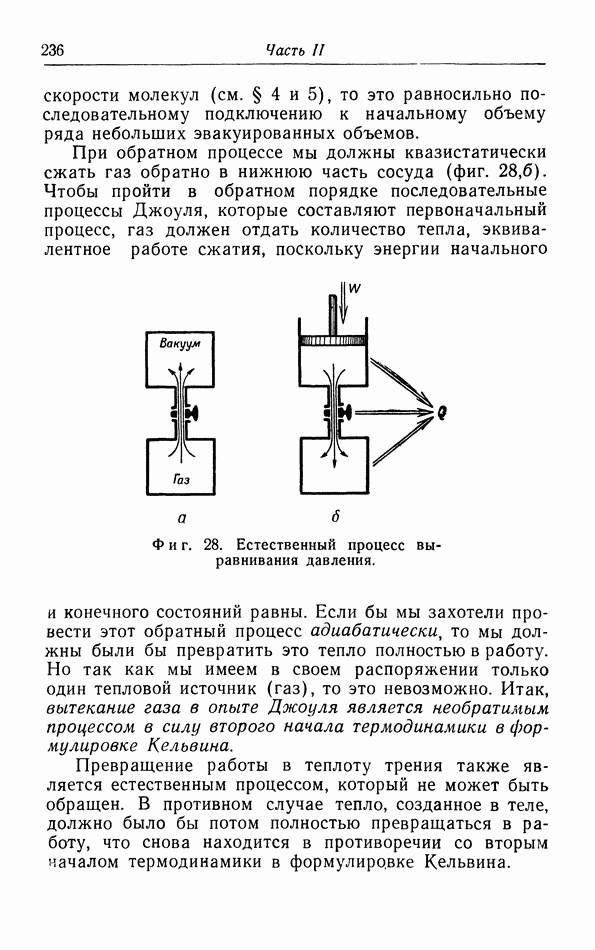
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Уравнение состояния твердых тел
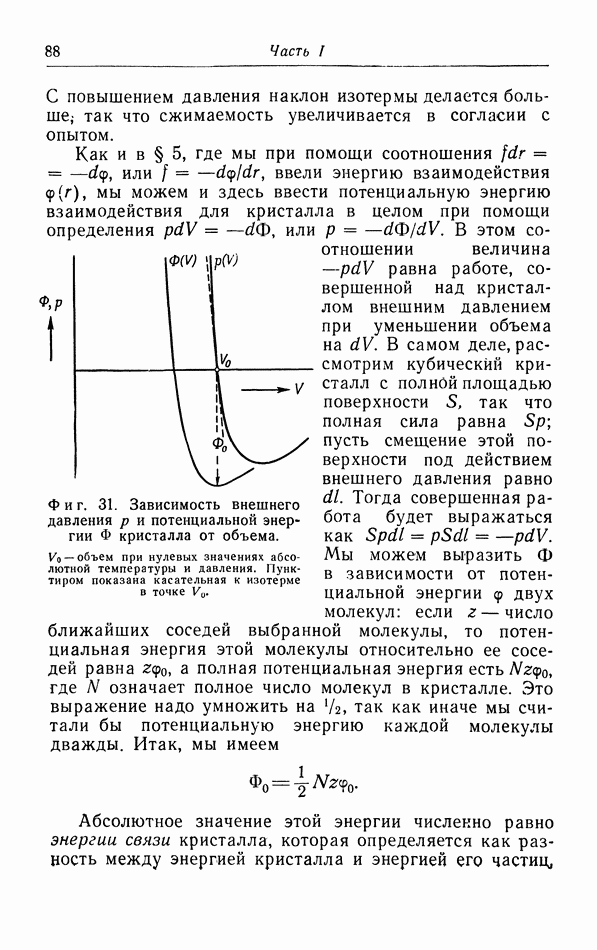
Реальные твердые тела не обладают идеальной решеткой в силу теплового движения атомов или молекул, которые колеблются около своих положений равновесия. Амплитуда этих колебаний увеличивается с повышением температуры. Однако при температурах ниже точки плавления влияние этих колебаний на состояние твердого тела не очень велико, так что пока мы будем ими полностью пренебрегать. Будем рассматривать твердое тело при абсолютном нуле, когда все атомы или молекулы находятся в покое. Для простоты ограничимся изучением таких твердых тел, в которых действуют силы, введенные нами в § 5 под названием межмолекулярных сил.
Одним из наиболее важных свойств этих межмолекулярных сил является их быстрое убывание при увеличении расстояния. Фактически радиус действия этих сил оказывается ограниченным ближайшими соседями.
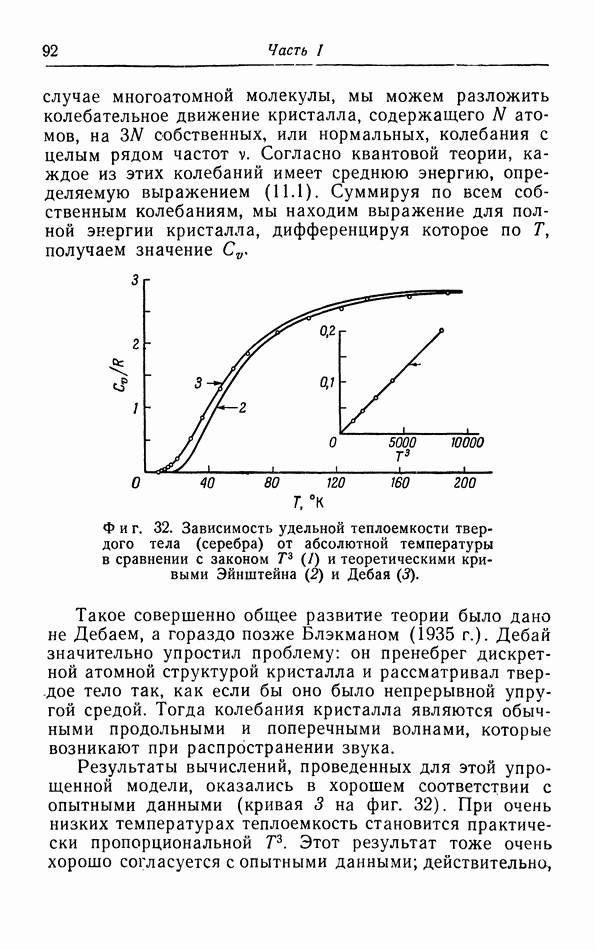
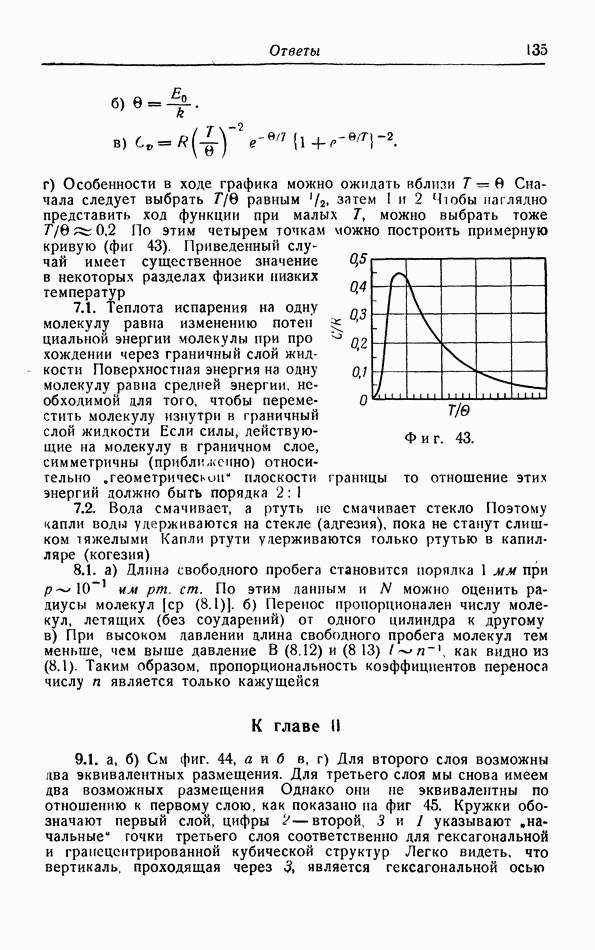
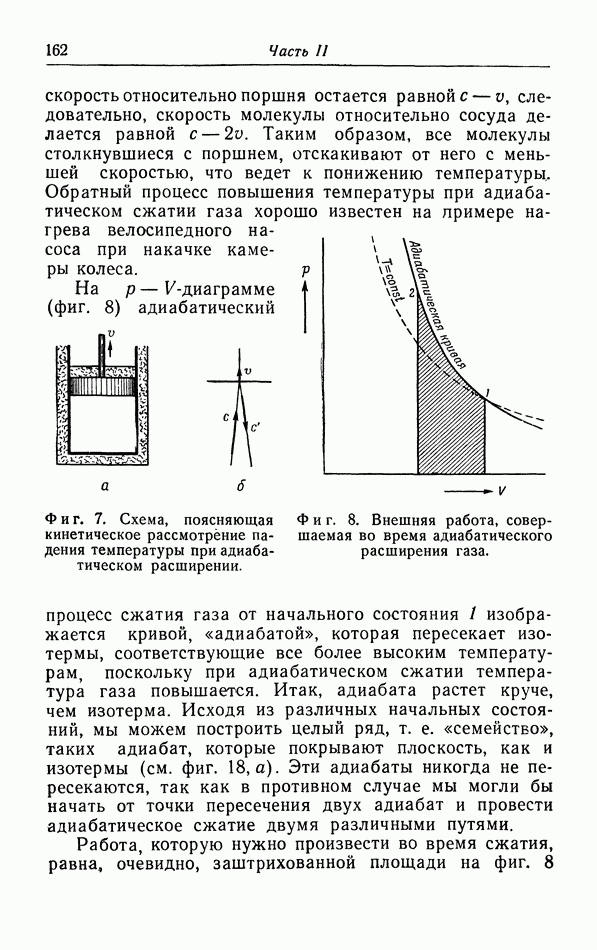
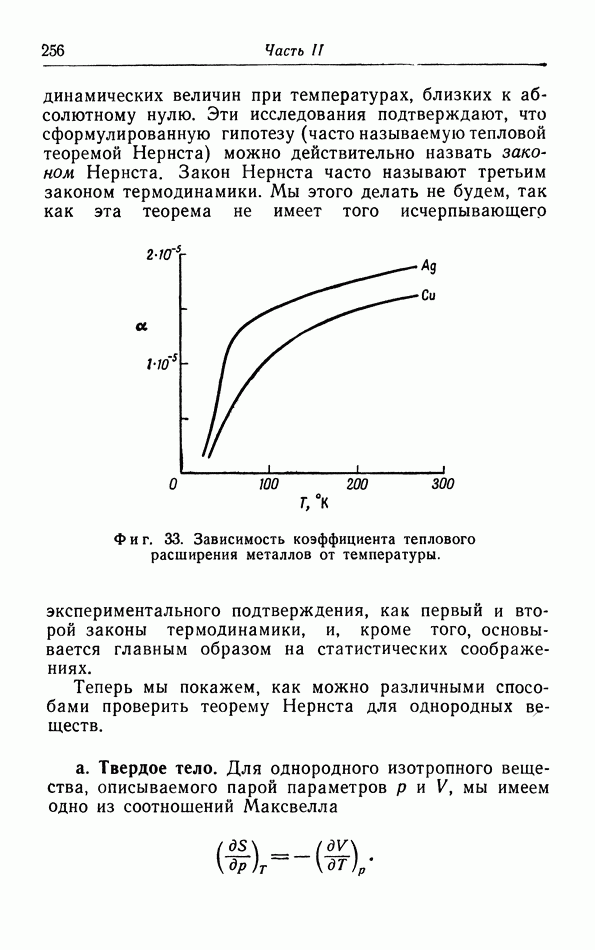
Если на кристал действует внешнее давление, то его объем, а следовательно, и все расстояния в решетке станут меньше. Зная силу взаимодействия между двумя молекулами (см. фиг. 11), можно легко рассчитать действующее на кристалл давление как функцию от объема  Результат показан на фиг. 31. Для объема
Результат показан на фиг. 31. Для объема  соответствующего расстоянию
соответствующего расстоянию  между ближайшими соседями, внешнее давление
между ближайшими соседями, внешнее давление  При постоянном внешнем давлении может быть реализована лишь часть изотермы
При постоянном внешнем давлении может быть реализована лишь часть изотермы  соответствующая объемам
соответствующая объемам  Наклон
Наклон  обратно пропорционален сжимаемости
обратно пропорционален сжимаемости

с повышением давления наклон изотермы делается больше, так что сжимаемость увеличивается в согласии с опытом.

Фиг. 31. Зависимость внешнего давления  и потенциальной энергии
и потенциальной энергии  кристалла от объема.
кристалла от объема.  — объем при нулевых значениях абсолютной температуры и давления. Пунктиром показана касательная к изотерме в точке
— объем при нулевых значениях абсолютной температуры и давления. Пунктиром показана касательная к изотерме в точке 
Как и в § 5, где мы при  соотношения
соотношения  или
или  ввели энергию взаимодействия
ввели энергию взаимодействия  мы можем и здесь ввести потенциальную энергию взаимодействия для кристалла в целом при
мы можем и здесь ввести потенциальную энергию взаимодействия для кристалла в целом при  определения
определения  или
или  . В этом соотношении величина
. В этом соотношении величина  равна работе, совершенной над кристаллом внешним давлением при уменьшении объема на
равна работе, совершенной над кристаллом внешним давлением при уменьшении объема на  . В самом деле, рассмотрихм кубический кристалл с полной площадью поверхности
. В самом деле, рассмотрихм кубический кристалл с полной площадью поверхности  так что полная сила равна
так что полная сила равна  пусть смещение этой поверхности под действием внешнего давления равно
пусть смещение этой поверхности под действием внешнего давления равно  Тогда совершенная работа будет выражаться как
Тогда совершенная работа будет выражаться как  Мы можем выразить
Мы можем выразить  в зависимости от потенциальной энергии
в зависимости от потенциальной энергии  двух молекул: если
двух молекул: если  число ближайших соседей выбранной молекулы, то потенциальная энергия этой молекулы относительно ее соседей равна
число ближайших соседей выбранной молекулы, то потенциальная энергия этой молекулы относительно ее соседей равна  а полная потенциальная энергия есть
а полная потенциальная энергия есть  где
где  означает полное число молекул в кристалле. Это выражение надо умножить на
означает полное число молекул в кристалле. Это выражение надо умножить на  так как иначе мы считали бы потенциальную энергию каждой молекулы дважды. Итак, мы имеем
так как иначе мы считали бы потенциальную энергию каждой молекулы дважды. Итак, мы имеем

Абсолютное значение этой энергии численно равно энергии связи кристалла, которая определяется как разность между энергией кристалла и энергией его частиц,
удаленных на бесконечное расстояние друг от друга (разреженный газ).  от
от  также представлена на фиг. 31. Когда внешнее давление
также представлена на фиг. 31. Когда внешнее давление  энергия
энергия  имеет минимальное значение; в области высоких давлений энергия быстро возрастает, так как молекулы входят в поля отталкивания соседних молекул; при отрицательных давлениях, когда объемы
имеет минимальное значение; в области высоких давлений энергия быстро возрастает, так как молекулы входят в поля отталкивания соседних молекул; при отрицательных давлениях, когда объемы  энергия также возрастает, так как теперь молекулы попадают в поля их взаимного притяжения.
энергия также возрастает, так как теперь молекулы попадают в поля их взаимного притяжения.
Как и в случае жидких пленок (ср. § 7), соотношение  не сохраняется, когда мы принимаем в расчет тепловое движение кристалла. Если мы хотим изотермически сжать кристалл, то тепло должно поглощаться окружающей средой. Соотношение
не сохраняется, когда мы принимаем в расчет тепловое движение кристалла. Если мы хотим изотермически сжать кристалл, то тепло должно поглощаться окружающей средой. Соотношение  можно теперь использовать лишь в том случае, если мы будем интерпретировать
можно теперь использовать лишь в том случае, если мы будем интерпретировать  как свободную энергию, которая отличается от потенциальной энергии.
как свободную энергию, которая отличается от потенциальной энергии.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
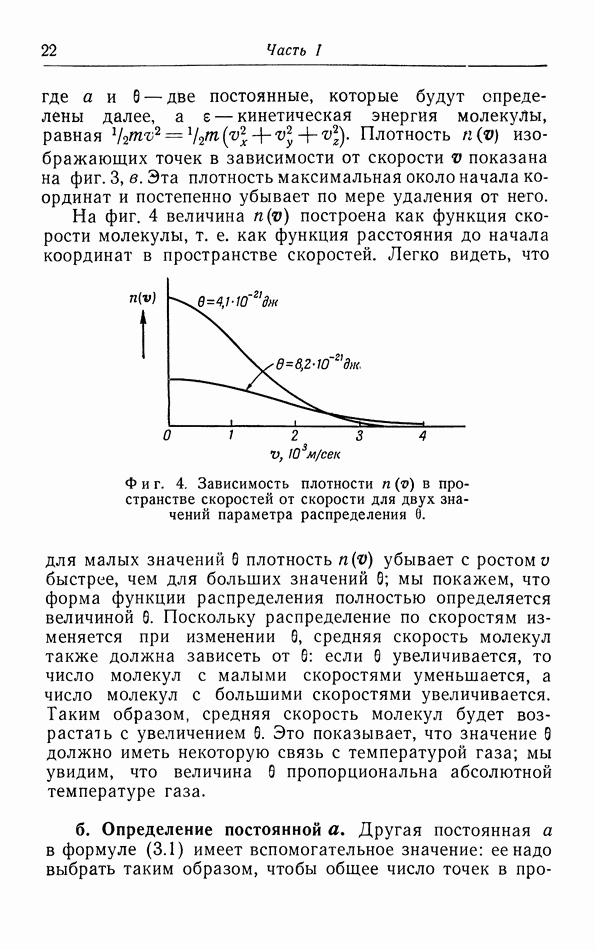
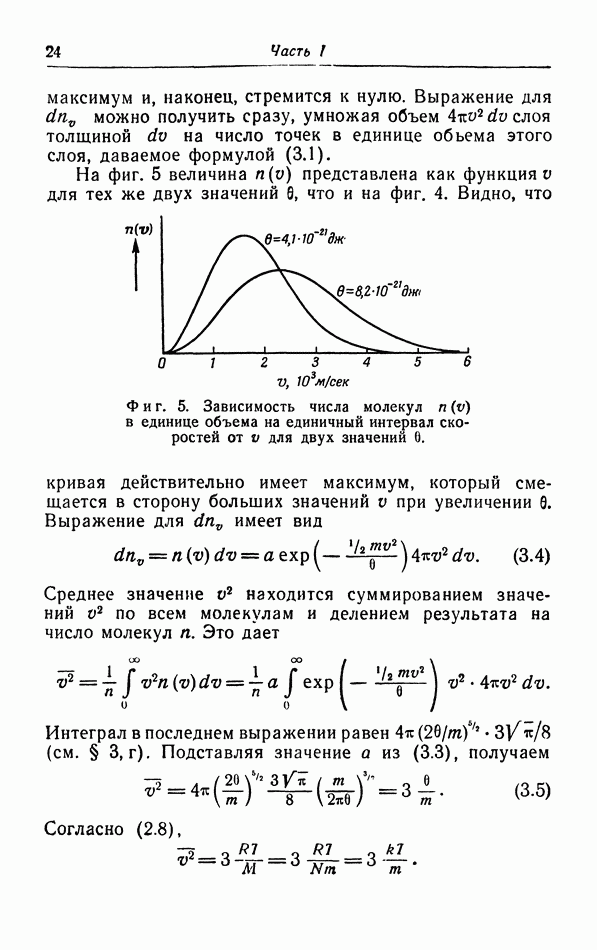
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
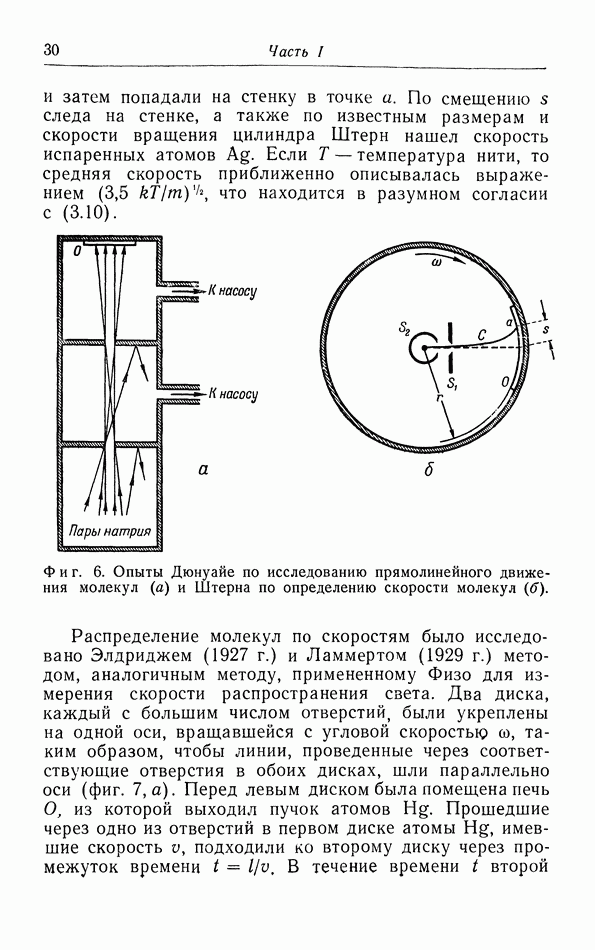
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
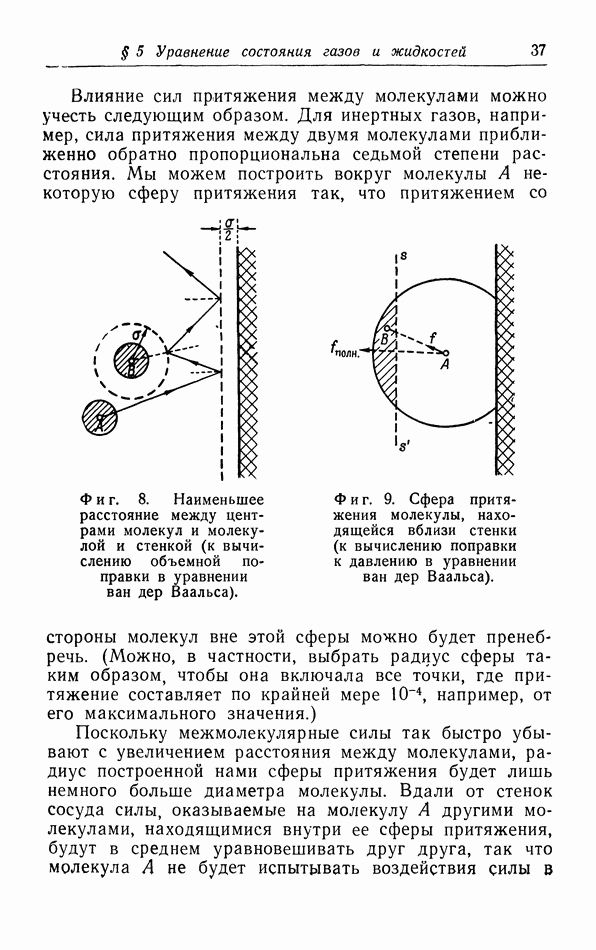
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
- б. Жидкие пленки.
- в. Капиллярное поднятие и понижение уровня жидкости.
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
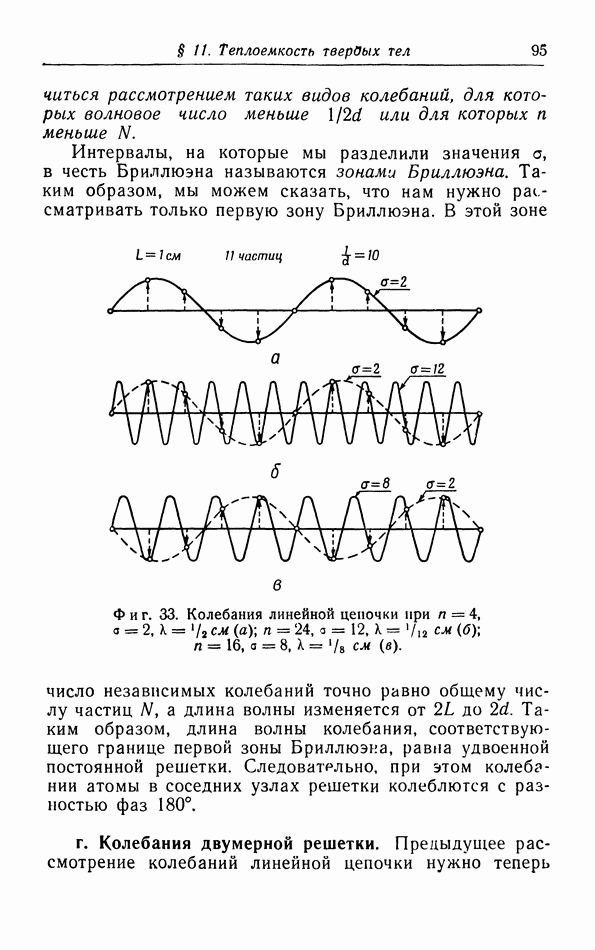
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
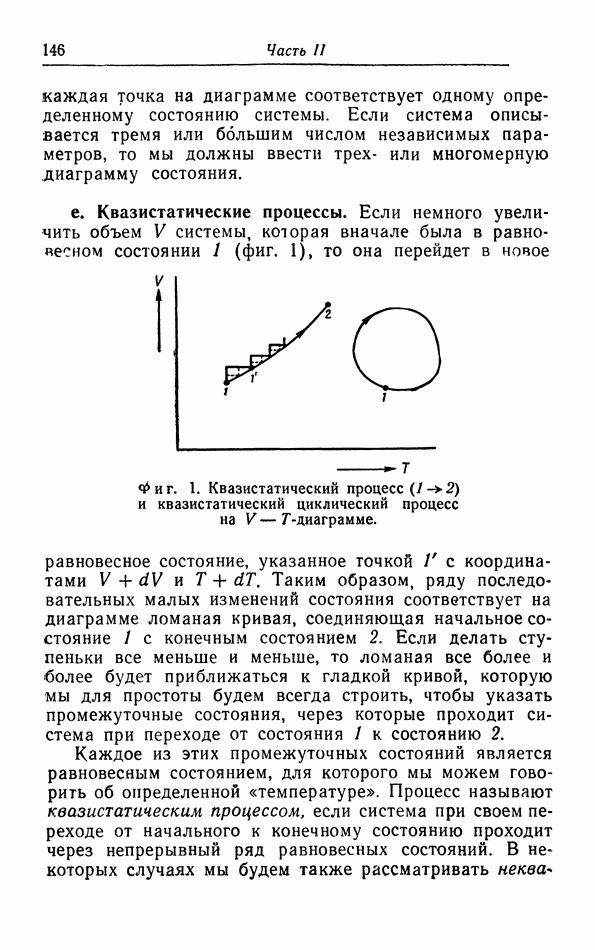
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
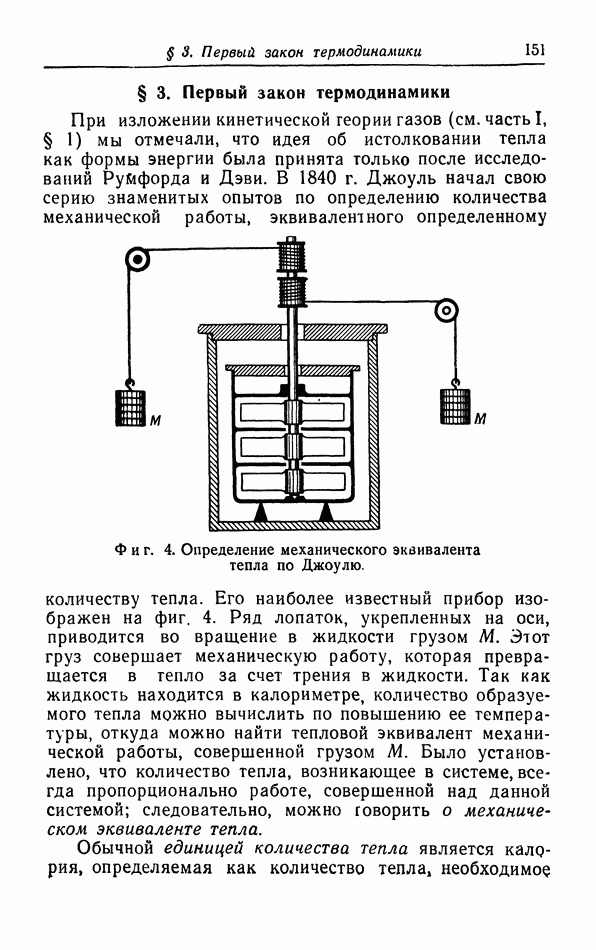
- § 3. Первый закон термодинамики
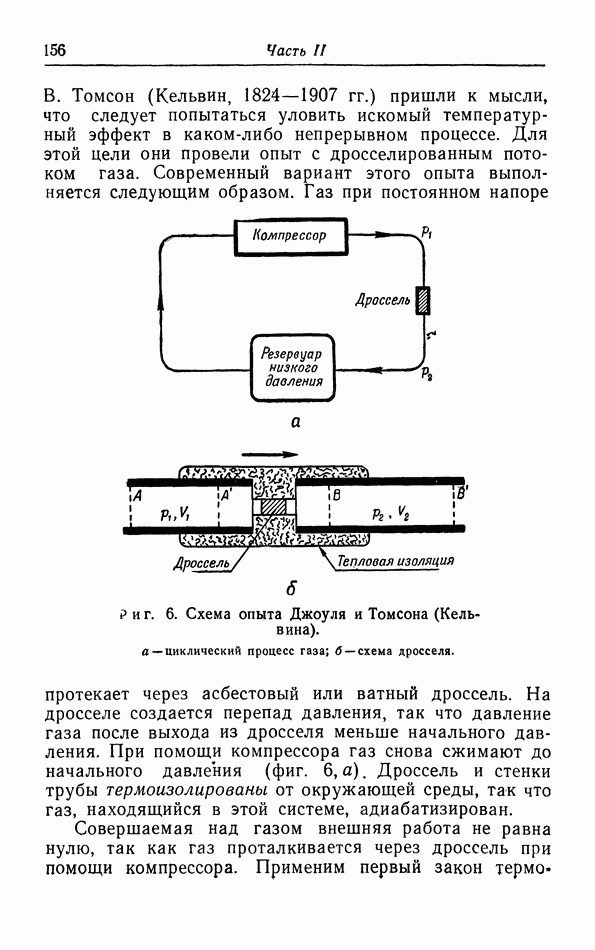
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
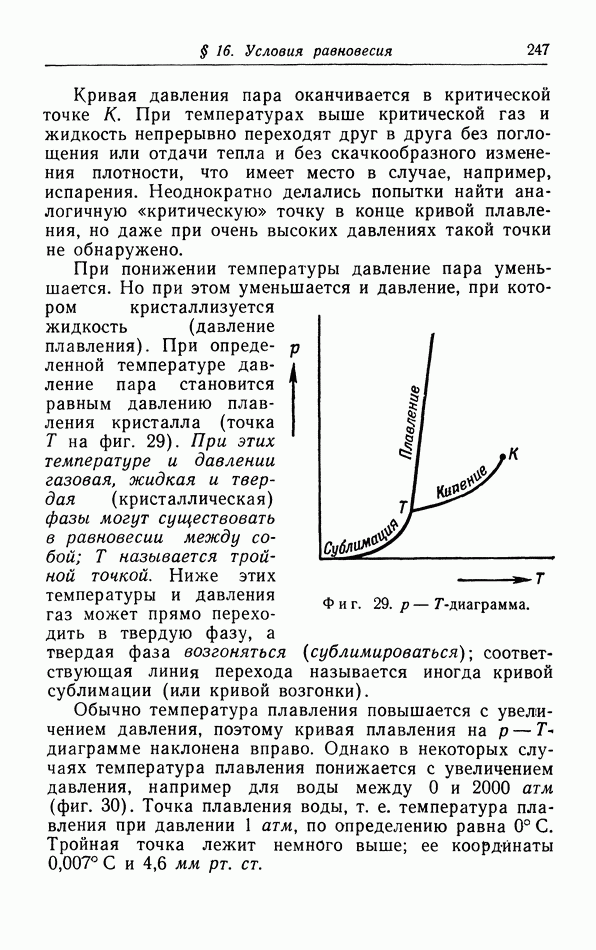
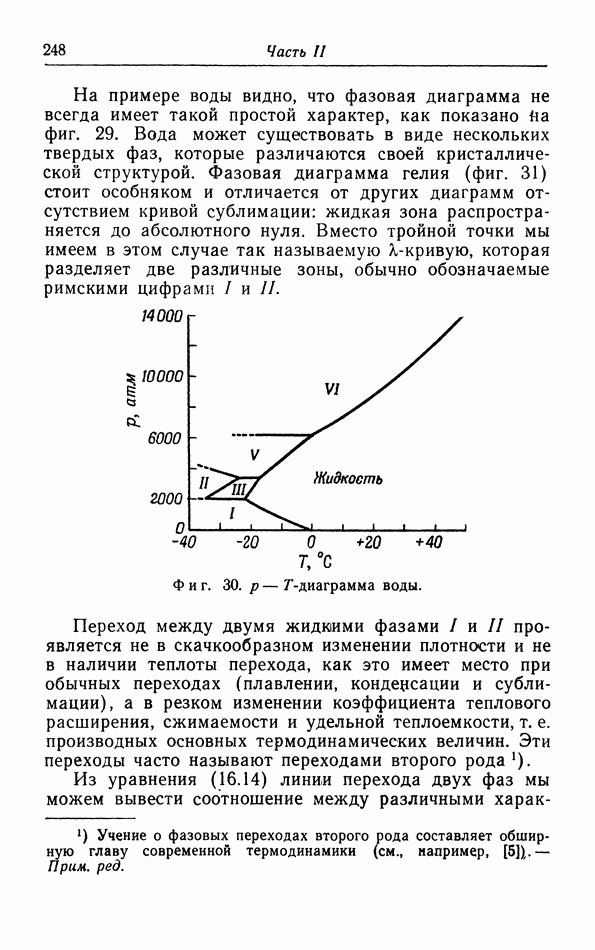
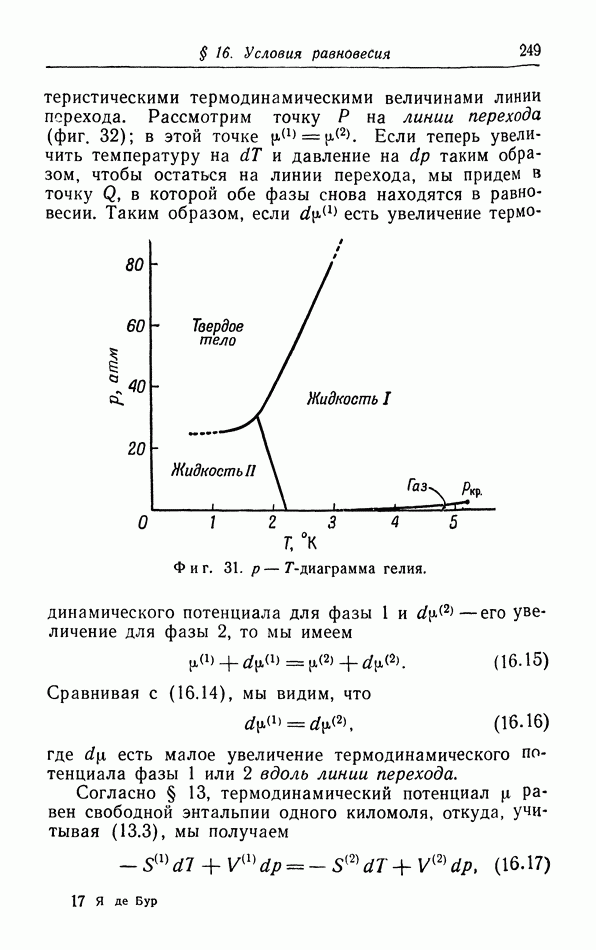
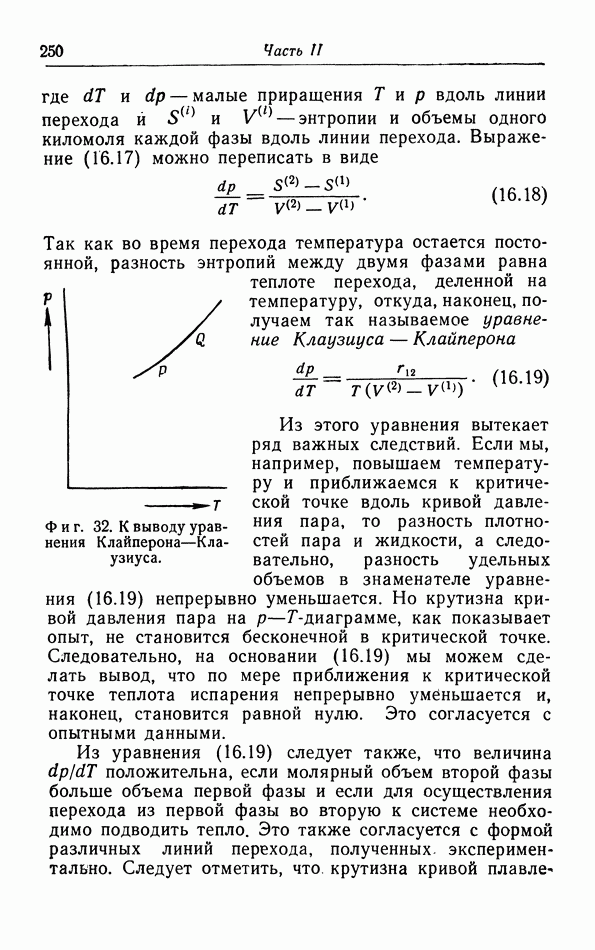
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
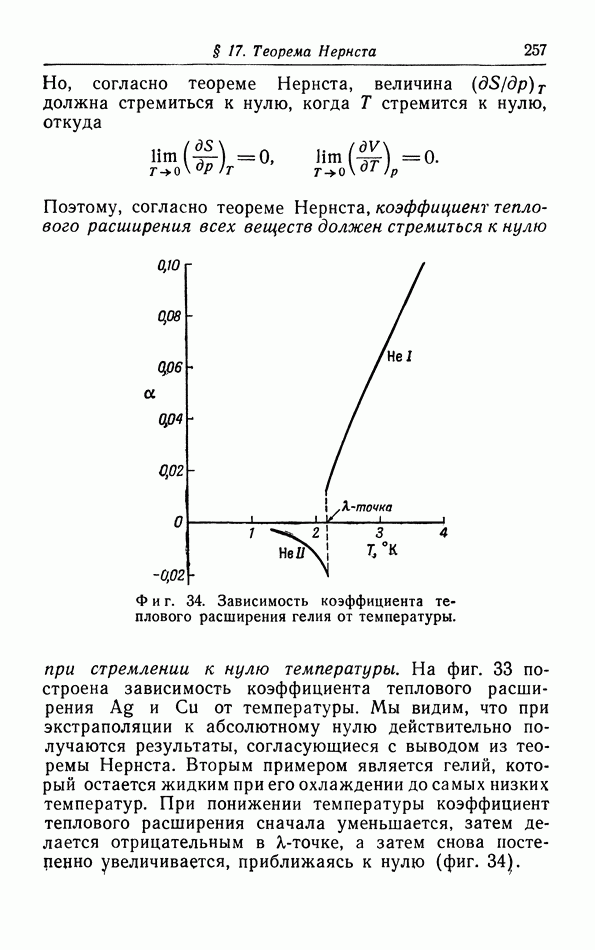
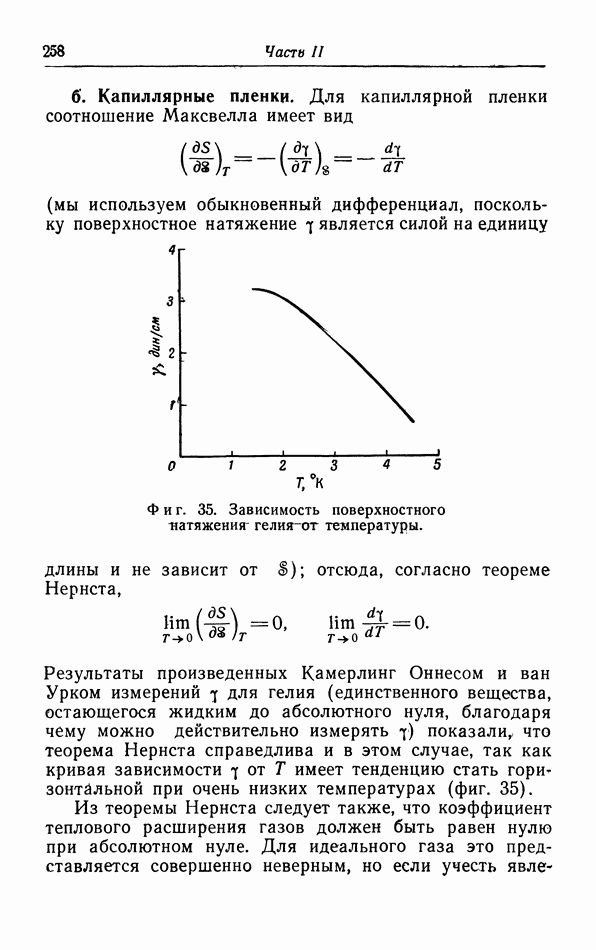
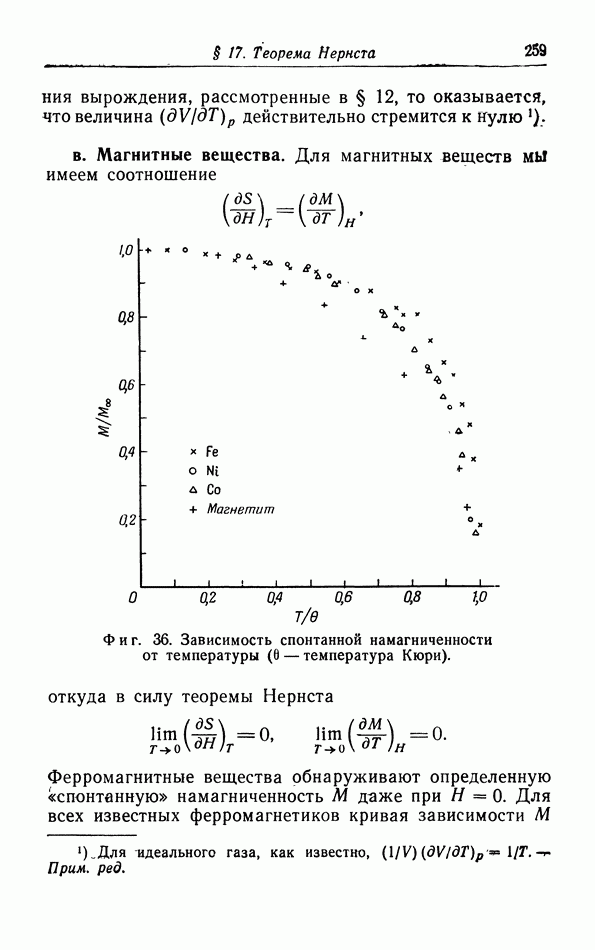
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам