| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
е. Теория Дебая.
Для вычисления средних энергий при помощи выражения (11.1) нужно определить частоты, соответствующие допускаемым волновым числам. Для этого необходимо решить динамическое уравнение движения. Подобные расчеты выполнили Борн, Карман
и Блэкман. Они показали, что для каждого значений о должно быть три решения (в случае, когда волновой вектор параллелен одной из кристаллических осей, мы можем интерпретировать эти решения как частоты двух поперечных и одной продольной стоячих волн с волновым числом а). Каждому из этих колебаний можно приписать среднюю колебательную энергию (11.1), и тогда полная энергия кристалла равна сумме вкладов каждого из  типов колебаний. Дифференцируя эту сумму по температуре, мы найдем удельную теплоемкость.
типов колебаний. Дифференцируя эту сумму по температуре, мы найдем удельную теплоемкость.
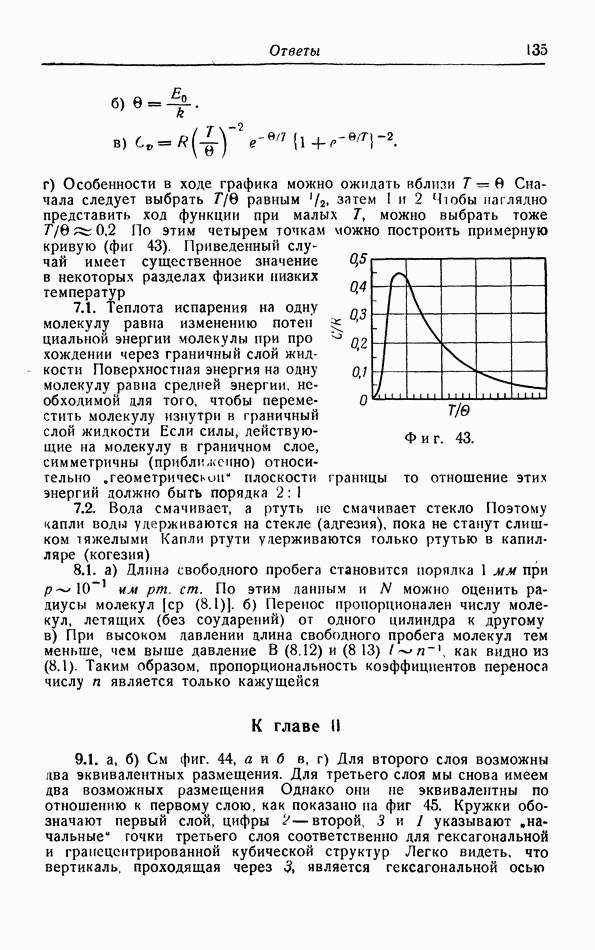
Дебай пренебрег дискретной структурой твердого тела, что значительно упростило задачу и позволило ему (в 1912 г.) вычислить  непосредственно без решения динамического уравнения. Это возможно потому, как указал Дебай, что при низких температурах, когда преобладают квантовые законы, существенное значение имеют лишь колебания с малой энергией
непосредственно без решения динамического уравнения. Это возможно потому, как указал Дебай, что при низких температурах, когда преобладают квантовые законы, существенное значение имеют лишь колебания с малой энергией  т. е. с низкой частотой, а следовательно, с большой длиной волны, так как только эти колебания дают заметный вклад в энергию. Но в случае длинных волн мы можем пренебречь дискретной структурой кристалла и полагать, что
т. е. с низкой частотой, а следовательно, с большой длиной волны, так как только эти колебания дают заметный вклад в энергию. Но в случае длинных волн мы можем пренебречь дискретной структурой кристалла и полагать, что  где с — скорость распространения в нем звука. Поскольку высокие частоты, т. е. малые длины волн, не дают вклада в энергию, Дебай предположил, что его соотношение справедливо для всех длин волн.
где с — скорость распространения в нем звука. Поскольку высокие частоты, т. е. малые длины волн, не дают вклада в энергию, Дебай предположил, что его соотношение справедливо для всех длин волн.
Поскольку Дебай пренебрег дискретной структурой при расчете  допустимо пренебречь конкретной формой первой зоны Бриллюэна и принять в качестве ее границы не куб, а октант сферы такого радиуса, чтобы число типов колебаний внутри этого октанта было равным
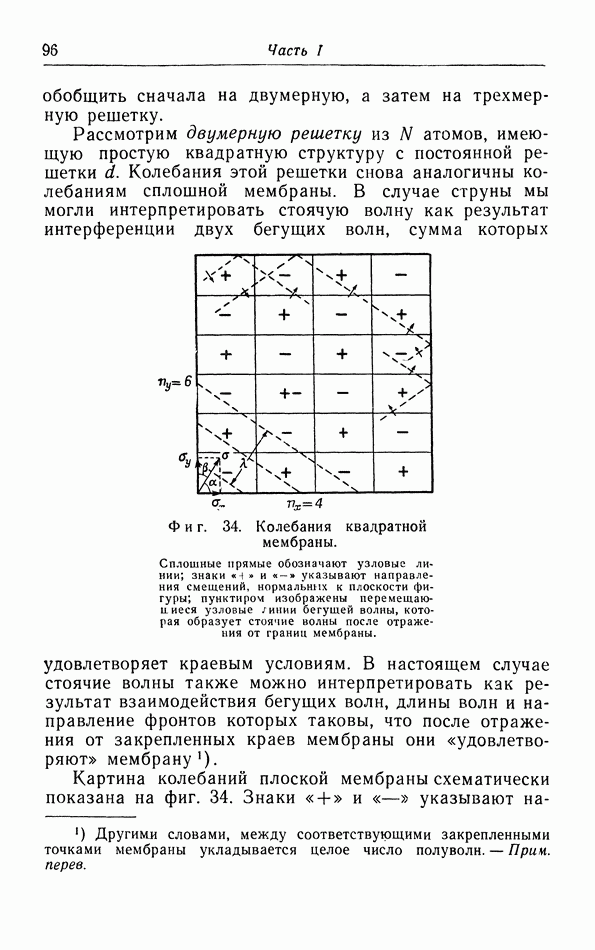
допустимо пренебречь конкретной формой первой зоны Бриллюэна и принять в качестве ее границы не куб, а октант сферы такого радиуса, чтобы число типов колебаний внутри этого октанта было равным  (см. фиг. 35). Итак, объем октанта должен быть равен объему куба. Пусть радиус октанта, т. е. максимальное значение а, есть
(см. фиг. 35). Итак, объем октанта должен быть равен объему куба. Пусть радиус октанта, т. е. максимальное значение а, есть  тогда мы должны положить
тогда мы должны положить

Отсюда, согласно Дебаю, минимальная длина волны одинакова для всех направлений распространения и
приблизительно в 1,61 раза больше постоянной решетки. Максимальное значение частоты определяется условием  используя соотношение
используя соотношение  находим, что
находим, что

Число собственных колебаний с частотами в пределах от  равно числу узловых точек в
равно числу узловых точек в  -пространстве между
-пространстве между  Все эти точки лежат в положительном октанте
Все эти точки лежат в положительном октанте  -пространства между двумя концентрическими сферами с радиусами
-пространства между двумя концентрическими сферами с радиусами  таким образом, соответствующий объем равен
таким образом, соответствующий объем равен  . В среднем одна точка приходится на объем
. В среднем одна точка приходится на объем  в
в  -пространстве, откуда числе собственных колебаний
-пространстве, откуда числе собственных колебаний  между
между  будет составлять
будет составлять

Согласно квантовой теории, каждое из этих колебаний имеет среднюю энергию (11.1); следовательно, полную энергию можно найти путем умножения  на (11.1) и интегрирования по всем частотам от 0 до
на (11.1) и интегрирования по всем частотам от 0 до 

Число колебаний имеет множитель 3, так как каждый вид колебания соответствует двум поперечным и одной продольной стоячим волнам. Как и в соответствующей теории Эйнштейна, введем характеристическую температуру  и исключим подставляя значение
и исключим подставляя значение  в соответствии с (11.8). Тогда выражение для
в соответствии с (11.8). Тогда выражение для  приобретает вид
приобретает вид

в последнем интеграле введена переменная  Можно видеть, что этот интеграл зависит только от верхнего предела
Можно видеть, что этот интеграл зависит только от верхнего предела  таким образом, мы можем записать
таким образом, мы можем записать

Это выражение можно сравнивать с (11.2).
При высоких температурах  так что интеграл делается равным энергия равной
так что интеграл делается равным энергия равной  как и следовало ожидать. При низких температурах и становится меньше
как и следовало ожидать. При низких температурах и становится меньше  при очень низких температурах верхний предел интеграла можно заменить на
при очень низких температурах верхний предел интеграла можно заменить на  после чего интеграл приобретает значение т. е. не зависит от
после чего интеграл приобретает значение т. е. не зависит от  Итак, при очень низких температурах и
Итак, при очень низких температурах и  имеют вид
имеют вид

Это известный дебаевский  -закон для теплоемкости твердых тел при очень низких температурах. Как мы уже знаем, закон
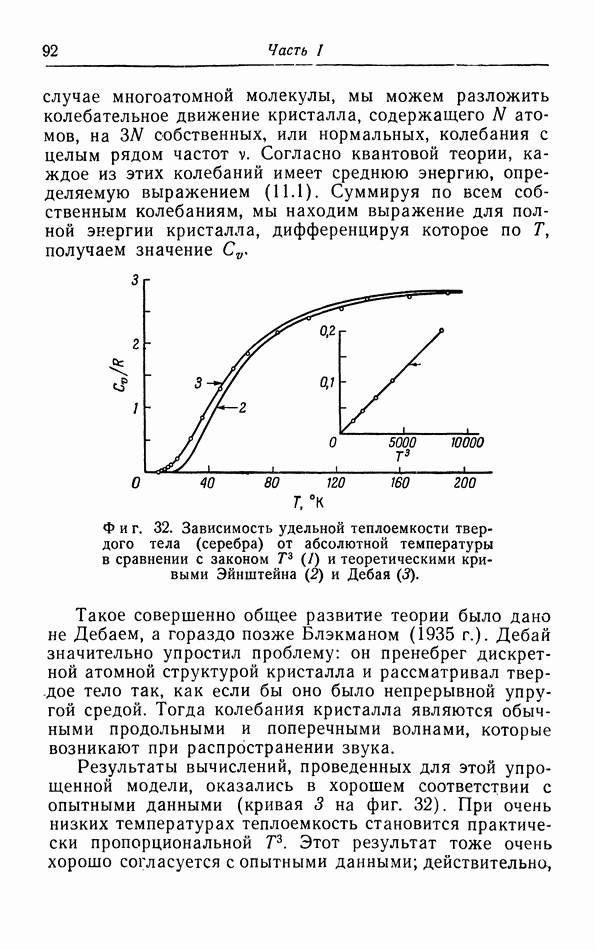
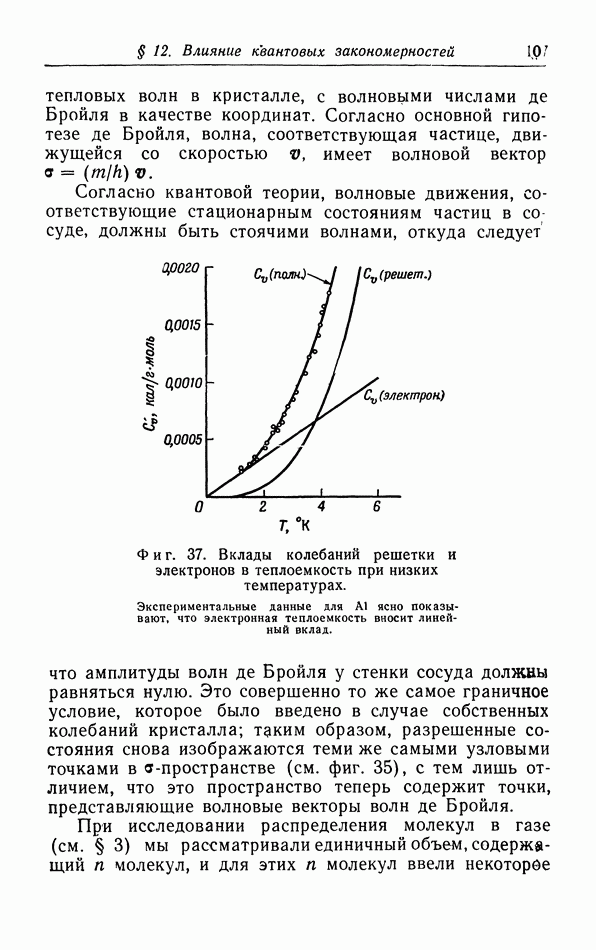
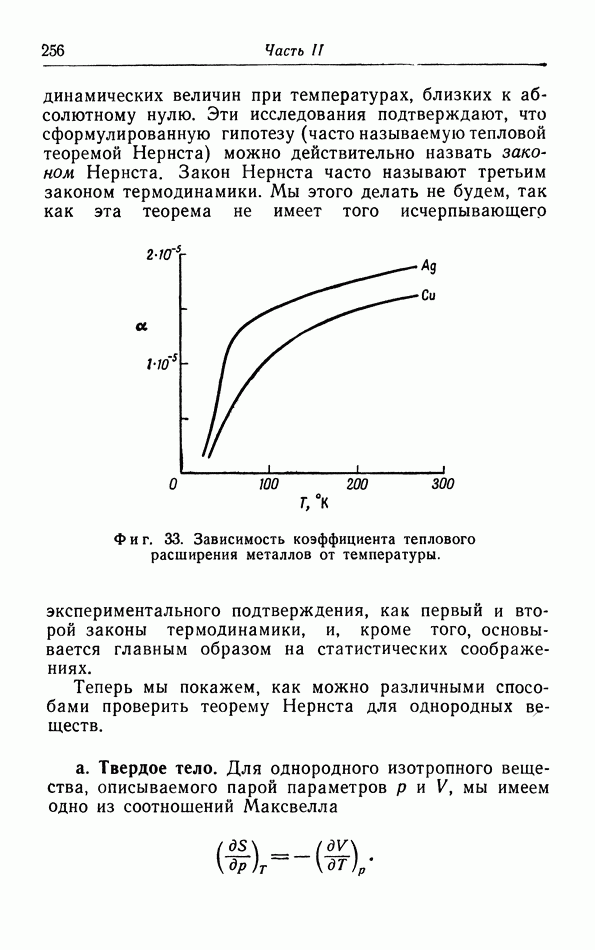
-закон для теплоемкости твердых тел при очень низких температурах. Как мы уже знаем, закон  находится в хорошем соответствии с опытными данными (см. кривую 1 на фиг. 32), что оправдывает использование приближения, введенного Дебаем. Однако в области температур, где высокие частоты еще дают заметный вклад в теплоемкость, имеются отклонения от
находится в хорошем соответствии с опытными данными (см. кривую 1 на фиг. 32), что оправдывает использование приближения, введенного Дебаем. Однако в области температур, где высокие частоты еще дают заметный вклад в теплоемкость, имеются отклонения от  -закона, которые можно объяснить на основе рассмотрения Блэкмана. При температурах, больших по сравнению с
-закона, которые можно объяснить на основе рассмотрения Блэкмана. При температурах, больших по сравнению с  теория Дебая снова дает правильный результат, так как при высоких температурах величина энергии стремится к классическому значению
теория Дебая снова дает правильный результат, так как при высоких температурах величина энергии стремится к классическому значению 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
- б. Жидкие пленки.
- в. Капиллярное поднятие и понижение уровня жидкости.
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
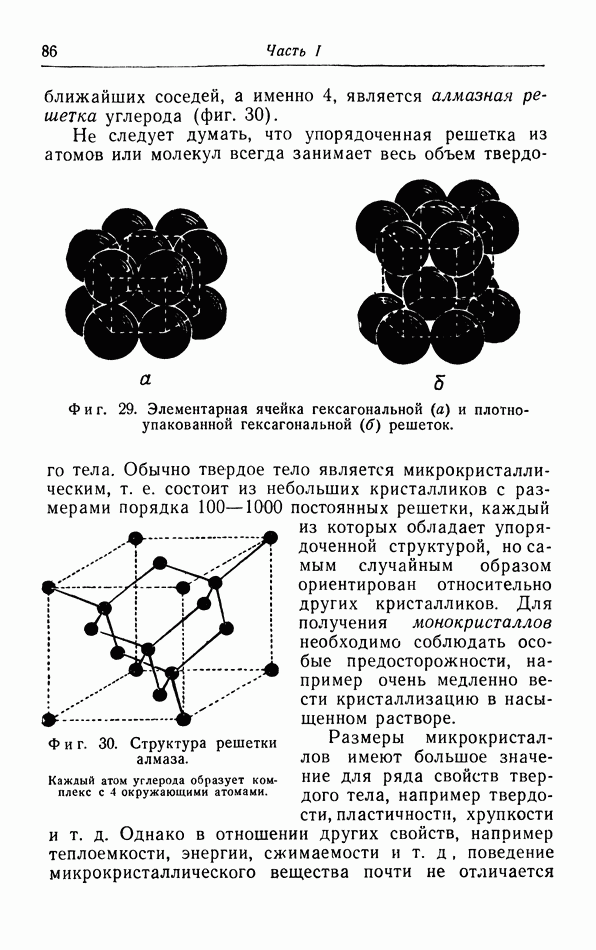
- § 9. Структура твердых тел
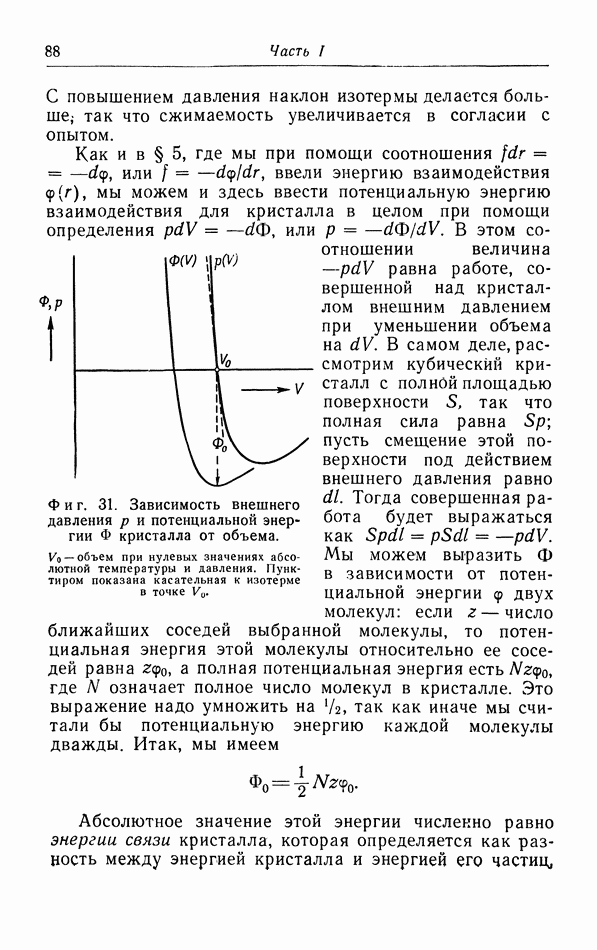
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
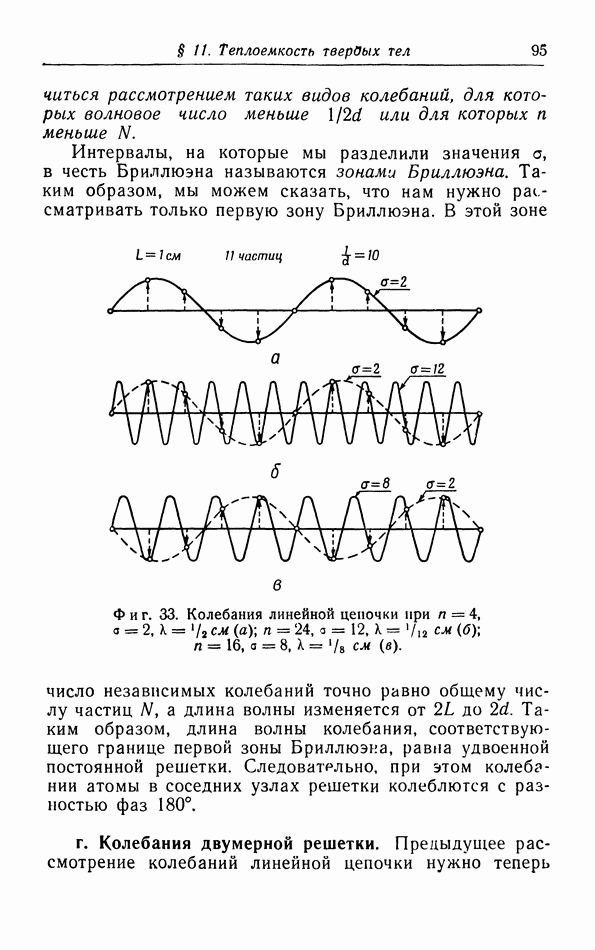
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
- § 3. Первый закон термодинамики
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
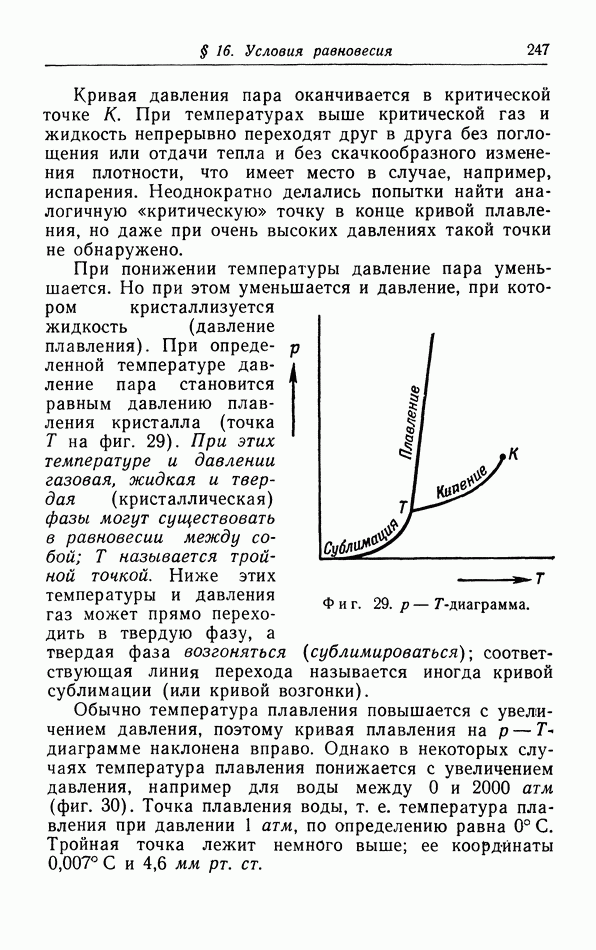
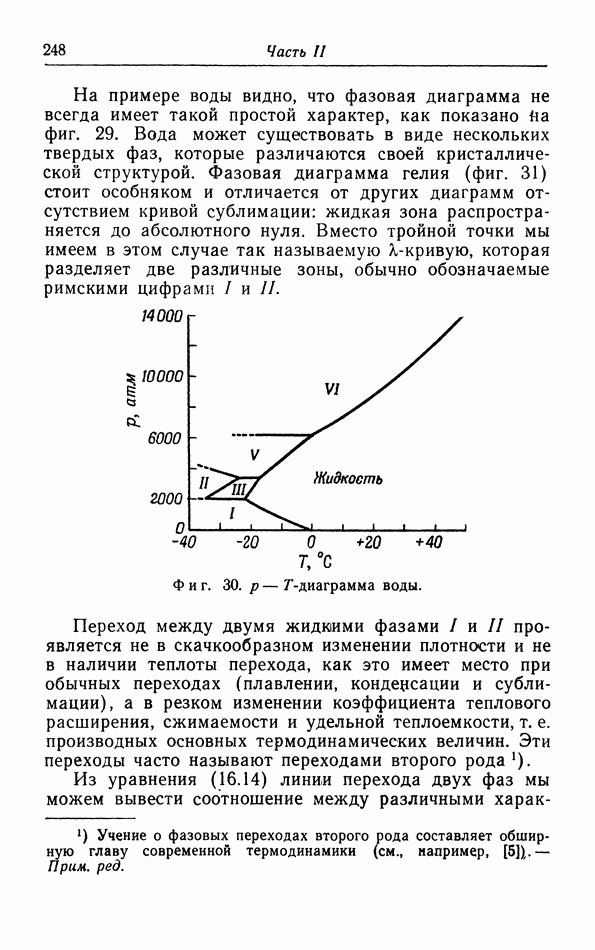
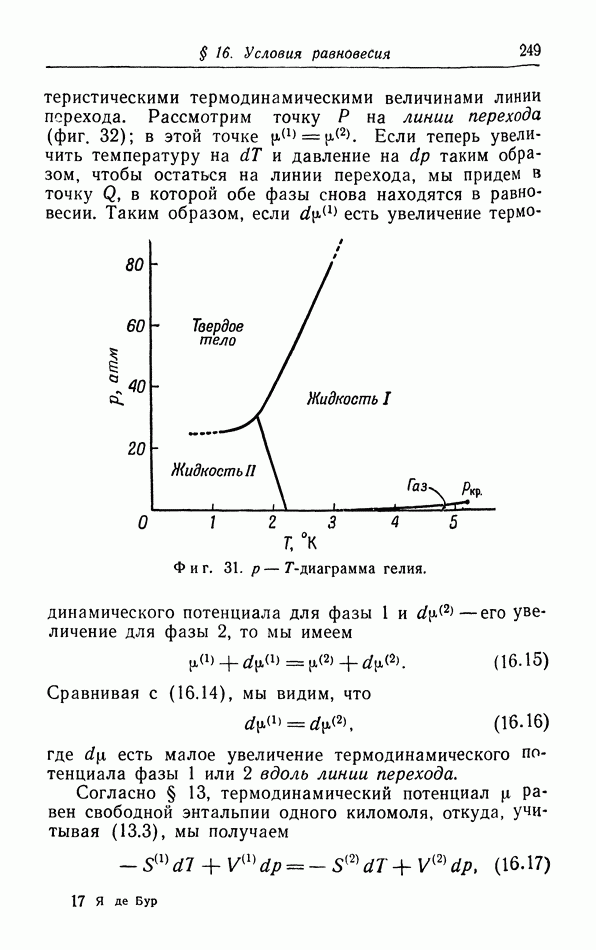
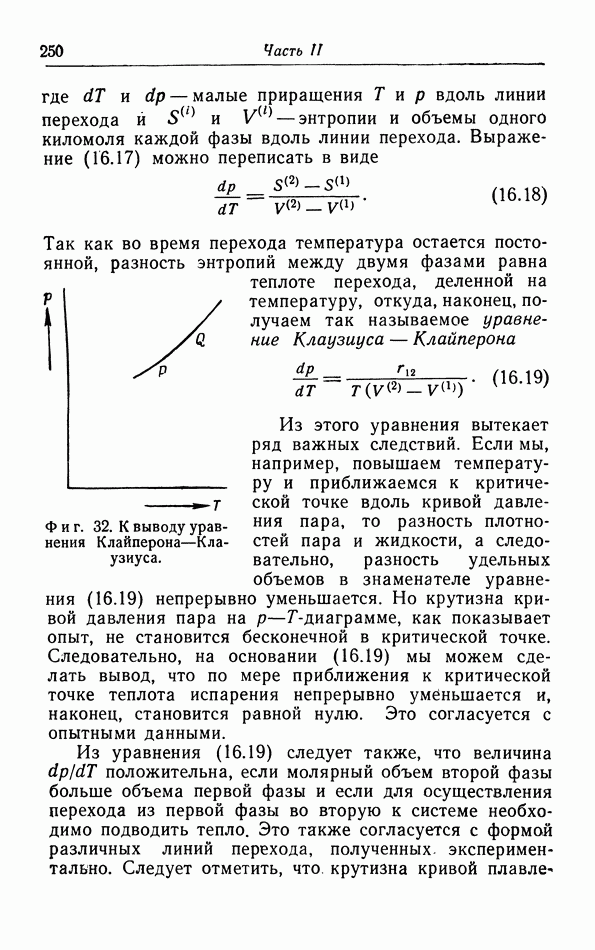
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам