ГЛАВА V. Теорема Нернста

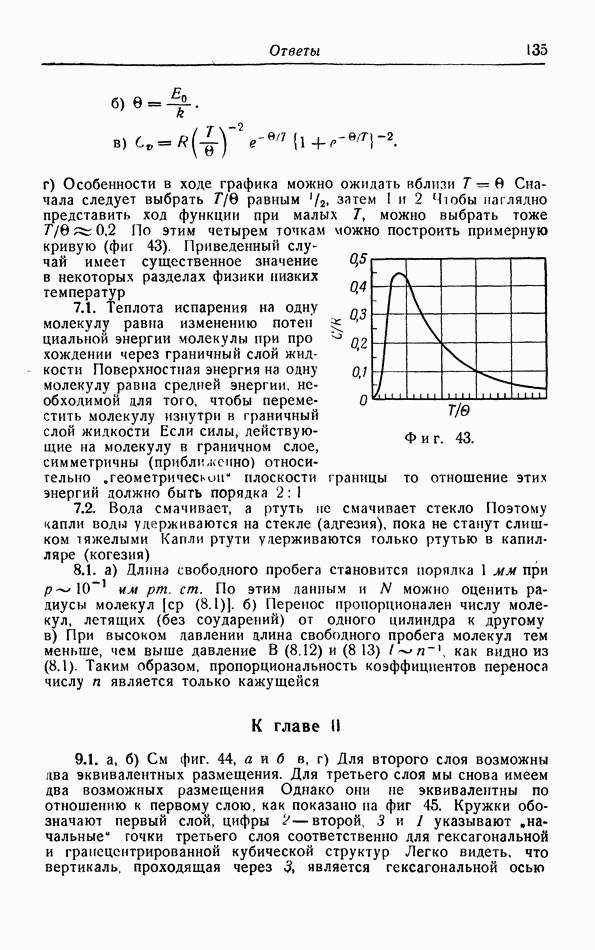
§ 17. Теорема Нернста

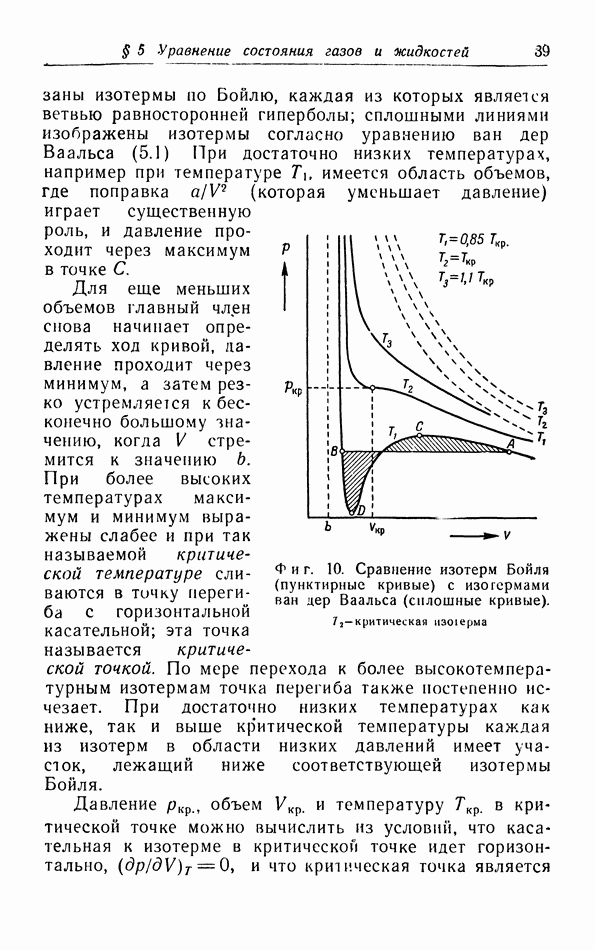
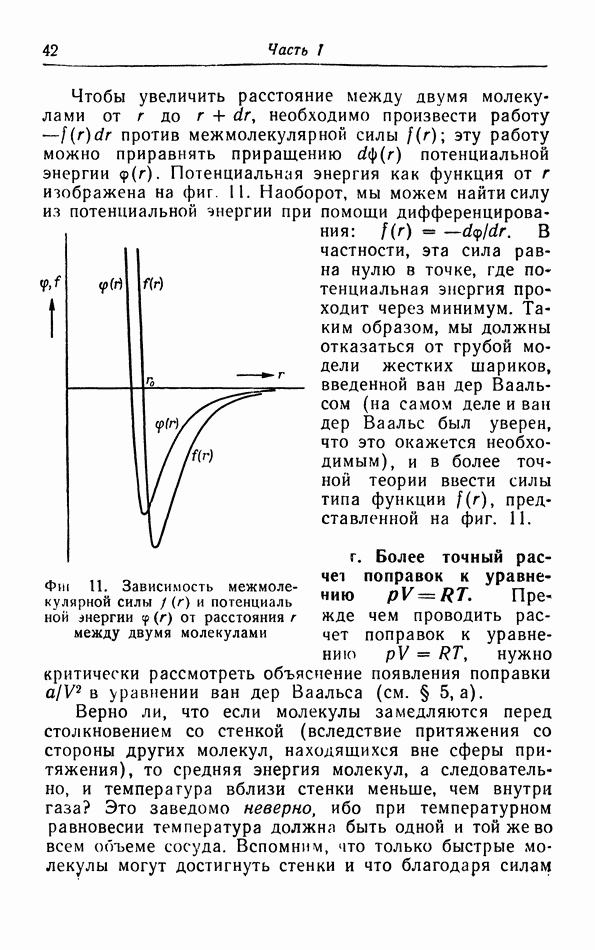
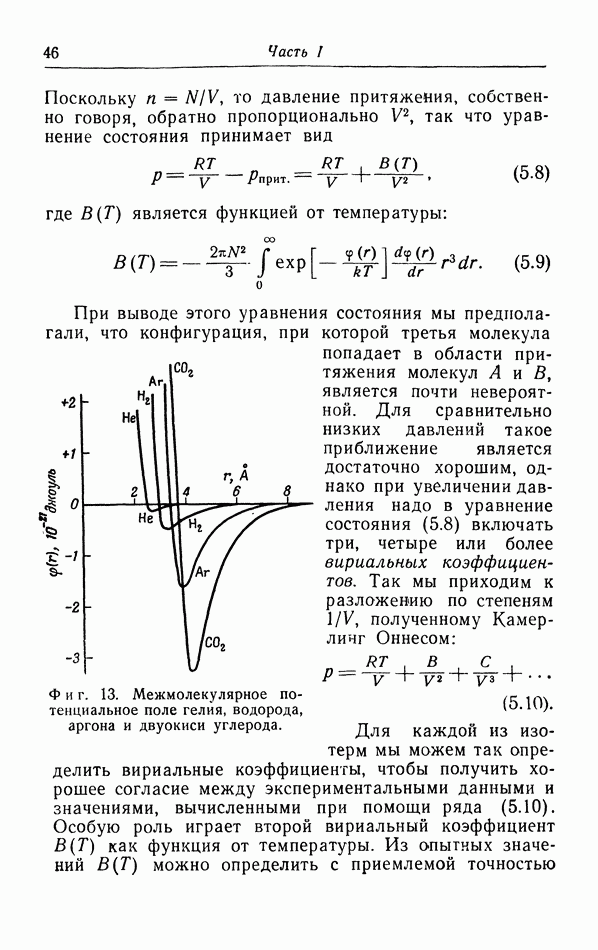
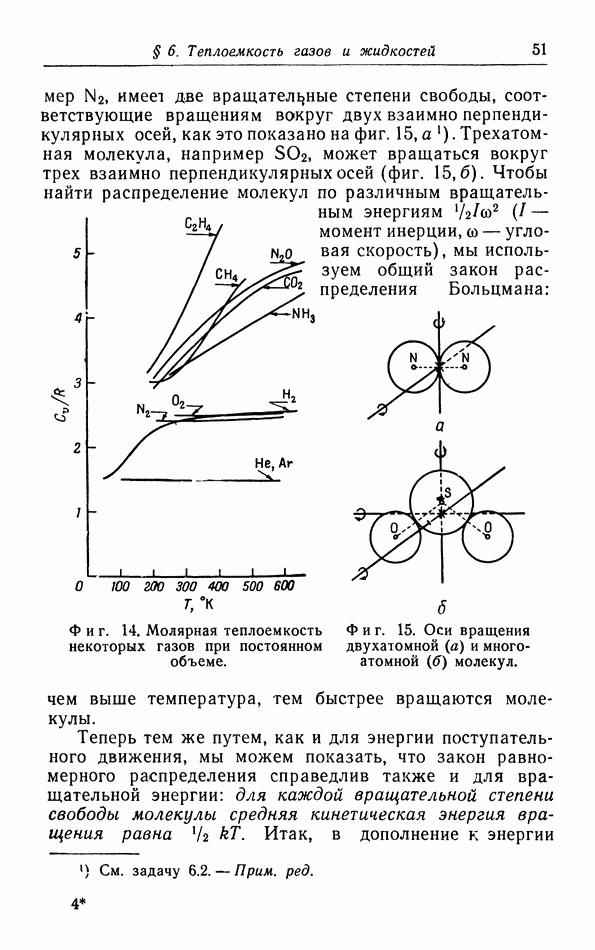
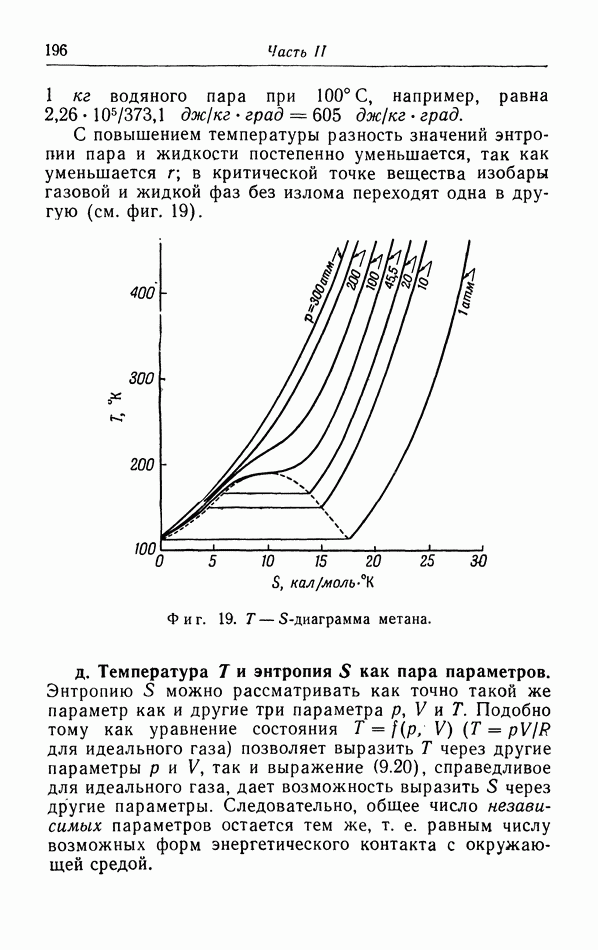
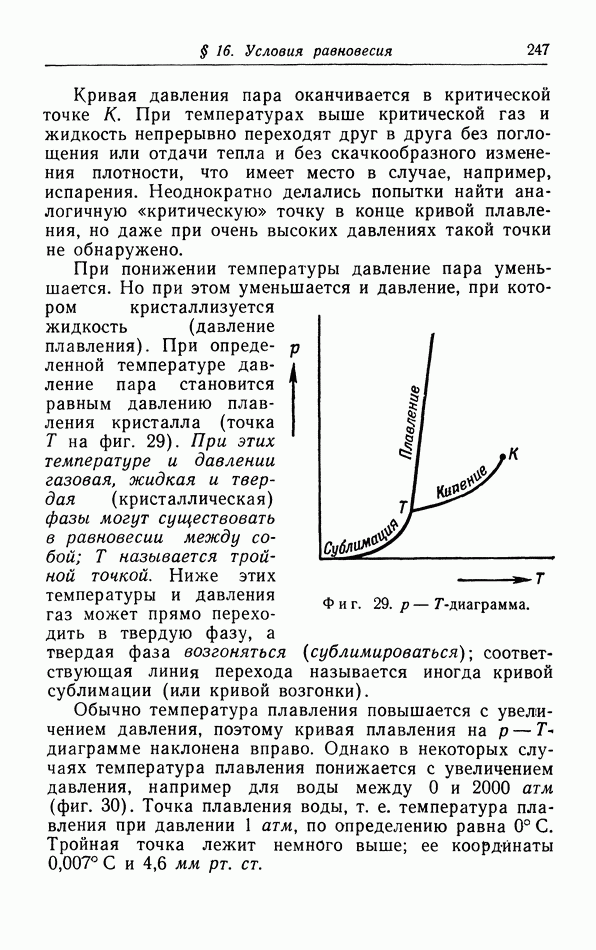
В § 9 мы упоминали статистическую интерпретацию энтропии как меры неупорядоченности системы. Когда мы все более и более понижаем температуру, система переходит в состояние наибольшей возможной упорядоченности. В кристаллах одноатомных веществ колебания постепенно замирают, и при абсолютном нуле остаются только колебания атомов около их положения равновесия; энергия этих колебаний представляет собой нулевую энергию. Это же самое происходит с атомами, образующими молекулу. Прекращается и вращение молекул, возможное в твердых телах, как, например, в водороде и этане. При определенной температуре вещество может перейти в другую кристаллическую фазу, соответствующую более низкой потенциальной энергии, как, например, олово при 20° С.

Ярким примером увеличения упорядоченности при понижении температуры является поведение сплава При высоких температурах атомы раслределены случайным образом по узловым точкам кубической решетки, но при низких температурах Наблюдается тенденция к переходу в упорядоченное состояние, в котором атомы чередуются в узлах решетки. При определенной температуре происходит даже переход, в результате которого увеличивается упорядоченность фазы, стабильной при более низкой температуре. Тенденция к упорядоченности объясняется тем, что энергия упорядоченного кристалла меньше энергии беспорядочной кристаллической структуры.

Вторым примером является существование ферромагнитного состояния различных магнитных веществ. В точке Кюри эти вещества переходят в более упорядоченное состояние, в котором все элементарные магнитики параллельны друг другу. Как мы указывали ранее в связи с опытами по размагничиванию, многие вещества, парамагнитные при обычных температурах, обнаруживают эту тенденцию при очень низких температурах.

Итак, во всех этих примерах мы видим одинаковую картину: чем ниже температура, тем сильнее проявляется тенденция к реализации состояния с наинизшей энергией, характеризующегося возможно более полной упорядоченностью. При высоких температурах достижению этого состояния с наинизшей энергией препятствует тепловое движение, создающее неупорядоченность. Итак, состояние при каждой определенной температуре является компромиссом между: 1) тенденцией к увеличению упорядоченности и к достижению состояния с наинизшей энергией и 2) беспорядочным тепловым движением, стремящимся увеличить энтропию.

Если бы мы сумели охладить вещество до абсолютного нуля, когда тепловое движение уже не нарушает упорядоченность состояния, то правдоподобно предположить, что это состояние соответствовало бы наинизшей возможной энтропии системы. Но что произойдет, если мы изменим это состояние при абсолютном нуле, например, сжатием кристалла? Кристалл будет оставаться в состоянии наинизшей энергии до тех пор, пока это допускается внешними параметрами (давлением). Но изменится ли энтропия, когда мы сжимаем вещество при абсолютном нуле?

Основываясь на большом количестве опытных данных, Нернст пришел к выводу: при абсолютном нуле все изменения состояния происходят при постоянной энтропии) (теорема Нернста, 1906 г.). Очевидно, что этот вывод никогда нельзя будет проверить на опыте, ибо невозможно произвести необходимые опыты при абсолютном нуле. Однако можно исследовать поведение различных

термодинамических величин при температурах, близких к абсолютному нулю. Эти исследования подтверждают, что сформулированную гипотезу (часто называемую тепловой теоремой Нернста) можно действительно назвать законом Нернста. Закон Нернста часто называют третьим законом термодинамики.

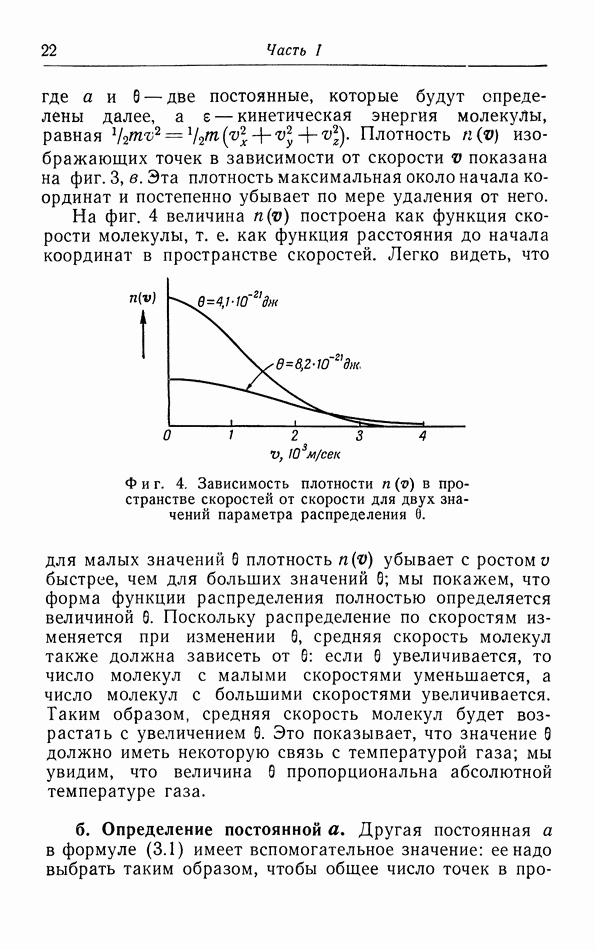
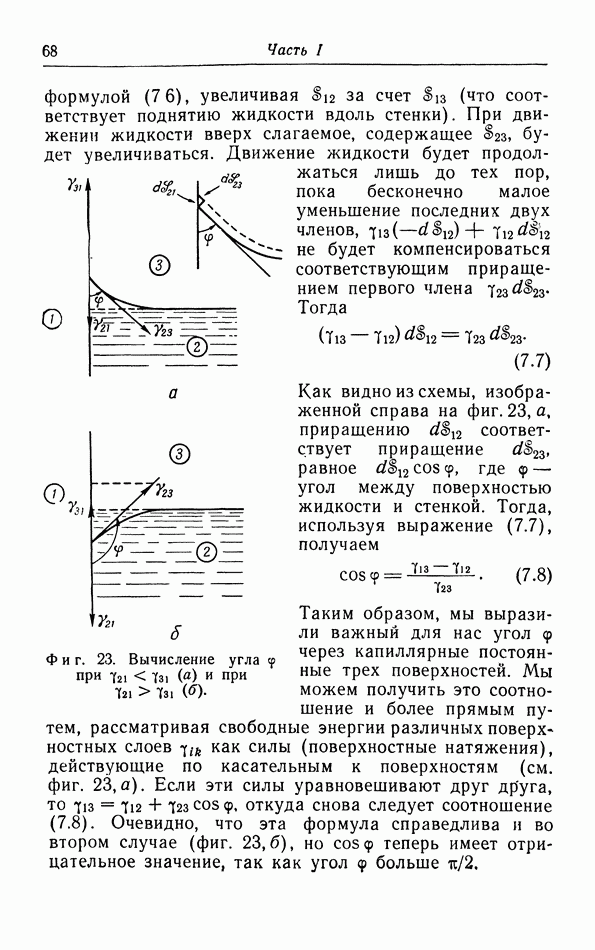
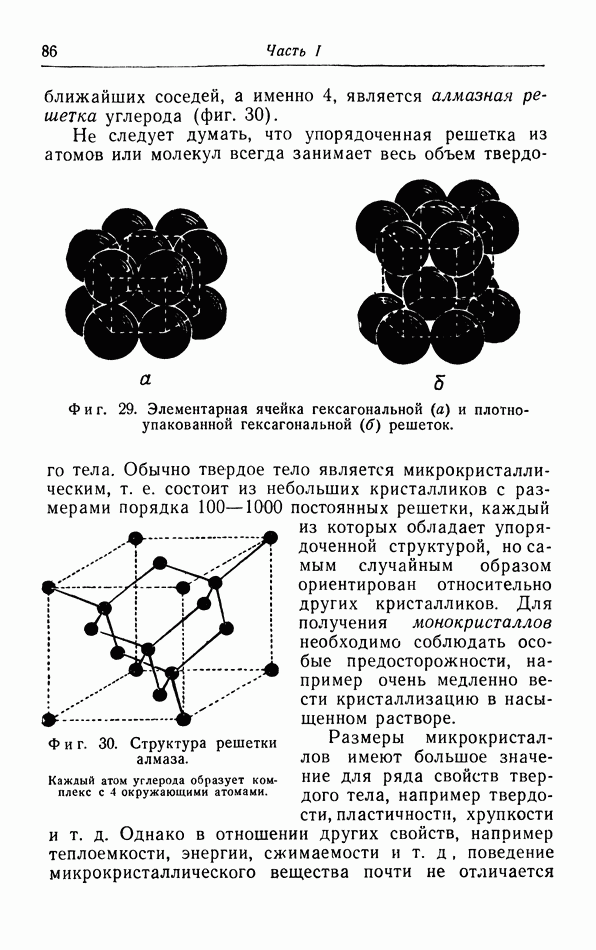
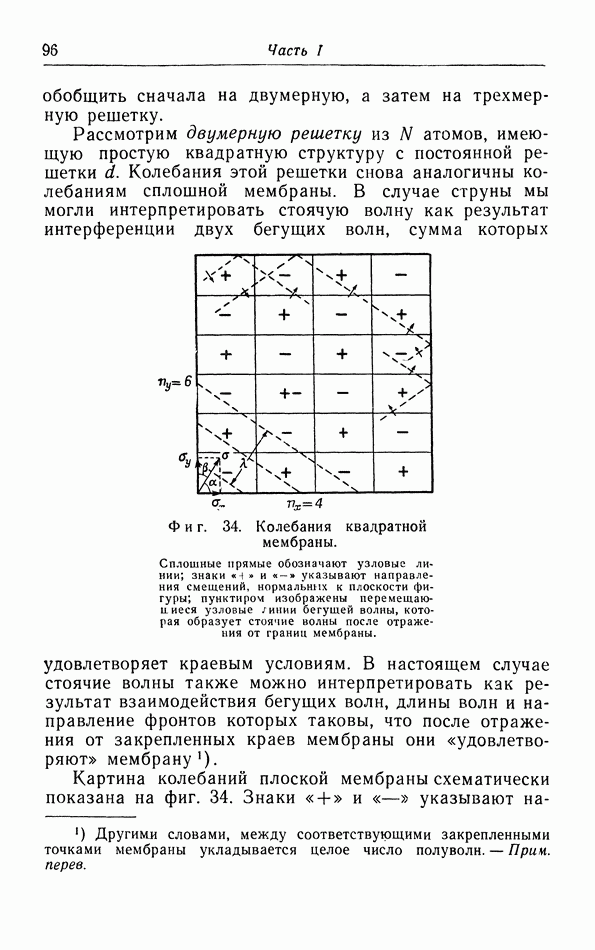
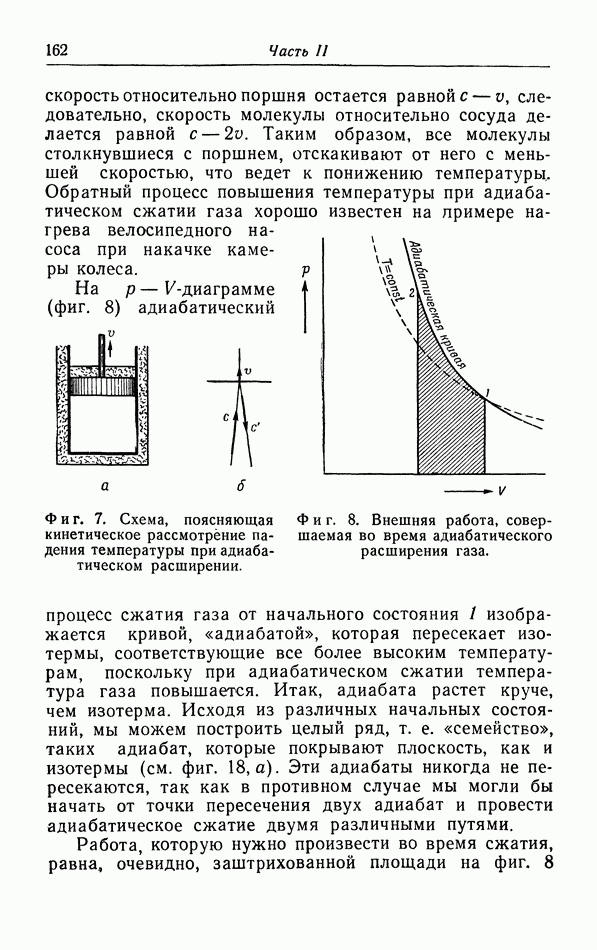
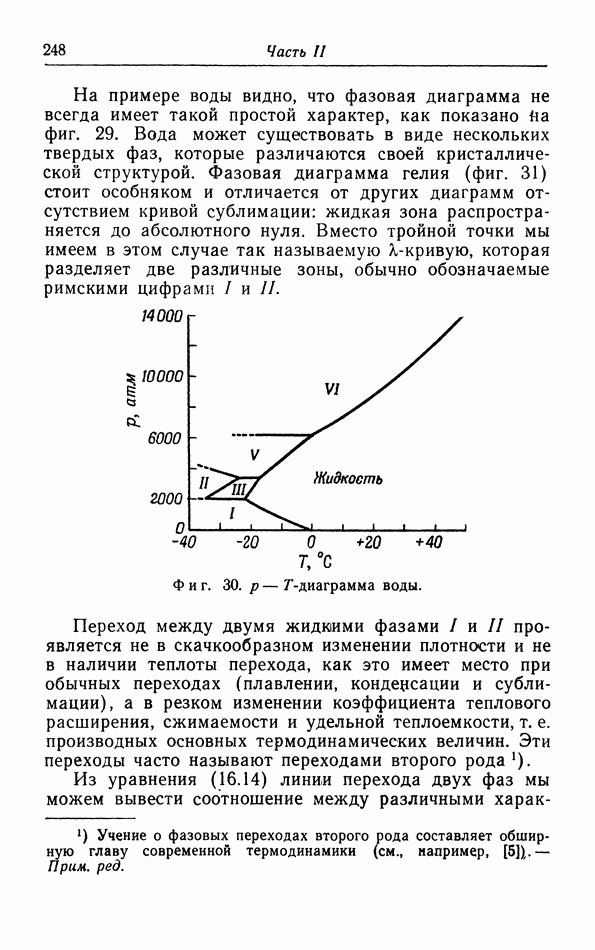
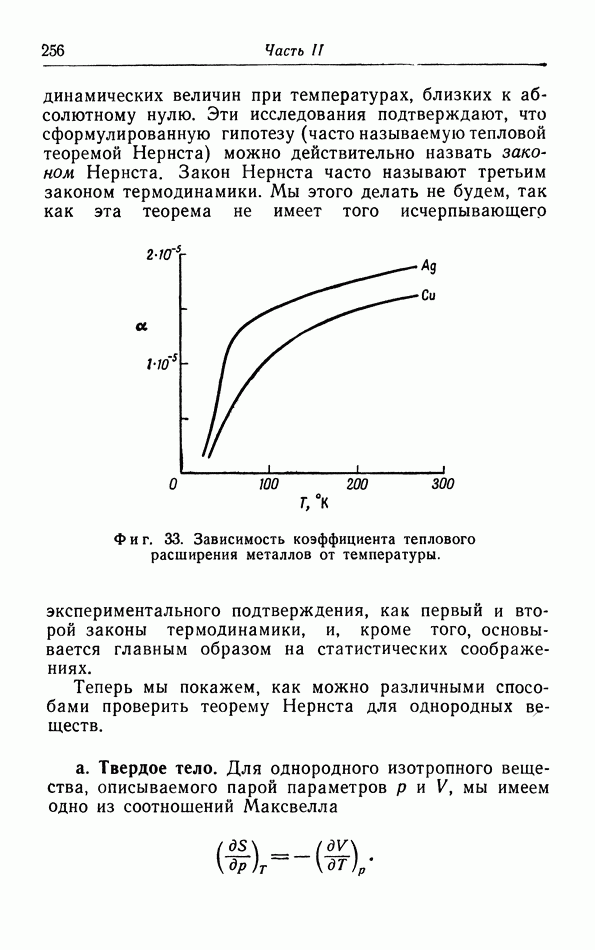
Фиг. 33. Зависимость коэффициента теплового расширения металлов от температуры.

Мы этого делать не будем, так как эта теорема не имеет того исчерпывающего экспериментального подтверждения, как первый и второй законы термодинамики, и, кроме того, основывается главным образом на статистических соображениях.

Теперь мы покажем, как можно различными способами проверить теорему Нернста для однородных веществ.

а. Твердое тело.

Для однородного изотропного вещества, описываемого парой параметров , мы имеем одно из соотношений Максвелла

Но, согласно теореме Нернста, величина должна стремиться к нулю, когда стремится к нулю, откуда

Поэтому, согласно теореме Нернста, коэффициент теплового расширения всех веиеств должен стремиться к нулю при стремлении к нулю температуры.

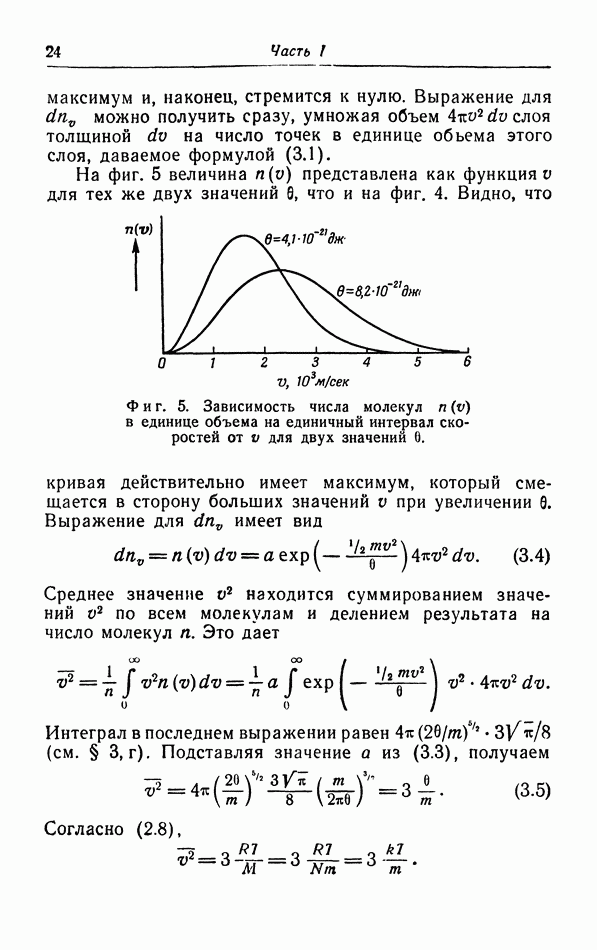
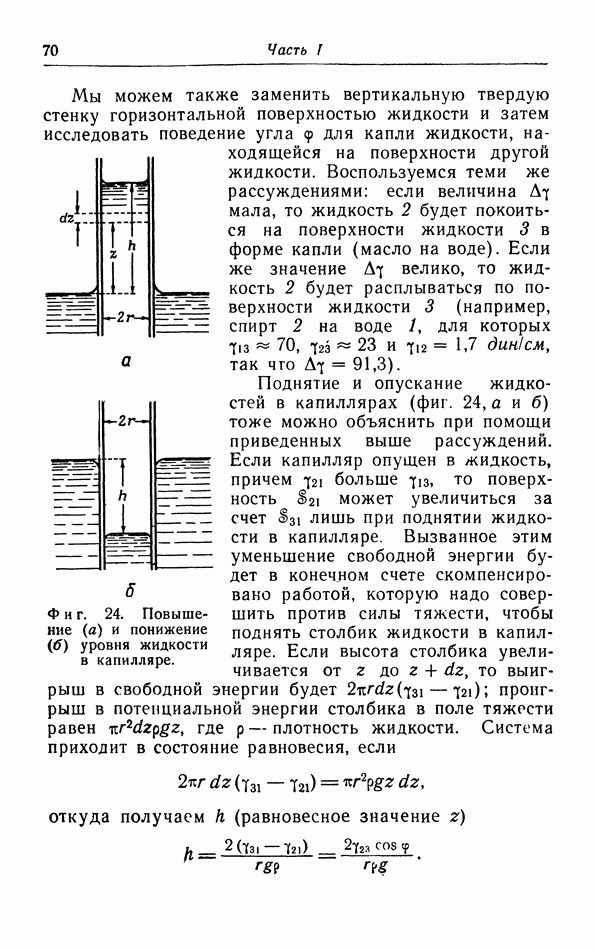
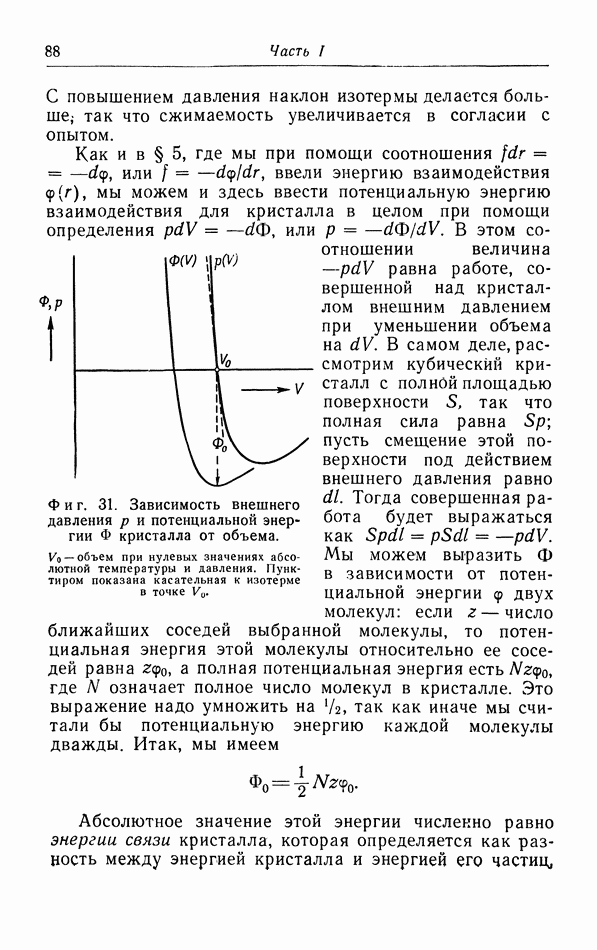
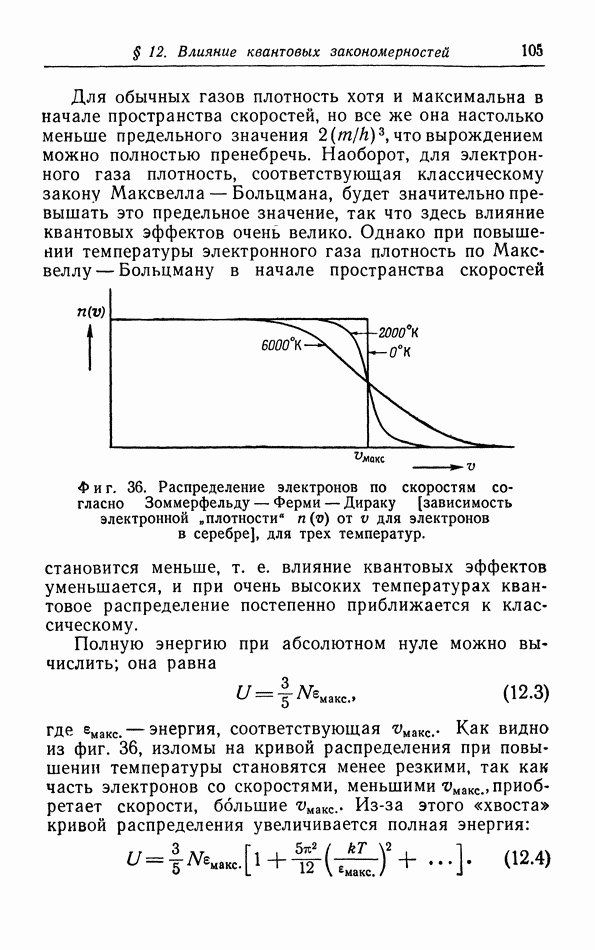
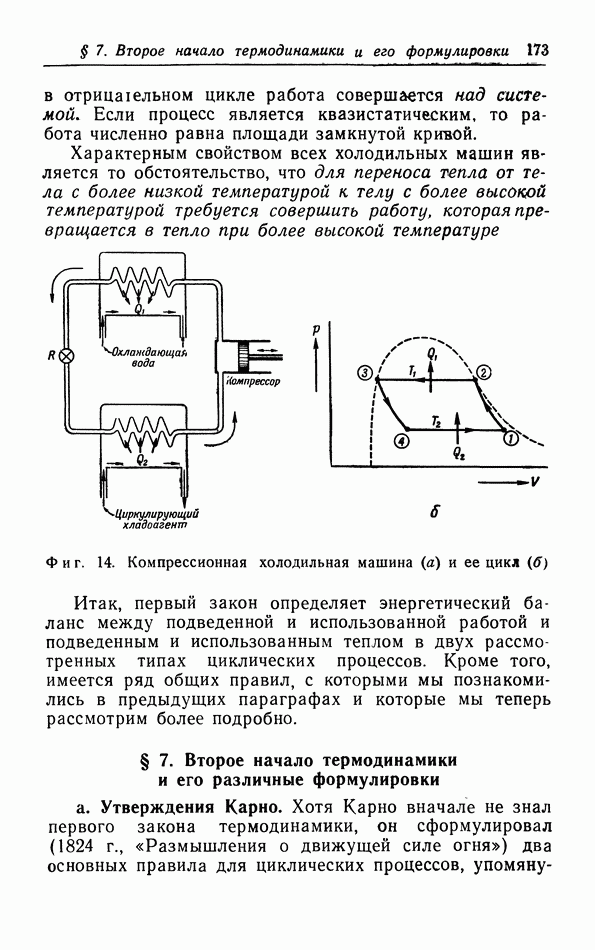
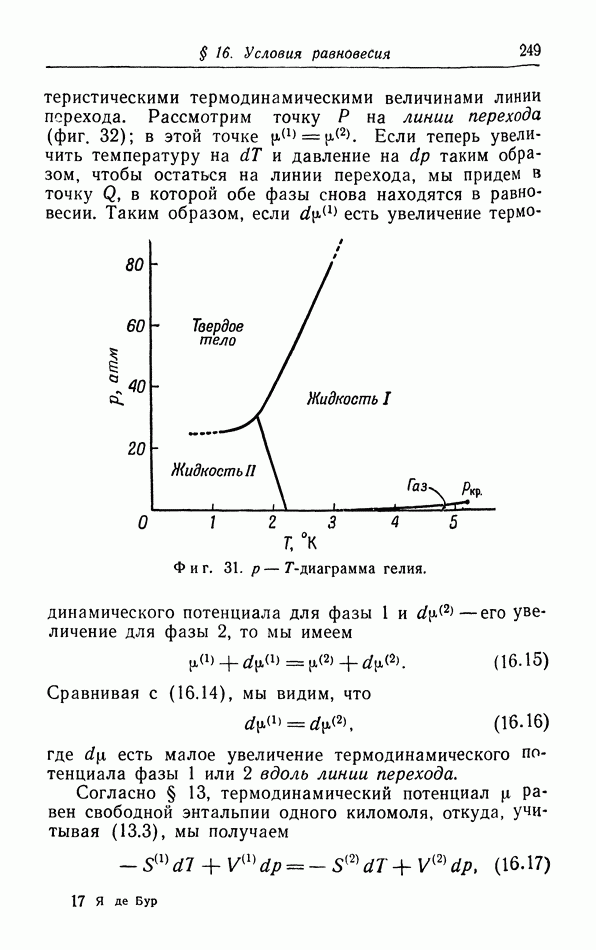
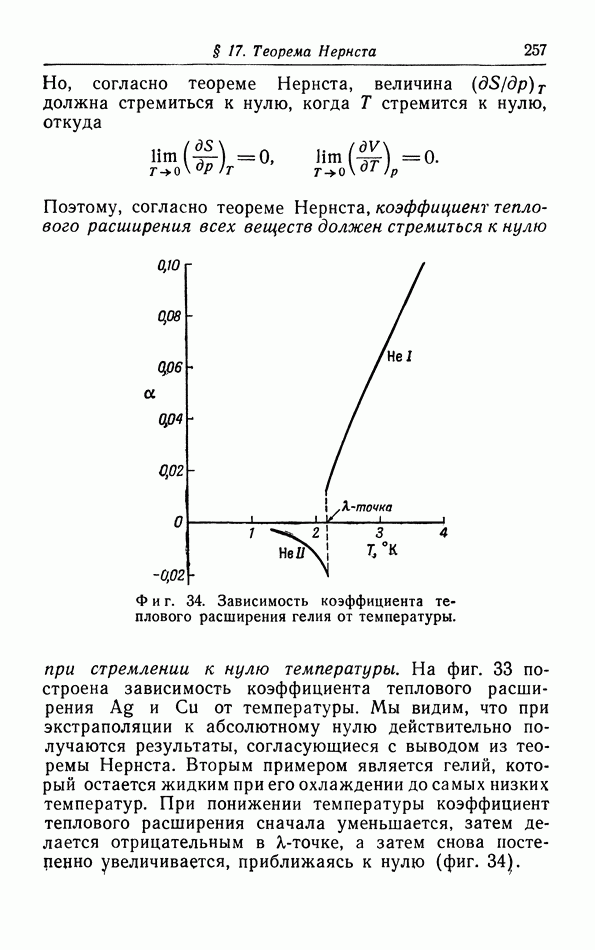
Фиг. 34. Зависимость коэффициента теплового расширения гелия от температуры.

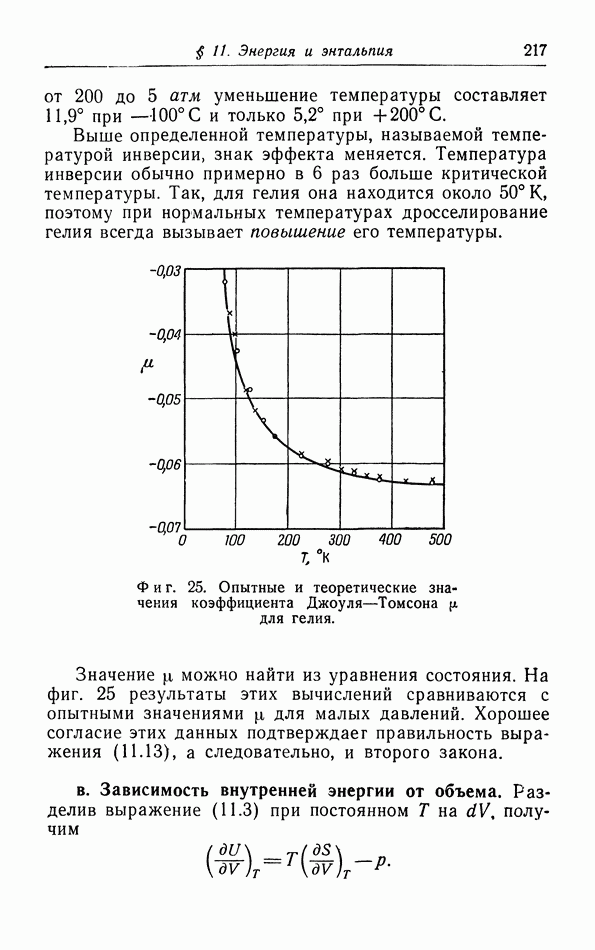
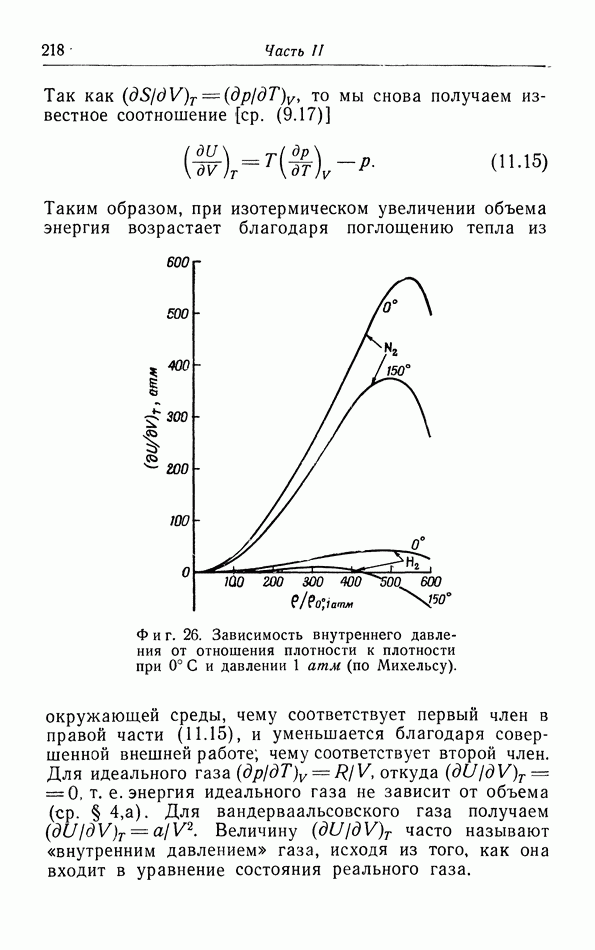
На фиг. 33 построена зависимость коэффициента теплового расширения от температуры. Мы видим, что при экстраполяции к абсолютному нулю действительно получаются результаты, согласующиеся с выводом из теоремы Нернста. Вторым примером является гелий, который остается жидким при его охлаждении до самых низких температур. При понижении температуры коэффициент теплового расширения сначала уменьшается, затем делается отрицательным в -точке, а затем снова постепенно увеличивается, приближаясь к нулю (фиг. 34).

б. Капиллярные пленки.

Для капиллярной пленки соотношение Максвелла имеет вид

(мы испояьзуем обыкновенный дифференциал, поскольку поверхностное натяжение является силой на единицу длины и не зависит от отсюда, согласно теореме Нернста,

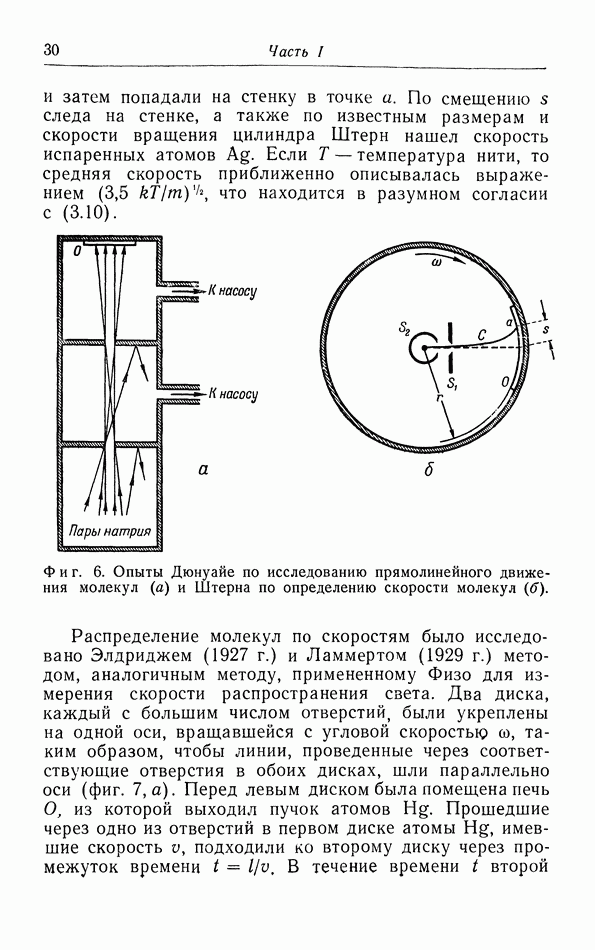
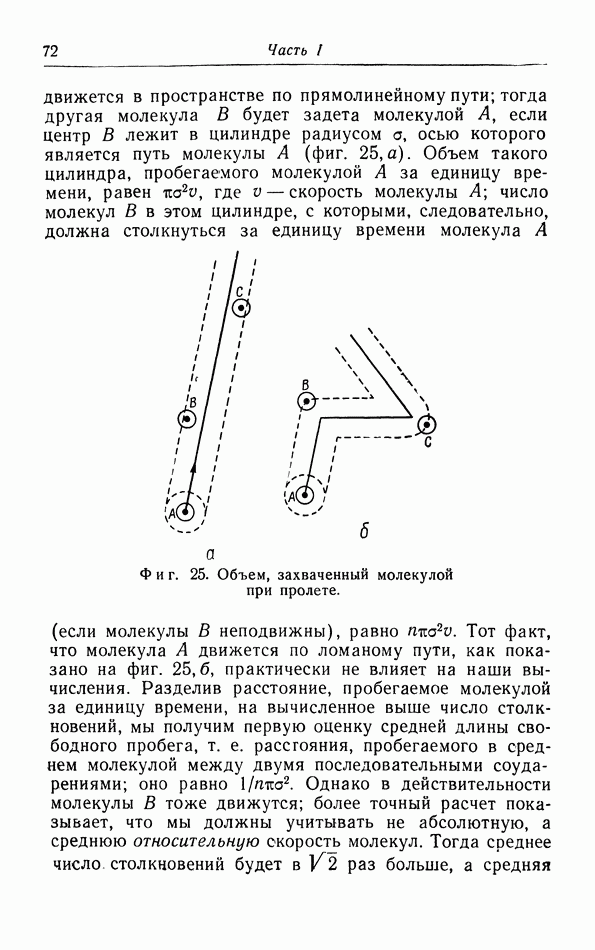
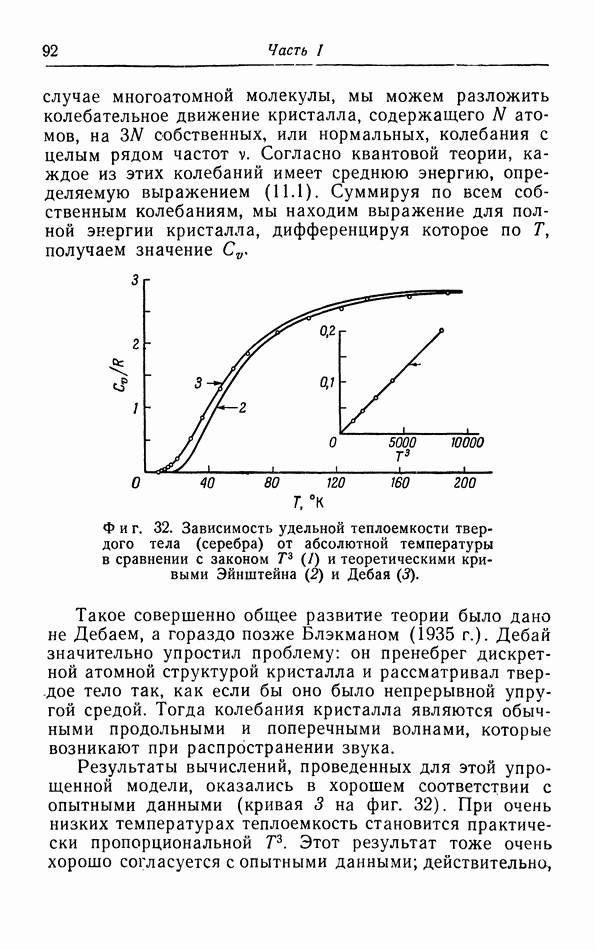
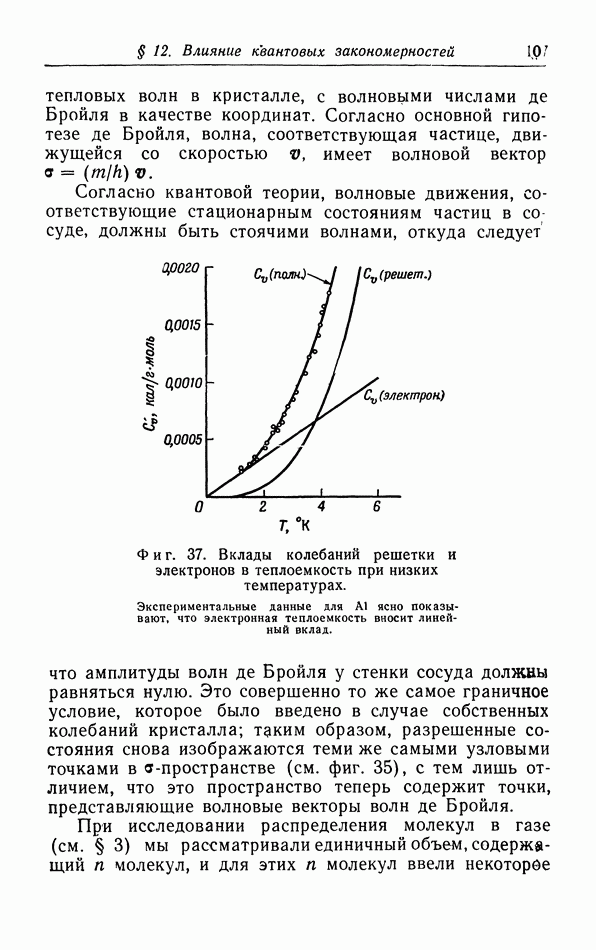
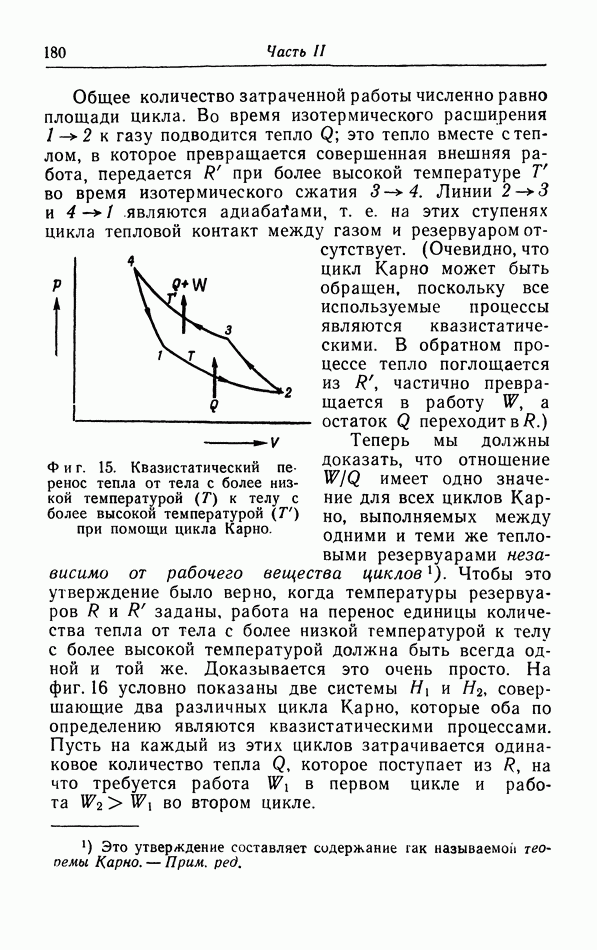
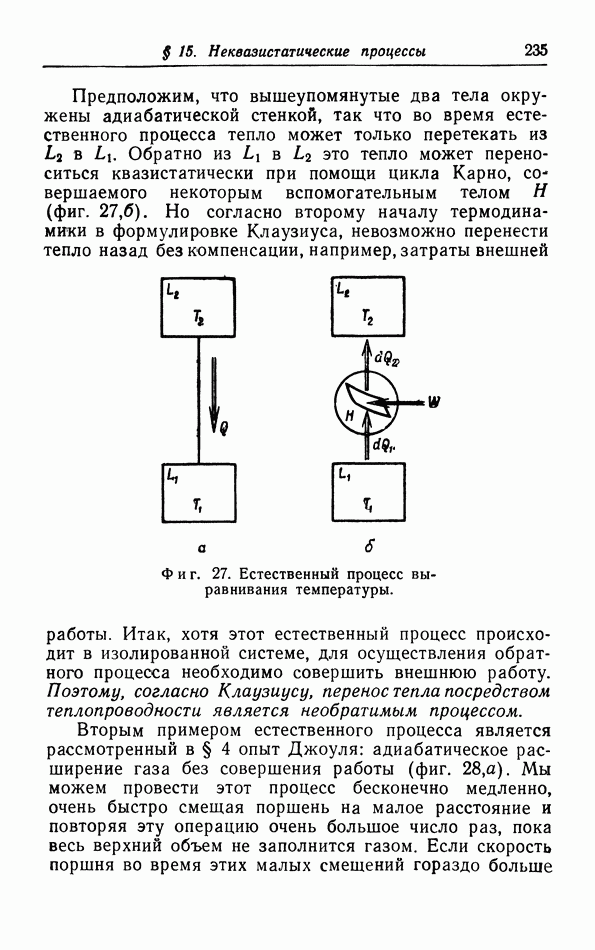
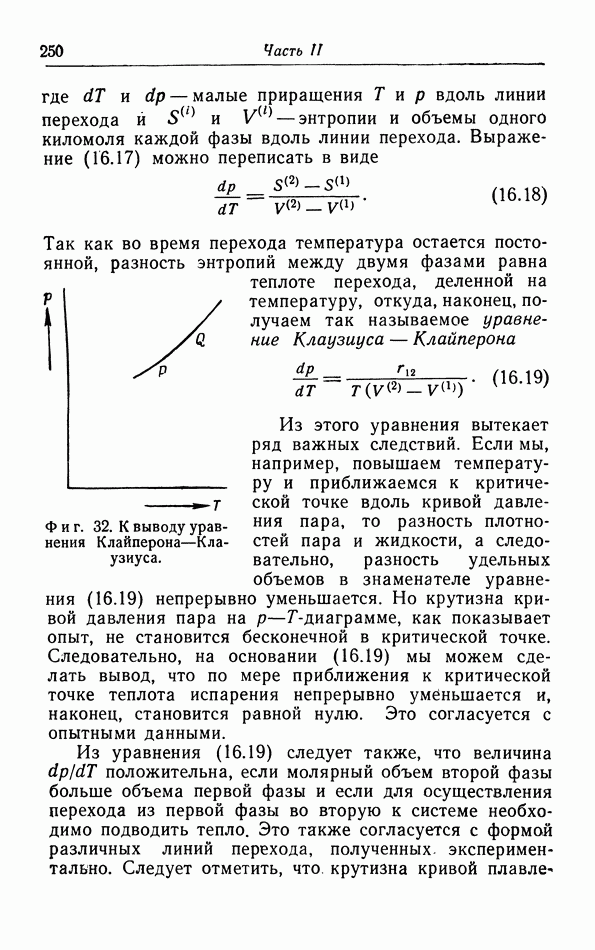
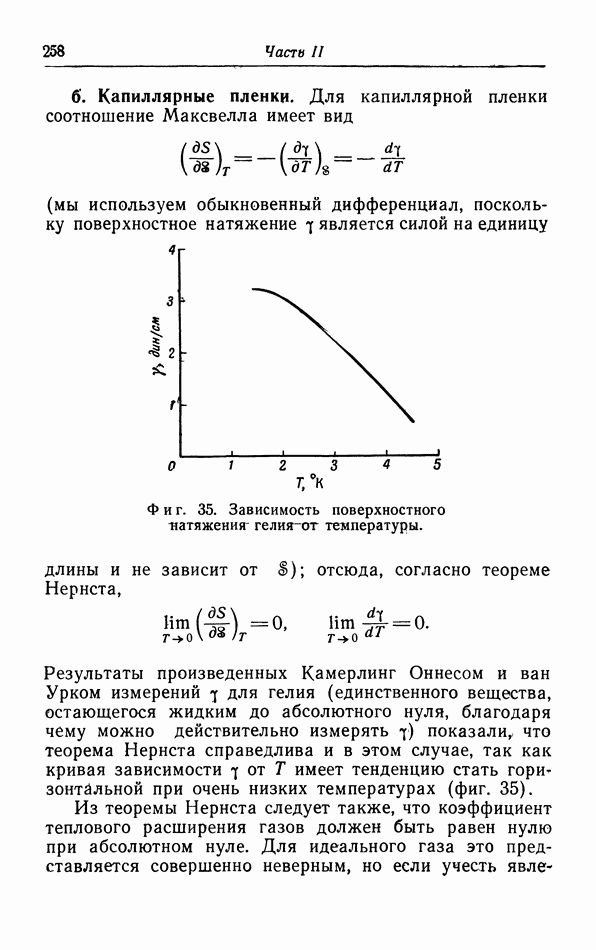
Результаты произведенных Камерлинг Оннесом и ван Урком измерений 7 для гелия (единственного вещества, остающегося жидким до абсолютного нуля, благодаря чему можно действительно измерять 7) показали, что теорема Нернста справедлива и в этом случае, так как кривая зависимости 7 от имеет тенденцию стать горизонтальной при очень низких температурах (фиг. 35).

Фиг. 35. Зависимость поверхностного натяжения гелия от температуры.

Из теоремы Нернста следует также, что коэффициент теплового расширения газов должен быть равен нулю при абсолютном нуле. Для идеального газа это представляется совершенно неверным, но если учесть

явления вырождения, рассмотренные в § 12, то оказывается, что величина действительно стремится к нулю.

в. Магнитные вещества.

Для магнитных зеществ мы имеем соотношение

откуда в силу теоремы Нернста

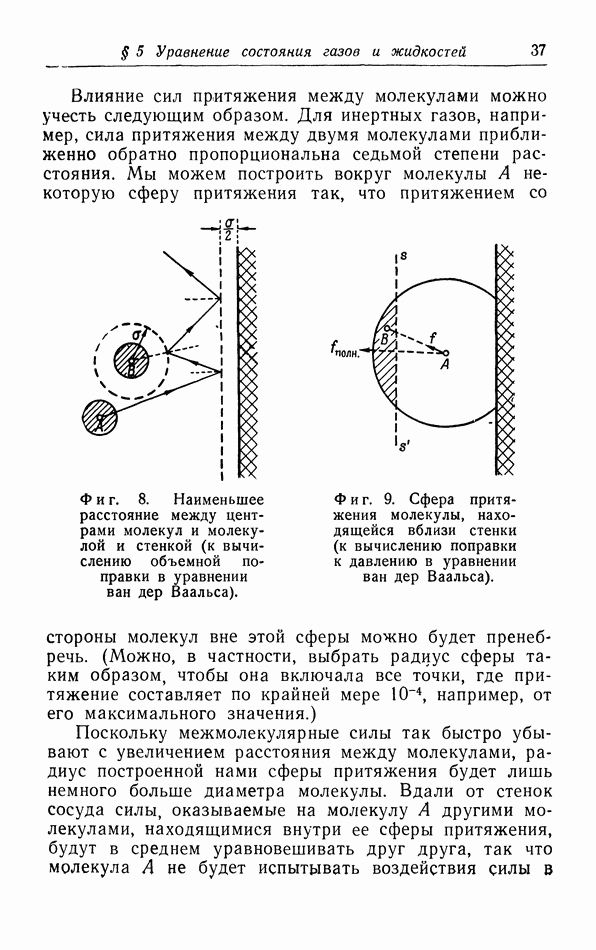
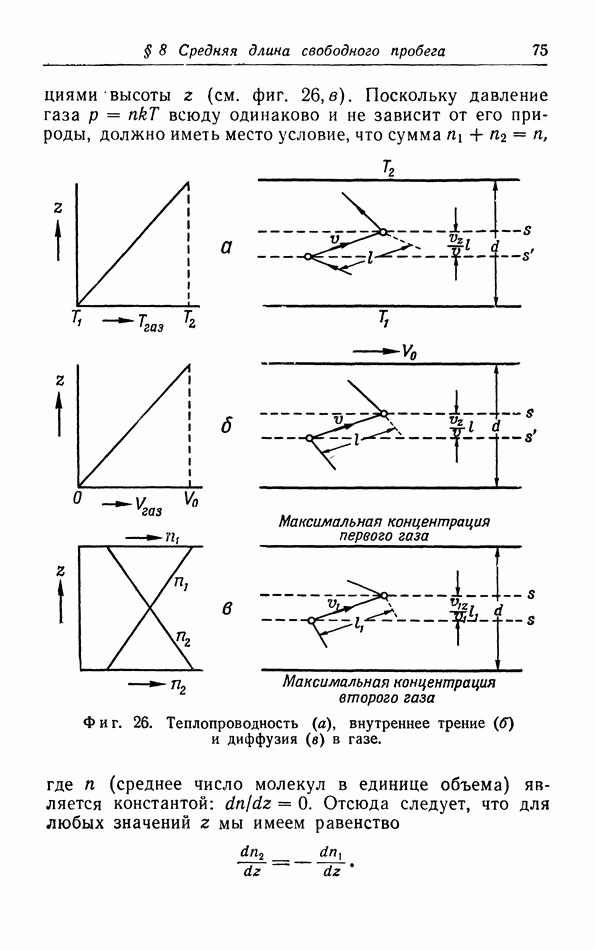
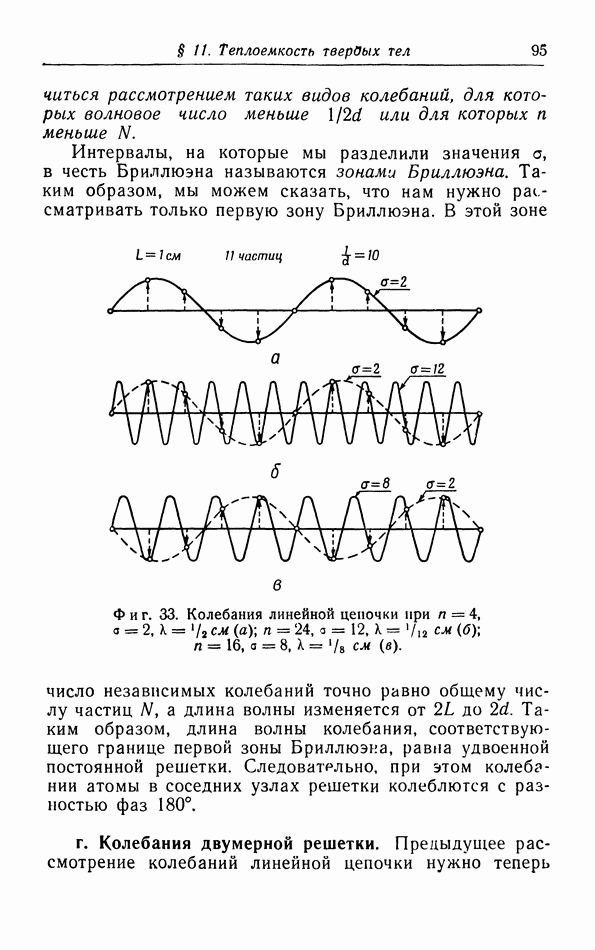
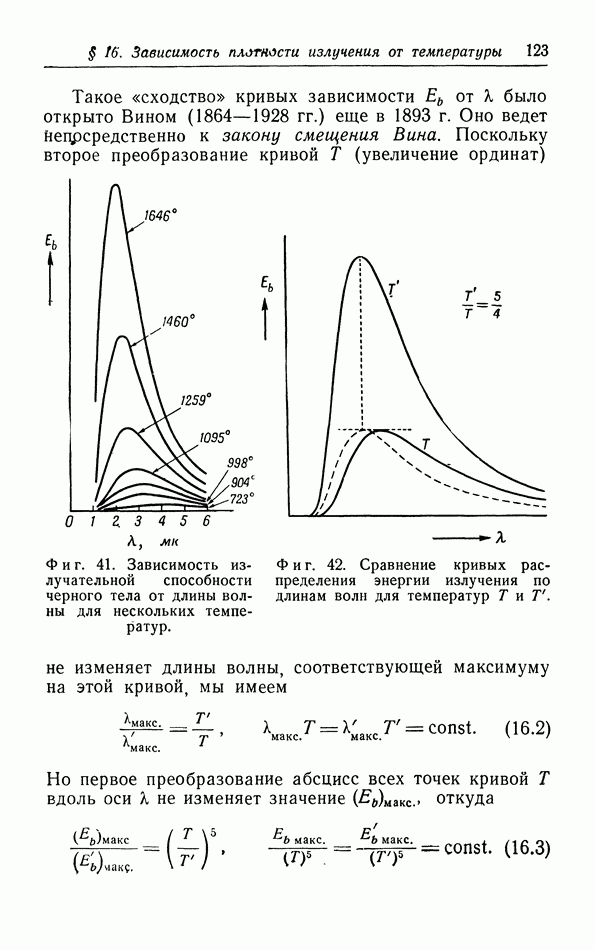
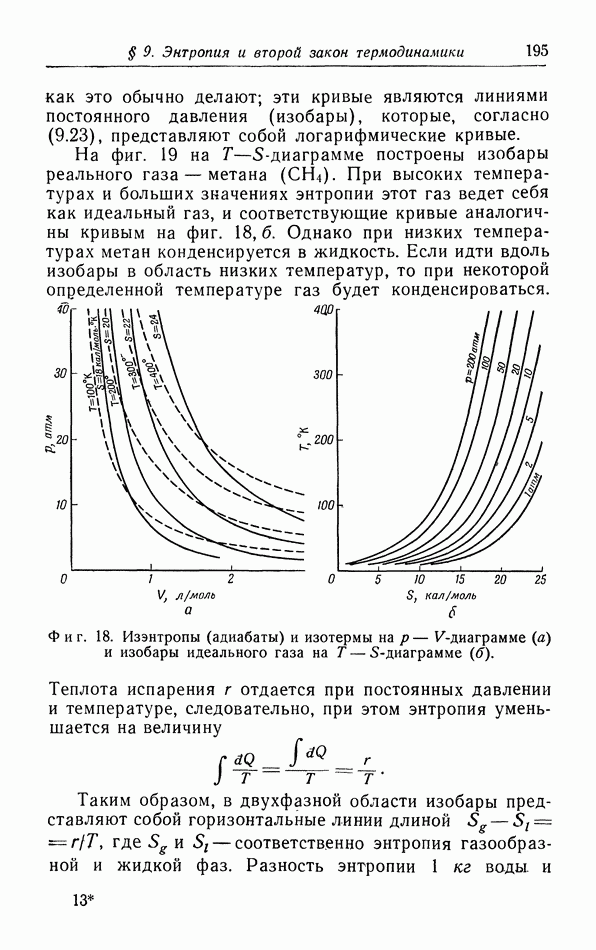
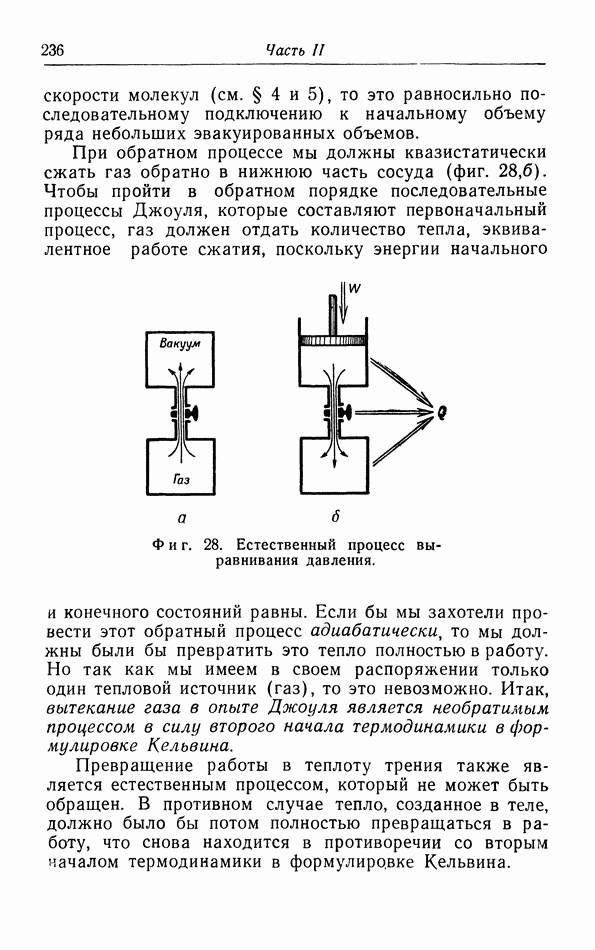
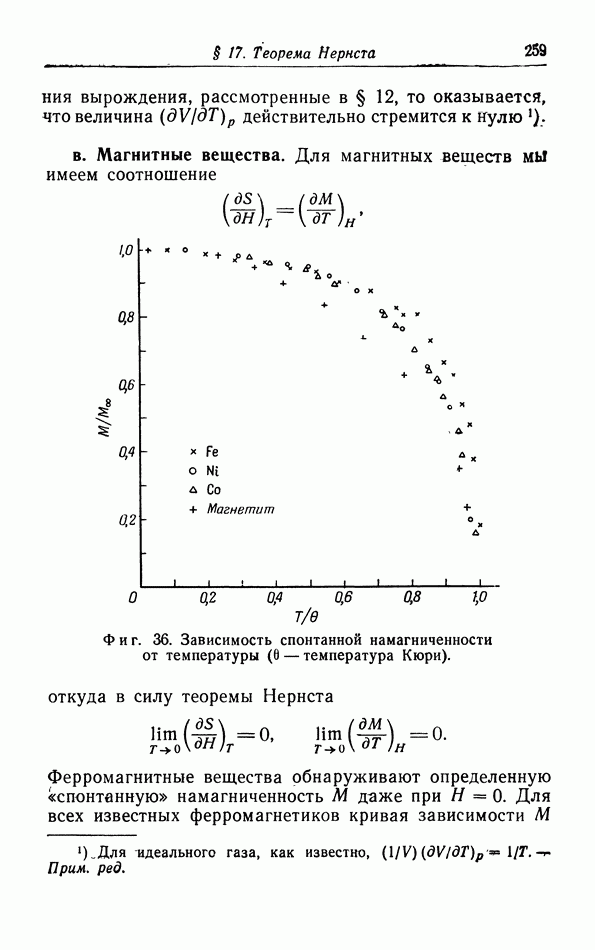
Фиг. 36. Зависимость спонтанной намагниченности от температуры ( — температура Кюри).

Ферромагнитные вещества обнаруживают определенную «спонтанную» намагниченность при Для всех известных ферромагнетиков кривая зависимости

от приближается к горизонтали при очень низких температурах, так что действительно 0. Точные измерения показали, что для очень низких температур зависимость спонтанной намагниченности от можно Представить как

в соответствии с теоремой Нернста.

Для парамагнитных веществ справедлив закон Кюри откуда если бы намагниченность вещества соответствовала закону Кюри до самых низких температур, то это противоречило бы теореме Нернста. Но, как мы отмечали при обсуждении опытов по размагничиванию (см. § 10), при очень низких температурах появляются отклонения от закона Кюри и вещество обнаруживает нерезко выраженные ферромагнитные свойства. Таким образом, мы можем считать, что теорема Нернста верна и в этом случае.