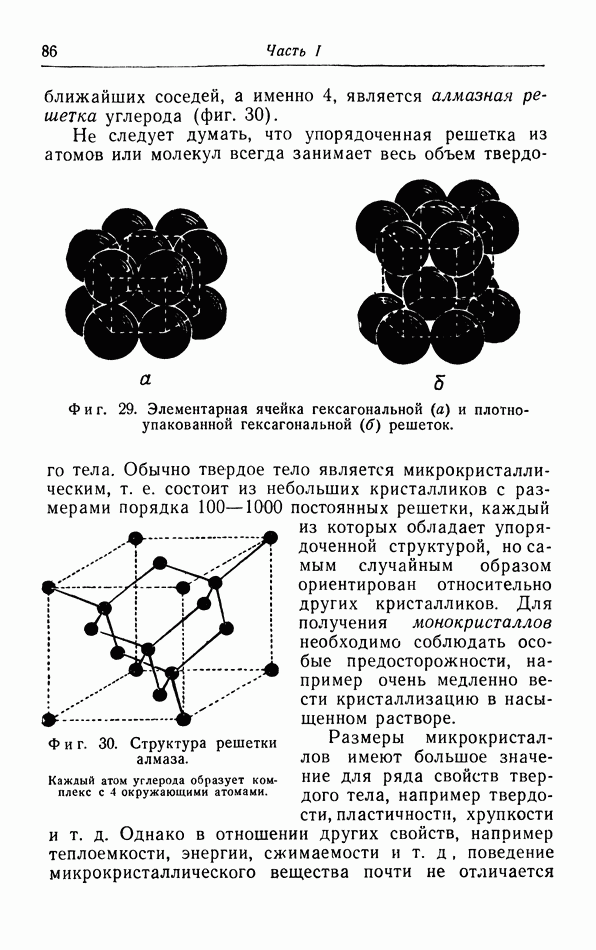
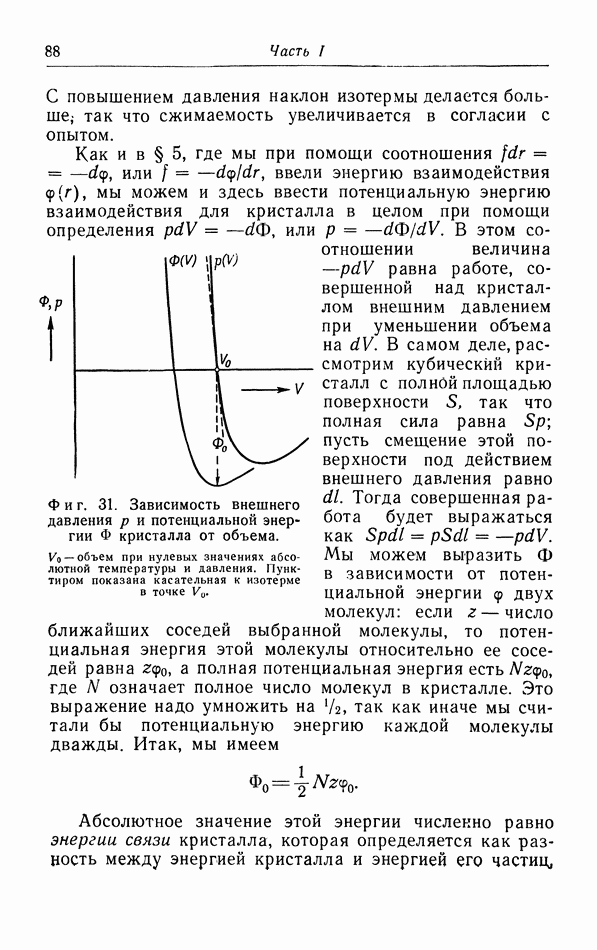
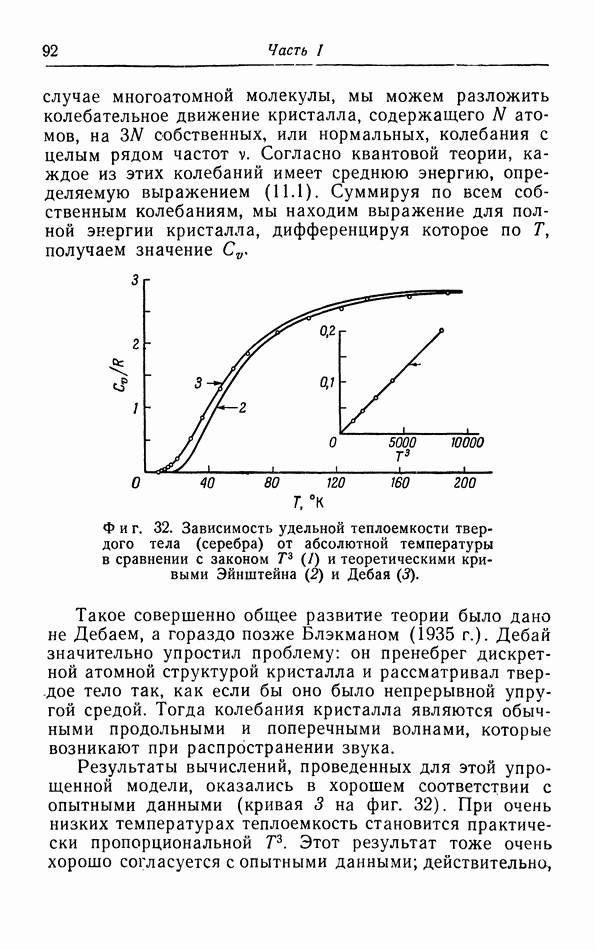
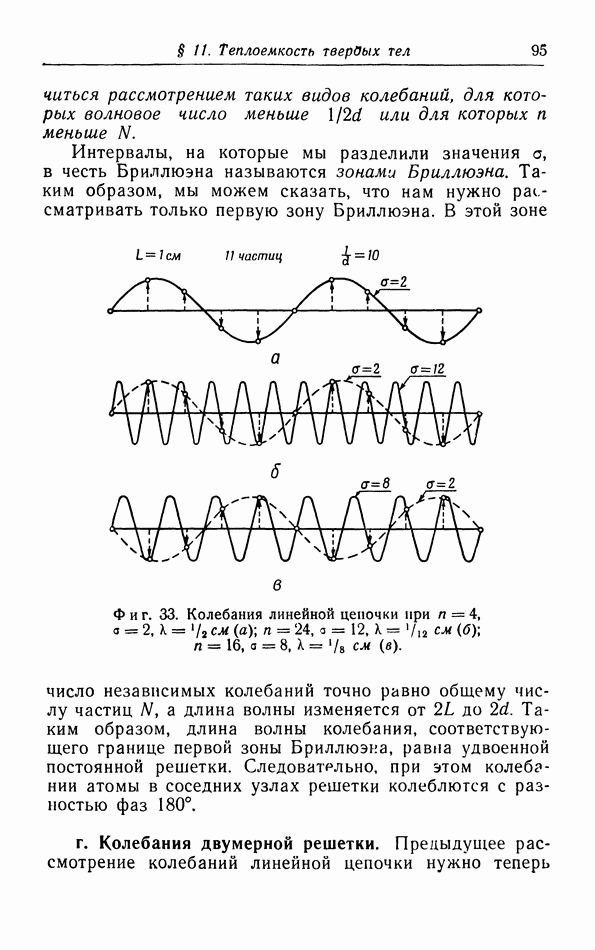
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
б. Расчет давления в кинетической теории газов.
Уравнение состояния идеального газа было теоретически выведено сначала Д. Бернулли (1738 г.), Джоулем (1851 г.), Крёнигом (1856 г.) и в окончательной форме Клаузиусом (1857 г ). Будем считать, что молекулы являются очень малыми точечными телами (с массой  и движутся в пространстве прямолинейно со скоростью V, имеющей компоненты
и движутся в пространстве прямолинейно со скоростью V, имеющей компоненты  .
.
Предположим, что стенка сосуда совершенно гладкая, так что молекулы отражаются от нее подобно тому, как свет отражается от зеркала. Поместим эту совершенно гладкую и твердую стенку перпендикулярно оси  как показано на фиг. 1, и положим, что некоторая молекула претерпевает столкновение в плоскости
как показано на фиг. 1, и положим, что некоторая молекула претерпевает столкновение в плоскости  Компоненты скорости
Компоненты скорости  после столкновения должны в таком случае удовлетворять соотношениям
после столкновения должны в таком случае удовлетворять соотношениям  и
и
Давление, оказываемое молекулами на стенку, равно среднему значению силы, действующей на единицу площади стенки вследствие ударов молекул. Согласно
одному из основных законов механики, сила, действующая на тело, равна изменению количества движения за единицу времени, а именно  Таким образом, средняя сила, действующая на молекулы со стороны стенки, равна изменению в единицу времени общего количества движения молекул в направлении, перпендикулярном к стенке. Сила, действующая на стенку со стороны молекул, равна этой же средней силе но направлена в обратную сторону.
Таким образом, средняя сила, действующая на молекулы со стороны стенки, равна изменению в единицу времени общего количества движения молекул в направлении, перпендикулярном к стенке. Сила, действующая на стенку со стороны молекул, равна этой же средней силе но направлена в обратную сторону.
Чтобы рассчитать изменение количества движения в направлении, перпендикулярном к стенке, для молекул, соударяющихся с элементом поверхности 1 сек, подсчитаем сначала количество молекул, достигающих этого элемента поверхности  в течение 1 сек. Рассмотрим пока только те молекулы, скорость которых по величине и направлению равна
в течение 1 сек. Рассмотрим пока только те молекулы, скорость которых по величине и направлению равна  тогда все молекулы, находящиеся в изображенном на фиг. 1 параллелепипеде с ребром
тогда все молекулы, находящиеся в изображенном на фиг. 1 параллелепипеде с ребром  и основанием
и основанием  ударятся о стенку в течение 1 сек. Количество этих молекул численно равно объему параллелепипеда
ударятся о стенку в течение 1 сек. Количество этих молекул численно равно объему параллелепипеда  умноженному на число молекул в единице объема, имеющих скорость V, т. е. равно
умноженному на число молекул в единице объема, имеющих скорость V, т. е. равно  Изменение количества движения каждой из этих молекул равно следовательно, полное изменение количества движения всех молекул этой группы, соударяющихся за 1 сек с элементом поверхности
Изменение количества движения каждой из этих молекул равно следовательно, полное изменение количества движения всех молекул этой группы, соударяющихся за 1 сек с элементом поверхности  будет равно
будет равно  Чтобы найти общее изменение количества движения всех молекул, сталкивающихся с
Чтобы найти общее изменение количества движения всех молекул, сталкивающихся с  за 1 сек, необходимо сложить вклады всех молекул, обладающих различными значениями
за 1 сек, необходимо сложить вклады всех молекул, обладающих различными значениями  Обозначая суммирование по всем этим молекулам через
Обозначая суммирование по всем этим молекулам через  получаем, что давление
получаем, что давление


Фиг. 1. Столкновение молекулы с абсолютно гладкой и упругой стенкой.
Суммирование следует производить лишь по тем молекулам. которые движутся слева направо, так как только эти молекулы действительно соударяются со стенкой. Если обозначить среднее значение  через
через  тогда, согласно определению среднего, величина
тогда, согласно определению среднего, величина  равна сумме
равна сумме  для всех движущихся направо молекул, деленной на их число. Итак,
для всех движущихся направо молекул, деленной на их число. Итак,

Подставляя в (2.3), получаем

Предположим теперь, что движение молекул происходит совершенно беспорядочно, т. е. они движутся по всевозможным направлениям и что средние значения числа молекул, движущихся в любом из этих направлений, одинаковы. Тогда среднее значение  не зависит от направления и поэтому
не зависит от направления и поэтому  Если
Если  численное значение скорости молекулы независимо от направления ее движения, то из соотношения
численное значение скорости молекулы независимо от направления ее движения, то из соотношения  получим
получим  откуда
откуда

Итак, давление пропорционально числу молекул в единице объема и среднему значению кинетической энергии  молекулы. Умножая
молекулы. Умножая  на
на  число молекул в единице объема, мы получаем плотность энергии
число молекул в единице объема, мы получаем плотность энергии

Давление равно  от плотности кинетической энергии газа.
от плотности кинетической энергии газа.
Если обозначить через  число Авогадро, т. е. число молекул в одном киломоле, объем которого равен V, то
число Авогадро, т. е. число молекул в одном киломоле, объем которого равен V, то
 Подставляя в (2.5), получаем
Подставляя в (2.5), получаем

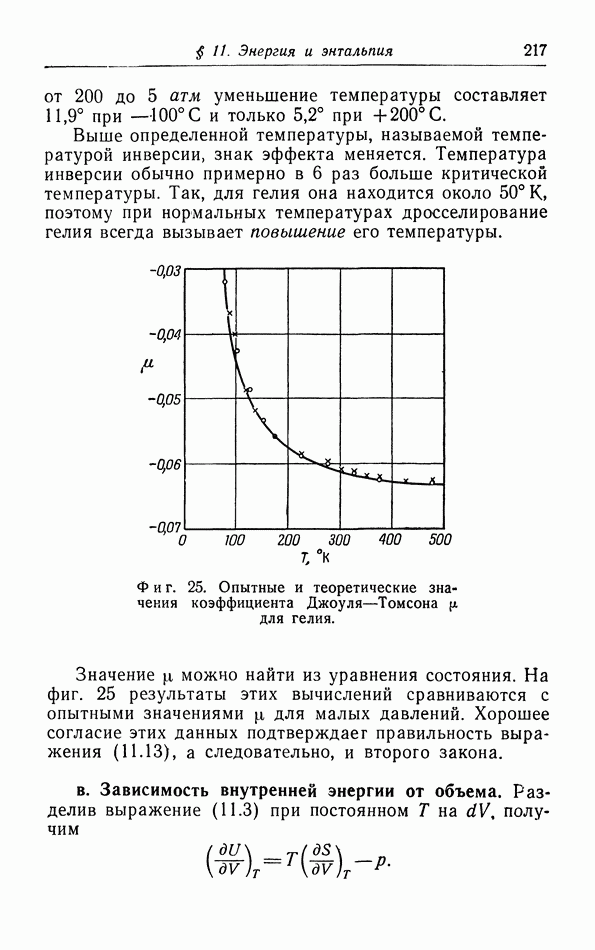
Таким образом, мы получили уравнение состояния (2.2) для идеального газа, если предположить, что значение  при заданной температуре не зависит от давления и что возрастает прямо пропорционально температуре согласно соотношению
при заданной температуре не зависит от давления и что возрастает прямо пропорционально температуре согласно соотношению

где  означает массу одного киломоля газа. Квадратный корень из среднего значения квадрата скорости называется «средней квадратичной скоростью», которая определяется выражением
означает массу одного киломоля газа. Квадратный корень из среднего значения квадрата скорости называется «средней квадратичной скоростью», которая определяется выражением

Интересно отметить, что формула (2.9) позволяет вычислить среднюю квадратичную скорость только по макроскопическим величинам: давлению  и плотности
и плотности  при этом не нужно делать каких-либо предположений о свойствах или массе молекул. В табл. 1 приведены рассчитанные по формуле (2.9) значения
при этом не нужно делать каких-либо предположений о свойствах или массе молекул. В табл. 1 приведены рассчитанные по формуле (2.9) значения  для ряда газов.
для ряда газов.
Таблица 1
Средняя квадратичная скорость при 15° С

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
- б. Жидкие пленки.
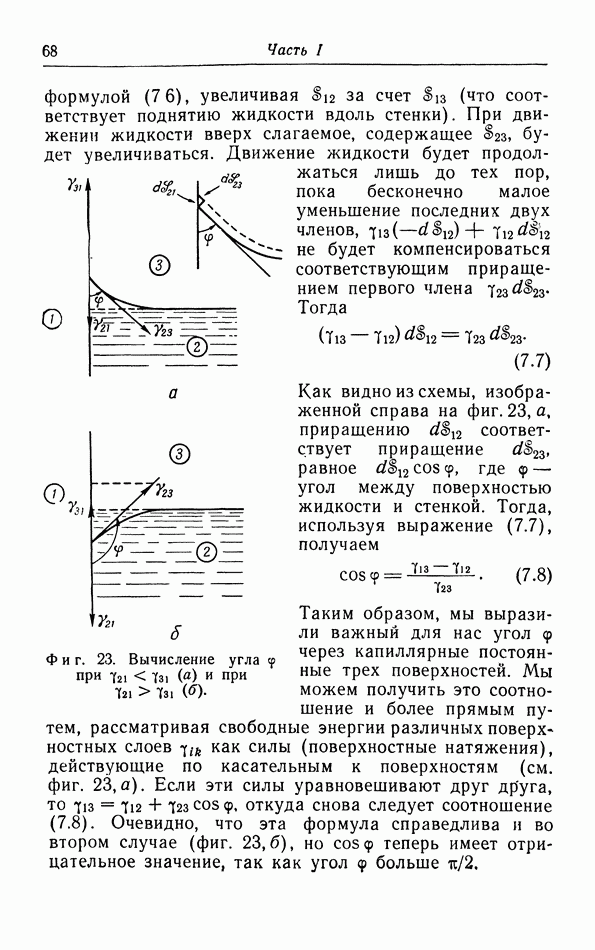
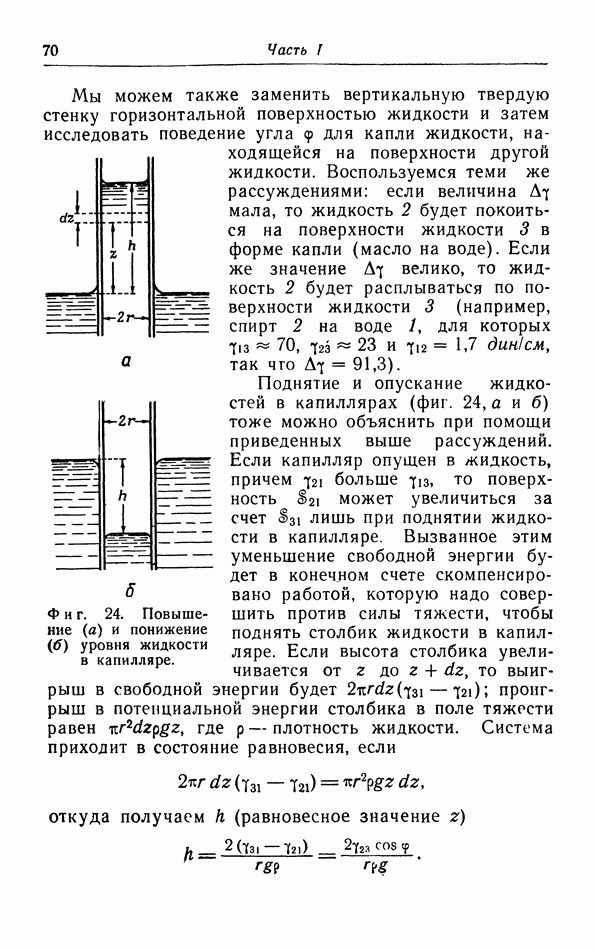
- в. Капиллярное поднятие и понижение уровня жидкости.
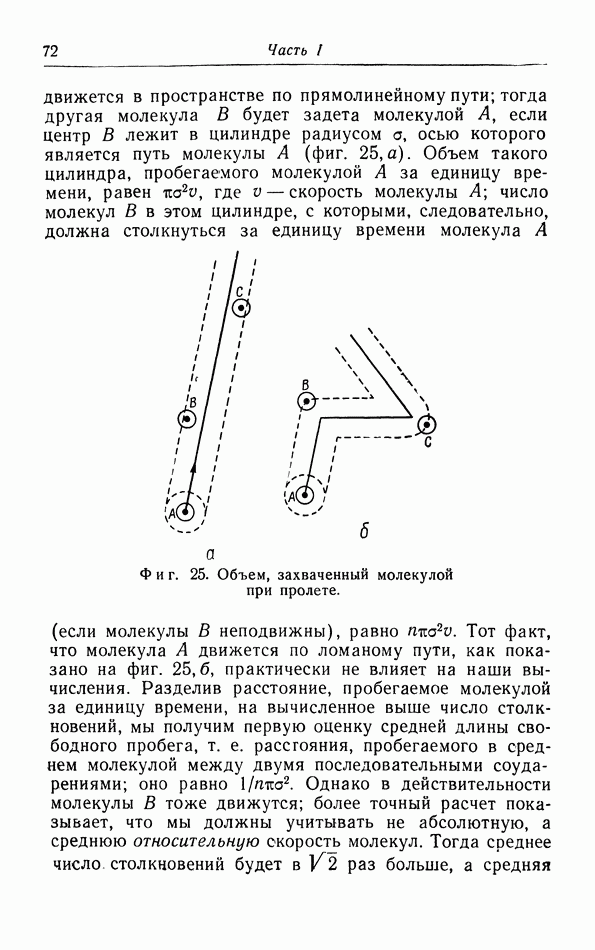
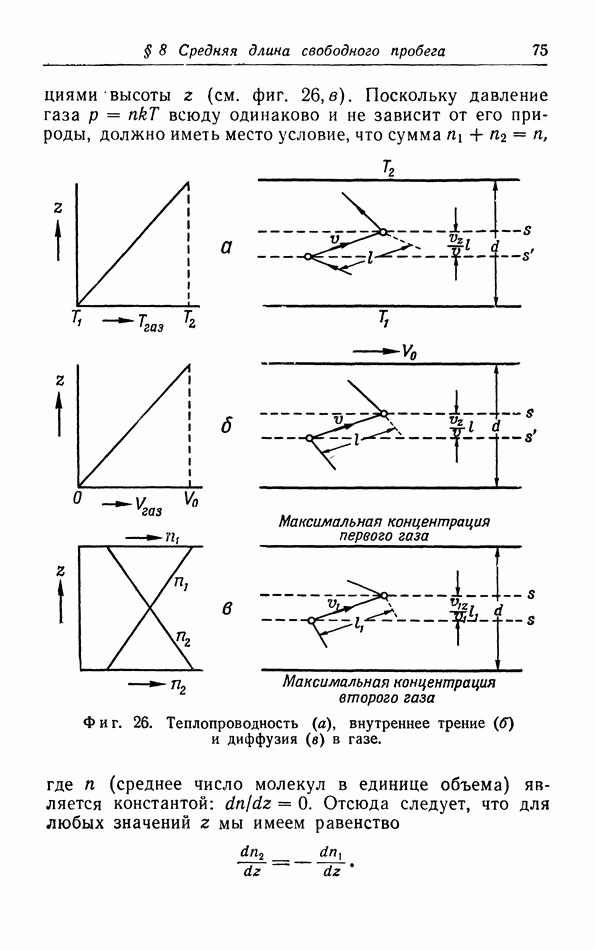
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
- § 3. Первый закон термодинамики
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
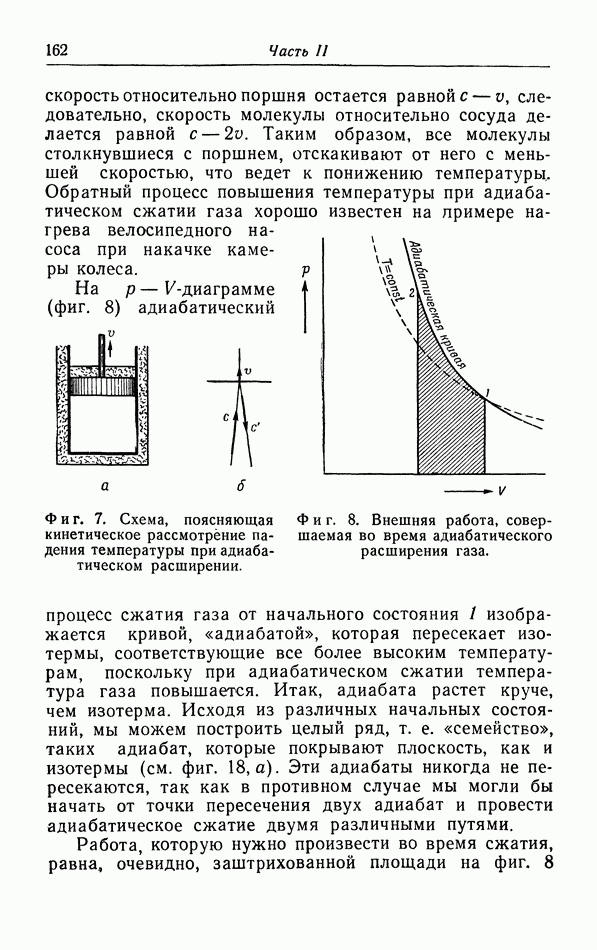
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
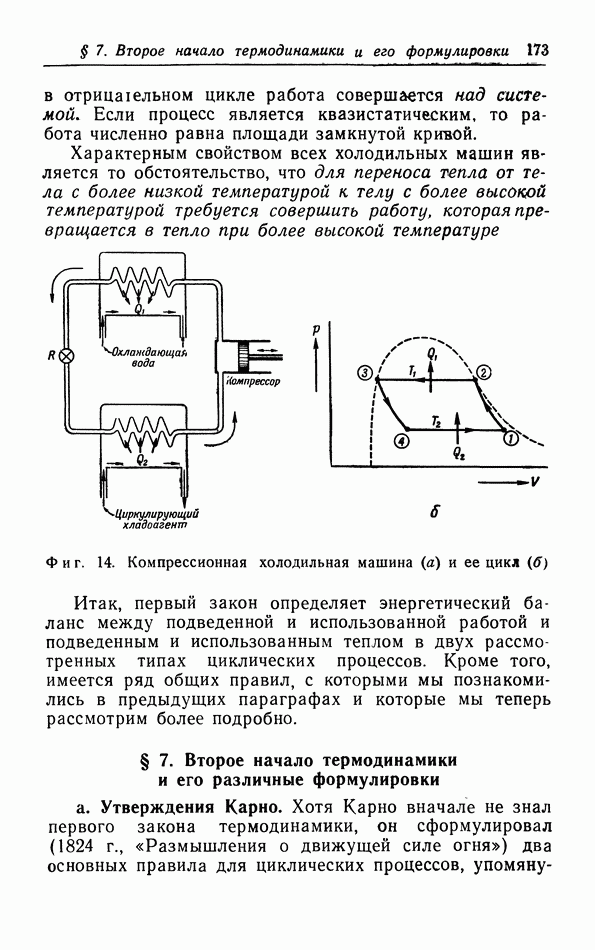
- § 6. Работа и теплота в циклических процессах
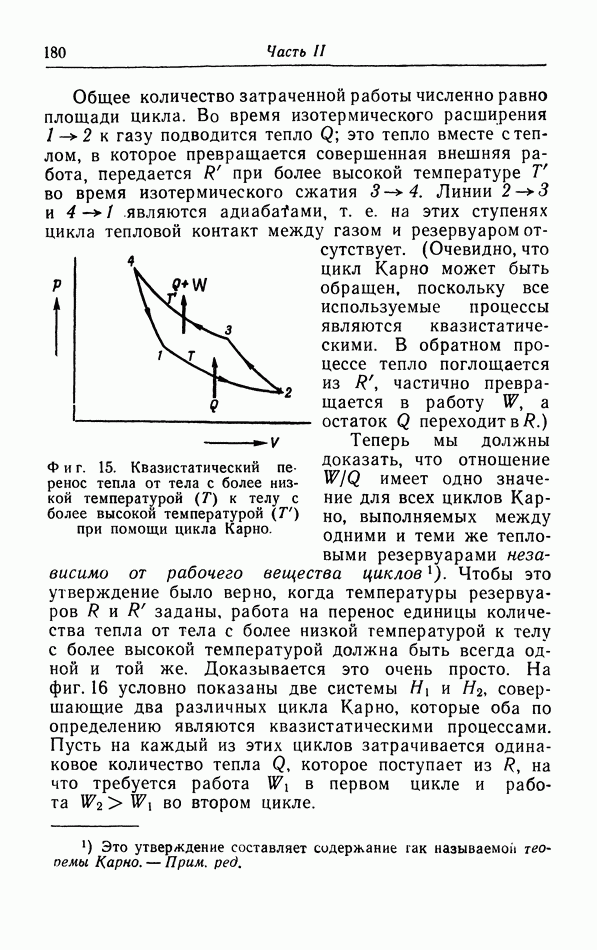
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
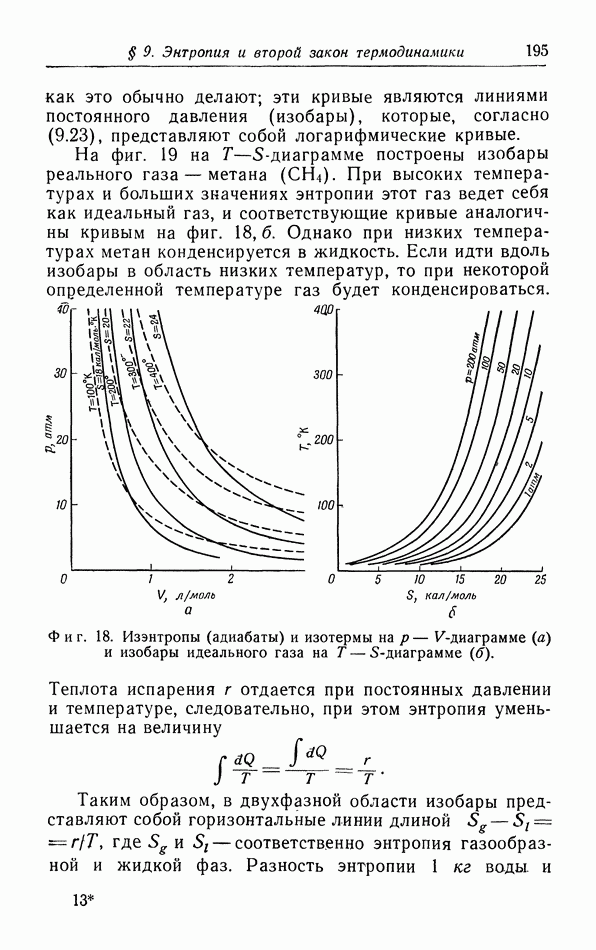
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
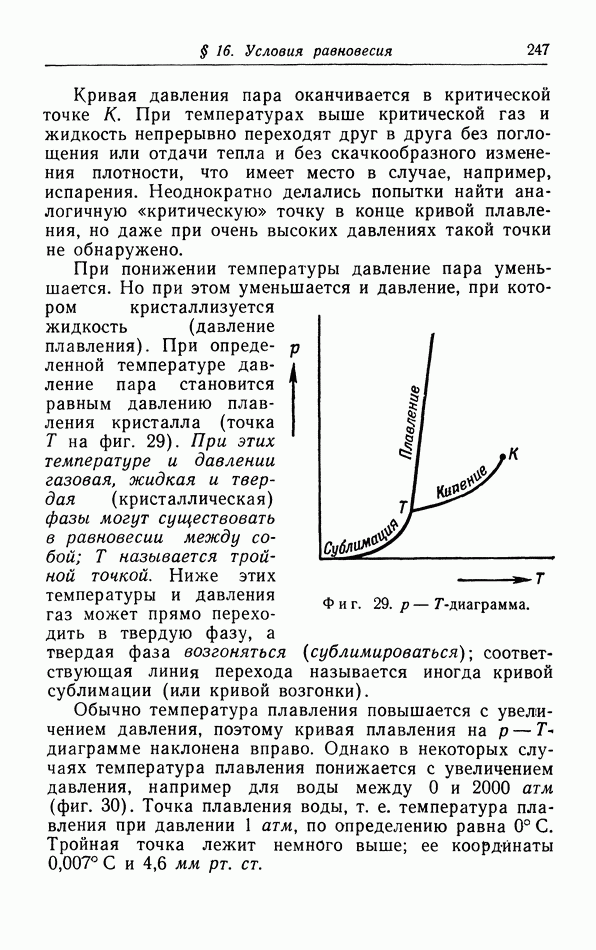
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
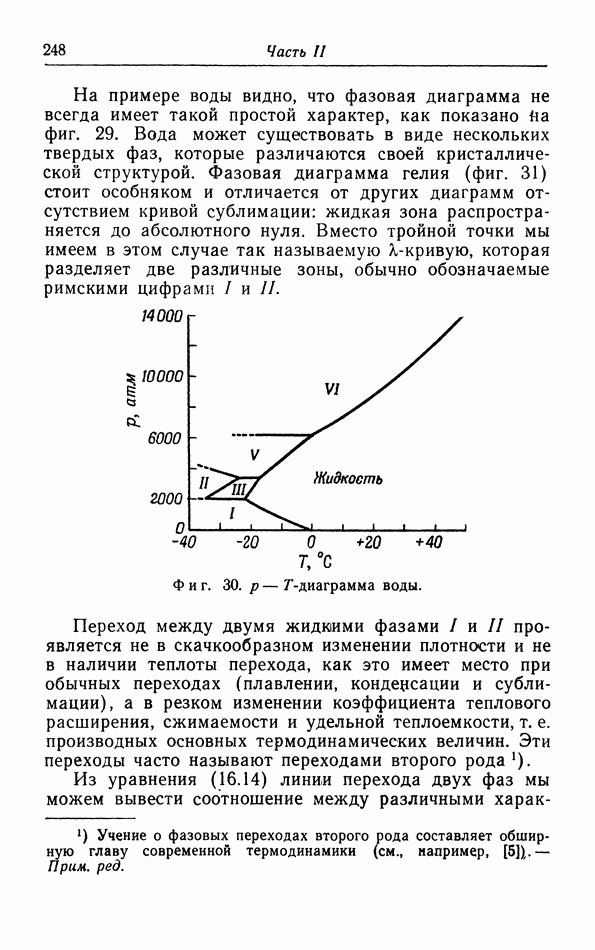
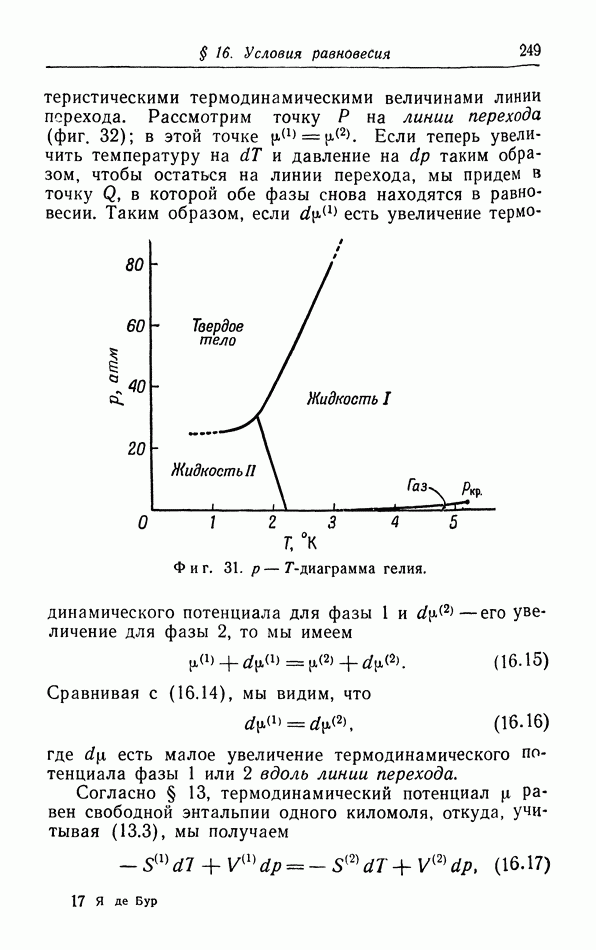
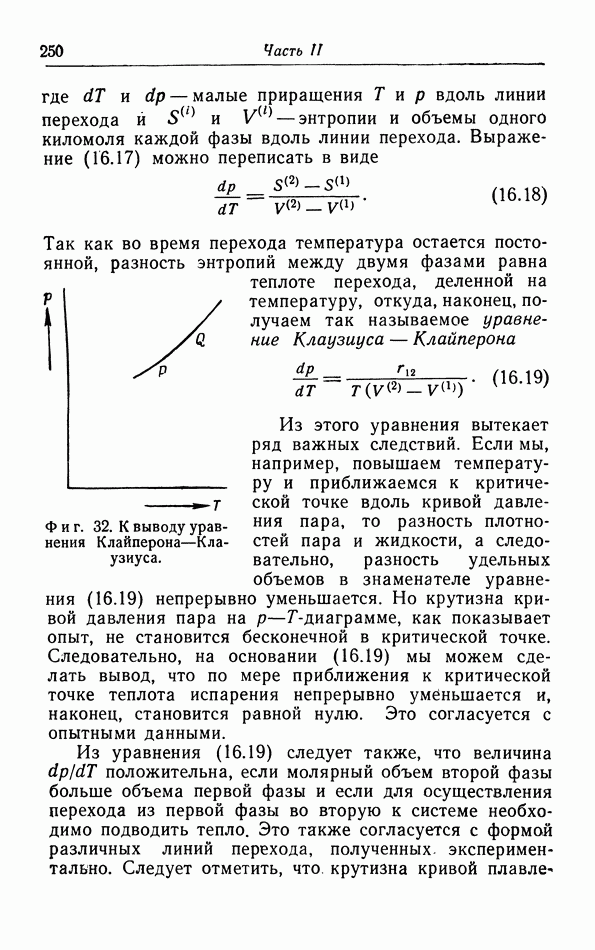
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам