| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
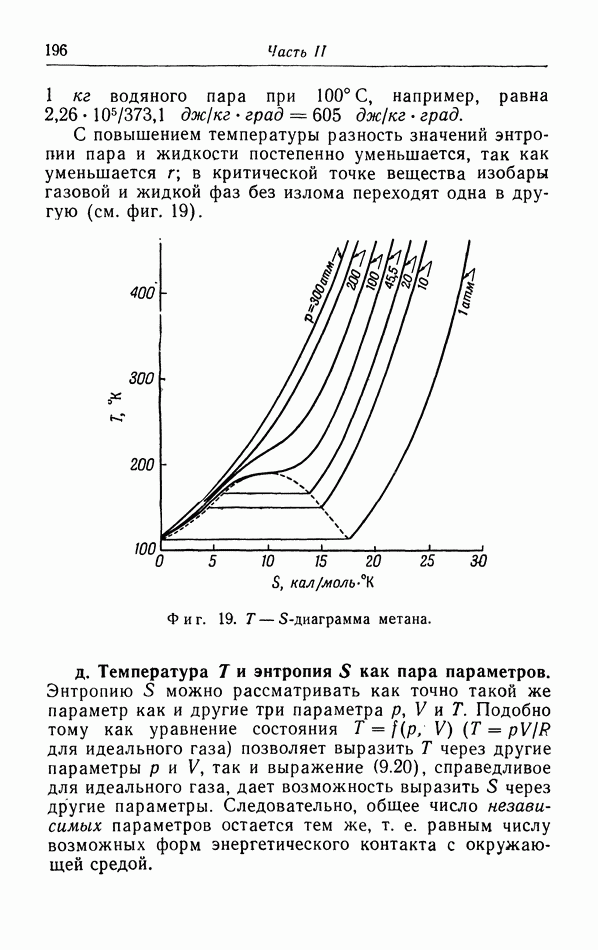
§ 10. Применения второго закона термодинамики
а. Другие формы записи второго закона.
В § 9 мы вывели следующее дифференциальное выражение для второго закона:

Теперь мы выведем аналогичное выражение, но в функции от параметров  Для этого будем считать V функцией от
Для этого будем считать V функцией от  Подставляя
Подставляя

в (10.1), получаем

три величины, в частности  каждую из которых мы можем считать функцией двух других, всегда удовлетворяют соотношению
каждую из которых мы можем считать функцией двух других, всегда удовлетворяют соотношению

При помощи этого соотношения мы можем упростить последнее слагаемое в выражении для  что дает
что дает

Так как  мы, согласно (5.7), имеем
мы, согласно (5.7), имеем

и, следовательно, выражение в квадратных скобках равно  откуда вторая форма записи второго закона в переменных Тир имеет вид
откуда вторая форма записи второго закона в переменных Тир имеет вид

б. Соотношение между ...
Как побочный результат мы получили соотношение между 

Применим выражение (10.4), чтобы найти разность  Для этого введем следующие поддающиеся измерению величины:
Для этого введем следующие поддающиеся измерению величины:
1. Коэффициент теплового расширения

2. Изотермическую сжимаемость, полученную с помощью выражения

Мы можем включить знак минус в определение величины  так как производная
так как производная  всегда отрицательна. Подставляя
всегда отрицательна. Подставляя

в выражение (10.4), получаем

Это соотношение часто используется для того, чтобы выразить  величину более интересную в теоретическом отношении, через величину
величину более интересную в теоретическом отношении, через величину  которая проще измеряется. Например, для металлического серебра
которая проще измеряется. Например, для металлического серебра  откуда при
откуда при  . Поскольку
. Поскольку  составляет примерно
составляет примерно  град, поправка довольно мала. Однако для жидкостей, не говоря уже о газах, она может быть сравнительно большой.
град, поправка довольно мала. Однако для жидкостей, не говоря уже о газах, она может быть сравнительно большой.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
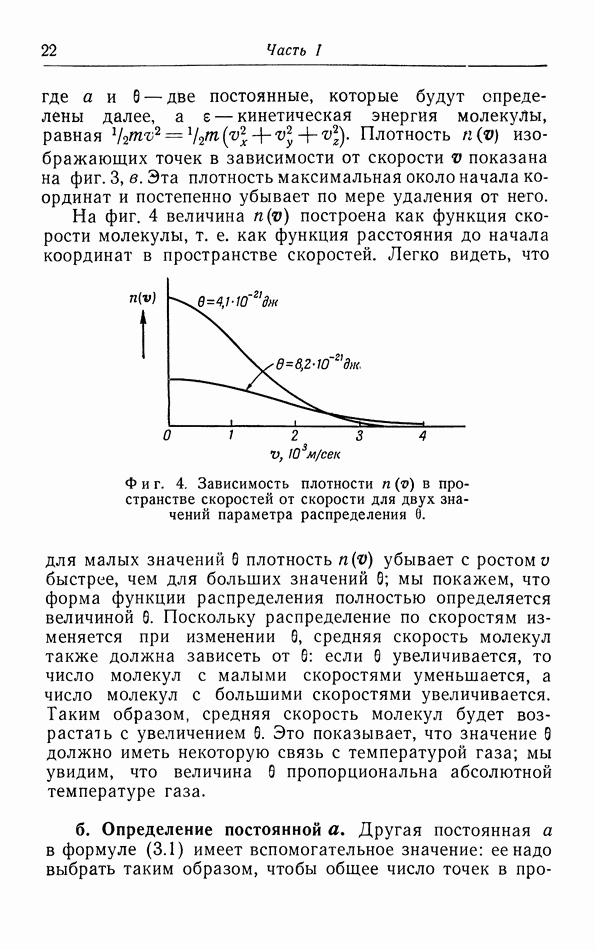
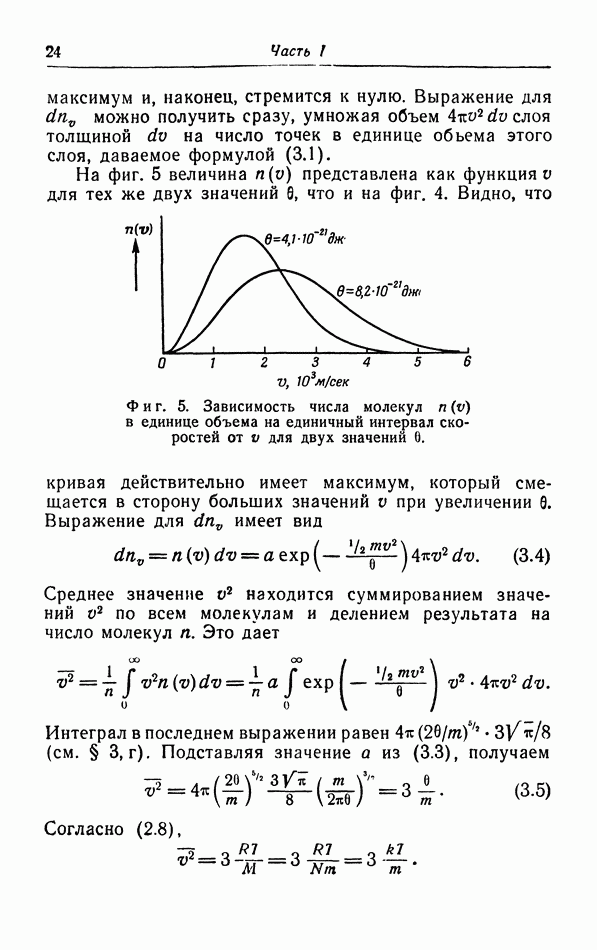
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
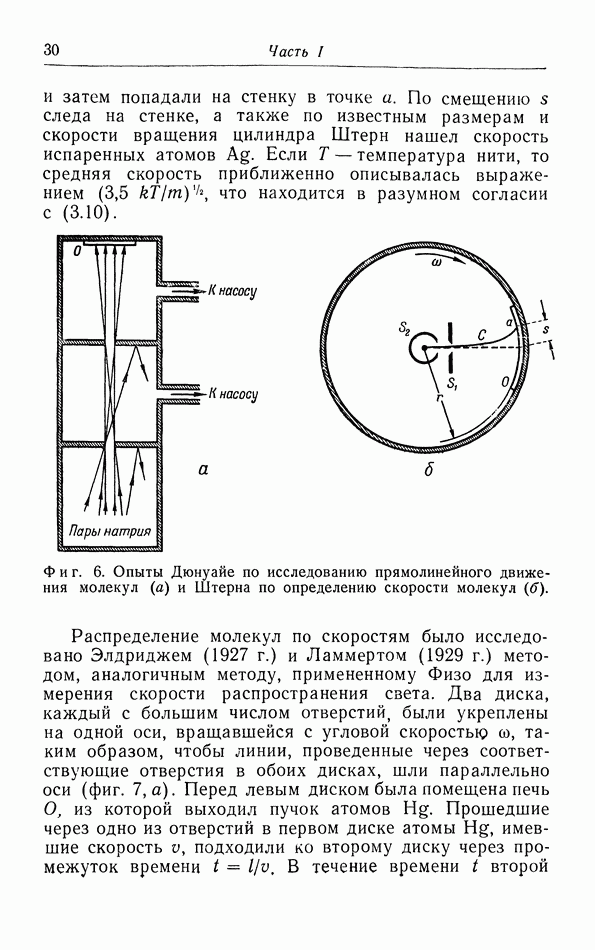
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
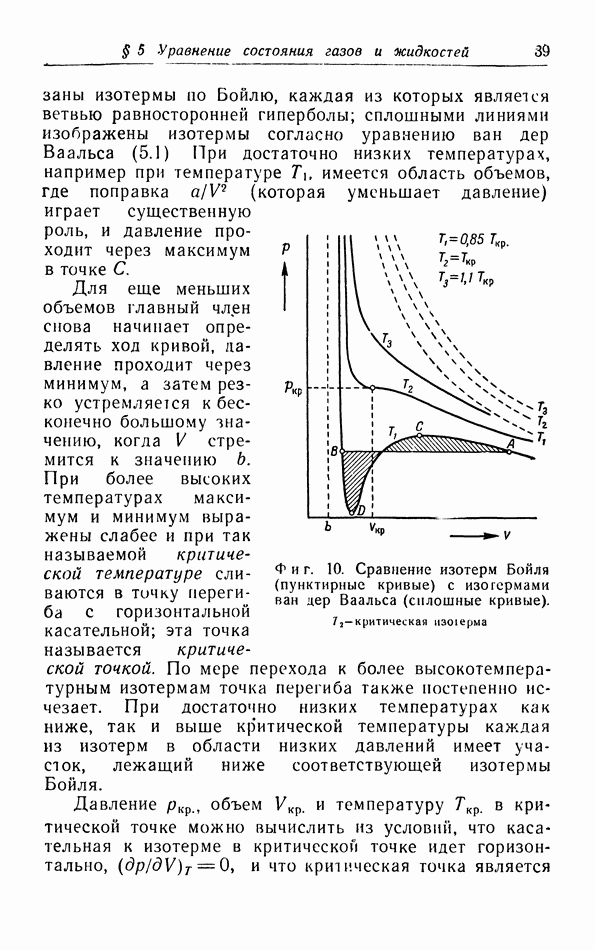
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
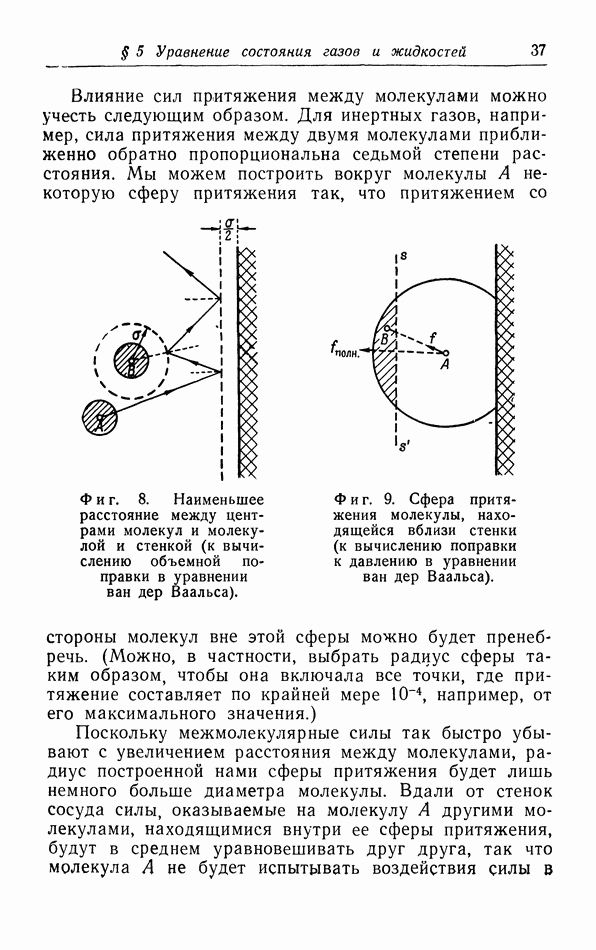
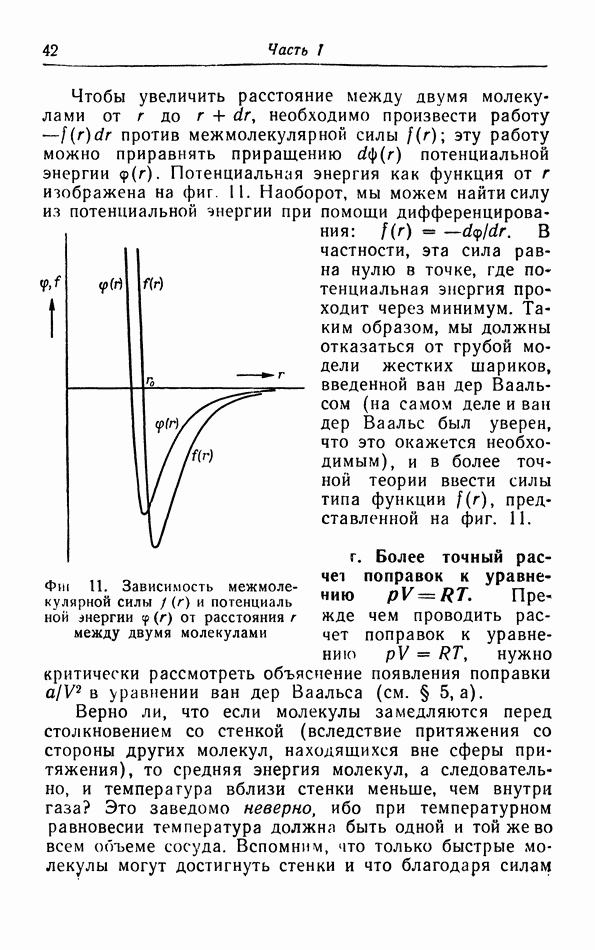
- в. Взаимодействие молекул.
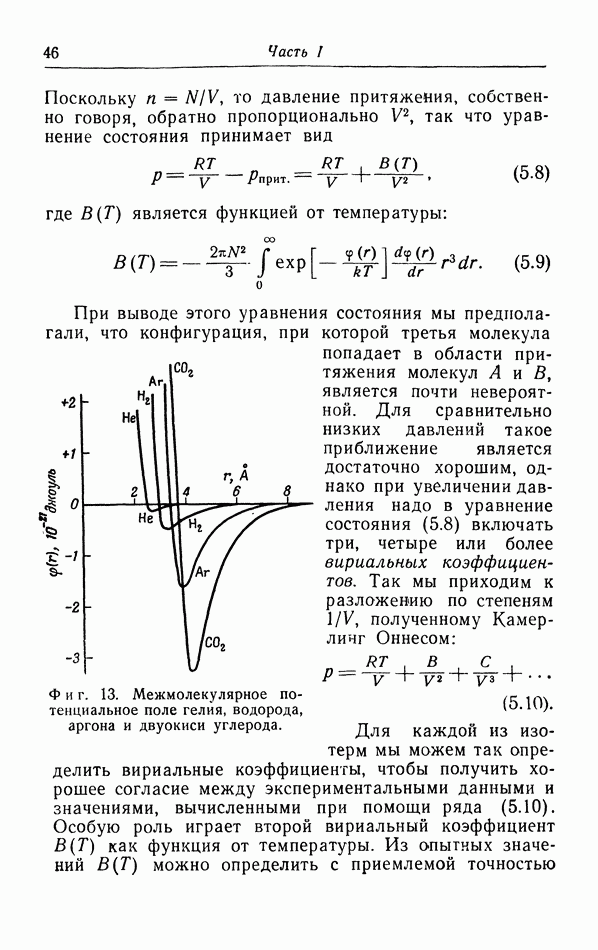
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
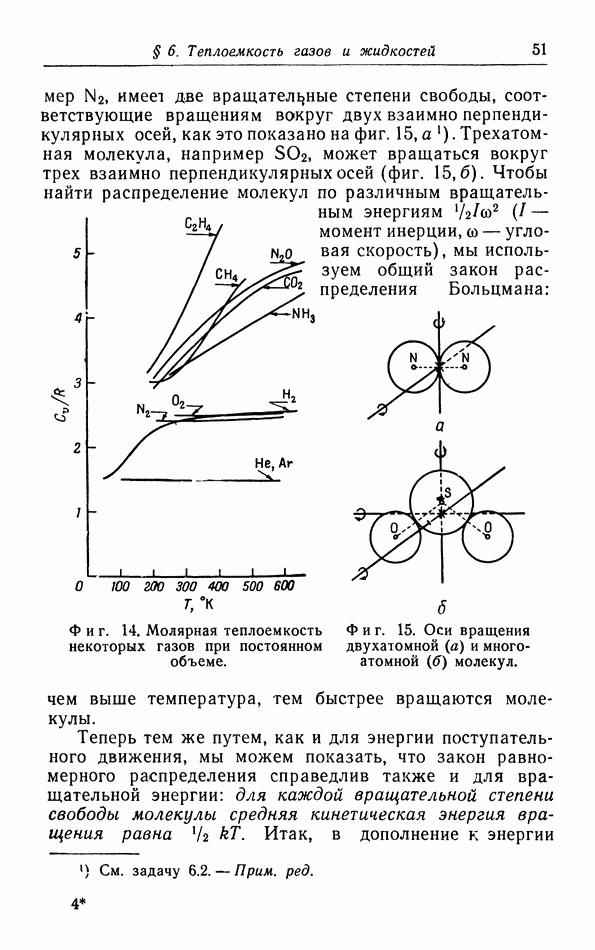
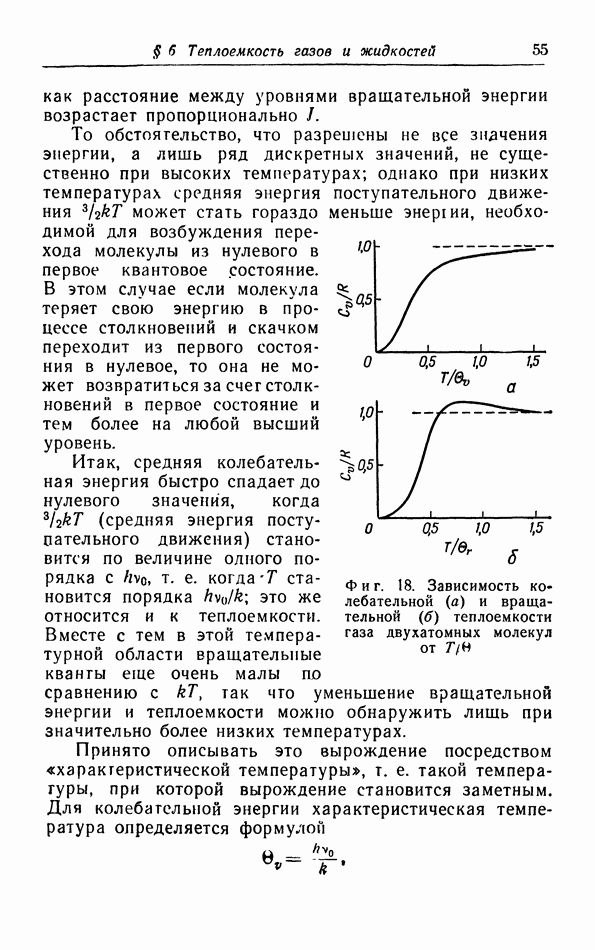
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
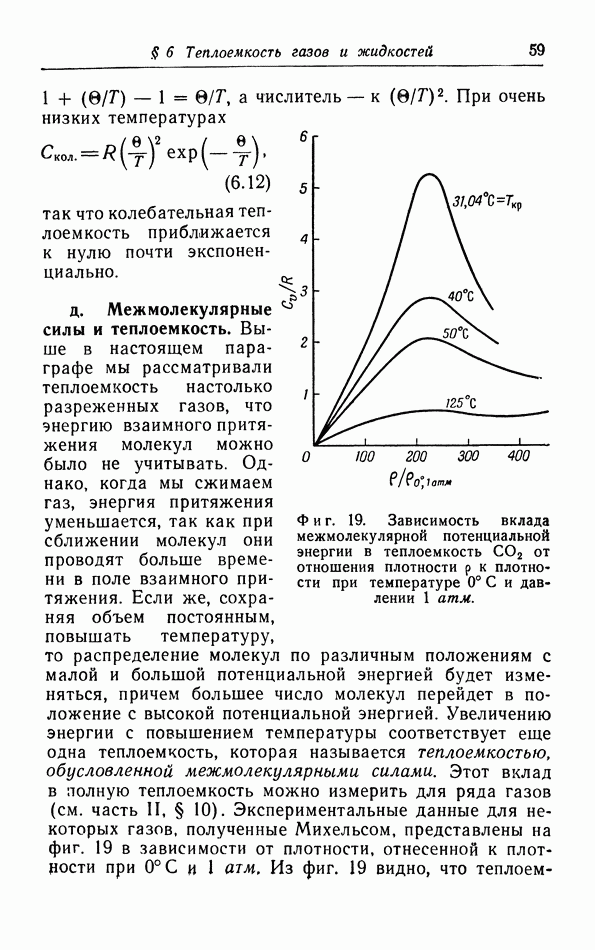
- д. Межмолекулярные силы и теплоемкость.
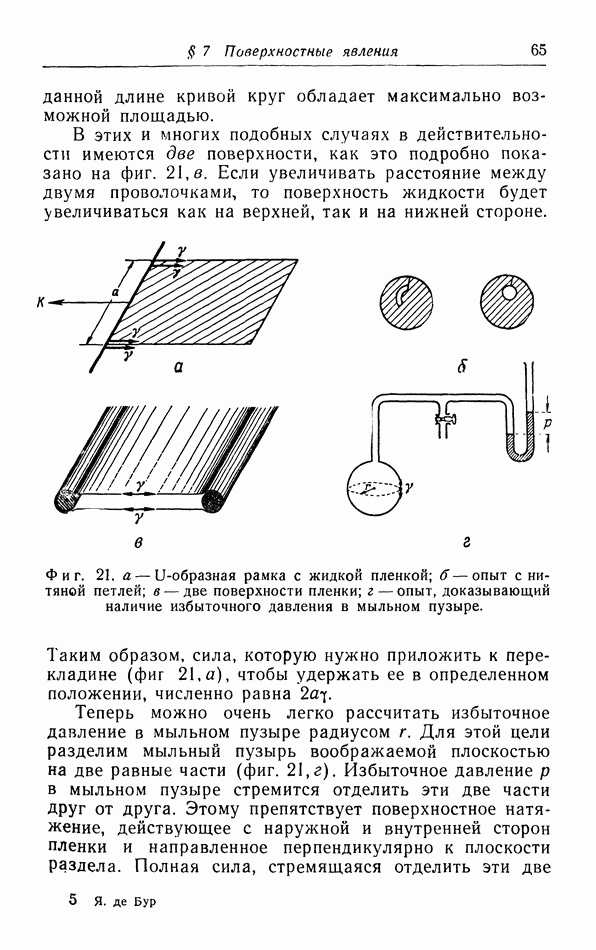
- § 7. Поверхностные явления
- б. Жидкие пленки.
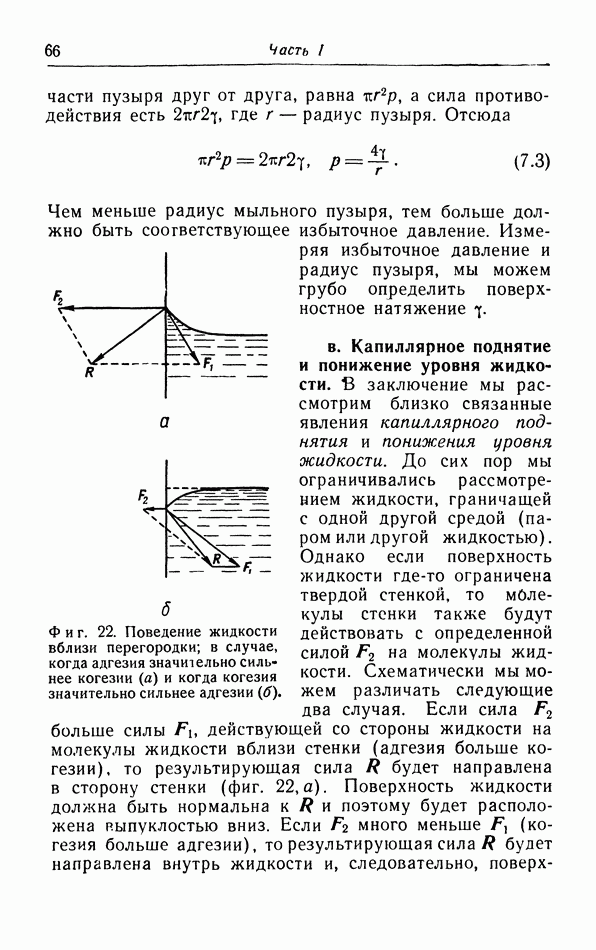
- в. Капиллярное поднятие и понижение уровня жидкости.
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
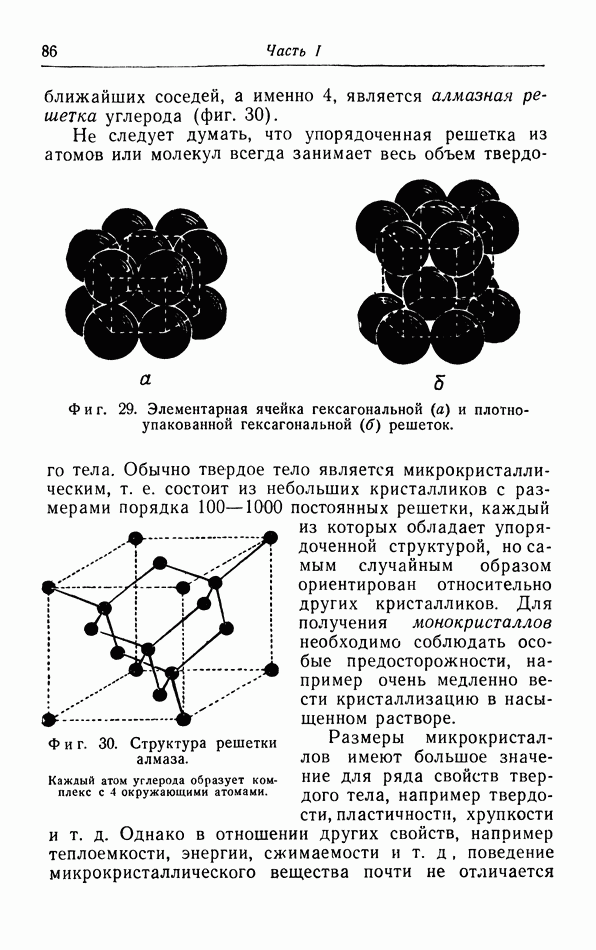
- § 9. Структура твердых тел
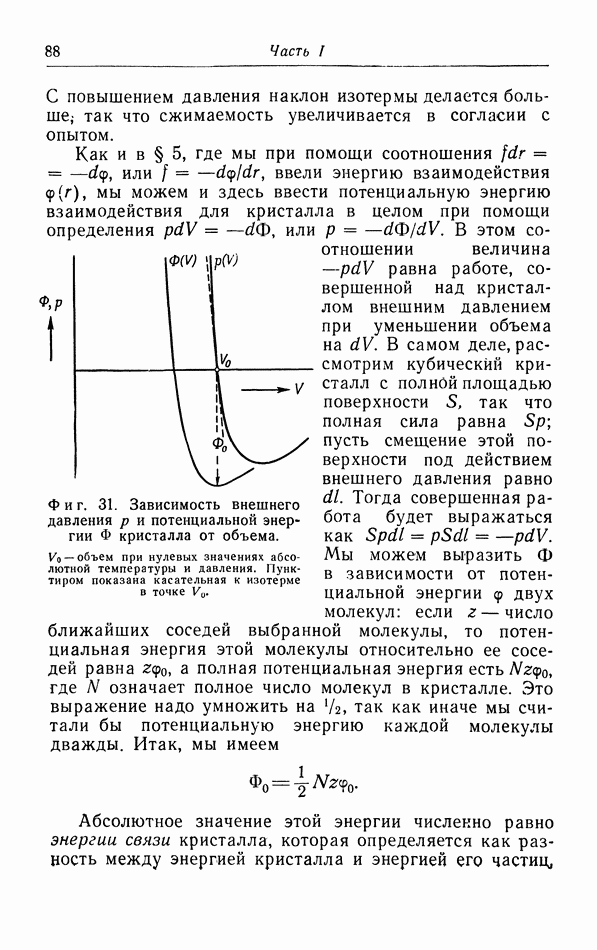
- § 10. Уравнение состояния твердых тел
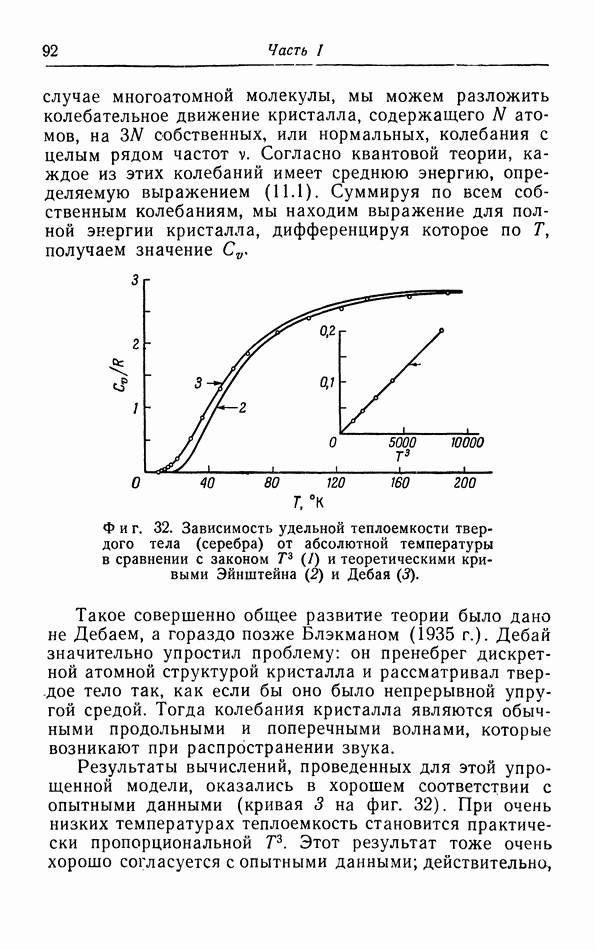
- § 11. Теплоемкость твердых тел
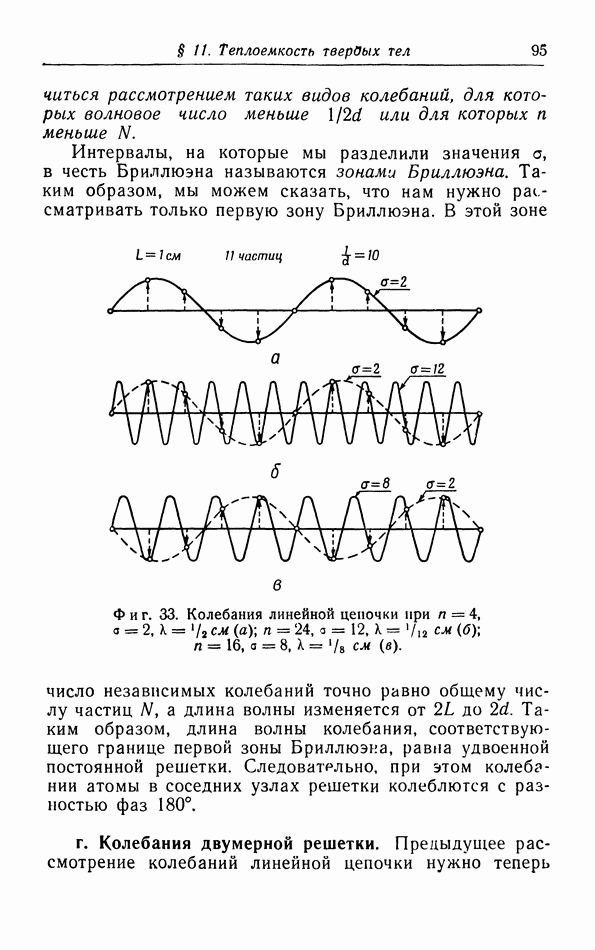
- в. Колебания линейной цепочки.
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
- § 3. Первый закон термодинамики
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
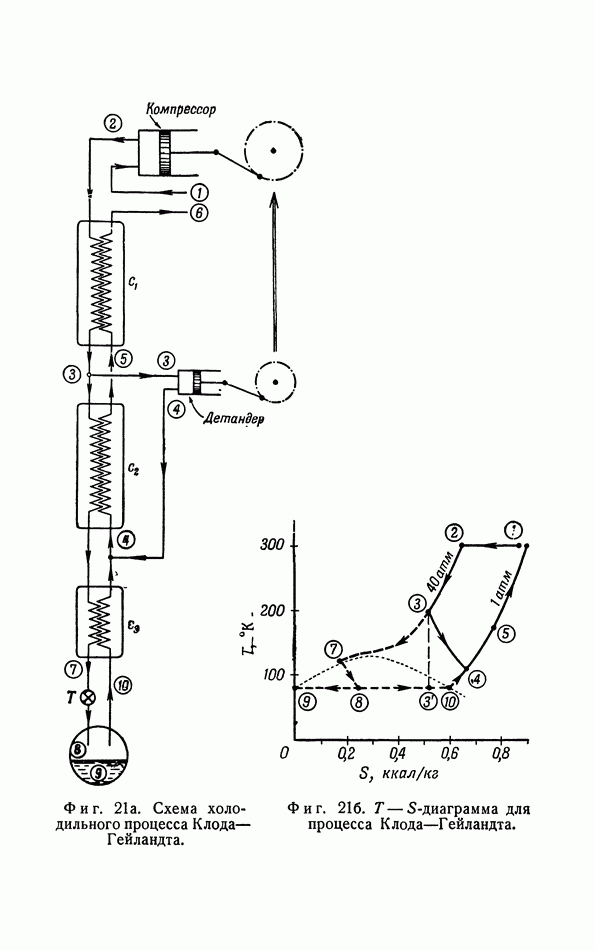
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
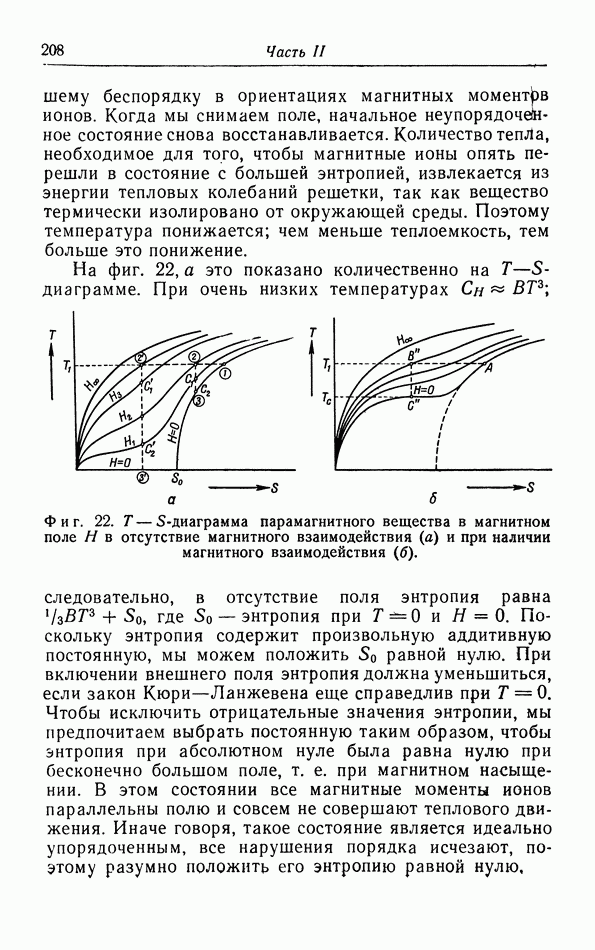
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
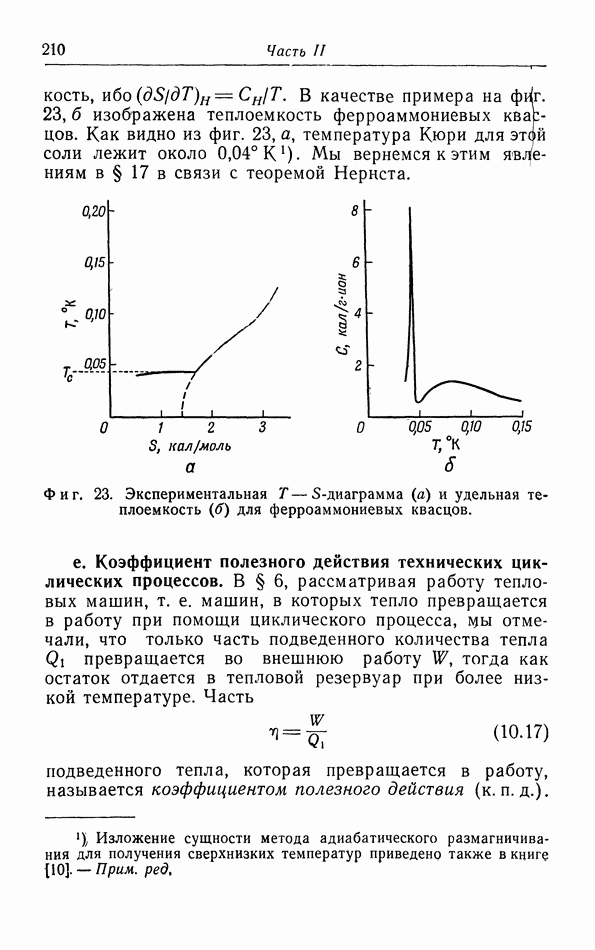
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
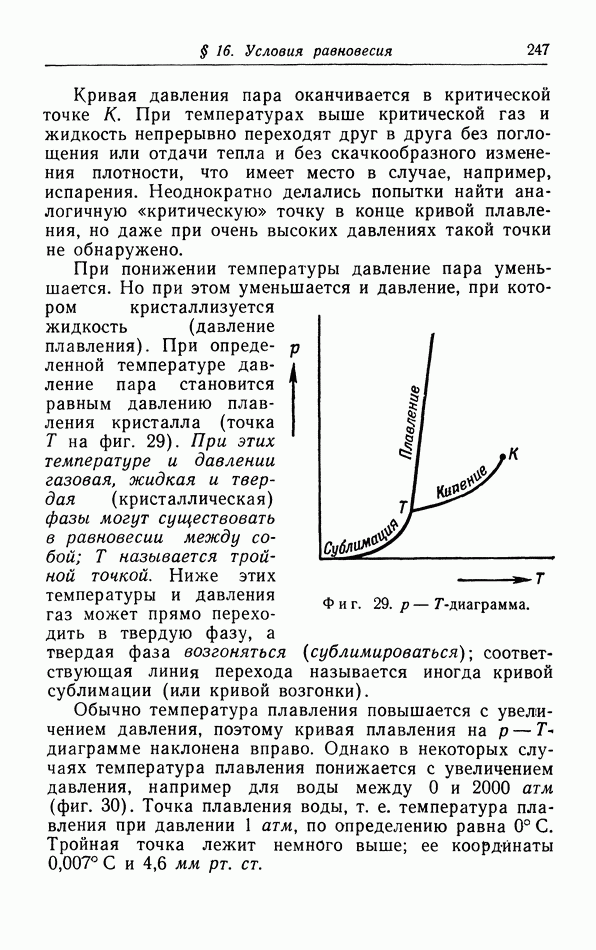
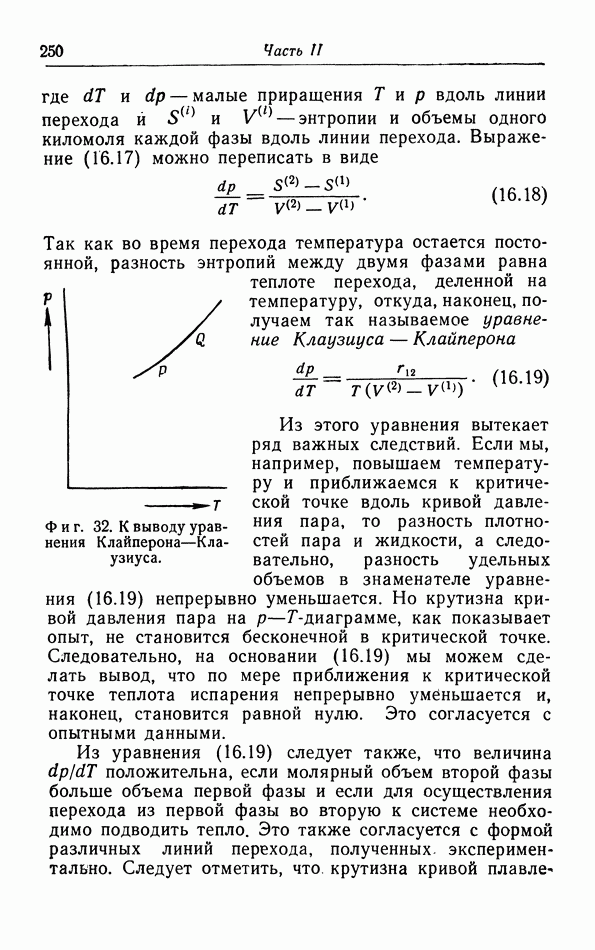
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
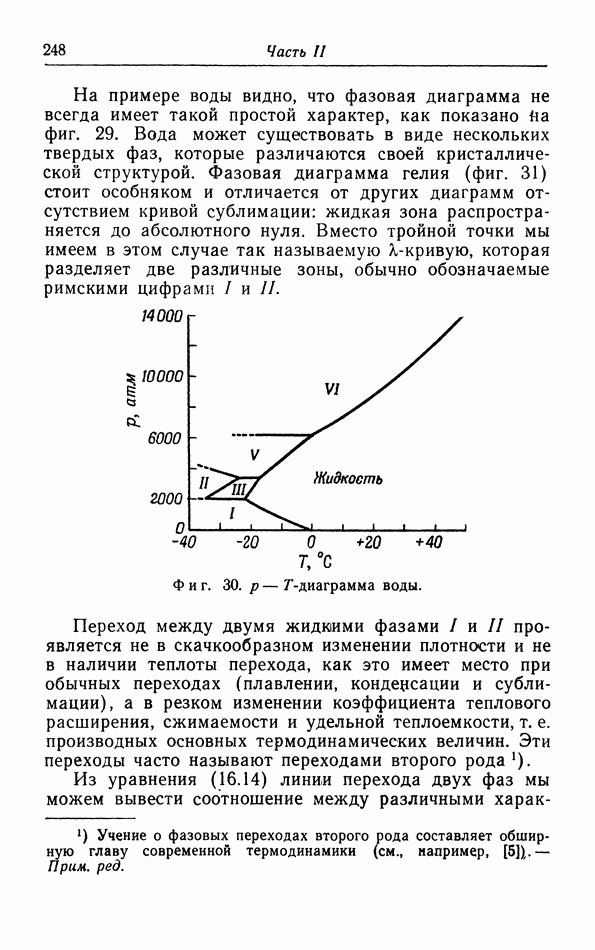
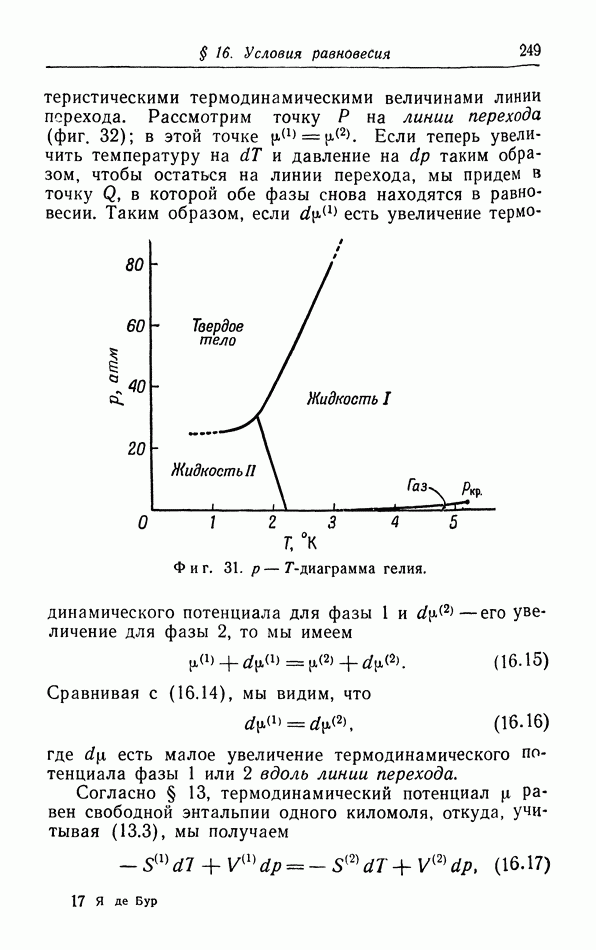
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам