| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
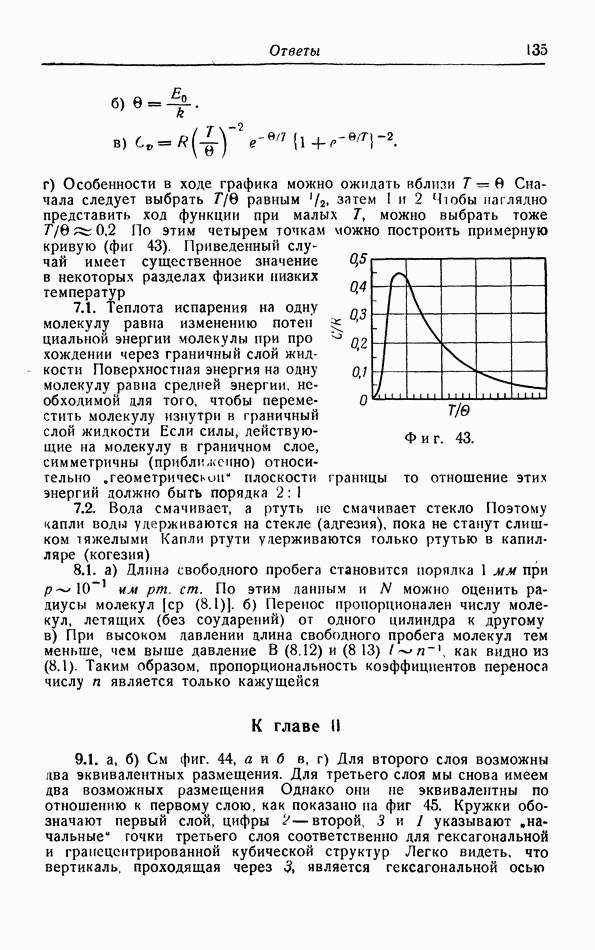
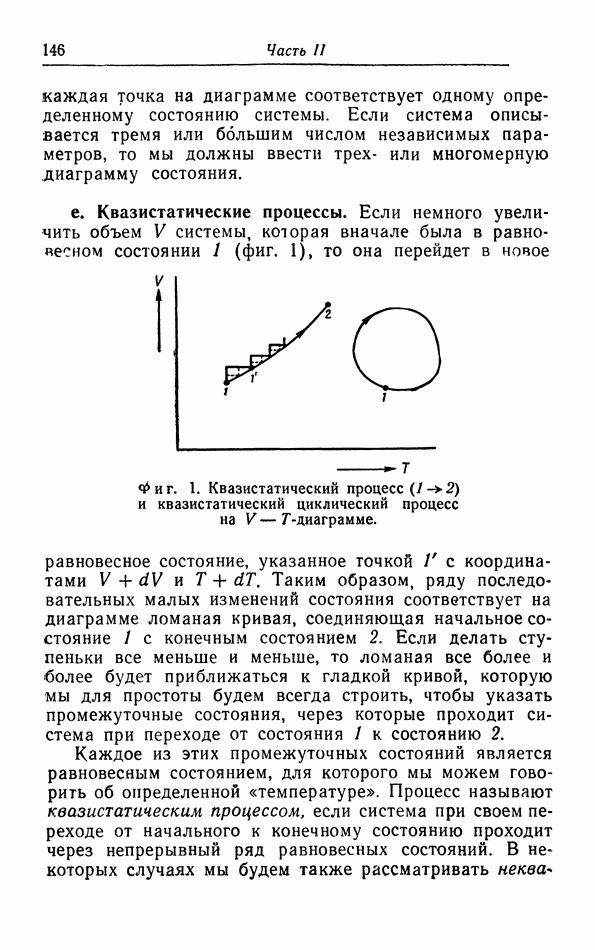
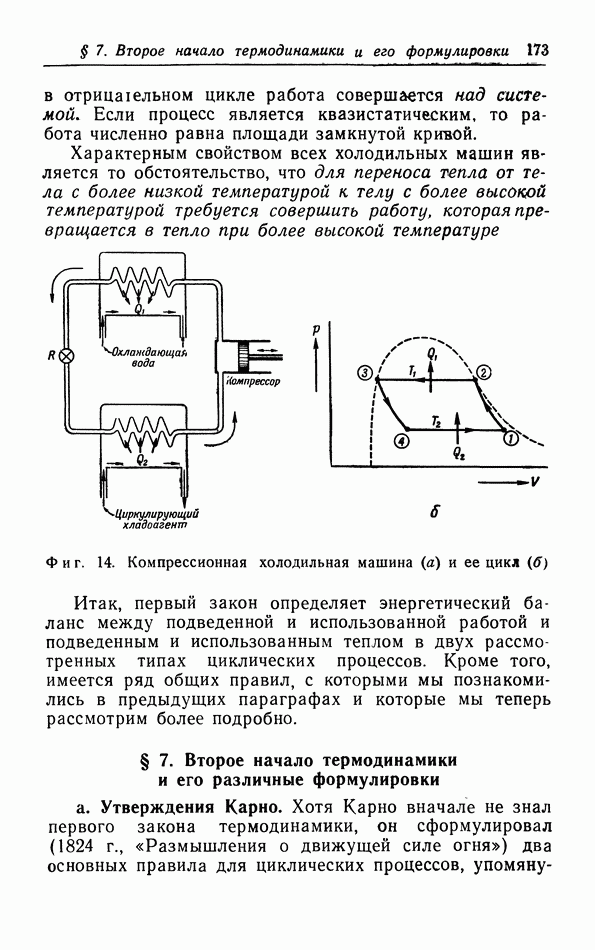
г. Неквазистатический изотермический процесс.
Кроме свойств неквазистатических адиабатических процессов, мы можем также вывести важные соотношения для изотермических процессов. Для таких процессов множитель  в выражении (15.2) можно вынести за знак интеграла, откуда, умножая на
в выражении (15.2) можно вынести за знак интеграла, откуда, умножая на  получаем 2
получаем 2

Согласно первому закону, который имеет совершенно общее значение,  откуда
откуда

или

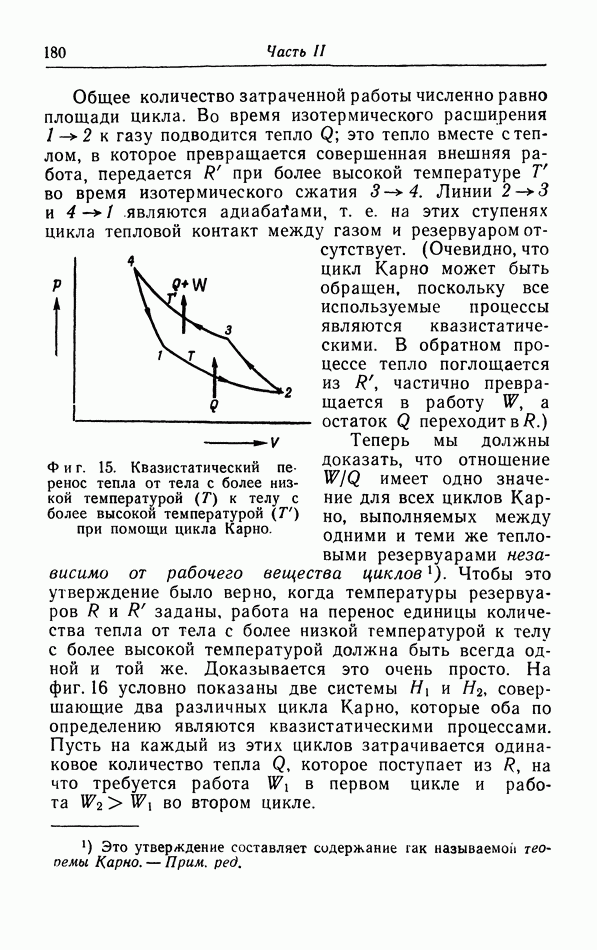
Внешняя работа, совершенная системой при неквазистатическом изотермическом процессе, меньше, чем уменьшение свободной энергии. Для квазистатического процесса сохраняется знак равенства; тогда неравенство (15.6) переходит в равенство (12.2). Итак, работа, совершенная при неквазистатическом изотермическом процессе, меньше работы, совершенной при
квазистатическом изотермическом процессе между теми же начальным и конечным состояниями.
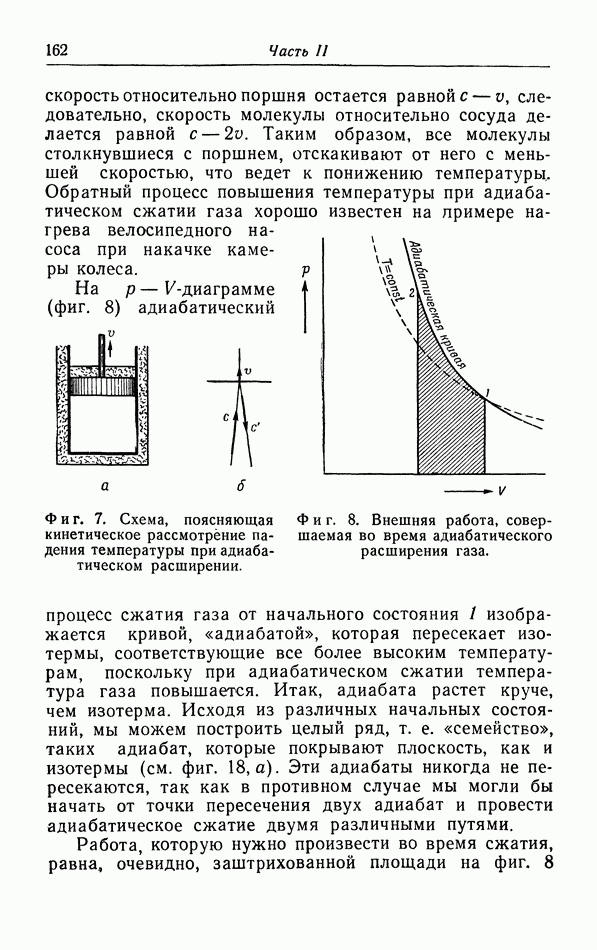
Мы можем представить это с точки зрения кинетической теории, рассматривая газ, который совершает работу во время расширения. Когда поршень выдвигается со скоростью давление на поршень со стороны газа уменьшается и будет равно приближенно  так как количество движения, передаваемого при соударении молекул с поршнем, определяется их относительной скоростью [см. часть I, формула (2.7)]. При
так как количество движения, передаваемого при соударении молекул с поршнем, определяется их относительной скоростью [см. часть I, формула (2.7)]. При  мы снова получаем обычное выражение для давления; но когда скорость поршня велика по сравнению со скоростями молекул, давление стремится к нулю, ибо тогда молекулы не могут догнать поршень.
мы снова получаем обычное выражение для давления; но когда скорость поршня велика по сравнению со скоростями молекул, давление стремится к нулю, ибо тогда молекулы не могут догнать поршень.
Если температура и объем остаются постоянными,  и
и

При неквазистатическом изотермическом процессе, происходящем при постоянном объеме, свободная энергия может только уменьшаться или оставаться постоянной.
Если же остаются постоянными температура и давление, то

и (15.6) приводится к виду

При неквазистатическом изотермическом процессе, происходящем при постоянном давлении, свободная энтальпия может только уменьшаться или оставаться постоянной.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
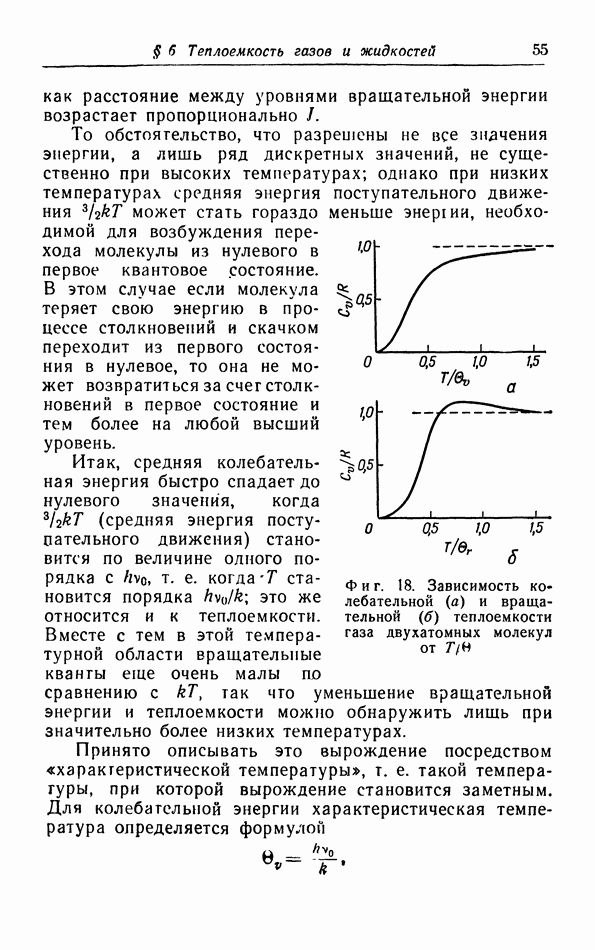
- г. Расчет колебательной теплоемкости двухатомной молекулы.
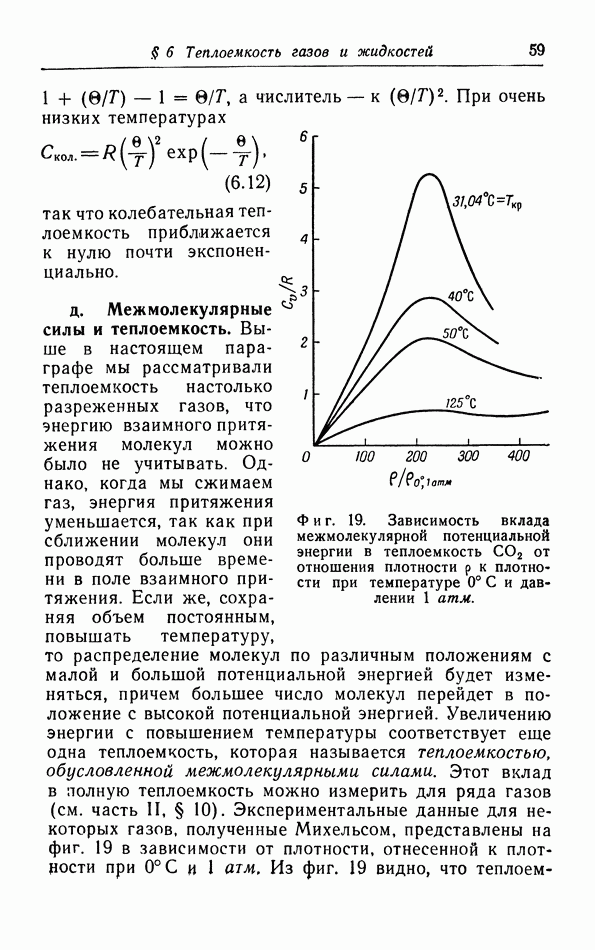
- д. Межмолекулярные силы и теплоемкость.
- § 7. Поверхностные явления
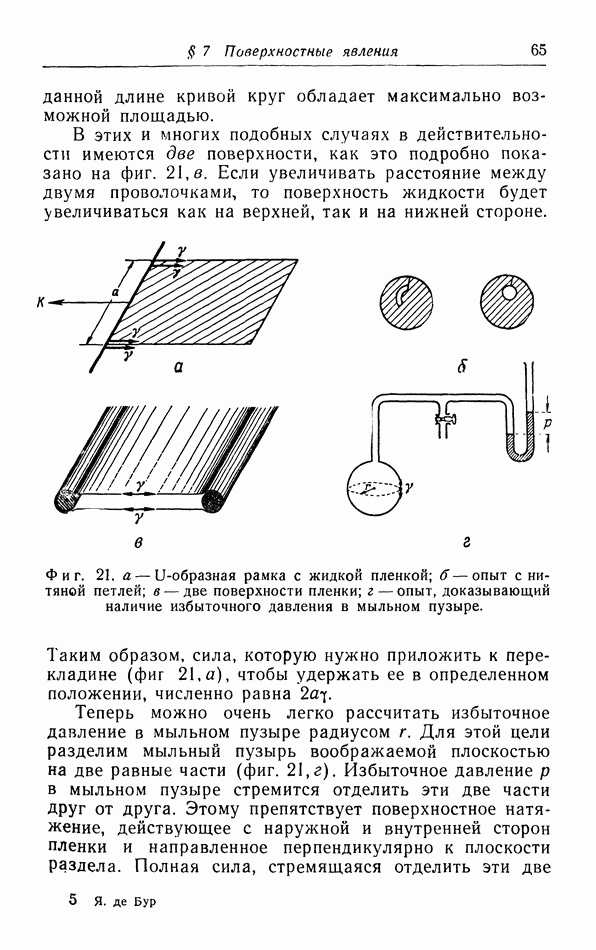
- б. Жидкие пленки.
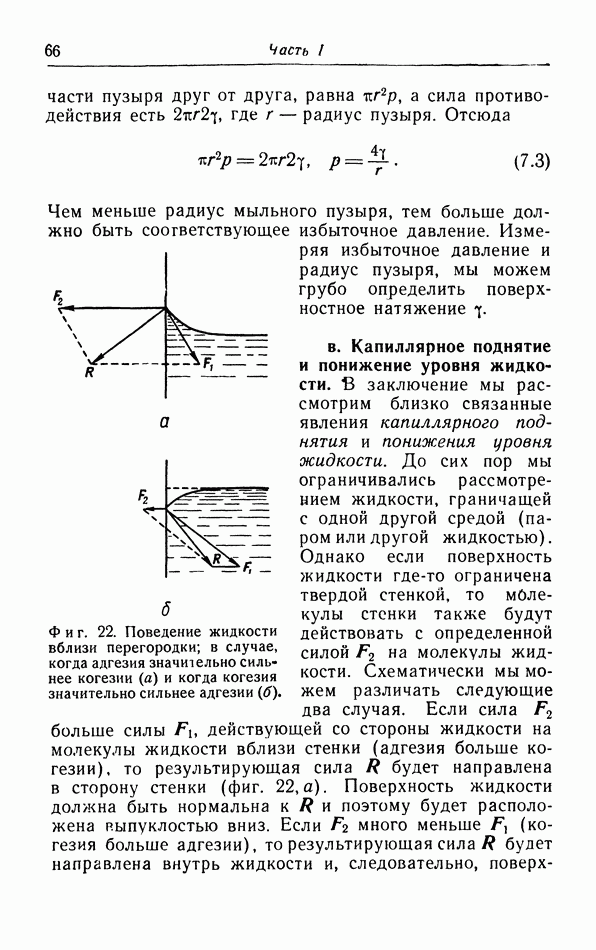
- в. Капиллярное поднятие и понижение уровня жидкости.
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
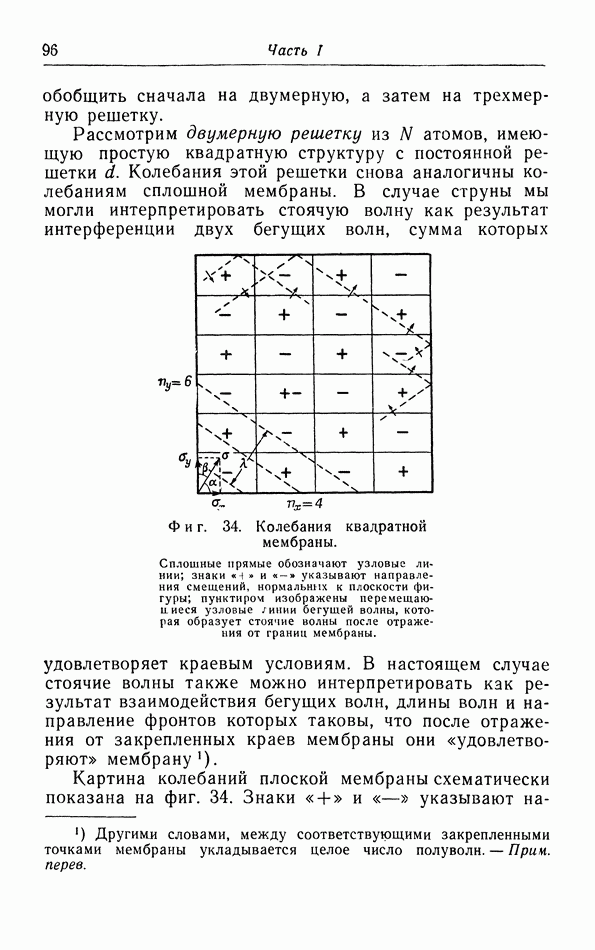
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
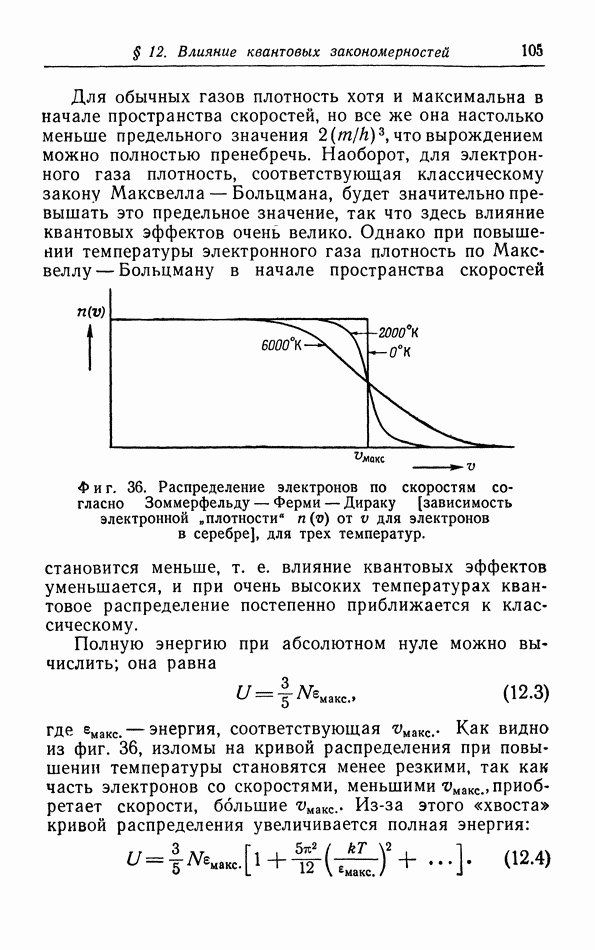
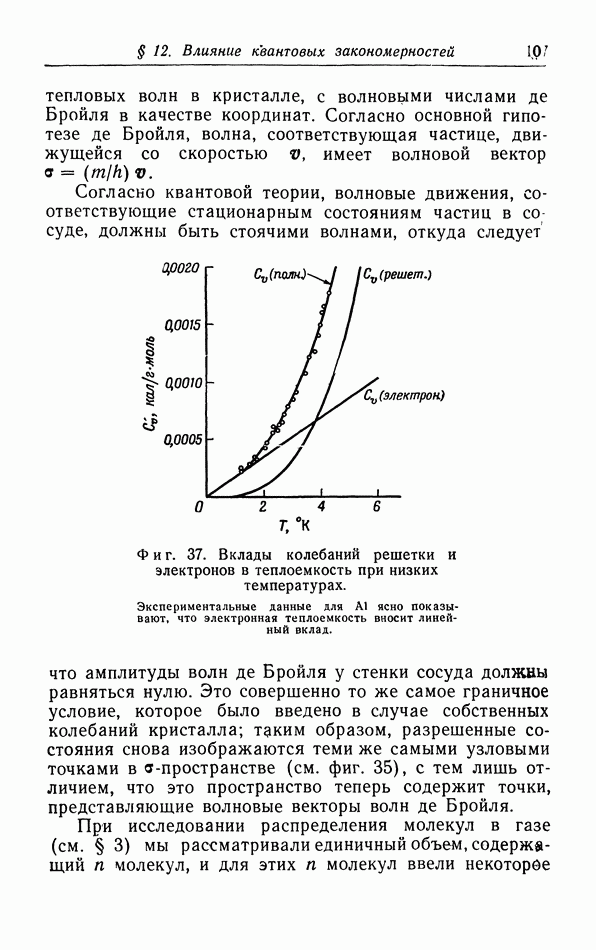
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
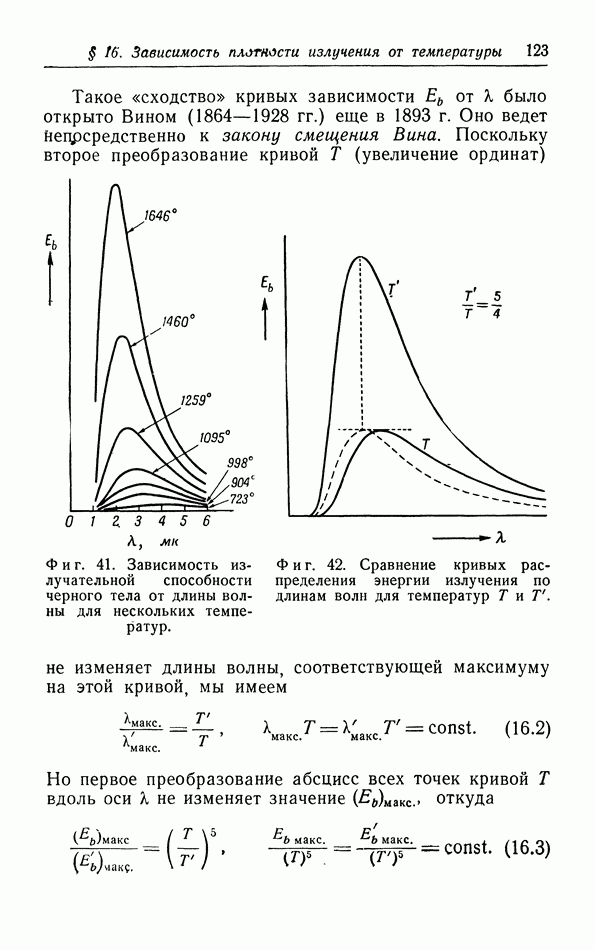
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
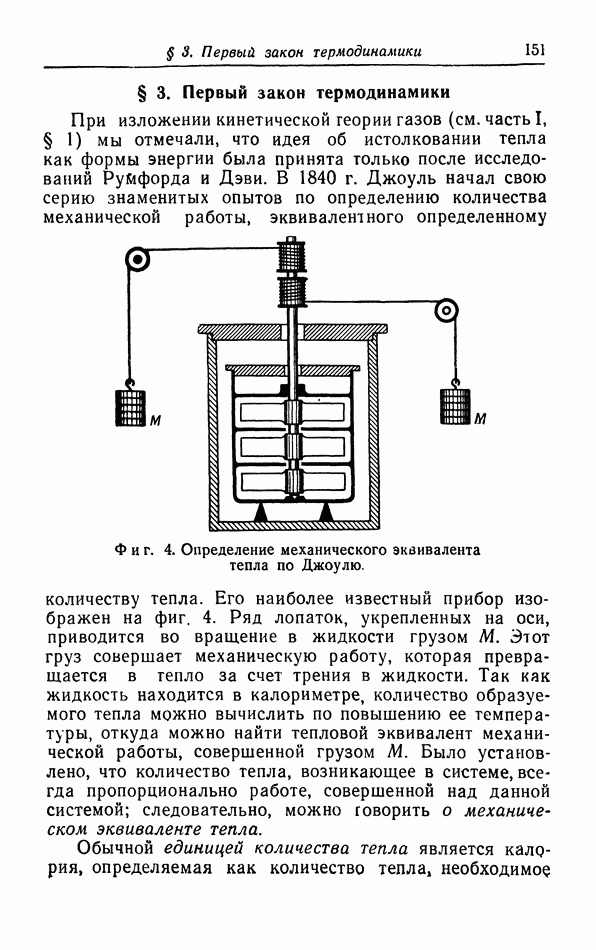
- § 3. Первый закон термодинамики
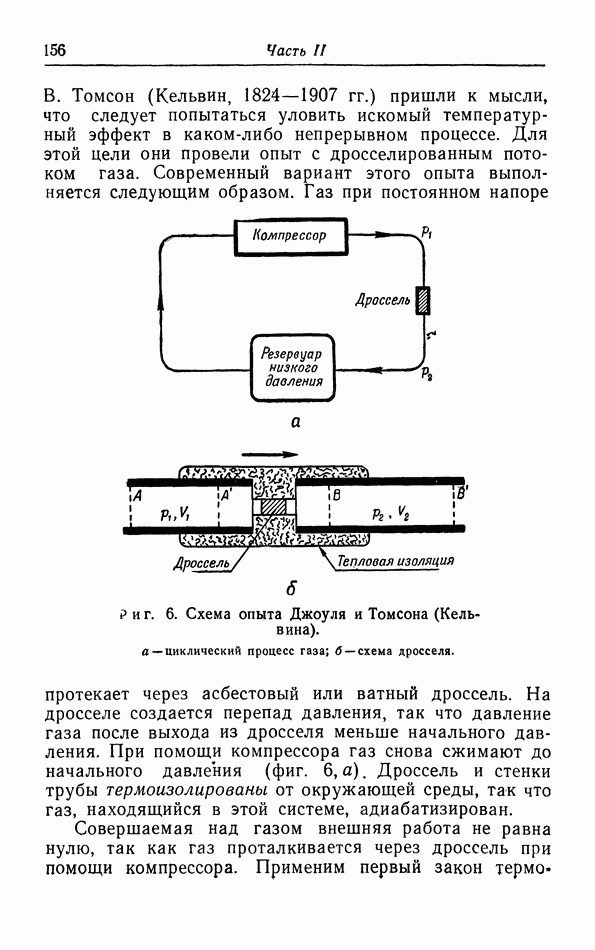
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
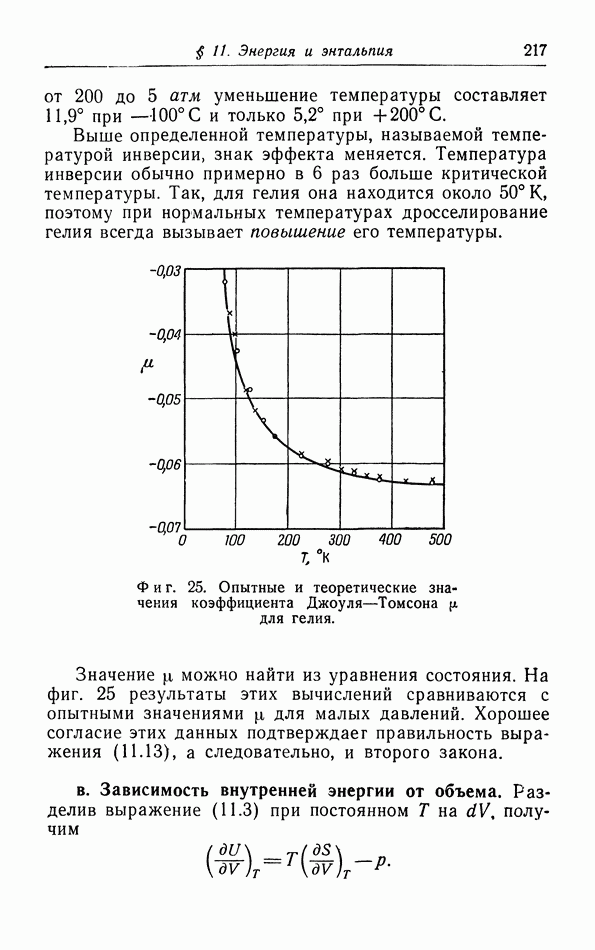
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
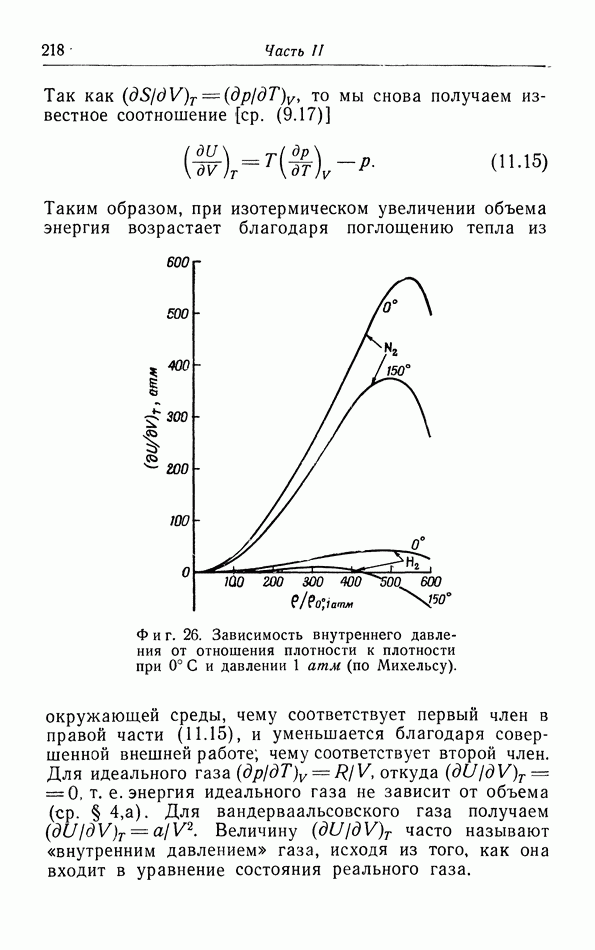
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
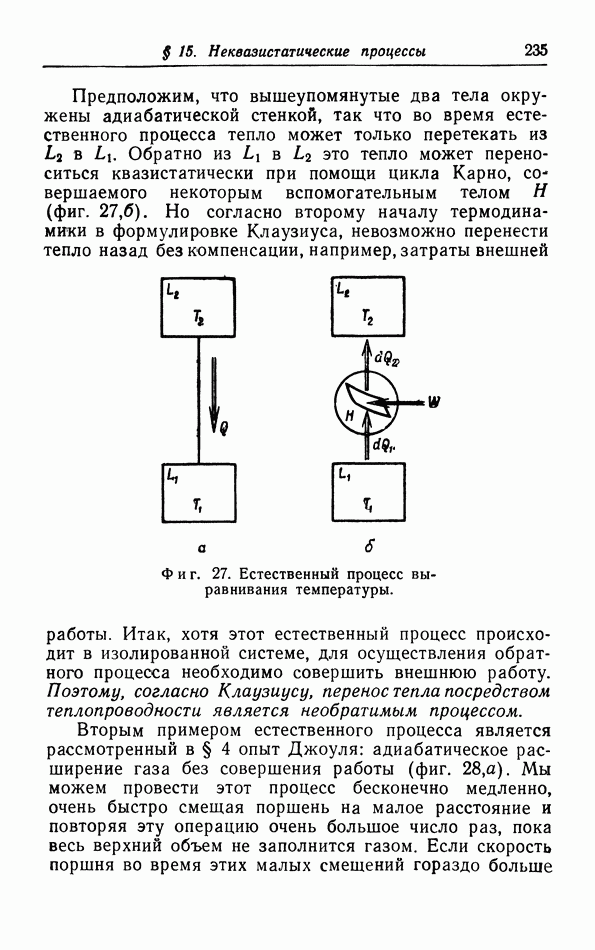
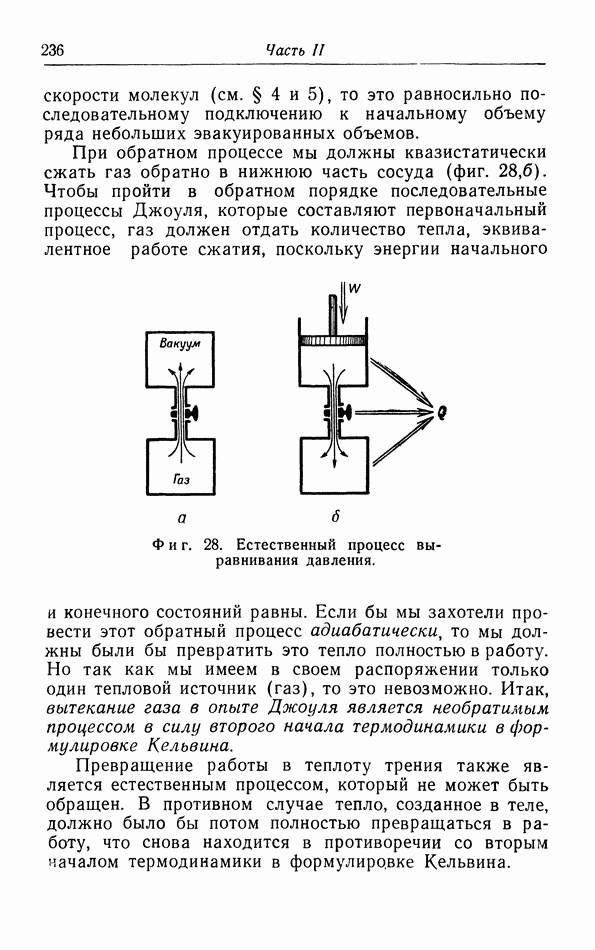
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
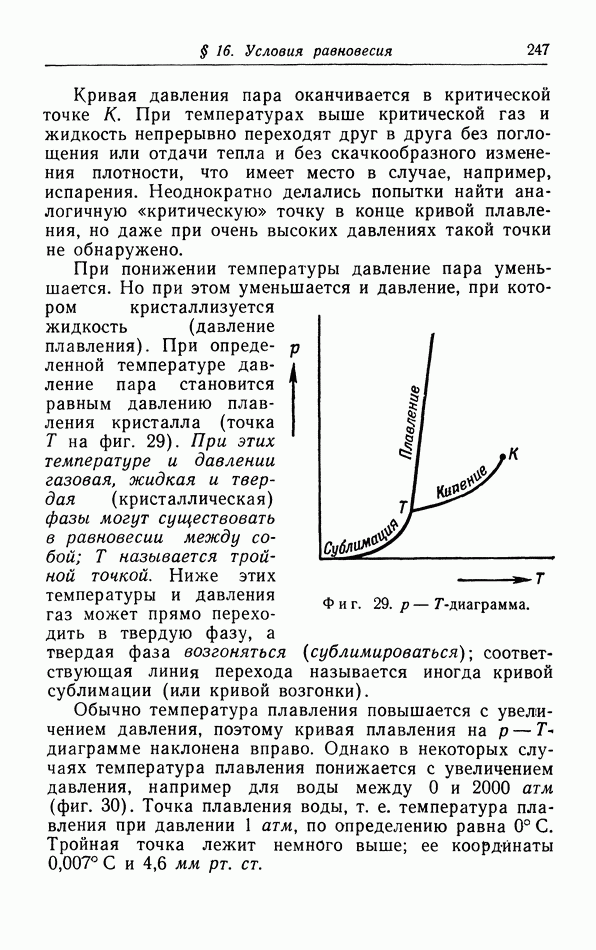
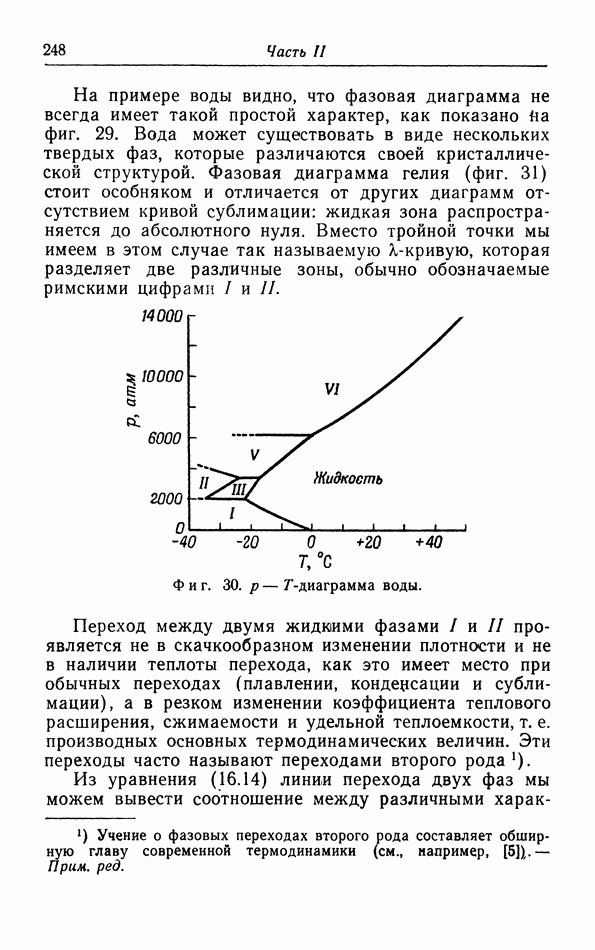
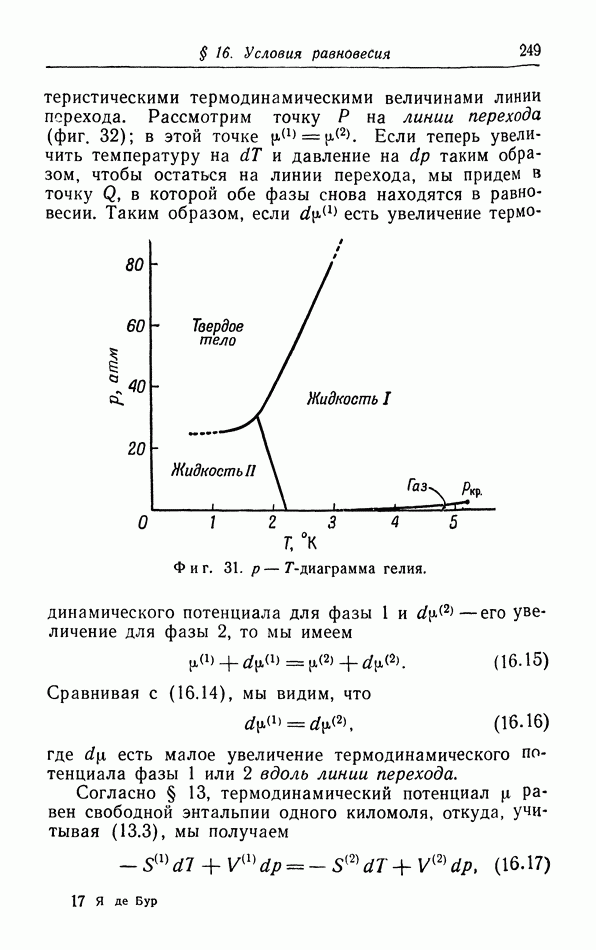
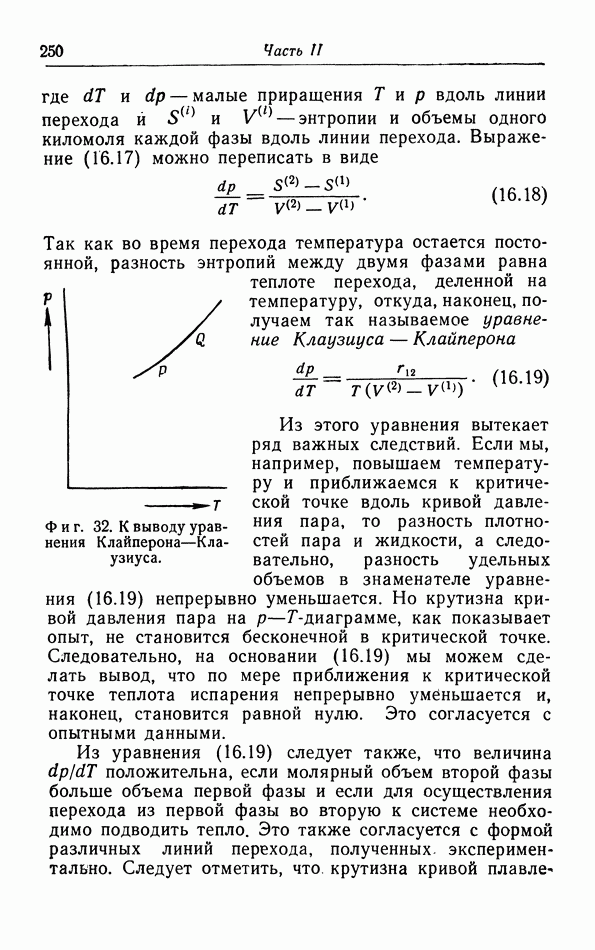
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам