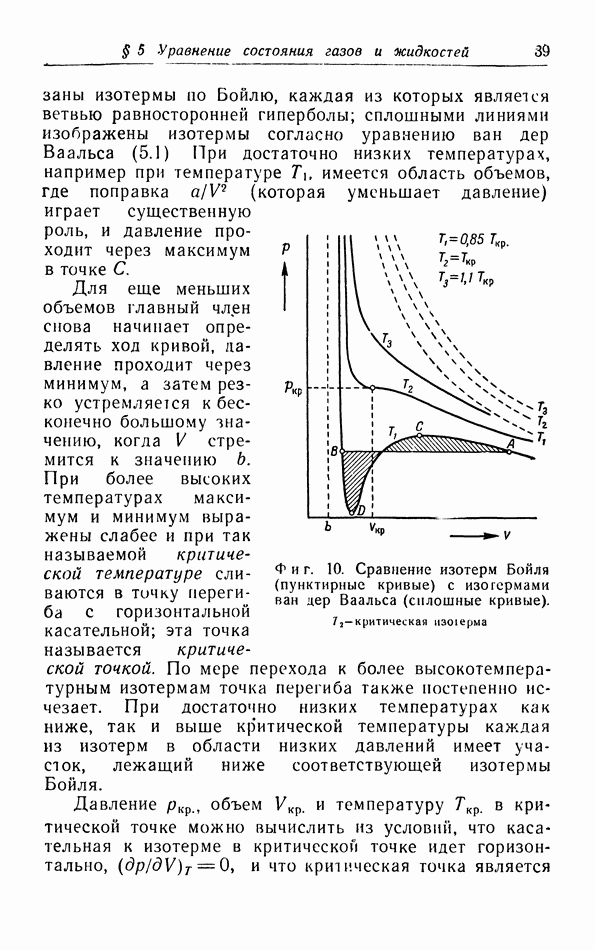
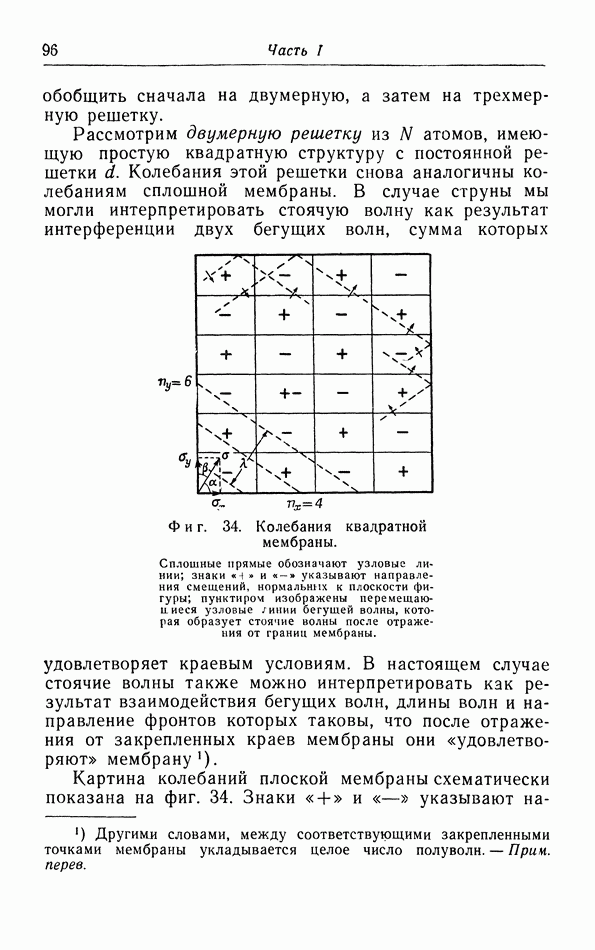
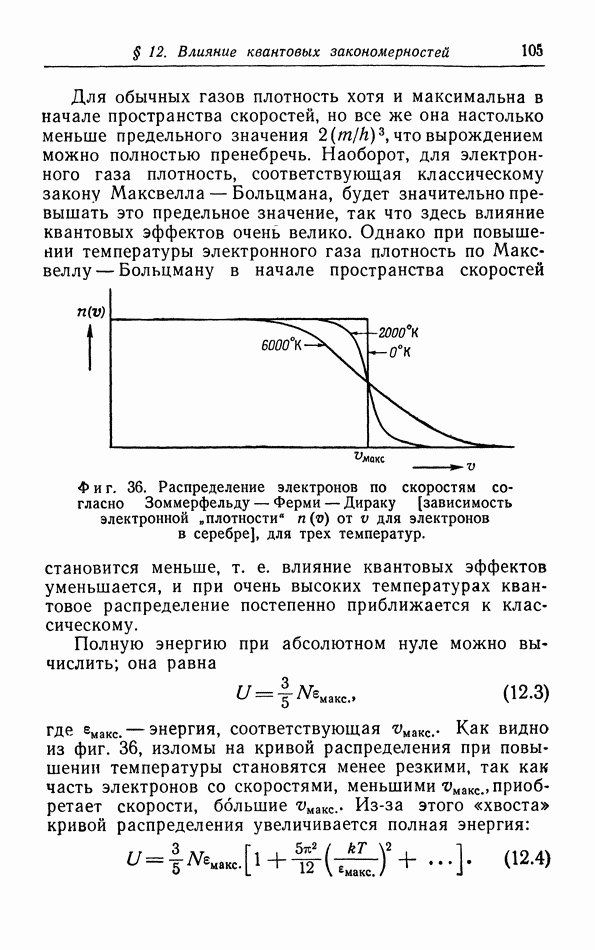
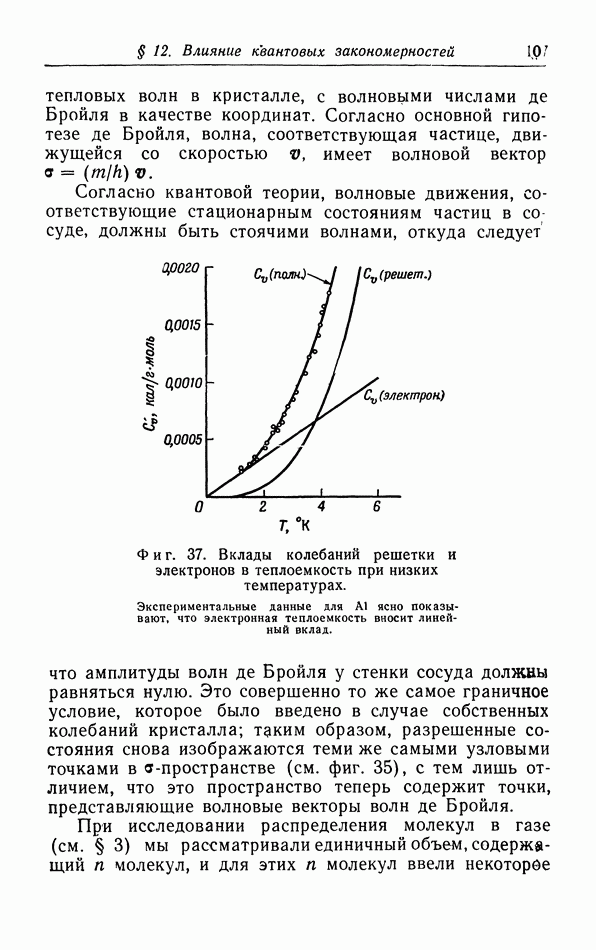
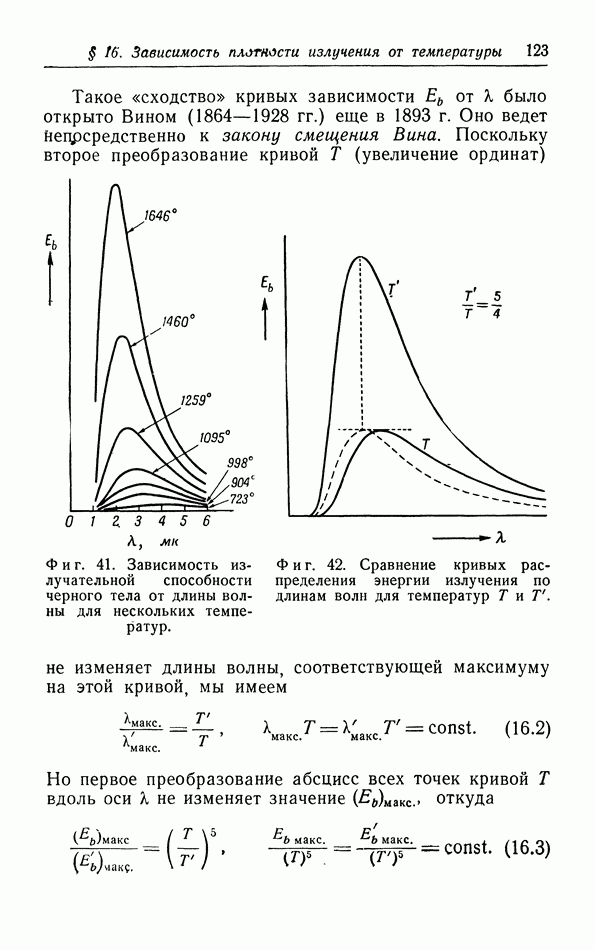
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
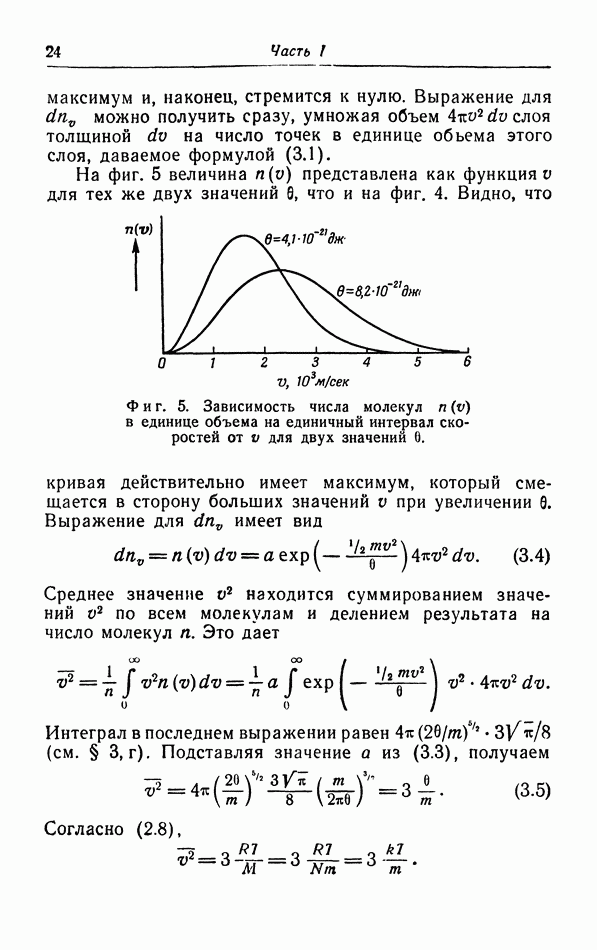
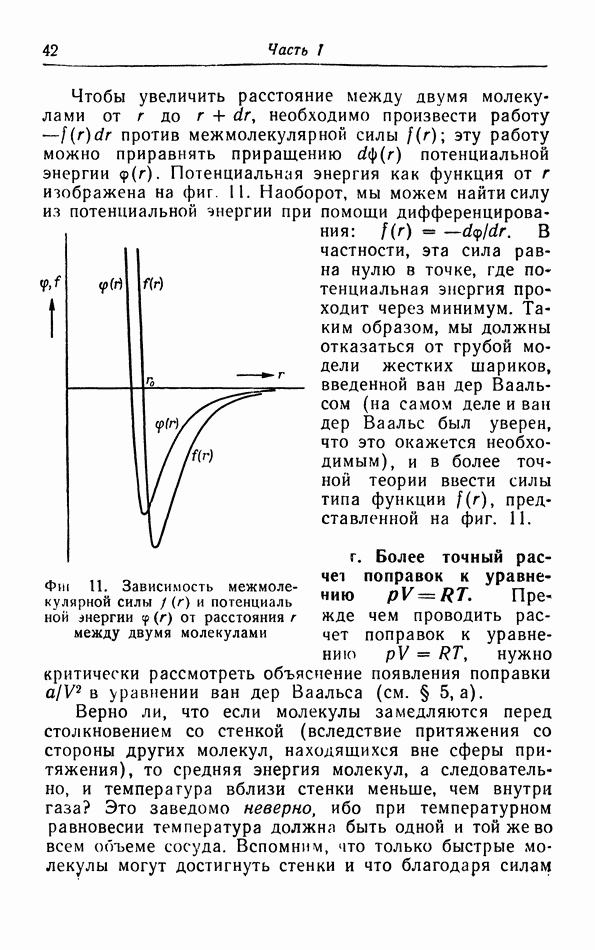
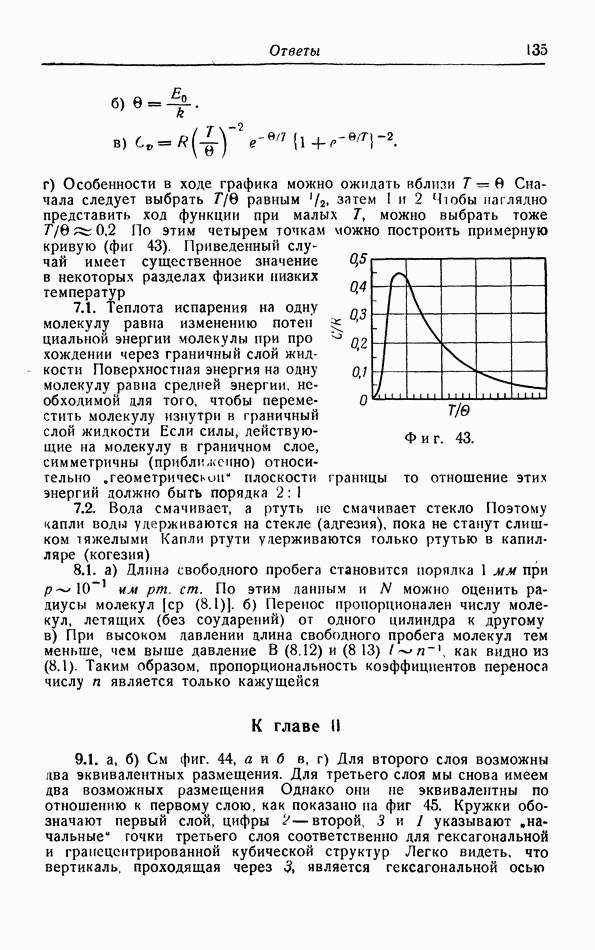
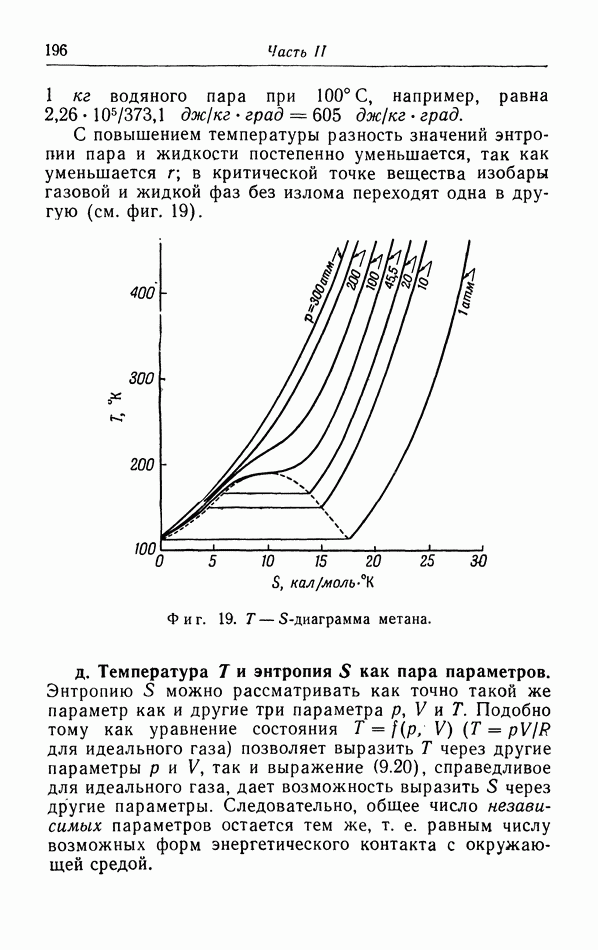
г. Более точный расчет поправок к уравнению pV=RT.
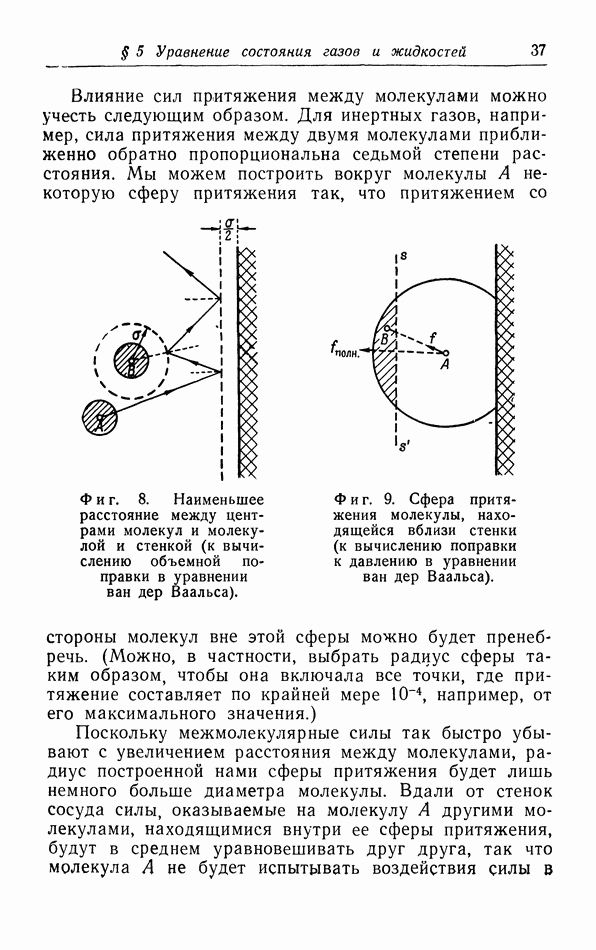
Прежде чем проводить расчет поправок к уравнению  нужно критически рассмотреть объяснение появления поправки
нужно критически рассмотреть объяснение появления поправки  в уравнении ван дер Ваальса (см. § 5, а).
в уравнении ван дер Ваальса (см. § 5, а).
Верно ли, что если молекулы замедляются перед столкновением со стенкой (вследствие притяжения со стороны других молекул, находящихся вне сферы притяжения), то средняя энергия молекул, а следовательно, и температура вблизи стенки меньше, чем внутри газа? Это заведомо неверно ибо при температурном равновесии температура должна быть одной и той же во всем объеме сосуда. Вспомним, что только быстрые молекулы могут достигнуть стенки и что благодаря силам
притяжения эти молекулы теряют как раз столько энергии, что средняя энергия молекул вблизи стенки остается равной средней энергии молекул внутри газа Медленные же молекулы вообще не достигают стенки и возвращаются под действием сил притяжения, не ударившись о стенку. Таким образом, мы приходим к заключению, что часть бомбардирующих молекул не достигает стенки: вблизи стенки плотность меньше, чем внутри газа. Это уменьшение плотности следует также из общего закона распределения Больцмана, так как молекулы вблизи стенки не испытывают притяжения со всех сторон, и, следовательно, их потенциальная энергия здесь больше, чем у молекул внутри газа.
Пойравка к давлению в уравнении ван дер Ваальса появляется за счет того, что число молекул, которые действительно сталкиваются со стенкой, уменьшается под действием сил притяжения, хотя средняя величина количества движения, передаваемого стенке одной молекулой, не зависит от сил притяжения.
Чтобы избежать вычисления уменьшения плотности вблизи стенки, прибегнем к следующему приему: рассмотрим объем газа, находящийся между стенкой и воображаемой плоскостью  (фиг. 12), которая помещена на некотором расстоянии от стенки. Давление, оказываемое стенкой на этот объем газа, должно быть равно давлению, оказываемому молекулами, находящимися слева от
(фиг. 12), которая помещена на некотором расстоянии от стенки. Давление, оказываемое стенкой на этот объем газа, должно быть равно давлению, оказываемому молекулами, находящимися слева от  на молекулы, находящиеся справа от
на молекулы, находящиеся справа от  так как давление в газе установилось. Таким образом, вместо давления на стенку мы можем вычислять давление, испытываемое плоскостью
так как давление в газе установилось. Таким образом, вместо давления на стенку мы можем вычислять давление, испытываемое плоскостью  Это давление складывается из давления, создаваемого переносом
Это давление складывается из давления, создаваемого переносом

Фиг. 12. Вычисление «давления притяжения».
количества движения, равного  при соударениях о стенку, и давления за счет межмолекулярных сил, оказываемого молекулами слева от
при соударениях о стенку, и давления за счет межмолекулярных сил, оказываемого молекулами слева от  на молекулы справа от
на молекулы справа от  Второе слагаемое, «давление притяжения», можно теперь вычислить простым способом.
Второе слагаемое, «давление притяжения», можно теперь вычислить простым способом.
Выберем молекулу А (см. фиг. 12), удаленную на расстояние  вправо от воображаемой плоскости
вправо от воображаемой плоскости  и попытаемся теперь вычислить силу, действующую на А со стороны молекул, которые находятся слева от 55 Элемент объема
и попытаемся теперь вычислить силу, действующую на А со стороны молекул, которые находятся слева от 55 Элемент объема  выбранный на расстоянии
выбранный на расстоянии  от А, будет содержать в среднем
от А, будет содержать в среднем  молекул. Однако в § 4 мы уже видели, что в точке, где потенциальная энергия меньше, число молекул несколько больше. Если вблизи
молекул. Однако в § 4 мы уже видели, что в точке, где потенциальная энергия меньше, число молекул несколько больше. Если вблизи  не имеется других молекул, то потенциальная энергия молекулы в положении В будет
не имеется других молекул, то потенциальная энергия молекулы в положении В будет  тогда среднее число молекул в
тогда среднее число молекул в  равно
равно  Таким образом, общая сила, действующая в направлении, перпендикулярном к стенке, со стороны молекул в объеме
Таким образом, общая сила, действующая в направлении, перпендикулярном к стенке, со стороны молекул в объеме  вблизи В на молекулу
вблизи В на молекулу  равна
равна

Введем теперь полярные координаты с полюсом в точке Лис полярной осью, идущей по нормали, опущенной из точки  на плоскость
на плоскость  Силы, действующие со стороны молекул в кольце радиусом
Силы, действующие со стороны молекул в кольце радиусом  на молекулу
на молекулу  равны по модулю. Объем кольца составляет
равны по модулю. Объем кольца составляет  следовательно, результирующая сила, действующая на молекулу
следовательно, результирующая сила, действующая на молекулу  со стороны молекул в кольце, перпендикулярна к стенке и равна
со стороны молекул в кольце, перпендикулярна к стенке и равна

Общую силу, действующую на  со стороны всех молекул в пространстве слева от 55 можно вычислить, производя интегрирование сначала по
со стороны всех молекул в пространстве слева от 55 можно вычислить, производя интегрирование сначала по  от О до
от О до  при фиксированном значении
при фиксированном значении  и затем по
и затем по  от
от  до
до 

Эта сила действует на все молекулы, заключенные в тонком слое вблизи плоскости 55; таким образом, если мы рассматриваем объем толщиной  и площадью
и площадью  то она действует на
то она действует на  молекул. Итак, давление притяжения можно найти, умножая силу, действующую на
молекул. Итак, давление притяжения можно найти, умножая силу, действующую на  на
на  и затем интегрируя результат по
и затем интегрируя результат по 

Чтобы выполнить это тройное интегрирование простым образом, сначала изменим пределы интегрирования по  т. е. будем интегрировать по
т. е. будем интегрировать по  от О до
от О до  по О от О до
по О от О до  наконец, для каждого значения
наконец, для каждого значения  и О по
и О по  от О до
от О до  Тогда
Тогда

Два из этих интегрирований выполняются теперь элементарно:

Выражение для давления притяжения  которое мы таким образом вывели с помощью неопределенной силы
которое мы таким образом вывели с помощью неопределенной силы  и потенциала
и потенциала  имеет вид
имеет вид

Поскольку  то давление притяжения, собственно говоря, обратно пропорционально V, так что уравнение состояния принимает вид
то давление притяжения, собственно говоря, обратно пропорционально V, так что уравнение состояния принимает вид

где  является функцией от температуры:
является функцией от температуры:

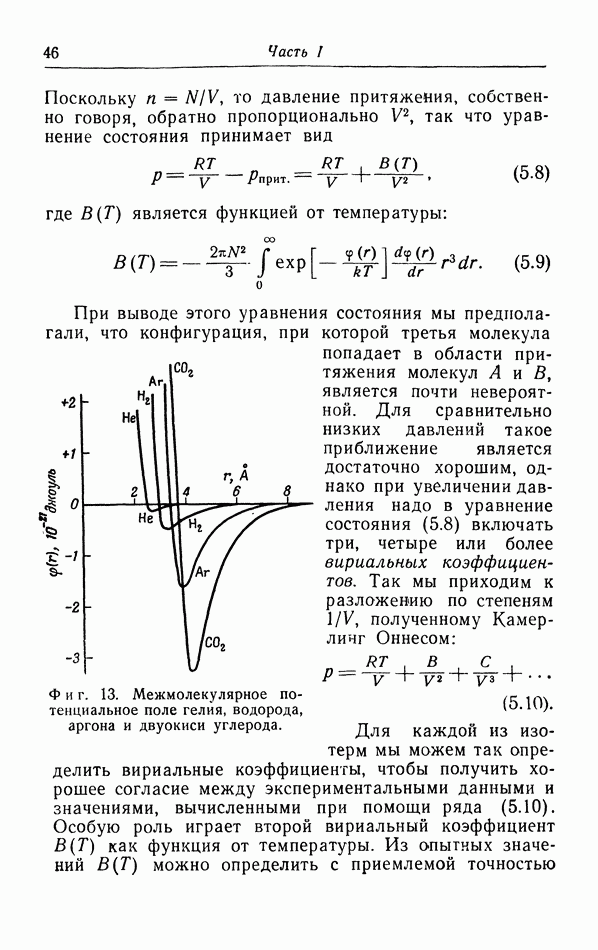
при выводе этого уравнения состояния мы предполагали, что конфигурация, при которой третья молекула попадает в области притяжения молекул  является почти невероятной. Для сравнительно низких давлений такое приближение является достаточно хорошим, однако при увеличении давления надо в уравнение состояния (5.8) включать три, четыре или более вириальных коэффициентов. Так мы приходим к разложению по степеням 1/V, полученному Камерлинг Оннесом:
является почти невероятной. Для сравнительно низких давлений такое приближение является достаточно хорошим, однако при увеличении давления надо в уравнение состояния (5.8) включать три, четыре или более вириальных коэффициентов. Так мы приходим к разложению по степеням 1/V, полученному Камерлинг Оннесом:


Фиг. 13. Межмолекулярное потенциальное поле гелия, водорода, аргона и двуокиси углерода.
Для каждой из изотерм мы можем так определить вириальные коэффициенты, чтобы получить хорошее согласие между экспериментальными данными и значениями, вычисленными при помощи ряда (5.10). Особую роль играет второй вириальный коэффициент  как функция от температуры. Из опытных значений
как функция от температуры. Из опытных значений  можно определить с приемлемой точностью
можно определить с приемлемой точностью
межмолекулярное потенциальное поле  используя для этой цели уравнение (5.9). На фиг. 13 показаны межмолекулярные потенциальные поля ряда газов, рассчитанные описанным путем.
используя для этой цели уравнение (5.9). На фиг. 13 показаны межмолекулярные потенциальные поля ряда газов, рассчитанные описанным путем.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- ГЛАВА I. Газы и жидкости
- § 1. Молекулярная структура газов и жидкостей
- § 2. Кинетическая теория идеального газа
- б. Расчет давления в кинетической теории газов.
- в. Расчет удельной теплоемкости в кинетической теории газов.
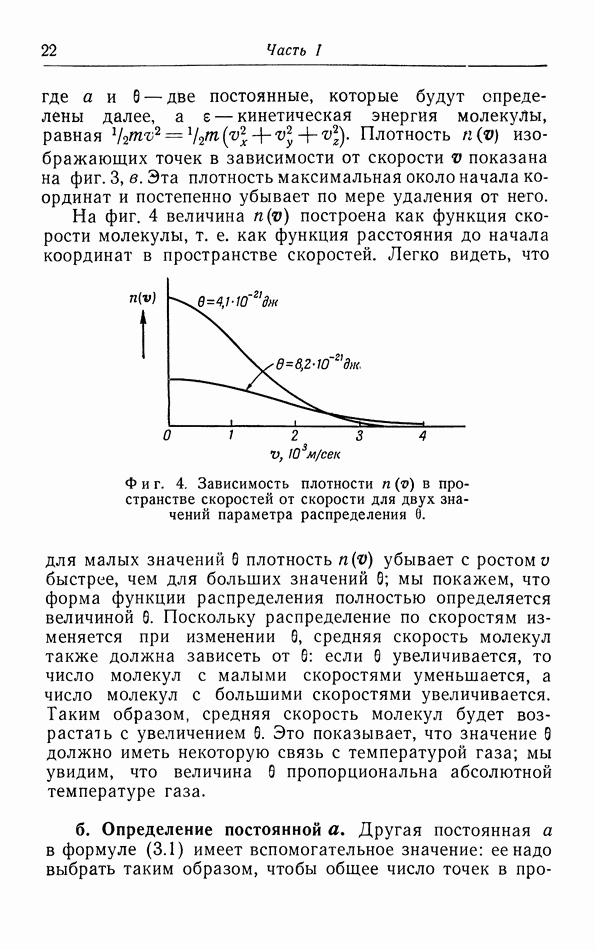
- § 3. Распределение молекул по скорости их движения
- г. Средняя квадратичная и средняя скорости.
- д. Броуновское движение.
- е. Опыты с молекулярными пучками.
- § 4. Общее распределение молекул по энергиям
- б. Возбужденные состояния.
- в. вращательная и колебательная энергии.
- г. Потенциальная энергия тяготения.
- д. Потенциальная энергия межмолекулярных сил.
- § 5. Уравнение состояния газов и жидкостей
- б. Обсуждение уравнения ван дер Ваальса.
- в. Взаимодействие молекул.
- г. Более точный расчет поправок к уравнению pV=RT.
- д. Закон соответственных состояний.
- е. Жидкая фаза.
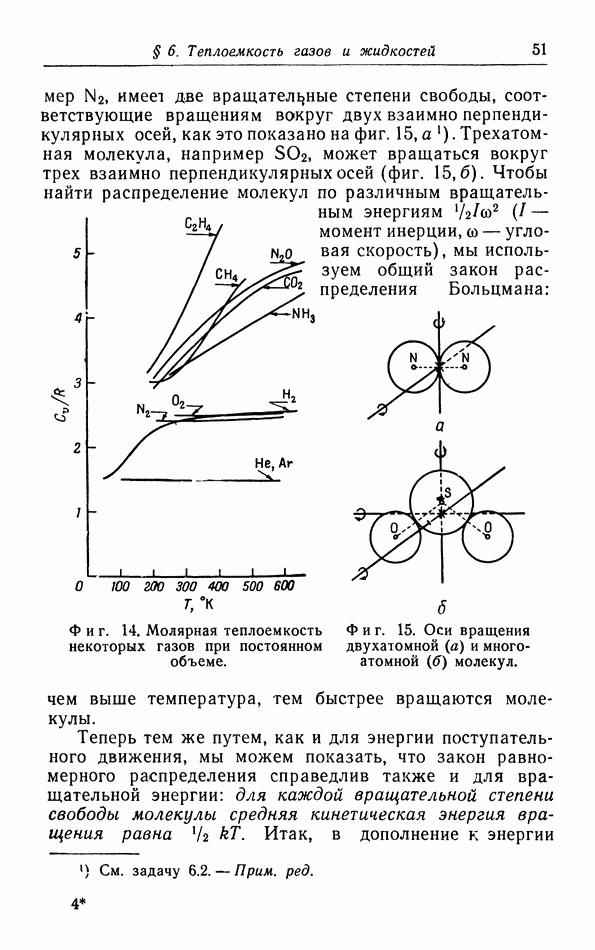
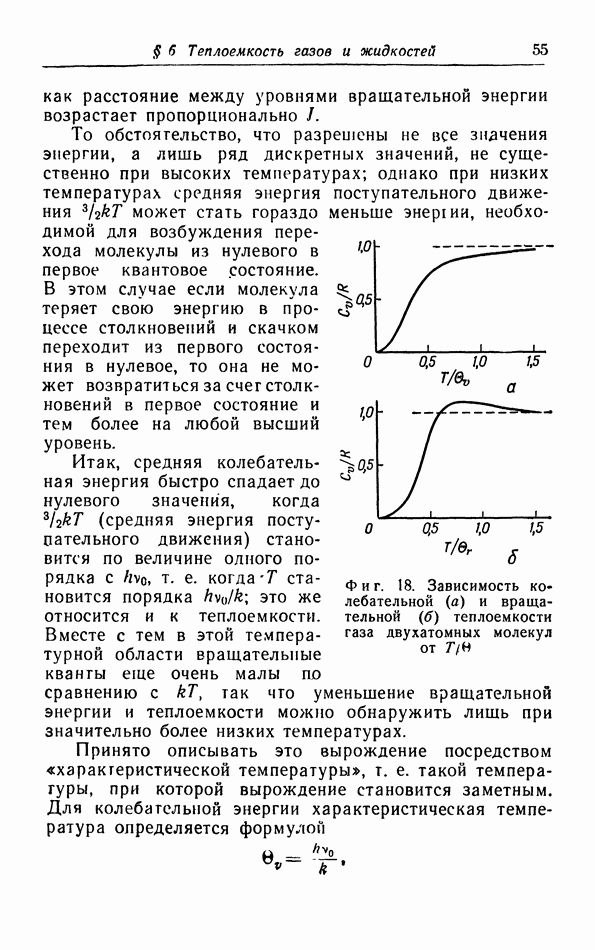
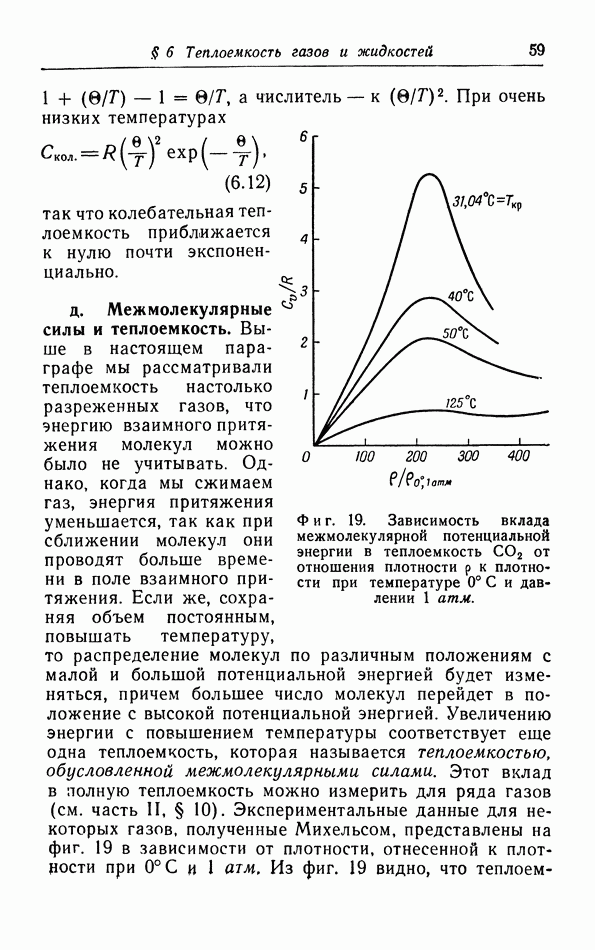
- § 6. Теплоемкость газов и жидкостей
- б. Классическая теория колебательной теплоемкости.
- в. Квантовая теория теплоемкости.
- г. Расчет колебательной теплоемкости двухатомной молекулы.
- д. Межмолекулярные силы и теплоемкость.
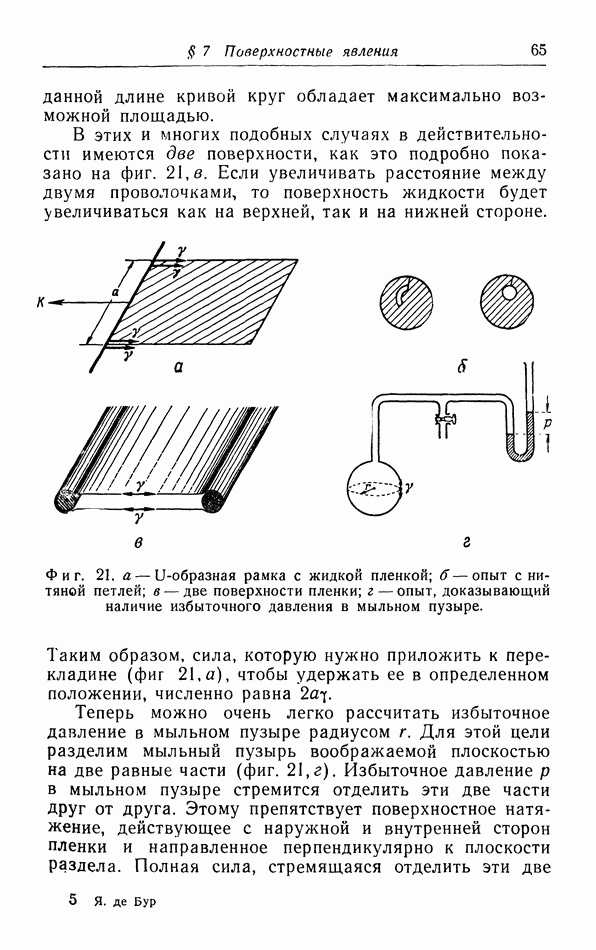
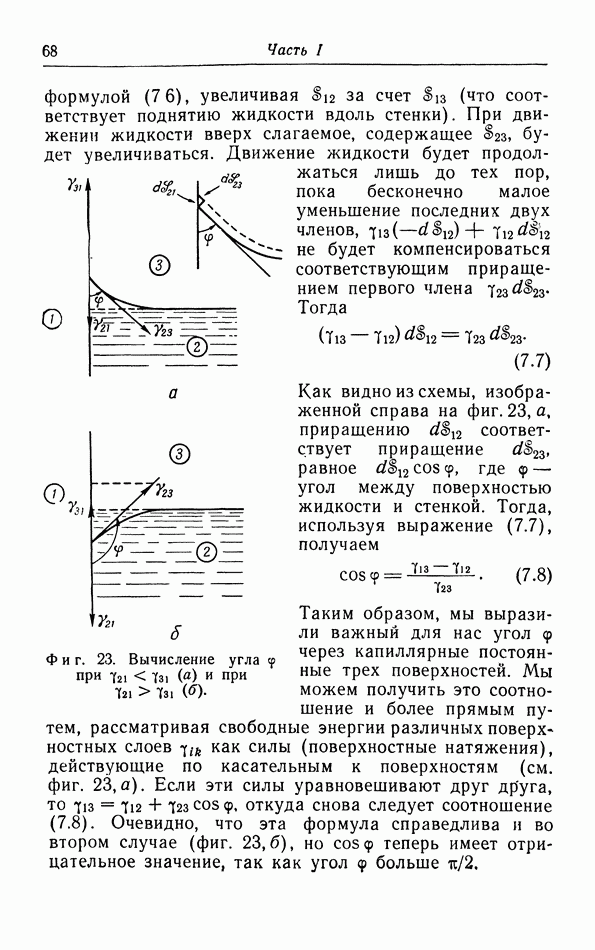
- § 7. Поверхностные явления
- б. Жидкие пленки.
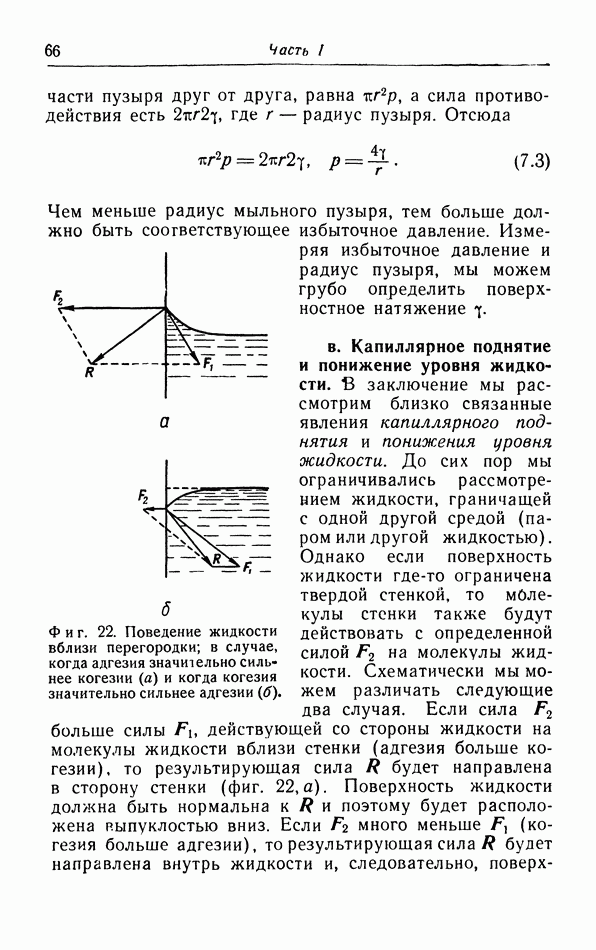
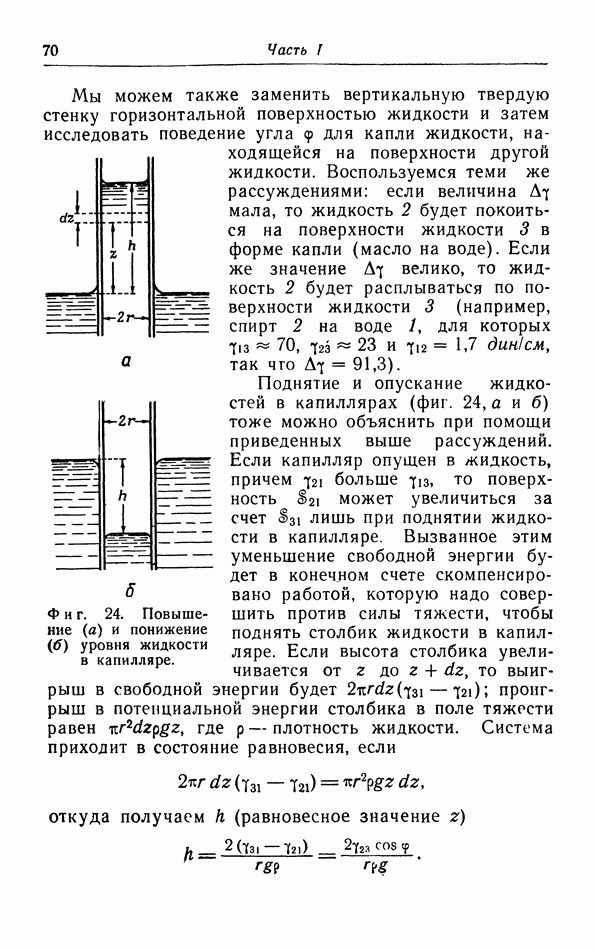
- в. Капиллярное поднятие и понижение уровня жидкости.
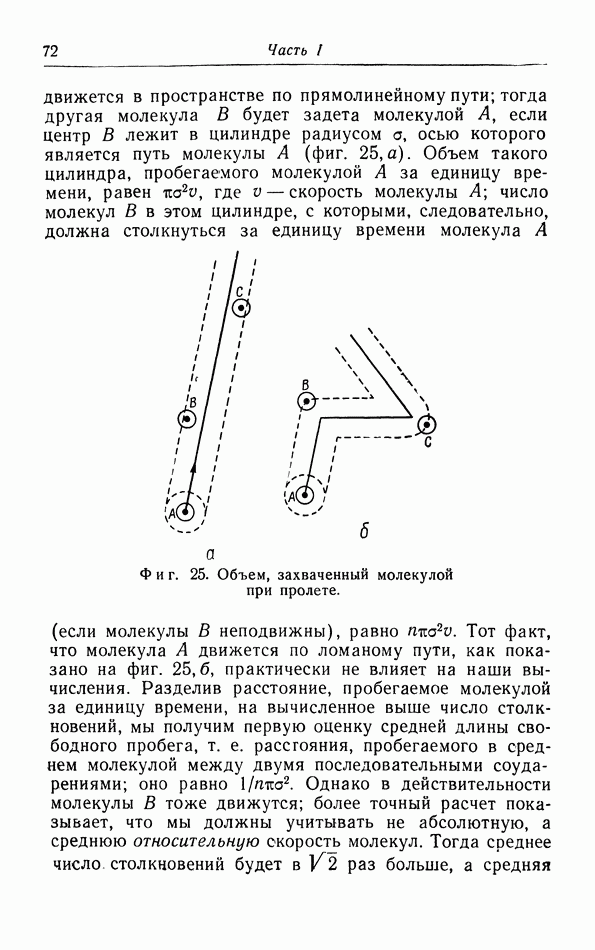
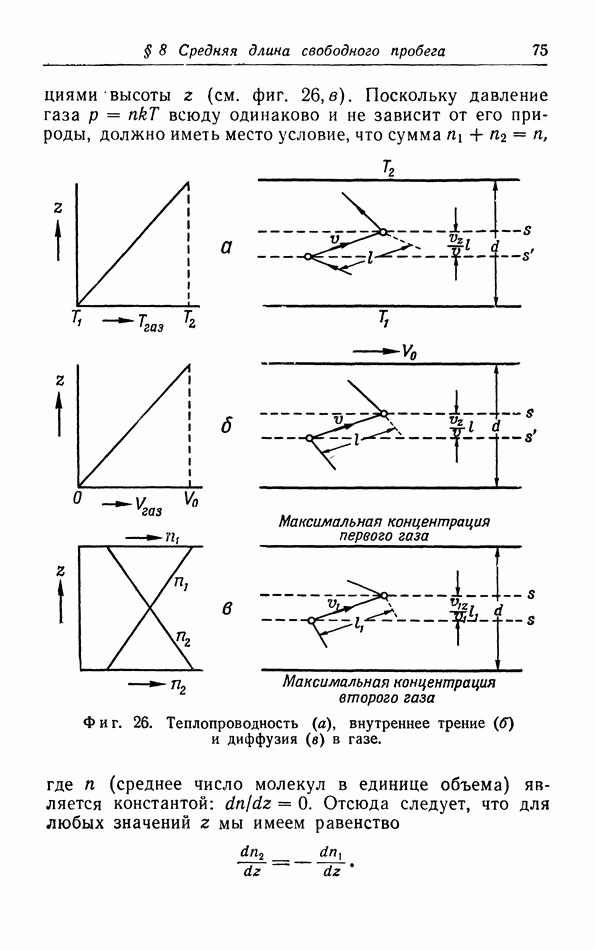
- § 8. Средняя длина свободного пробега, теплопроводность, вязкость и диффузия
- ГЛАВА II. Твердые тела
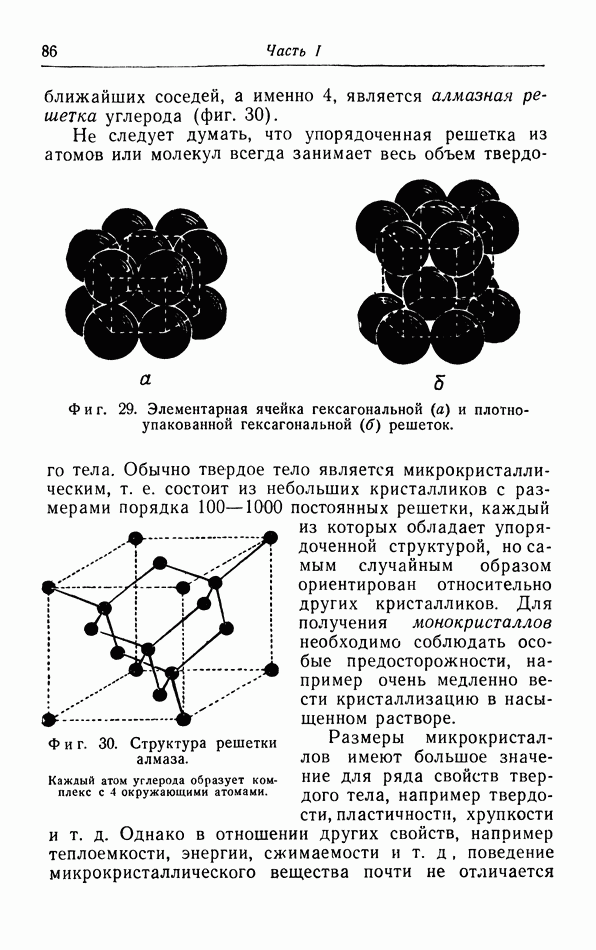
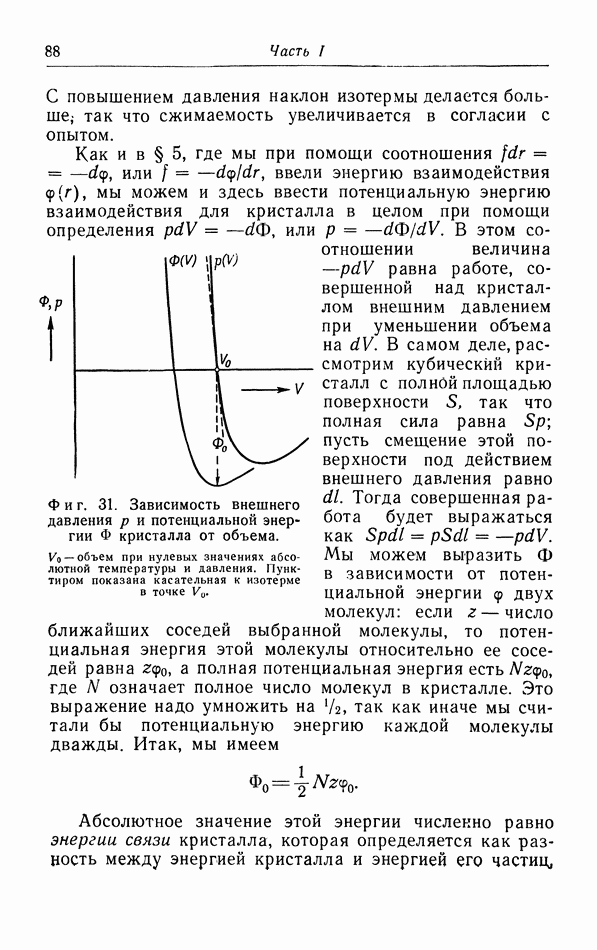
- § 9. Структура твердых тел
- § 10. Уравнение состояния твердых тел
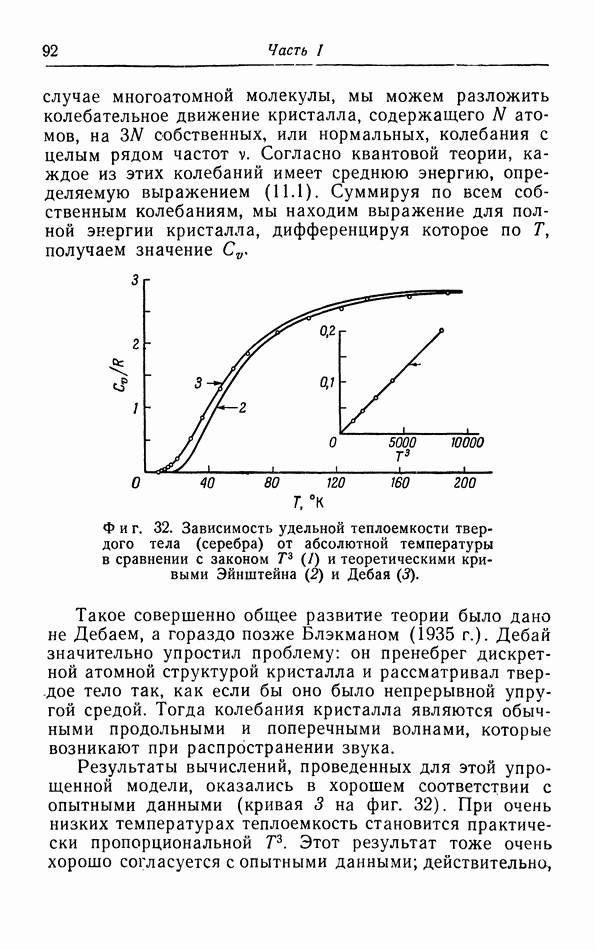
- § 11. Теплоемкость твердых тел
- в. Колебания линейной цепочки.
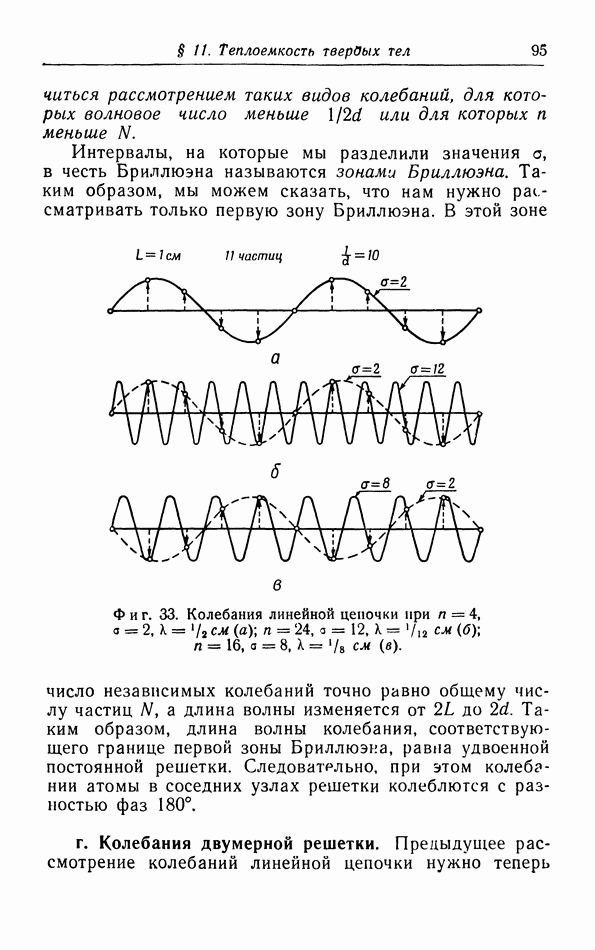
- г. Колебания двумерной решетки.
- д. Колебания трехмерной решетки.
- е. Теория Дебая.
- § 12. Влияние квантовых закономерностей на распределение частиц по скоростям
- ГЛАВА III. Излучение
- § 13. Тепловое излучение и свет
- § 14. Испускание, поглощение и плотность излучения
- б. Яркость и излучательная способность.
- в. Плотность излучения.
- г. Закон Кирхгофа.
- § 15. Фотонная гипотеза. Давление излучения
- § 16. Зависимость плотности излучения от температуры и длины волны
- б. Закон смещения Вина.
- в. Закон излучения Релея — Джинса.
- г. Закон излучения Планка.
- ГЛАВА I. Первый закон термодинамики
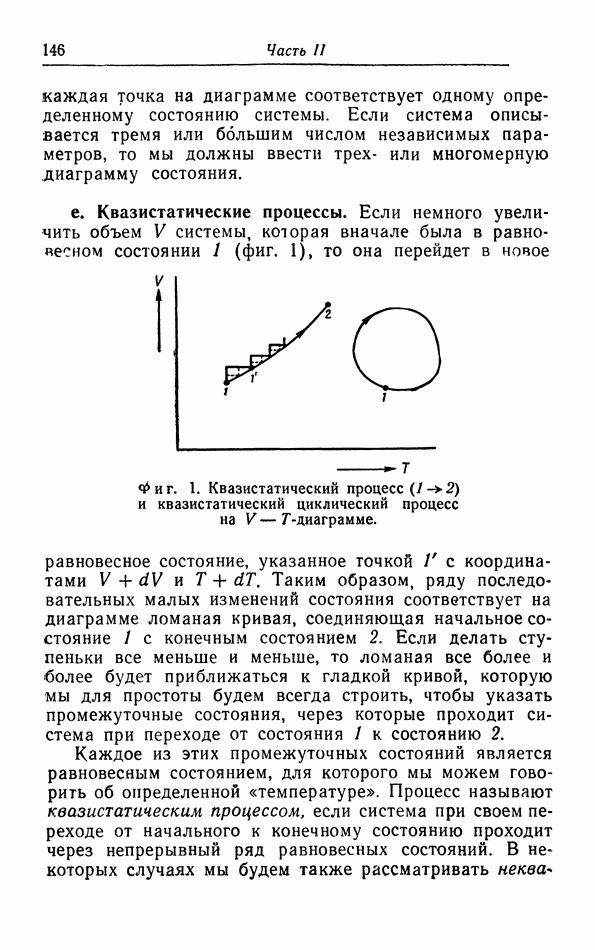
- § 1. Термодинамическое состояние и его изменения
- § 2. Работа при квазистатических процессах
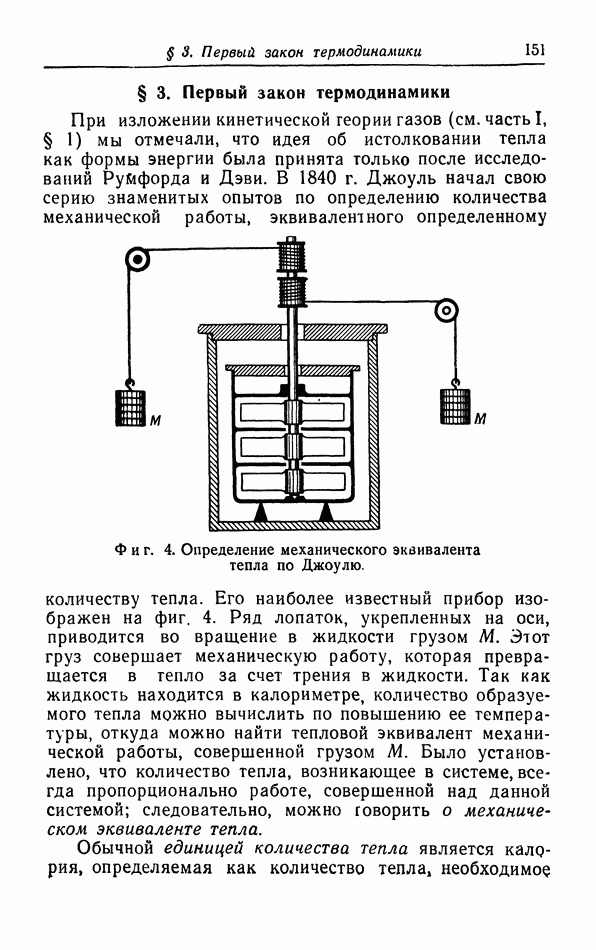
- § 3. Первый закон термодинамики
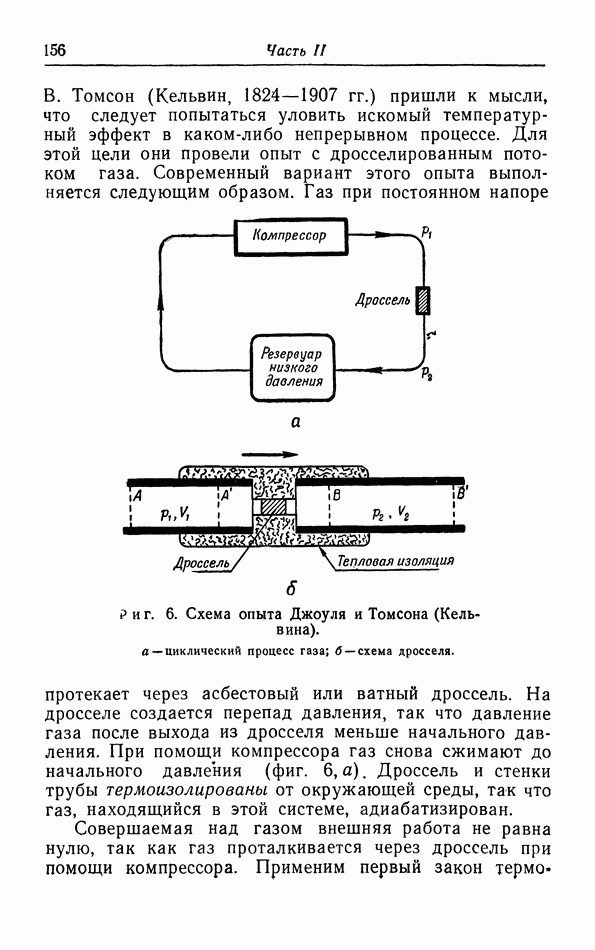
- § 4. Опыты Джоуля и Томсона
- § 5. Дальнейшие приложения первого закона
- б. Теплоемкость.
- в. Работа при адиабатических процессах.
- ГЛАВА II. Второй закон термодинамики
- § 6. Работа и теплота в циклических процессах
- § 7. Второе начало термодинамики и его различные формулировки
- § 8. Температура
- § 9. Энтропия и второй закон термодинамики
- § 10. Применения второго закона термодинамики
- в. Изэнтропические изменения состояния.
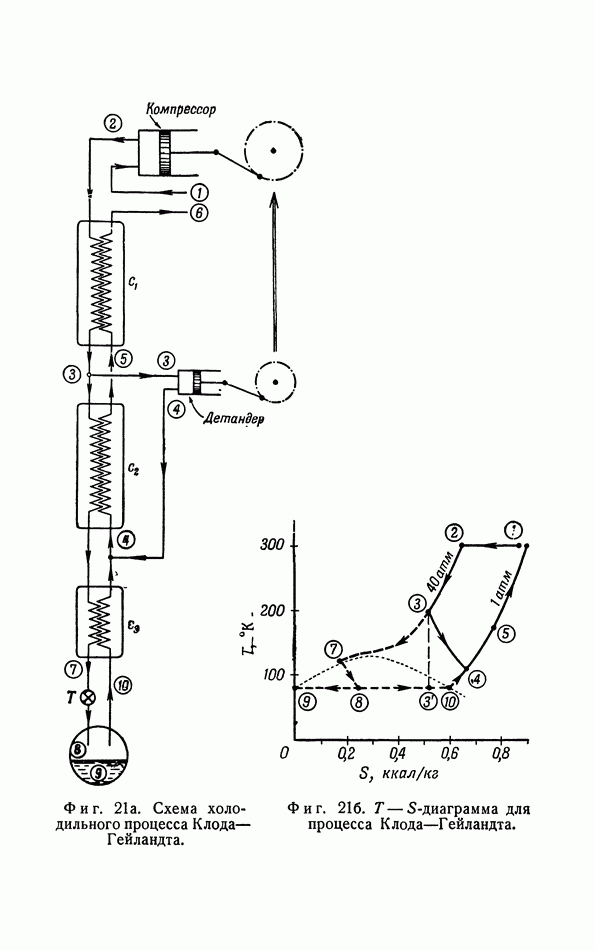
- г. Изэнтропические холодильные процессы (процесс Ж. Клода).
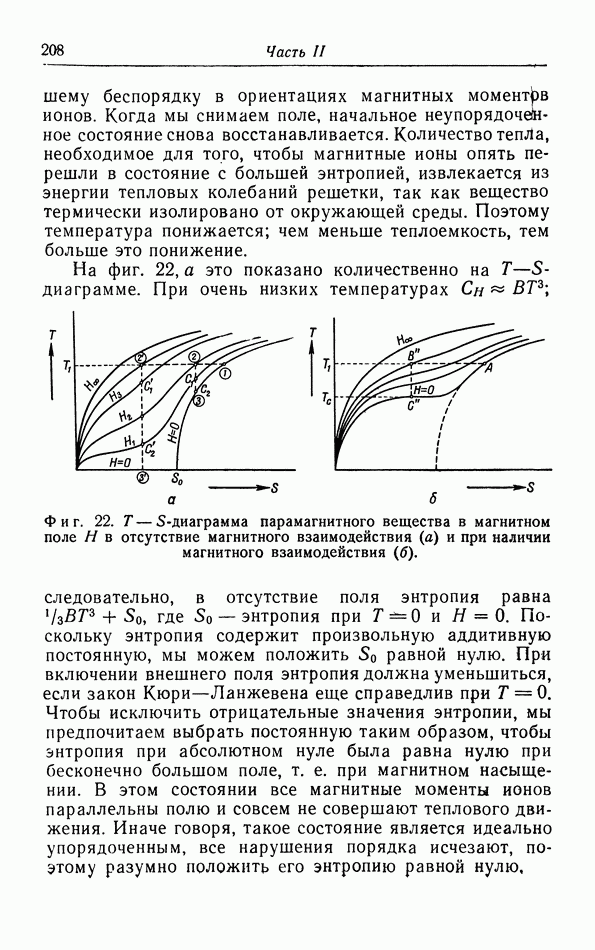
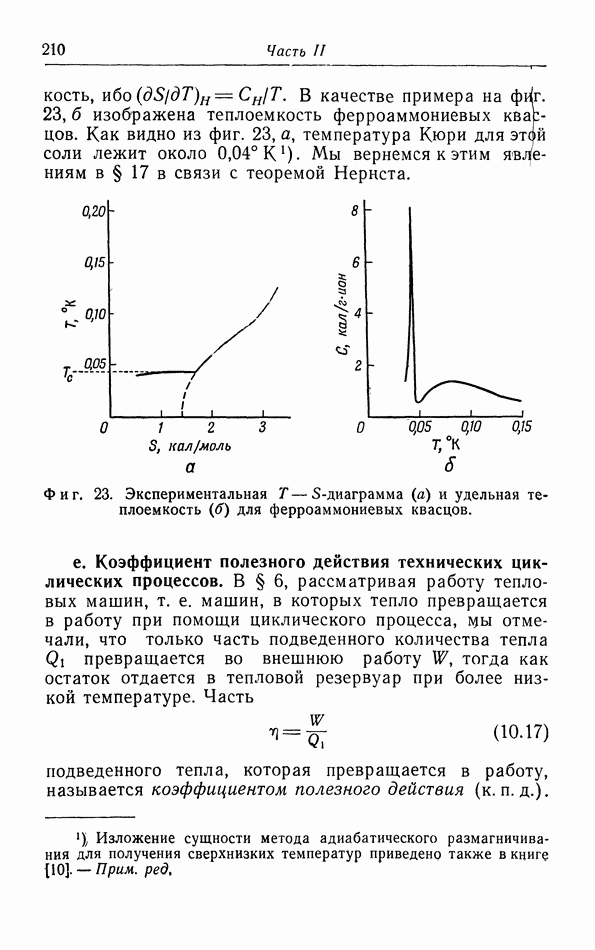
- д. Иззнтропические холодильные процессы (адиабатическое размагничивание).
- е. Коэффициент полезного действия технических циклических процессов.
- ГЛАВА III. Характеристические функции
- § 11. Энергия и энтальпия
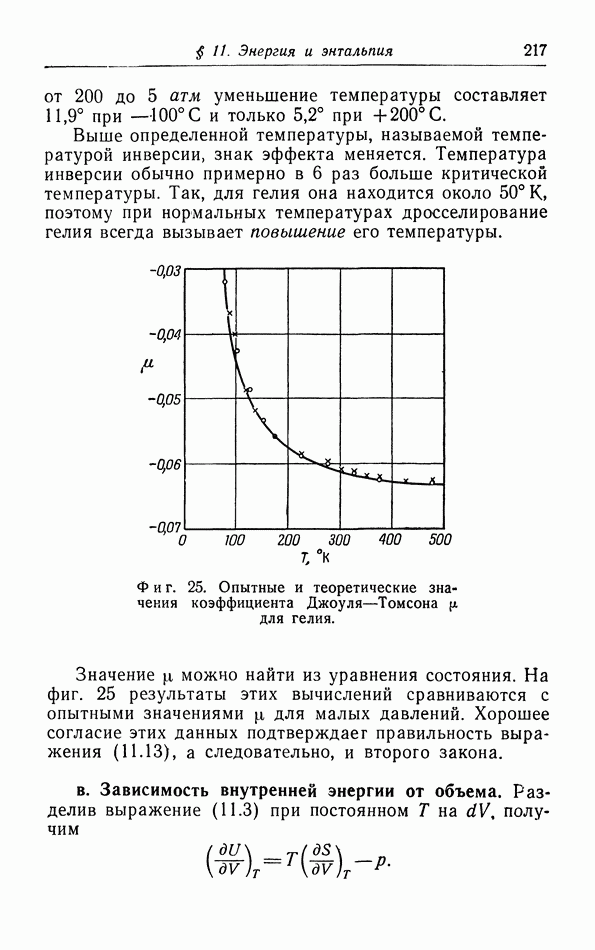
- б. Расчет процессов Джоуля и Джоуля — Томсона (Кельвина).
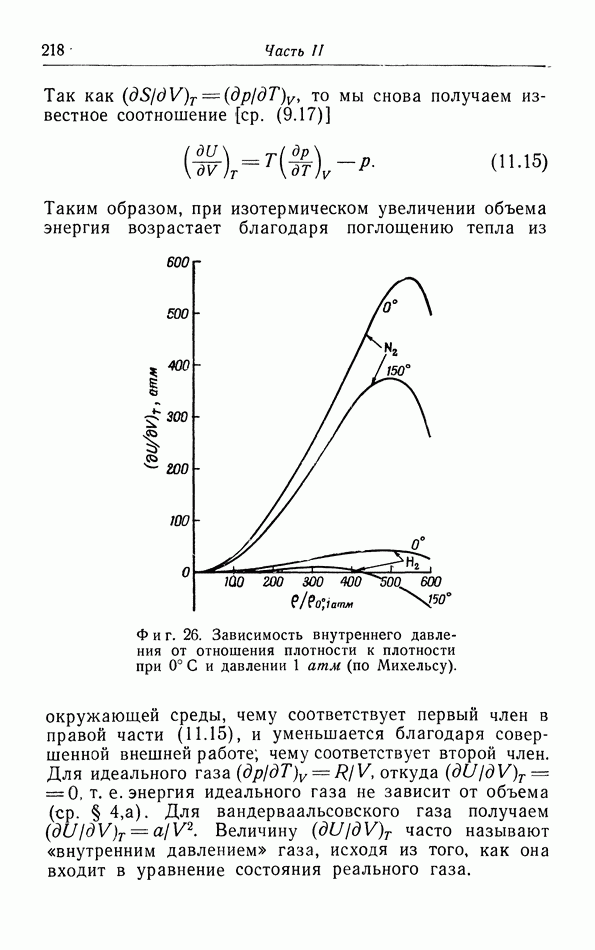
- в. Зависимость внутренней энергии от объема.
- г. Вывод закона Стефана — Больцмана.
- д. Характеристические функции U и H.
- § 12. Свободная энергия
- б. Свободная энергия и поверхностное натяжение.
- в. Свободная энергия и гальванические элементы.
- § 13. Свободная энтальпия и термодинамический потенциал
- б. Термодинамический потенциал.
- в. Системы с более чем одним компонентом.
- § 14. Соотношения Максвелла
- ГЛАВА IV. Неквазистатические процессы. Равновесие
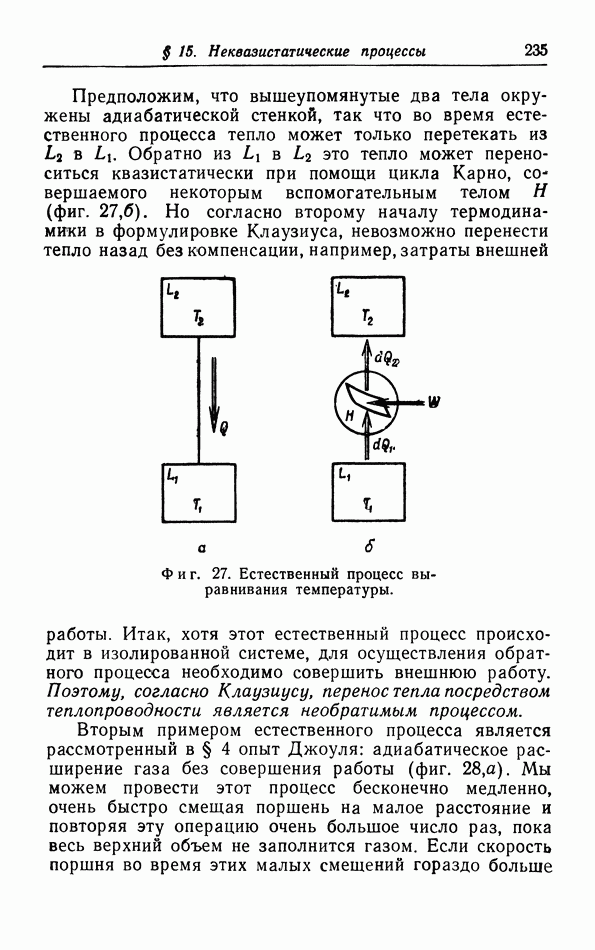
- § 15. Неквазистатические процессы
- б. Подвод тепла и изменение энтропии.
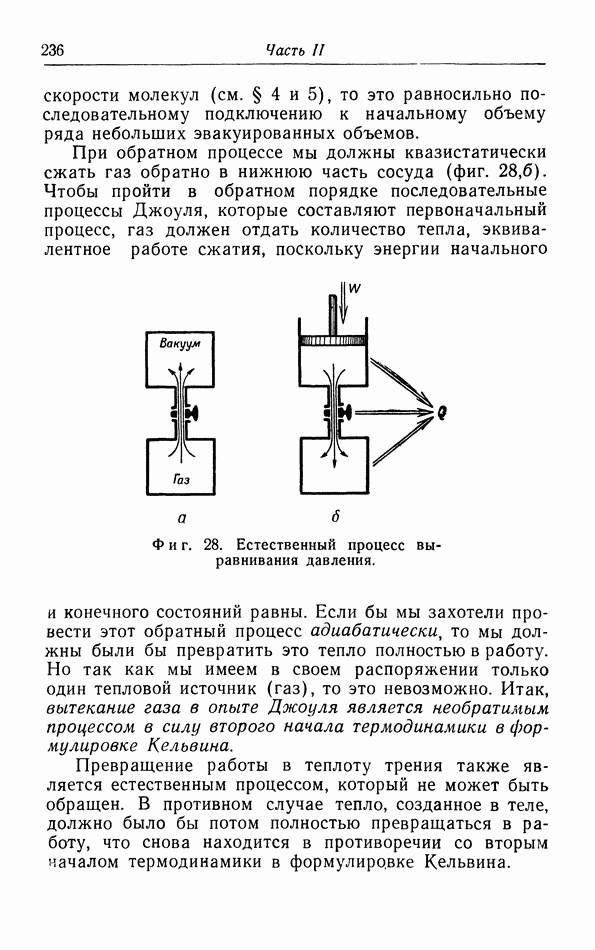
- в. Увеличение энтропии в адиабатических системах.
- г. Неквазистатический изотермический процесс.
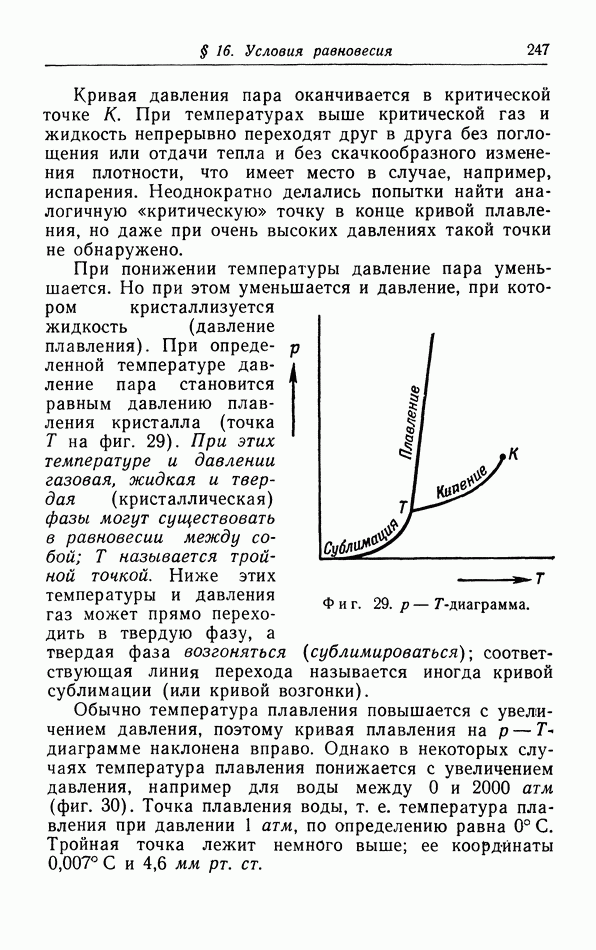
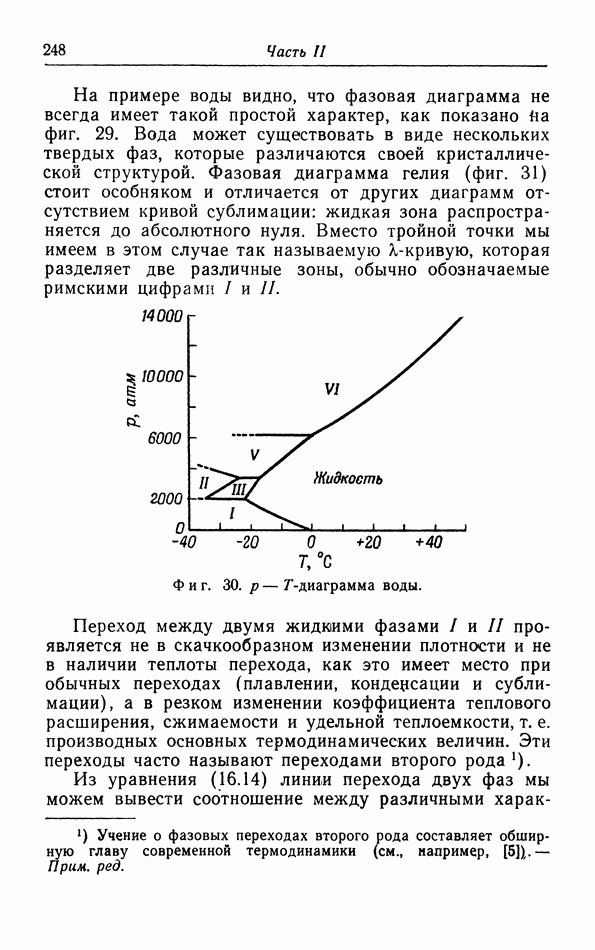
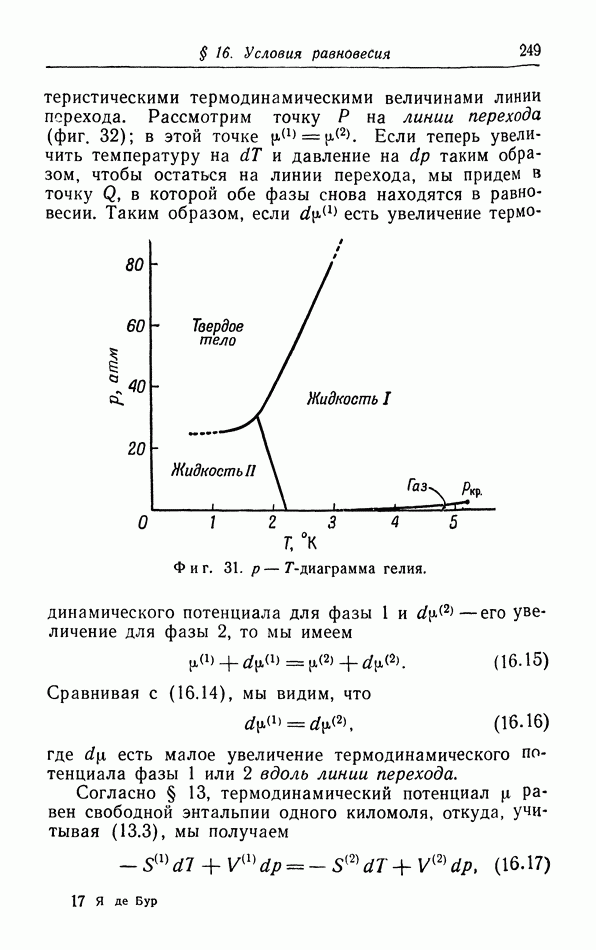
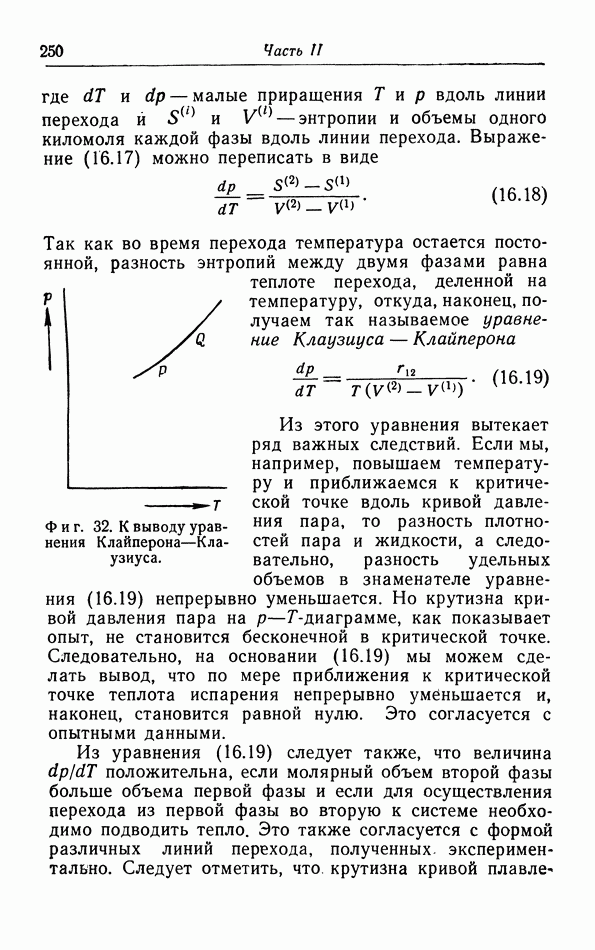
- § 16. Условия равновесия
- б. Первое условие равновесия.
- в. Второе условие равновесия.
- г. Третье условие равновесия.
- д. p-T-диаграмма.
- е. Равновесие фаз в случае более чем одного компонента. Правило фаз.
- ГЛАВА V. Теорема Нернста
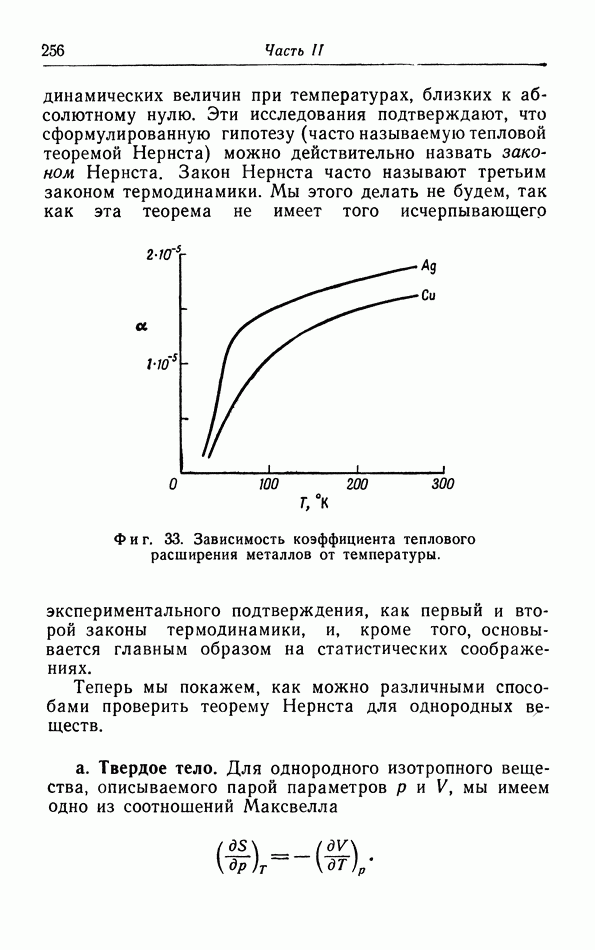
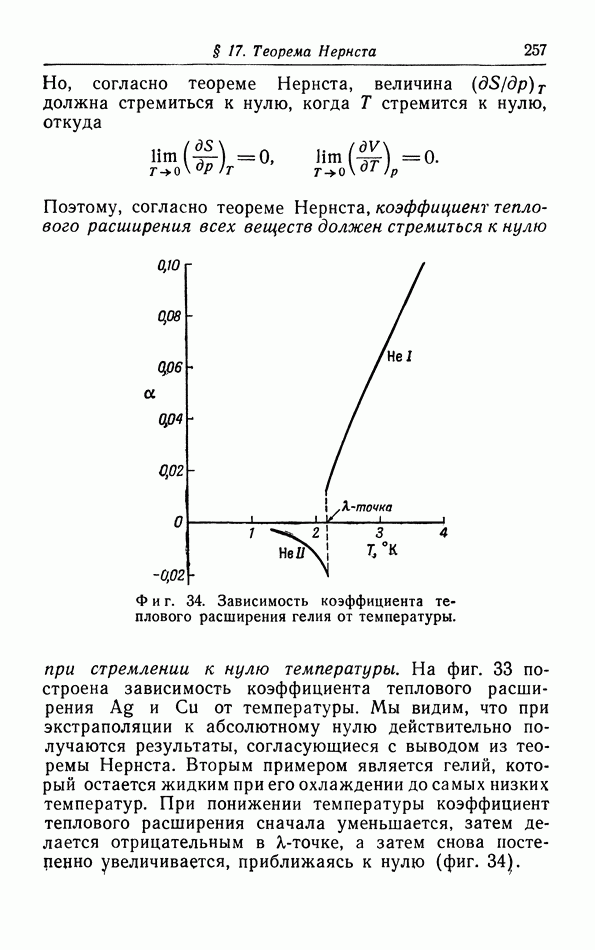
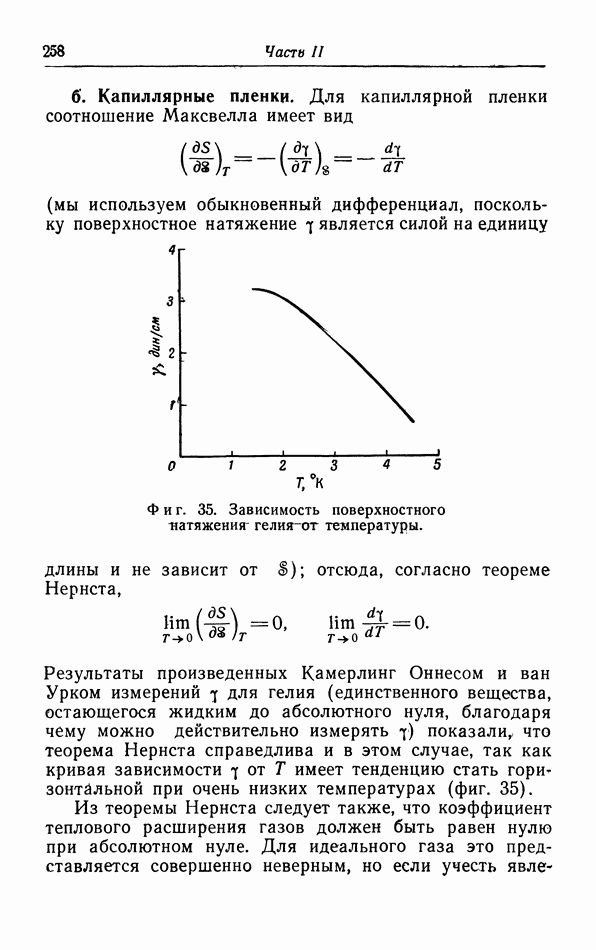
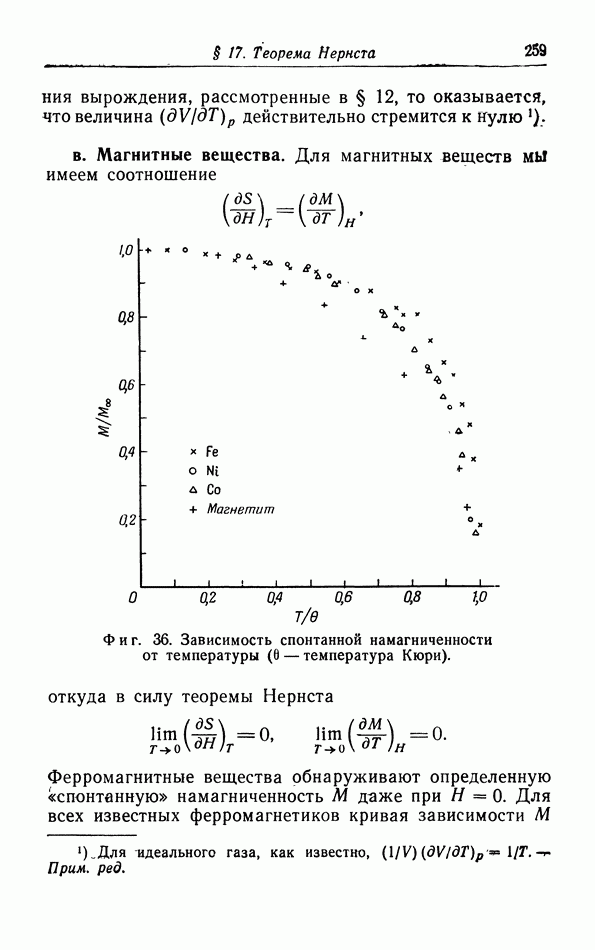
- § 17. Теорема Нернста
- § 18. Применение теоремы Нернста к фазовым переходам