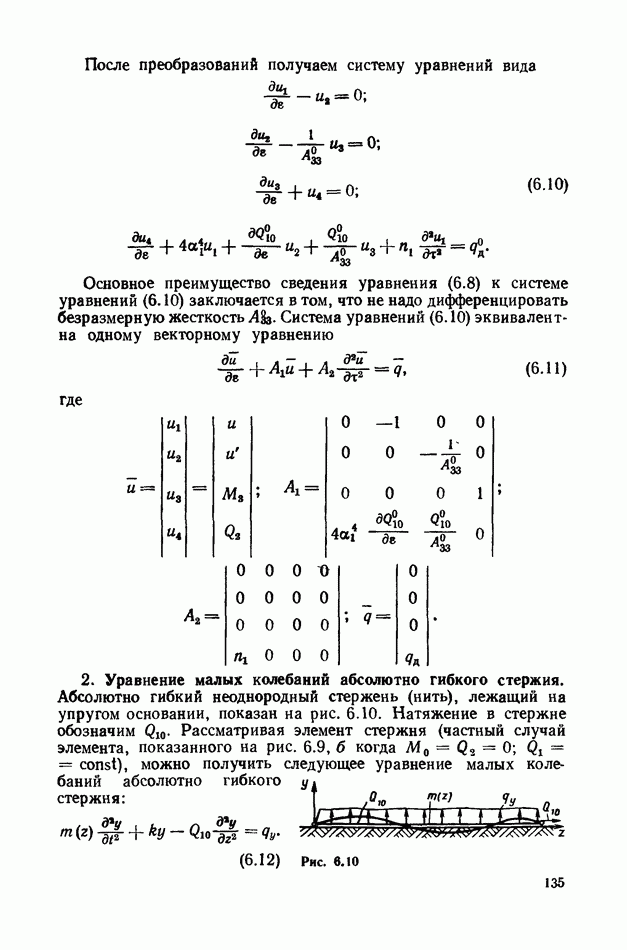
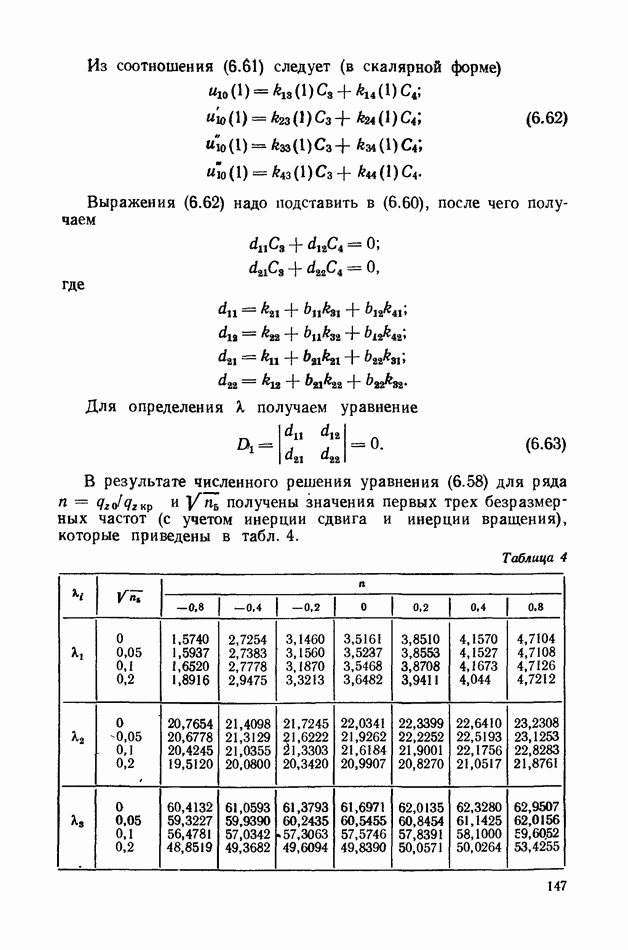
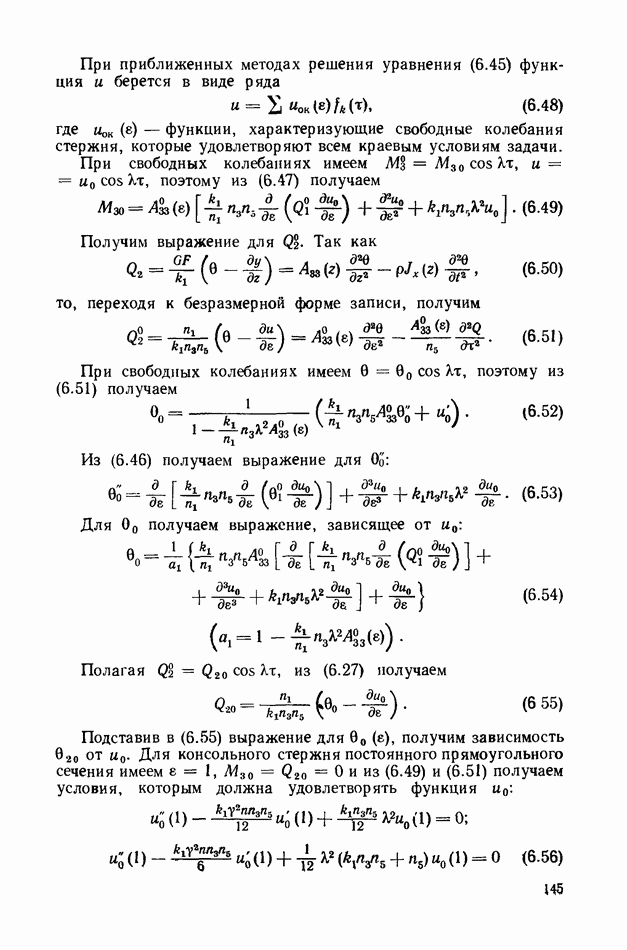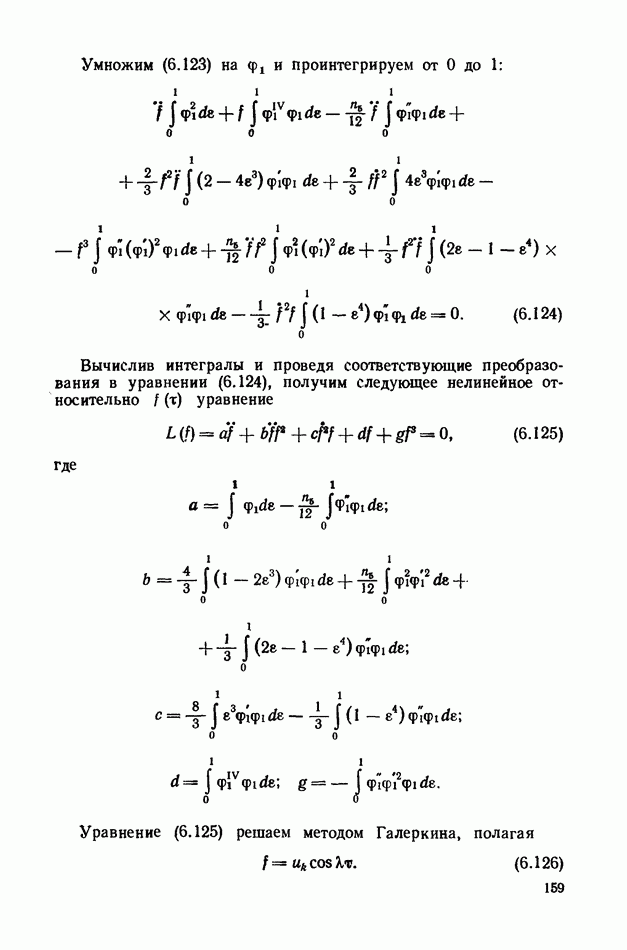| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Основные правила дифференцирования векторов.
1. Производная суммы векторов равна сумме производных слагаемых. Если  то
то

2. а) Производная произведения вектора на скаляр 

б) Производная скалярного произведения двух векторов 

в) Производная векторного произведения 


Рис. 1.10
3. Рассмотрим производную вектора постоянной длйны. Если вектор а при изменении скалярного аргумента меняет свое направление, но сохраняет свою длину, имеем

Дифференцируя (1.45) в соответствии с (1.43) и в силу коммутативности скалярного произведения, получим

Из соотношения (1.46) следует, что вектор ортогонален вектору а. Покажем, что производная от единичного вектора  (рис. 1.10), положение которого на плоскости задается скалярным аргументом (угол
(рис. 1.10), положение которого на плоскости задается скалярным аргументом (угол  есть тоже единичный вектор.
есть тоже единичный вектор.
Вектор  перпендикулярен вектору
перпендикулярен вектору  и его можно записать в виде
и его можно записать в виде  где
где  единичный вектор, перпендикулярный к вектору
единичный вектор, перпендикулярный к вектору  . С другой стороны,
. С другой стороны,  можно представить как
можно представить как

Поэтому

так как 
4. Рассмотрим вектор постоянного направления, который можно представить в виде

где  единичный вектор неизменного направления. Дифференцируя (1.48), получим
единичный вектор неизменного направления. Дифференцируя (1.48), получим

Из (1.49) следует, что вектор параллелен, исходному вектору а, т. е. необходимым и достаточным условием сохранения вектором а своего направления в пространстве является равенство нулю векторного произведения 
Найдем условия, при выполнении которых вектор а параллелен плоскости. Если вектор а, изменяясь (по длине и по направлению), остается все время параллельным некоторой плоскости, то он перпендикулярен любому вектору с, нормальному этой плоскости, т. е.

Если вектор а, изменяясь, остается в плоскости, то и векторы, характеризующие его производные  лежат в этой плоскости, поэтому скалярно-векторное (смешанное) произведение векторов
лежат в этой плоскости, поэтому скалярно-векторное (смешанное) произведение векторов  равно нулю:
равно нулю:

Выполнение (1.50) и (1.51) является необходимым и достаточным условием для того, чтобы вектор а, изменяясь по направлению и величине, оставался в плоскости, параллельной неизменной плоскости.
Рассмотрим производные единичных векторов  по координате
по координате  Так как производная от вектора по скалярному аргументу есть вектор, то представим его в виде разложения по базисным векторам
Так как производная от вектора по скалярному аргументу есть вектор, то представим его в виде разложения по базисным векторам 

где  элементы некоторой матрицы
элементы некоторой матрицы 
Покажем, что матрица  кососимметрична, т. е.
кососимметрична, т. е.  Умножив скалярно (1.52) на
Умножив скалярно (1.52) на  получим
получим

Так как  то после дифференцирования по
то после дифференцирования по  имеем
имеем

откуда в соответствии с (1.52) получаем

Из (1.54) следует  т. е. матрица
т. е. матрица  имеет всего три независимых элемента:
имеет всего три независимых элемента:

Элементы матрицы  характеризуют геометрию кривой, с которой связан трехгранник осей. Геометрический смысл введенных величин
характеризуют геометрию кривой, с которой связан трехгранник осей. Геометрический смысл введенных величин  устанавливается в § 3.
устанавливается в § 3.
Аналогичные выражения можно получить и для производных векторов базиса 

Вместо матрицы  можно перейти к вектору
можно перейти к вектору  и выражения для производных (1.52), (1.57) записать в виде
и выражения для производных (1.52), (1.57) записать в виде

В развернутой форме записи имеем

Проделав аналогичные выкладки, можно получить следующее выражение для вторых производных:

или в развернутой форме записи

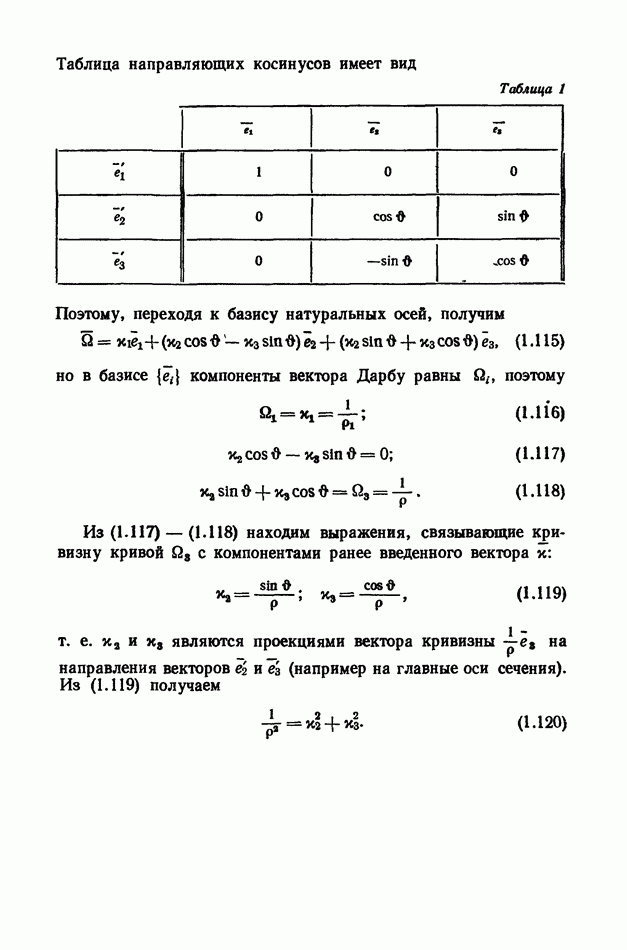
При перемещении трехгранника осей по пространственной кривой оси поворачиваются по отношению к первоначальному положению. Новое положение осей, как это было показано в § 1 п. 3, можно определить с помощью трех независимых углов  поэтому и вектор и, характеризующий изменение положения осей, должен зависеть от этих углов.
поэтому и вектор и, характеризующий изменение положения осей, должен зависеть от этих углов.
Получим эти зависимости, воспользовавшись выражениями (1.60) и соотношениями

Дифференцируя  имеем
имеем

Исключая из  получим
получим

Исключая  получаем
получаем

Дважды встречающиеся индексы можно заменять на любые другие (новые), например в первом слагаемом в левой части  можно заменить на
можно заменить на  в результате получим
в результате получим

Из выражения (1.67) получим

Найдем выражение для  Полагая
Полагая  имеем
имеем

Получим развернутые выражения для вторых слагаемых в скобках:

Окончательно получаем

или

Проделав аналогичные выкладки, можно получить следующие выражения для 

Подставив в (1.71) — (1.73) вместо  их выражения через углы
их выражения через углы  получим
получим

В выражениях  отсчитываются от положения осей
отсчитываются от положения осей  которое принято за начальное.
которое принято за начальное.
Систему соотношений (1.74) — (1-76) можно записать в виде одного векторного соотношения, удобного при преобразованиях:

где

Вектор  не равен вектору
не равен вектору  который характеризует геометрию кривой в начальном состоянии. Вектор
который характеризует геометрию кривой в начальном состоянии. Вектор  имеет компоненты в базисе равные компонентам вектора
имеет компоненты в базисе равные компонентам вектора  в базисе
в базисе  Выражение (1.77) дает возможность установить, как изменяется вектор
Выражение (1.77) дает возможность установить, как изменяется вектор  характеризующий геометрию кривой, если геометрия кривой в начальном состоянии
характеризующий геометрию кривой, если геометрия кривой в начальном состоянии  известна. Найдем вектор
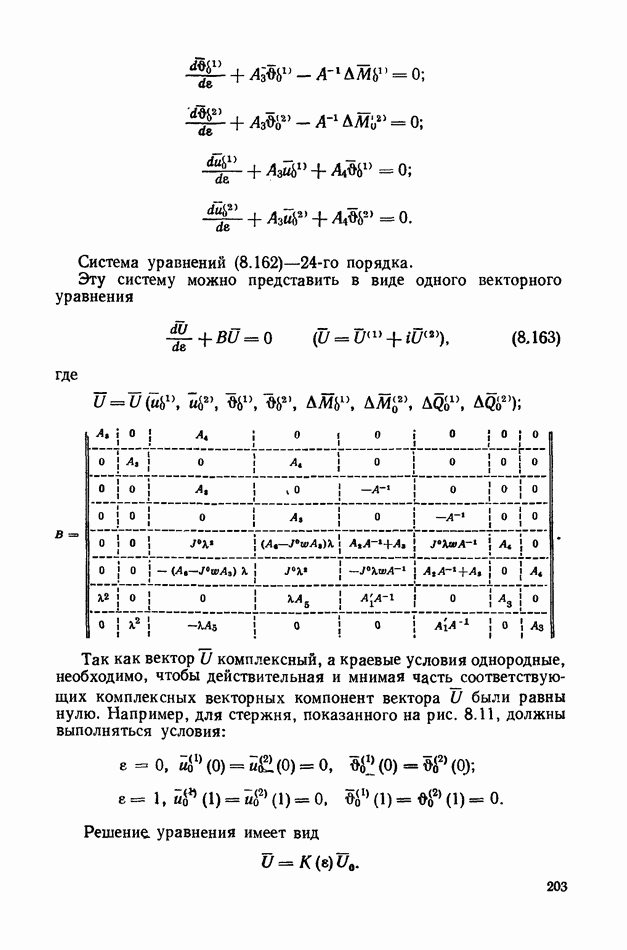
известна. Найдем вектор  характеризующий начальное состояние кривой, считая, что по отношению к декартовой системе координат
характеризующий начальное состояние кривой, считая, что по отношению к декартовой системе координат  известно положение базиса в каждой точке кривой. Углы, характеризующие положение базиса
известно положение базиса в каждой точке кривой. Углы, характеризующие положение базиса  относительно базиса
относительно базиса  обозначим
обозначим  .
.
Базисные векторы  связаны между собой матрицей
связаны между собой матрицей

Следует отметить, что единичные векторы  от
от  не зависят. Дифференцируя
не зависят. Дифференцируя  по
по  получим
получим

Так как  то после преобразований выражения (1.79) получим
то после преобразований выражения (1.79) получим

Далее находим

или в векторной форме записи

Установим геометрический смысл компонент вектора 

Рис. 1.11
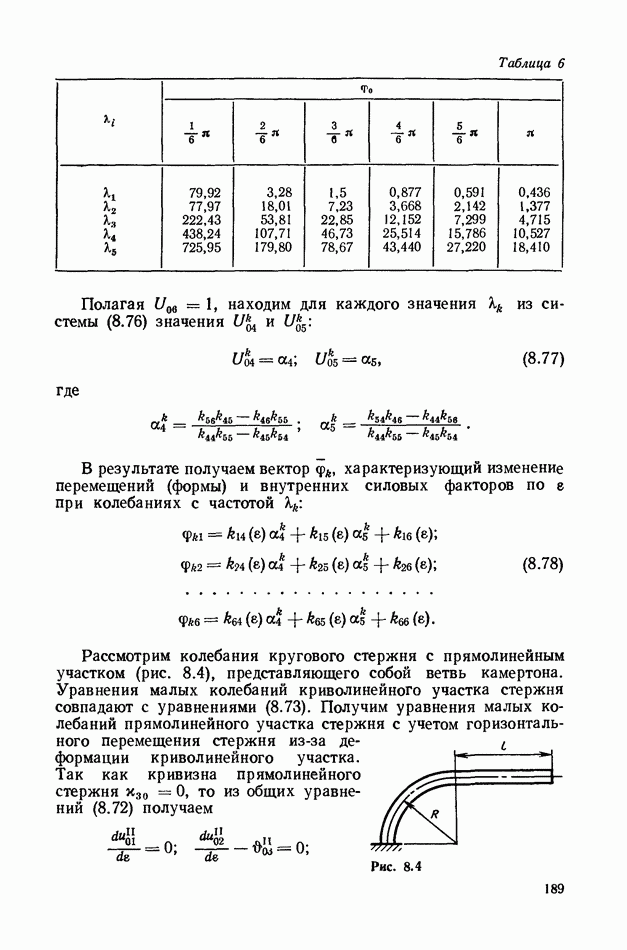
Рассмотрим частный случай плоской кривой, лежащей в плоскости  его). В этом случае при перемещении базиса по кривой векторы
его). В этом случае при перемещении базиса по кривой векторы  поворачиваются на угол
поворачиваются на угол  остальные два угла
остальные два угла  тождественно равны нулю, поэтому из
тождественно равны нулю, поэтому из  имеем
имеем

т. е.  кривизна кривой;
кривизна кривой;  радиус кривизны кривой в произвольной точке (более подробно о геометрических свойствах кривых будет сказано в § 3).
радиус кривизны кривой в произвольной точке (более подробно о геометрических свойствах кривых будет сказано в § 3).
Аналогично можно показать, что  есть кривизна плоской кривой в плоскости
есть кривизна плоской кривой в плоскости  следовательно, в общем случае пространственной кривой
следовательно, в общем случае пространственной кривой  проекции кривизны пространственной кривой на плоскостях, определяемые векторами
проекции кривизны пространственной кривой на плоскостях, определяемые векторами  Рассмотрим частный случай кривой — прямую. При перемещении начала базиса по прямой возможен только поворот осей относительно вектора
Рассмотрим частный случай кривой — прямую. При перемещении начала базиса по прямой возможен только поворот осей относительно вектора  (совпадающего с этой прямой), т. е.
(совпадающего с этой прямой), т. е.  Например, прямая является осью естественно закрученного стержня, у которого положение главных осей сечения (по которым направлены векторы
Например, прямая является осью естественно закрученного стержня, у которого положение главных осей сечения (по которым направлены векторы  зависит от координаты
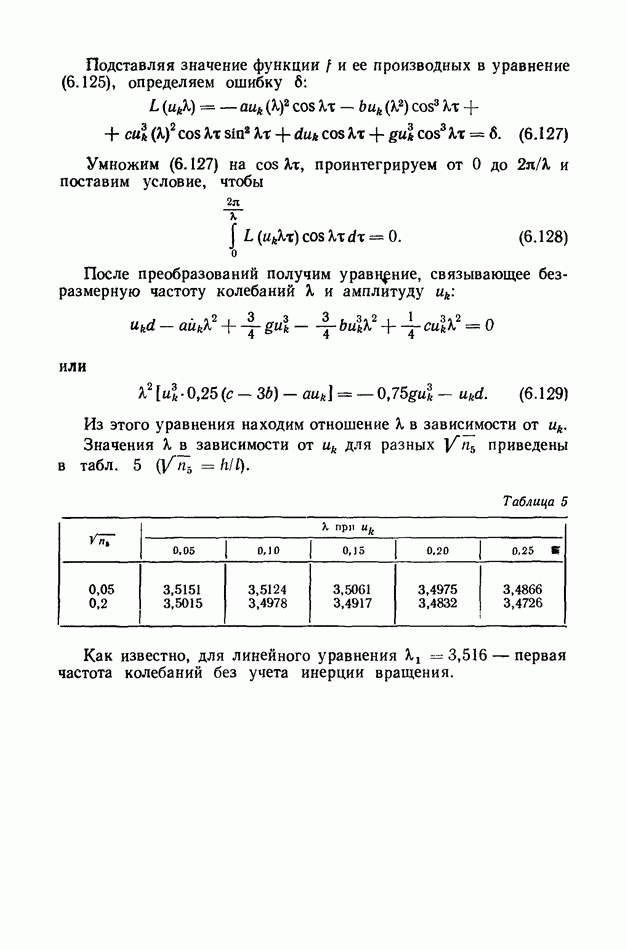
зависит от координаты 
Из выражений (1.81) — (1.83) получаем

В этом частном случае проекция  вектора
вектора  характеризует вращение связанного трехгранника осей относительно прямой, а для общего случая — относительно касательной к пространственной кривой. Аналогичный геометрический смысл имеют и компоненты вектора
характеризует вращение связанного трехгранника осей относительно прямой, а для общего случая — относительно касательной к пространственной кривой. Аналогичный геометрический смысл имеют и компоненты вектора  Напримердля плоской кривой в плоскости
Напримердля плоской кривой в плоскости  из (1-76) получаем (при
из (1-76) получаем (при  )
)

Кривизна кривой в новом положении равна кривизне в начальном положении плюс изменение кривизны, вызванное «деформацией» кривой.
Получим выражения для производной вектора  по координате
по координате 

где  -локальная частная производная, характеризующая изменение вектора а в связанной системе координат.
-локальная частная производная, характеризующая изменение вектора а в связанной системе координат.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
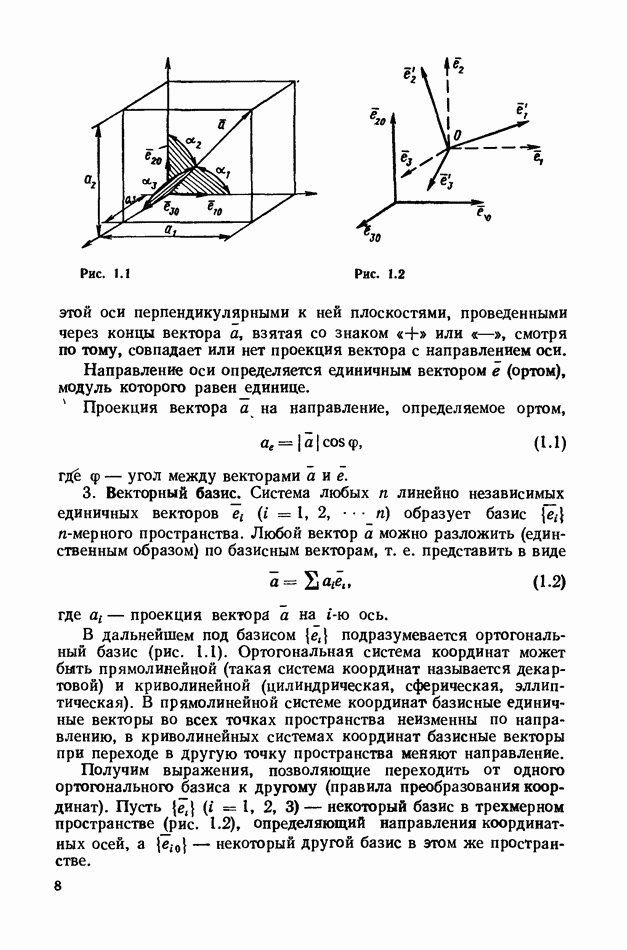
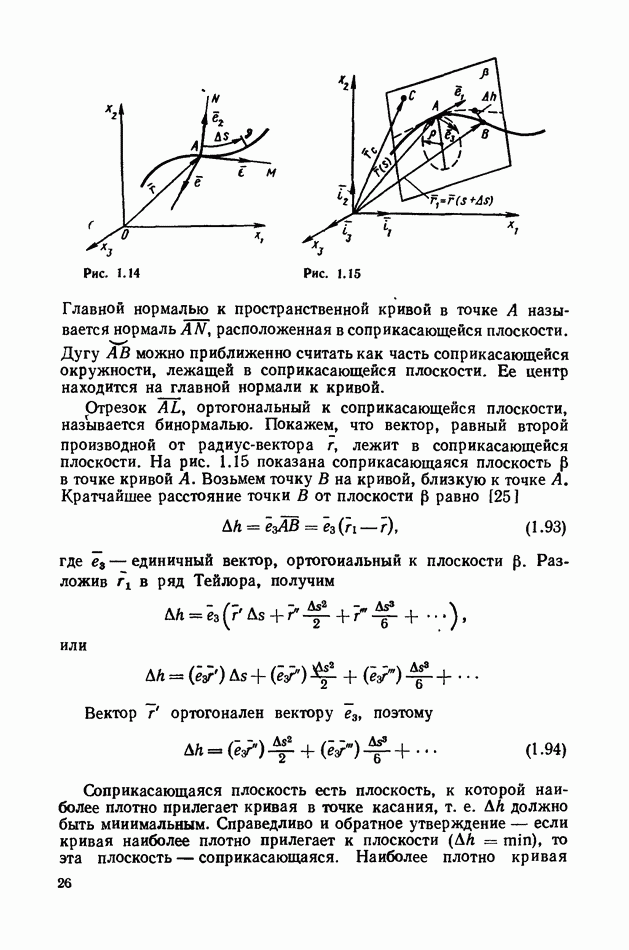
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
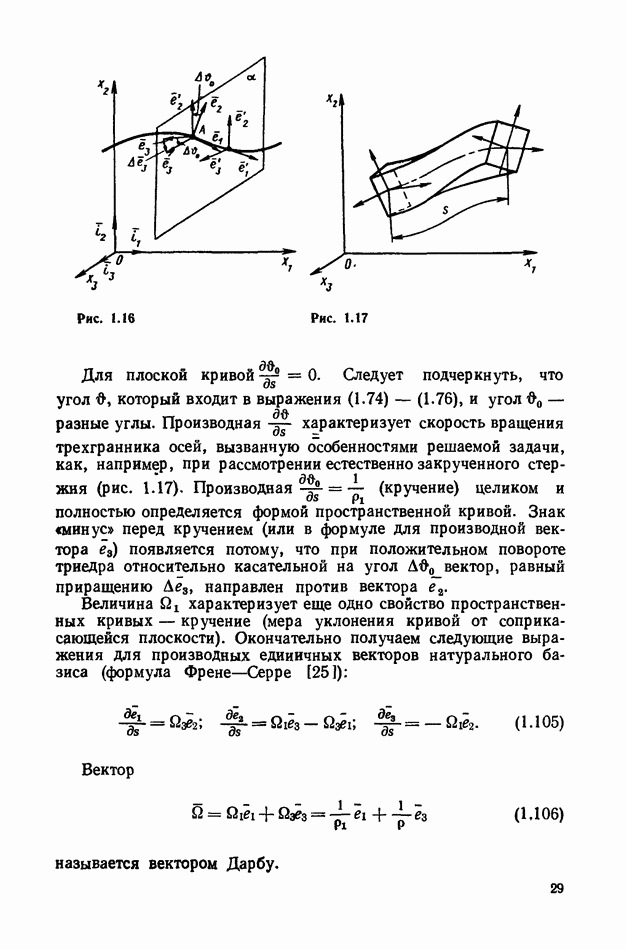
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
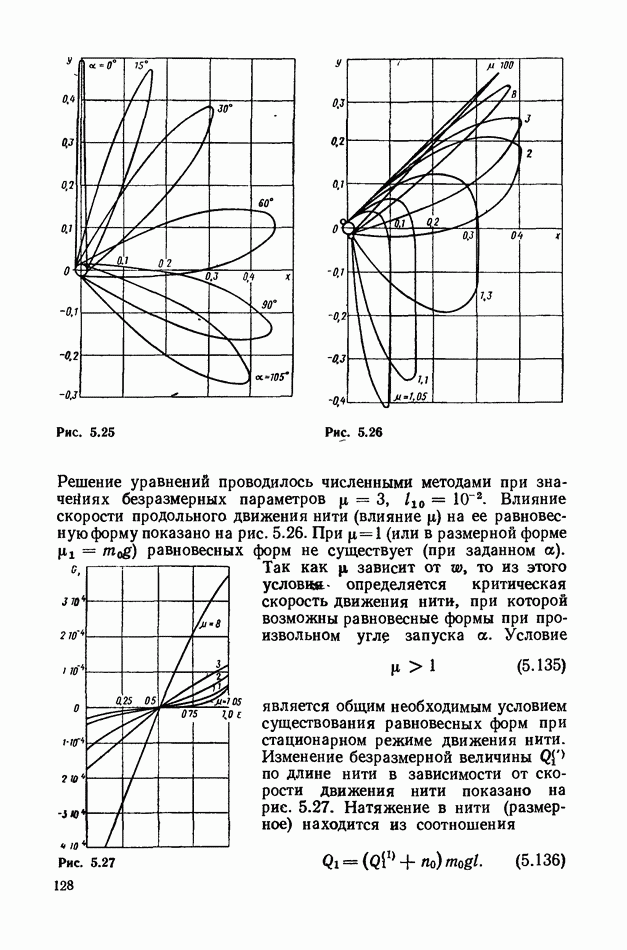
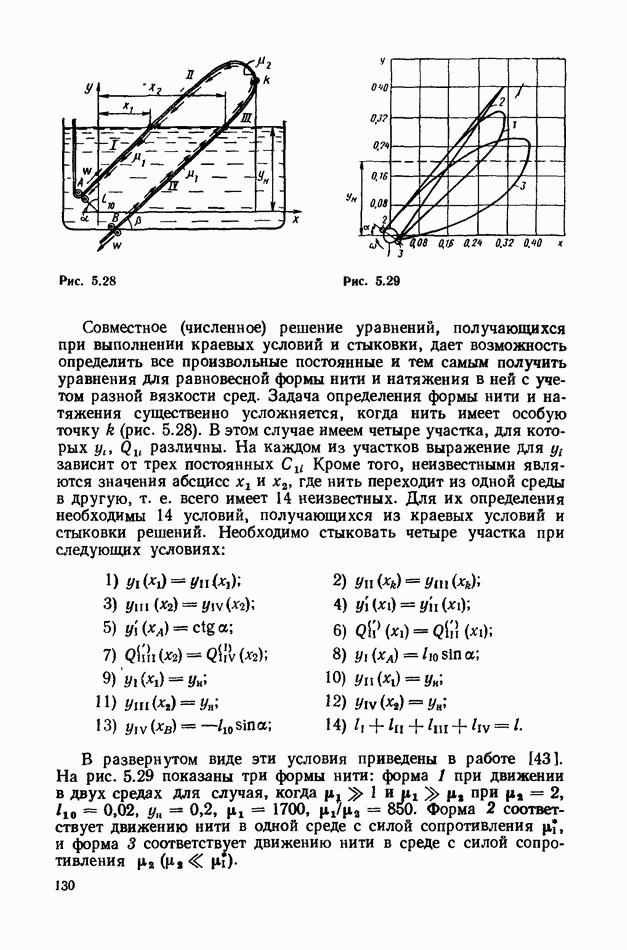
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.