| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 32. Малые колебания движущихся стержней
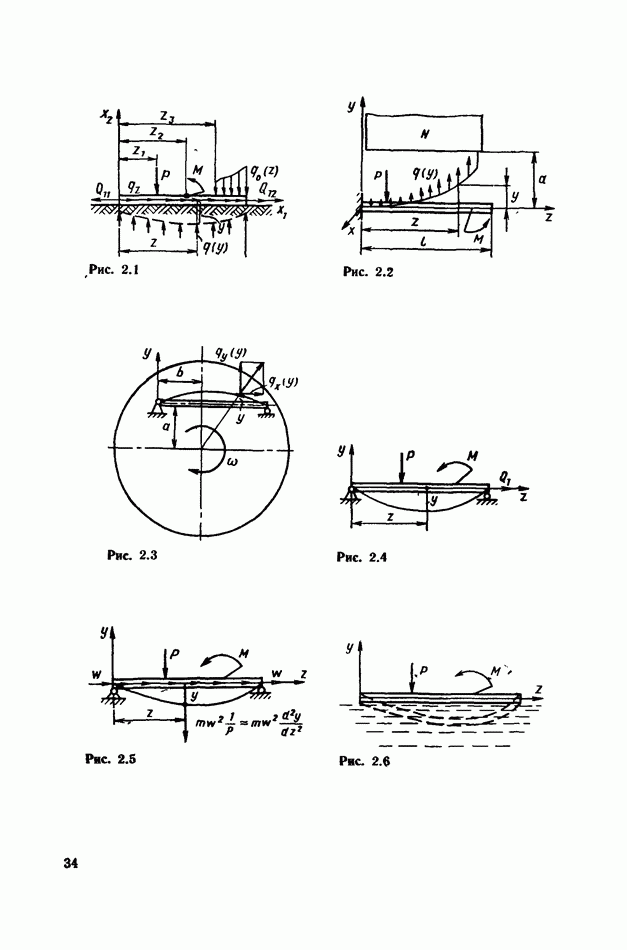
Рассмотрим малые колебания стержней относительно прямолинейного движения (рис. 6.14). Подобного рода задачи возникают при исследовании вибраций ленточных пил, передач с гибкой связью, намоточных устройств, лентопротяжных механизмов.
1. Уравнения малых колебаний гибкого стержня, имеющего продольное движение.
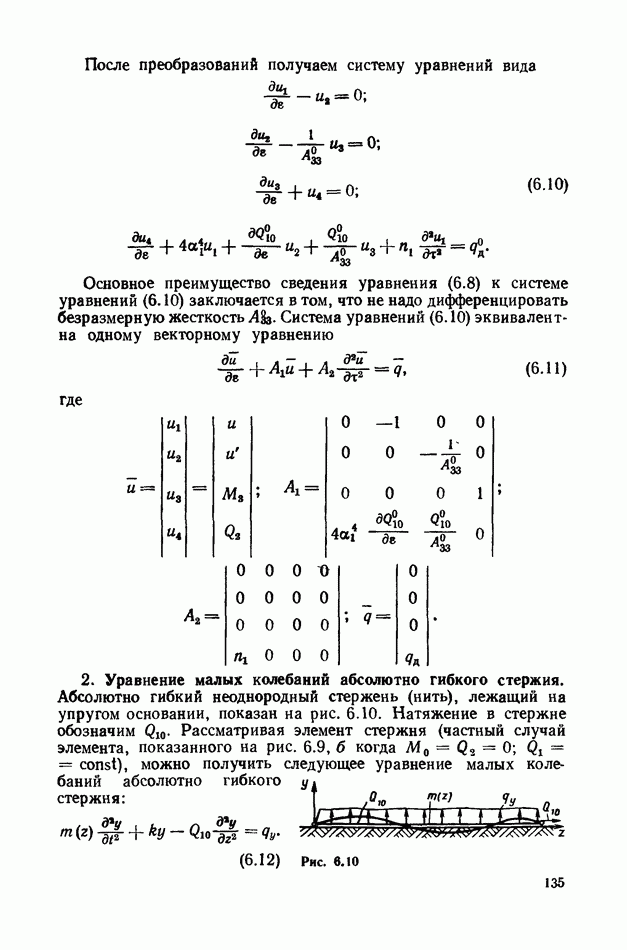
Ограничимся случаем, когда инерцией вращения и сдвига при исследовании колебаний стержня постоянного сечения можно пребречь. Уравнение малых колебаний стержня получим, воспользовавшись переменными Эйлера, для которых имеем (6.2), (4.32)

Полагая  получим (6.64) в безразмерной форме
получим (6.64) в безразмерной форме

поэтому уравнение малых колебаний (6.8) при  примет вид (опуская, индекс «нуль» в безразмерной скорости и осевом усилии)
примет вид (опуская, индекс «нуль» в безразмерной скорости и осевом усилии)

В частном случае  при постоянной скорости движения из (6.65) получаем уравнение
при постоянной скорости движения из (6.65) получаем уравнение

2. Определение частот и форм колебаний.
Основная особенность уравнения (6.66) заключается в том, что оно содержит нечетную производную по времени (из-за силы Кориолиса), что осложняет определение собственных чисел краевой задачи. Наличие слагаемого с нечетной производной говорит о возможной неконсервативности задачи, при которой собственные значения могут быть комплексными числами. В ряде случаев установить, является ли рассматриваемая задача консервативной или неконсервативной, можно сразу.

Рис. 6.14
Например, для случая, показанного на рис. 6.14, задача является консервативной, так как кинетическая энергия, поступающая в единицу времени через сечение  равна кинетической энергии элементов стержня, выходящих из сечения В. Поэтому участок стержня между сечениями
равна кинетической энергии элементов стержня, выходящих из сечения В. Поэтому участок стержня между сечениями  колебания которого рассматриваются, имеет неизменный запас энергии, т. е. задача является консервативной. Для консервативной задачи собственные значения X, если искать решение (6.66) [или в более общем случае
колебания которого рассматриваются, имеет неизменный запас энергии, т. е. задача является консервативной. Для консервативной задачи собственные значения X, если искать решение (6.66) [или в более общем случае  в виде
в виде  являются действительными числами. Подставив выражение для и в (6.66), получим (полагая
являются действительными числами. Подставив выражение для и в (6.66), получим (полагая 

В уравнении  следует считать комплексным числом
следует считать комплексным числом  поэтому уравнение (6.67) эквивалентно двум уравнениям (разделяя действительные и мнимые части)
поэтому уравнение (6.67) эквивалентно двум уравнениям (разделяя действительные и мнимые части)

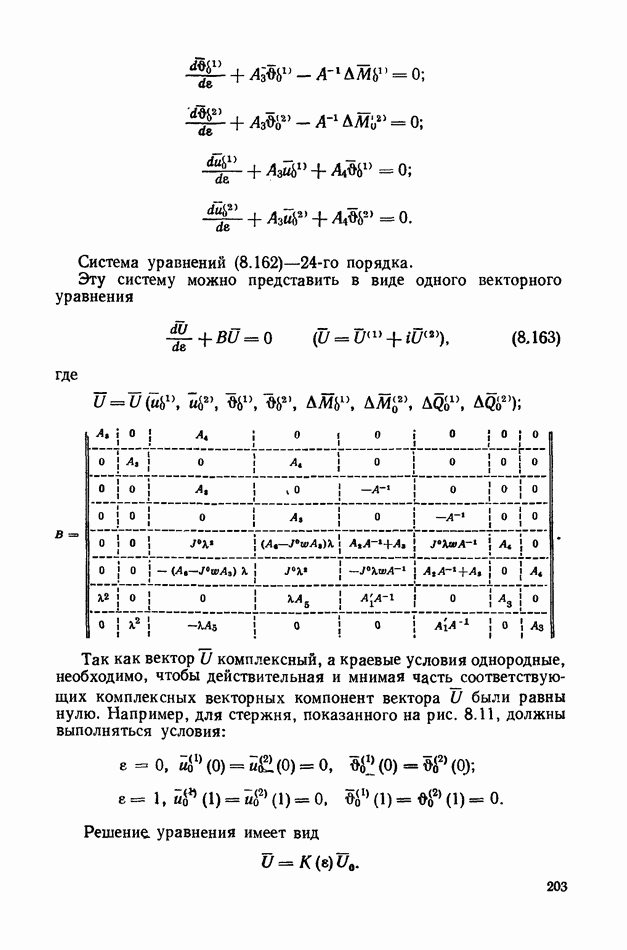
Систему уравнений (6.68) можно представить в виде одного векторного уравнения второго порядка

где

Задаваясь X при фиксированной скорости  получаем
получаем

Решение (6.70) должно удовлетворять комплексным краевым условиям:

что эквивалентно следующим краевым условиям:

Выполнение краевых условий при  приводит к следующим значениям первых четырех компонент вектора С:
приводит к следующим значениям первых четырех компонент вектора С:

Выполнение краевых условий при  приводит к системе четырех однородных уравнений вида
приводит к системе четырех однородных уравнений вида

Значения  которые обращают определитель системы (6.71) в нуль
которые обращают определитель системы (6.71) в нуль

являются частотами.
При определении частот колебаний для уравнений, не содержащих нечетных производных по времени, как, например, для системы уравнений (6.44), определитель (6.63) в зависимости от значений к может менять знак. Поэтому при численном счете определить значения К, при которых определитель меняет знак, особого труда не представляет. Качественный характер изменения определителя (6.63) показан на рис. 6.15 пунктирной линией.

Рис. 8.15 Для уравнений малых колебаний, содержащих нечетные производные по времени, определитель  при изменении
при изменении  знака не меняет. Качественный характер изменения
знака не меняет. Качественный характер изменения  от X показан на рис. 6.15 сплошной линией. Такой характер изменения определителя от К существенно осложняет
от X показан на рис. 6.15 сплошной линией. Такой характер изменения определителя от К существенно осложняет
численное определение собственных значений  Наиболее эффективным методом определения
Наиболее эффективным методом определения  обращающих
обращающих  в нуль, является метод наискорейшего спуска.
в нуль, является метод наискорейшего спуска.
Для каждого из найденных значений  из системы (6.71) находим
из системы (6.71) находим  в зависимости от
в зависимости от 

Понимая под формой колебаний  действительную часть комплексной функции
действительную часть комплексной функции  получаем (положив,
получаем (положив, 

3. Приближенное определение частот колебаний.
Для приближенного определения частот колебаний движущегося стержня воспользуемся принципом возможных перемещений. Решение уравнения (6.66) ищем в виде (при 

где  функции, удовлетворяющие краевым условиям задачи. В качестве таких функций можно взять функции, удовлетворяющие уравнению
функции, удовлетворяющие краевым условиям задачи. В качестве таких функций можно взять функции, удовлетворяющие уравнению

Определяем возможные перемещения:

(функции  удовлетворяют условию ортогональности).
удовлетворяют условию ортогональности).
В соответствии с принципом возможных перемещений получаем систему уравнений

или в развернутой форме записи

где

Можно показать (интегрируя по частям), что коэффициенты  удовлетворяют условиям
удовлетворяют условиям

Система уравнений (6.78) эквивалента векторному уравнению

где

Решение уравнения (6.80) ищем в виде  и Для получаем характеристическое уравнение
и Для получаем характеристическое уравнение

Например, для двух слагаемых ряда (6.74) получаем уравнение для определения двух безразмерных частот

или

Частоты колебаний стержня равны

4. Малые колебания нити.
Уравнения малых колебаний движущегося гибкого стержня получим из уравнения (6.66), полагая  Перейдя к переменным Эйлера и безразмерным величинам, в соответствии с выводом (6.65) получаем
Перейдя к переменным Эйлера и безразмерным величинам, в соответствии с выводом (6.65) получаем

5. Определение частот и форм точным методом.
Решение уравнения (6.85) ищем в виде  что приводит к уравнению относительно
что приводит к уравнению относительно 

Полагая  получим
получим

где

Корни уравнения (6.87)

поэтому решение (6.86) имеет вид

Функция  должна удовлетворять краевым условиям задачи:
должна удовлетворять краевым условиям задачи:  что приводит к уравнению
что приводит к уравнению

или

Условие (6.91) выполняется, если

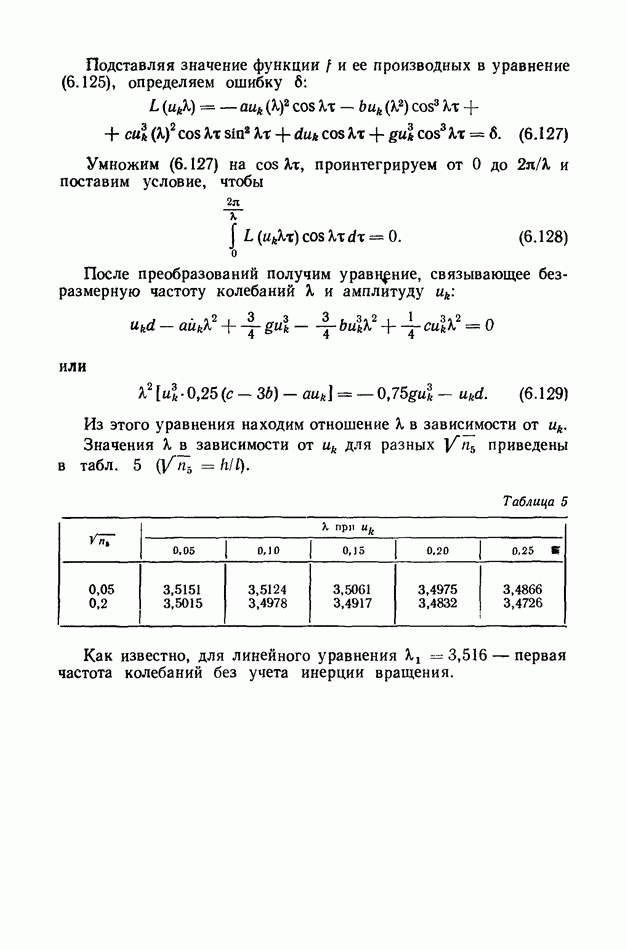
Из (6.92) получаем точные значения частот колебаний движущейся нити 

Как следует из (6.93), все частоты при  стремятся к нулю.
стремятся к нулю.
Критическое значение безразмерной скорости продольного движения нити

совпадает со скоростью (безразмерной) распространения возмущений по нити.
Определив  находим корни
находим корни 

где

Произвольные постоянные  и С а связаны соотношением
и С а связаны соотношением  для любого
для любого  Поэтому собственные функции краевой задачи следующие
Поэтому собственные функции краевой задачи следующие

Общее решение уравнения (6.86) имеет вид

Разделив действительные и мнимые части, получим, например, для 

где

При  и из (6.94) получается известное решение уравнений малых колебаний струны.
и из (6.94) получается известное решение уравнений малых колебаний струны.
Функции  удовлетворяют уравнению
удовлетворяют уравнению

где

Можно показать, что функции  удовлетворяют условию ортогональности (на интервале 0; 1) следующего вида:
удовлетворяют условию ортогональности (на интервале 0; 1) следующего вида:

Интегрируя, получим

После преобразований имеем

Для  получаем значения
получаем значения

6. Свободные колебания.
Если при  струна имела отклонения и скорости, т. е.
струна имела отклонения и скорости, т. е.

где  и
и  известные функции, то получаем два выражения:
известные функции, то получаем два выражения:

Умножаем (6.95) на  а (6.96) на
а (6.96) на  складываем и интегрируем от
складываем и интегрируем от  до 1, имеем
до 1, имеем

Второе уравнение для определения  получим, умножив (6.95) на а (6.96) на
получим, умножив (6.95) на а (6.96) на  вычитая получающиеся выражения и проинтегрировав
вычитая получающиеся выражения и проинтегрировав

В результате получим систему двух уравнений (6.97) и (6.98) для определения  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
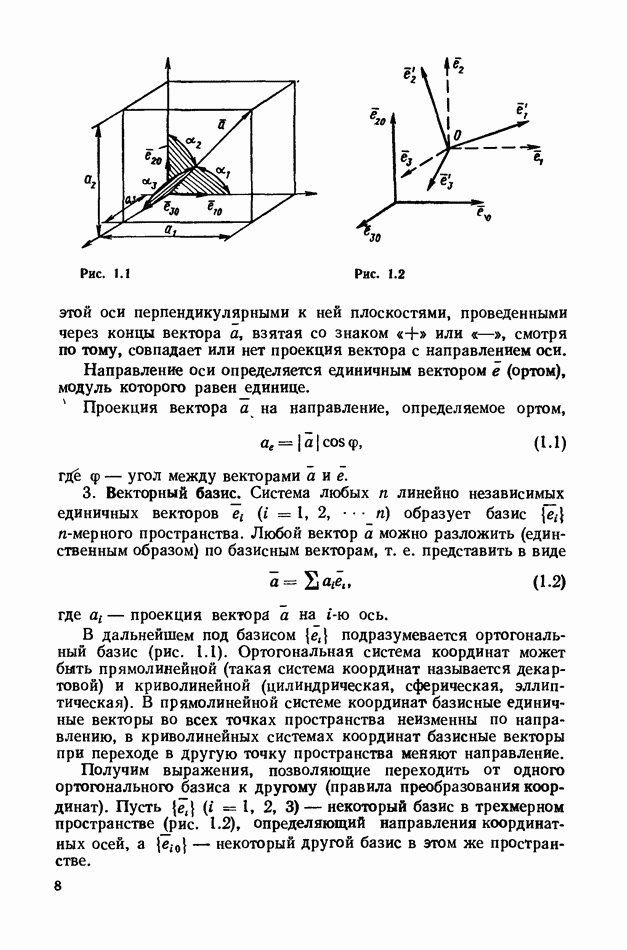
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
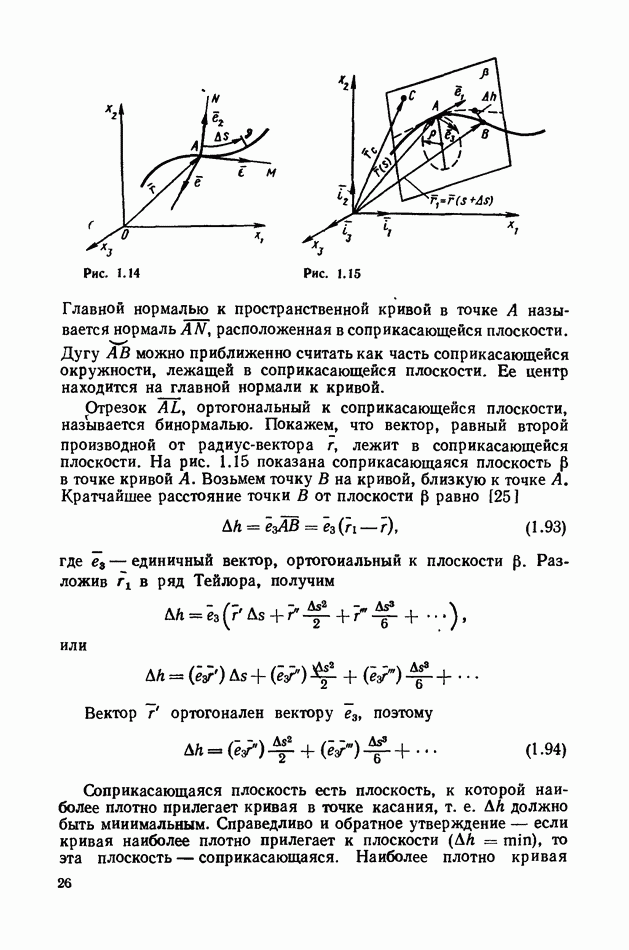
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
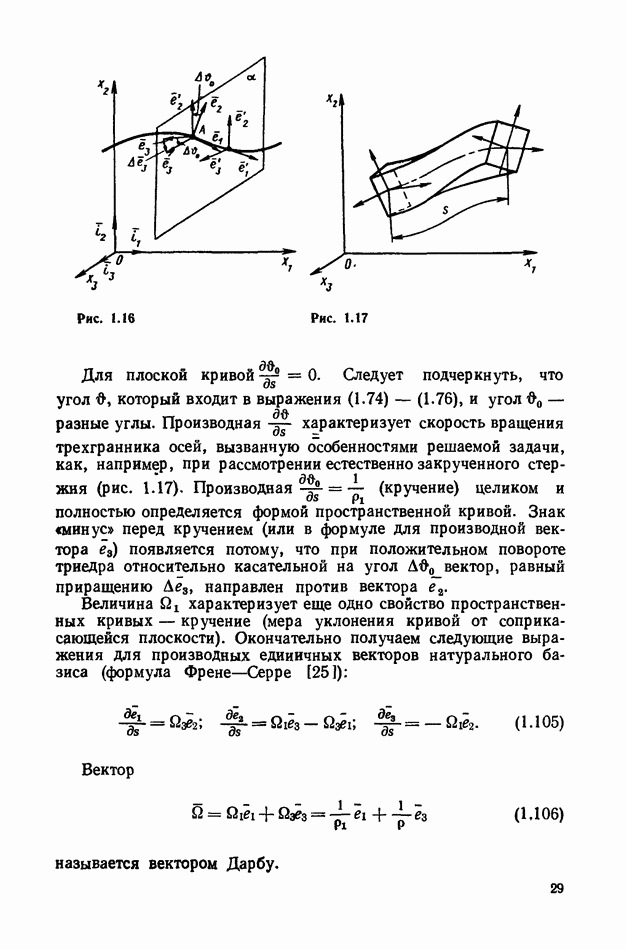
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
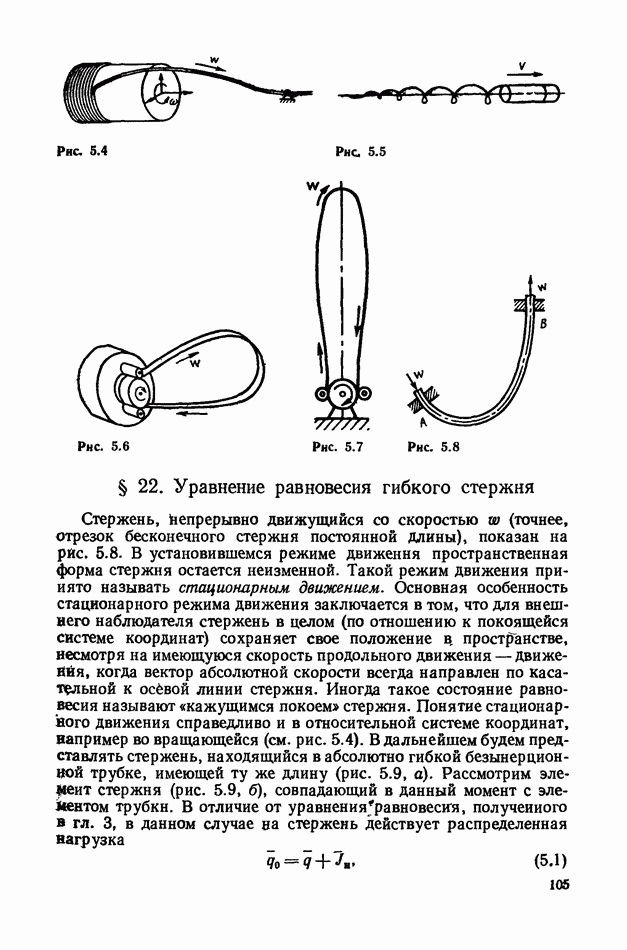
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
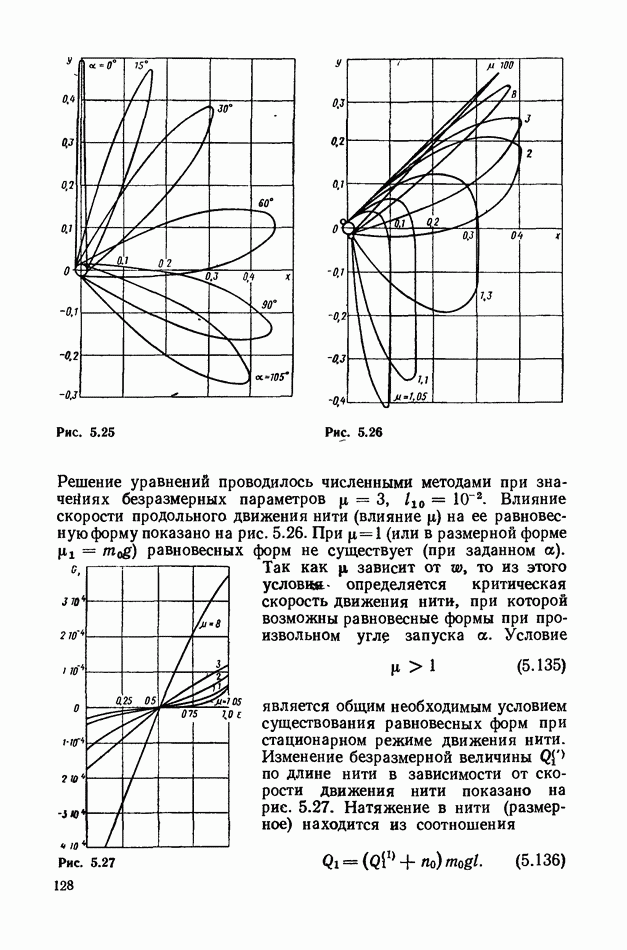
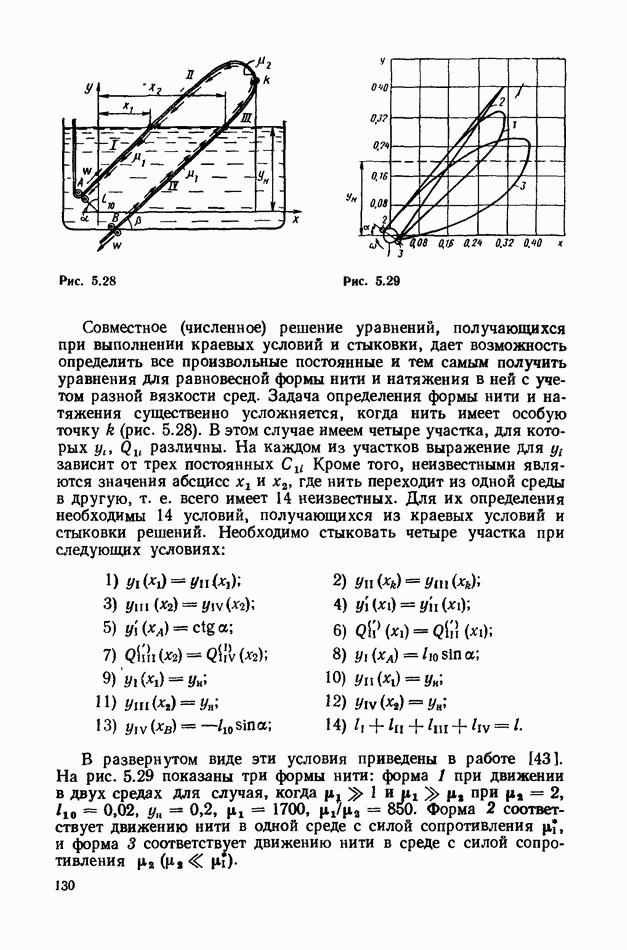
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.