| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Векторный базис.
Система любых  линейно независимых единичных векторов
линейно независимых единичных векторов  образует базис
образует базис  -мерного пространства. Любой вектор а можно разложить (единственным образом) по базисным векторам, т. е. представить в виде
-мерного пространства. Любой вектор а можно разложить (единственным образом) по базисным векторам, т. е. представить в виде

где  проекция вектора а на
проекция вектора а на  ось.
ось.
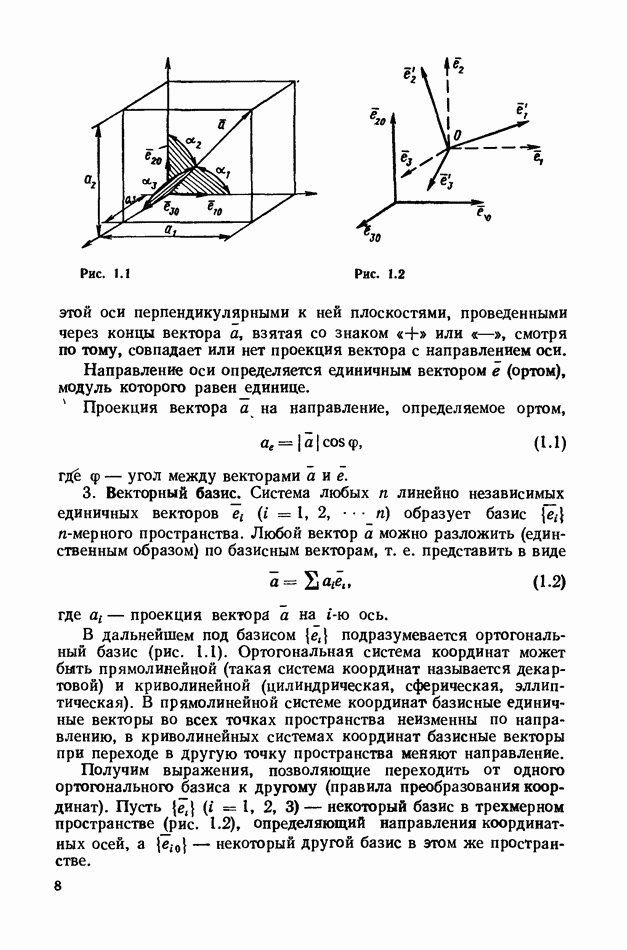
В дальнейшем под базисом  подразумевается ортогональный базис (рис. 1.1). Ортогональная система координат может бить прямолинейной (такая система координат называется декартовой) и криволинейной (цилиндрическая, сферическая, эллиптическая). В прямолинейной системе координат базисные единичные векторы во всех точках пространства неизменны по направлению, в криволинейных системах координат базисные векторы при переходе в другую точку пространства меняют направление.
подразумевается ортогональный базис (рис. 1.1). Ортогональная система координат может бить прямолинейной (такая система координат называется декартовой) и криволинейной (цилиндрическая, сферическая, эллиптическая). В прямолинейной системе координат базисные единичные векторы во всех точках пространства неизменны по направлению, в криволинейных системах координат базисные векторы при переходе в другую точку пространства меняют направление.
Получим выражения, позволяющие переходить от одного ортогонального оазиса к другому (правила преобразования координат). Пусть  — некоторый базис в трехмерном пространстве (рис. 1.2), определяющий направления координатных осей, а
— некоторый базис в трехмерном пространстве (рис. 1.2), определяющий направления координатных осей, а  некоторый другой базис в этом же пространстве.
некоторый другой базис в этом же пространстве.
Каждый из векторов базиса можна разложить по векторам исходного базиса 

или

где  проекции базисных векторов
проекции базисных векторов  на направления, определяемые векторами
на направления, определяемые векторами 
В системе (1.3) коэффициенты  определяют матрицу
определяют матрицу

которая называется матрицей перехода от базиса  к базису
к базису 
Выражения (1.2) — (1.3) можно представить в более компактной форме, введя следующее соглашение: если индекс употреблен дважды, то подразумевается, что этот индекс принимает все значения, которые указываются в знаке суммы  знак суммы можно опустить:
знак суммы можно опустить:

Повторяющиеся индексы называют немыми, так как их замена на любые другие, не встречающиеся в данной записи, не изменяет выражения. Неповторяющиеся индексы называют свободными [21].
В качестве примера найдем значения элементов матрицы  Рассмотрим случай, когда новые базисные векторы
Рассмотрим случай, когда новые базисные векторы  в новом положении координатных осей остались параллельными исходным базисным векторам с одинаковыми индексами (см. рис. 1.2). Такое перемещение координатных осей в пространстве называется поступательным. При преобразовании базисных векторов
в новом положении координатных осей остались параллельными исходным базисным векторам с одинаковыми индексами (см. рис. 1.2). Такое перемещение координатных осей в пространстве называется поступательным. При преобразовании базисных векторов  поэтому
поэтому  где
где  единичная матрица.
единичная матрица.
В качестве второго примера найдем матрицу перехода  при произвольных перемещении и повороте тройки базисных векторов (см. рис. 1.2). Так как при поступательном перемещении координатных осей базисные векторы совпадают с исходными, то можно
при произвольных перемещении и повороте тройки базисных векторов (см. рис. 1.2). Так как при поступательном перемещении координатных осей базисные векторы совпадают с исходными, то можно

Рис. 1.3

Рис. 1.4

Рис. 1.5
рассмотреть только преобразование базисных векторов, связанное с поворотом. Произвольный поворот координатных осей можно представить как три независимых поворота [15]. Рассмотрим поворот исходных координатных осей относительно оси, совпадающей с направлением  на положительный угол
на положительный угол  (рис. 1.3). Получаем
(рис. 1.3). Получаем

Соответствующая матрица перехода

Элементы матрицы (как и элементы любой матрицы поворота координатных осей) можно рассматривать как направляющие косинусы между векторами базисов  и
и
Второй поворот на положительный угол  осуществим относительно оси, совпадающей с направлением вектора
осуществим относительно оси, совпадающей с направлением вектора  (рис. 1.4). При этом
(рис. 1.4). При этом

Соответствующая матрица перехода

Наконец, последний поворот координатных осей осуществим относительно оси, совпадающей по направлению с  положительный угол (рис. 1.5). После поворота базисные векторы
положительный угол (рис. 1.5). После поворота базисные векторы  совпадают с векторами
совпадают с векторами  Соответствующая матрица перехода
Соответствующая матрица перехода

Компоненты произвольного вектора а при каждом из поворотов преобразуются следующим образом:

поэтому

Матрица перехода от базиса  к базису
к базису 

или

или

Матрица  позволяет определить положение элемента стержня в пространстве при его произвольных поворотах. Матрица
позволяет определить положение элемента стержня в пространстве при его произвольных поворотах. Матрица  поворота координатных осей имеет следующую особенность: ее обратная матрица
поворота координатных осей имеет следующую особенность: ее обратная матрица  равна транспонированной матрице
равна транспонированной матрице

Так как  то элементы
то элементы  матрицы
матрицы  удовлетворяют следующим шести условиям:
удовлетворяют следующим шести условиям:

Систему (1.13) можно записать более компактно, если воспользоваться соглашением о суммировании и символами Кронекера  :
:

Возможны и другие варианты трех последовательных, поворотов координатных осей. Соответствующие углы, определяющие поворот осей, выбираются в зависимости от решаемых задач.
Наибольшей популярностью в теоретической механике пользуются углы Эйлера [15], однако в механике стержней и нитей более удобными при решении являются углы, которые при малом отклонении осей остаются малыми. Матрица  перехода при малых углах принимает вид
перехода при малых углах принимает вид

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
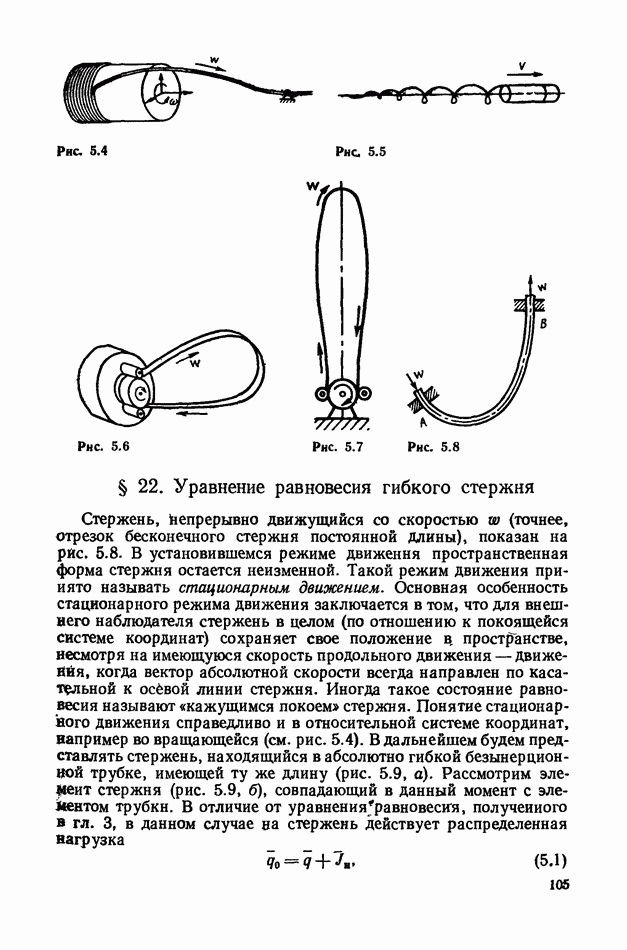
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.