| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
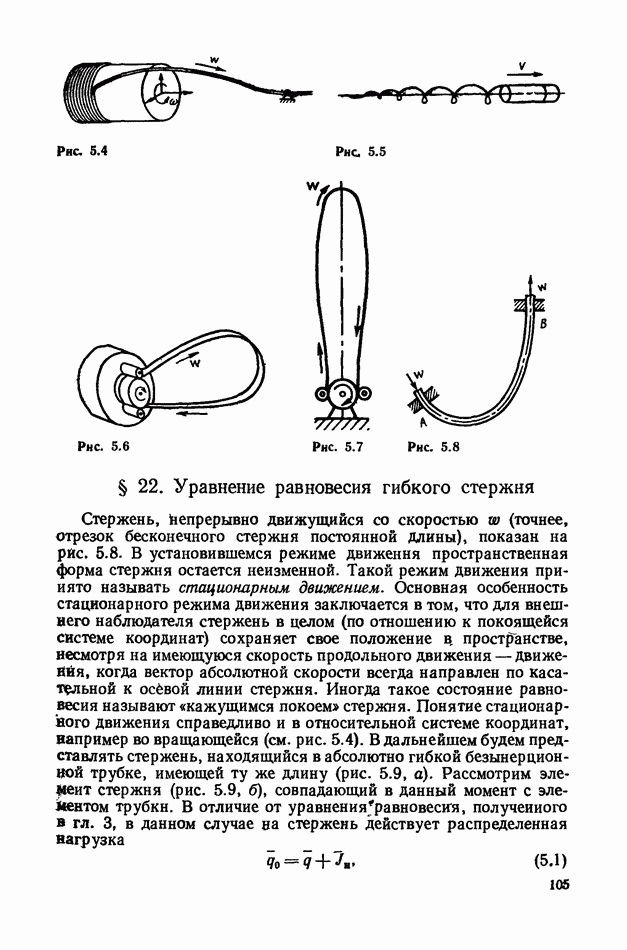
§ 22. Уравнение равновесия гибкого стержня
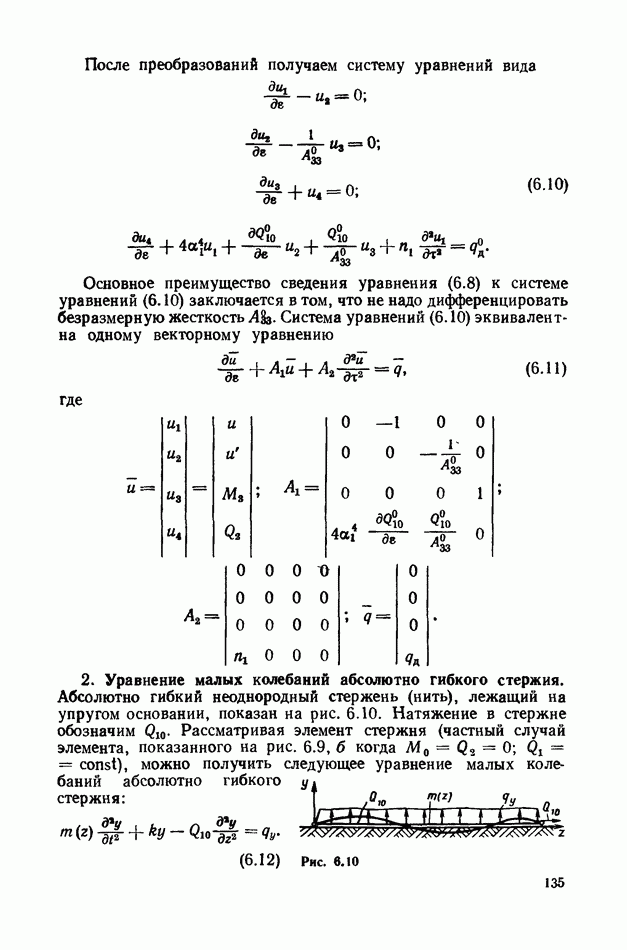
Стержень, Непрерывно движущийся со скоростью  (точнее, отрезок бесконечного стержня постоянной длины), показан на рис. 5.8. В установившемся режиме движения пространственная форма стержня остается неизменной. Такой режим движения принято называть стационарным движением. Основная особенность стационарного режима движения заключается в том, что для внешнего наблюдателя стержень в целом (по отношению к покоящейся системе координат) сохраняет свое положение в пространстве, несмотря на имеющуюся скорость продольного движения — движения, когда вектор абсолютной скорости всегда направлен по касательной к осёвой линии стержня. Иногда такое состояние равновесия называют «кажущимся покоем» стержня. Понятие стационарного движения справедливо и в относительной системе координат, например во вращающейся (см. рис. 5.4). В дальнейшем будем представлять стержень, находящийся в абсолютно гибкой безынерционной трубке, имеющей ту же длину (рис. 5.9, а). Рассмотрим элемент стержня (рис. 5.9, б), совпадающий в данный момент с элементом трубки. В отличие от уравнения равновесия, полученного в гл. 3, в данном случае на стержень действует распределенная нагрузка
(точнее, отрезок бесконечного стержня постоянной длины), показан на рис. 5.8. В установившемся режиме движения пространственная форма стержня остается неизменной. Такой режим движения принято называть стационарным движением. Основная особенность стационарного режима движения заключается в том, что для внешнего наблюдателя стержень в целом (по отношению к покоящейся системе координат) сохраняет свое положение в пространстве, несмотря на имеющуюся скорость продольного движения — движения, когда вектор абсолютной скорости всегда направлен по касательной к осёвой линии стержня. Иногда такое состояние равновесия называют «кажущимся покоем» стержня. Понятие стационарного движения справедливо и в относительной системе координат, например во вращающейся (см. рис. 5.4). В дальнейшем будем представлять стержень, находящийся в абсолютно гибкой безынерционной трубке, имеющей ту же длину (рис. 5.9, а). Рассмотрим элемент стержня (рис. 5.9, б), совпадающий в данный момент с элементом трубки. В отличие от уравнения равновесия, полученного в гл. 3, в данном случае на стержень действует распределенная нагрузка

где  распределенная нагрузка (вызванная силамн инерции)
распределенная нагрузка (вызванная силамн инерции)

( - масса единицы длины стержня).
- масса единицы длины стержня).

Рис. 5.9
При стационарном движении нерастяжимого стержня справедливо условие  Переходя к переменным Эйлера и учитывая, что
Переходя к переменным Эйлера и учитывая, что  получим
получим

Так как при стационарном движении все величины, характеризующие состояние стержня, не зависят от времени, то вместо частных производных можно использовать полные производные по  поэтому получаем следующее уравнение равновесия:
поэтому получаем следующее уравнение равновесия:

Переходя к безразмерной форме записи (аналогично § 11), получим

где  безразмерные величины.
безразмерные величины.
Уравнение (5.5) можно представить в виде

которое эквивалентно (по записи) уравнению (3.41), т. е. можно исследовать состояние кажущегося покоя стержня, используя уравнение (5 5). Тогда продольное движение стержня эквивалентно дополнительной распределенной нагрузке и можно рассматривать равновесие, «забыв» о продольном движении, а затем в конечном решении к осевой силе  добавить слагаемое
добавить слагаемое 
Как следует из выражения для  основная особенность полученного уравнения (5.6) заключается в том, что изменяется только осевое усилие, увеличивающееся на одну и ту же величину
основная особенность полученного уравнения (5.6) заключается в том, что изменяется только осевое усилие, увеличивающееся на одну и ту же величину 
Переходя к локальным производным в (5.4), имеем

В проекциях на связанные оси уравнение (5 7) принимает вид

При движении по криволинейной пространственной трубке элемент стержня вращается с некоторой угловой скоростью  поэтому на него действует дополнительная распределенная инерционная нагрузка — распределенный момент
поэтому на него действует дополнительная распределенная инерционная нагрузка — распределенный момент  равный
равный

или переходя к переменным Эйлера

где  матрица главных моментов инерции элемента стержня, длина которого равна единице. Перейдя к локальным производным, получаем уравнение (в безразмерных величинах)
матрица главных моментов инерции элемента стержня, длина которого равна единице. Перейдя к локальным производным, получаем уравнение (в безразмерных величинах)

В скалярной форме имеем

Уравнение для перемещений остается без изменения, так как при установившемся движении форма стержня может быть определена как форма неподвижной трубки, с которой совпадает стержень. Для гибких тонких стержней распределенный момент, вызванный инерцией вращения, как правило, является малым, и им можно пренебречь  Если слагаемое, зависящее от скорости продольного движения, объединить с осевой силой [как это сделано в
Если слагаемое, зависящее от скорости продольного движения, объединить с осевой силой [как это сделано в  то уравнения, характеризующие стационарное движение стержня, эквивалентны уравнениям равновесия. Сила
то уравнения, характеризующие стационарное движение стержня, эквивалентны уравнениям равновесия. Сила  входящая в уравнение моментов, может быть заменена на
входящая в уравнение моментов, может быть заменена на  так как справедливо равенство
так как справедливо равенство

и уравнение (5.12) (при  тождественно совпадает с уравнением (3.98).
тождественно совпадает с уравнением (3.98).
Рассмотрим несколько частных случаев общих уравнений стационарного движения стержня, имеющих прикладное значение. Во введении к этой главе приведен пример, где используется быстродвижущийся гибкий стержень для охлаждения реактора (ленточный радиатор).

Рис. 5.10
Получим уравнения стационарного движения ленточного радиатора. Ленточные радиаторы предназначены для отвода тепла от различного типа силовых установок, в частности от силовых установок космических кораблей (рис. 5.10) [51]. В условиях космоса тепло может быть отведено в окружающее пространство только путем излучения. Обычные радиаторы, предназначенные для отвода тепла, при больших значениях отводимой энергии имеют большую массу, что для космических кораблей недопустимо. При необходимости отвода энергии около 1 МВт вес радиатора равен почти половине веса силовой установки. Применение ленточного радиатора позволяет снизить вес радиатора почти на 60% [51]. Кроме того, ленточный радиатор менее чувствителен к столкновениям с частицами, которые представляют большую угрозу для обычных радиаторов.
Действие обычного радиатора основано на циркуляции рабочей жидкости силовой установки или вторичной охлаждающей жидкости по системе входных и выходных камер, служащих кожухами для множества более тонких трубочек, расположенных внутри. Внешние поверхности этих маленьких трубочек и составляют как раз всю теплообменную поверхность радиатора. Камеры делают из значительно более толстого материала, чтобы выдержать все бесчисленные столкновения с частицами за весь срок службы. Трубки меньшего диаметра могут иметь более тонкие стенки, чем камеры, и в случае проникновения частицы поврежденная трубка может быть удалена из системы, чтобы предотвратить потерю жидкости. Несмотря на применение тонкостенных трубок, общая масса их составляет почти половину массы всего радиатора.
Ленточный радиатор состоит из вращающегося барабана или другой контактной поверхности, нагревающейся при работе силовой установки, и замкнутой гибкой ленты (см. рис. 5.10). Часть непрерывно движущейся ленты находится в контакте с нагретой поверхностью (барабаном) и за время контакта нагревается. После выхода из контакта с барабаном нагретый участок ленты движется в окружающем пространстве, охлаждается и снова входит в контакт с барабаном. Цикл повторяется.
Скорость, с которой лента отводит тепло от вращающегося барабана, намного превосходит скорость излучения тепла в пространство. Следовательно, площадь контакта между лентой и вращающимся барабаном должна быть много меньше, чем площадь, с которой излучается тепло. Отношение этих площадей и скорость движения позволяют регулировать процесс отвода тепла от силовой установки. Ленточный радиатор в сравнении с обычной трубчатой (змеевиковой) системой характеризуется простотой и
надежностью в эксплуатации, дает возможность избавиться от охлаждающей жидкости. Это приводит к уменьшению веса силовой установки. Расчет ленточного радиатора включает как расчет термодинамических процессов, так и расчет, связанный с определением прочности и долговечности. Для более интенсивного отвода тепла от нагретой поверхности следует увеличить скорость движения ленты, что приводит к увеличению средних значений напряжений в ней и к более быстрому накоплению циклов напряжений, тем самым к уменьшению долговечности. Поэтому выбор оптимальных режимов работы ленточного радиатора надо рассматривать как совместную термодинамическую и механическую задачу.

Рис. 5.11
Ограничимся в дальнейшем только механической частью расчета ленточного радиатора и получим уравнения равновесия ленты Для режимов работы в космосе и в земных условиях. Уравнения стационарного движения ленты получим в системе координат  вращающейся с угловой скоростью цилиндров 1 и 2 (рис. 5.11), прижимающих ленту к барабану. В относительной системе координат лента имеет продольное движение со скоростью
вращающейся с угловой скоростью цилиндров 1 и 2 (рис. 5.11), прижимающих ленту к барабану. В относительной системе координат лента имеет продольное движение со скоростью  кроме того, на ленту действует распределенная нагрузка
кроме того, на ленту действует распределенная нагрузка  Воспользуемся уравнением равновесия стержня (5.6), которое запишем во вращающейся системе координат
Воспользуемся уравнением равновесия стержня (5.6), которое запишем во вращающейся системе координат  Полагая
Полагая

и переходя к безразмерной форме записи, получим (принимая во внимание, что 

После преобразований получаем следующие уравнения равновесия ленты (опуская индекс «нуль» в безразмерных величинах):

Полученная система уравнений  является нелинейной, поэтому точно
является нелинейной, поэтому точно  решить практически невозможно. Рассмотрим один из возможных вариантов приближенного решения, использующий особенность применяемых лент — их малую изгибную жесткость. Чем меньше отношение толщины ленты к среднему радиусу кривизны при стационарном движении, тем меньше влияет на форму ее изгибная жесткость. Возможны конструкции лент из набора цепочек, которые имеют нулевую изгибную жесткость. При малой изгибной жесткости для получения безразмерных сил и моментов следует использовать другие множители, например, вместо
решить практически невозможно. Рассмотрим один из возможных вариантов приближенного решения, использующий особенность применяемых лент — их малую изгибную жесткость. Чем меньше отношение толщины ленты к среднему радиусу кривизны при стационарном движении, тем меньше влияет на форму ее изгибная жесткость. Возможны конструкции лент из набора цепочек, которые имеют нулевую изгибную жесткость. При малой изгибной жесткости для получения безразмерных сил и моментов следует использовать другие множители, например, вместо  следует брать
следует брать  . В этом случае имеем
. В этом случае имеем

Тогда  равно
равно 
При приближенном решении системы  в качестве первого приближения естественно взять предельный случай, когда изгибная жесткость ленты равна нулю, т. е. допустить, что ленту можно рассматривать как абсолютно гибкий стержень (нить). Для нити
в качестве первого приближения естественно взять предельный случай, когда изгибная жесткость ленты равна нулю, т. е. допустить, что ленту можно рассматривать как абсолютно гибкий стержень (нить). Для нити  поэтому при малой изгибной жесткости можно считать, что
поэтому при малой изгибной жесткости можно считать, что  являются малыми величинами и их можно представить в виде разложения по малому параметру
являются малыми величинами и их можно представить в виде разложения по малому параметру  При малой жесткости
При малой жесткости  ее можно считать малым параметром порядка
ее можно считать малым параметром порядка  Разложение имеет вид
Разложение имеет вид

Аналогично можно представить  .
.

Подставив выражения для  и приравняв коэффициенты при одинаковых степенях
и приравняв коэффициенты при одинаковых степенях  получим следующие системы уравнений для первого и последующих приближений (опуская индекс «нуль» в безразмерных величинах):
получим следующие системы уравнений для первого и последующих приближений (опуская индекс «нуль» в безразмерных величинах):

В системе линейных уравнений неизвестными являются  Основная трудность при решении системы
Основная трудность при решении системы  заключается в том, что задача в целом является двухточечной краевой задачей. Так как используемый при решении метод малого параметра приводит по каждому приближению (кроме первого) к линейным уравнениям, то для решения может быть использован метод прогонки, позволяющий свести двухточечную задачу к одноточечной [2].
заключается в том, что задача в целом является двухточечной краевой задачей. Так как используемый при решении метод малого параметра приводит по каждому приближению (кроме первого) к линейным уравнениям, то для решения может быть использован метод прогонки, позволяющий свести двухточечную задачу к одноточечной [2].
Рассмотрим систему нелинейных уравнений  которая представляет собой систему уравнений равновесия движущейся нити в поле центробежных сил. Ограничимся приближенным решением, полагая
которая представляет собой систему уравнений равновесия движущейся нити в поле центробежных сил. Ограничимся приближенным решением, полагая  . В этом случае находим приближенные выражения для
. В этом случае находим приближенные выражения для 

Считая, что форма леиты симметрична относительно оси х (это подтверждается экспериментальными исследованиями), поместим начало системы координат так, что при  (см. рис. 5.11).
(см. рис. 5.11).
Из уравнения для  имеем:
имеем:  откуда
откуда  Тогда неизвестное натяжение
Тогда неизвестное натяжение

Натяжение в ленте с учетом продольной скорости движения находим из (5.26):

Из ограничения на величину осевой силы  можно установить предельную скорость движения ленты (или предельную угловую скорость обкатывания прижимными валиками барабана). Например, если нельзя допустить, чтобы напряжения в ленте превышали предел текучести
можно установить предельную скорость движения ленты (или предельную угловую скорость обкатывания прижимными валиками барабана). Например, если нельзя допустить, чтобы напряжения в ленте превышали предел текучести  то из (5.37) имеем
то из (5.37) имеем

где  площадь поперечного сечения ленты.
площадь поперечного сечения ленты.
Удовлетворяя краевым условиям и для  окончательно получим
окончательно получим

Полученные выражения для  являются приближенными. Потребуем, чтобы уравнение (5.28) удовлетворялось интегрально, т. е.
являются приближенными. Потребуем, чтобы уравнение (5.28) удовлетворялось интегрально, т. е.

Подставив в (5.39) выражения для  после преобразований получаем уравнение для определения произвольной постоянной
после преобразований получаем уравнение для определения произвольной постоянной 

откуда


Рис. 5.12
Знак  найдем из условия, что при
найдем из условия, что при  рис. 5.11), что соответствует положительному значению корня. Из рис. 5.11 следует, что
рис. 5.11), что соответствует положительному значению корня. Из рис. 5.11 следует, что  Исключая из выражений для
Исключая из выражений для  параметр
параметр  получаем уравнение эллипса
получаем уравнение эллипса

Форма лецты показана пунктирной линией. Столь большое отличие в формах объясняется тем, что лецта, показанная сплошной линией, нарисована для случая с конечной изгибной жесткостью. Полученное решение можно уточнить, воспользовавшись системой уравнений  Изложенный алгоритм решения нелинейных задач статики гибких стержней, имеющих малую жесткость, может быть использован не только при решении задач, когда внешние распределенные нагрузки пропорциональны координатам, но и для любых других зависимостей
Изложенный алгоритм решения нелинейных задач статики гибких стержней, имеющих малую жесткость, может быть использован не только при решении задач, когда внешние распределенные нагрузки пропорциональны координатам, но и для любых других зависимостей  их координат и их первых производных.
их координат и их первых производных.
Рассмотрим случай работы ленточного радиатора в земных условиях, когда вращение ленты относительно оси барабана нежелательно. Для того чтобы лента не меняла своего положения в пространстве, необходимо вращать с угловой скоростью  барабан (рис. 5.12), зафиксировав положение прижимных валиков 1 и 2. В этом случае на ленту действуют другие распределенные силы, а именно сила веса и сила
барабан (рис. 5.12), зафиксировав положение прижимных валиков 1 и 2. В этом случае на ленту действуют другие распределенные силы, а именно сила веса и сила  аэродинамического сопротивления зависящая от скорости продольного движения
аэродинамического сопротивления зависящая от скорости продольного движения  Так как вектор
Так как вектор  можно представить через проекции на оси
можно представить через проекции на оси  (приведя к безразмерной форме)
(приведя к безразмерной форме)

то из уравнения (5.6) получаем следующую систему уравнений равновесия гибкой ленты с учетом сил веса и аэродинамического сопротивления (опуская индекс «нуль»):

Уравнения (5.20)-(5.22) остаются без изменения. Уравнения (5.42), (5.43) позволяют получить первые два интеграла

Для случая, когда изгибная жесткость ленты мала, можно воспользоваться методом малого параметра, как это было сделано при решении предыдущей задачи [перейдя к безразмерным величинам (5.23)]. Основная особенность данной задачи заключается в том, что считать осевое усилие (даже приближенно) постоянным по длине ленты (как это было сделано в предыдущей задаче) нельзя из-за наличия продольных аэродинамических сил, т. е. для получения первого приближения следует решать систему трех уравнений вида

Метод решения системы (5.46)-(5.48) изложен в § 24.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
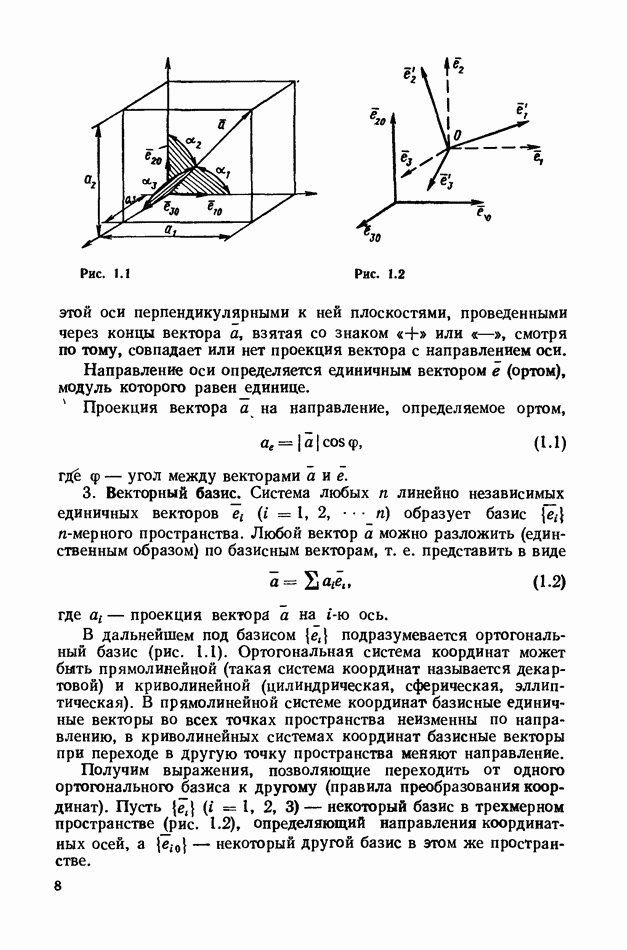
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
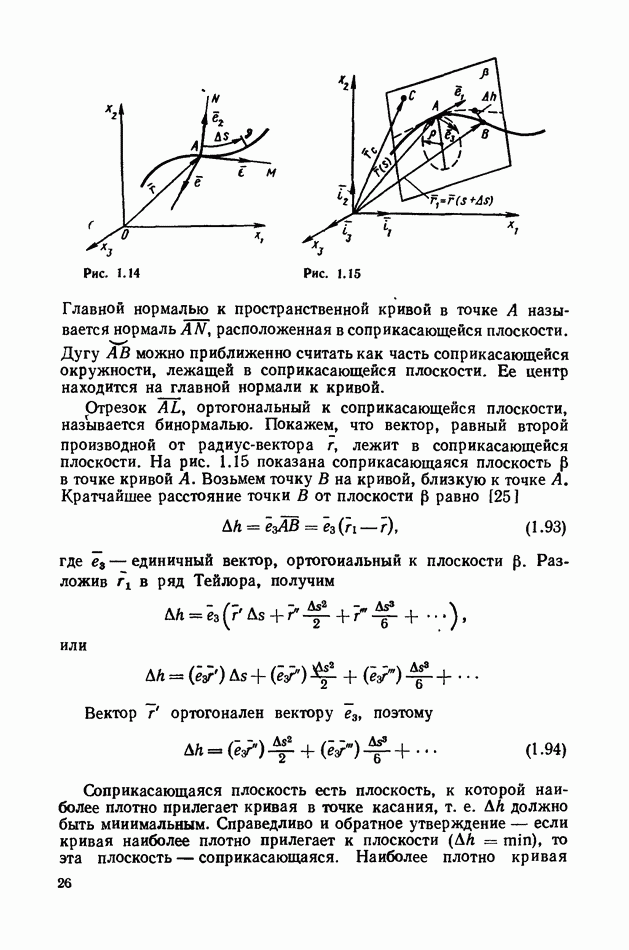
- § 3. Основные положения дифференциальной геометрии
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
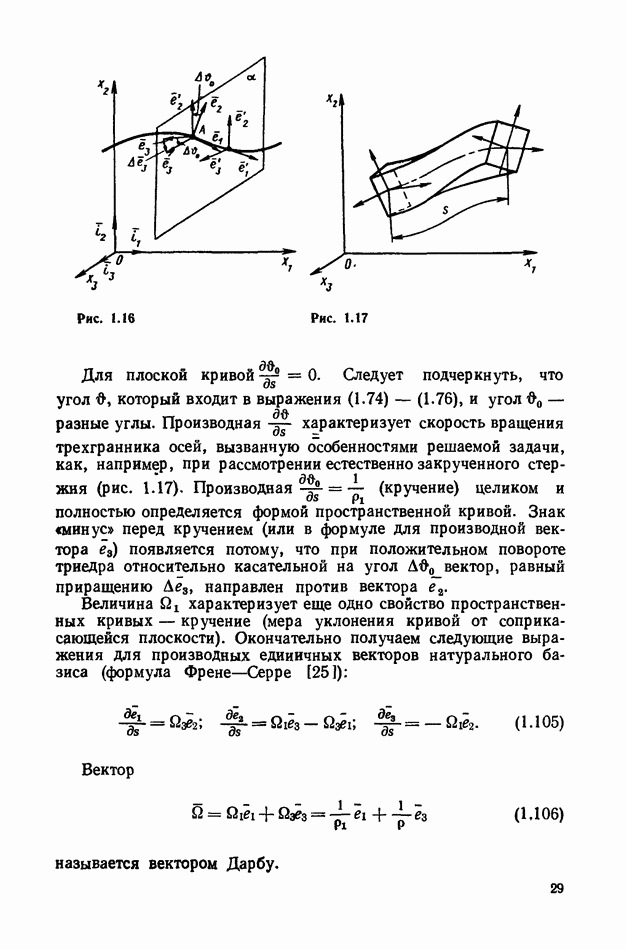
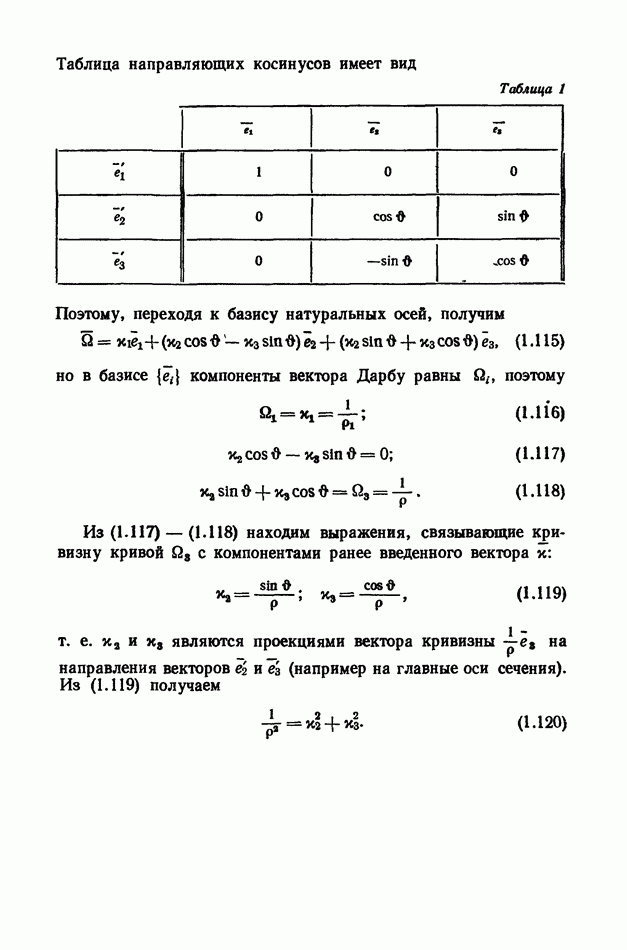
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.