| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 46. Примеры приближенного определения частот
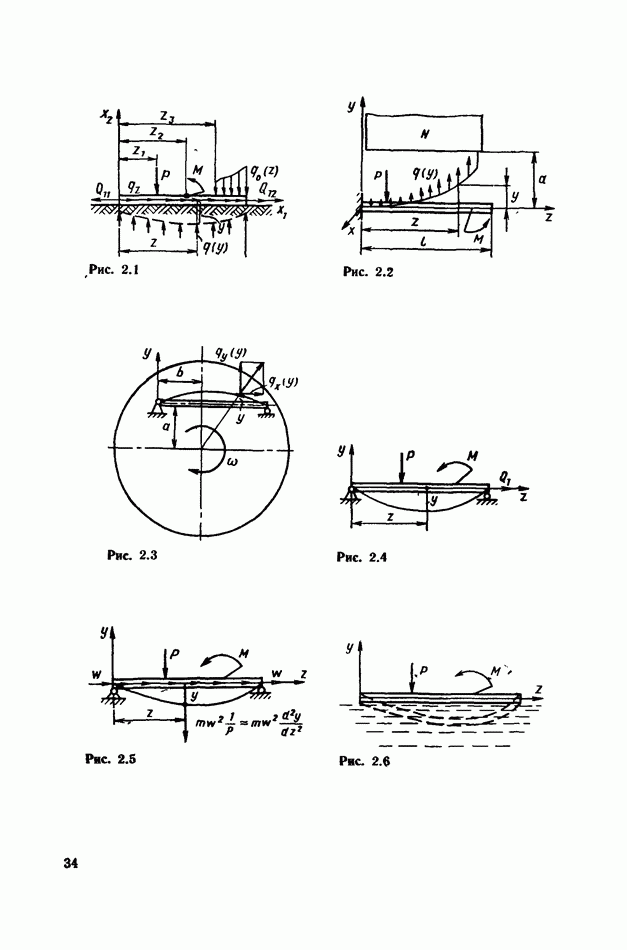
В качестве примеров приближенного определения частот рассмотрим колебания движущегося кругового стержня (см. рис. 8.11) и вращающегося кольца (рис. 8.12).
1. Колебания в плоскости осевой линии стержня.
Прямолинейный бесконечный стержень (см. рис. 8.11) был изогнут моментами  и закреплен. Участок стержня между сечениями
и закреплен. Участок стержня между сечениями  имеет постоянный радиус кривизны
имеет постоянный радиус кривизны  Затем стержень был приведен в движение с продольной скоростью до. Рассмотрим свободные колебания стержня в плоскости чертежа, пренебрегая инерцией вращения
Затем стержень был приведен в движение с продольной скоростью до. Рассмотрим свободные колебания стержня в плоскости чертежа, пренебрегая инерцией вращения 
Для определения частот, как следует из уравнений (8.155), необходимо найти начальное напряженное состояние стержня  На участок стержня между сечениями
На участок стержня между сечениями  действует равномерно распределенная нагрузка
действует равномерно распределенная нагрузка  (в безразмерной форме).
(в безразмерной форме).

Рис. 8.12
Решая статическую задачу, можно получить значения  (вызванные инерционными силами
(вызванные инерционными силами 

поэтому  и уравнения (8.155), (8.156) принимают вид
и уравнения (8.155), (8.156) принимают вид

Последовательно исключая из системы уравнений  [как это было сделано при выводе уравнения
[как это было сделано при выводе уравнения  получим следующее уравнение относительно
получим следующее уравнение относительно 

Воспользуемся методом Галеркина при решении уравнения (8.169), предварительно определив функции  удовлетворяющие краевым условиям задачи.
удовлетворяющие краевым условиям задачи.
Берем приближенное выражение для функции  в виде степенного ряда
в виде степенного ряда

Так как стержень нерастяжим и длина его между сечениями  не изменяется, то первая форма колебаний имеет вид, показанный на рис. 8.11, б штрихпунктирной линией 1. Однако для получения приближенных функций, характеризующих формы колебаний, удобнее предположить, что возможна и нулевая форма. Последнюю в дальнейшем можно не использовать, так как она возможна только для растяжимого стержня. Введем для этой функции обозначение
не изменяется, то первая форма колебаний имеет вид, показанный на рис. 8.11, б штрихпунктирной линией 1. Однако для получения приближенных функций, характеризующих формы колебаний, удобнее предположить, что возможна и нулевая форма. Последнюю в дальнейшем можно не использовать, так как она возможна только для растяжимого стержня. Введем для этой функции обозначение 
функция  должна удовлетворять условиям:
должна удовлетворять условиям:  Из уравнения (8.168) следует (так как
Из уравнения (8.168) следует (так как 

Наименьшее необходимое число слагаемых ряда (8.170), при которых функция  удовлетворяет всем однородным краевым условиям задачи, равно шести, т. е.
удовлетворяет всем однородным краевым условиям задачи, равно шести, т. е.

Из условий  следует, что
следует, что 
Выполнение остальных условий приводит к системе уравнений

Из системы (8.172) получаем

Для получаем выраженйе с двумя произвольными параметрами  (один из которых, например
(один из которых, например  равен единице):
равен единице):

Находим функцию из (8.167):

Так как при  то
то  Оставшийся произвольный параметр
Оставшийся произвольный параметр  найдем из условия: при
найдем из условия: при 

Из (8.175) получаем 
Зная  и находим
и находим

В результате имеем три функции  и удовлетворяющие всем краевым условиям задачи. Функции и приближенно описывают первую форму колебаний.
и удовлетворяющие всем краевым условиям задачи. Функции и приближенно описывают первую форму колебаний.
Функцию, приближенно характеризующую первую форму колебаний, ищем в форме ряда (8.170) [с числом слагаемых на единицу больше, чем в (8.171)] со своими неопределенными коэффициентами 

Функция  должна удовлетворять краевым условиям:
должна удовлетворять краевым условиям:  иго
иго  поэтому получаем
поэтому получаем

Полагая  получим
получим

Для определения оставшихся двух неизвестных коэффициентов  необходимо иметь два дополнительных условия. Первое условие, связывающее эти коэффициенты, получим при
необходимо иметь два дополнительных условия. Первое условие, связывающее эти коэффициенты, получим при

Второе условие найдем, потребовав, чтобы векторы, характеризующие формы колебаний  удовлетворяли условию ортогональности
удовлетворяли условию ортогональности

где

В развернутом виде из (8.179) получаем

На получающиеся приближенные значения компонент векторов  можно наложить менее жесткое требование, а именно, чтобы ортогональны были только компоненты в этом случае условие (8.180) принимает вид
можно наложить менее жесткое требование, а именно, чтобы ортогональны были только компоненты в этом случае условие (8.180) принимает вид

Из уравнений (8.178) и (8.180) находим  Приближенное выражение для второй формы колебаний найдем, приняв
Приближенное выражение для второй формы колебаний найдем, приняв

Функция (8.181) содержит три произвольных коэффициента  которые находят из трех условий:
которые находят из трех условий:

Если требовать только ортогональность компонент  то получаем систему уравнений для определения
то получаем систему уравнений для определения  :
:

Считая, что функции  известны, ищем решение уравнения (8.169), воспользовавшись методом Галеркина и полагая
известны, ищем решение уравнения (8.169), воспользовавшись методом Галеркина и полагая

В соответствии с методом Галеркина из соотношения 1

получаем систему уравнений относительно функций 

где

Так, например, для двух слагаемых ряда (8.185) получаем систему уравнений

Полагая  получим для определения
получим для определения  уравнение
уравнение

Рассмотрим более детально свойства коэффициентов  от которых зависят значения
от которых зависят значения 

Интегрируя второе слагаемое в правой части выражения (8.190), получаем

Так как функции  и их первые производные удовлетворяют однородным краевым условиям, то окончательно получаем
и их первые производные удовлетворяют однородным краевым условиям, то окончательно получаем

Из полученного выражения (8.192) следует

Рассмотрим коэффициенты 

Интегрируя слагаемые в правой части (8.194) по частям, можно показать, что

поэтому коэффициенты  удовлетворяют условию
удовлетворяют условию

После преобразований можно получить следующее выражение:

Из (8.195) следует, что при 

Интегрируя правую часть выражения для коэффициентов  по частям, можно показать, что эти коэффициенты удовлетворяют условиям
по частям, можно показать, что эти коэффициенты удовлетворяют условиям

В соответствии с установленными свойствами коэффициентов определитель (8.189) принимает вид

Раскрыв определитель, получим

или

где

Покажем, что коэффициенты  больше нуля (для случая, когда функции и ортогональны):
больше нуля (для случая, когда функции и ортогональны):

Для того чтобы  достаточно выполнение условия
достаточно выполнение условия

Полученное условие (8.202) есть неравенство Коши-Буняковского, т. е. всегда выполняется, поэтому  Аналогично можно показать, что и
Аналогично можно показать, что и 
Из (8.200) находим значения  (предполагая, что и
(предполагая, что и 

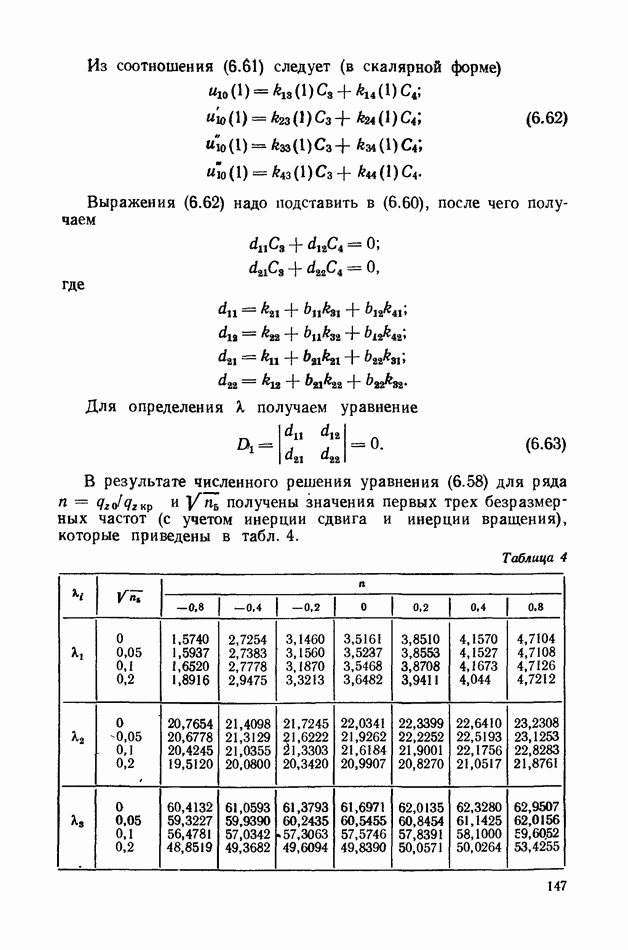
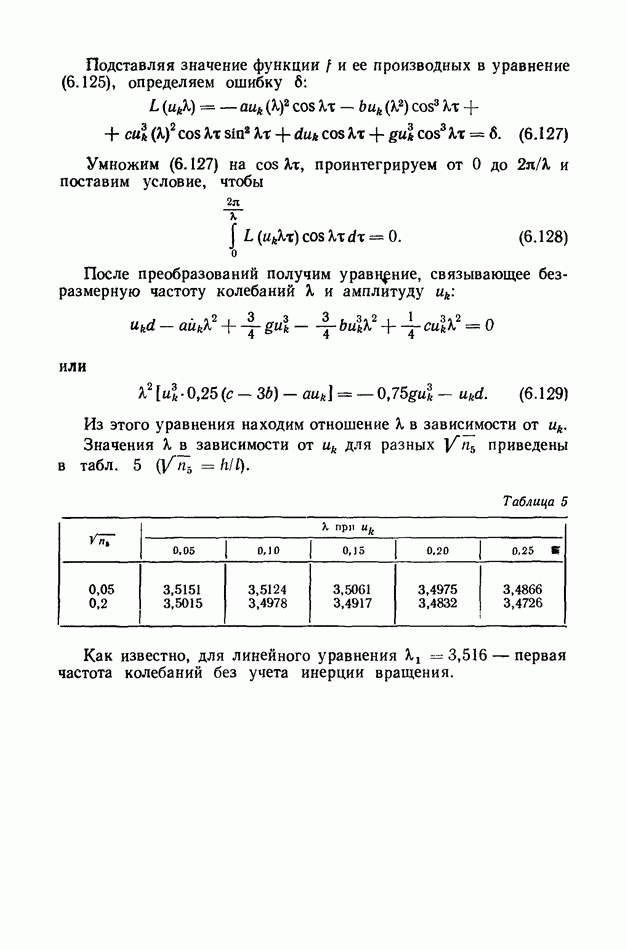
Безразмерные частоты

Как следует из решения, для того чтобы установить влияние скорости продольного движения на частоты колебаний стержня, надо искать решение уравнения (8.169), используя две приближенные формы колебаний. Если ограничиться только одной формой колебаний, то, например, первая частота  т. е. от скорости
т. е. от скорости  не зависит.
не зависит.
Из формул (8.203) следует, что при  т. е. вторая частота при больших
т. е. вторая частота при больших  является грубой. Для уточнения значения второй частоты следует брать три слагаемых ряда (8.185). При этом получающиеся две первые частоты, как правило, дают хорошее приближение к действительным значениям, т. е. для получения приближенного значения
является грубой. Для уточнения значения второй частоты следует брать три слагаемых ряда (8.185). При этом получающиеся две первые частоты, как правило, дают хорошее приближение к действительным значениям, т. е. для получения приближенного значения  частот надо брать
частот надо брать  слагаемых ряда (8.185).
слагаемых ряда (8.185).
2. Рассмотрим колебания в плоскости стержня (см. рис. 8.11,б), пренебрегая инерцией вращения. После преобразований аналогичных выводу уравнения (8.169) можно из системы (8.143)-(8.154) получить уравнение относительно 

При приближенном решении уравнения (8.204) воспользуемся методом, излаженным в п. 1.
Возьмем в качестве функции, характеризующей первую форму колебаний, степенную функцию вида

Функции должны удовлетворять краевым условиям:  поэтому
поэтому 
Полагая  находим коэффициенты
находим коэффициенты  поэтому
поэтому

Получим функцию, характеризующую вторую форму колебаний:

Для определения коэффициентов  имеем систему уравнений
имеем систему уравнений

откуда

Коэффициент  найдем из условия ортогональности функций
найдем из условия ортогональности функций  или после вычислений получаем
или после вычислений получаем  .
.
Функция  имеет вид
имеет вид

Решение уравнения (8.204), ограничившись двумя формами колебаний, ищем в виде

Используя метод Галеркина, получаем два уравнения: 1

из которых следуют уравнения относительно функций и 

где
(см. скан)
Характеристическое уравнение системы (8.211) аналогично уравнению (8.200), а зависимость безразмерных частот  от коэффициентов системы (8.211) аналогична выражениям (8.203).
от коэффициентов системы (8.211) аналогична выражениям (8.203).
3. Рассмотрим колебания вращающегося кольца в плоскости чертежа (рис. 8.12). Уравнение малых колебаний кругового стержня в плоскости было получено в п. 1 (уравнение 8.169). В этом случае функции, характеризующие формы колебаний, должны удовлетворять условию периодичности, поэтому ищем решение, полагая

Воспользовавшись методом Галеркина, получаем систему уравнений

где

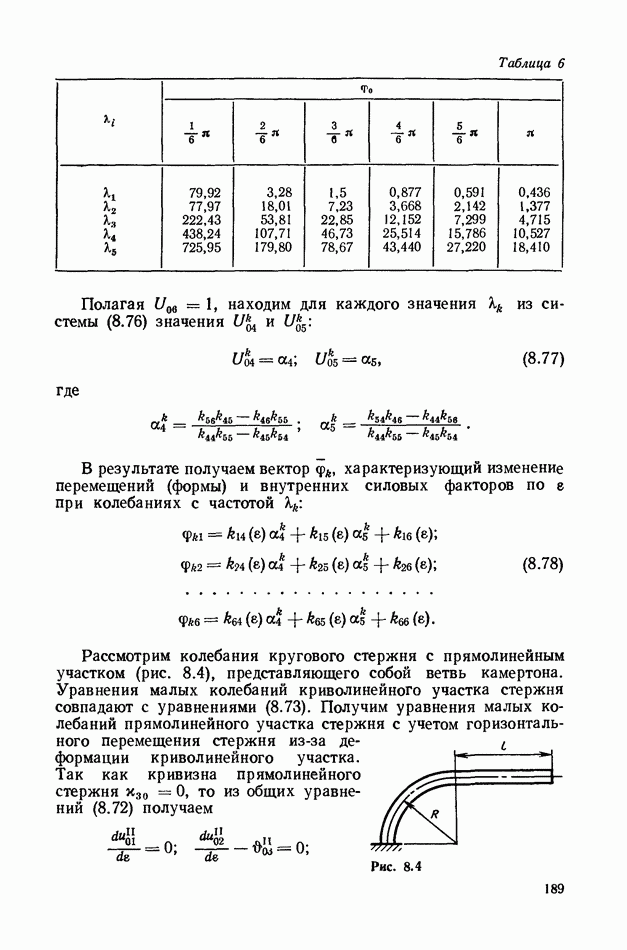
Безразмерные частоты

т. е. не зависят от скорости  .
.

Рис. 8.13
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
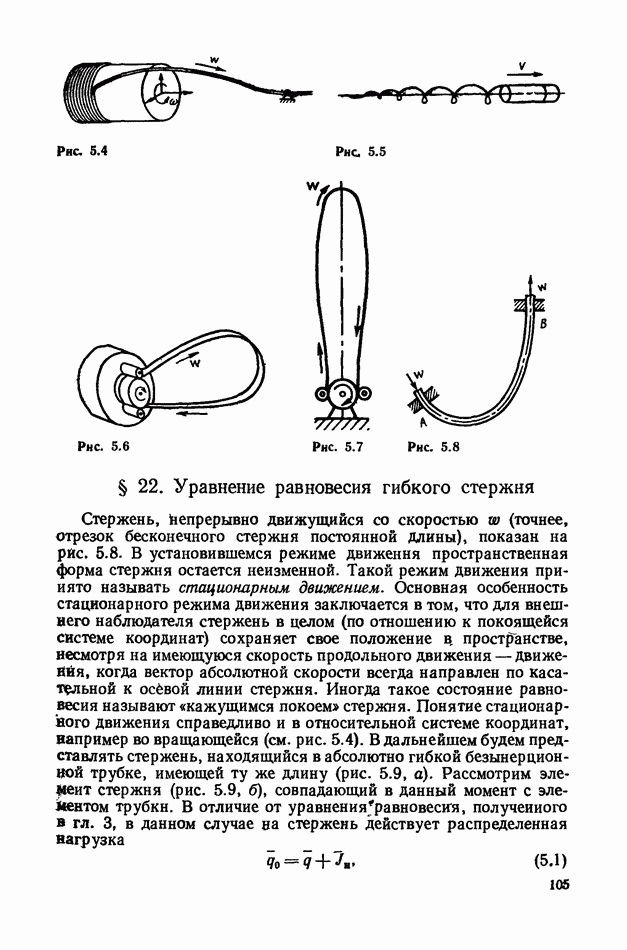
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.