| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
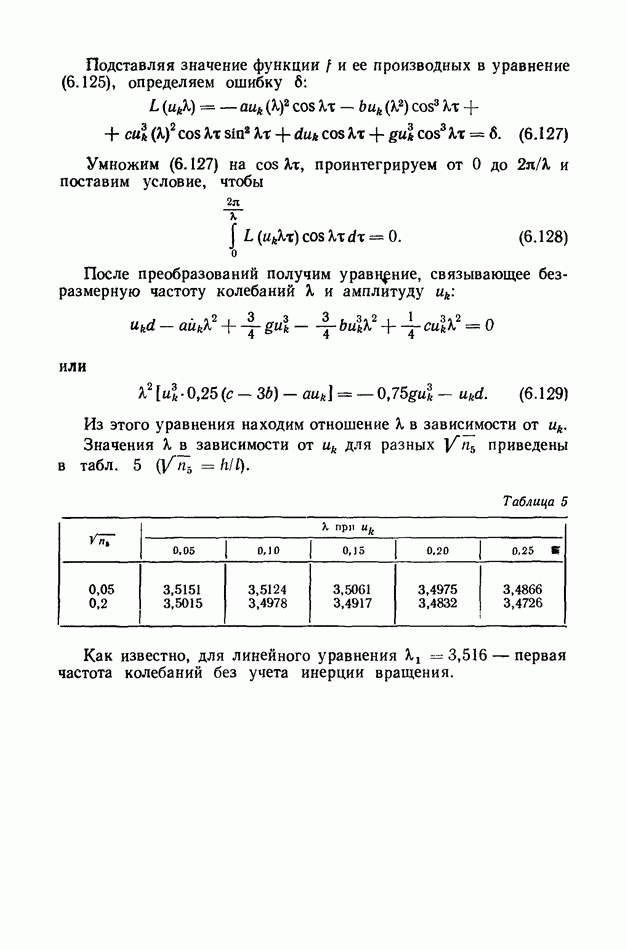
§ 28. Малые колебания прямолинейных стержней
При колебаниях стержней или в более общем случае — движении прогибы стержня и внутренние силовые факторы зависят не только от координаты  (или безразмерной координаты в), но и от времени
(или безразмерной координаты в), но и от времени  поэтому следует перейти к частным производным, т. е. расшифровывая приращения функции (например, прогиба
поэтому следует перейти к частным производным, т. е. расшифровывая приращения функции (например, прогиба  связанного с переходом от сечения с координатой
связанного с переходом от сечения с координатой  в соседнее сечение с координатой
в соседнее сечение с координатой  полагать
полагать

В данной главе рассмотрен наиболее простой случай колебаний прямолинейного стержня, когда движение стержня происходит в плоскости чертежа (рис. 6.9, а).
1. Уравнение малых колебаний гибкого стержня.
Статика прямолинейных гибких стержней рассматривалась в гл. 2 и было получено основное уравнение равновесия прямолинейного стержня (2.8) в предположении, что прогибы стержня являются малыми. При колебаниях стержня на его элемент действует (при малых прогибах) сила инерции (рис. 6.9, б)

В случае малых колебаний можно считать, что элемент стержня смещается только по нормали, т. е. координата  элемента от времени не зависит, поэтому при описании движения стержня можно использовать переменные Лагранжа (в рассматриваемом случае
элемента от времени не зависит, поэтому при описании движения стержня можно использовать переменные Лагранжа (в рассматриваемом случае  и для распределенной силы инерции получаем
и для распределенной силы инерции получаем

Перейдем к безразмерным величинам, полагая  где
где  жесткость в начале координат. Массу единицы длины можно выразить через массу единицы длины стержня в начале координат
жесткость в начале координат. Массу единицы длины можно выразить через массу единицы длины стержня в начале координат  и безразмерную функцию
и безразмерную функцию  Безразмерная распределенная нагрузка
Безразмерная распределенная нагрузка  поэтому после преобразований получаем
поэтому после преобразований получаем


Рис. 6.9
Движение стержня может быть вызвано как отклонением от состояния равновесия, так и приложенными к стержню силами, зависящими отвремени, т. е. в общем случае правая часть уравнения (2.8) (приведенного к безразмерной форме) может быть представлена в виде

поэтому уравнение малых колебаний прямолинейного стержня относительно состояния равновесия имеет вид

где  соответственно статическая и динамическая нагрузки приложенные к стержню. Уравнение (6.6) является линейным дифференциальным уравнением в частных производных.
соответственно статическая и динамическая нагрузки приложенные к стержню. Уравнение (6.6) является линейным дифференциальным уравнением в частных производных.
Если под  понимают полный безразмерный прогиб стержня, то его можно представить в виде
понимают полный безразмерный прогиб стержня, то его можно представить в виде  где
где  прогиб, вызванный статически приложенными силами и — динамический прогиб, вызванный силами
прогиб, вызванный статически приложенными силами и — динамический прогиб, вызванный силами  или, при свободных колебаниях, отклонением от состояния равновесия.
или, при свободных колебаниях, отклонением от состояния равновесия.
Подставив выражение для  в (6.6), получим
в (6.6), получим

т. е. для определения  получили два независимых уравнения, поэтому при исследовании малых колебаний можно рассматривать только динамическую составляющую прогиба.
получили два независимых уравнения, поэтому при исследовании малых колебаний можно рассматривать только динамическую составляющую прогиба.
Уравнение (6.8) не учитывает инерцию вращения элемента стержня [показанный на рис. 6.9, б пунктиром инерционный момент  считается равным нулю] и инерцию сдвига, о чем более подробно будет сказано в § 36. Для численных методов определения частот и форм колебаний уравнение (6.8) удобнее представить в виде системы уравнений первого порядка (относительно производной по в), введя следующие функции:
считается равным нулю] и инерцию сдвига, о чем более подробно будет сказано в § 36. Для численных методов определения частот и форм колебаний уравнение (6.8) удобнее представить в виде системы уравнений первого порядка (относительно производной по в), введя следующие функции:

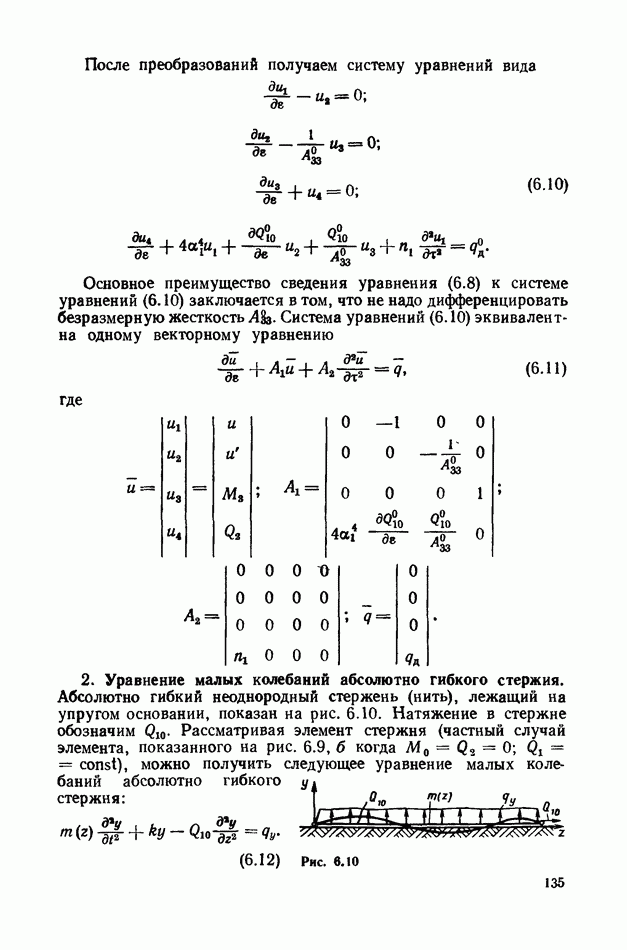
После преобразований получаем систему уравнений вида

Основное преимущество сведения уравнения (6.8) к системе уравнений (6.10) заключается в том, что не надо дифференцировать безразмерную жесткость  Система уравнений (6.10) эквивалентна одному векторному уравнению
Система уравнений (6.10) эквивалентна одному векторному уравнению

где

2. Уравнение малых колебаний абсолютно гибкого стержня.
Абсолютно гибкий неоднородный стержень (нить), лежащий на упругом основании, показан на рис. 6.10. Натяжение в стержне обозначим  Рассматривая элемент стержня (частный случай элемента, показанного на рис. 6.9, б когда
Рассматривая элемент стержня (частный случай элемента, показанного на рис. 6.9, б когда  можно получить следующее уравнение малых колебаний абсолютно гибкого стержня:
можно получить следующее уравнение малых колебаний абсолютно гибкого стержня:


Рис. 8.10
Полагая  получим (6.12) в безразмерной форме:
получим (6.12) в безразмерной форме:

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
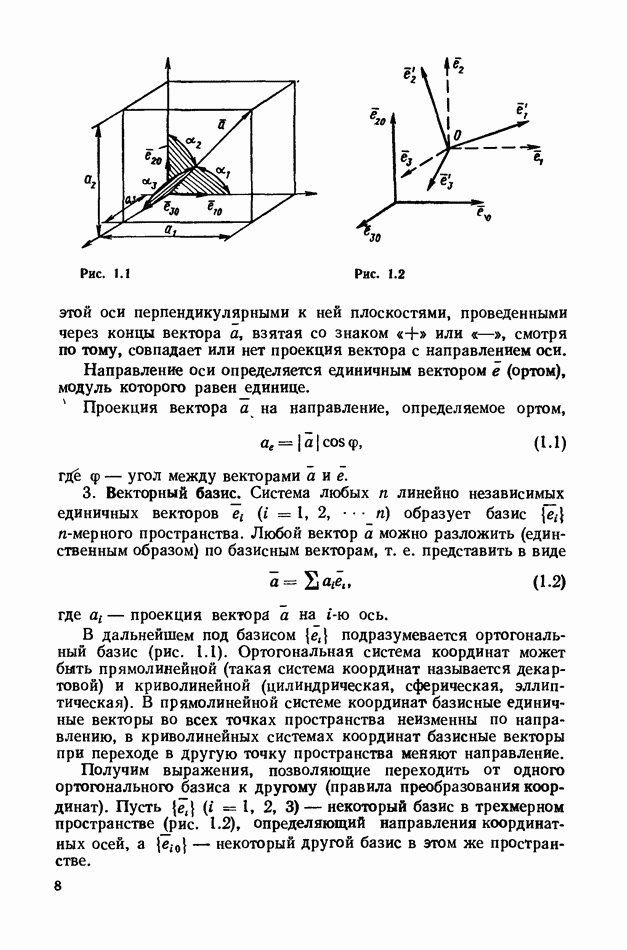
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
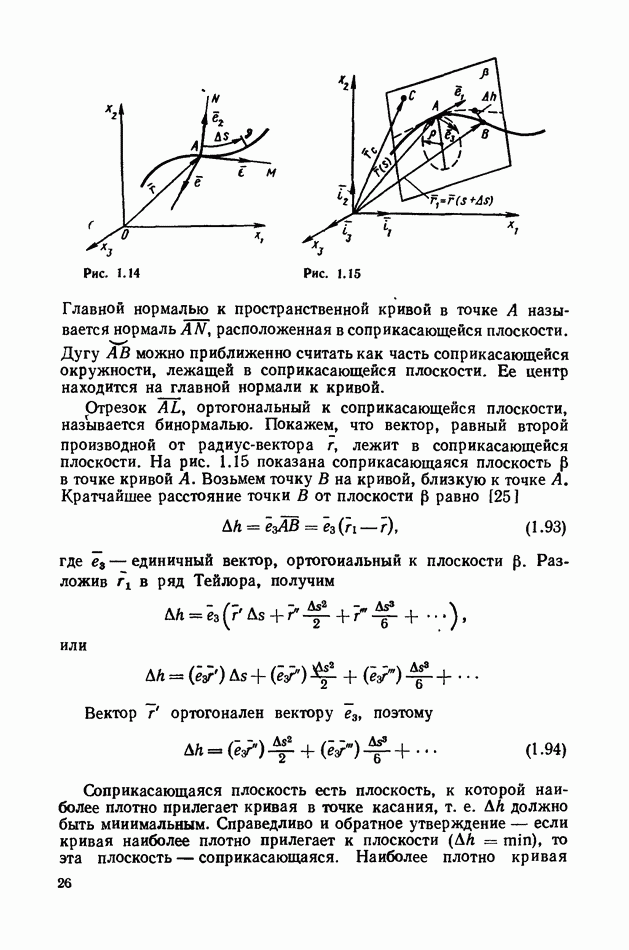
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
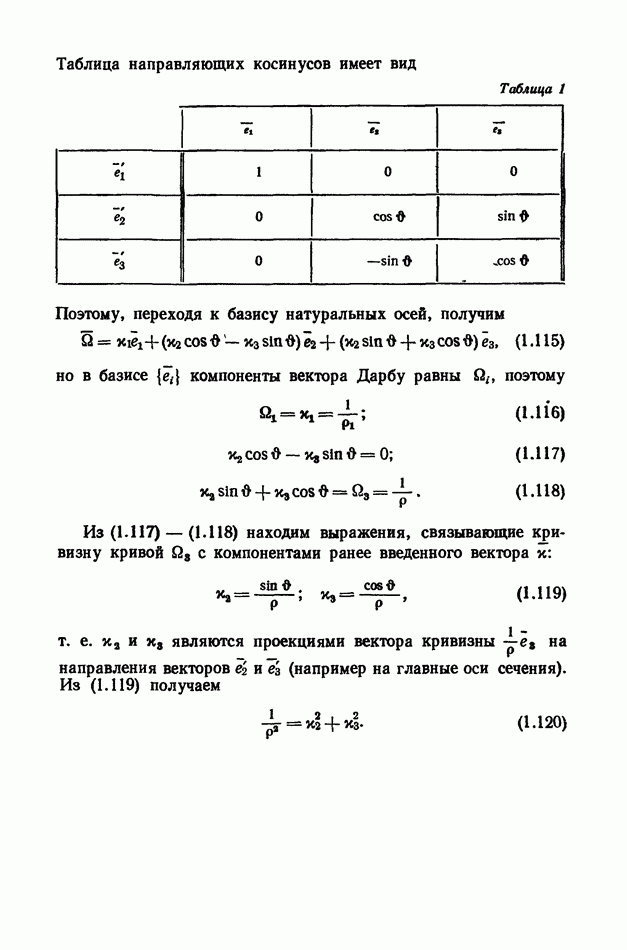
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
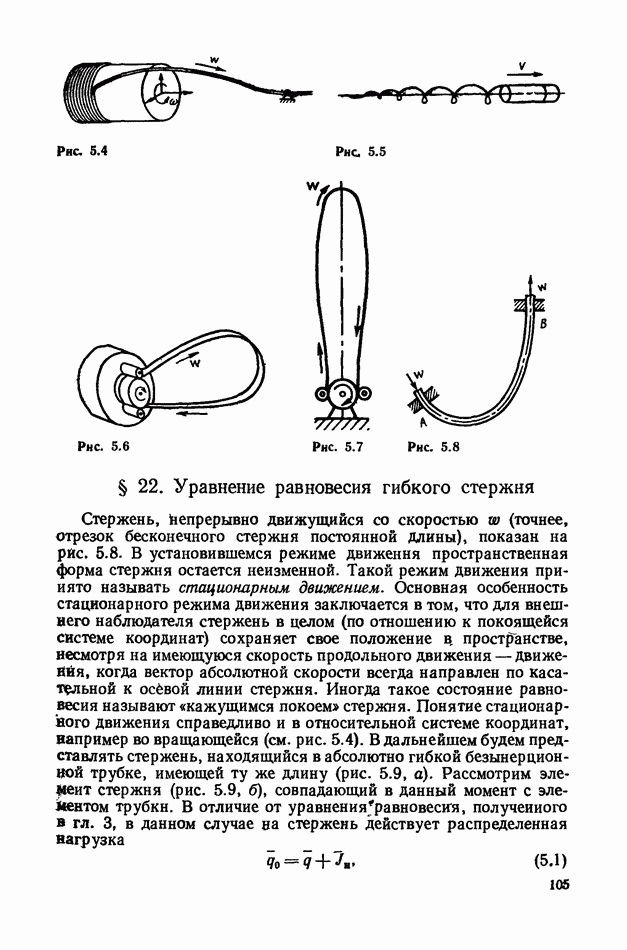
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.