| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Приближенные методы решения задач
Многие задачи механики стержней, с которыми приходится сталкиваться инженеру-расчетчику, не поддаются точному решению. К таким задачам относятся, например, задачи статики и динамики стержней с переменным сечением, нелинейные задачи с нелинейными краевыми условиями и т. д. Для решения подобных задач используют приближенные методы как численные,
так и аналитические, или методы, представляющие их комбинацию. Часто оказывается, что полученные точные решения из-за чрезвычайной сложности записи являются практически бесполезными для математической и физической интерпретации или численных расчетов, т. е. для получения нужной информации прибегают к упрощениям или аппроксимациям.
Среди приближенных методов наибольшее распространение получили методы, использующие вариационные принципы, и методы возмущений (асимптотических разложений) по большим или малым значениям параметра или координаты. Полученные в предыдущих параграфах уравнения равновесия стержней и нитей, как правило, являются нелинейными и в общем случае нечмогут быть решены в аналитической форме за исключением частных случаев. При решении уравнений равновесия обычно используют или численные методы, или приближенные, использующие вариационные принципы механики. При численных методах решения задач усложняются тем, что все задачи механики стержней относятся к двухточечным краевым задачам.
Рассмотрим задачу о нагруженной балке, лежащей на упругом основании [уравнение (2.9)]. Для численного решения этой системы уравнений необходимо знать о (0), однако компонент вектора  неизвестен.
неизвестен.
Поэтому при численном счете задаются неизвестными компонентами  каждый раз решая систему уравнений, пока не найдут значения
каждый раз решая систему уравнений, пока не найдут значения  при которых вектор
при которых вектор  удовлетворяет краевым условиям на правом конце. Несмотря на кажущуюся сложность этих методов, их решение на ЭВМ довольно эффективно. Для сокращения времени счета используют методы целенаправленного поиска начальных значений у, (0), дающих решение задачи. Если используют уравнения в безразмерной форме, то полученное решение охватывает целый класс родственных задач.
удовлетворяет краевым условиям на правом конце. Несмотря на кажущуюся сложность этих методов, их решение на ЭВМ довольно эффективно. Для сокращения времени счета используют методы целенаправленного поиска начальных значений у, (0), дающих решение задачи. Если используют уравнения в безразмерной форме, то полученное решение охватывает целый класс родственных задач.
Следует подчеркнуть, что классическое решение дифференциальных уравнений равновесия стержня или нити (представление решения в квадратурах), как правило, практически мало полезно, так как все равно, получение числовых результатов требует применения численных методов для выражений анализа решений. Это может быть гораздо сложнее, чем численное решение исходных уравнений.
Уравнения равновесия стержней и нитей можно получить  из общи вариационных принципов механики, поэтому их можно использовать и для приближенных методов расчета. Прежде чем изложить методы приближенных решений, напомним положения вариационного исчисления и основные вариационные принципы, используемые в механике стержней и нитей.
из общи вариационных принципов механики, поэтому их можно использовать и для приближенных методов расчета. Прежде чем изложить методы приближенных решений, напомним положения вариационного исчисления и основные вариационные принципы, используемые в механике стержней и нитей.
1. Основные положения вариационного исчисления. В инженерной практике наряду с задачами определения экстремальных
значений функций  возникает необходимость определения экстремальных значений выражений вида
возникает необходимость определения экстремальных значений выражений вида

которые называются функционалами. Задачей вариационного исчисления является определение функций, например функции у, которые сообщают экстремальные значения функционалам.
Исследуем на экстремум простейший функционал (2.64) для случая, когда граничные точки для допустимых функций у фиксированы:  Допустимыми функциями называются непрерывные функции (с непрерывными производными), принимающие известные значения на концах интервала интегрирования. Необходимым условием экстремума является обращение в нуль первой вариации функционала. Для получения первой вариации функционала перейдем от функции у к близкой к ней, полагая
Допустимыми функциями называются непрерывные функции (с непрерывными производными), принимающие известные значения на концах интервала интегрирования. Необходимым условием экстремума является обращение в нуль первой вариации функционала. Для получения первой вариации функционала перейдем от функции у к близкой к ней, полагая

где а — малое число;  — произвольная функция (вариация функции
— произвольная функция (вариация функции  которая обращается в нуль при
которая обращается в нуль при  Приращение функционала
Приращение функционала

Разложив первое слагаемое в правой части в ряд Тейлора по степеням а, получим (ограничившись линейной частью разложения)

или

Интегрируя  по частям, получим
по частям, получим

Подставив (2.68) в выражение для первой вариации функционала (2.67), имеем

Вариация  является произвольной функцией, не равной
является произвольной функцией, не равной  дественно нулю, поэтому условие (2.69) будет выполняться, если положить
дественно нулю, поэтому условие (2.69) будет выполняться, если положить

Полученное уравнение (2.70) есть уравнение Эйлера. В развернутом виде имеем

Если функция  не зависит от
не зависит от  уравнение Эйлера имеет первый интеграл. В этом случае из (2.71) получим
уравнение Эйлера имеет первый интеграл. В этом случае из (2.71) получим

Умножив (2.72) на у, получаем производную от выражения

поэтому

Если функционал

зависит от  то, проделав аналогичные выкладки, получим следующее уравнение для определения у:
то, проделав аналогичные выкладки, получим следующее уравнение для определения у:

Функционал может зависеть от двух и более неизвестных функций, например

Чтобы функции  доставляли экстремум функционалу (2.77), необходимо, чтобы функции
доставляли экстремум функционалу (2.77), необходимо, чтобы функции  удовлетворяли системе уравнений вида
удовлетворяли системе уравнений вида

Часто встречаются задачи, в которых на искомые функции у накладываются дополнительные ограничения. Такая задача называется задачей на условный экстремум, и она формулируется следующим образом: требуется найти функцию у, которая сообщает экстремум функционалу

при условии, что функция у удовлетворяет дополнительному условию

Ограничения, которым должна удовлетворять функция (2.80), могут от производных функций у и не зависеть. При решении рассматривают функционал вида

где к  множитель Лагранжа, и ищут экстремум функционала
множитель Лагранжа, и ищут экстремум функционала

Уравнение Эйлера имеет вид

или

Уравнение (2.84) совместно с уравнением (2.80) дают систему двух уравнений для определения неизвестных функций  . В случае, когда имеется ряд ограничений
. В случае, когда имеется ряд ограничений  рассматривается функция вида
рассматривается функция вида

где  — множители Лагранжа.
— множители Лагранжа.
Если ограничения на функцию у заданы в интегральной форме вида

то такие задачи называются изопериметрическими. Требуется найти экстремум функционала

при условии

Изопериметрическую задачу можно свести к общей задаче на условный экстремум, полагая

Дифференцируя (2.89) по получим

Требуется найти функции  доставляющие экстремум функционалу (2.87) при наличии уравнения связи (2.90). Воспользовавшись множителем Лагранжа, имеем
доставляющие экстремум функционалу (2.87) при наличии уравнения связи (2.90). Воспользовавшись множителем Лагранжа, имеем

Так как функция  зависит от двух неизвестных функций
зависит от двух неизвестных функций  то для их определения получаем систему уравнений
то для их определения получаем систему уравнений

или


Рис. 2.15
Из уравнения (2.94) следует, что  для изопериметрической задачи множитель Лагранжа есть постоянное число.
для изопериметрической задачи множитель Лагранжа есть постоянное число.
Уравнение (2.93) и условие (2.88) дают возможность определить функцию у и неизвестный множитель Лагранжа 
Рассмотрим следующий пример. Нить заданной длины, которая находится в равновесии в поле тяжести, показана на рис. 2.15. Форма, которую нить имеет в состоянии равновесия (по сравнению с другими возможными формами, показанными пунктирными линиями), должна удовлетворять экстремальному условию: координата у о (центр тяжести) для истинной формы равновесия имеет наименьшее значение (что эквивалентно условию минимума потенциальной энергии нити). Координата центра тяжести

Условие минимума  эквивалентно условию минимума функционала
эквивалентно условию минимума функционала

при дополнительном ограничении

Воспользовавшись множителем Лагранжа, получаем следующий функционал:

Уравнение Эйлера для функционала  имеет первый интеграл
имеет первый интеграл

или

Из (2.99) получаем

Уравнение (2.100) можно проинтегрировать, положив  имеем
имеем

Продифференцировав (2.101) по  получим
получим

Из (2.102) получаем  После преобразований
После преобразований

Из уравнения (2.103) следует, что нить в поле тяжести в состоянии равновесия имеет форму, которая описывается цепной линией.
Для определения трех постоянных величин  и К имеем следующие три уравнения:
и К имеем следующие три уравнения:

Подставив в (2.106) выражение для у, получим

Из уравнений (2.104) и (2.105) можно исключить 

Возводим уравнения (2.107) и (2.108) в квадрат и вычитаем одно из другого:

Из (2.109) после преобразований получаем

Уравнение (2.110) зависит только от Определив  находим из (2.107) или
находим из (2.107) или  а из (2.104) или (2.105)
а из (2.104) или (2.105)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
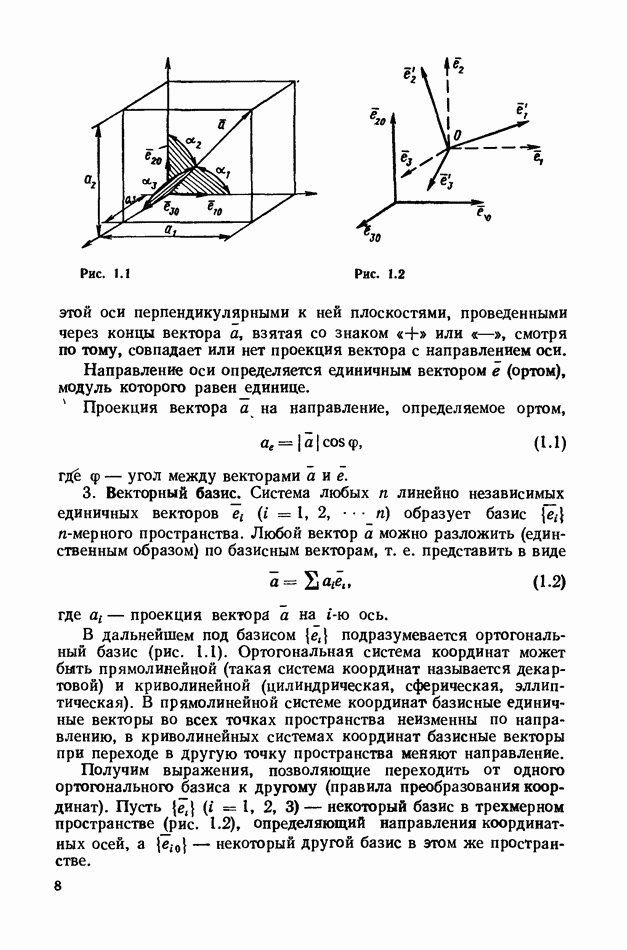
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
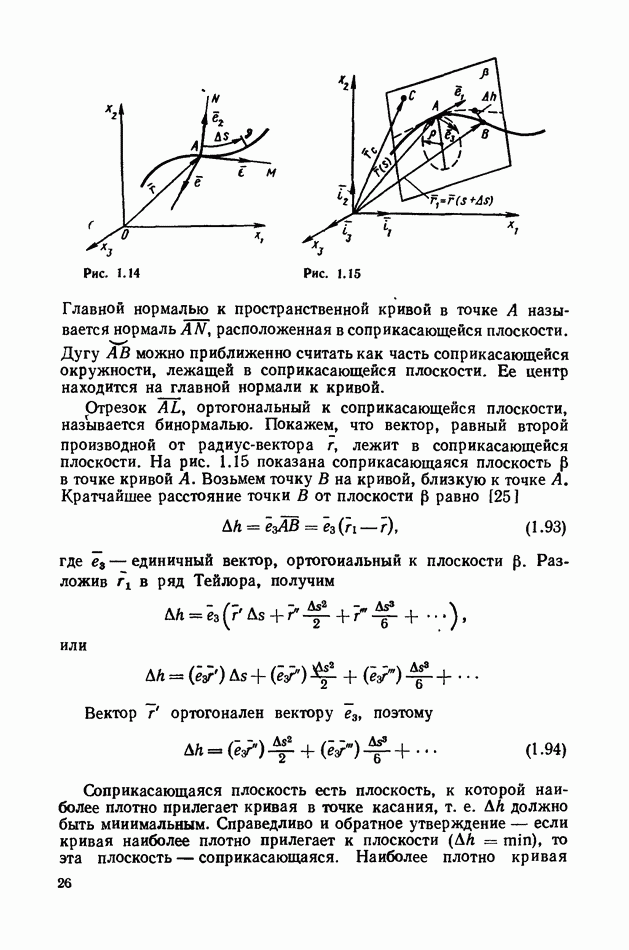
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
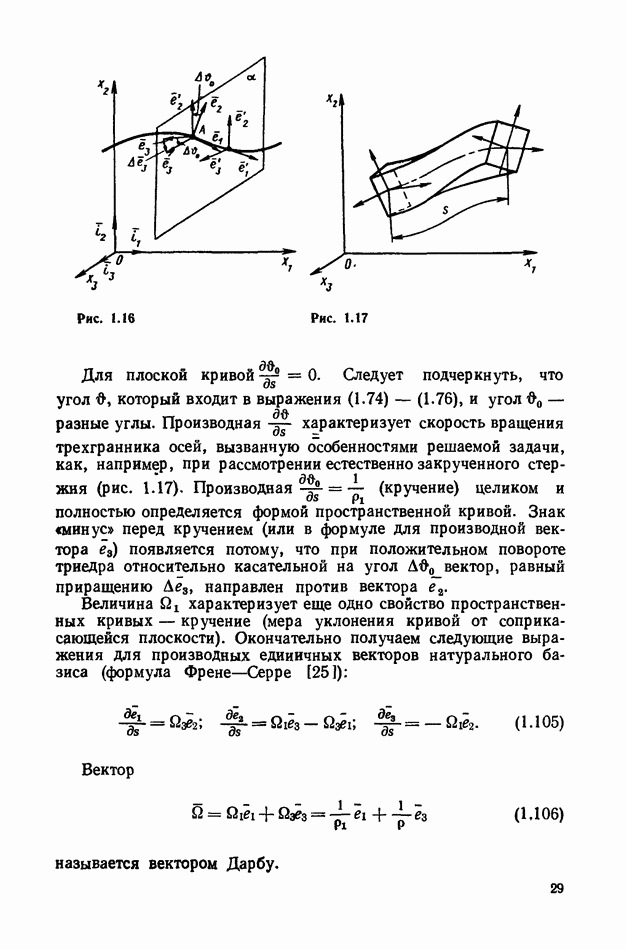
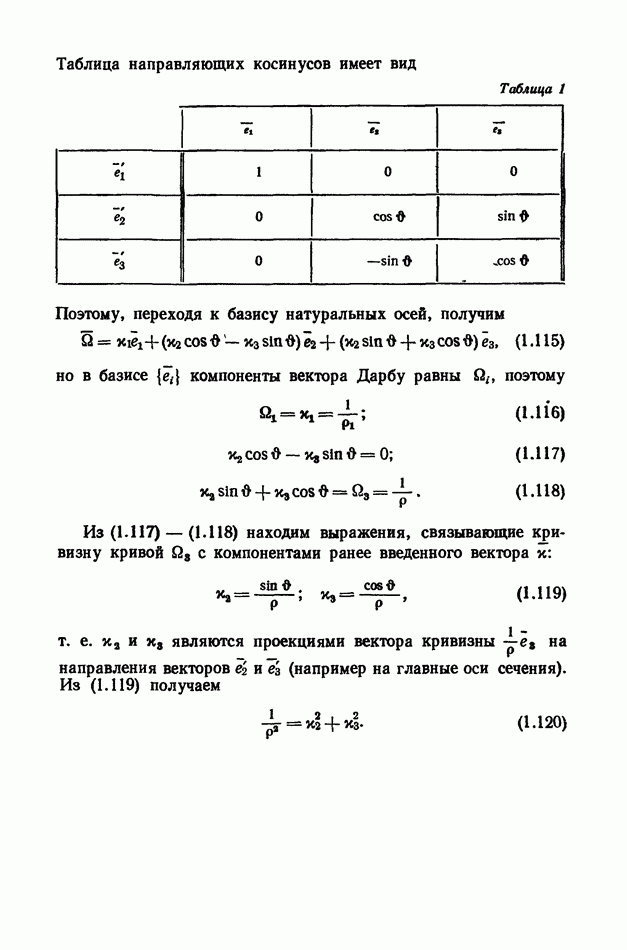
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
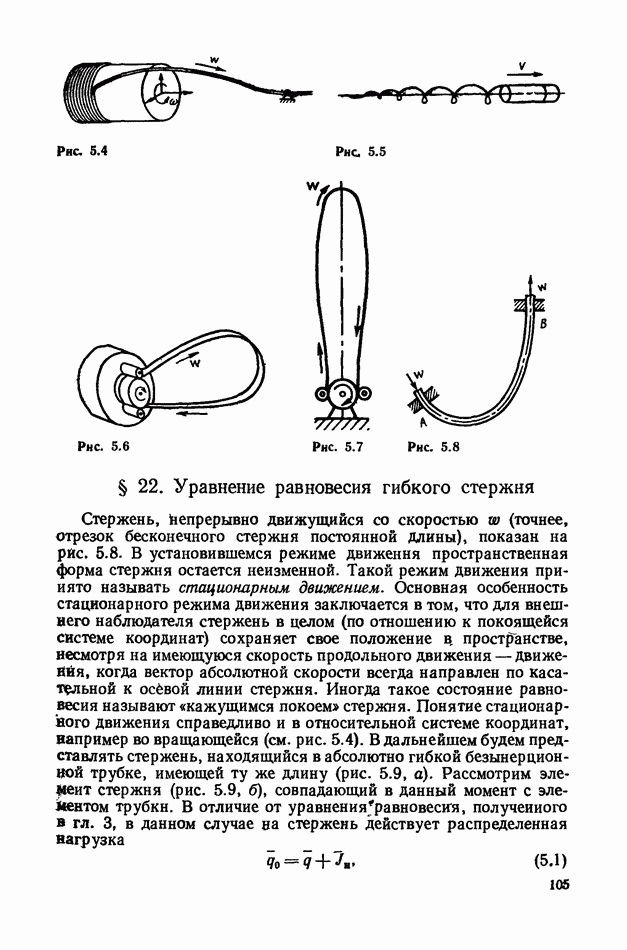
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.