| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 29. Численные методы определения частот и форм колебаний стержня
1. Определение частот.
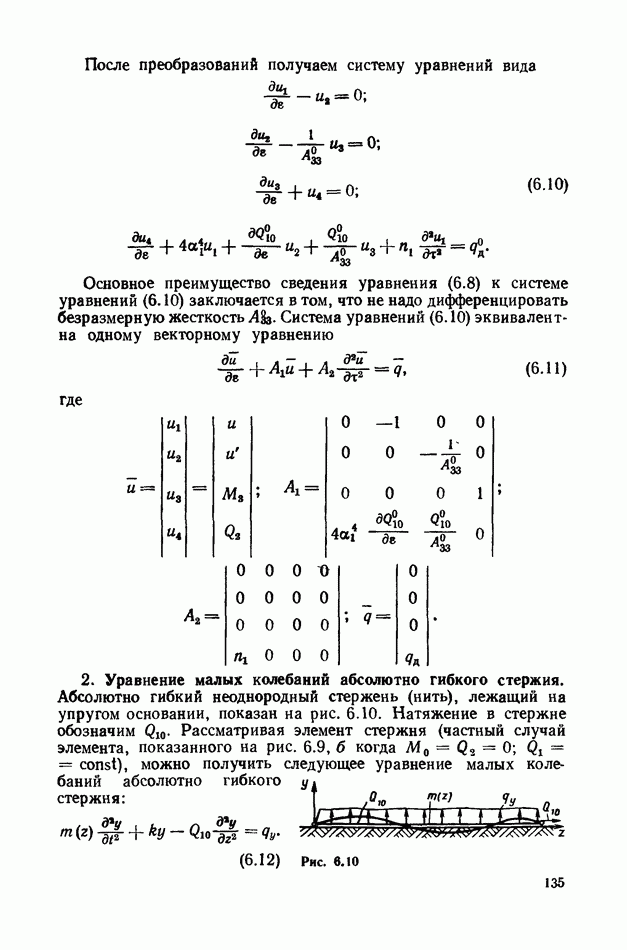
Рассмотрим свободные колебания стержня (положим  при которых решение (6.8) ищем в виде
при которых решение (6.8) ищем в виде  где
где  безразмерная частота, равная
безразмерная частота, равная  размерная частота). Подставив выражение для
размерная частота). Подставив выражение для  в (6.8), получаем
в (6.8), получаем

где

Решение уравнения (6.14) при  аналогично решению уравнения (2.9) и имеет вид
аналогично решению уравнения (2.9) и имеет вид

где С — произвольный вектор.
Метод численного определения матрицы  изложен в гл. 2.
изложен в гл. 2.
Отличие между решениями (2.9) и (6.15) заключается в том, что в статике элементы матрицы А известны, а при исследовании малых колебаний матрица А имеет элемент, зависящий от неизвестного параметра К. Поэтому при численном определении матрицы  приходится задаваться параметром К (безразмерной частотой) и искать такие значения
приходится задаваться параметром К (безразмерной частотой) и искать такие значения  при которых вектор
при которых вектор  удовлетворяет краевым условиям задачи. Например, для консольно закрепленного стержня компоненты вектора
удовлетворяет краевым условиям задачи. Например, для консольно закрепленного стержня компоненты вектора  должны удовлетворять следующим краевым условиям:
должны удовлетворять следующим краевым условиям:  (следовательно,
(следовательно,  Это приводит к системе уравнений
Это приводит к системе уравнений

или

Значения при которых элементы матрицы  удовлетворяют условию (6.16), дают спектр безразмерных частот стержня.
удовлетворяют условию (6.16), дают спектр безразмерных частот стержня.

Рис. 6.11
В качестве примера определим безразмерные частоты стержня переменного сечения (рис. 6.11). В этом случае имеем  зависят от закона изменения ширины сечения
зависят от закона изменения ширины сечения  для которой рассмотрим два случая:
для которой рассмотрим два случая:

 безразмерных коэффициентов и
безразмерных коэффициентов и  получаем соответственно
получаем соответственно

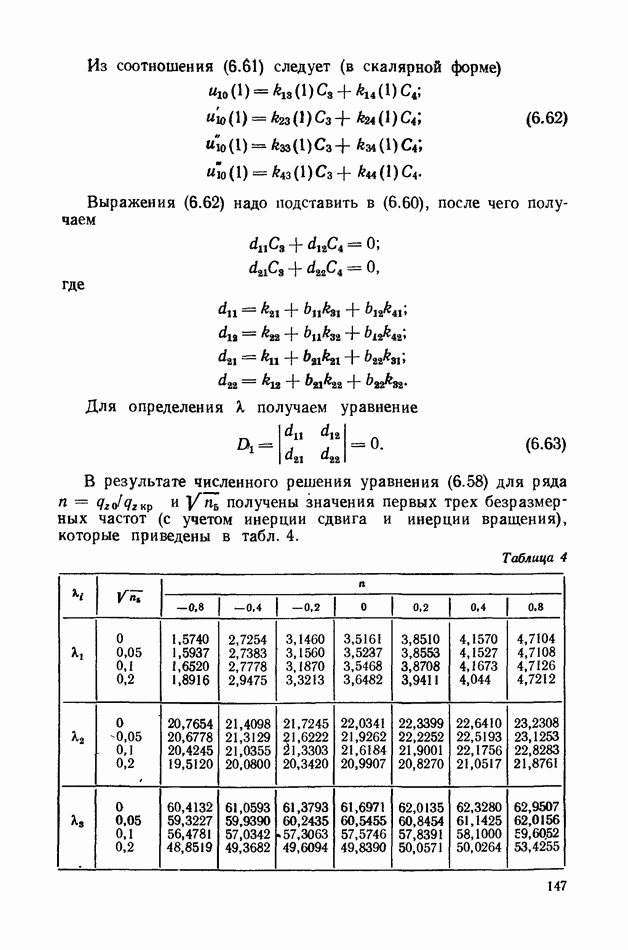
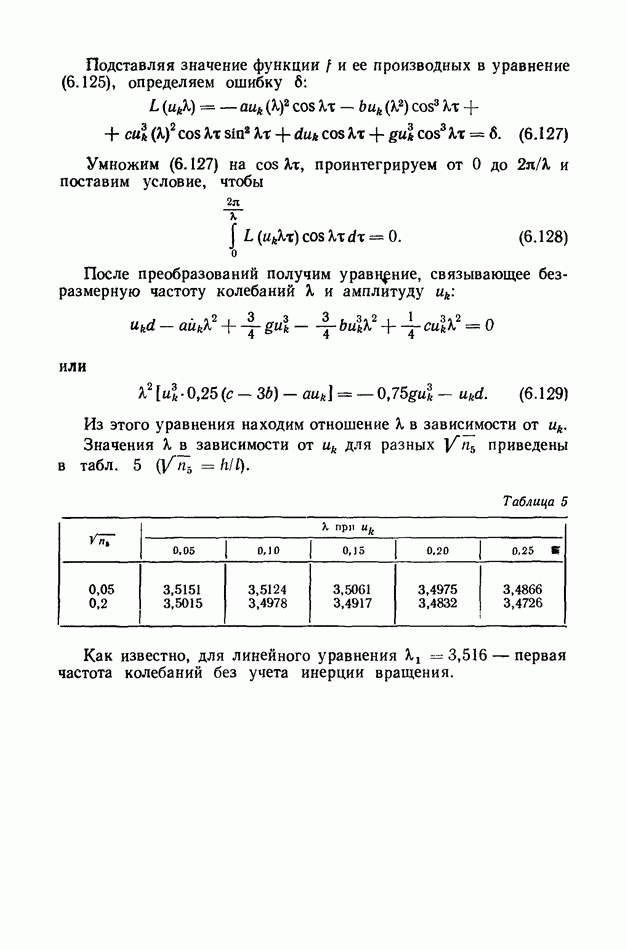
В результате численного решения уравнения получаем три первых значения безразмерных частот колебаний в зависимости от  для двух случаев изменения
для двух случаев изменения  (табл. 2 и 3).
(табл. 2 и 3).
Таблица 2 (см. скан)
Таблица 3 (см. скан)
Для частного случая стержня постоянного сечения  при
при  из (6.8) получаем
из (6.8) получаем

и соответствующее ему характеристическое уравнение  откуда получаем значения корней
откуда получаем значения корней

и соответствующее им точное аналитическое решение

где

Функции  так же, как и функции (2.53), называют функциями Крылова.
так же, как и функции (2.53), называют функциями Крылова.
Для производных  по
по  справедливы соотношения
справедливы соотношения

Соотношения (6.20) позволяют получить значения более высоких производных, а тем самым и матрицу  которая для рассматриваемого частного случая имеет вид
которая для рассматриваемого частного случая имеет вид

Для определения к, например для консольного стержня, получаем

или

Численное решение уравнения (6.18) дает для значения 
2. Определение форм колебаний.
Для каждого из определенных значений  формы колебаний для общего случая (когда элементы матрицы А зависят от
формы колебаний для общего случая (когда элементы матрицы А зависят от  ) можно найти только численным счетом.
) можно найти только численным счетом.
Из уравнений (6.16) находим

поэтому для компонент вектора  соответствующих
соответствующих  имеем
имеем

где  форма колебаний, соответствующая
форма колебаний, соответствующая  частоте;
частоте;  и Фал — функции, характеризующие изменение по
и Фал — функции, характеризующие изменение по  первой производной
первой производной  момента и перерезывающей силы, соответствующие
момента и перерезывающей силы, соответствующие  частоте колебаний стержня, т. е. каждой частоте колебаний соответствует вектор решений
частоте колебаний стержня, т. е. каждой частоте колебаний соответствует вектор решений  собственный вектор краевой задачи.
собственный вектор краевой задачи.
Для определения  соответствующих (для стержня переменного сечения), надо решить уравнение (6.14) два раза, чтобы получить элементы двух столбцов матрицы
соответствующих (для стержня переменного сечения), надо решить уравнение (6.14) два раза, чтобы получить элементы двух столбцов матрицы  Например, для консольного стержня условия следующие: при
Например, для консольного стержня условия следующие: при  .
.
Для уравнения (6.18) при консольном закреплении стержня собственные формы [функции  равны]
равны]

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. Сведения из векторного анализа
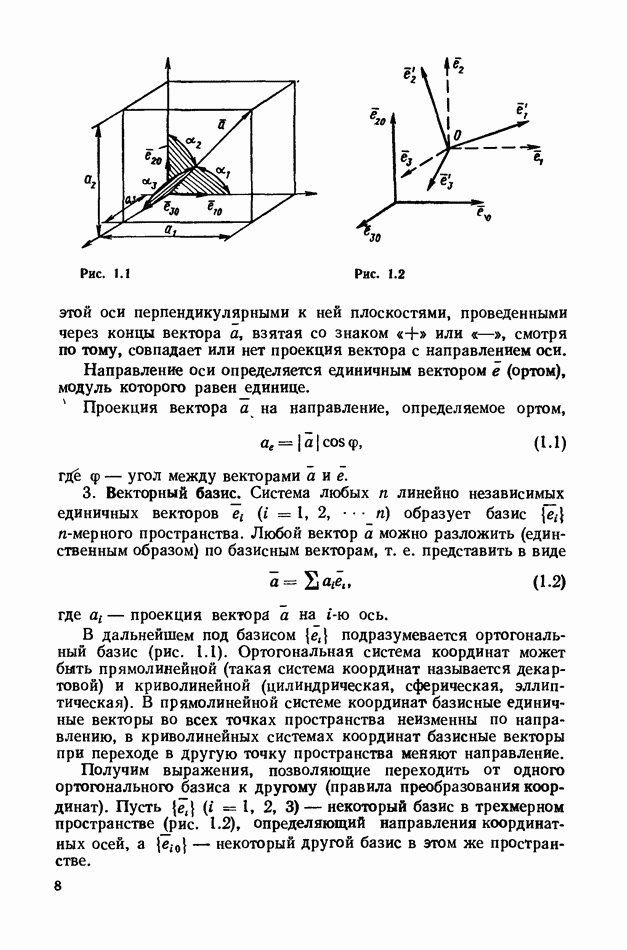
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
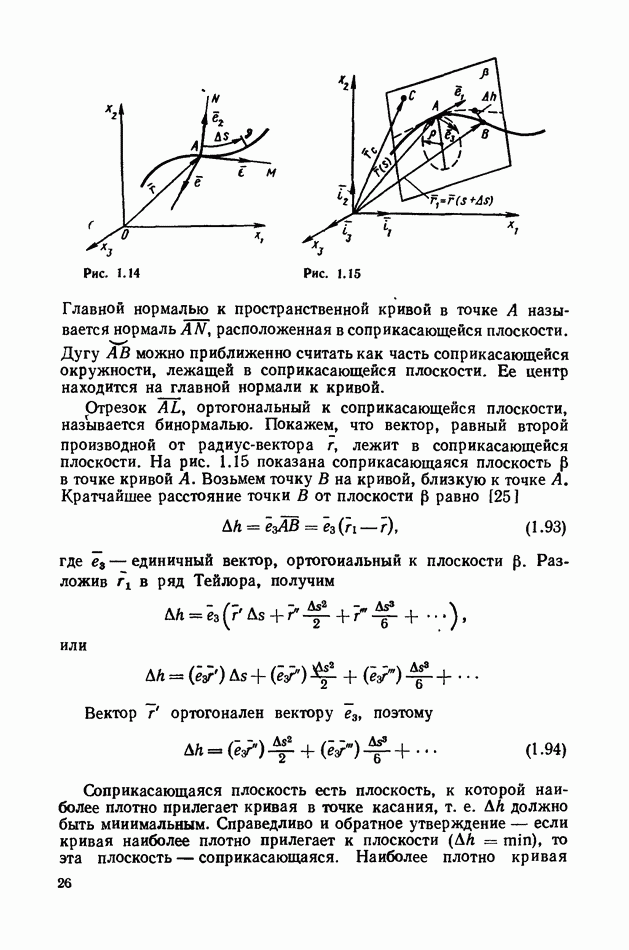
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
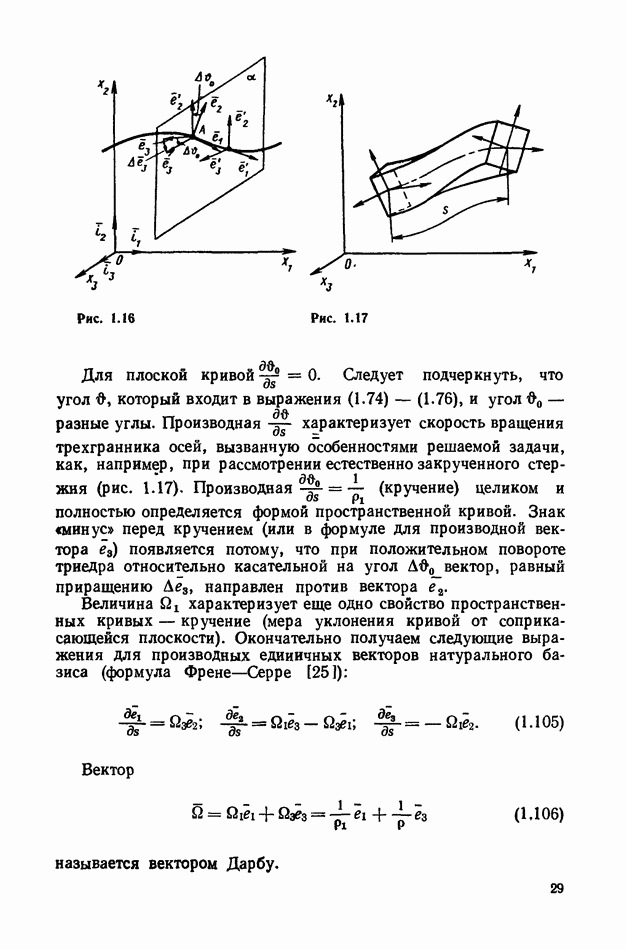
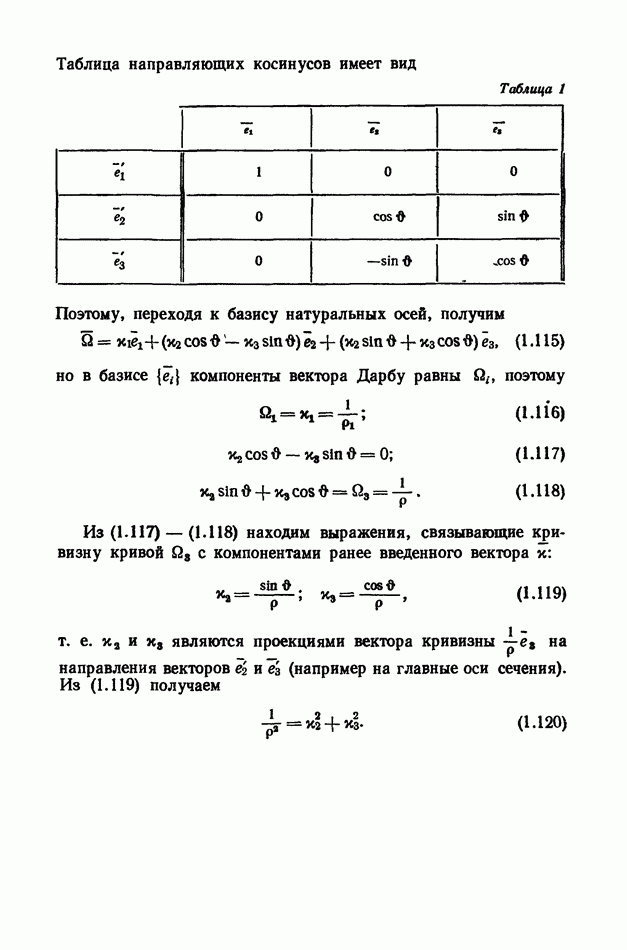
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
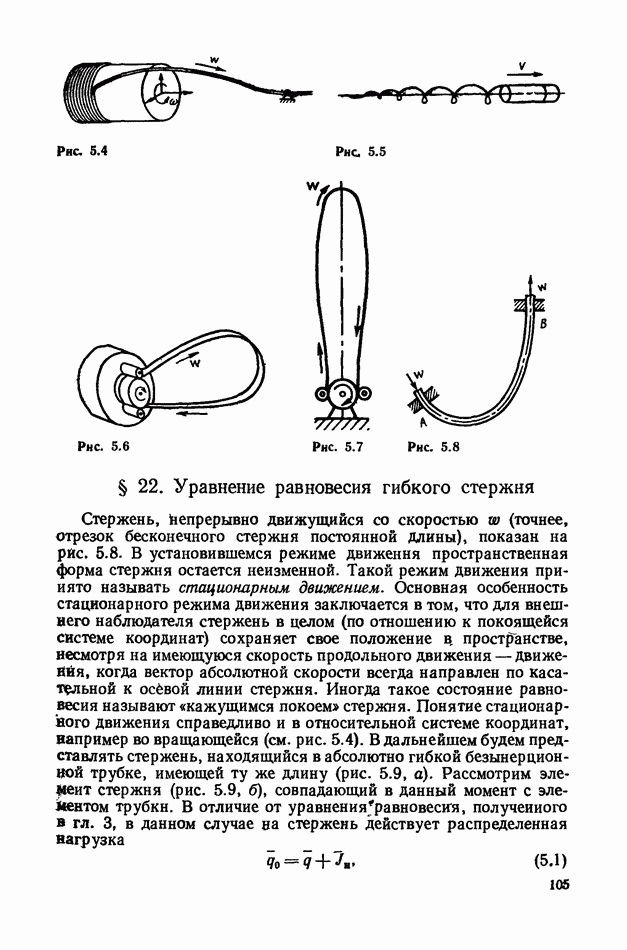
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.