| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Векторные уравнения равновесия стержней
1. Векторные уравнения равновесия стержня.
При исследовании статики стержня введем две системы координат: неподвижную декартовую с единичными векторами  (рис. 3.1), относительно которой определяется положение стержня, и подвижную, жестко связанную с сечениями стержня, относительно которой рассматриваются малые упругие деформации элемента стержня. Дуга
(рис. 3.1), относительно которой определяется положение стержня, и подвижную, жестко связанную с сечениями стержня, относительно которой рассматриваются малые упругие деформации элемента стержня. Дуга  осевой линии отсчитывается от некоторой фиксированной точки, выбор которой произволен.
осевой линии отсчитывается от некоторой фиксированной точки, выбор которой произволен.

Рис. 3.1
Связанные оси могут Оыть ориентированы произвольно, но для получения более простых уравнений равновесия (и движения) целесообразно их ориентировать следующим образом. Начало координат должно совпадать с центром тяжести площади поперечного сечения стержня, одна из осей (например ось, определяемая единичным вектором  направлена по касательной к осевой линии стержня в сторону возрастания координаты
направлена по касательной к осевой линии стержня в сторону возрастания координаты  а две другие оси — по главным центральным осям сечения.
а две другие оси — по главным центральным осям сечения.
Для абсолютно гибкого стержня (нити) в качестве связанных осей целесообразно брать естественные оси. Естественные оси могут быть взяты и при рассмотрении деформаций стержня, поперечное сечение которого имеет более чем одиу пару осей симметрии. Оси, связанные с главными осями сечения, будем называть главными осями (в отличие от естественных осей).
Два положения стержня показаны на рис. 3.1: первое положение соответствует иенагруженному состоянию (естественному), при котором осевая линия стержня есть пространственная кривая; второе положение соответствует нагруженному состоянию.. Под действием медленно нарастающих силы  и момента
и момента  (рассматривается статика) стержень, деформируясь, переходит из состояния 1 в состояние 2. Из рис. 3.1 следует, что упругие перемещения могут быть настолько болыними, что форма осевой линии нагруженного стержня может как угодно сильно отличаться от первоначальной формы. Внешние силы в процессе деформации стержня изменяются по направлению (на рис. 3.1 направления векторов
(рассматривается статика) стержень, деформируясь, переходит из состояния 1 в состояние 2. Из рис. 3.1 следует, что упругие перемещения могут быть настолько болыними, что форма осевой линии нагруженного стержня может как угодно сильно отличаться от первоначальной формы. Внешние силы в процессе деформации стержня изменяются по направлению (на рис. 3.1 направления векторов  в момент приложения к стержню показаны пунктиром).
в момент приложения к стержню показаны пунктиром).
Для решения нелинейных задач статики гибких стержней необходимо знать поведение внешних нагрузок в процессе деформации стержня, а также необходимо учитывать изменение связей (например, перемещение шарнира на рис. 3.2). Конечное состояние гибкого стержня будет различным, если стержень в первом случае нагружать «мертвой» силой («мертвой» называется нагрузка, сохраняющая при деформировании системы свое направление), а во втором следящей, т. е. силой, которая в процессе деформации стержня сохраняет свое направление но отношению к стержню (например образует неизменные углы со связанным триедром). В более общем случае нагруженйя на стержень кроме сосредоточенных могут действовать распределенные силы и моменты, поэтому при выводе уравнений равновесия будем их учитывать.
Рассмотрим элементы стержня длиной  и нанесем все действующие на него силы (рис. 3.3). На рис. 3.3 приняты следующие обозначения: вектор внутренних усилий
и нанесем все действующие на него силы (рис. 3.3). На рис. 3.3 приняты следующие обозначения: вектор внутренних усилий  где
где  осевое усилие;
осевое усилие;  перерезывающие усилия; вектор внутренних моментов
перерезывающие усилия; вектор внутренних моментов  Мгег
Мгег  где
где  крутящий момент;
крутящий момент;  изгибающие моменты;
изгибающие моменты;  проекции вектора распределенной нагрузки
проекции вектора распределенной нагрузки  на связанные оси;
на связанные оси;  Из проекции вектора
Из проекции вектора  распределенного момента на связанные оси. Направления осей связанного триедра, определяемые единичными векторами
распределенного момента на связанные оси. Направления осей связанного триедра, определяемые единичными векторами  совпадают с направлением главных осей сечения стержня. Элемент находится в равновесии, следовательно, сумма всех сил и сумма моментов равны нулю и получаем два векторных уравнения
совпадают с направлением главных осей сечения стержня. Элемент находится в равновесии, следовательно, сумма всех сил и сумма моментов равны нулю и получаем два векторных уравнения

или

В векторной форме записи уравнения инвариантны по отношению к любой системе координат. Для перехода от (3.3) (3.4) к уравнениям, записанным в каком-либо базисе, необходимо представить векторы в виде разложения по векторам данного базиса. Более подробно о других формах записи уравнений равновесия сказано в § 13.
В системе уравнений  неизвестными являются векторы
неизвестными являются векторы  известными — действующие распределенные нагрузки, а также сосредоточенные силы и моменты, приложенные к стержню (см. рис. 3.1), и условия закрепления стержня. Система уравнений,
известными — действующие распределенные нагрузки, а также сосредоточенные силы и моменты, приложенные к стержню (см. рис. 3.1), и условия закрепления стержня. Система уравнений,  не является полной, таккак определить
не является полной, таккак определить  из этой системы в общем случае нельзя. Дело в том, что в уравнение (3.4) входит единичный вектор
из этой системы в общем случае нельзя. Дело в том, что в уравнение (3.4) входит единичный вектор  натурального триедра, положение которого
натурального триедра, положение которого

Рис. 3.2

Рис. 3.3.
в пространстве неизвестно и зависит от деформации стержня.

Рис. 3.4
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
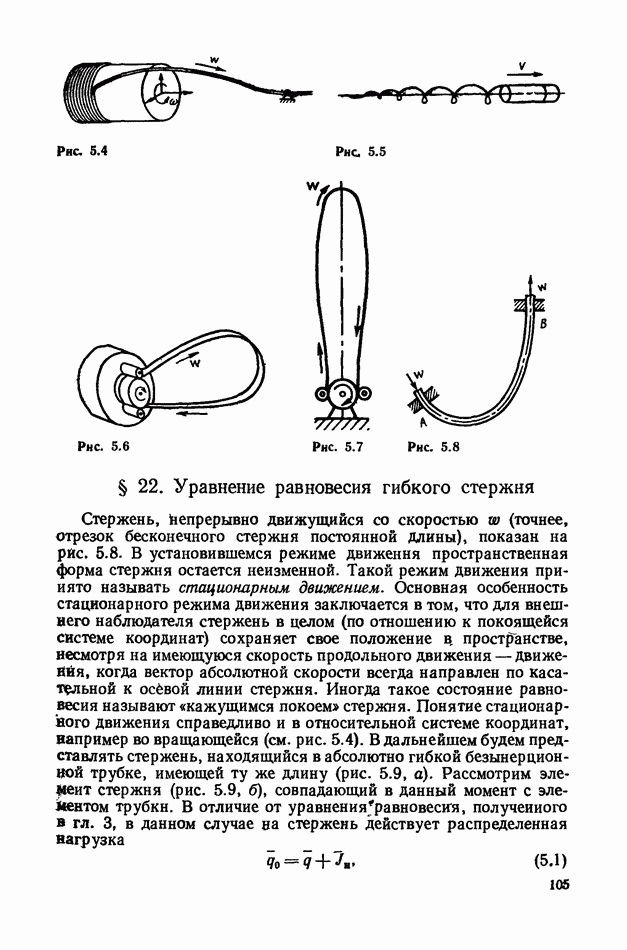
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
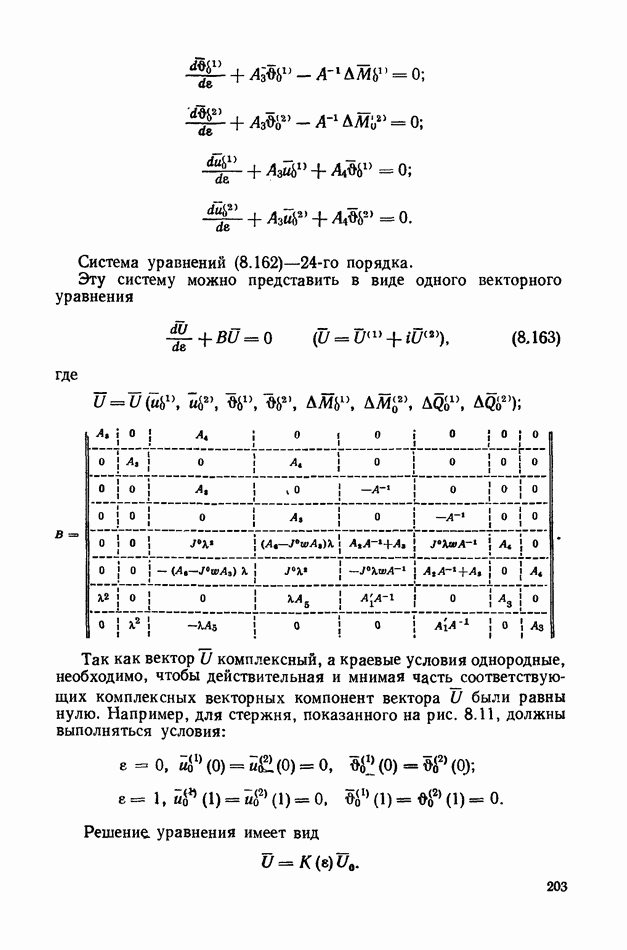
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
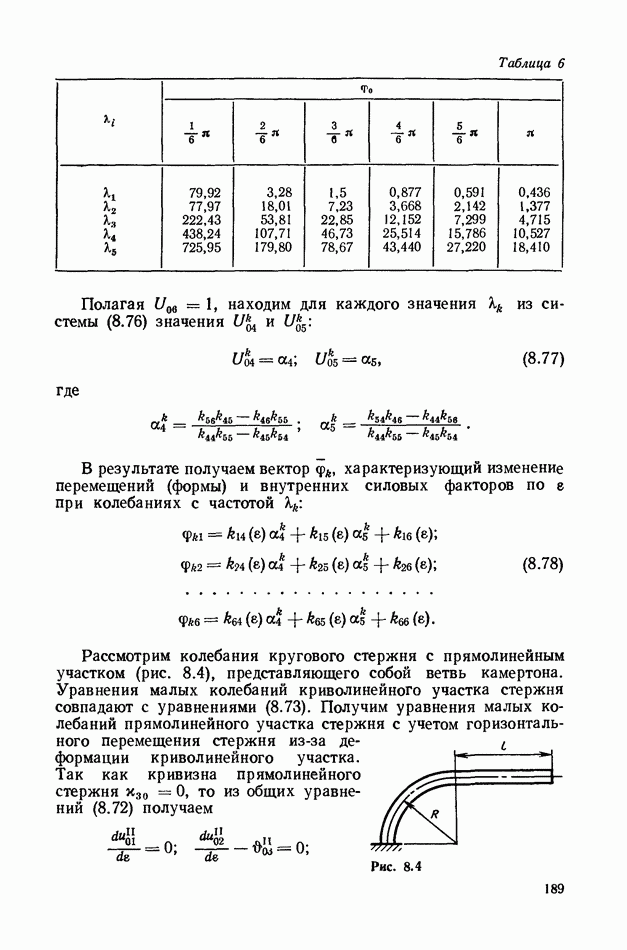
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
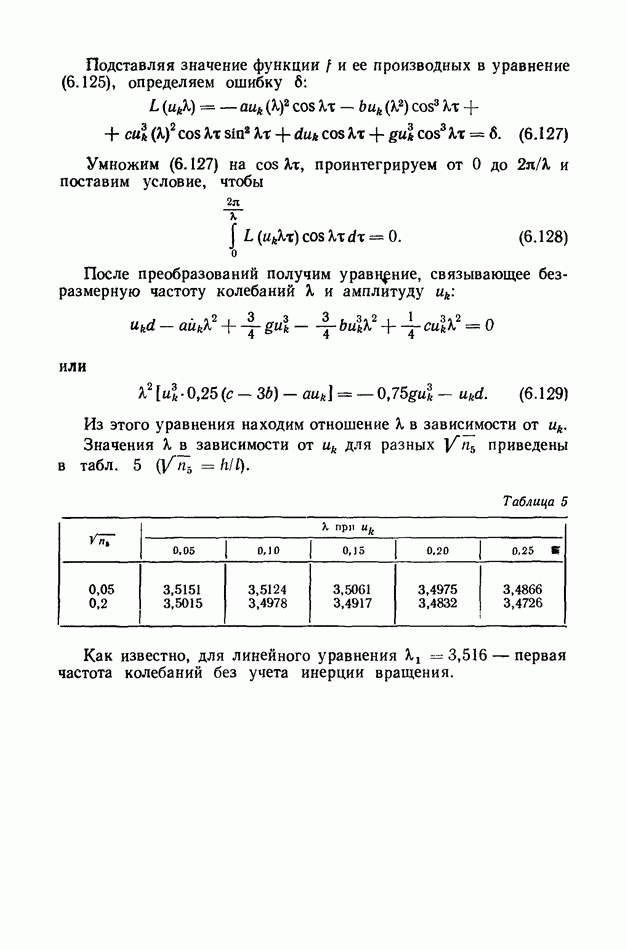
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.