| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Принцип возможных перемещений.
При решении задач статики и динамики стержней очень эффективными являются приближенные методы, использующие принцип возможных перемещений Напомним формулировку принципа возможных перемещений, которая дается в курсе теоретической механики [17]. Необходимое и достаточное условие равновесия системы, подчиненной стационарным идеальным связям, заключается в равенстве нулю работы сил, приложенных к системе, на всех ее возможных перемещениях (Идеальными связями называются такие связи, сумма работ реакций которых на любом возможном перемещении систем равна нулю.)
Аналитическая запись принципа возможных перемещений имеет вид 

где  сумма работ внешних сил
сумма работ внешних сил  на возможных перемещениях
на возможных перемещениях  Если внешние силы
Если внешние силы  консервативны, то их можно представить через потенциальную энергию системы
консервативны, то их можно представить через потенциальную энергию системы  в виде
в виде

 координаты центров масс системы материальных точек).
координаты центров масс системы материальных точек).
Из (2.111) получаем

или

где  вариация потенциальной энергии системы. Условие (2.113) — условие экстремальности потенциальной энергии в положении равновесия системы.
вариация потенциальной энергии системы. Условие (2.113) — условие экстремальности потенциальной энергии в положении равновесия системы.
Следовательно, из принципа возможных перемещений следует, что необходимые и достаточные условия равновесия системы с идеальными связями под действием консервативных сил совпадают с необходимым (но недостаточным) условием экстремума потенциальной энергии. Принцип возможных перемещений может быть использован при решении задач статики наряду с более привычными уравнениями статики.

Рис. 2.16

Рис. 2.17
Для применения принципа возможных перемещений при решении задач механики стержней необходимо обобщить этот принцип так, чтобы его можно было распространить на упругие системы. Для упругих систем (или в более общем случае для деформируемых систем, например стержней) необходимо принимать во внимание не только работу внешних сил, но и работу внутренних сил (результирующих напряжений), вызванных возможными отклонениями упругой системы от состояния равновесия. Остановимся более подробно на понятии возможного перемещения для стержней. Возможным (или виртуальным) перемещением называется всякое малое перемещение точек осевой линии стержня из исходного состояния без нарушения связей, наложенных на стержень. Например для стержня, показанного на рис 2 16, любая функция  мало отличающаяся от функции
мало отличающаяся от функции  и удовлетворяющая ее краевым условиям, может рассматриваться как возможные перемещения для точек осевой линии стержня Любое возможное перемещение
и удовлетворяющая ее краевым условиям, может рассматриваться как возможные перемещения для точек осевой линии стержня Любое возможное перемещение  стержня является непрерывной функцией.
стержня является непрерывной функцией.
Рассмотрим, как формулируется принцип возможных перемещений для произвольно нагруженного стержня (рис. 2.17), который до приложения внешней нагрузки был прямолинейным. При статическом приложении нагрузки  стержень деформируется, в связи с чем силы совершают работу, которая переходит в его энергию деформации Пренебрегая потерями энергии, вызванными внутренним трением, имеем
стержень деформируется, в связи с чем силы совершают работу, которая переходит в его энергию деформации Пренебрегая потерями энергии, вызванными внутренним трением, имеем

где  энергия деформации стержня (равная работе внутренних сил); А — работа внешних сил.
энергия деформации стержня (равная работе внутренних сил); А — работа внешних сил.
Применительно к деформируемым системам принцип возможных перемещений формулируется следующим образом:
если деформируемая система находится в равновесии под действием внешних сил, то работа этих сил на возможных деформациях системы, совместимых со связями, наложенными на систему,

Рис. 2.18
равна работе внутренних сил на этих же деформациях, т. е.

Работа  есть работа внешних (обобщенных) сил, приложенных к конструкции, на возможных обобщенных перемещениях точек приложения этих сил (вызванных возможными деформациями конструкции).
есть работа внешних (обобщенных) сил, приложенных к конструкции, на возможных обобщенных перемещениях точек приложения этих сил (вызванных возможными деформациями конструкции).
На возможных перемещениях внешние силы сохраняют свое значение, поэтому работа каждой из обобщенных сил равна произведению силы на обобщенное возможное перемещение, т. е.

где  обобщенная сила;
обобщенная сила;  возможное обобщенное перемещение.
возможное обобщенное перемещение.
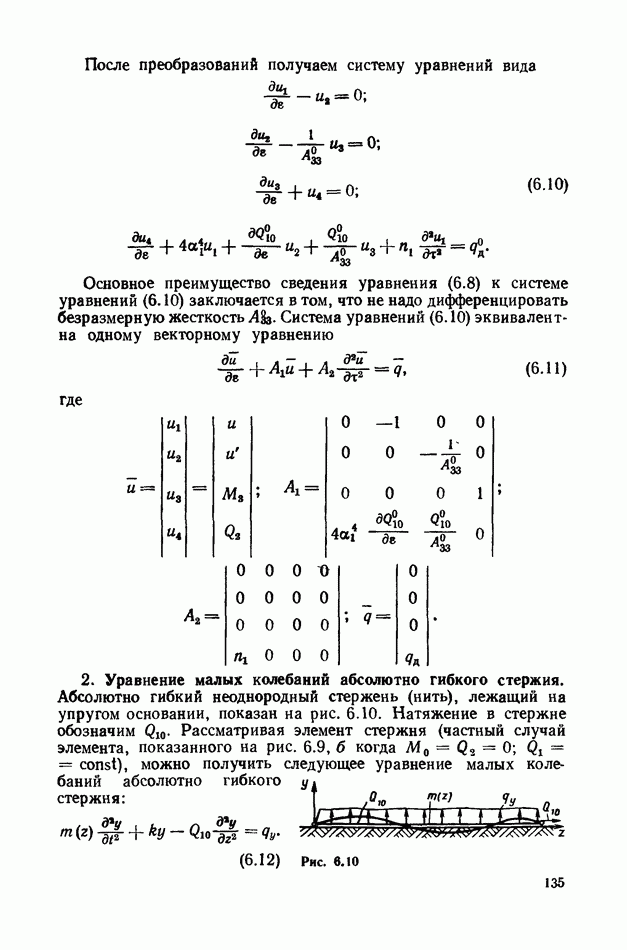
Получим выражение для возможной работы сил, приложенных к стержню, лежащему на упругом основании (слое) (рис. 2.18, а). На рис. 2.18, б показаны возможные перемещения балки — 
Работа внешних сил на возможных перемещениях в рассматриваемом случае

Покажем, что из условия (2.115) можно получить уравнение равновесия стержня. Рассмотрим стержень, лежащий на упругом слое (см. рис. 2.18, а). Потенциальная энергия и ее вариация, вызванная возможными деформациями стержня, соответственно равны

Работа внешних сил на возможных перемещениях

или

Интегрируя (2.119) по частям, получим

Свободные слагаемые в силу краевых условий равны нулю.
Аналогично проинтегрировав последнее слагаемое в (2.120), получим

Приравняв выражения для  , после преобразований имеем
, после преобразований имеем 

Так как возможное перемещение является произвольной функцией, не равной тождественно нулю, то из (2.121) следует

Полученное выражение (2.122) есть уравнение равновесия стержня для случая, показанного на рис. 2.18, а.
Выражение (2.121) можно представить в более компактной и общей форме записи

где  есть уравнение равновесия стержня. Если у является точным решением уравнения равновесия, то
есть уравнение равновесия стержня. Если у является точным решением уравнения равновесия, то  Если у не является решением уравнения равновесия (задано приближенно), то соотношение (2.123) является дополнительным интегральным условием (кроме краевых условий), которому должно удовлетворять приближенное выражение для у. Выражение (2.123) можно преобразовать к безразмерной фордое, как это делалось в предыдущих параграфах, и получить
Если у не является решением уравнения равновесия (задано приближенно), то соотношение (2.123) является дополнительным интегральным условием (кроме краевых условий), которому должно удовлетворять приближенное выражение для у. Выражение (2.123) можно преобразовать к безразмерной фордое, как это делалось в предыдущих параграфах, и получить

где  безразмерный прогиб.
безразмерный прогиб.

Рис. 2.19
Условие (2.123) является основным соотношением для приближенного решения задачи о равновесии" стержней. Как для линейных уравнений равновесия, так и для нелинейных уравнений равновесия представим прогиб у в виде ряда

где а, — произвольные числа;  функции (известные), удовлетворяющие краевым условиям как геометрическим,
функции (известные), удовлетворяющие краевым условиям как геометрическим,  физическим, характеризующим связи, наложенные на стержень. Возможные перемещения точек осевой линии стержня естественно искать в виде функции, подобной прогибам, т. е. в виде
физическим, характеризующим связи, наложенные на стержень. Возможные перемещения точек осевой линии стержня естественно искать в виде функции, подобной прогибам, т. е. в виде

где  независимые произвольные величины. Подставив (2.125) и (2.126) в (2.123), получим
независимые произвольные величины. Подставив (2.125) и (2.126) в (2.123), получим

Так как величина  независима, то из (2.127) получаем систему уравнений вида
независима, то из (2.127) получаем систему уравнений вида

Для линейных уравнений равновесия из (2.128) после интегрирования получим систему линейных алгебраических уравнений относительно 

При изложении приближенного решения использовали выражение (2 124) с известными функциями  Естественно возникает вопрос, как эти функции получить. Очень эффективными для приближенного решения являются степенные функции, удовлетворяющие условиям ортогональности Изложим метод получения таких функций на примере стержня, показанного на рис. 2.19, а, перейдя к безразмерной координате
Естественно возникает вопрос, как эти функции получить. Очень эффективными для приближенного решения являются степенные функции, удовлетворяющие условиям ортогональности Изложим метод получения таких функций на примере стержня, показанного на рис. 2.19, а, перейдя к безразмерной координате  Для получения отличного от нуля выражения для безразмерного прогиба
Для получения отличного от нуля выражения для безразмерного прогиба  надо взять число слагаемых степенного ряда на единицу больше числа
надо взять число слагаемых степенного ряда на единицу больше числа
граничных условий, что дает следующее приближенное выражение:

Удовлетворив краевым условиям и полагая  получим следующую функцию:
получим следующую функцию:

Эта функция при изменении  в интервале
в интервале  больше нуля (рис. 2.19, б). Получим вторую функцию
больше нуля (рис. 2.19, б). Получим вторую функцию  взяв на одно слагаемое больше:
взяв на одно слагаемое больше:

Полагая  получим
получим

В выражение (2.133) входит произвольный параметр  который можно определить, потребовав, чтобы
который можно определить, потребовав, чтобы  были ортогональны на интервале
были ортогональны на интервале  что дает
что дает

После вычислений получаем

Функция  на интервале
на интервале  один раз обращается в нуль (рис. 2.19, в). Функция
один раз обращается в нуль (рис. 2.19, в). Функция  будет содержать два свободных параметра
будет содержать два свободных параметра  (полагая
(полагая  которые находят из условий ортогональности
которые находят из условий ортогональности

 сггаъ
сггаъ 
Алгоритм получения необходимого числа функций  для конкретной задачи (конкретных краевых условий) можно запрограммировать для счета на ЭВМ. В результате получаем приближенное выражение для безразмерного прогиба в виде
для конкретной задачи (конкретных краевых условий) можно запрограммировать для счета на ЭВМ. В результате получаем приближенное выражение для безразмерного прогиба в виде

где  произвольные константы. Возникает вопрос о точности получаемых приближенных решений и о необходимом числе слагаемых ряда (2.136), но так как точное решение отсутствует, то получить абсолютную оценку сходимости приближенных решений нельзя. Поэтому судить о сходимости приближенных решений можно только по относительным оценкам, сравнивая между собой решения с различным числом слагаемых ряда (2.136). Например, получив решения для двух приближенных выражений
произвольные константы. Возникает вопрос о точности получаемых приближенных решений и о необходимом числе слагаемых ряда (2.136), но так как точное решение отсутствует, то получить абсолютную оценку сходимости приближенных решений нельзя. Поэтому судить о сходимости приближенных решений можно только по относительным оценкам, сравнивая между собой решения с различным числом слагаемых ряда (2.136). Например, получив решения для двух приближенных выражений  найдем их разность
найдем их разность  которая может служить оценкой точности получаемых решений. Если максимальное значение
которая может служить оценкой точности получаемых решений. Если максимальное значение  интервале
интервале  меньше или равно допустимому), которое задается исходя из требований, предъявляемых к точности решения
меньше или равно допустимому), которое задается исходя из требований, предъявляемых к точности решения

где  допускаемая погрешность в решении, то можно считать, что
допускаемая погрешность в решении, то можно считать, что  решение исходной задачи. Если
решение исходной задачи. Если  то следует получить решение для
то следует получить решение для  и сравнить его с решением
и сравнить его с решением  т. е. проверить выполнение условия (2.137):
т. е. проверить выполнение условия (2.137):

Решение  при котором выполняется условие
при котором выполняется условие

можно считать приближенным решением задачи (если интерес представляют только прогибы). Когда необходимо получить приближенное решение, характеризующее с заданной степенью точности не только прогибы, но и внутренние силовые факторы (пропорциональные  то необходимо, чтобы выполнялись условия
то необходимо, чтобы выполнялись условия

где  допустимые значения погрешностей первых трех производных решения.
допустимые значения погрешностей первых трех производных решения.
Рассмотрим приближенное решение уравнения равновесия шарнирно закрепленного стержня, лежащего на линейном упругом слое (рис. 2.20). В качестве функций  можно взять тригонометрические функции
можно взять тригонометрические функции


Рис. 2.20
Уравнение равновесия стержня 

Приближенное решение уравнения равновесия ищем в видег

Возможный прогиб стержня можно взять в виде

В соответствии с принципом возможных перемещений получаем систему уравнений

из которой определяют неизвестные коэффициенты 

или

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
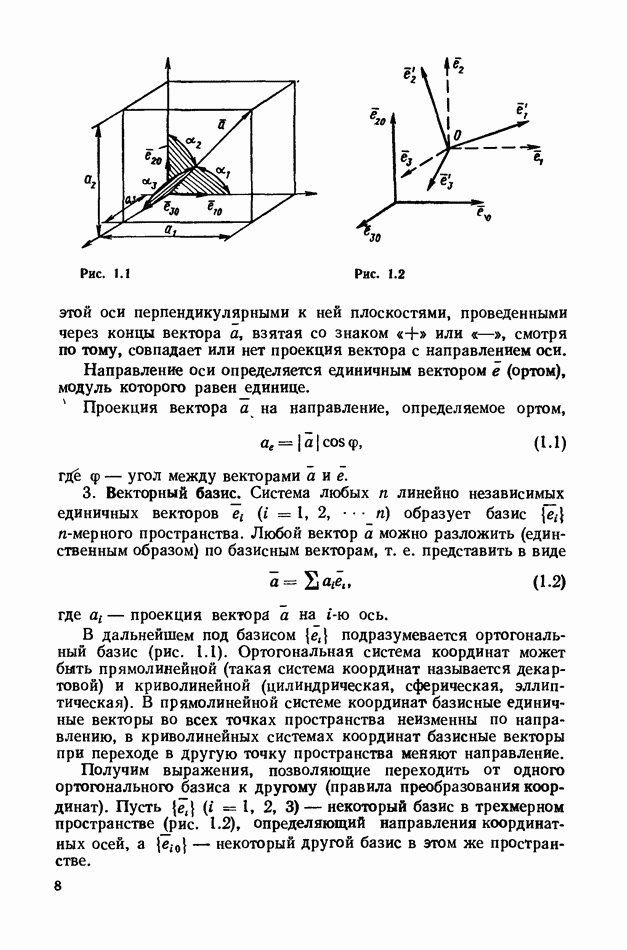
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
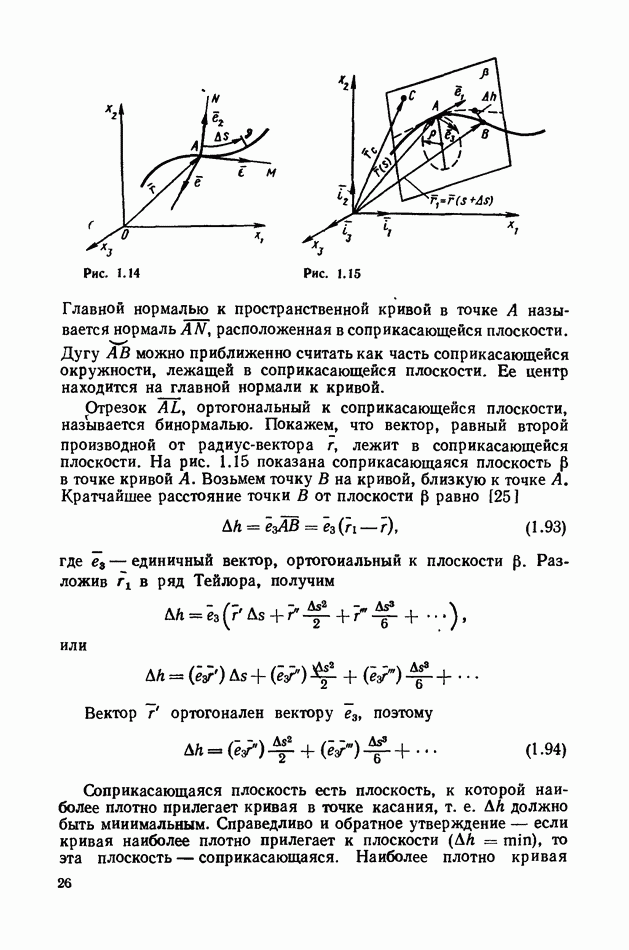
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
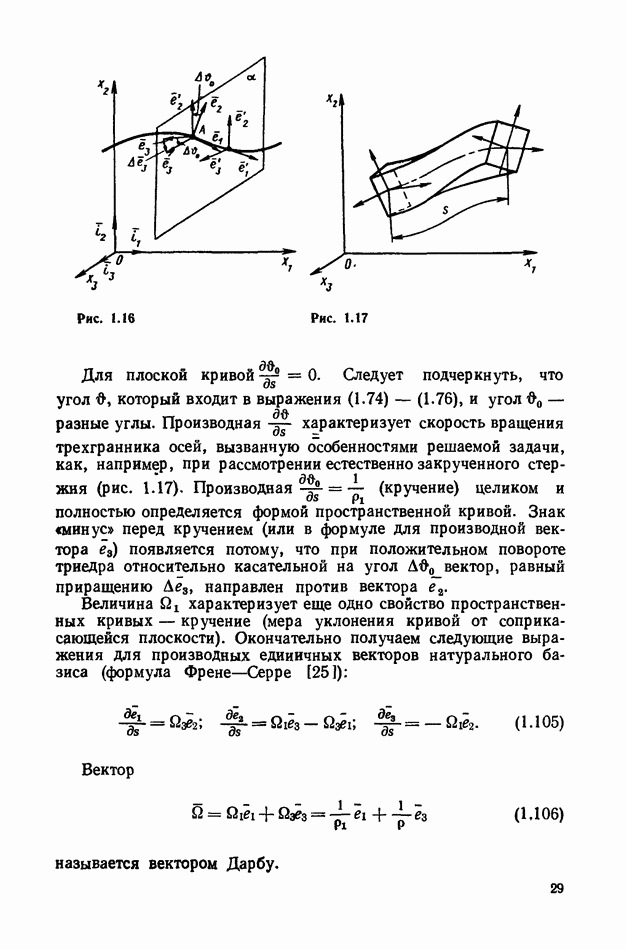
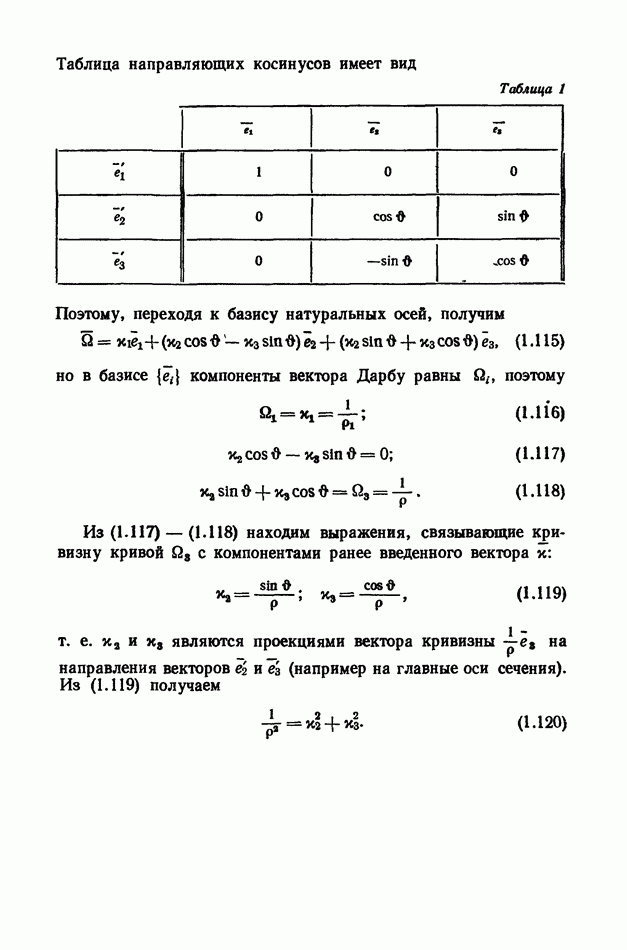
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
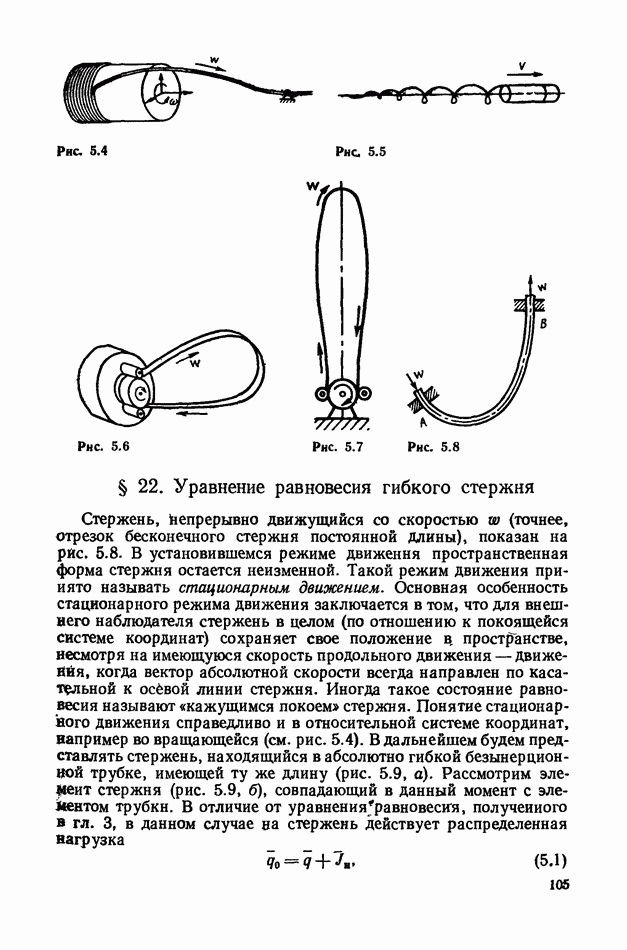
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.