| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
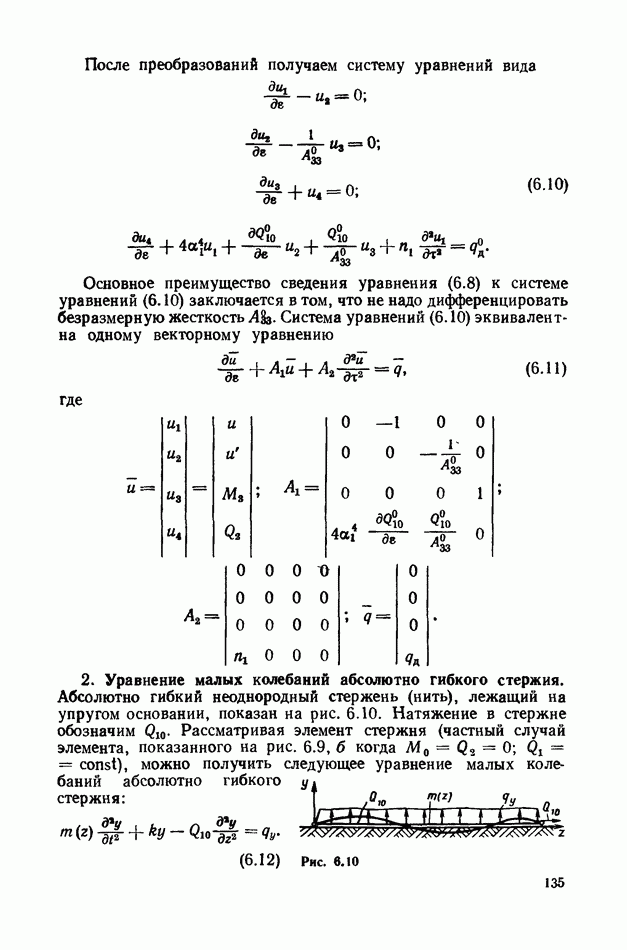
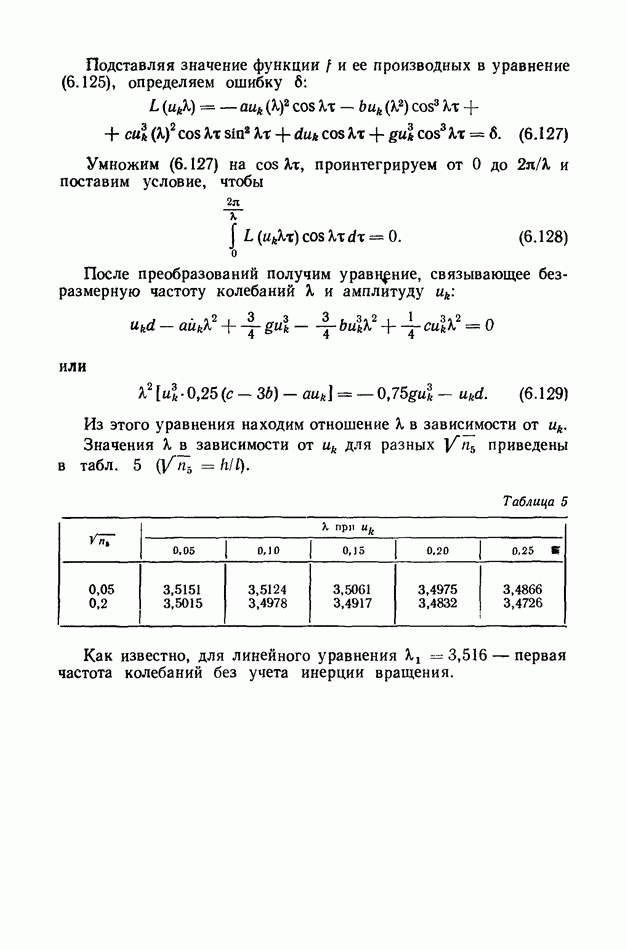
2. Переменные Эйлера.
Нерастяжимый стержень показан на рис. 4.4. Он имеет продольное движение [например, ветвь передачи с гибкой связью (рис. 4.5) [33] со скоростью  кроме того, имеет еще переносное движение со скоростью
кроме того, имеет еще переносное движение со скоростью  т. е. полная скорость элемента стержня
т. е. полная скорость элемента стержня

Если стержень нерастяжим, то  зависит только от времени. Если стержень растяжимый, то продольная скорость
зависит только от времени. Если стержень растяжимый, то продольная скорость  зависит и от времени, и от координаты
зависит и от времени, и от координаты  . В последнем случае при изучении движения участка стержня постоянной длины, находящегося между точками
. В последнем случае при изучении движения участка стержня постоянной длины, находящегося между точками  переменные Лагранжа неудобны. Нас интересует поведение участка стержня между точками
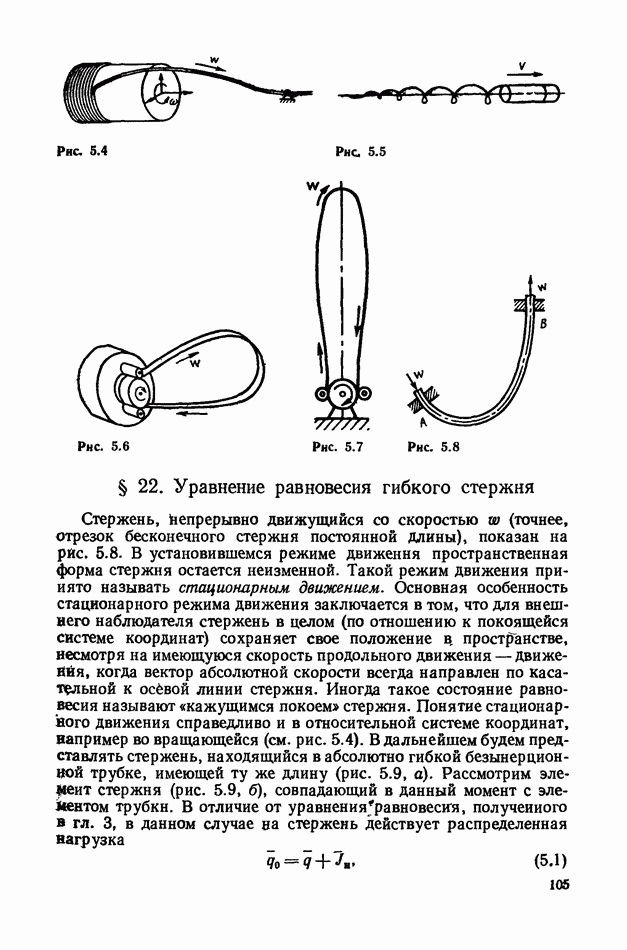
переменные Лагранжа неудобны. Нас интересует поведение участка стержня между точками  в целом, а не движение индивидуальных точек. Для большей наглядности метода Эйлера представим, что стержень находится в абсолютно гибкой безынерционной трубке (см. рис. 4.4). Для описания движения достаточно знать положение трубки во времени и внутренние силовые факторы в стержне в фиксированном сечении трубки. Та ко 2 разделение движения на переносное (скорость о) и относительное (скорость
в целом, а не движение индивидуальных точек. Для большей наглядности метода Эйлера представим, что стержень находится в абсолютно гибкой безынерционной трубке (см. рис. 4.4). Для описания движения достаточно знать положение трубки во времени и внутренние силовые факторы в стержне в фиксированном сечении трубки. Та ко 2 разделение движения на переносное (скорость о) и относительное (скорость  весьма эффективно при изучении динамики шлангов (абсолютно гибких стержней) и стержней, заполненных движущейся жидкостью (рис. 4.6). В этом случае движение жидкости рассматривается совместно с движением шланга (трубки).
весьма эффективно при изучении динамики шлангов (абсолютно гибких стержней) и стержней, заполненных движущейся жидкостью (рис. 4.6). В этом случае движение жидкости рассматривается совместно с движением шланга (трубки).

Рис. 4.6.
Если жидкость несжимаема, то относительная скорость  при заданном расходе не зависит от движения шланга, т. е. ее можно считать известной.
при заданном расходе не зависит от движения шланга, т. е. ее можно считать известной.
Так как стержень по отношению к трубке движется (см. рис. 4,4)  элемента стержня зависит от времени), то полная производная координат точек осевой линии стержня по времени
элемента стержня зависит от времени), то полная производная координат точек осевой линии стержня по времени

где 
Первое слагаемое характеризует изменение во времени координат сечения трубки при фиксированном  и называется местной производной.
и называется местной производной.
Второе слагаемое  характеризует изменение координат точек осевой линии стержня при его движении по трубке и называется переносной или конвективной производной.
характеризует изменение координат точек осевой линии стержня при его движении по трубке и называется переносной или конвективной производной.
Вторая производная  по времени (компоненты абсолютного ускорения)
по времени (компоненты абсолютного ускорения)

Если продольное движение стержня установившееся (при котором  до
до  или
или  зависит только от
зависит только от  то выражения для компонент ускорения
то выражения для компонент ускорения

Рассмотрим трехгранник осей  связанный с осевой линией стержня, имеющего продольное движение. В этом случае векторы
связанный с осевой линией стержня, имеющего продольное движение. В этом случае векторы  зависят от
зависят от  поэтому полная производная
поэтому полная производная  по времени (см. § 15)
по времени (см. § 15)

или

Так как частная производная  характеризует местное изменение во времени векторов
характеризует местное изменение во времени векторов  при фиксированном
при фиксированном  то угловая скорость со есть местная угловая скорость, т. е. угловая скорость трубки, а не элемента стержня.
то угловая скорость со есть местная угловая скорость, т. е. угловая скорость трубки, а не элемента стержня.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
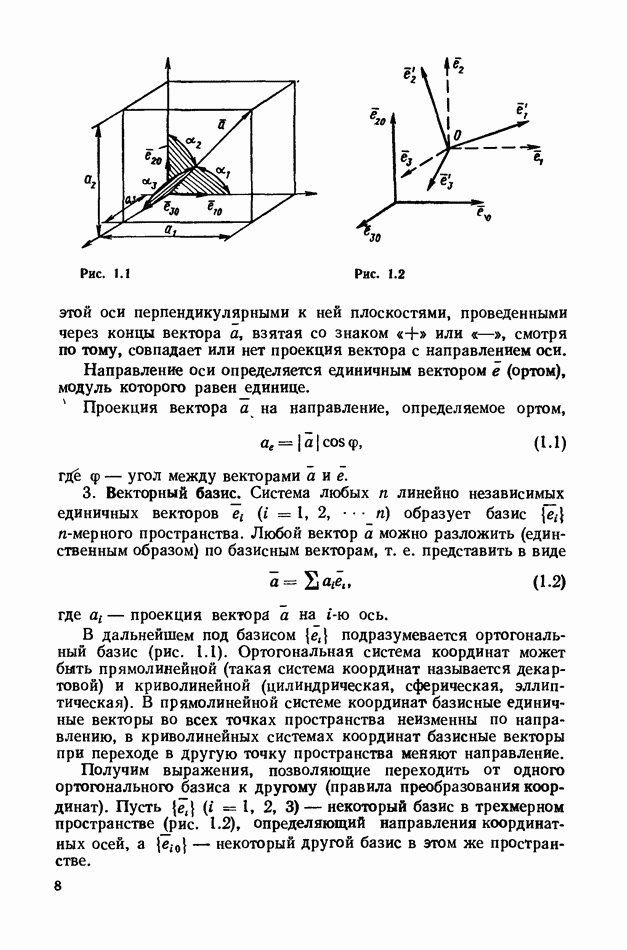
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
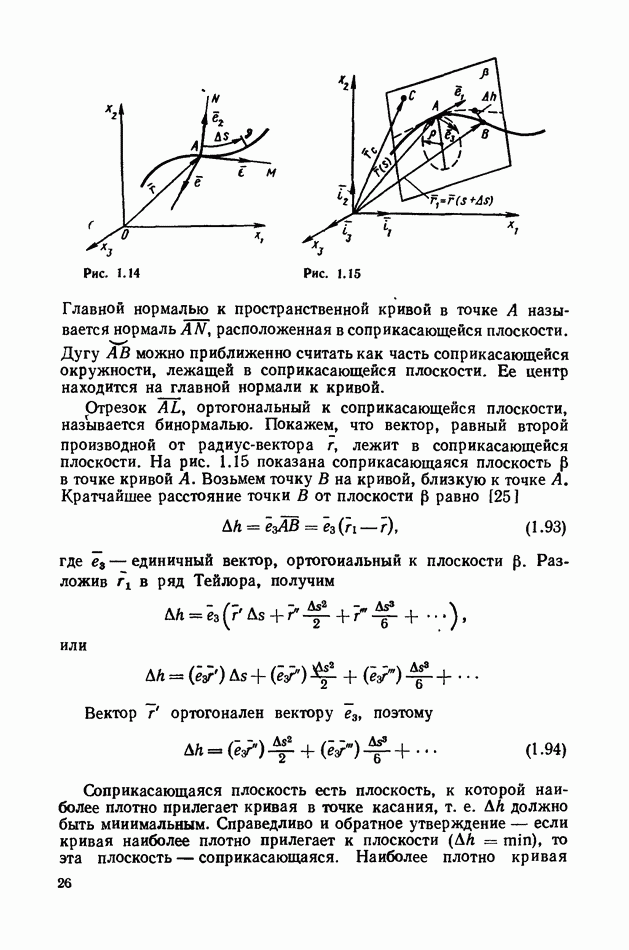
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
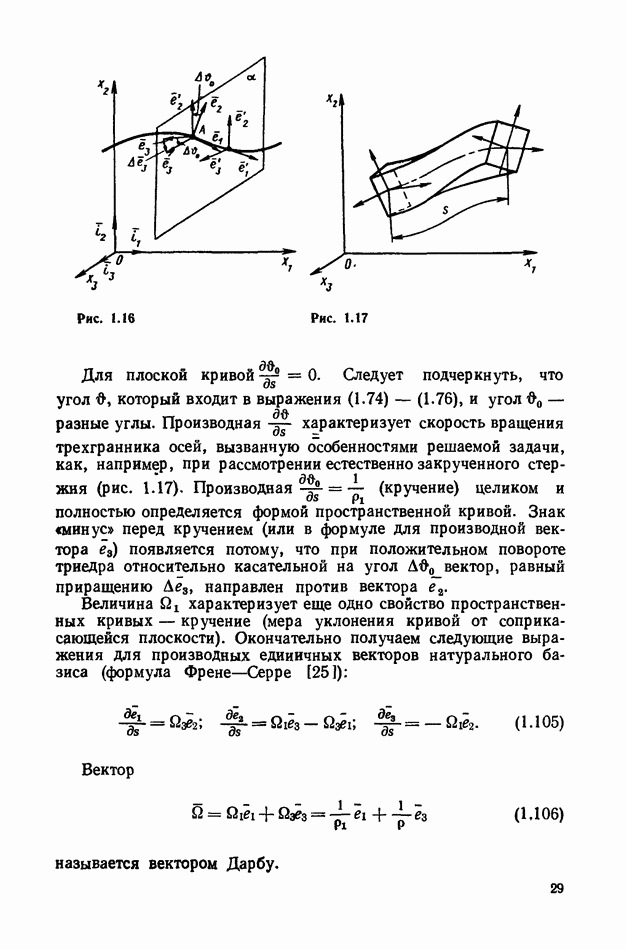
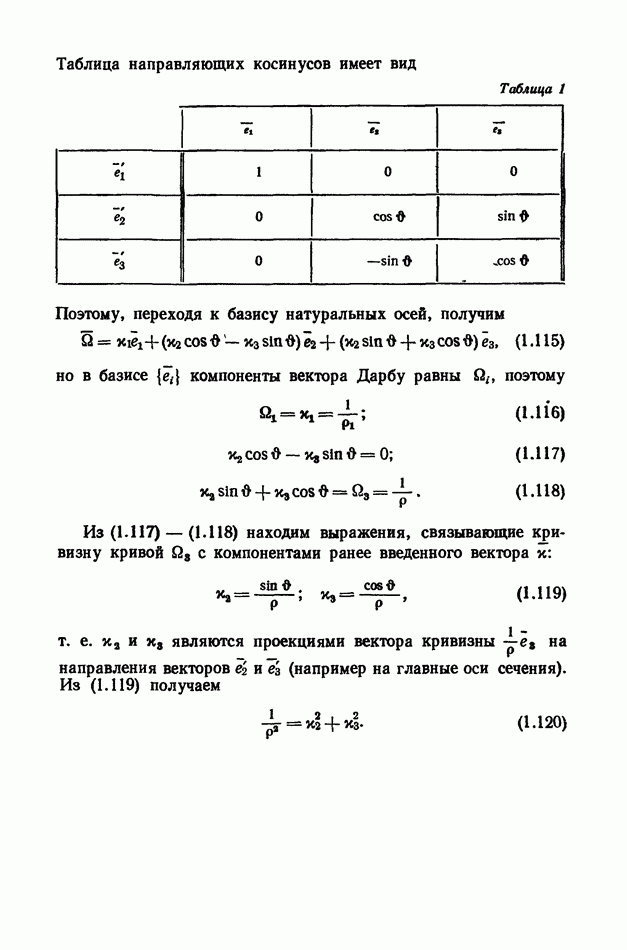
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.