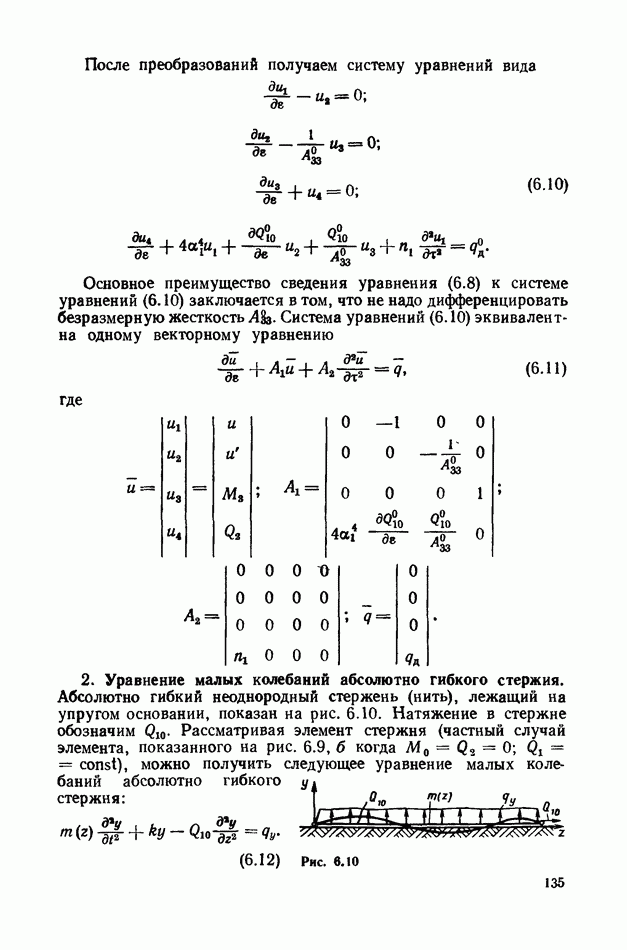
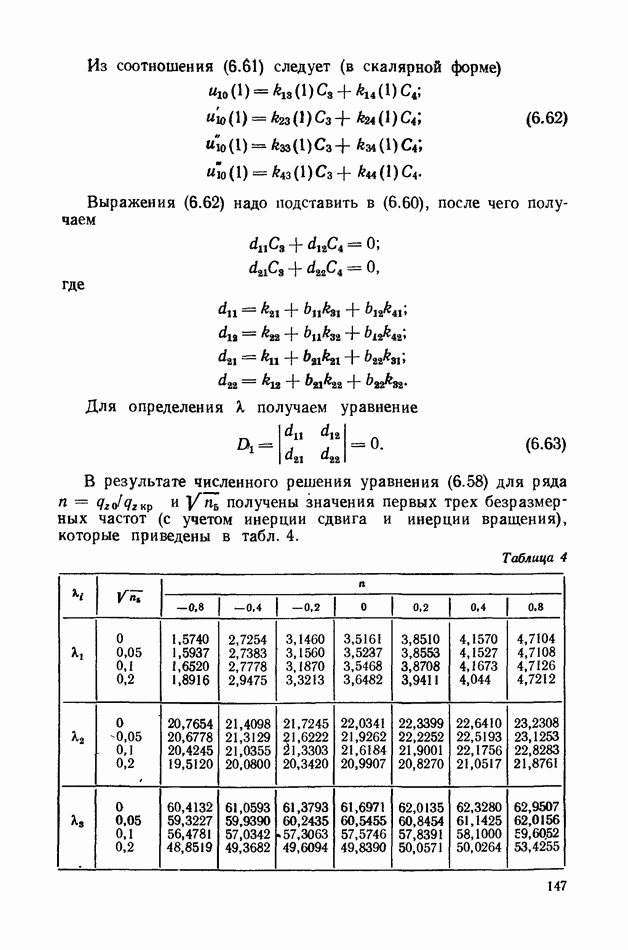
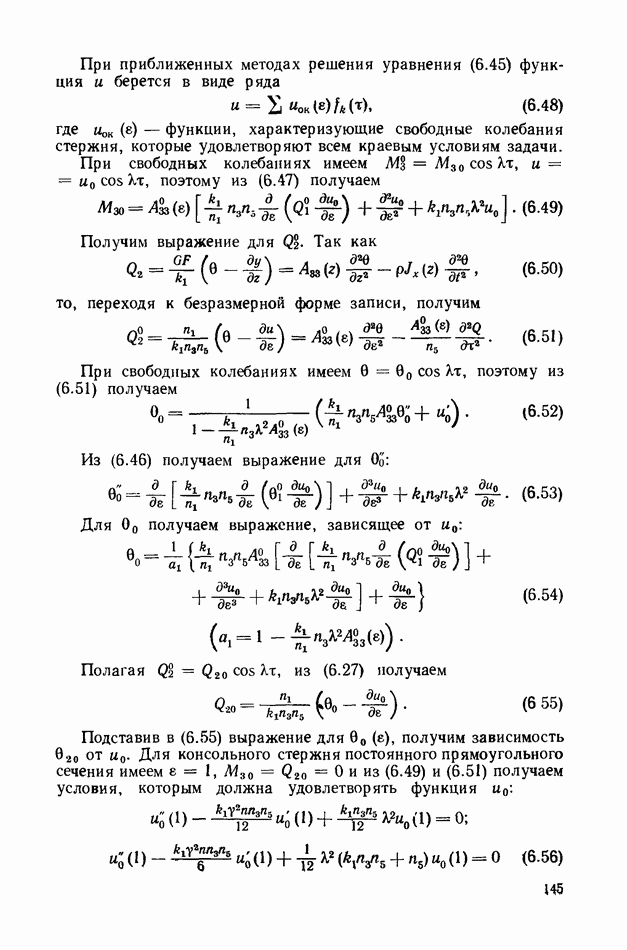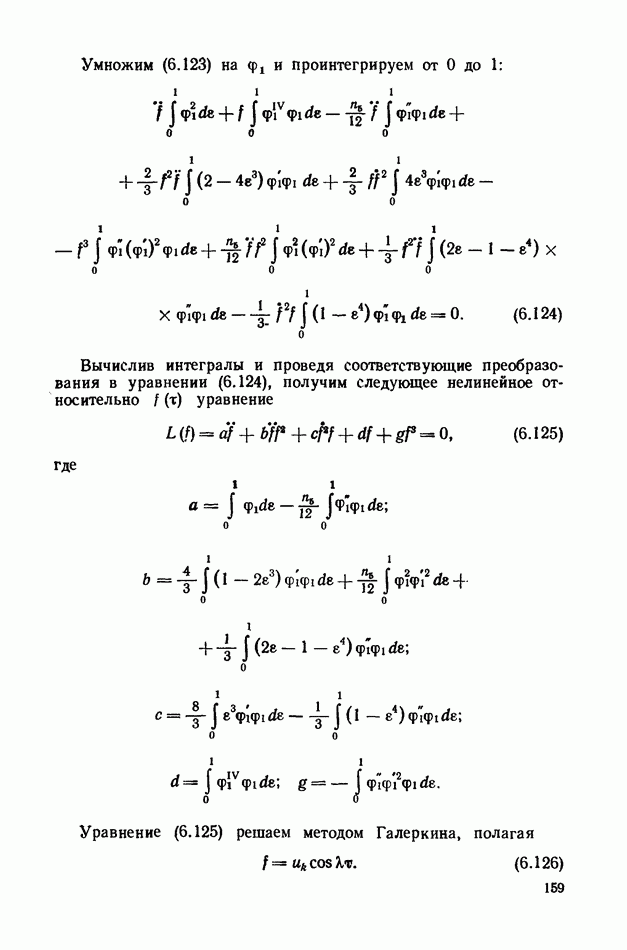| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 6. Динамика прямолинейных гибких стержней
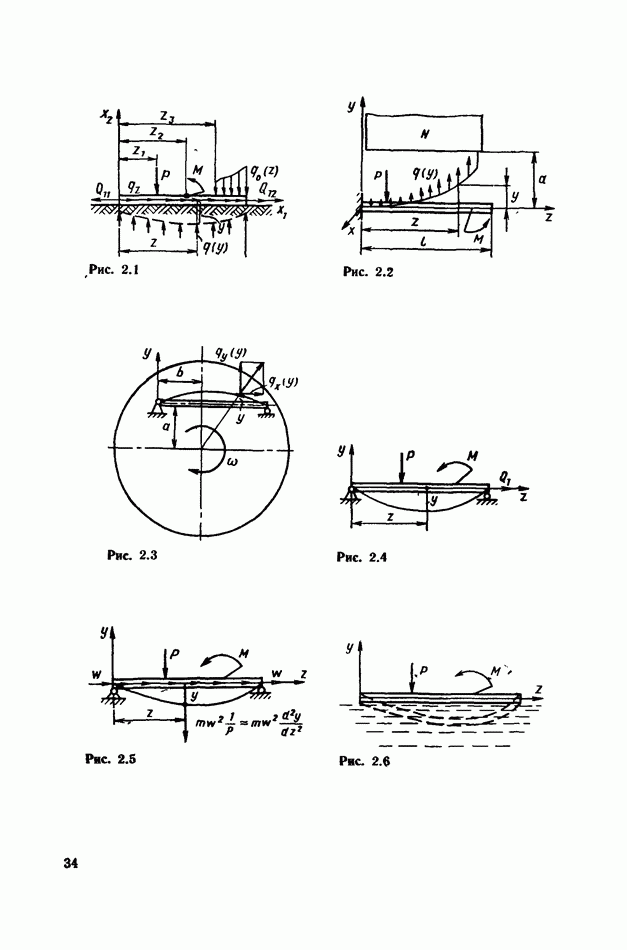
§ 27. Введение
Многие прикладные задачи динамики конструкций требуют анализа динамических процессов, возникающих при работе, и в частности, анализа колебаний элементов конструкций, представляющих собой гибкие и абсолютно гибкие стержни.
Несмотря на кажущуюся простоту расчетной схемы (когда упругие элементы рассматриваются как стержни), возникающие вопросы при исследовании динамических процессов являются не всегда простыми как по применяемым методам решения, так и по содержанию конечных результатов. В качестве примеров на рис. 6.1-6.8 показаны реальные конструкции и элементы конструкций, которые можно рассматривать как гибкие или абсолютно гибкие стержни. На рис. 6.1 показана ракета, которая из-за случайных возмущений или в результате действия управляющих усилий может совершать малые изгибные колебания. Различного вида высокие конструкции, мачты, трубы и т. д. (см. рис. 6.2), находящиеся в потоке воздуха, из-за срыва потока (вихрей Кармана) могут очень сильно раскачаться в плоскости, перпендикулярной к вектору скорости потока. Аналогичные задачи возникают и при расчете висящих мостов, которые в первом приближении могут рассматриваться как одномерные конструкции (стержни). Крыло самолета в первом приближении (см. рис. 6.3) можно рассматривать как стержень [5].

Рис. 6.1

Рис. 6.2

Рис. 6.3

Рис. 6.4

Рис. 6.5

Рис. 6.6
В потоке воздуха на крыло действуют аэродинамические силы, которые могут вызвать нарастающие колебания крыла (флаттер крула). Одна из основных задач при исследовании флаттера элементов конструкций заключается в определении критической скорости потока, при превышении которой возможны нарастающие колебания.
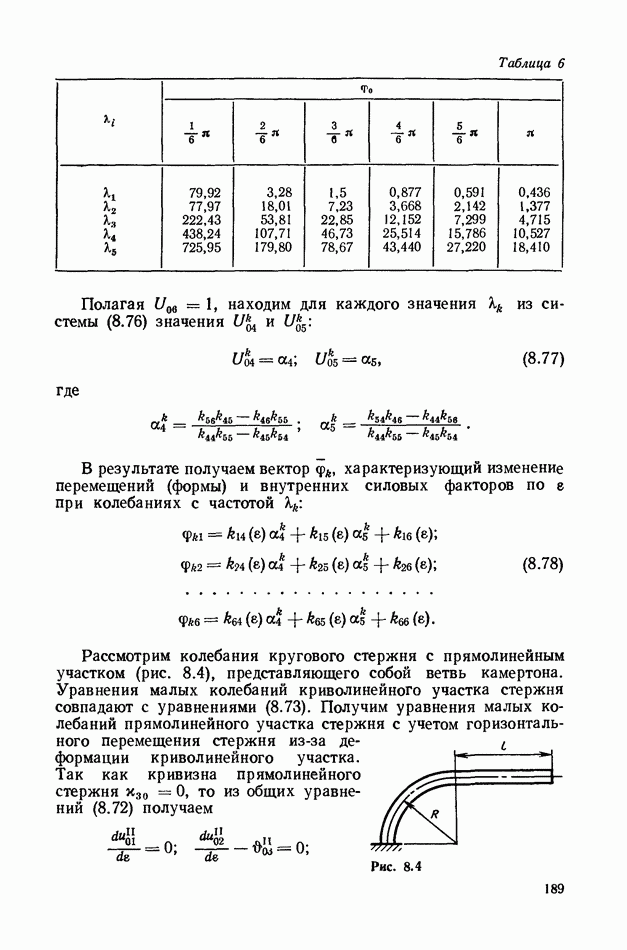
Во многих приборах в качестве упругих элементов используют различного рода стержни, например в приборах времени (в часах) спиральные стержни (см. рис. 6.3) [45, 49], от работы которых зависит точность хода часов. При определении периода автоколебаний балансира требуется учитывать инерционность спирали, что приводит к необходимости исследования колебаний криволинейного стержня. В ряде приборов (в том числе и в приборах времени) используют камертоны (см. рис. 6.5) [8, 9, 49], например при определении ускорения движущегося тела. На ускоренно движущемся объекте ветви камертона нагружаются осевой инерционной нагрузкой, от которой зависят частоты колебаний камертона. По замеренной, первой частоте колебаний можно определить ускорение объекта.
При сверлении глубоких отверстий (см. рис. 6.6) [40] для охлаждения сверла в зону резания и удаления стружки подается жидкость, которая существенно влияет на режим сверления. В зависимости от параметров потока жидкости (скорости и давления) возможны неустойчивые изгибные колебания вращающегося сверла в отверстии. Эта задача аналогична классической задаче об устойчивости шипа в подшипнике [5]. Движущаяся в намоточном устройстве нить показана на рис. 6.7. Из-за неравномерности вращения катушек возникают ее колебания, которые отрицательно сказываются на работе устройства. Цилиндрические пружины (см. рис. 6.8), широко распространенные в машиностроении и приборостроении, также относятся к стержням, но к более сложным — пространственно-криволинейным.

Рис. 6.12

Рис. 7.13
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. Сведения из векторного анализа
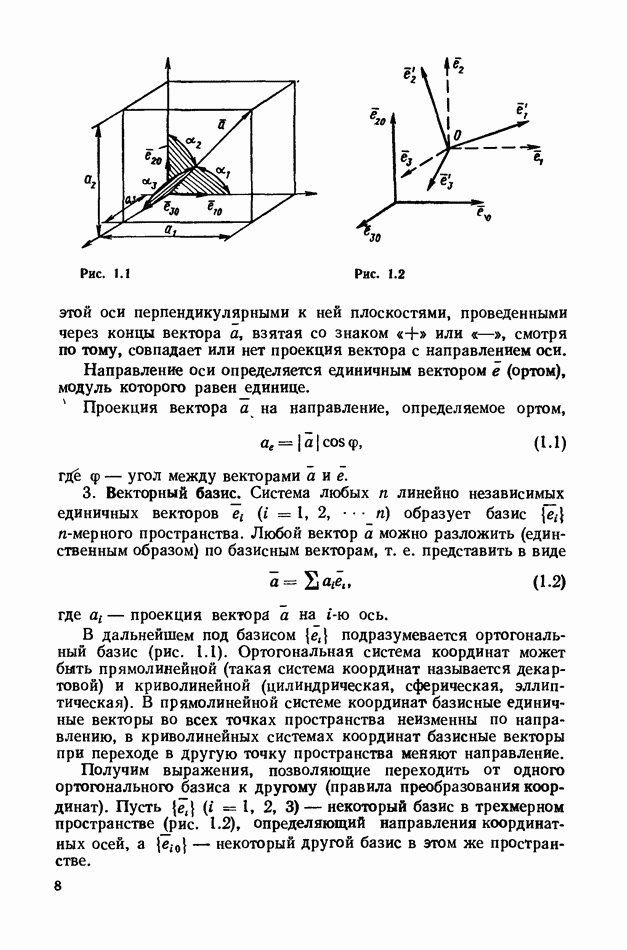
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
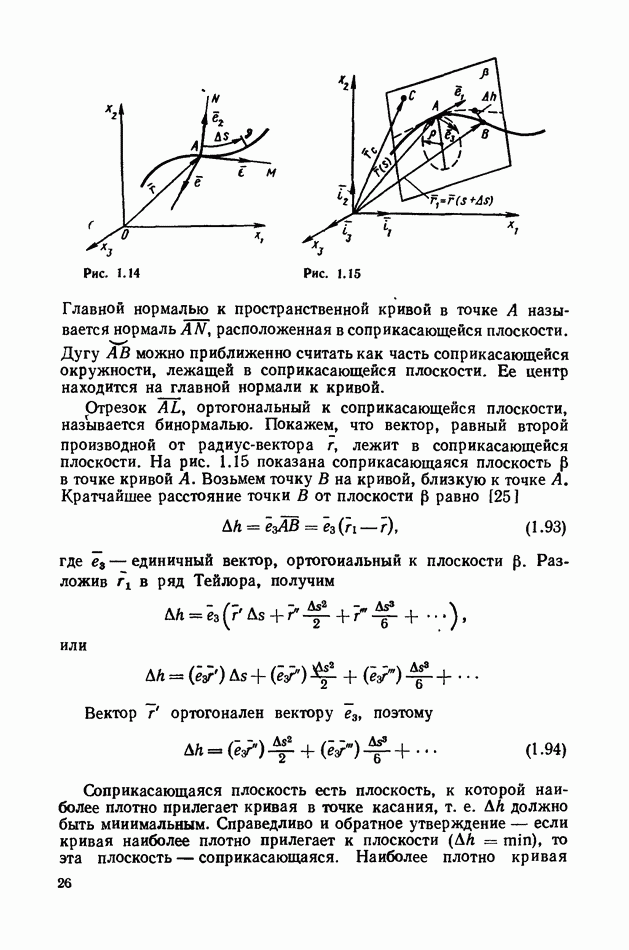
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
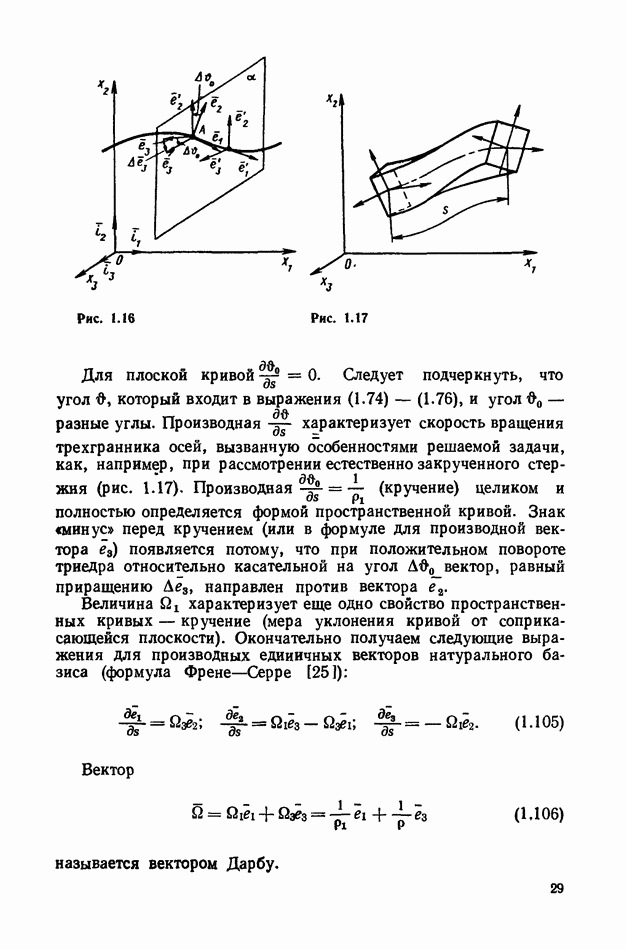
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
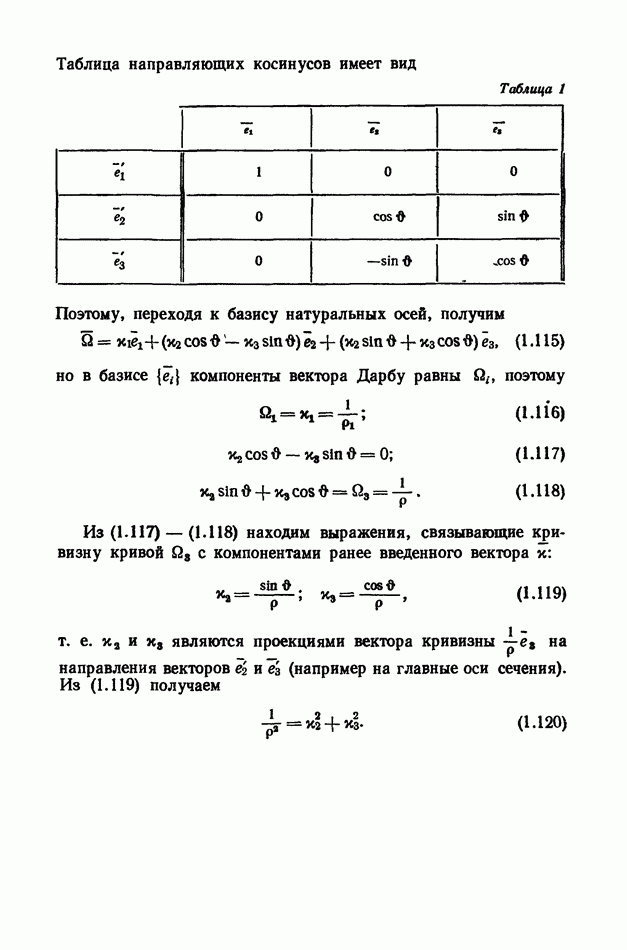
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
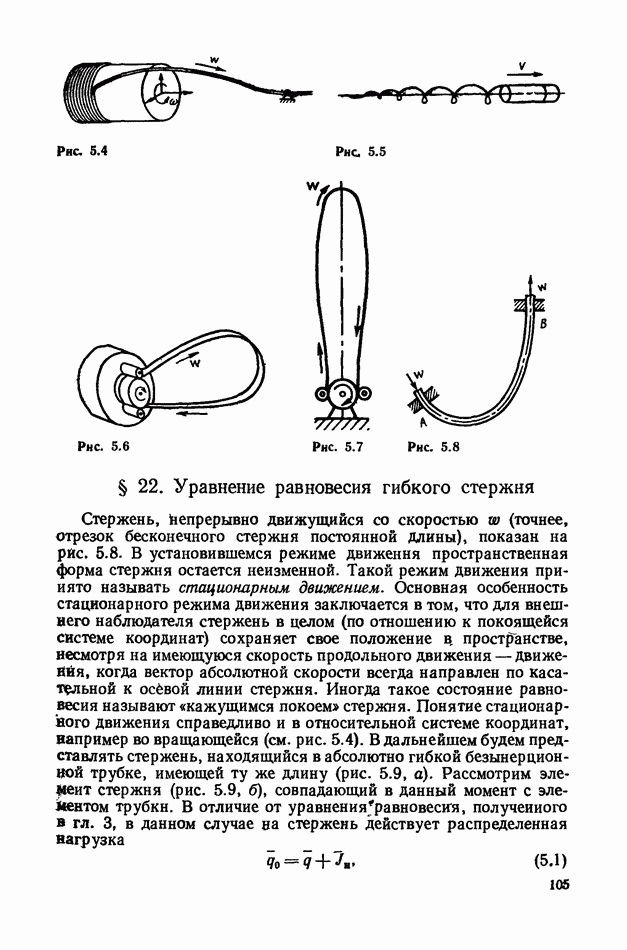
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
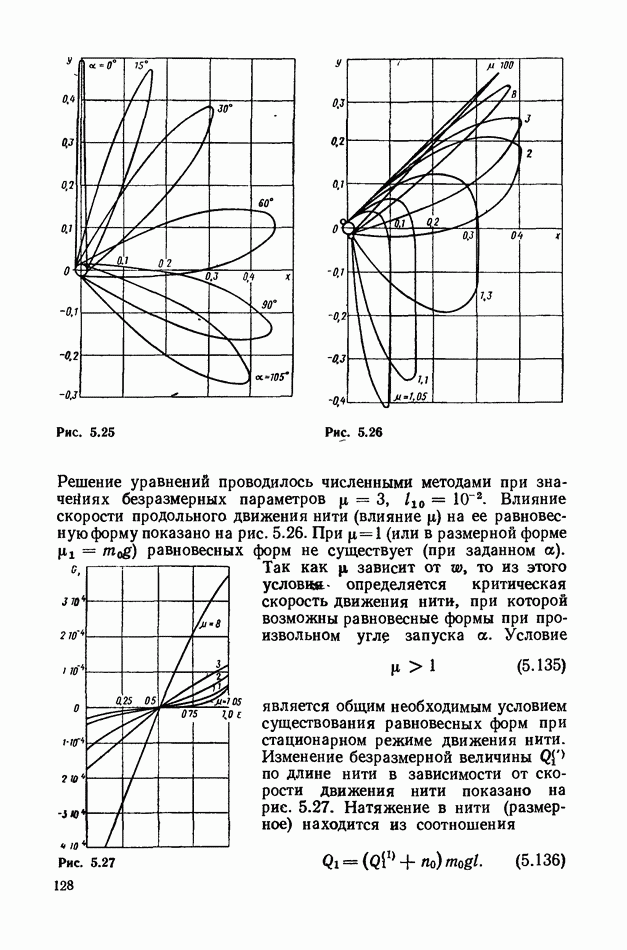
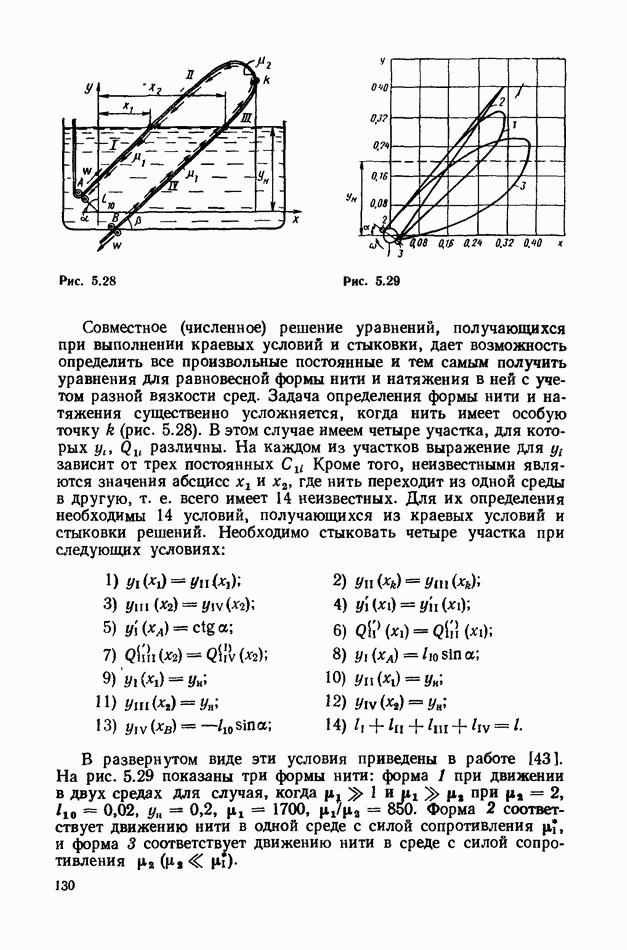
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.