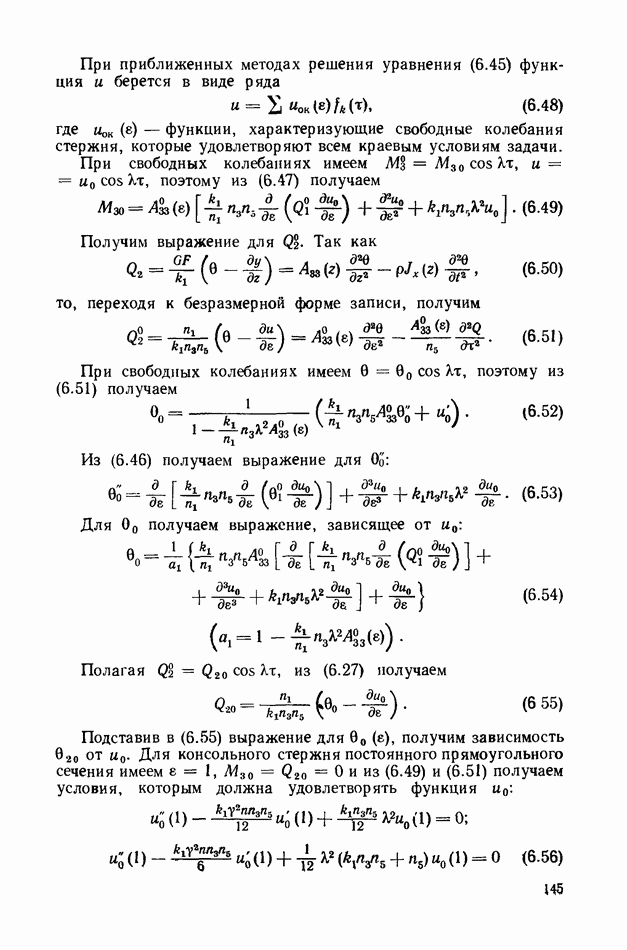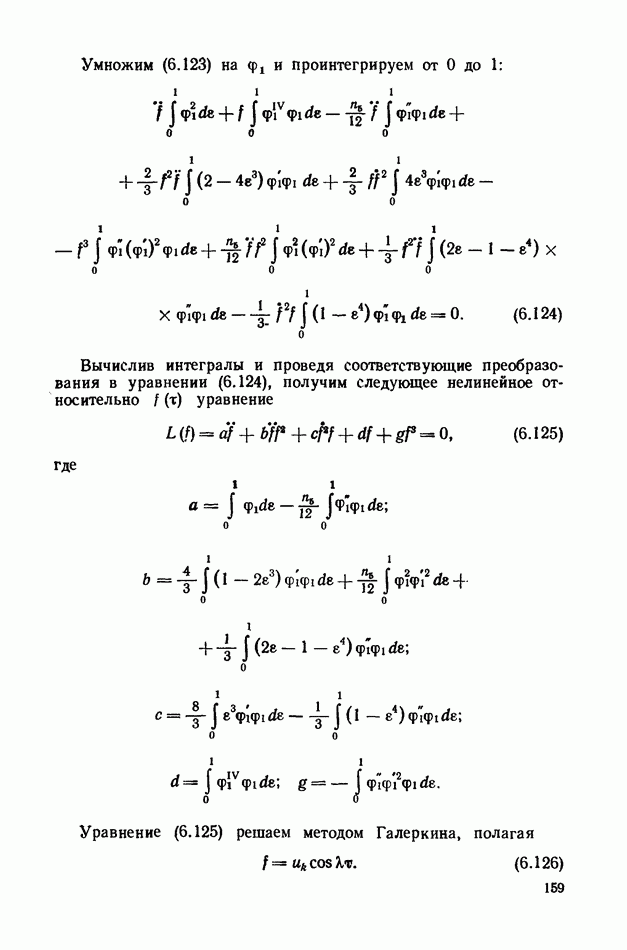| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 33. Свободные нелинейные колебания стержня
1. Вывод нелинейных уравнений колебаний гибкого стержня.
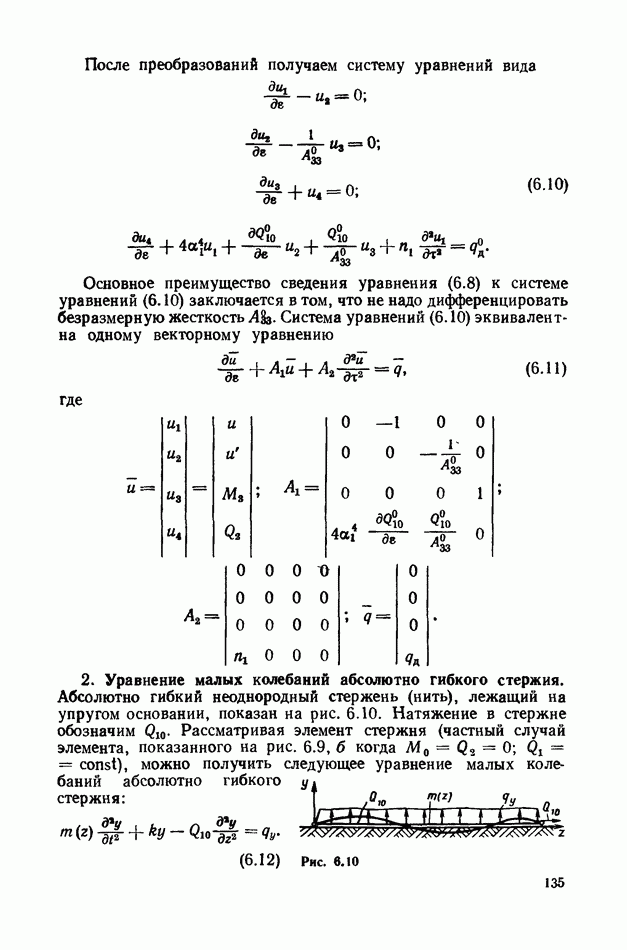
Элемент стержня с действующими на него силами и моментами (включая момент инерции вращения) показан на рис. 6.16. Проектируя силы на оси  соответственно, имеем два уравнения вида
соответственно, имеем два уравнения вида

где


Рис. 6.16
После преобразований из уравнений (6.99) и (6.100) получаем

Сумма моментов, действующих на элемент, равна

где

После преобразований получаем выражение

Умножим (6.101) на  и сложим с (6.102):
и сложим с (6.102):

где 
Продифференцируем 

Так как

то получаем следующее выражение:

Разделив действительную и мнимую части в уравнении (6.109), получим два нелинейных уравнения

В результате получаем систему трех уравнений (6.110), (6.111), и (6.104) с тремя неизвестными,  стержень не действуют внешние силы, направленные по оси стержня. Поэтому продольное усилие
стержень не действуют внешние силы, направленные по оси стержня. Поэтому продольное усилие  вызвано силами инерции из-за смещений элементов стержня по направлению к оси
вызвано силами инерции из-за смещений элементов стержня по направлению к оси  . В линейной постановке принимают, что смещения элементов при колебаниях происходят только по оси у. Горизонтальные смещения элементов стержня в первом приближении пропорциональны квадратам смещений по оси у, поэтому сила
. В линейной постановке принимают, что смещения элементов при колебаниях происходят только по оси у. Горизонтальные смещения элементов стержня в первом приближении пропорциональны квадратам смещений по оси у, поэтому сила  нелинейно зависит от перемещений по оси у. Уравнение (6.110) содержит как линейные слагаемые, так и нелинейные, т. е. является основным уравнением, описывающим нелинейные колебания. Из этого уравнения в частном случае получается уравнение линейных колебаний стержня. Уравнение (6.111) является чисто нелинейным и при линейном рассмотрении обычно не учитывается.
нелинейно зависит от перемещений по оси у. Уравнение (6.110) содержит как линейные слагаемые, так и нелинейные, т. е. является основным уравнением, описывающим нелинейные колебания. Из этого уравнения в частном случае получается уравнение линейных колебаний стержня. Уравнение (6.111) является чисто нелинейным и при линейном рассмотрении обычно не учитывается.
При точном решении система уравнений решается совместно, однако это возможно только численными методами. Ограничимся приближенным решением, для которого достаточно найти приближенное выражение для продольной силы  Предварительно преобразуем уравнение (6.110), исключив из него силу
Предварительно преобразуем уравнение (6.110), исключив из него силу 

В уравнение (6.112) входит неизвестная сила  возникающая вследствие изгиба стержня. Выражение для
возникающая вследствие изгиба стержня. Выражение для  можно найти, рассмотрев равновесие отсеченной части стержня (см. рис. 6.16):
можно найти, рассмотрев равновесие отсеченной части стержня (см. рис. 6.16):

Определим приближенно силу  задавшись вертикальными смещениями в виде
задавшись вертикальными смещениями в виде  тогда производные
тогда производные  и по координате
и по координате 

Выражение для после разложения в ряд принимает вид (ограничимся только двумя слагаемыми ряда)

Получим выражение для  и для вторых производных
и для вторых производных  по
по  которые входят в выражение (6.113):
которые входят в выражение (6.113):

Подставив выражения (6.117) и (6.118) в соотношение (6.113), получим

Приведем уравнение (6.112) к безразмерному виду

2. Определение низшей частоты колебаний.
Для решения уравнения (6.120) воспользуемся методом Галеркина, приняв

где  производная по
производная по  от первой собственной функции линейной задачи.
от первой собственной функции линейной задачи.
В линейной постановке имеем  где
где  — первая собственная функция для уравнения
— первая собственная функция для уравнения

Подставив а в уравнение (6.120), получим

Умножим (6.123) на  и проинтегрируем от
и проинтегрируем от  до
до 

Вычислив интегралы и проведя соответствующие преобразования в уравнении (6.124), получим следующее нелинейное относительно  уравнение
уравнение

где

Уравнение (6.125) решаем методом Галеркина, полагая

Подставляя значение функции  и ее производных в уравнение (6.125), определяем ошибку 8:
и ее производных в уравнение (6.125), определяем ошибку 8:

Умножим (6.127) на  проинтегрируем от
проинтегрируем от  до
до  и поставим условие, чтобы
и поставим условие, чтобы

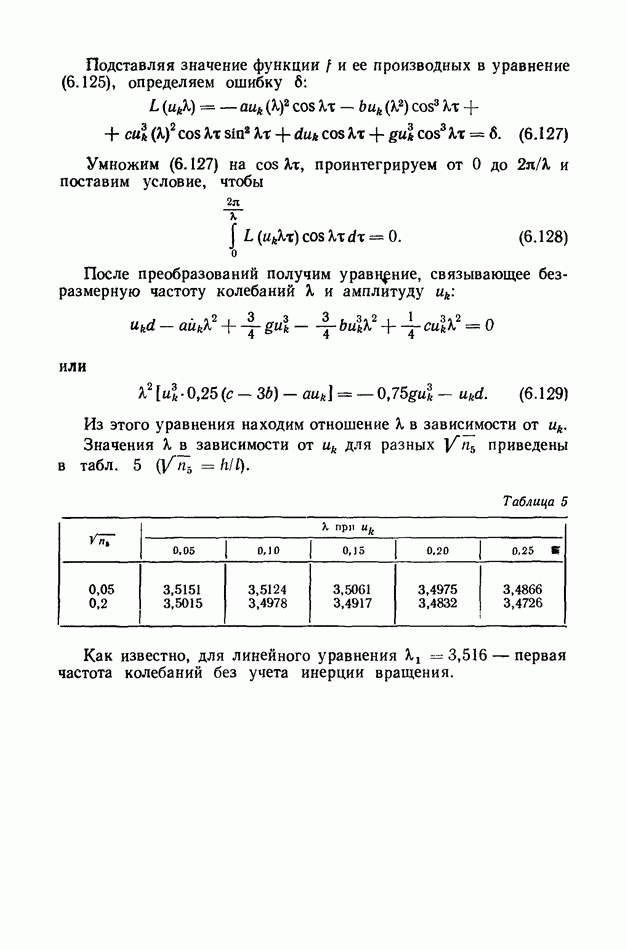
После преобразований получим уравнение, связывающее безразмерную частоту колебаний к и амплитуду 

или

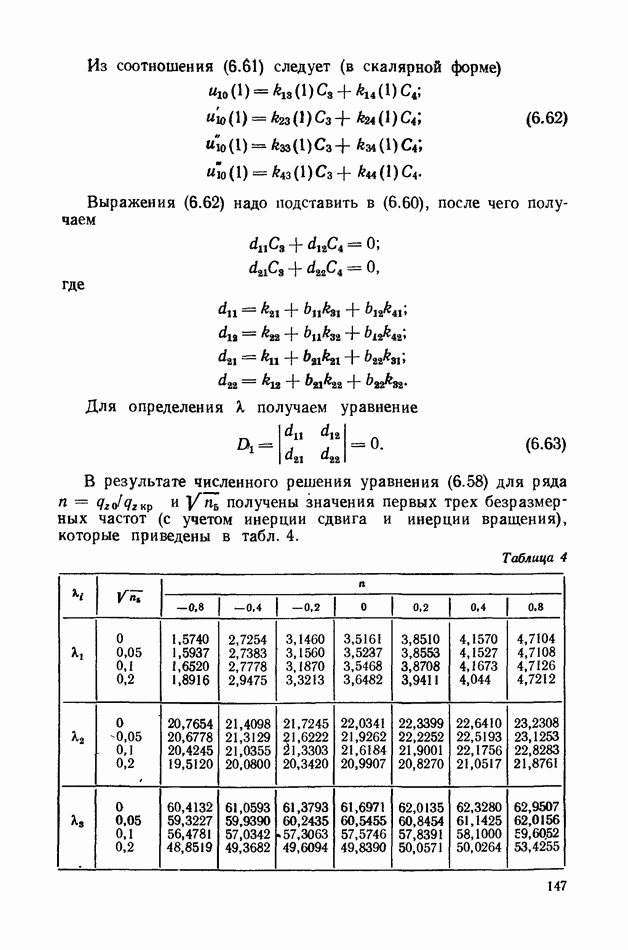
Из этого уравнения находим отношение к в зависимости от  Значения к в зависимости от
Значения к в зависимости от  для разных
для разных  приведены в табл.
приведены в табл. 
Таблица 5 (см. скан)
Как известно, для линейного уравнения  — первая частота колебаний без учета инерции вращения.
— первая частота колебаний без учета инерции вращения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. Сведения из векторного анализа
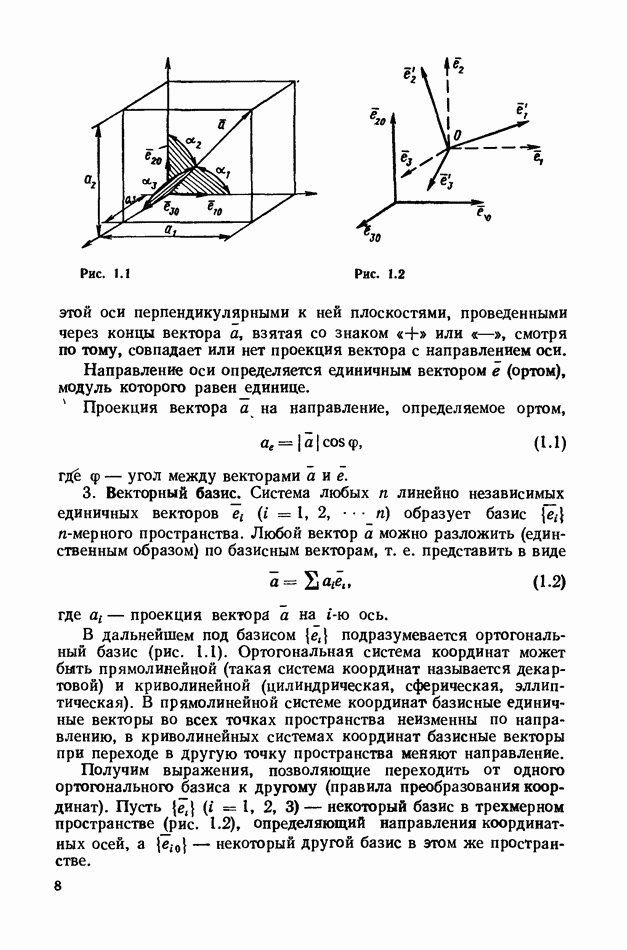
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
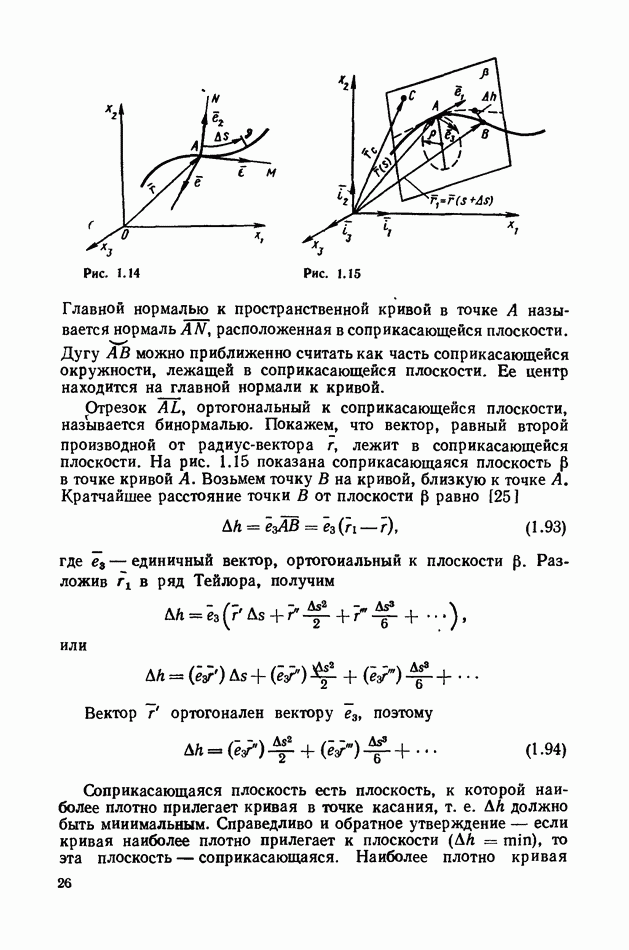
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
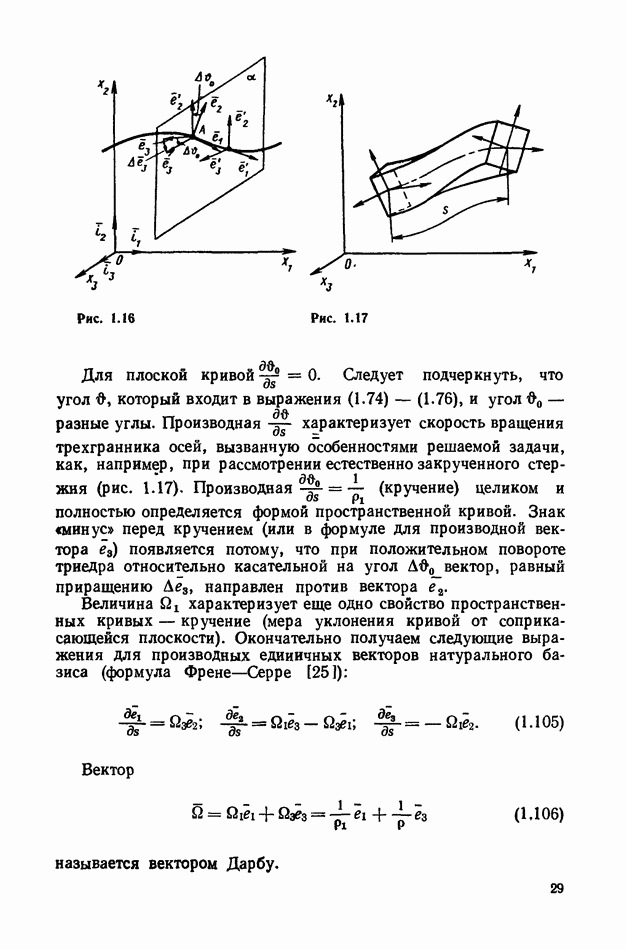
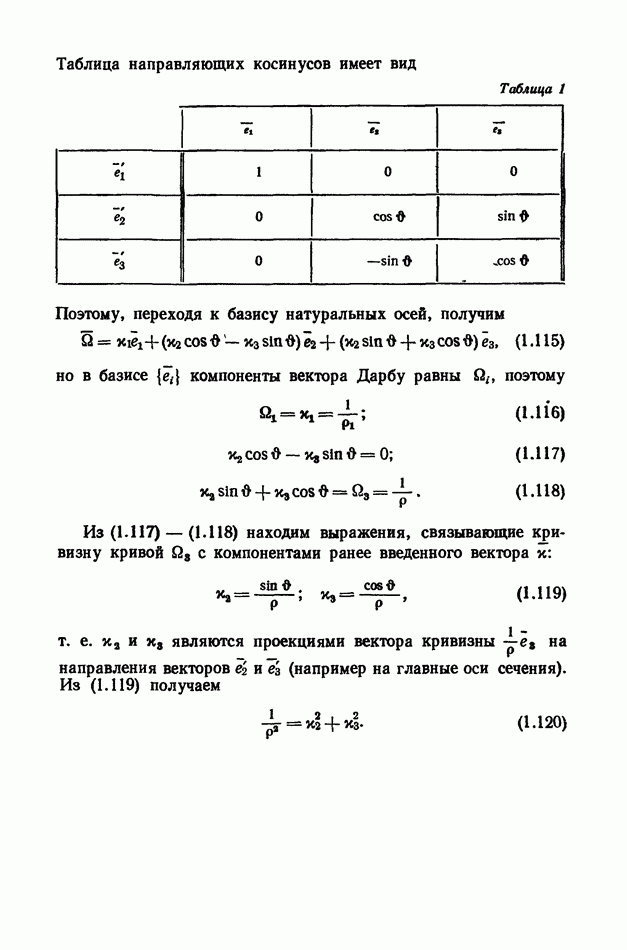
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
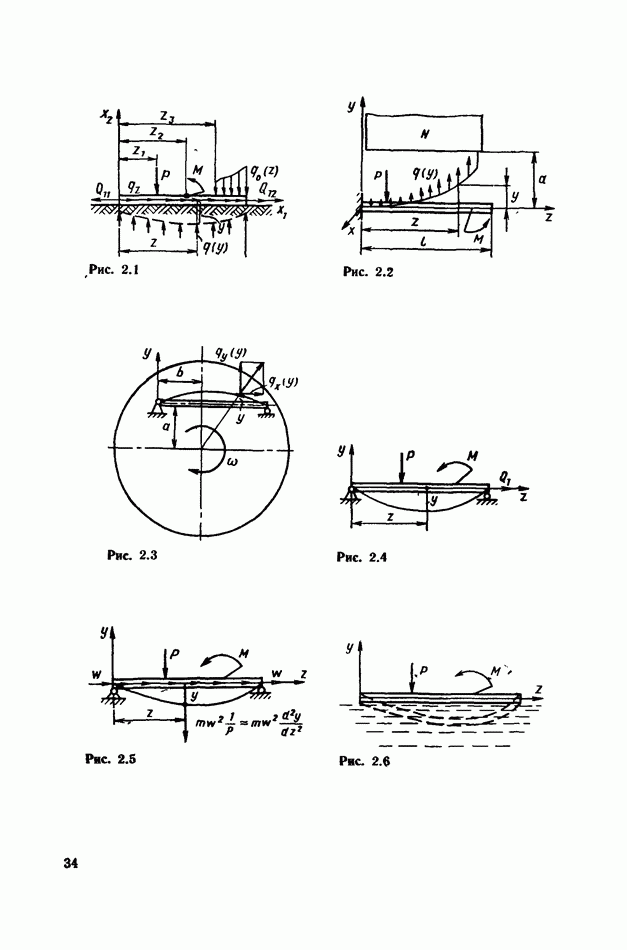
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
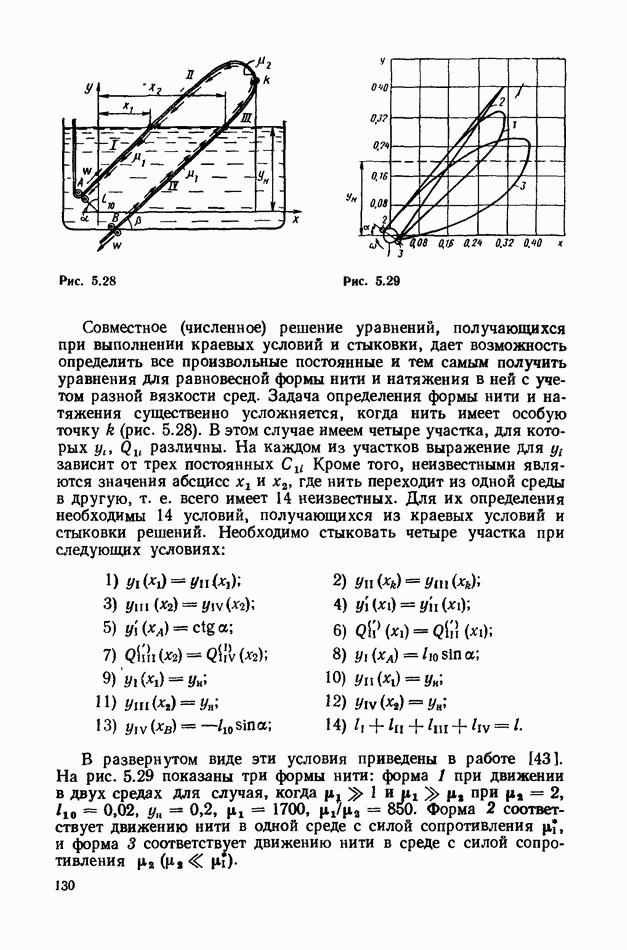
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.