| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 14. Основные теоремы статики нити
Если нить нагружена распределенными силами, направленными по нормали к нити, то натяжение в нити постоянно (теорема 1). Подобный случай нагружения нити имеет место, когда невесомая нить расположена на криволинейной идеально гладкой поверхности (рис. 3.13). Так как в этом случае  то из уравнения (3.102) получаем
то из уравнения (3.102) получаем 
В состоянии равновесия нить, находящаяся на идеально гладкой поверхности, располагается по геодезической линии этой поверхности (теорема 2). Геодезической линией на поверхности называется такая линия, у которой соприкасающаяся плоскость в каждой ее точке проходит через нормаль к поверхности в этой точке. Если нить находится в равновесии, то и любая ее часть находится в равновесии. Рассмотрим элемент нити (рис. 3.14), который находится в равновесии под действием силы натяжения и реакции поверхности 
Предположим, что главная нормаль к нити (вектор  и нормаль к поверхности
и нормаль к поверхности  не совпадают. Векторы
не совпадают. Векторы  лежат в плоскости, ортогональной к вектору
лежат в плоскости, ортогональной к вектору  поэтому
поэтому  Уравнение равновесия элемента нити имеет вид
Уравнение равновесия элемента нити имеет вид

или

Из уравнения (3.113) следует


Рис. 3.13

Рис. 3.14
Два вектора могут быть равными, если они имеют одно и то же направление, т. е. в рассматриваемом случае нормаль к нити совпадает с нормалью к поверхности  Но вектор
Но вектор  лежит в соприкасающейся плоскости, которая проходит через его, значит, линия расположения нити есть геодезическая, что и требовалось показать.
лежит в соприкасающейся плоскости, которая проходит через его, значит, линия расположения нити есть геодезическая, что и требовалось показать.
При равновесии нити в поле параллельных сил она принимает форму плоской кривой, плоскость которой параллельна направлению внешних сил (теорема  поле параллельных сил уравнение равновесия нити имеет вид
поле параллельных сил уравнение равновесия нити имеет вид

где  постоянный по направлению единичный вектор.
постоянный по направлению единичный вектор.
Умножив векторно уравнение (3.115) на вектор  получим
получим

Рассмотрим производную от векторного произведения:

но  поэтому из (3.117) имеем
поэтому из (3.117) имеем

или

Вектор  ортогонален вектору
ортогонален вектору  или, что то же, ортогонален вектору
или, что то же, ортогонален вектору  Кроме того, вектор
Кроме того, вектор  имеет в пространстве неизменное направление, что может быть только тогда, когда нить есть плоская кривая.
имеет в пространстве неизменное направление, что может быть только тогда, когда нить есть плоская кривая.
При равновесии в центральном поле сил нить принимает форму плоской кривой, плоскость которой проходит через центр сил
(теорема 4). Умножим векторио уравнение равновесия на 

так как

то имеем

Рассмотрим производную

Из (3.120) следует

Постоянный вектор  ортогонален вектору
ортогонален вектору  (ортогонален вектору в каждой точке кривой), т. е. форма нити есть плоская кривая.
(ортогонален вектору в каждой точке кривой), т. е. форма нити есть плоская кривая.

Рис. 3.15
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
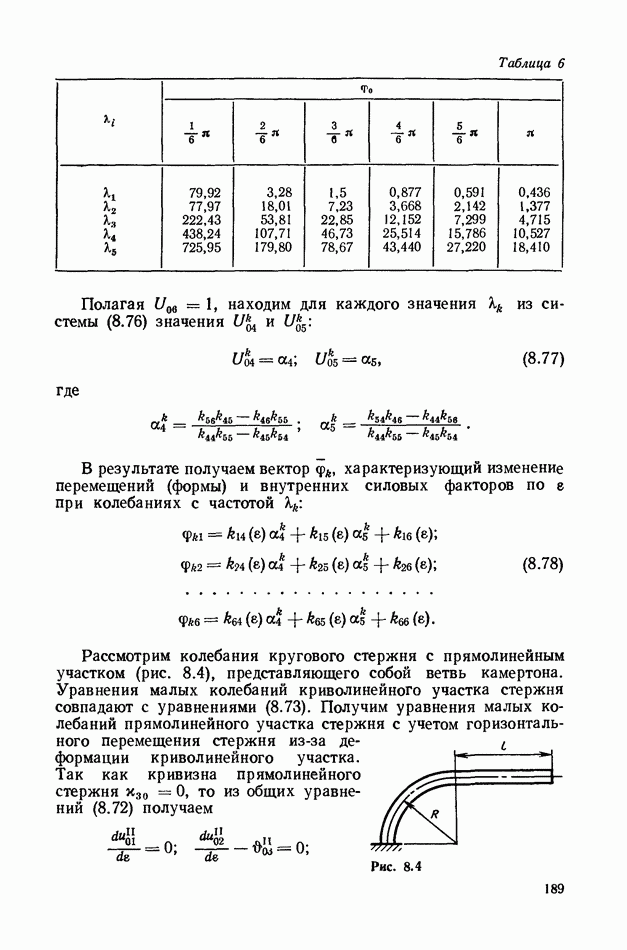
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
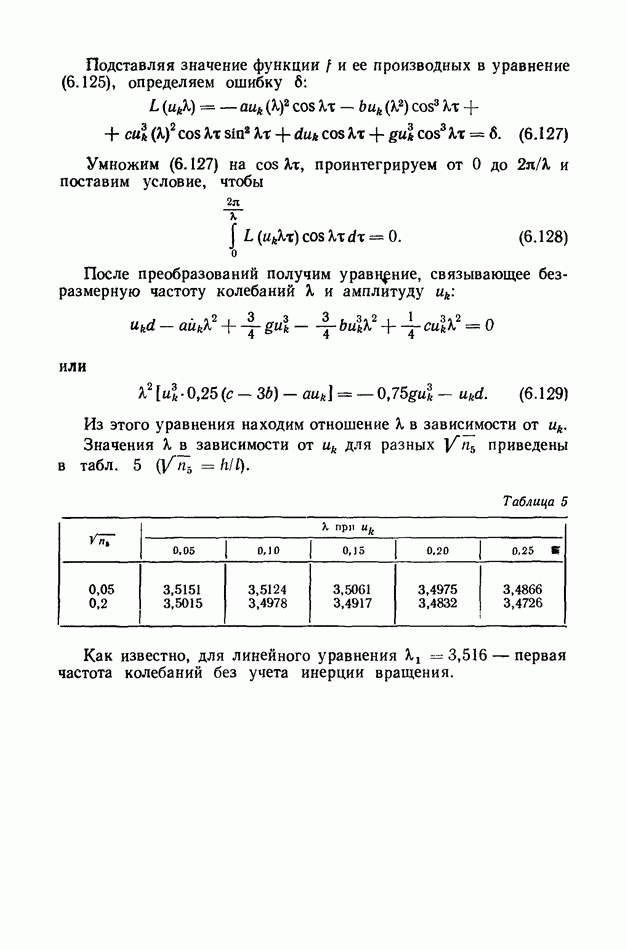
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.