| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 24. Стационарное движение нити в вязкой покоящейся среде
1. Рассмотрим более подробно стационарное движение абсолютно гибкого стержня в покоящейся вязкой среде. Подобного рода задачи возникают, например, при изучении процесса смотки и намотки проводников в радиотехнической и текстильной промышленности (рис. 5.13). Для покрытия изоляцией гибкий проводник пропускают через жидкость, которая при движении проводника в воздухе высыхает и покрывает его изолирующим слоем (рис. 5.14). С точки зрения производительности технологического процесса скорость движения провода желательно сделать как

Рис. 5.13

Рис. 5.14
можно больше, однако при ее увеличении растут силы сопротивления (А и, как следствие, осевое усилие  Поэтому для каждого типа провода и размера
Поэтому для каждого типа провода и размера  свободного участка между выходом и входом существует своя предельная скорость (с учетом аэродинамических сил), при которой максимальные осевые напряжения не превышают допустимых напряжений. Для назначения оптимальных режимов процесса необходимо знать зависимость напряжения в проводе от скорости его продольного
свободного участка между выходом и входом существует своя предельная скорость (с учетом аэродинамических сил), при которой максимальные осевые напряжения не превышают допустимых напряжений. Для назначения оптимальных режимов процесса необходимо знать зависимость напряжения в проводе от скорости его продольного  движения.
движения.
Под действием на нить силы веса и осевой силы сопротивления она в равновесии приобретает форму плоской кривой. Поэтому из системы (5.42)-(5.43) получаем (при  в безразмерной форме следующие уравнения:
в безразмерной форме следующие уравнения:

К уравнениям (5.54)-(5.55) следует добавить уравнение

Сила сопротивления  считается постоянной по длине нити. Экспериментальному определению сил сопротивления при продольном движении нити посвящено много работ [1, 14], из которых следует, что сила сопротивления пропорциональна квадрату скорости движения нити, т. е.
считается постоянной по длине нити. Экспериментальному определению сил сопротивления при продольном движении нити посвящено много работ [1, 14], из которых следует, что сила сопротивления пропорциональна квадрату скорости движения нити, т. е.  Зависимость
Зависимость  от скорости
от скорости  необходима для определения продольной скорости движения нити. Коэффициент пропорциональности а определяется экспериментально [14].
необходима для определения продольной скорости движения нити. Коэффициент пропорциональности а определяется экспериментально [14].
Интегрируя уравнения (5.54) и (5.55), получаем [39]

множив (1) на  и (2) на у, сложив полученные выражения и проинтегрировав по в, получим [с учетом (5.56)]
и (2) на у, сложив полученные выражения и проинтегрировав по в, получим [с учетом (5.56)]

Исключая  из соотношений (5.57) и (5.58), имеем
из соотношений (5.57) и (5.58), имеем

Из (5.60) и (5.61) находим х и у, которые подставляем в (5.56); в результате имеем

Соотношение (5.61) можно преобразовать к виду

Введем новые переменные  полагая
полагая

после чего уравнение (5.63) принимает вид

Интегрируя (5.65) и переходя к старым переменным, получаем

Следует отметить, что полученное выражение (5.66) справедливо только при  так как только в этом случае
так как только в этом случае  конечны.
конечны.
Для определения четырех постоянных  имеем четыре краевых условий, например для случая, показанного на рис.
имеем четыре краевых условий, например для случая, показанного на рис. 
Из уравнений (5.62) и (5.66) получаем четыре алгебраических уравнения для определения 

В уравнениях (5.69) и  можно исключить, воспользовавшись соотношениями (5.64). Определив
можно исключить, воспользовавшись соотношениями (5.64). Определив  из (5.66) находим
из (5.66) находим  а затем из
а затем из  Определив
Определив  , находим из
, находим из  а затем
а затем


Рис. 5.15
Решение задачи существенно упрощается в зависимости от выбранных осей. Например, для осей  рис. 5.13) имеем следующие краевые условия:
рис. 5.13) имеем следующие краевые условия:  и, что приводит к более простым уравнениям для определения произвольных постоянных. В этом случае получаем систему уравнений (исключая
и, что приводит к более простым уравнениям для определения произвольных постоянных. В этом случае получаем систему уравнений (исключая  для определения
для определения 

2. Рассмотрим частный случай краевых условий, показанный на рис. 5.15. Имеем следующие краевые условия:  Для определения
Для определения  получаем систему уравнений
получаем систему уравнений

При  выражение (5.75) обращается в тождество, а из соотношений (5.64) получаем
выражение (5.75) обращается в тождество, а из соотношений (5.64) получаем

При этих значениях  из уравнений (5.73) и (5.74) можно определить
из уравнений (5.73) и (5.74) можно определить 

Знак произвольной постоянной  найдем из условия, что при
найдем из условия, что при  Из уравнения (5.60) получаем
Из уравнения (5.60) получаем 
откуда следует, что  должно быть отрицательным. Произвольную постоянную
должно быть отрицательным. Произвольную постоянную  находят из уравнения (5.69):
находят из уравнения (5.69):

Определив  из (5.66), получаем уравнения для определения
из (5.66), получаем уравнения для определения 

Определив из  находим
находим  [воспользовавшись соотношением (5.62)]:
[воспользовавшись соотношением (5.62)]:

Две формы равновесия нити при стационарном движении для безразмерного параметра  при двух значениях безразмерной силы сопротивления
при двух значениях безразмерной силы сопротивления  показаны на рис. 5.16. Натяжение в нити определяем из выражения
показаны на рис. 5.16. Натяжение в нити определяем из выражения

График изменения  в зависимости от
в зависимости от  показан на рис. 5.17.
показан на рис. 5.17.
Из выражения (5.81) следует, что  в точках
в точках  (рис. 5.16) обращается в нуль, т. е. натяжение в нити в этих точках равно
(рис. 5.16) обращается в нуль, т. е. натяжение в нити в этих точках равно 
3. Для нити дополнительным необходимым условием существования равновесных форм (кроме независимости всех величин от времени) является положительность натяжения  так как сжимающие усилия она воспринимать не может. Из графика рис. 5.17 следует, что натяжение в нити
так как сжимающие усилия она воспринимать не может. Из графика рис. 5.17 следует, что натяжение в нити  достигает минимального значения при
достигает минимального значения при  т. е.
т. е.


Рис. 5.16

Рис. 5.17

Рис. 5.18

Рис. 5.19
Предельное значение скорости движения нити при которой возможен стационарный режим движения (возможна равновесная форма при стационарном движении в покоящейся вязкой среде), находят из условия

Возвращаясь к явным выражениям для  в зависимости от
в зависимости от  (считая, что
(считая, что  пропорционально квадрату скорости), из (5.82) получим
пропорционально квадрату скорости), из (5.82) получим

Из соотношения (5.83) следует, что стационарное движение нити в поле сил тяжести возможно только при наличии вязкой среда  но не для всякой нити возможен стационарный режим. Стационарный режим возможен, если предельная скорость, получающаяся из (5.82), есть действительная величина, что имеет место при
но не для всякой нити возможен стационарный режим. Стационарный режим возможен, если предельная скорость, получающаяся из (5.82), есть действительная величина, что имеет место при

Получим еще одно ограничение на скорость движения нити. Из выражения (5.80) следует, что  принимает действительные значения при выполнении условия
принимает действительные значения при выполнении условия  или
или

На рис. 5.18 показаны области значений  для которых выполняются неравенства
для которых выполняются неравенства  Все три неравенства выполняются в области
Все три неравенства выполняются в области  являющейся областью возможных значений скорости движения нити. При этих скоростях возможен стационарный режим нити для случая, когда она движется от точки А к В (см. рис. 5.15). Следует подчеркнуть, что область I получена для случая, когда сила сопротивления
являющейся областью возможных значений скорости движения нити. При этих скоростях возможен стационарный режим нити для случая, когда она движется от точки А к В (см. рис. 5.15). Следует подчеркнуть, что область I получена для случая, когда сила сопротивления  пропорциональна квадрату скорости. Возможны, конечно, и другие (экспериментально полученные) зависимости
пропорциональна квадрату скорости. Возможны, конечно, и другие (экспериментально полученные) зависимости  от
от 
Рассмотрим случай, когда нить движется из точки В в точку А (рис. 5.19). При изменении направления движения нити изменйтся
направление сил аэродинамического сопротивления  в предыдущем решении следует заменить
в предыдущем решении следует заменить  на
на  а выражение для произвольной постоянной
а выражение для произвольной постоянной  взять с плюсом.
взять с плюсом.
Выражение для силы в этом случае принимает вид

Сохраняя начало отсчета в точке А, из (5.86) следует, что минимальное натяжение имеет место в точке В:

Предельное значение скорости получаем из (5.87), полагая 

Из (5.88) следует, что

Неравенство (5.85) остается без изменения. На рис. 5.20 показана область II, где выполняются все неравенства (5.85), (5.88) и (5.89). Область II есть область значений скоростей продольного движения нити [при движении из точки  (рис. 5.18)], при которых возможен стационарный режим. Для обоих рассмотренных случаев движения нити (при
(рис. 5.18)], при которых возможен стационарный режим. Для обоих рассмотренных случаев движения нити (при  имеется одна и та же критическая скорость движения, которую находим из условия
имеется одна и та же критическая скорость движения, которую находим из условия

При  (что эквивалентно
(что эквивалентно  стационарное движение существовать не может, так как координаты точек нити, как следует из (5.80), становятся мнимыми.
стационарное движение существовать не может, так как координаты точек нити, как следует из (5.80), становятся мнимыми.
4. Рассмотрим движение нити по горизонтальной поверхности (рис. 5.21). 3 этом случае силы веса нити на оси  не дают проекций. Сила сопротивления
не дают проекций. Сила сопротивления  равна сумме двух слагаемых, зависящих от аэродинамического сопротивления нити и от трения между нитью и плоскостью. Считаем, что суммарная сила сопротивления зависит только от скорости движения нити, как и в предыдущем случае.
равна сумме двух слагаемых, зависящих от аэродинамического сопротивления нити и от трения между нитью и плоскостью. Считаем, что суммарная сила сопротивления зависит только от скорости движения нити, как и в предыдущем случае.

Рис. 5.20

Рис. 5.21
Для того чтобы исследовать этот случай, необходимо изменить только уравнение (5.55), принимающее вид

Интегрируя уравнения (5.54) и (5.91), получим

Из (5.92) и (5.93) с учетом (5.56) находим

Из уравнений (5.92) и (5.93) получим (после исключения 

Исключая из  и интегрируя получающееся уравнение, имеем
и интегрируя получающееся уравнение, имеем

Так как при  то из (5.96) получаем
то из (5.96) получаем  Исключая
Исключая  из (5.96), имеем
из (5.96), имеем

Из уравнений (5.95) и (5.97) следует

Удовлетворяя краевым условиям по  получаем из (5.98) два уравнения для определения
получаем из (5.98) два уравнения для определения 

и находим

Оставшуюся произвольную постоянную  найдем из уравнения (5.96) при
найдем из уравнения (5.96) при 

т. е.  Определив произвольные постоянные, находим
Определив произвольные постоянные, находим  [из соотношений (5.97) и (5.98)]:
[из соотношений (5.97) и (5.98)]:

Интересная особенность данной задачи заключается в том, что равновесная форма нити представляет собой две сходящиеся в точке  прямые (рис. 5.22). Натяжение в нити
прямые (рис. 5.22). Натяжение в нити

В точке  натяжение в нити равно
натяжение в нити равно  Этот результат можно получить и из теоремы об изменении количества движения элемента нити. Предельное значение скорости, при котором возможно стационарное движение, получим из (5.104):
Этот результат можно получить и из теоремы об изменении количества движения элемента нити. Предельное значение скорости, при котором возможно стационарное движение, получим из (5.104):

т. е. при  стационарное движение возможно при любой скорости. При движении нити в горизонтальной плоскости форма нити и натяжение в ней не зависят от направления движения в отличие от случая движения нити в вертикальной плоскости.
стационарное движение возможно при любой скорости. При движении нити в горизонтальной плоскости форма нити и натяжение в ней не зависят от направления движения в отличие от случая движения нити в вертикальной плоскости.
5. Рассмотренное в пп. 3 и 4 стационарное движение является частным случаем возможного в реальных условиях стационарного движения, поэтому более подробно остановимся на общем случае (рис. 5.23). Начало системы координат взято в точке, делящей расстояние между точками выхода А и входом В пополам, что упрощает решение.
Из рис. 5.23 следует, что на кривой, которая характеризует форму нити при стационарном режиме движения, имеется точка  где натяжение
где натяжение  равно нулю, и из уравнения (5.51) получаем (так как в точке
равно нулю, и из уравнения (5.51) получаем (так как в точке 

откуда и следует, что  (так как в общем случае
(так как в общем случае  (в точке
(в точке  выполняется условие
выполняется условие  [это следует из уравнения (5.57)]. Перейдем в уравнении (5.55) от
[это следует из уравнения (5.57)]. Перейдем в уравнении (5.55) от  к независимой переменной
к независимой переменной  используя соотношение
используя соотношение  Величину
Величину  из (5.55) исключим, воспользовавшись уравнением (5.57), после чего получим
из (5.55) исключим, воспользовавшись уравнением (5.57), после чего получим

В точке  т. е. точка
т. е. точка  есть особая точка для уравнения (5.106), поэтому свободную часть нити представим
есть особая точка для уравнения (5.106), поэтому свободную часть нити представим

Рис. 5.22

Рис. 5.23
состоящей из ветвей  и
и  Стыкуя решения для каждой из ветвей в точке
Стыкуя решения для каждой из ветвей в точке  получим общее решение. Интегрируя уравнения (5.106), имеем (для участка
получим общее решение. Интегрируя уравнения (5.106), имеем (для участка 

После второго интегрирования получаем для участка  (учитывая, что при
(учитывая, что при 

Аналогичное выражение можно получить и для участка 

Для определения пяти произвольных постоянных имеем: три краевых условия  условие стыковки решений в точке
условие стыковки решений в точке  и условие, связывающее длины участков
и условие, связывающее длины участков 

Из условия стыковки следует 
Подставив в (5.110) выражения для  после преобразований и интегрирования можно получить следующее выражение для
после преобразований и интегрирования можно получить следующее выражение для 

Рассмотрим интегрирование одного из выражений для  более подробно:
более подробно:

где 
Из (5.113) получаем

или

После интегрирования (5.115) получаем (5.111). Так как  , то из (5.110) имеем
, то из (5.110) имеем

Из выполнения краевых условий получаем еще три уравнения для определения  :
:

Определив из уравнений (5.116)-(5.119) произвольные постоянные, получаем конкретную равновесную форму, которую принимает нить при заданной скорости продольного движения до и известной силе сопротивления 
Натяжение в нити найдем, воспользовавшись уравнением

которое после преобразований принимает вид (для каждой из ветвей)

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
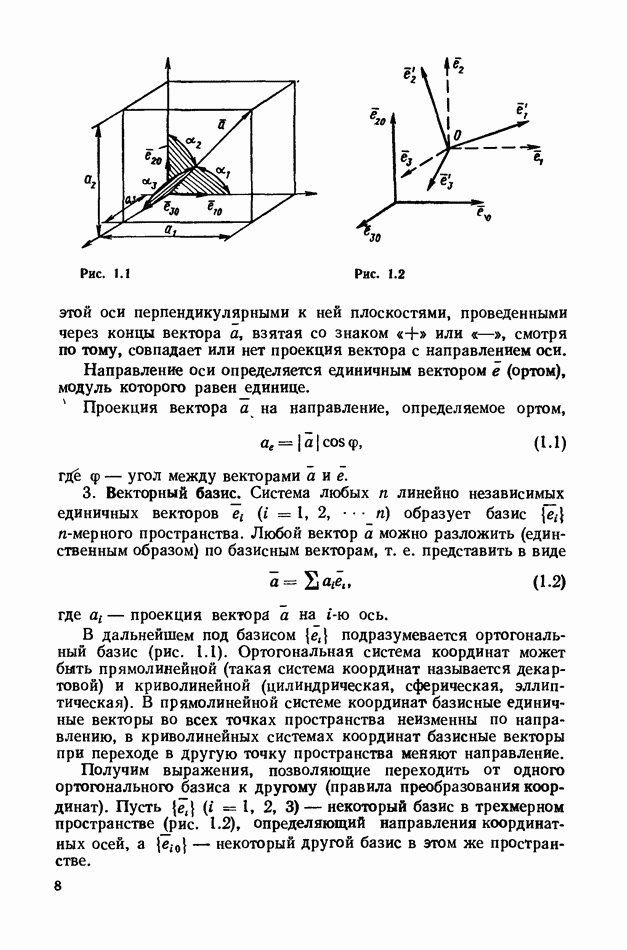
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
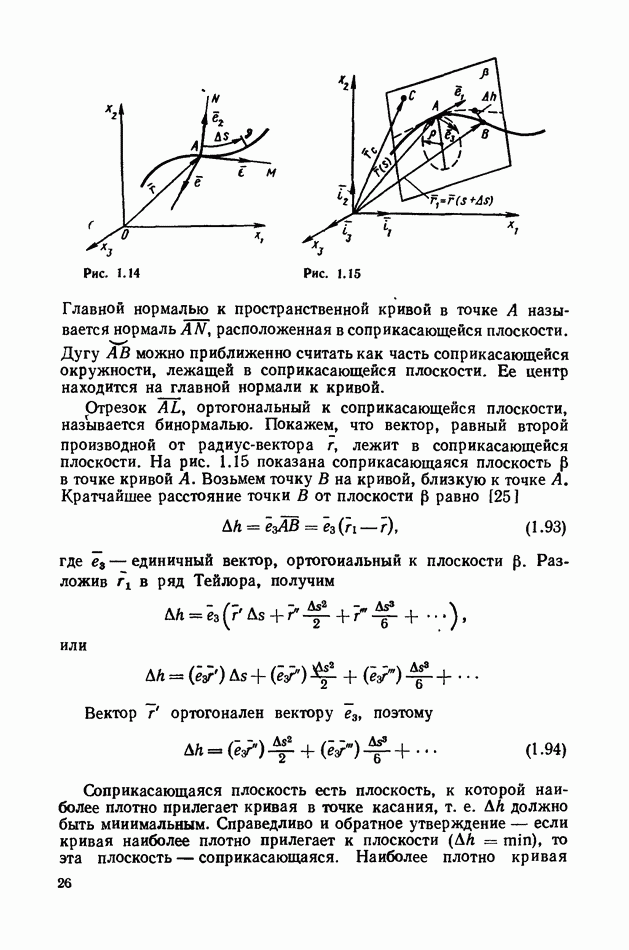
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
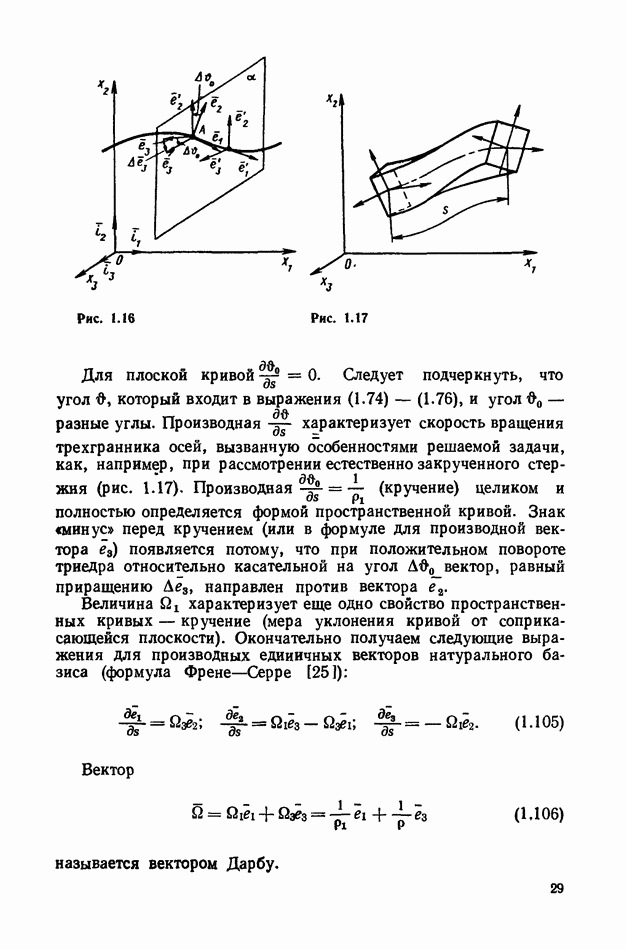
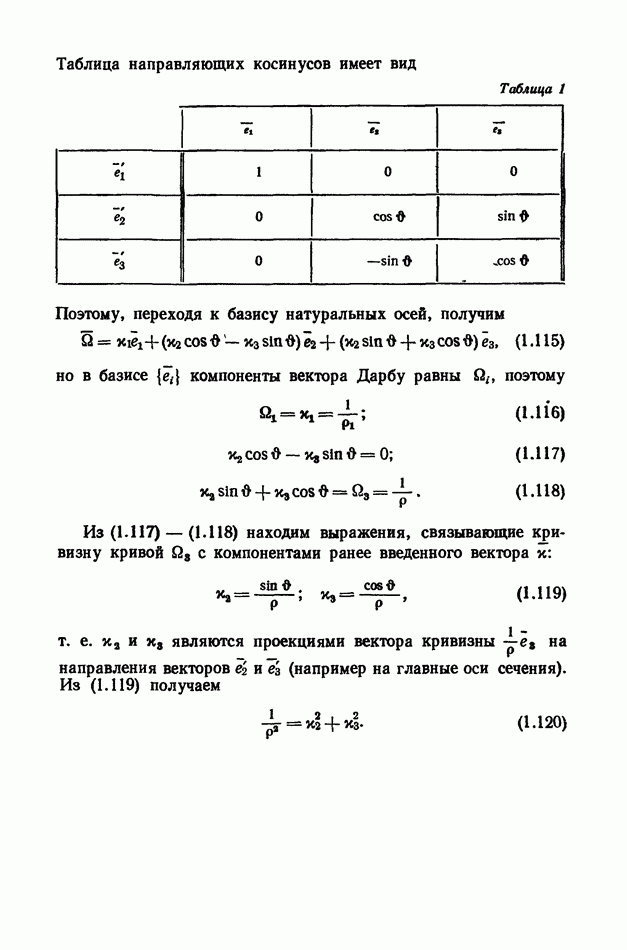
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.