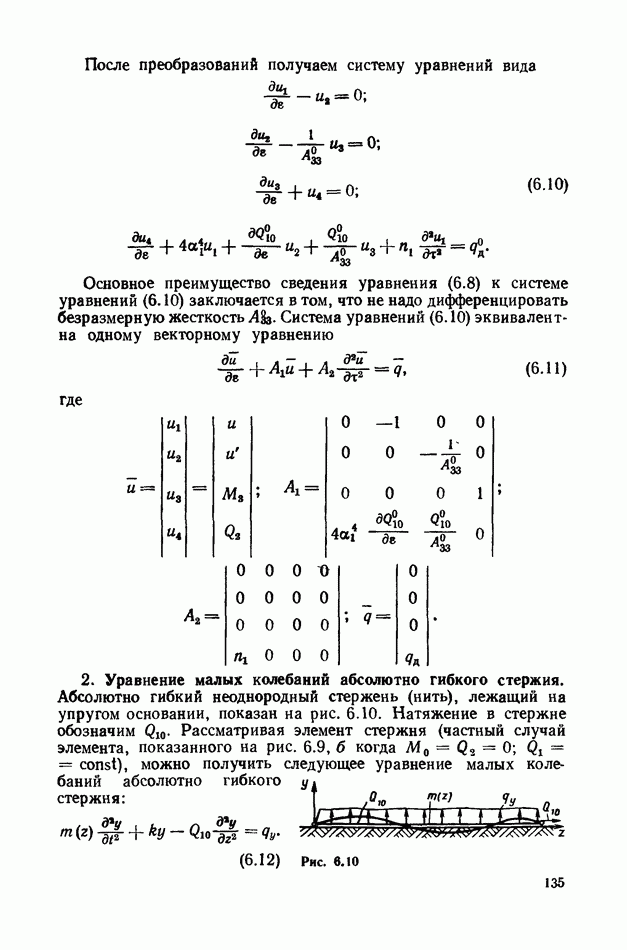
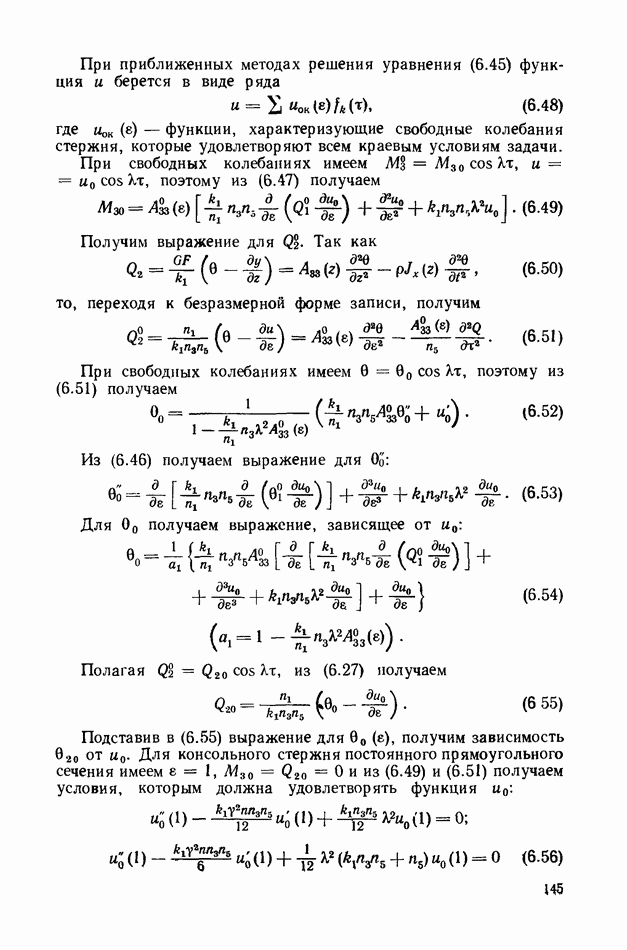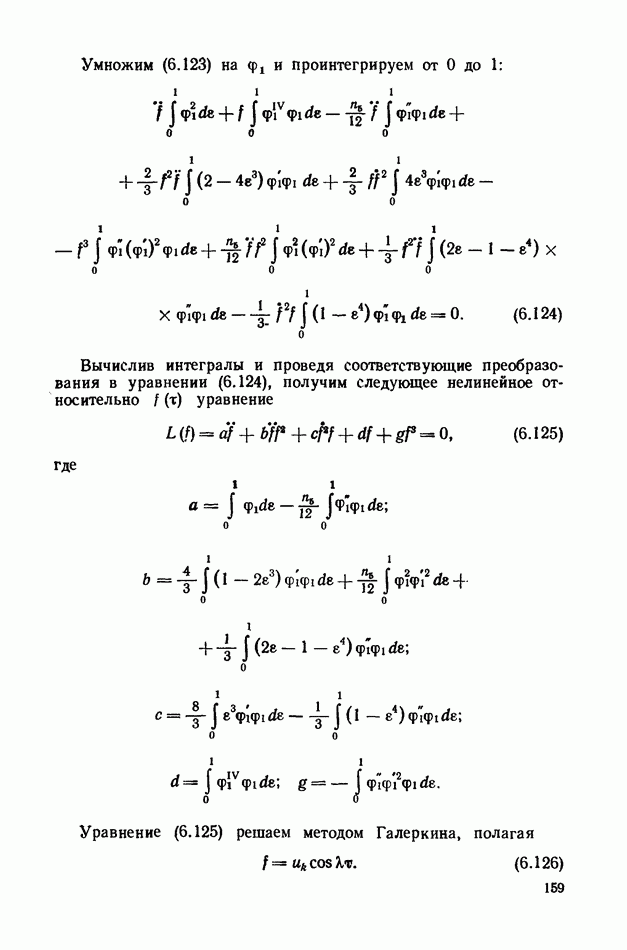| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Принцип минимума потенциальной энергии.
Наиболее распространенный приближенный метод решения задач статики упругих систем основан на том, что из всех возможных равновесных состояний (которые может принять упругая система под действием внешних статически приложенных сил) она принимает такое, в котором ее потенциальная энергия имеет минимальное значение, т. е. [28]

При нагружении системы внешними силами вследствие деформации системы силы совершают работу, которая переходит в потенциальную энергию системы. Это приводит к дополнительному условию

где А — работа внешних сил. Условие (2.147) справедливо только для упругих систем, у которых при деформировании энергия не расходуется на необратимые процессы. Для стержня, лежащего
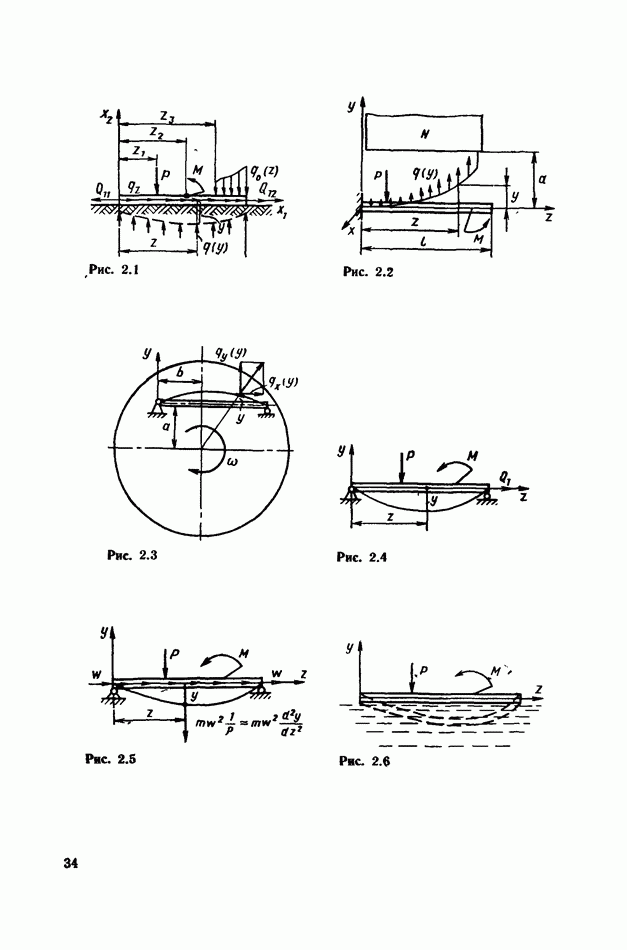
на упругом основании (см. рис. 2.14), уравнения потенциальной энергии системы и работы внешних сил имеют вид

где  -масса жидкости, приходящаяся на единицу длины стержня (трубки). В соответствии с результатами п. 1 имеем вариационную задачу на условный экстремум, поэтому рассмотрим вместо (2.146) функционал вида
-масса жидкости, приходящаяся на единицу длины стержня (трубки). В соответствии с результатами п. 1 имеем вариационную задачу на условный экстремум, поэтому рассмотрим вместо (2.146) функционал вида

где  множитель Лаграджа.
множитель Лаграджа.
Для упругой системы, которая подчиняется закону Гука, потенциальную энергию можно записать как квадратичную функцию от перемещений точек приложения сил:

где  перемещения (линейные и угловые) сечений, где приложены сила и моменты;
перемещения (линейные и угловые) сечений, где приложены сила и моменты;  коэффициенты жесткости;
коэффициенты жесткости;  общее число приложенных сил и моментов. Работу внешних сил при статическом нагруженни можно представить в виде
общее число приложенных сил и моментов. Работу внешних сил при статическом нагруженни можно представить в виде

где  — общее обозначение для сил и моментов.
— общее обозначение для сил и моментов.
Форма записи (2.151) для работы сил  справедлива только для случая, когда перемещения совпадают с направлением приложенных сил. В более общем случае, например при пространственной деформации стержня, работу внешних сил мджно представить в виде
справедлива только для случая, когда перемещения совпадают с направлением приложенных сил. В более общем случае, например при пространственной деформации стержня, работу внешних сил мджно представить в виде

где  -скалярное произведение. Для дальнейших преобразований важно, что потенциальная энергия системы есть однородная функция второй степени, а работа внешних сил — первой степени. Напомним основные свойства однородных функций (полиномов).
-скалярное произведение. Для дальнейших преобразований важно, что потенциальная энергия системы есть однородная функция второй степени, а работа внешних сил — первой степени. Напомним основные свойства однородных функций (полиномов).
Однородными функциями называются функции, состоящие из слагаемых одного и того же измерения. Например, функция

есть однородный полином второй степени. Если умножить  на общий множитель
на общий множитель  то вся функция
то вся функция  приобретет множитель
приобретет множитель  Еслн такую же операцию проделать с однородным полиномом
Еслн такую же операцию проделать с однородным полиномом  степени, то функция приобретает множитель
степени, то функция приобретает множитель  Это свойство является основным при определении однородных функций. Для однородной функции степени
Это свойство является основным при определении однородных функций. Для однородной функции степени  справедливо тождество
справедливо тождество

Предположим, что однородная функция  степени
степени  имеет непрерывные производные по всем аргументам. Фиксируя аргументы
имеет непрерывные производные по всем аргументам. Фиксируя аргументы  имеем
имеем

Дифференцируя левую и правую части (2.155) по  получим (используя правило дифференцирования сложной функции)
получим (используя правило дифференцирования сложной функции)

Полагая в  получаем соотношение (теорема Эйлера)
получаем соотношение (теорема Эйлера)

Условие экстремума функционала  в рассматриваемом случае записываем в виде
в рассматриваемом случае записываем в виде

Умножив (2.158) на  , и сложив соотношения, получим
, и сложив соотношения, получим

В силу теоремы Эйлера имеем

поэтому из (2.159) получаем

Так как  то из (2.160) находим множитель Лагранжа
то из (2.160) находим множитель Лагранжа  Для упругих систем, подчиняющихся закону Гука, и для
Для упругих систем, подчиняющихся закону Гука, и для
внешних сил, работу которых можно записать в виде  поэтому можно рассматривать функционал (без дополнительных условий)
поэтому можно рассматривать функционал (без дополнительных условий)

Можно показать, что экстремум функционала (2.161) есть максимум, поэтому экстремум

есть минимум.
Из принципа минимума потенциальной энергии [функционала (2.162)], так же как и из принципа возможных перемещений, может быть выведено уравнение равновесия стержня. Полученное из принципа минимума потенциальной энергии условие

является очень эффективным для приближенных решений задач статики стержней. Дифференциальные уравнения, получающиеся при исследовании вариационных задач (например, уравнение равновесия стержня), интегрируются в конечном виде лишь в частных случаях. Возникает необходимость в разработке методов решения вариационных задач с использованием исходных функционалов [например,  не переходя к дифференциальным уравнениям. Такие методы решения вариационных задач принято называть прямыми методами. Одним из таких методов является метод Ритца.
не переходя к дифференциальным уравнениям. Такие методы решения вариационных задач принято называть прямыми методами. Одним из таких методов является метод Ритца.
Для прямолинейных стержней функционал  зависит от прогибов стержня и их первых производных:
зависит от прогибов стержня и их первых производных:

поэтому представим у в виде ряда с неопределенными коэффициентами

где  неопределенные коэффициенты;
неопределенные коэффициенты;  известные функции, удовлетворяющие только геометрическим краевым условиям в отличие от приближенного метода решения по принципу возможных перемещений, когда необходимо, чтобы аппроксимирующие функции
известные функции, удовлетворяющие только геометрическим краевым условиям в отличие от приближенного метода решения по принципу возможных перемещений, когда необходимо, чтобы аппроксимирующие функции  удовлетворяли как геометрическим, так и силовым краевым условиям.
удовлетворяли как геометрическим, так и силовым краевым условиям.
В качестве таких функций могут быть взяты ортогональные полиномы (в данном случае более простые), которые будут рассмотрены в § 10. После подстановки выражения для у в функционал  получаем
получаем

что приводит к системе уравнений для определения неизвестных коэффициентов 

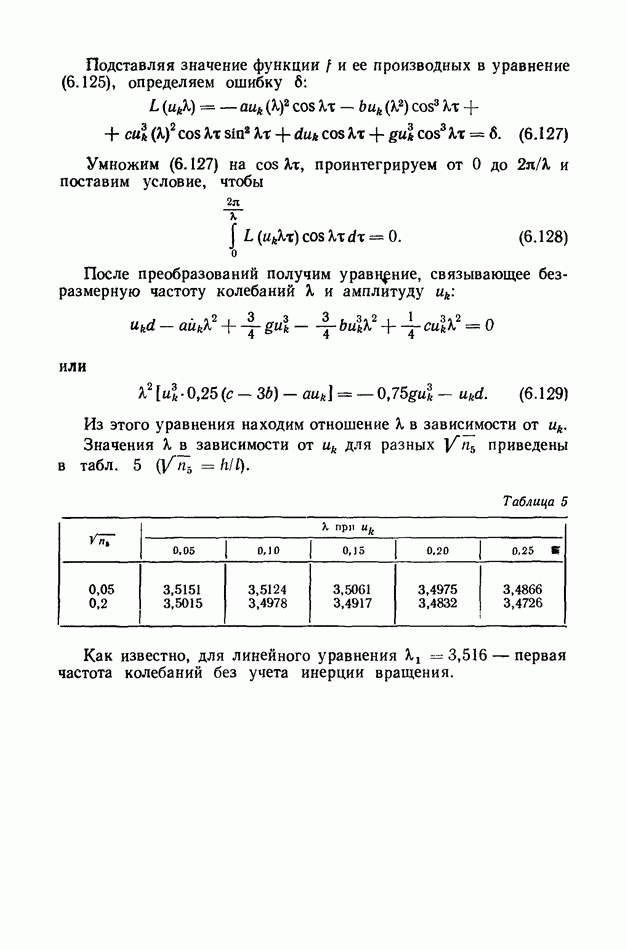
Определив из  получаем приближенное выражение для у. Найдем приближенное выражение для прогибов стержня для случая, показанного на рис. 2.14. Для получения
получаем приближенное выражение для у. Найдем приближенное выражение для прогибов стержня для случая, показанного на рис. 2.14. Для получения  воспользуемся выражением для
воспользуемся выражением для  :
:

Представим (2.168) в безразмерной форме: 1

где

Ограничимся двучленным приближением, приняв

Подставив (2.170) в выражение (2.169), после преобразований получаем два независимых уравнения для определения 

или

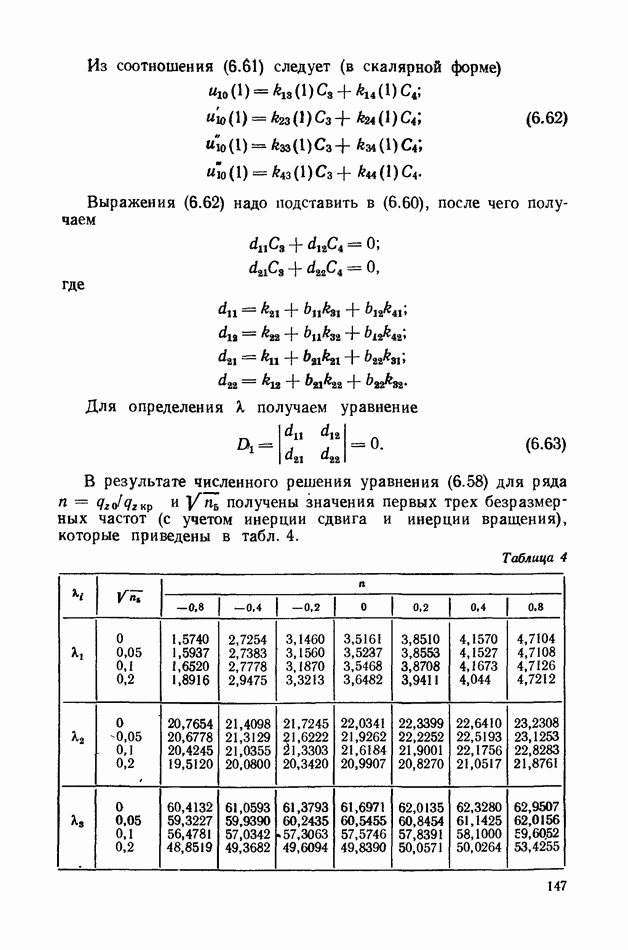
Из полученных выражений для  можно найти критическое значение скорости
можно найти критическое значение скорости  течения жидкости, при которой возможна статическая неустойчивость трубки, лежащей на упругом основании. Минимальное значение скорости
течения жидкости, при которой возможна статическая неустойчивость трубки, лежащей на упругом основании. Минимальное значение скорости  найдем из условия равенства нулю знаменателя выражения (2.172):
найдем из условия равенства нулю знаменателя выражения (2.172):

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
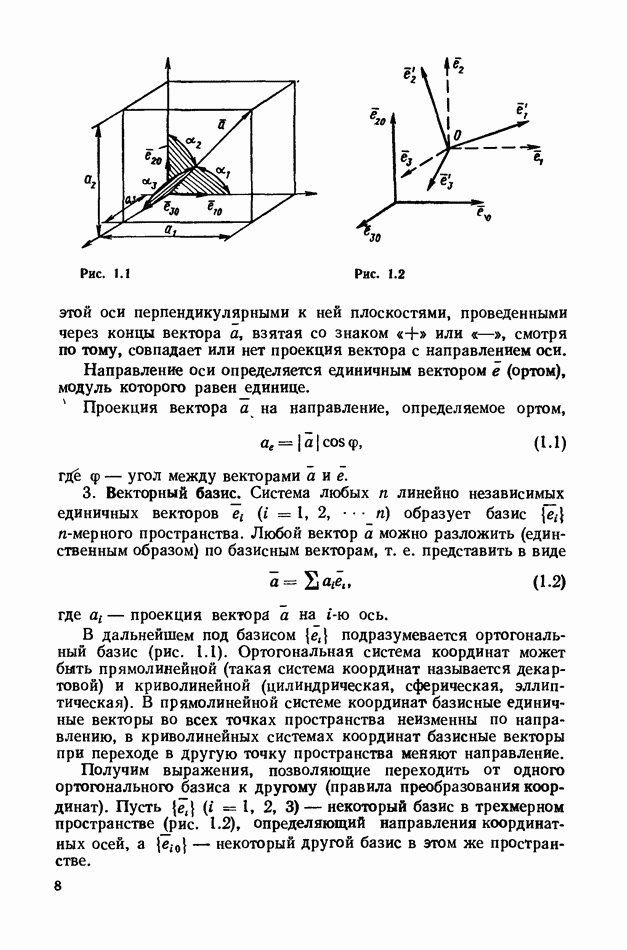
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
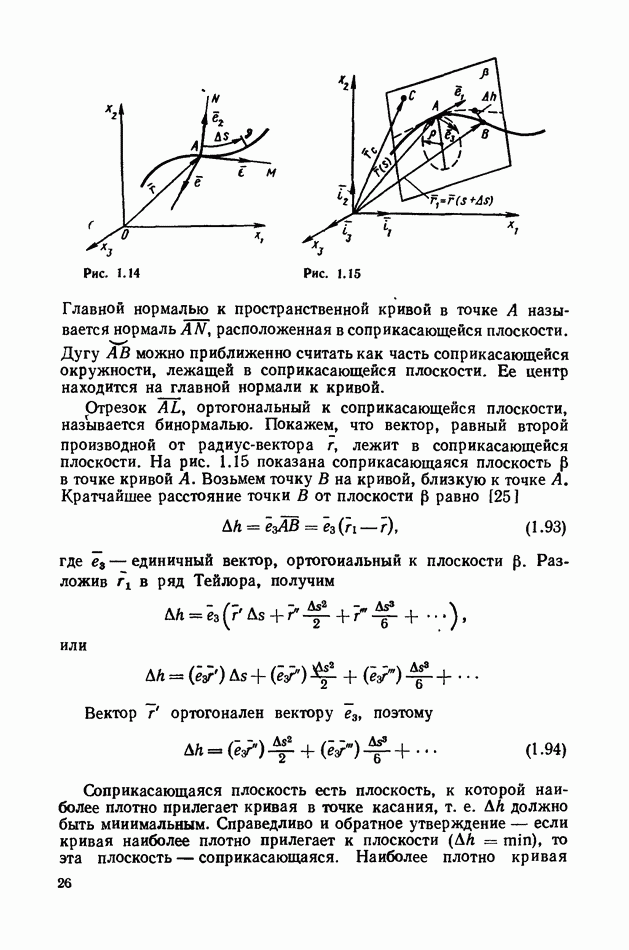
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
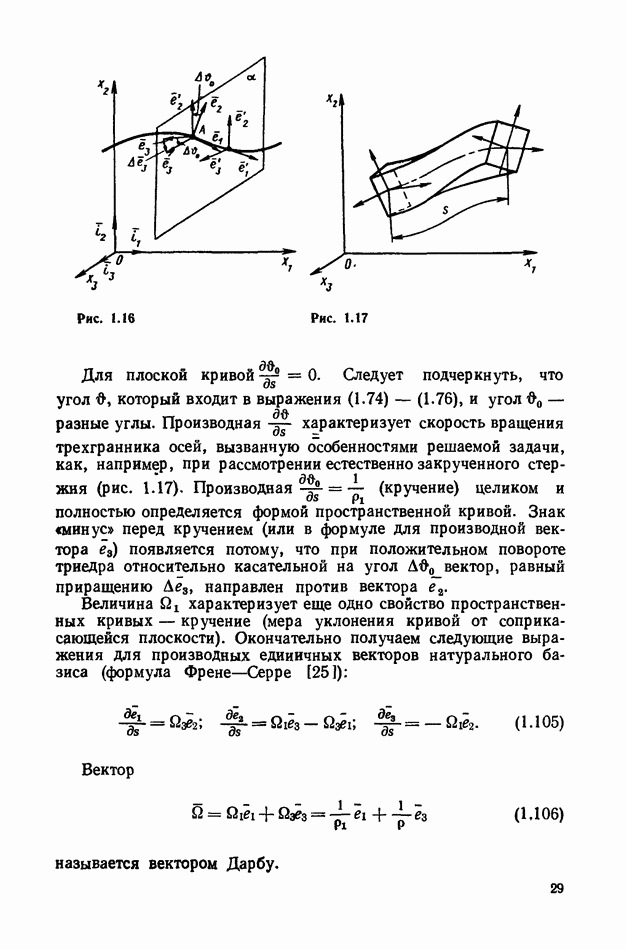
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
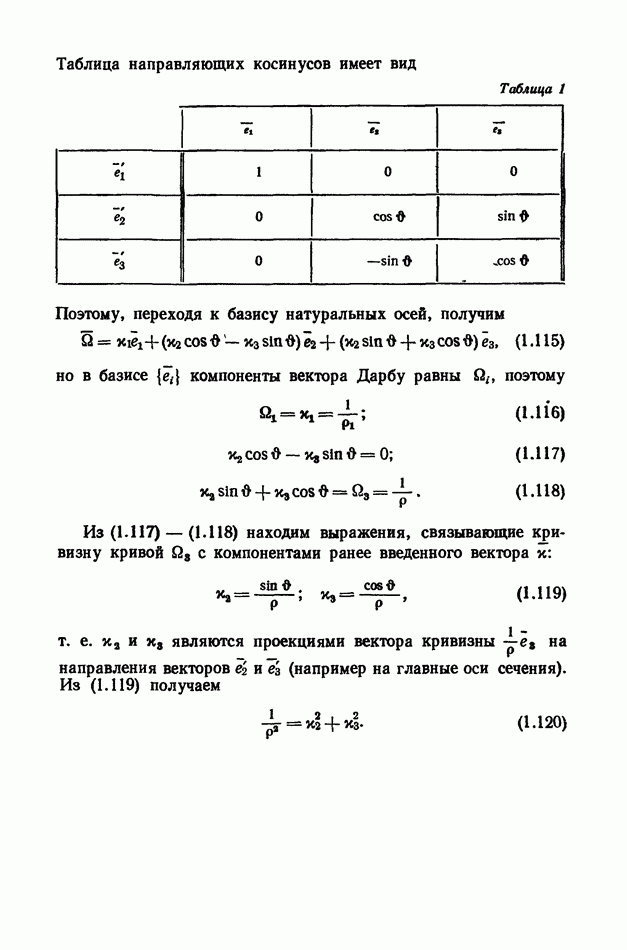
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
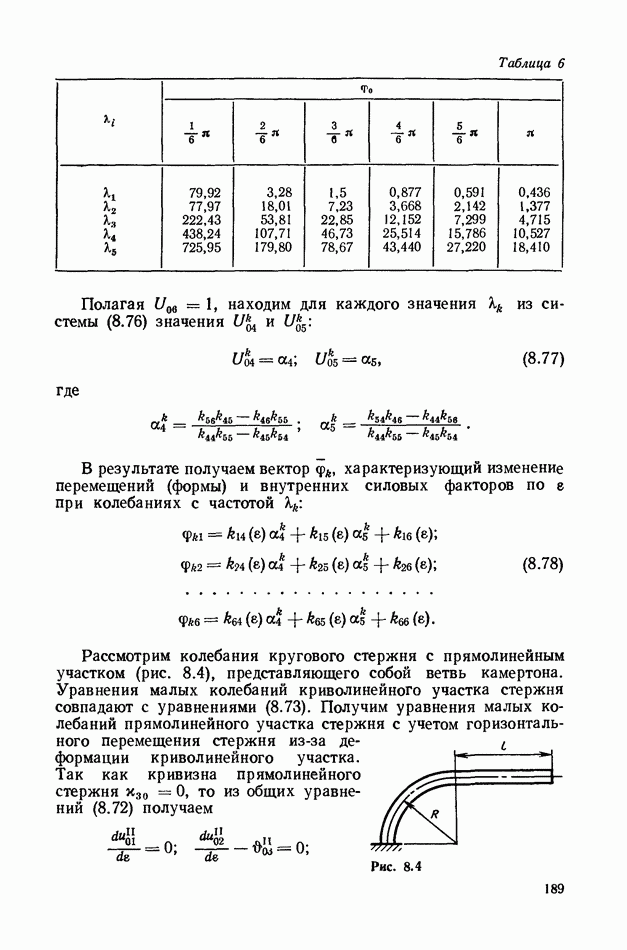
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.