| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Пространственная кривая.
Касательная к пространственной кривой определяется так же, как и для случая плоской кривой. Для кривой в пространстве к касательной в точке  можно провести бесчисленное множество нормалей, лежащих в плоскости, перпендикулярной к вектору
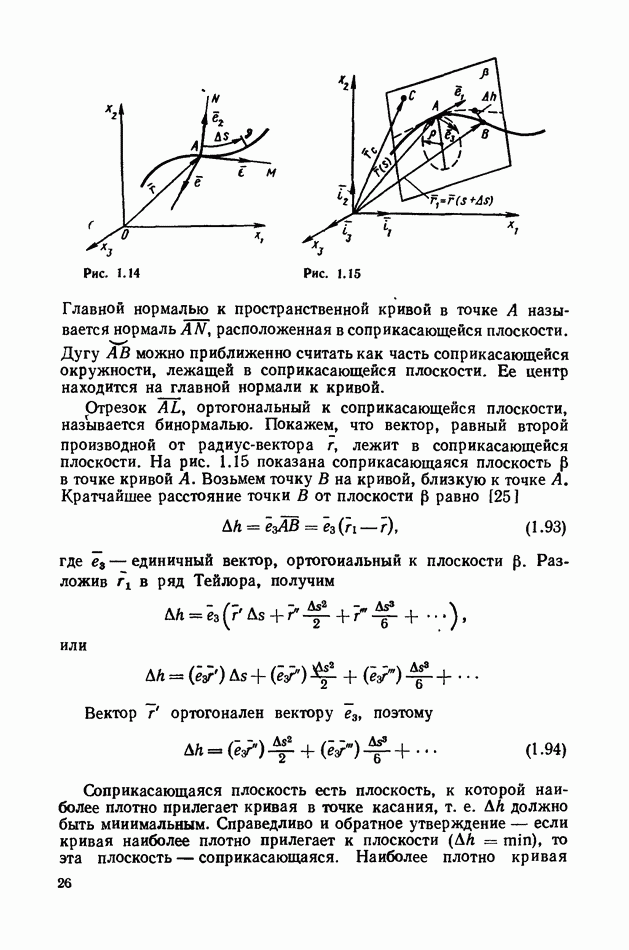
можно провести бесчисленное множество нормалей, лежащих в плоскости, перпендикулярной к вектору  (рис. 1 14). Возьмем точку В, близкую к точке А. Пространственную дугу
(рис. 1 14). Возьмем точку В, близкую к точке А. Пространственную дугу  можно приближенно считать дугой плоской кривой. Плоскость, проходящую через касательную
можно приближенно считать дугой плоской кривой. Плоскость, проходящую через касательную  и точку В, можно считать плоскостью, в которой лежит дуга
и точку В, можно считать плоскостью, в которой лежит дуга  При
При  эта плоскость займет строго определенное положение, которое характеризуется наиболее плотным прилеганием кривой юэтой плоскости. Эта плоскость называется соприкасающейся плоскостью к пространственной кривой в точке А.
эта плоскость займет строго определенное положение, которое характеризуется наиболее плотным прилеганием кривой юэтой плоскости. Эта плоскость называется соприкасающейся плоскостью к пространственной кривой в точке А.

Рис. 1.14

Рис. 1.15
Главной нормалью к пространственной кривой в точке А называется нормаль  расположенная в соприкасающейся плоскости.
расположенная в соприкасающейся плоскости.
Дугу А В можно приближенно считать как часть соприкасающейся окружности, лежащей в соприкасающейся плоскости. Ее центр находится на главной нормали к кривой.
Отрезок  ортогональный к соприкасающейся плоскости, называется бинормалью. Покажем, что вектор, равный второй производной от радиус-вектора
ортогональный к соприкасающейся плоскости, называется бинормалью. Покажем, что вектор, равный второй производной от радиус-вектора  лежит в соприкасающейся плоскости. На рис. 1.15 показана соприкасающаяся плоскость
лежит в соприкасающейся плоскости. На рис. 1.15 показана соприкасающаяся плоскость  в точке кривой А. Возьмем точку В на кривой, близкую к точке А. Кратчайшее расстояние точки В от плоскости
в точке кривой А. Возьмем точку В на кривой, близкую к точке А. Кратчайшее расстояние точки В от плоскости  равно
равно 

где  единичный вектор, ортогональный к плоскости
единичный вектор, ортогональный к плоскости  Разложив
Разложив  в ряд Тейлора, получим
в ряд Тейлора, получим

или

Вектор  ортогонален вектору
ортогонален вектору  поэтому
поэтому

Соприкасающаяся плоскость есть плоскость, к которой наиболее плотно прилегает кривая в точке касания, т. е.  должно быть минимальным. Справедливо и обратное утверждение — если кривая наиболее плотно прилегает к плоскости
должно быть минимальным. Справедливо и обратное утверждение — если кривая наиболее плотно прилегает к плоскости  то эта плоскость — соприкасающаяся. Наиболее плотно кривая
то эта плоскость — соприкасающаяся. Наиболее плотно кривая
будет прилегать в точке касания к плоскости, если эту плоскость провести через векторы  . В этом случае
. В этом случае  и разложение
и разложение  в ряд (1.94) начнется только со слагаемого, содержащего
в ряд (1.94) начнется только со слагаемого, содержащего  вектор
вектор  (ортогональный к вектору
(ортогональный к вектору  лежит в соприкасающейся плоскости.
лежит в соприкасающейся плоскости.
Вводя единичный вектор нормали  вектор
вектор  можно представить в виде
можно представить в виде

Если взять произвольную точку С (рис. 1.15), лежащую в соприкасающейся плоскости, то векторы  лежат в одной плоскости, поэтому должно выполняться условие (1.51)
лежат в одной плоскости, поэтому должно выполняться условие (1.51)

которое является уравнением соприкасающейся плоскости. Для случая параметрического задания кривой в декартовой системе координат условие (1.96) эквивалентно

В соприкасающейся плоскости можно провести соприкасающуюся окружность (см. рис. 1.15), что по аналогии с плоской кривой дает возможность получить одну из геометрических характеристик пространственной кривой — радиус кривизны или обратную ему величину — кривизну кривой в произвольной точке. Так как приращение вектора  лежит в соприкасающейся плоскости, то, возвращаясь к соотношению (1.95), имеем
лежит в соприкасающейся плоскости, то, возвращаясь к соотношению (1.95), имеем

т.е.

и из (1.95) получаем

Если на базисные векторы  ортогонального базиса, связанного с пространственной кривой, дополнительные условия не наложены (например, чтобы они совпадали с главными осями сечения стержня), то целесообразно вектор
ортогонального базиса, связанного с пространственной кривой, дополнительные условия не наложены (например, чтобы они совпадали с главными осями сечения стержня), то целесообразно вектор  направить по главной нормали, а вектор
направить по главной нормали, а вектор  по бинормали (см. рис. 1.14). Такой базис
по бинормали (см. рис. 1.14). Такой базис
(триедр) называется естественным или натуральным. При перемещении естественного трехгранника по пространственной кривой положение векторов  непрерывно изменяется, поэтому, рассмотрев производные по
непрерывно изменяется, поэтому, рассмотрев производные по  имеем в соответствии с общим случаем (1.52)
имеем в соответствии с общим случаем (1.52)

или

Основное отличие соотношений (1.60) от (1.101) заключается в том, что при выводе соотношений (1.60) никаких дополнительных условий на направление вектора не накладывалось (кроме основного условия, что вектор  ортогонален
ортогонален  При выводе соотношений (1.101) направление вектора
При выводе соотношений (1.101) направление вектора  строго определено — вектор
строго определено — вектор  направлен по нормали к кривой, что является частным случаем связанного трехгранника осей. Вектор, характеризующий геометрические свойства кривой и представленный через проекции на оси естественного трехгранника, принято обозначать
направлен по нормали к кривой, что является частным случаем связанного трехгранника осей. Вектор, характеризующий геометрические свойства кривой и представленный через проекции на оси естественного трехгранника, принято обозначать  и называть вектором Дарбу. В дальнейшем для этих векторов
и называть вектором Дарбу. В дальнейшем для этих векторов  используют единое обозначение как для случая, когда используются естественные оси (в механике нитей), так и для случая общих связанных осей. Из сопоставления выражений (1.99) и (1.101) следует
используют единое обозначение как для случая, когда используются естественные оси (в механике нитей), так и для случая общих связанных осей. Из сопоставления выражений (1.99) и (1.101) следует

Найдем проекцию вектора  . Вектор ортогонален вектору
. Вектор ортогонален вектору  Кроме того, этот вектор, как следует из правой части (1.101), лежит в плоскости а (проходящей через точку
Кроме того, этот вектор, как следует из правой части (1.101), лежит в плоскости а (проходящей через точку  ортогональной к соприкасающейся плоскости (так как
ортогональной к соприкасающейся плоскости (так как  поэтому можно рассмотреть изменение направления вектора
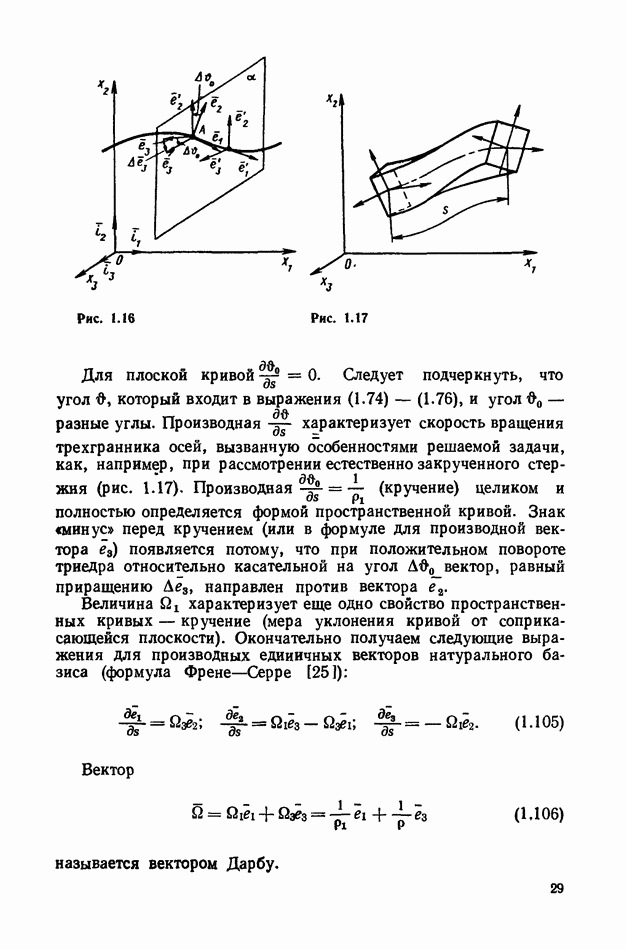
поэтому можно рассмотреть изменение направления вектора  в плоскости (рис. 1.16).
в плоскости (рис. 1.16).
Из рисунка следует

поэтому из (1.101) и (1.103) следует

где  кручение кривой.
кручение кривой.

Рис. 1.16

Рис. 1.17
Для плоской кривой  . Следует подчеркнуть, что угол который входит в выражения (1.74) — (1.76), и угол
. Следует подчеркнуть, что угол который входит в выражения (1.74) — (1.76), и угол  разные углы. Производная характеризует скорость вращения трехгранника осей, вызванную особенностями решаемой задачи, как, например, при рассмотрении естественно закрученного стержня (рис. 1.17). Производная
разные углы. Производная характеризует скорость вращения трехгранника осей, вызванную особенностями решаемой задачи, как, например, при рассмотрении естественно закрученного стержня (рис. 1.17). Производная  (кручение) целиком и полностью определяется формой пространственной кривой. Знак «минус» перед кручением (или в формуле для производной вектора
(кручение) целиком и полностью определяется формой пространственной кривой. Знак «минус» перед кручением (или в формуле для производной вектора  появляется потому, что при положительном повороте триедра относительно касательной на угол
появляется потому, что при положительном повороте триедра относительно касательной на угол  вектор, равный приращению
вектор, равный приращению  направлен против вектора
направлен против вектора 
Величина характеризует еще одно свойство пространственных кривых — кручение (мера уклонения кривой от соприкасающейся плоскости). Окончательно получаем следующие выражения для производных единичных векторов натурального базиса (формула Френе-Серре [25]):

Вектор

называется вектором Дарбу.

Рис. 1.18

Рис. 1.19
Выражения для вторых производных единичных векторов естественного трехгранника осей 

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава I. Сведения из векторного анализа
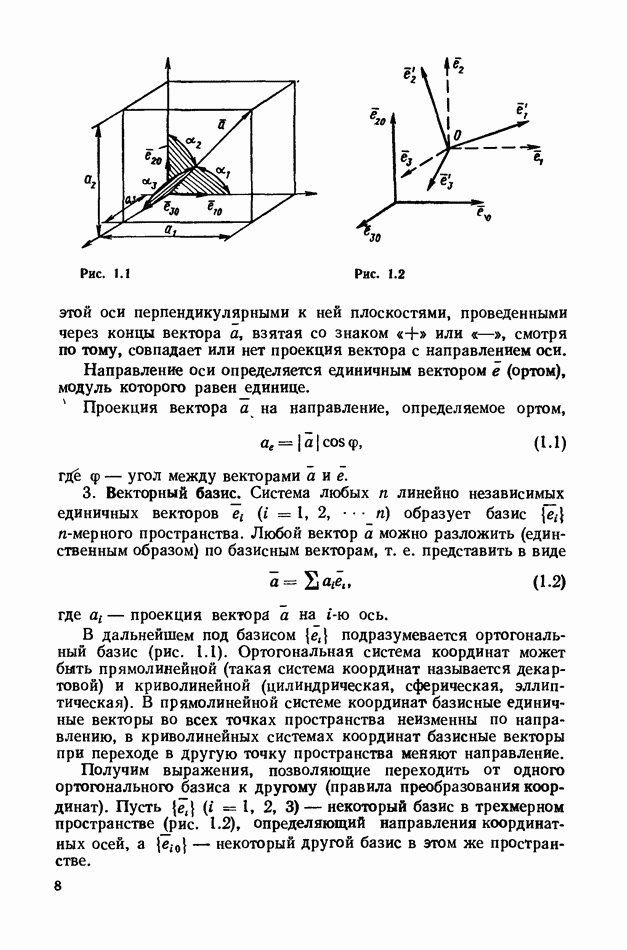
- 1. Скаляры и векторы.
- 2. Проекция вектора на произвольное направление.
- 3. Векторный базис.
- 4. Скалярное произведение двух векторов.
- 5. Векторное произведение двух векторов.
- 6. Смешанное или скалярно-векторное произведение
- 7. Двойное векторное произведение. Тождество Лагранжа.
- § 2. Основные положения векторного анализа
- 1. Геометрическое значение производной векторной функции.
- 2. Основные правила дифференцирования векторов.
- § 3. Основные положения дифференциальной геометрии
- 2. Пространственная кривая.
- 3. Выражения для кривизны и кручения через декартовые прямоугольные координаты точки кривой.
- 4. Связь кривизны и кручения осевой линии стержня с направляющими косинусами осей связанного трехгранника.
- Глава 2. Статика прямолинейных стержней
- § 5. Основные сведения из теории дифференциальных уравнений
- § 6. Элементарные обобщенные функции
- § 7. Балки на упругом основании
- § 8. Приближенные методы решения задач
- 2. Принцип возможных перемещений.
- 3. Принцип минимума потенциальной энергии.
- Глава 3. Статика пространственно-криволинейных стержней
- § 9. Основные положения и допущения механики гибких стержней
- § 10. Векторные уравнения равновесия стержней
- 2. Частные Случаи векторных уравнений равновесия.
- 3. Векторное уравнение для перемещений.
- 4. Векторное уравнение для момента.
- 5. Уравнения равновесия в безразмерной форме.
- § 11. Векторные уравнения равновесия нитей
- § 12. Уравнения равновесия стержней в проекциях на неподвижные оси
- 2. Уравнения равновесия стержня в случае, когда ось стержня — плоская кривая.
- 3. Уравнения равновесия нити в проекциях на неподвижные оси.
- 4. Частные случаи уравнений равновесия нити в неподвижных осях.
- § 13. Уравнения равновесия в связанной системе координат
- 2. Уравнения равновесия иити в связанной системе координат.
- 3. Равновесие нити, связанной с вращающейся системой координат.
- § 14. Основные теоремы статики нити
- Глава 4. Кинематика гибких стержней
- § 15. Производные базисных векторов по времени
- § 16. Абсолютная и локальная производные вектора по времени
- § 17. Уравнение, связывающее векторы
- § 18. Переменные Лагранжа и Эйлера в механике стержней
- 2. Переменные Эйлера.
- § 19. Уравнение неразрывности
- § 20. Кинематические уравнения для скоростей и ускорений
- Глава 5. Стационарное движение гибких стержней
- § 22. Уравнение равновесия гибкого стержня
- § 23. Уравнения равновесия при стационарном движении нити
- § 24. Стационарное движение нити в вязкой покоящейся среде
- § 25. Стационарное движение баллистической антенны
- § 26. Стационарное движение нити в средах разной вязкости
- Глава 6. Динамика прямолинейных гибких стержней
- § 28. Малые колебания прямолинейных стержней
- § 29. Численные методы определения частот и форм колебаний стержня
- § 30. Уравнения колебаний стержня с учетом инерции вращения и сдвига
- 2. Уравнение вращения элемента стержня.
- 3. Уравнения изгибных колебаний стержня переменного сечения.
- 4. Уравнения изгибных колебаний стержня постоянного сечения.
- 5. Краевые условия с учетом инерции вращения и сдвига.
- § 31. Влияние осевой силы на частоты колебаний стержня
- § 32. Малые колебания движущихся стержней
- § 33. Свободные нелинейные колебания стержня
- Глава 7. Уравнения движения гибкого стержня и нити
- § 35. Уравнения движения стержня в проекциях на связанные оси
- § 36. Уравнения движения стержня в плоскости
- § 37. Уравнения движения нити
- § 38. Прямолинейное движение нити
- § 39. Уравнения движения стержня, имеющего продольное движение
- Глава 8. Малые колебания пространственно-криволинейных стержней
- 2. Уравнения малых колебаний в проекциях на связанные оси.
- 3. Уравнения колебаний стержня в плоскости.
- § 41. Определение частот и форм колебаний пространственно-криволинейных стержней
- 2. Определение форм колебаний гибкого стержня.
- § 42. Определение частот и форм колебаний плоского кругового стержня
- § 43. Малые колебания нитей
- 1. Уравнение малых пространственных колебаний.
- 2. Уравнения колебаний нити в плоскости.
- 3. Получим уравнение колебаний нити относительно вертикальной плоскости
- § 44. Малые колебания стержней относительно стационарного движения
- 2. Уравнения малых колебаний стержня, имеющего при стационарном движении плоскую форму.
- 3. Уравнения колебаний стержня в плоскости.
- § 45. Определение частот колебаний стержня, имеющего продольное движение
- § 46. Примеры приближенного определения частот
- 4. Малые колебания нити относительно стационарного движения.