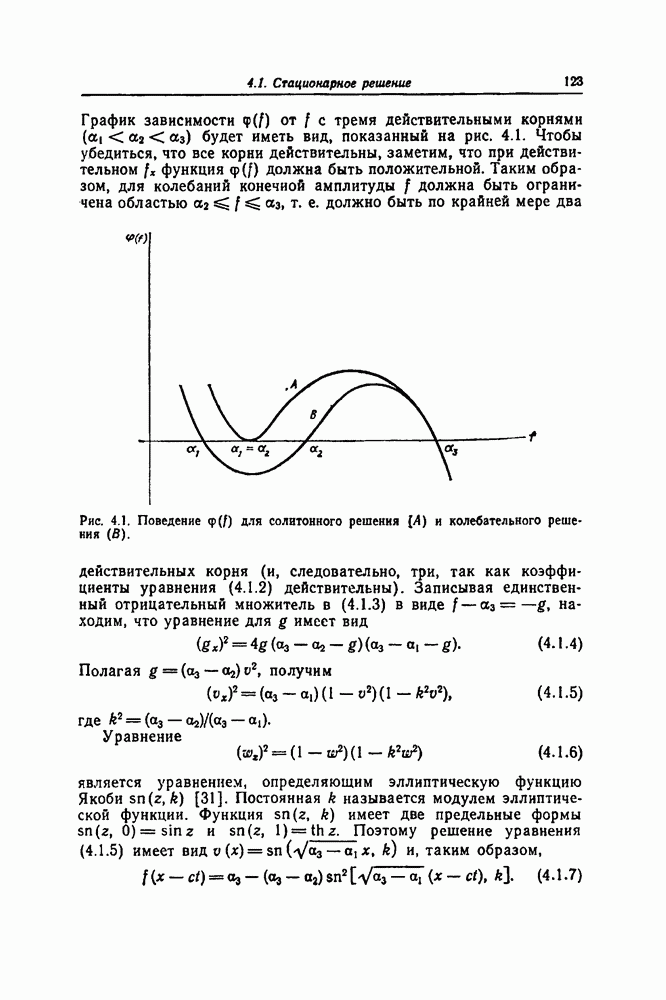
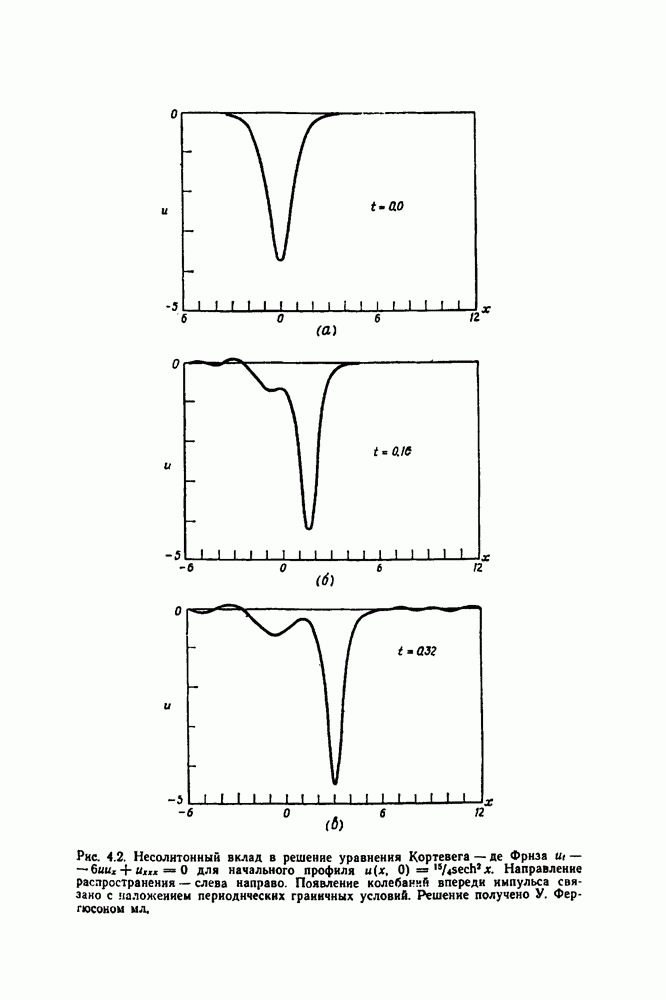
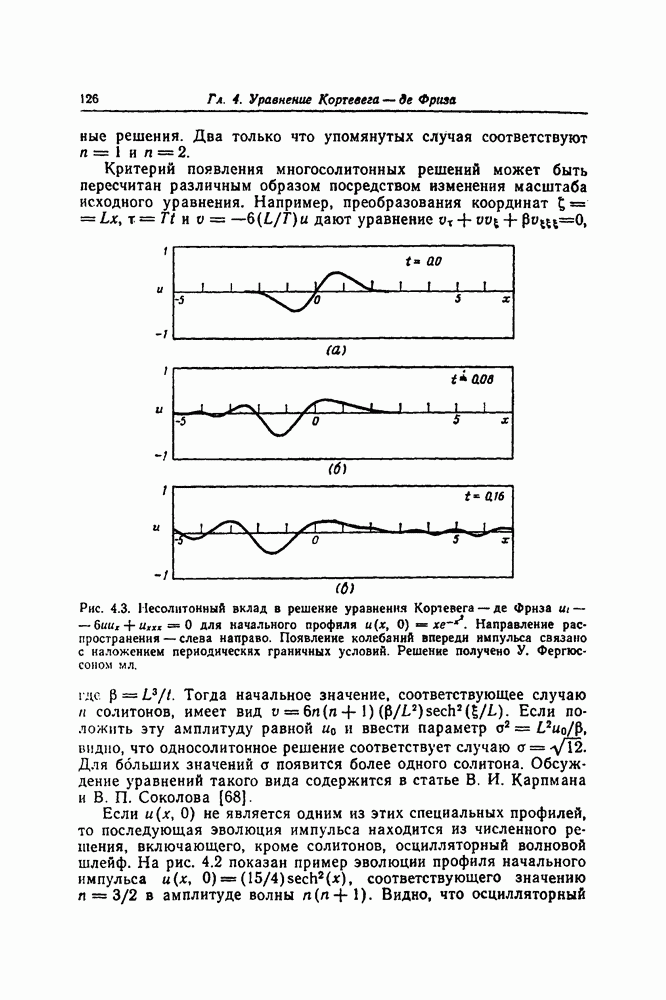
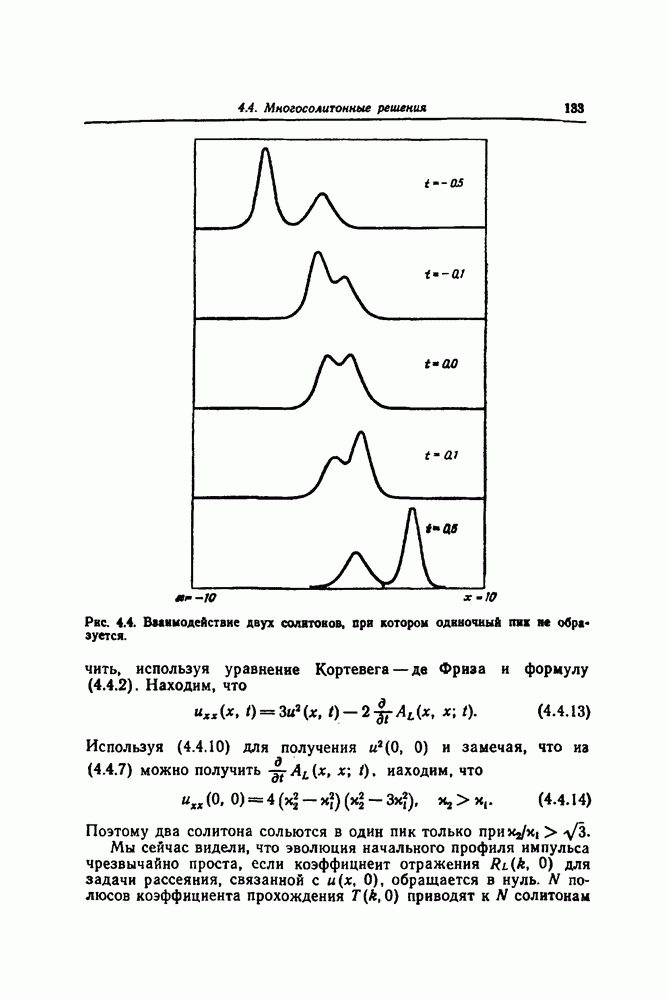
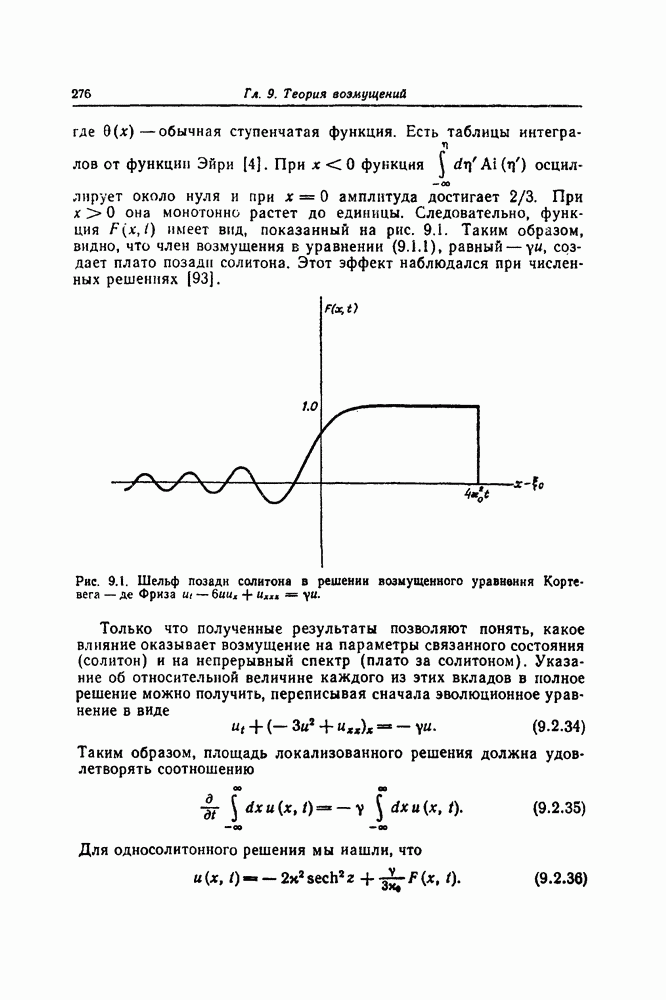
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
Если бы функция  в уравнении (1.1.1) содержала параметр, например а, так что
в уравнении (1.1.1) содержала параметр, например а, так что  то можно было бы ожидать, что изменение формы потенциала при изменении параметра а приведет к некоторому соответствующему изменению собственных значений
то можно было бы ожидать, что изменение формы потенциала при изменении параметра а приведет к некоторому соответствующему изменению собственных значений  т. е. можно было бы ожидать зависимости
т. е. можно было бы ожидать зависимости  от а. Естественно задать вопрос: существуют ли потенциальные функции
от а. Естественно задать вопрос: существуют ли потенциальные функции  для которых
для которых  при изменении а остается постоянным? Сразу же напрашивается достаточно тривиальный пример — замена любой функции
при изменении а остается постоянным? Сразу же напрашивается достаточно тривиальный пример — замена любой функции  на
на  просто переносит неоднородность потенциала или показателя преломления вдоль оси х, что изменяет положение запертой частицы или смещает звуковой канал и не влияет на энергию связанного состояния или частоту локализованной волны. Таким образом, это измененне а не влияет на собственные значения
просто переносит неоднородность потенциала или показателя преломления вдоль оси х, что изменяет положение запертой частицы или смещает звуковой канал и не влияет на энергию связанного состояния или частоту локализованной волны. Таким образом, это измененне а не влияет на собственные значения  Для сравнения с последующими результатами следует отметить, что функции
Для сравнения с последующими результатами следует отметить, что функции  удовлетворяют линейному дифференциальному уравнению в частных производных
удовлетворяют линейному дифференциальному уравнению в частных производных  Мы покажем, что есть и другие, более интересные возможности, которые приводят к нелинейным уравнениям в частных производных. В частности будет показано, что функции
Мы покажем, что есть и другие, более интересные возможности, которые приводят к нелинейным уравнениям в частных производных. В частности будет показано, что функции  удовлетворяющие дифференциальному уравнению
удовлетворяющие дифференциальному уравнению

тоже оставляют собственные значения неизменными. Если считать параметр а временем (конечно, соответствующее уравнение Штурма — Лиувилля не является зависящим от времени уравнением Шрёдингера), то уравнение (1.2.1) является уравнением Кортевега — де Фриза.
Таким образом, нахождение решений уравнения Кортевега — де Фриза может быть связано с определением зависящих от параметра
потенциалов в уравнении Штурма — Лиувилля и наоборот. Упомянутая в разд. 1.1 задача рассеяния касалась определения волновой функции у при заданном потенциале  В данном случае речь идет об определении потенциала по некоторой заданной информации о волновой функции (более детально это будет рассмотрено в гл. 4). Задача определения потенциала по информации о волновой функции называется обратной задачей рассеяния.
В данном случае речь идет об определении потенциала по некоторой заданной информации о волновой функции (более детально это будет рассмотрено в гл. 4). Задача определения потенциала по информации о волновой функции называется обратной задачей рассеяния.
Используя метод Лакса [77], мы можем легко видеть, что уравнение Кортевега — де Фриза является одним из бесконечного числа уравнений, описывающих такое изменение потенциала уравнения Шрёдингера, при котором собственные значения остаются постоянными. Чтобы убедиться в этом, удобно записать уравнение Шредингера, или Штурма — Лиувилля, в виде

где  Дифференцируя это уравнение по времени, получим
Дифференцируя это уравнение по времени, получим

Так как  то
то  Нас интересует такая зависимость и и, следовательно, у от времени, при которой
Нас интересует такая зависимость и и, следовательно, у от времени, при которой  Рассмотрим случай, когда зависимость у от времени может быть выражена в виде
Рассмотрим случай, когда зависимость у от времени может быть выражена в виде  где В — некоторый линейный дифференциальный оператор, подлежащий определению (не обязательно единственный). Конечно, пространственное изменение удается уравнением (1.2.2). Теперь уравнение (1.2.3) может быть записано в виде
где В — некоторый линейный дифференциальный оператор, подлежащий определению (не обязательно единственный). Конечно, пространственное изменение удается уравнением (1.2.2). Теперь уравнение (1.2.3) может быть записано в виде

где  Мы замечаем, что X будет постоянным
Мы замечаем, что X будет постоянным  при условии, что В выбирается таким образом, чтобы оно удовлетворяло уравнению
при условии, что В выбирается таким образом, чтобы оно удовлетворяло уравнению  . В общем случае это операторное уравнение; однако, как мы сейчас увидим, некоторые ограничения на вид В могут привести к тому, что выражение для
. В общем случае это операторное уравнение; однако, как мы сейчас увидим, некоторые ограничения на вид В могут привести к тому, что выражение для  не будет содержать дифференциальных операторов, а будет только функцией
не будет содержать дифференциальных операторов, а будет только функцией  и ее пространственных производных. В этом случае мы тем самым построили дифференциальное уравнение в частных производных для
и ее пространственных производных. В этом случае мы тем самым построили дифференциальное уравнение в частных производных для  такое, что если оно удовлетворяется, то
такое, что если оно удовлетворяется, то  т. е. собственные значения остаются постоянными во времени.
т. е. собственные значения остаются постоянными во времени.
В качестве первого примера дифференциального оператора В, который может приводить к постоянным собственным значениям, рассмотрим  где сначала допускается, что а может быть функцией
где сначала допускается, что а может быть функцией  и ее пространственных производных. Затем по
и ее пространственных производных. Затем по
определению 

Если в этом последнем выражении коэффициенты при  обращаются в нуль, т. е. если
обращаются в нуль, т. е. если  то
то  и соотношение (1.2.4) принимает вид
и соотношение (1.2.4) принимает вид

Поэтому  будет равно нулю и, таким образом, X не будет зависеть от времени при условии, что и удовлетворяет уравнению в частных производных
будет равно нулю и, таким образом, X не будет зависеть от времени при условии, что и удовлетворяет уравнению в частных производных  Так как решением этого уравнения является любая функция от
Так как решением этого уравнения является любая функция от  мы виднм, что любой потенциал вида
мы виднм, что любой потенциал вида  будет оставлять
будет оставлять  не зависящим от времени. Этот в каком-то смысле неинтересный пример, в котором параметр
не зависящим от времени. Этот в каком-то смысле неинтересный пример, в котором параметр  просто переносит потенциал вдоль оси х со скоростью —а, уже упоминался косвенно в предыдущем рассмотрении.
просто переносит потенциал вдоль оси х со скоростью —а, уже упоминался косвенно в предыдущем рассмотрении.
Чтобы получить более интересный пример, можно было бы попытаться взять В в виде  где
где  являются в общем случае функциями и и ее пространственных производных и снова, как и в предыдущем примере,
являются в общем случае функциями и и ее пространственных производных и снова, как и в предыдущем примере,  Однако простые вычисления показывают, что никакого обобщения предыдущего результата при этом не получаетоя: мы просто приходим к тому же самому дифференциальному уравнению в частных производных для и.
Однако простые вычисления показывают, что никакого обобщения предыдущего результата при этом не получаетоя: мы просто приходим к тому же самому дифференциальному уравнению в частных производных для и.
Если мы сделаем следующий шаг и рассмотрим  мы найдем, что
мы найдем, что

Если теперь снова потребовать, чтобы коэффициенты при  обращались в нуль, то получится новое дифференциальное уравнение в частных производных. Обращение в нуль этих коэффициентов дает простые дифференциальные соотношения, которые легко проинтегрировать. Мы находим, что
обращались в нуль, то получится новое дифференциальное уравнение в частных производных. Обращение в нуль этих коэффициентов дает простые дифференциальные соотношения, которые легко проинтегрировать. Мы находим, что  где
где  произвольные функции времени, появляющиеся в результате интегрирования. Тогда из (1.2.7) имеем
произвольные функции времени, появляющиеся в результате интегрирования. Тогда из (1.2.7) имеем

Снова из соотношения  следует дифференциальное уравнение в частных производных для и. Чтобы упростить коэффициенты полученного уравнения, можно положить постоянную а равной —4. Функцию
следует дифференциальное уравнение в частных производных для и. Чтобы упростить коэффициенты полученного уравнения, можно положить постоянную а равной —4. Функцию  также можно положить равной нулю, так как простым преобразованием к новый независимым
также можно положить равной нулю, так как простым преобразованием к новый независимым
переменным, задаваемым соотношениями  ее можно исключить из окончательного уравнения для и. Таким образом, находим, что новое уравнение для и имеет вид
ее можно исключить из окончательного уравнения для и. Таким образом, находим, что новое уравнение для и имеет вид

Если и определяется этим уравнением, то левая часть уравнения (1.2.4) обращается в нуль, и, следовательно, мы снова получим, что  С точностью до множителя
С точностью до множителя  , который можно устранить, полагая
, который можно устранить, полагая  это уравнение совпадает с нелинейным дифференциальным уравнением (1.2.1). Это одна
это уравнение совпадает с нелинейным дифференциальным уравнением (1.2.1). Это одна  стандартных форм уравнения Кортевега — де Фриза. Таким образом, если эволюция потенциала, входящего в уравнение Шрёдингера, определяется уравнением Кортевега — де Фриза, то собственное значение к остается постоянным.
стандартных форм уравнения Кортевега — де Фриза. Таким образом, если эволюция потенциала, входящего в уравнение Шрёдингера, определяется уравнением Кортевега — де Фриза, то собственное значение к остается постоянным.
Наконец, поскольку функции  в операторе
в операторе  теперь известны, известна и зависимость решения у от времени. Она дается уравнением
теперь известны, известна и зависимость решения у от времени. Она дается уравнением

Функцию  мы также положили равной нулю, так как от нее можно избавиться, введя новую зависимую переменную
мы также положили равной нулю, так как от нее можно избавиться, введя новую зависимую переменную 
Следует отметить, что и изменение у в пространстве, описываемое уравнением

и его изменение во времени (уравнение 1.2.10)) выражаются с помощью линейных дифференциальных уравнений.
Как и следовало теперь Ожидать, можно построить [77, 42] бесконечную последовательность уравнений более высокого порядка, характеризуемых нечетными линейными операторами  Однако в настоящее время в прикладных физических задачах эти эволюционные уравнения более высокого порядка, по-видимому, не возникают, и здесь они рассматриваться не будут. Вместо этого мы проанализируем два простых решения уравнения Кортевега — де Фриза (1.2.9).
Однако в настоящее время в прикладных физических задачах эти эволюционные уравнения более высокого порядка, по-видимому, не возникают, и здесь они рассматриваться не будут. Вместо этого мы проанализируем два простых решения уравнения Кортевега — де Фриза (1.2.9).
Односолитонное решение уравнения Кортевега — де Фриза
Простейшим решением уравнения Кортевега — де Фриза является стационарное решение, которое можно получить, полагая  Решение представляет собой возмущение, движущееся в положительном направлении оси с постоянной скоростью с.
Решение представляет собой возмущение, движущееся в положительном направлении оси с постоянной скоростью с.
В гл. 4 будет показано, что это решение уравнения Кортевега — де Фриза имеет вид

В этом решении проявляется общая черта нелинейных волн — связь между амплитудой и скоростью импульса. Импульсы с большей амплитудой движутся быстрее и, кроме того, они уже. Простое интегрирование показывает, что ширина и амплитуда импульса связаны соотношением

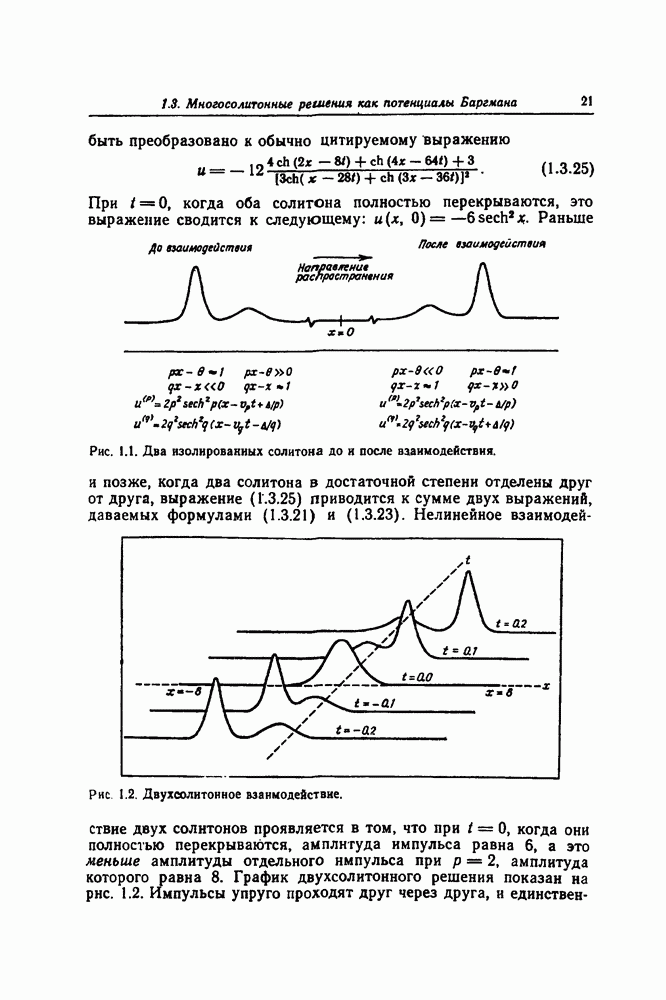
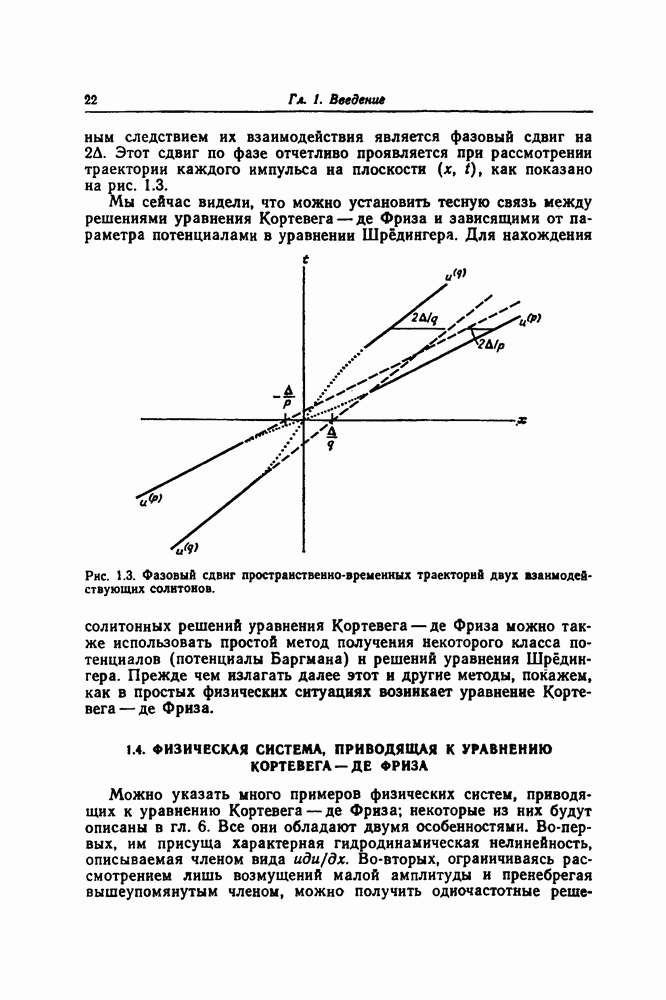
Решение (1.2.12), представляющее собой локализованное возмущение, симметричное относительно своей средней точки, является односолитонным решением уравнения Кортевега — де Фриза. Однако истинно солитонный характер этого возмущения еще не очевиден. Существенная черта солитона состоит в том, что приведенное выше аналитическое выражение сохраняется (за исключением смещения по фазе) и при взаимодействии двух или более таких импульсов. Чтобы убедиться в этом, мы должны рассмотреть решение, более сложное, чем приведенное выше стационарное решение. В последующих главах будут описаны способы получения многосолитонных решений, основанные на методе обратной задачи рассеяния. Чтобы дать предварительный обзор этих более общих результатов, мы получим здесь двухсолитониое решение с помощью простого метода, предшествующего более сложным методам обратной задачи рассеяния. Этот метод был предложен Баргманом [11) для радиального уравнения Шрёдингера, но в равной мере он применим и в данном случае, когда областью изменения независимой переменной является вся ось х. Метод делает очевидной тесную связь между потенциалами и многосолитонными решениями.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- 1.1. УРАВНЕНИЕ ШТУРМА-ЛИУВИЛЛЯ
- 1.2. УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 1.3. МНОГОСОЛИТОННЫЕ РЕШЕНИЯ КАК ПОТЕНЦИАЛЫ БАРГМАНА
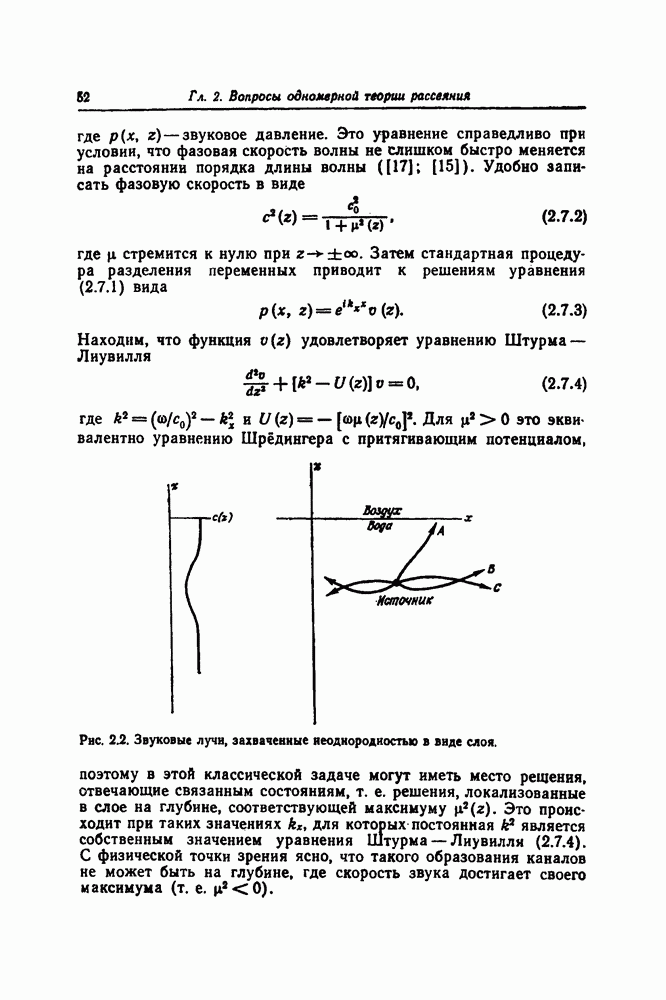
- 1.4. ФИЗИЧЕСКАЯ СИСТЕМА, ПРИВОДЯЩАЯ К УРАВНЕНИЮ КОРТЕВЕГА — ДЕ ФРИЗА
- 1.5. РАСПРОСТРАНЕНИЕ НА СЛУЧАИ ДРУГИХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.6. ПЛАН ДАЛЬНЕЙШЕГО ИЗЛОЖЕНИЯ
- Глава 2. ВОПРОСЫ ОДНОМЕРНОЙ ТЕОРИИ РАССЕЯНИЯ
- 2.2. РАССЕЯНИЕ ОСЦИЛЛЯТОРОМ
- 2.3. УПРУГО ЗАКРЕПЛЕННАЯ СТРУНА
- 2.4. УРАВНЕНИЕ ШРЕДИНГЕРА
- 2.5. РАССЕЯНИЕ ПОТЕНЦИАЛОМ ВИДА sech
- 2.6. СООТВЕТСТВУЮЩИЕ УРАВНЕНИЯ ШТУРМА — ЛИУВИЛЛЯ
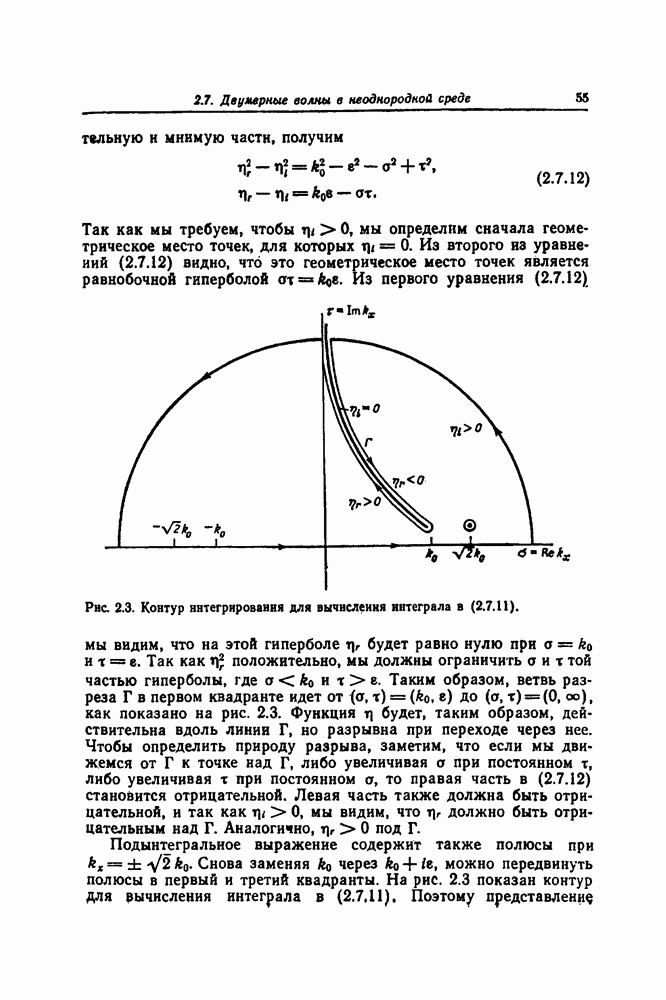
- 2.7. ДВУМЕРНЫЕ ВОЛНЫ В НЕОДНОРОДНОЙ СРЕДЕ
- 2.8. ОБЩИЙ ПОДХОД К ПРОБЛЕМЕ РАССЕЯНИЯ
- 2.9. «ОБРЕЗАННЫЕ» ПОТЕНЦИАЛЫ
- 2.10. РАССЕЯНИЕ ИМПУЛЬСОВ — УРАВНЕНИЯ МАРЧЕНКО
- 2.11. ЗАДАЧА РАССЕЯНИЯ ЗАХАРОВА — ШАБАТА
- 2.12. СВЯЗЬ МЕЖДУ УРАВНЕНИЕМ ШРЕДИНГЕРА И УРАВНЕНИЯМИ ЗАХАРОВА — ШАБЛТА: УРАВНЕНИЯ РИККАТИ
- Глава 3. ОДНОМЕРНАЯ ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ
- 3.2. НАЛИЧИЕ СВЯЗАННЫХ СОСТОЯНИЯ
- 3.3. БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ
- 3.4. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ-РАЦИОНАЛЬНАЯ ФУНКЦИЯ
- 3.5. ПОТЕНЦИАЛЫ БАРГМАНА
- 3.8. МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ ЗАХАРОВА — ШАБАТА ДЛЯ ДЕЙСТВИТЕЛЬНЫХ ПОТЕНЦИАЛОВ
- 3.7. БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ ДЛЯ СИСТЕМЫ ЗАХАРОВА — ШАБАТА
- 3.8. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ ДЛЯ СИСТЕМЫ ЗАХАРОВА — ШАБАТА В ВИДЕ РАЦИОНАЛЬНОЯ ФУНКЦИИ
- 3.9. СИСТЕМА ЗАХАРОВА — ШАБАТА С КОМПЛЕКСНЫМ ПОТЕНЦИАЛОМ
- Глава 4. УРАВНЕНИЕ КОРТЕВЕГА—ДЕ ФРИЗА
- 4.2. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РЕШЕНИЙ
- 4.3. ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 4.4. МНОГОСОЛИТОННЫЕ РЕШЕНИЯ
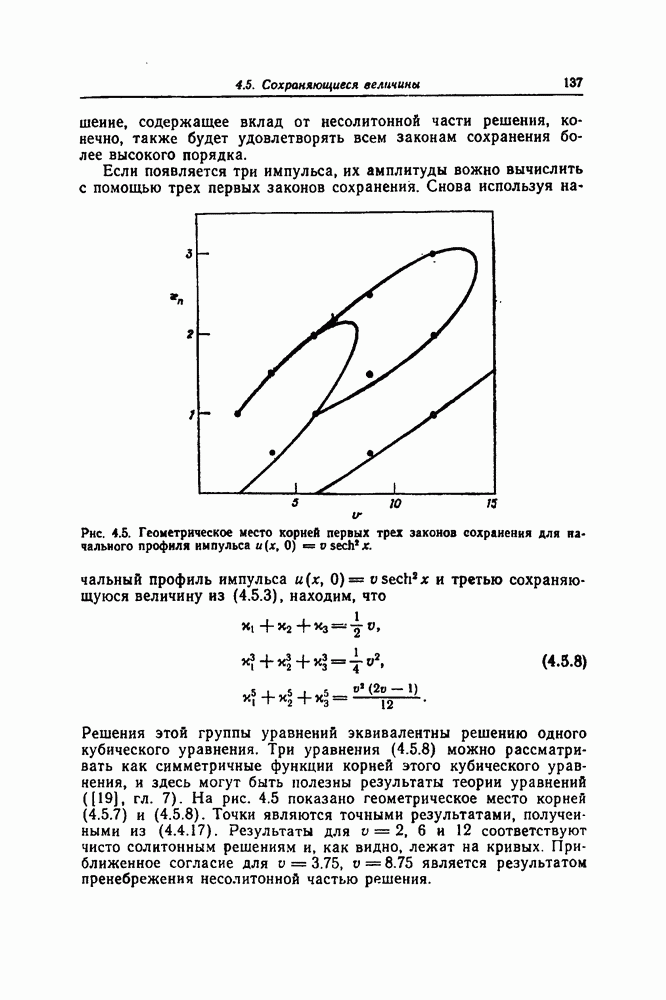
- 4.5. СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
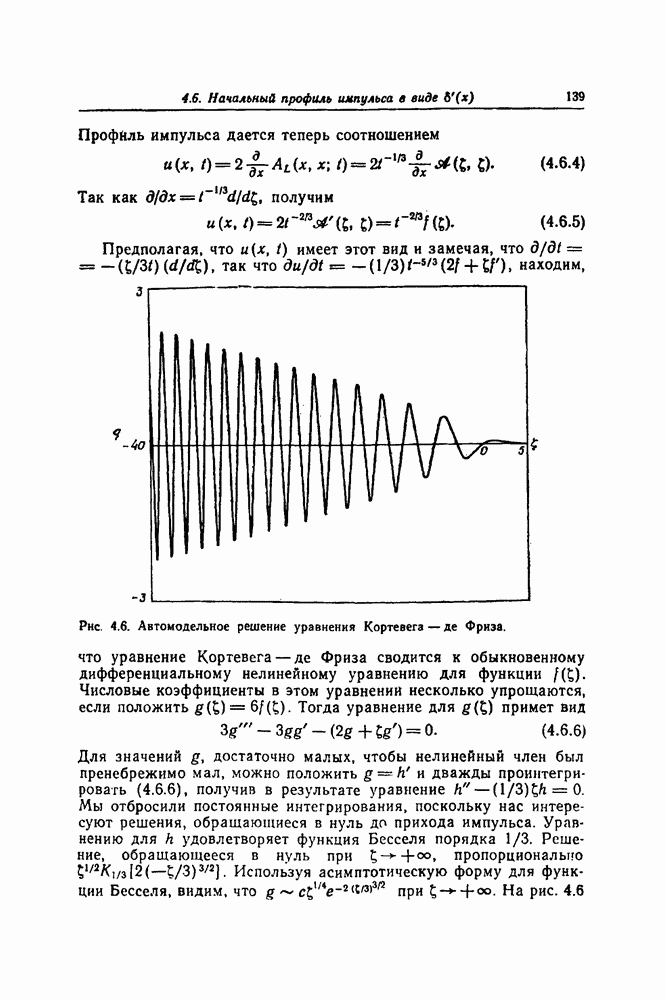
- 4.6. НАЧАЛЬНЫЙ ПРОФИЛЬ ИМПУЛЬСА В ВИДЕ ДЕЛЬТА-ФУНКЦИИ: АВТОМОДЕЛЬНОЕ РЕШЕНИЕ
- 4.7. ДРУГОЙ ПОДХОД К ЛИНЕЙНЫМ УРАВНЕНИЯМ ДЛЯ УРАВНЕНИЯ КОРТЕВЕГА-ДЕ ФРИЗА
- Глава 5. НЕКОТОРЫЕ ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ, СВЯЗАННЫЕ С СИСТЕМОЙ ЗАХАРОВА — ШАБАТА
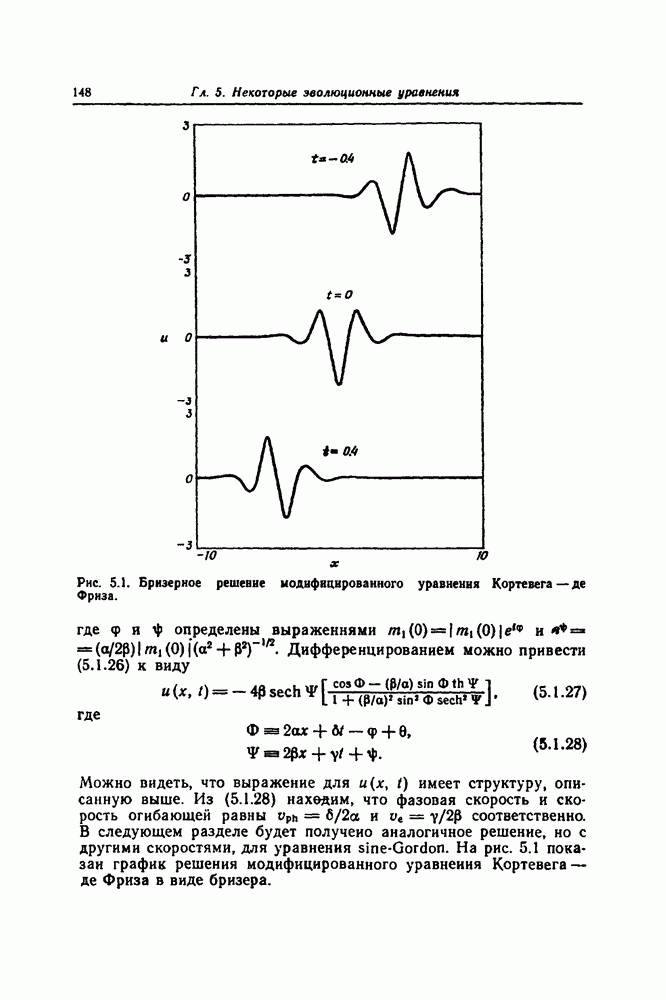
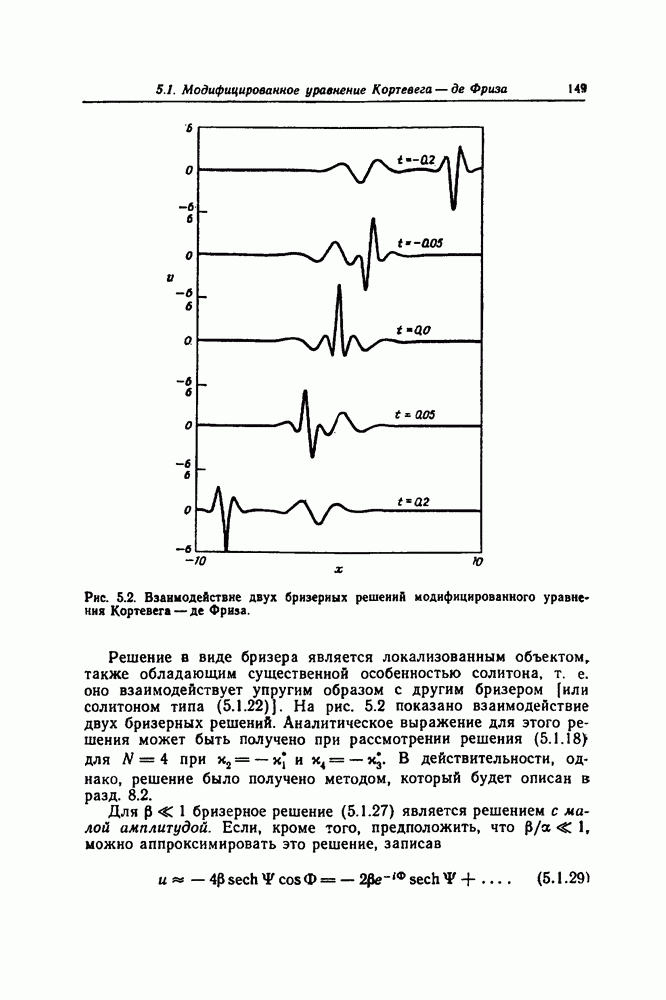
- 5.1. МОДИФИЦИРОВАННОЕ УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 5.2. УРАВНЕНИЕ SINE-GORDON
- 5.3. КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- 5.4. ОБЩИЙ КЛАСС РАЗРЕШИМЫХ НЕЛИНЕЙНЫХ ЭВОЛЮЦИОННЫХ УРАВНЕНИЙ
- Глава 6. ПРИЛОЖЕНИЯ I
- 6.1. ВОЛНЫ НА МЕЛКОЙ ВОДЕ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 6.2. ВОЛНЫ НА МЕЛКОЙ ВОДЕ И КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- 6.3. ИОННО-ЗВУКОВЫЕ ВОЛНЫ В ПЛАЗМЕ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
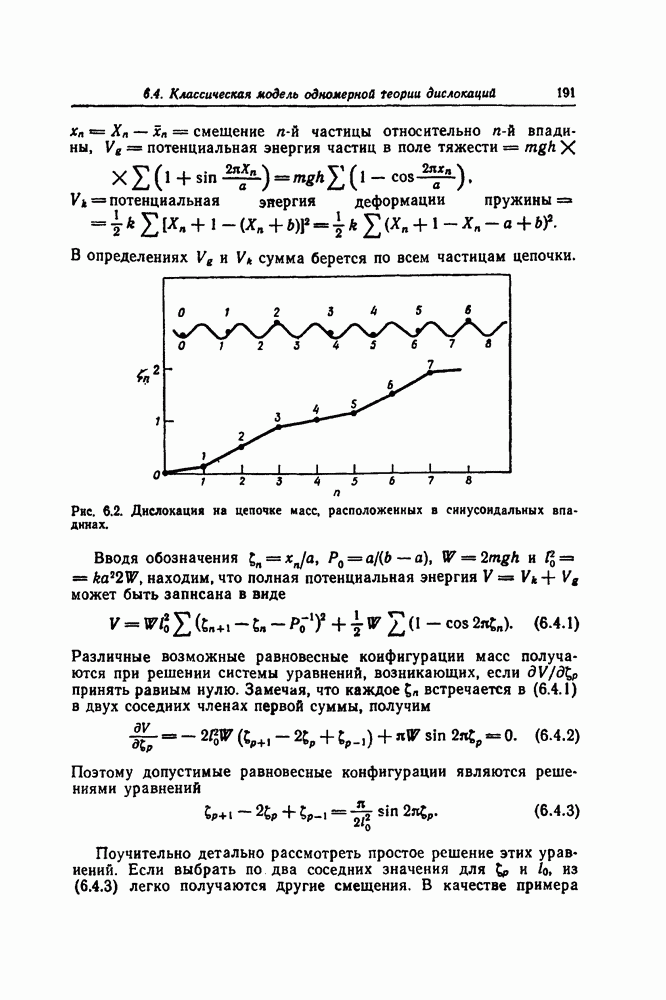
- 6.4. КЛАССИЧЕСКАЯ МОДЕЛЬ ОДНОМЕРНОЙ ТЕОРИИ ДИСЛОКАЦИИ — УРАВНЕНИЕ SINE-GORDON
- 6.5. ВЫБОР ПАРАМЕТРОВ РАЗЛОЖЕНИЯ
- Глава 7. ПРИЛОЖЕНИЯ II
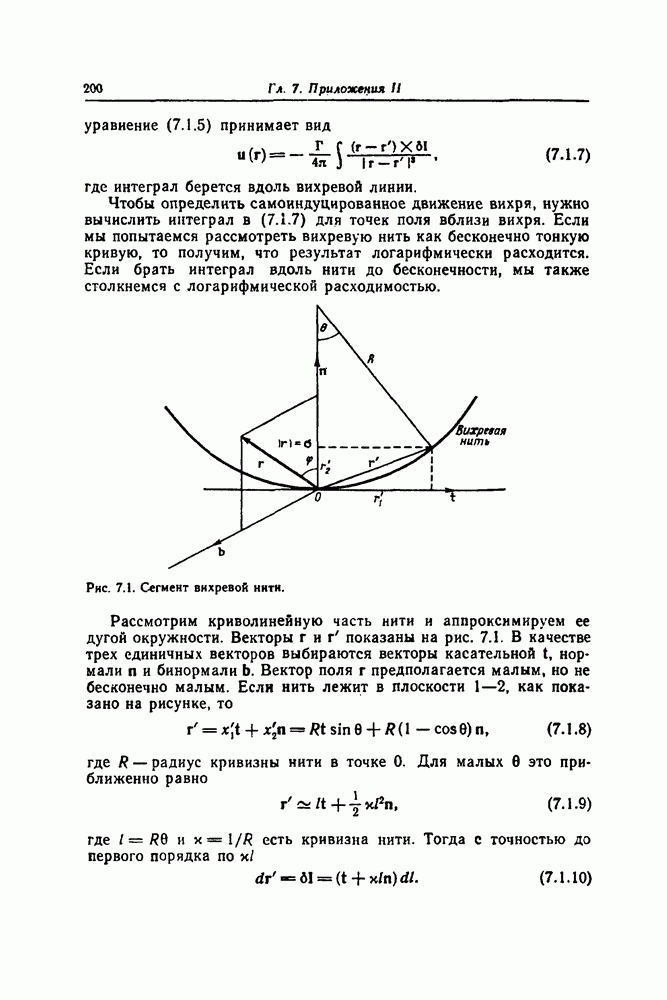
- 7.1. САМОИНДУЦИРОВАННЫЙ ВИХРЬ
- 7.2. ДВИЖЕНИЕ НИТИ
- 7.3. ФОРМА ОДНОСОЛИТОНИОИ НИТИ
- 7.4. ДРУГИЕ СОЛИТОННЫЕ УРАВНЕНИЯ
- 7.5. ОПИСАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 7.6. ДВУХУРОВНЕВЫЙ АТОМ
- 7.7. УРАВНЕНИЯ МОДЕЛИ
- 7.8. НЕПОДВИЖНЫЕ АТОМЫ — ПРЕДЕЛ SINE-CORDON
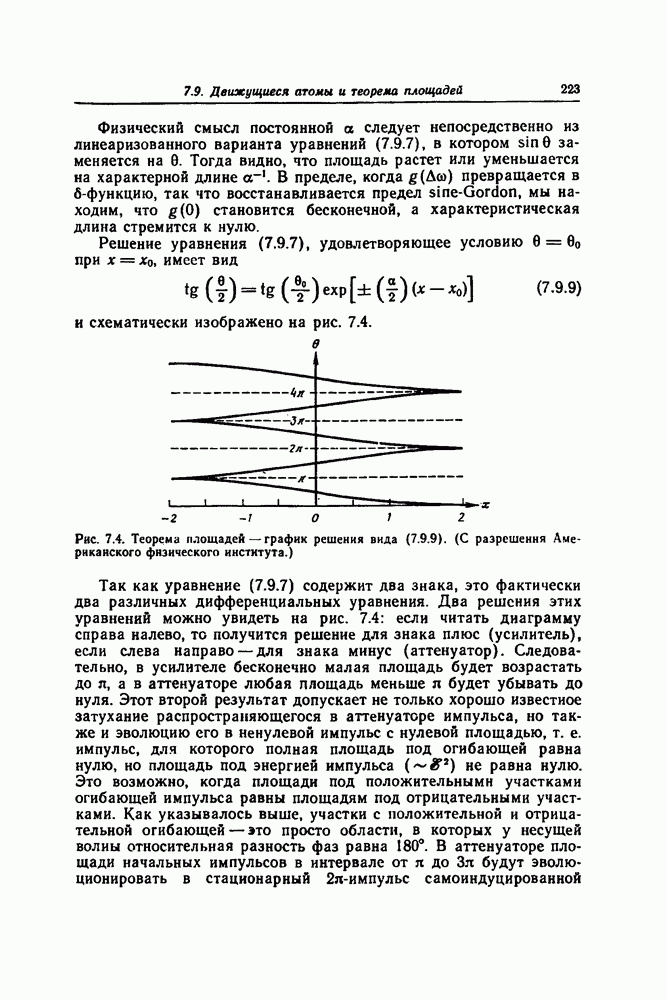
- 7.9. ДВИЖУЩИЕСЯ АТОМЫ И ТЕОРЕМА ПЛОЩАДЕЙ
- 7.10. РЕШЕНИЕ МЕТОДОМ ОБРАТНОЙ ЗАДАЧИ
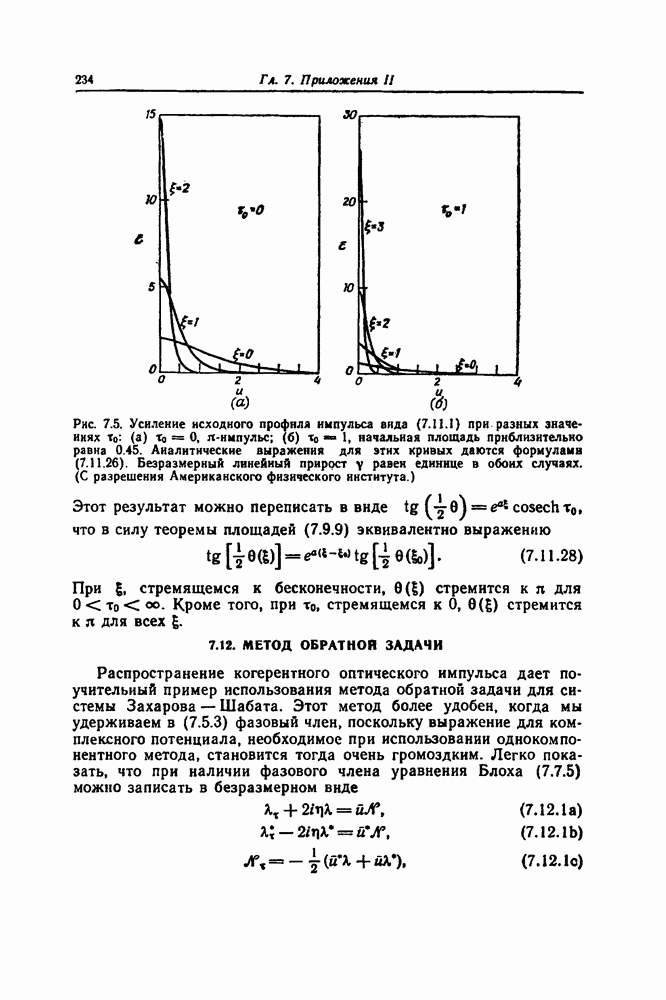
- 7.11. РАСПРОСТРАНЕНИЕ В УСИЛИТЕЛЕ
- 7.12. МЕТОД ОБРАТНОЙ ЗАДАЧИ
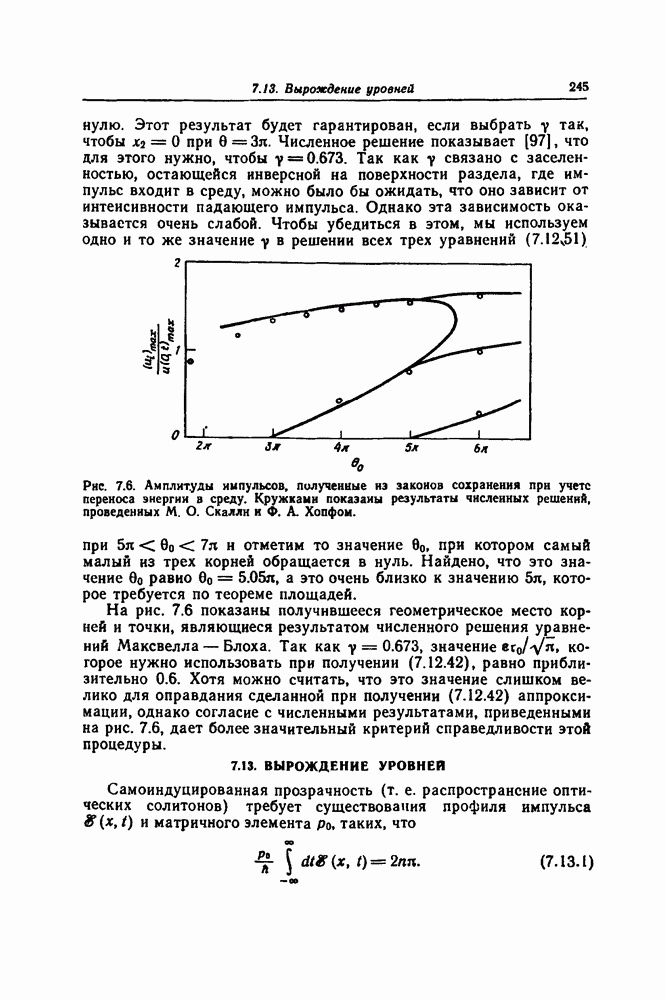
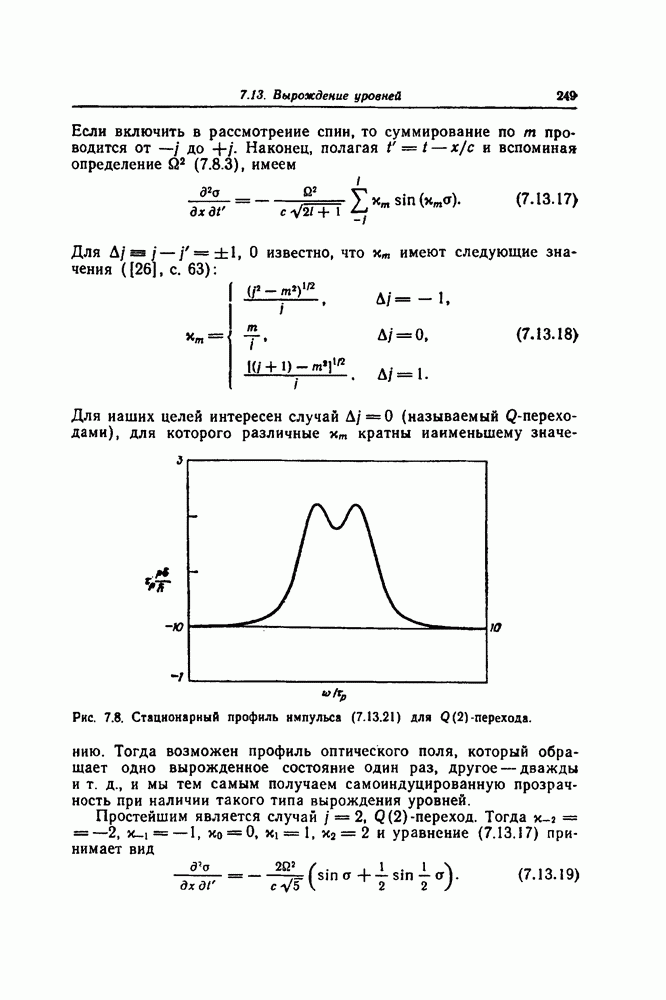
- 7.13. ВЫРОЖДЕНИЕ УРОВНЕЙ
- Глава 8. ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
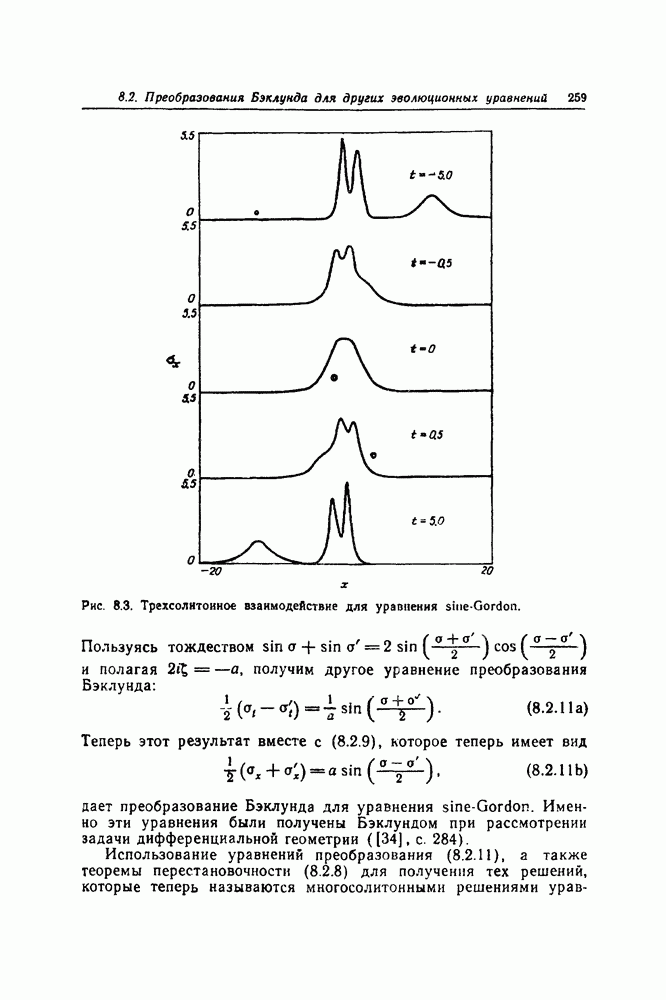
- 8.2. ПРЕОБРАЗОВАНИЯ БЭКЛУНДА ДЛЯ НЕКОТОРЫХ ДРУГИХ ЭВОЛЮЦИОННЫХ УРАВНЕНИЯ
- 8.3. БОЛЕЕ ОБЩИЕ ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
- Главе 9. ТЕОРИЯ ВОЗМУЩЕНИЯ
- УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 9.2. ВОЗМУЩЕНИЕ ОДНОСОЛИТОННОГО РЕШЕНИЯ
- КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЁДИНГЕРА
- 9.4. ЗАТУХАНИЕ ЕДИНИЧНОГО СОЛИТОНА