| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
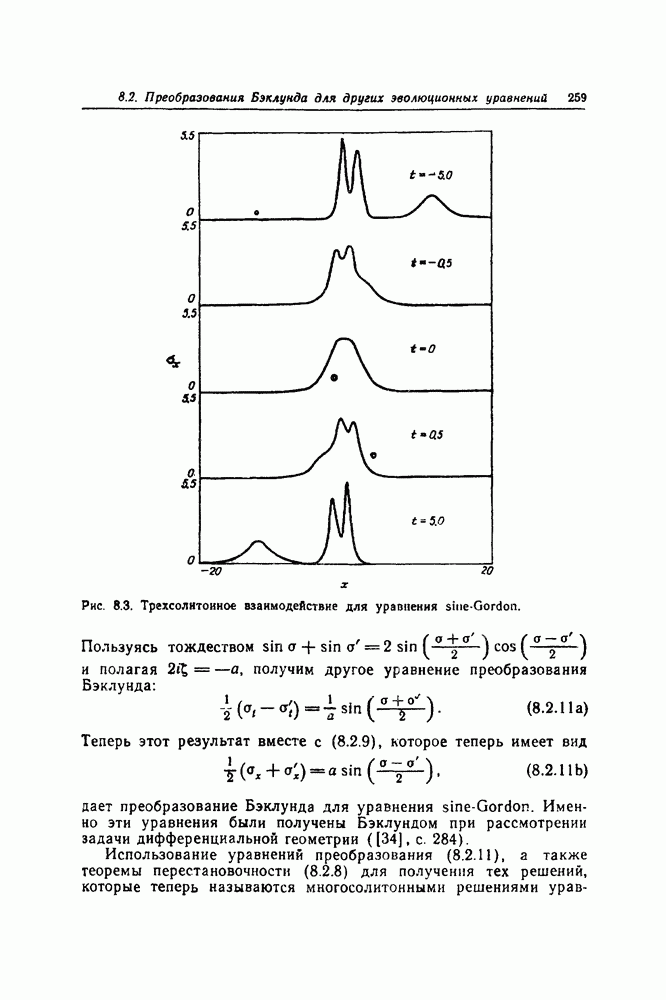
8.3. БОЛЕЕ ОБЩИЕ ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
Рассмотренные в двух предыдущих разделах преобразования, при которых исходная функция  и преобразованная функция
и преобразованная функция  удовлетворяют одному и тому же дифференциальному уравнению в частных производных, являются специальным классом преобразований Бэклунда. В общем случае функции
удовлетворяют одному и тому же дифференциальному уравнению в частных производных, являются специальным классом преобразований Бэклунда. В общем случае функции  могут удовлетворять различным уравнениям. Кроме того, необязательно, чтобы была какая-либо связь с уравнением Штурма — Лиувилля. В этом разделе мы кратко рассмотрим разработанный Клэрэном [23] метод построения как ранее рассмотренных преобразований Бэклунда, так и преобразований более общего вида, когда функции
могут удовлетворять различным уравнениям. Кроме того, необязательно, чтобы была какая-либо связь с уравнением Штурма — Лиувилля. В этом разделе мы кратко рассмотрим разработанный Клэрэном [23] метод построения как ранее рассмотренных преобразований Бэклунда, так и преобразований более общего вида, когда функции  удовлетворяют различным дифференциальным уравнениям в частных производных.
удовлетворяют различным дифференциальным уравнениям в частных производных.
Рассмотрим преобразования Бэклунда, связывающие дифференциальные уравнения второго порядка в частных производных вида  где
где  функции x, у и z, а также
функции x, у и z, а также  где
где  Такого типа уравнения часто называют уравнениями Монжа — Ампера. Преобразования Бэклунда, связывающие два таких уравнения второго порядка, задаются парой дифференциальных уравнений первого порядка
Такого типа уравнения часто называют уравнениями Монжа — Ампера. Преобразования Бэклунда, связывающие два таких уравнения второго порядка, задаются парой дифференциальных уравнений первого порядка

Классификация различных типов получающихся преобразований требует детального рассмотрения. Это было проделано Клэрэном (1903) [23] и подытожено в работе [46]. Краткий обзор содержится в книге Форсайта [39]. В некоторых случаях это более простое преобразование, называемое контактным. В других случаях оно называется преобразованием Бэклунда. Форсайт показал также ([39], с. 441), что произвольно выбранное уравнение Монжа — Ампера нельзя связать с преобразованием Бэклунда [Нужно иметь возможность удовлетворить четырем уравнениям с тремя неизвестными.)
Для определения  заметим сначала, что условие интегруемости (т. е. равенство смешанных вторых производных)
заметим сначала, что условие интегруемости (т. е. равенство смешанных вторых производных)
требует, чтобы функции (8.3.1) удовлетворяли соотношению

Замечая, что каждая из четырех переменных  зависит от х и у, и обозначая штрихами частные производные, имеем
зависит от х и у, и обозначая штрихами частные производные, имеем

Аналогичное выражение справедливо для  Используя (8.3.1) для исключения
Используя (8.3.1) для исключения  и группируя члены, находим, что
и группируя члены, находим, что

Считая функцию  известной, мы видим, что пока по крайней мере один из коэффициентов
известной, мы видим, что пока по крайней мере один из коэффициентов  или
или  не равен нулю, уравнение (8.3.4) является дифференциальным уравнением в частных производных для функции
не равен нулю, уравнение (8.3.4) является дифференциальным уравнением в частных производных для функции 
Пример — уравнение Лиувилля
В качестве примера построения методом Клэрэна преобразования Бэклунда, связывающего два различных уравнения, получим преобразование между нелинейным уравнением Лиувилля  и линейным уравнением
и линейным уравнением  Последнее уравнение является волновым уравнением в характеристических координатах. Общее решение волнового уравнения, выраженное через две произвольные функции, конечно, известно. Мы увидим, что используя преобразование Бэклунда, можно получить общее решение уравнения Лиувилля.
Последнее уравнение является волновым уравнением в характеристических координатах. Общее решение волнового уравнения, выраженное через две произвольные функции, конечно, известно. Мы увидим, что используя преобразование Бэклунда, можно получить общее решение уравнения Лиувилля.
Так как уравнение Лиувилля содержит  но не
но не  или
или  из условия совместности (8.3.4) мы ожидаем, что
из условия совместности (8.3.4) мы ожидаем, что  и
и  Итак, мы начнем с уравнений преобразования вида
Итак, мы начнем с уравнений преобразования вида

Производная по у от (8.3.5а) дает

Используя  и то, что
и то, что  имеем
имеем

Две производные по  дают
дают

Это означает (поскольку  зависит главным образом от
зависит главным образом от  , что
, что  является линейной функцией
является линейной функцией  Аналогичным образом можно
Аналогичным образом можно
показать, что  является линейной функцией
является линейной функцией  и можно записать
и можно записать

Как указывалось выше, мы должны наложить ограничение  Можно избежать относительно скучного анализа и легко получить простое преобразование, полагая
Можно избежать относительно скучного анализа и легко получить простое преобразование, полагая  Тогда уравнения преобразования суть
Тогда уравнения преобразования суть

а условие совместности (8.3.4) записывается в виде 

где был использован факт, что  удовлетворяет уравнению Лиувилля. Теперь неизвестные функции
удовлетворяет уравнению Лиувилля. Теперь неизвестные функции  определяются из рассмотрения различных производных от
определяются из рассмотрения различных производных от  В частности,
В частности,

С этими соотношениями выражение для  сводится к следующему:
сводится к следующему:

Кроме того, уравнения (8.3.12) являются дифференциальными уравнениями в частных производных, имеющими решения

Из (8.3.13) мы можем получить

Если ввести новые независимые переменные

то уравнение (8.3.15) можно записать в виде

где переменные разделены и  является постоянной разделения. (Выбор знака соответствует действительным показателям экспонент в уравнении Лиувилля.) Таким образом, выражения для
является постоянной разделения. (Выбор знака соответствует действительным показателям экспонент в уравнении Лиувилля.) Таким образом, выражения для  имеют вид
имеют вид

Теперь, используя (8.3.7), можно определить постоянные интегрирования  Находим
Находим

Этому уравнению можно удовлетворить, выбирая либо  либо к
либо к  При первом выборе постоянных мы получим преобразование в виде
При первом выборе постоянных мы получим преобразование в виде

Последний выбор постоянных дает то же самое однопараметрическое преобразование Бэклунда.
Уравнения преобразования (8.3.20) могут быть использованы для получения общего решения уравнения Лиувилля. С этой целью заметим сначала, что общее решение волнового уравнения  можно записать в виде
можно записать в виде  Полагая
Полагая  линеаризуем уравнения преобразования и получим
линеаризуем уравнения преобразования и получим

Общее решение этих линейных уравнений легко определяется. Если положить  то находим, что общее решение уравнения Лиувилля имеет вид
то находим, что общее решение уравнения Лиувилля имеет вид

В этом примере, где с помощью преобразования Бэклунда уравнение Лиувилля преобразуется в простое линейное уравнение, Получено общее решение нелинейного уравнения. Для преобразования нелинейного уравнения в самого себя, как в случае солитенных уравнений, метод дает только частные решения.
Известны некоторые другие преобразования различных дифференциальных уравнений в частных производных, и можно показать, что они являются примерами преобразований Бэклунда. Нелинейное уравнение Бюргерса  связано с линейным уравнением диффузии
связано с линейным уравнением диффузии  посредством преобразования ([39], [54], [25])
посредством преобразования ([39], [54], [25])

В обозначениях данного раздела это соотношение эквивалентно

Как намечено в упр. 1, использованный выше метод можно применить для получения дополнительного уравнения

Уравнения (8.3.24) и (8.3.25) составляют преобразование Бэклунда, связывающее уравнение Бюргерса с уравнением диффузии В гл. 5 мы видели, что уравнение Кортевега — де Фриза и модифицированное уравнение Кортевега — де Фриза связаны преобразованием Миуры. Чтобы получить преобразование Бэклунда, можно присоединить к преобразованию Миуры дополнительное уравнение. Эта процедура излагается в упр. 5.
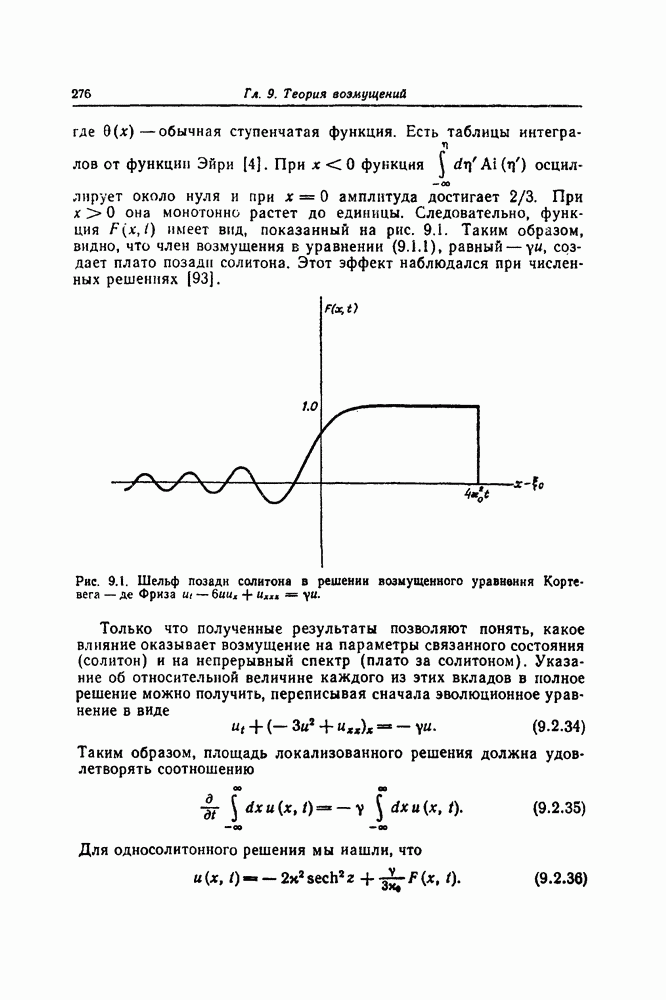
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- 1.1. УРАВНЕНИЕ ШТУРМА-ЛИУВИЛЛЯ
- 1.2. УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 1.3. МНОГОСОЛИТОННЫЕ РЕШЕНИЯ КАК ПОТЕНЦИАЛЫ БАРГМАНА
- 1.4. ФИЗИЧЕСКАЯ СИСТЕМА, ПРИВОДЯЩАЯ К УРАВНЕНИЮ КОРТЕВЕГА — ДЕ ФРИЗА
- 1.5. РАСПРОСТРАНЕНИЕ НА СЛУЧАИ ДРУГИХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.6. ПЛАН ДАЛЬНЕЙШЕГО ИЗЛОЖЕНИЯ
- Глава 2. ВОПРОСЫ ОДНОМЕРНОЙ ТЕОРИИ РАССЕЯНИЯ
- 2.2. РАССЕЯНИЕ ОСЦИЛЛЯТОРОМ
- 2.3. УПРУГО ЗАКРЕПЛЕННАЯ СТРУНА
- 2.4. УРАВНЕНИЕ ШРЕДИНГЕРА
- 2.5. РАССЕЯНИЕ ПОТЕНЦИАЛОМ ВИДА sech
- 2.6. СООТВЕТСТВУЮЩИЕ УРАВНЕНИЯ ШТУРМА — ЛИУВИЛЛЯ
- 2.7. ДВУМЕРНЫЕ ВОЛНЫ В НЕОДНОРОДНОЙ СРЕДЕ
- 2.8. ОБЩИЙ ПОДХОД К ПРОБЛЕМЕ РАССЕЯНИЯ
- 2.9. «ОБРЕЗАННЫЕ» ПОТЕНЦИАЛЫ
- 2.10. РАССЕЯНИЕ ИМПУЛЬСОВ — УРАВНЕНИЯ МАРЧЕНКО
- 2.11. ЗАДАЧА РАССЕЯНИЯ ЗАХАРОВА — ШАБАТА
- 2.12. СВЯЗЬ МЕЖДУ УРАВНЕНИЕМ ШРЕДИНГЕРА И УРАВНЕНИЯМИ ЗАХАРОВА — ШАБЛТА: УРАВНЕНИЯ РИККАТИ
- Глава 3. ОДНОМЕРНАЯ ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ
- 3.2. НАЛИЧИЕ СВЯЗАННЫХ СОСТОЯНИЯ
- 3.3. БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ
- 3.4. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ-РАЦИОНАЛЬНАЯ ФУНКЦИЯ
- 3.5. ПОТЕНЦИАЛЫ БАРГМАНА
- 3.8. МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ ЗАХАРОВА — ШАБАТА ДЛЯ ДЕЙСТВИТЕЛЬНЫХ ПОТЕНЦИАЛОВ
- 3.7. БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ ДЛЯ СИСТЕМЫ ЗАХАРОВА — ШАБАТА
- 3.8. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ ДЛЯ СИСТЕМЫ ЗАХАРОВА — ШАБАТА В ВИДЕ РАЦИОНАЛЬНОЯ ФУНКЦИИ
- 3.9. СИСТЕМА ЗАХАРОВА — ШАБАТА С КОМПЛЕКСНЫМ ПОТЕНЦИАЛОМ
- Глава 4. УРАВНЕНИЕ КОРТЕВЕГА—ДЕ ФРИЗА
- 4.2. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РЕШЕНИЙ
- 4.3. ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 4.4. МНОГОСОЛИТОННЫЕ РЕШЕНИЯ
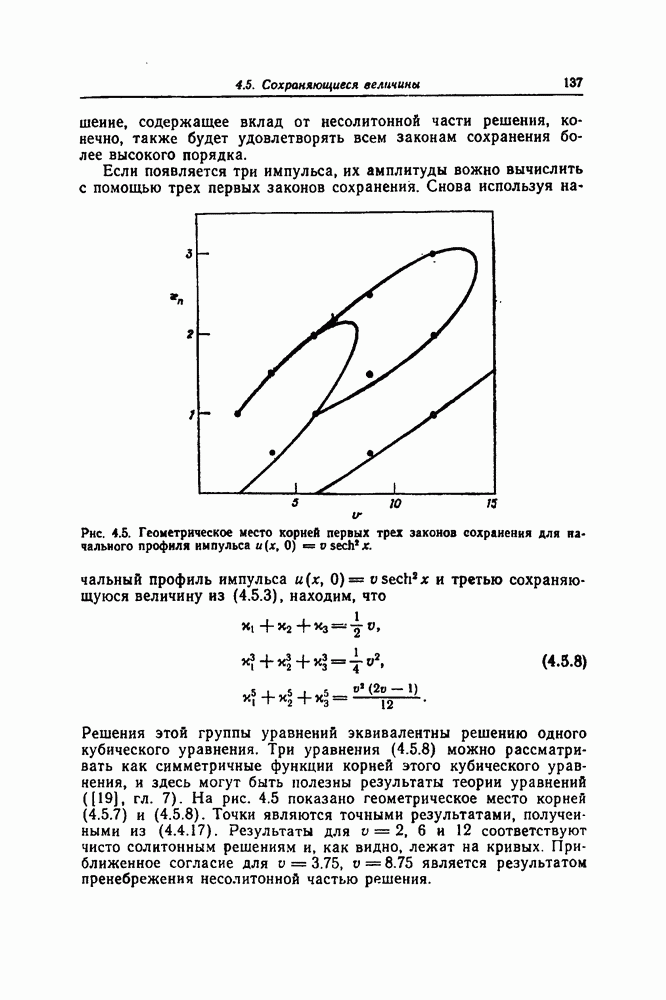
- 4.5. СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
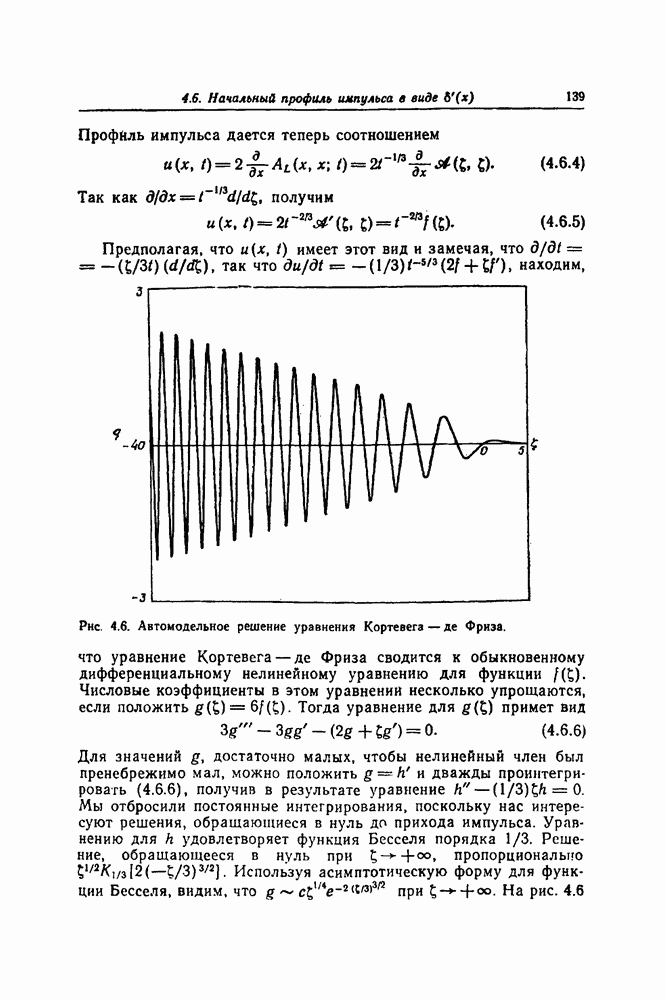
- 4.6. НАЧАЛЬНЫЙ ПРОФИЛЬ ИМПУЛЬСА В ВИДЕ ДЕЛЬТА-ФУНКЦИИ: АВТОМОДЕЛЬНОЕ РЕШЕНИЕ
- 4.7. ДРУГОЙ ПОДХОД К ЛИНЕЙНЫМ УРАВНЕНИЯМ ДЛЯ УРАВНЕНИЯ КОРТЕВЕГА-ДЕ ФРИЗА
- Глава 5. НЕКОТОРЫЕ ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ, СВЯЗАННЫЕ С СИСТЕМОЙ ЗАХАРОВА — ШАБАТА
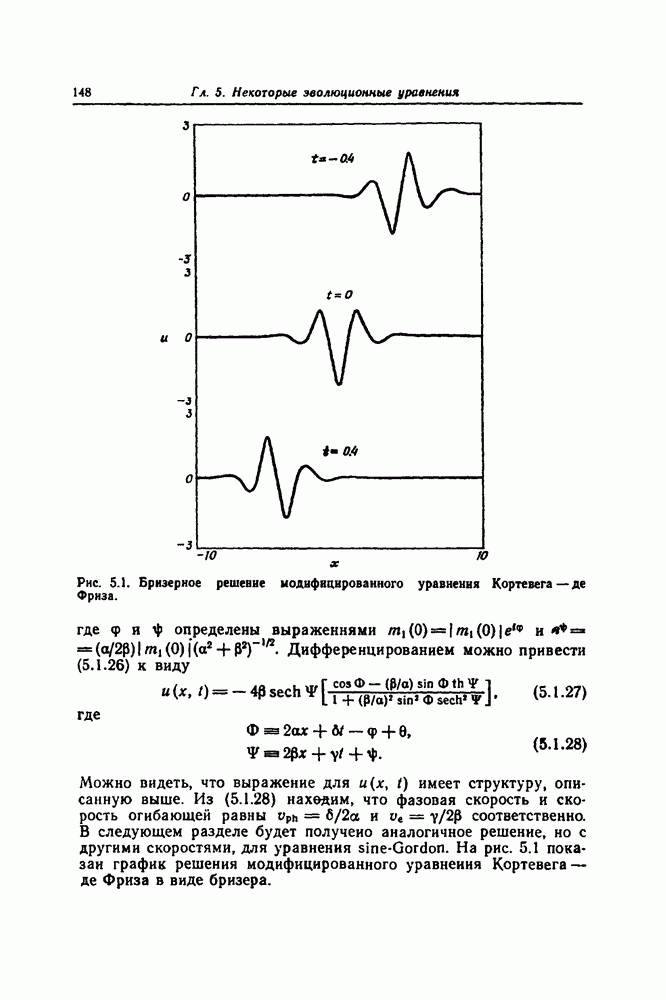
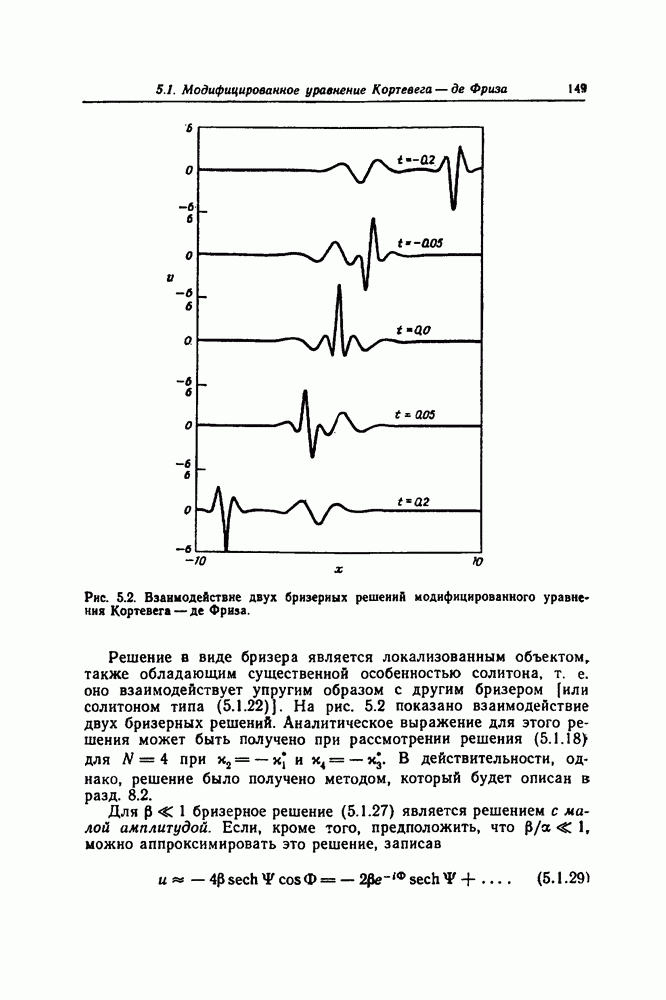
- 5.1. МОДИФИЦИРОВАННОЕ УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 5.2. УРАВНЕНИЕ SINE-GORDON
- 5.3. КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- 5.4. ОБЩИЙ КЛАСС РАЗРЕШИМЫХ НЕЛИНЕЙНЫХ ЭВОЛЮЦИОННЫХ УРАВНЕНИЙ
- Глава 6. ПРИЛОЖЕНИЯ I
- 6.1. ВОЛНЫ НА МЕЛКОЙ ВОДЕ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 6.2. ВОЛНЫ НА МЕЛКОЙ ВОДЕ И КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- 6.3. ИОННО-ЗВУКОВЫЕ ВОЛНЫ В ПЛАЗМЕ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
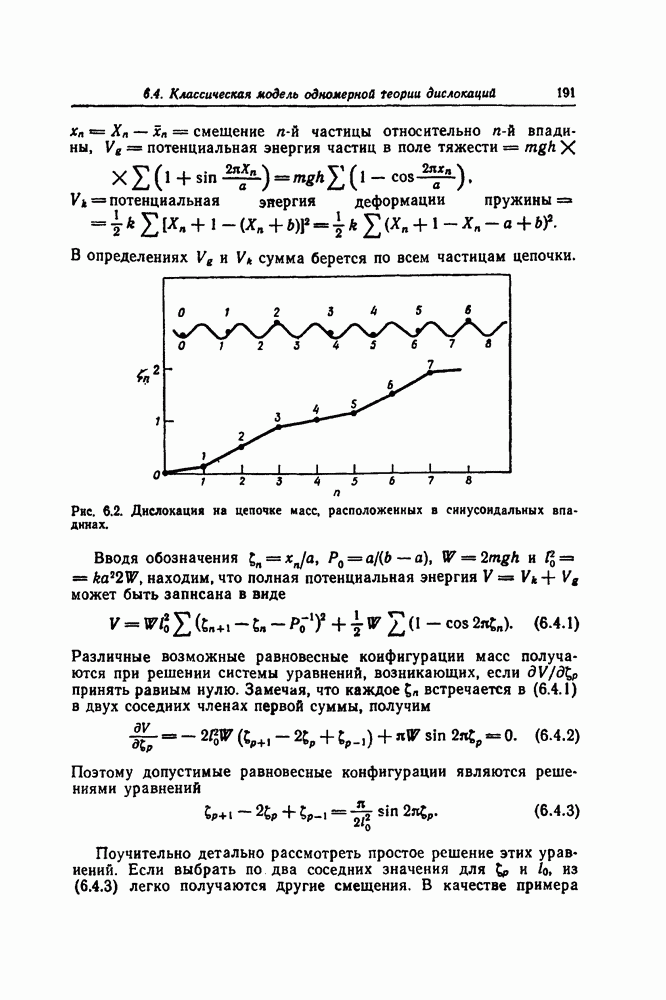
- 6.4. КЛАССИЧЕСКАЯ МОДЕЛЬ ОДНОМЕРНОЙ ТЕОРИИ ДИСЛОКАЦИИ — УРАВНЕНИЕ SINE-GORDON
- 6.5. ВЫБОР ПАРАМЕТРОВ РАЗЛОЖЕНИЯ
- Глава 7. ПРИЛОЖЕНИЯ II
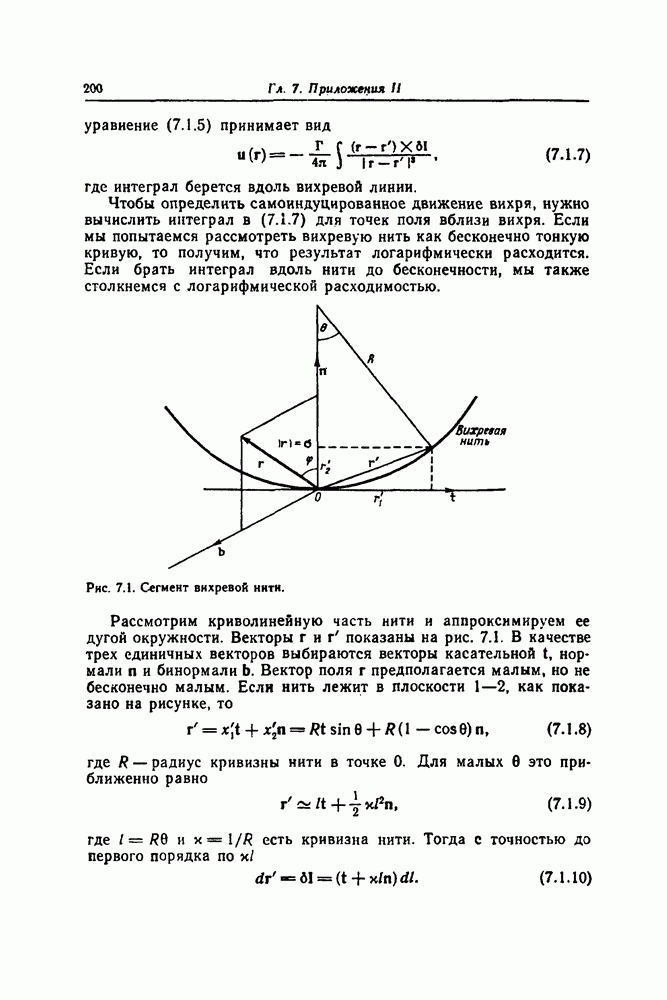
- 7.1. САМОИНДУЦИРОВАННЫЙ ВИХРЬ
- 7.2. ДВИЖЕНИЕ НИТИ
- 7.3. ФОРМА ОДНОСОЛИТОНИОИ НИТИ
- 7.4. ДРУГИЕ СОЛИТОННЫЕ УРАВНЕНИЯ
- 7.5. ОПИСАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 7.6. ДВУХУРОВНЕВЫЙ АТОМ
- 7.7. УРАВНЕНИЯ МОДЕЛИ
- 7.8. НЕПОДВИЖНЫЕ АТОМЫ — ПРЕДЕЛ SINE-CORDON
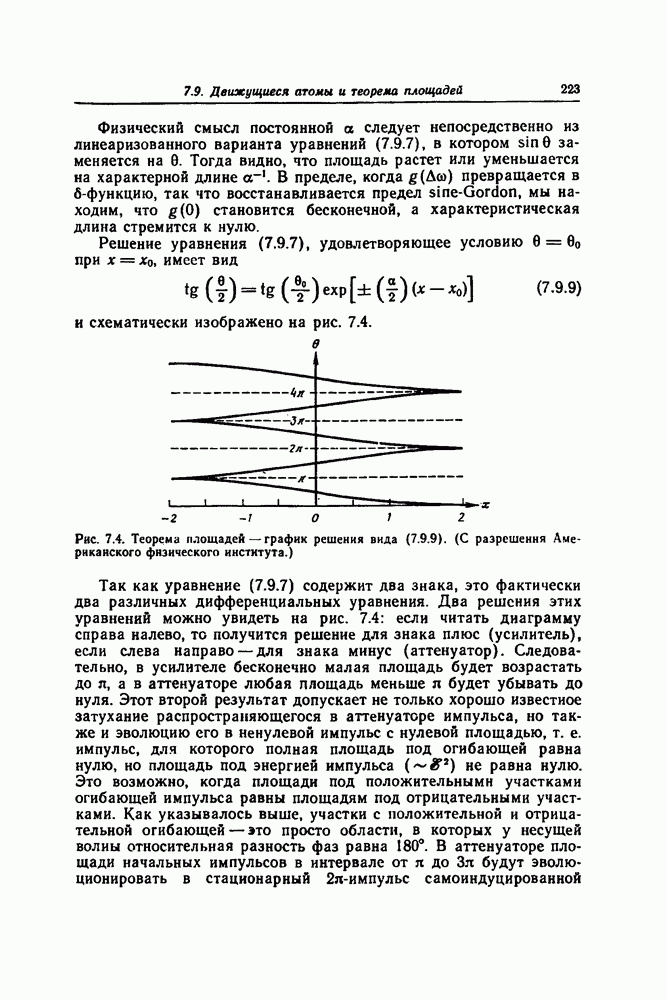
- 7.9. ДВИЖУЩИЕСЯ АТОМЫ И ТЕОРЕМА ПЛОЩАДЕЙ
- 7.10. РЕШЕНИЕ МЕТОДОМ ОБРАТНОЙ ЗАДАЧИ
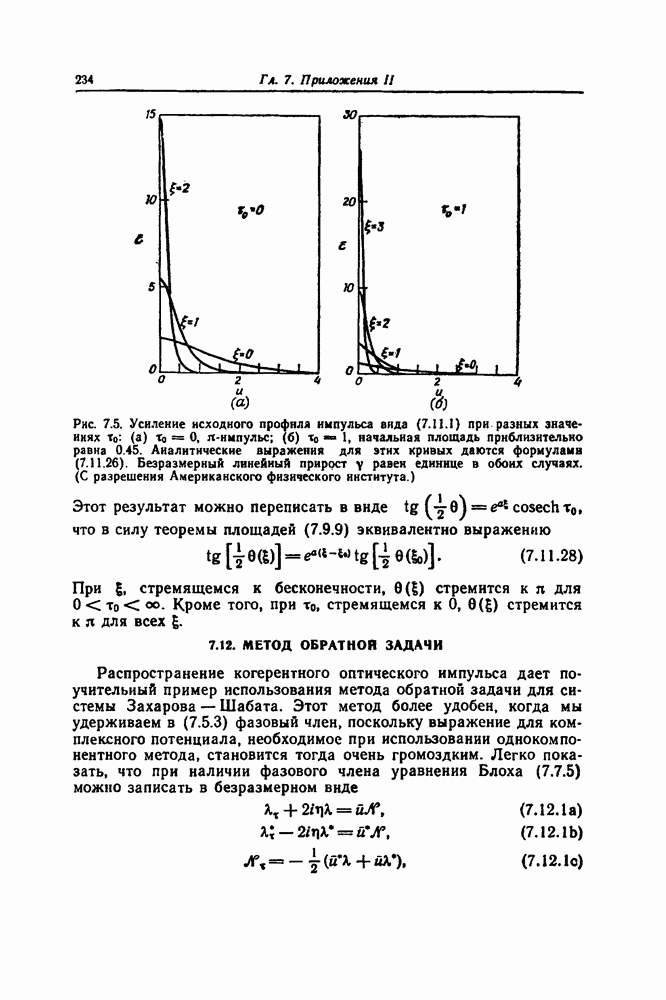
- 7.11. РАСПРОСТРАНЕНИЕ В УСИЛИТЕЛЕ
- 7.12. МЕТОД ОБРАТНОЙ ЗАДАЧИ
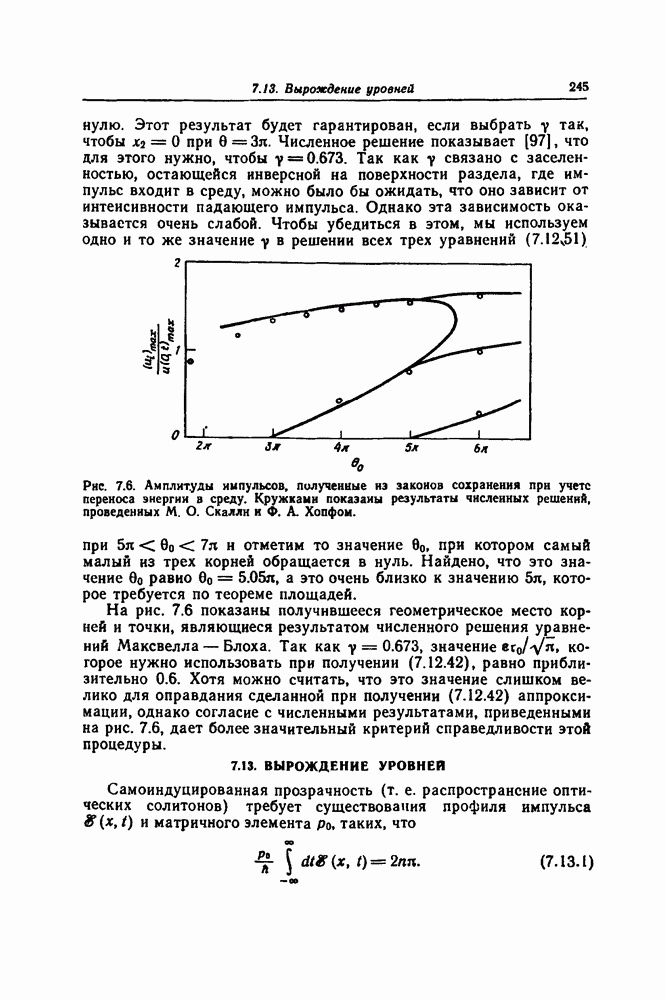
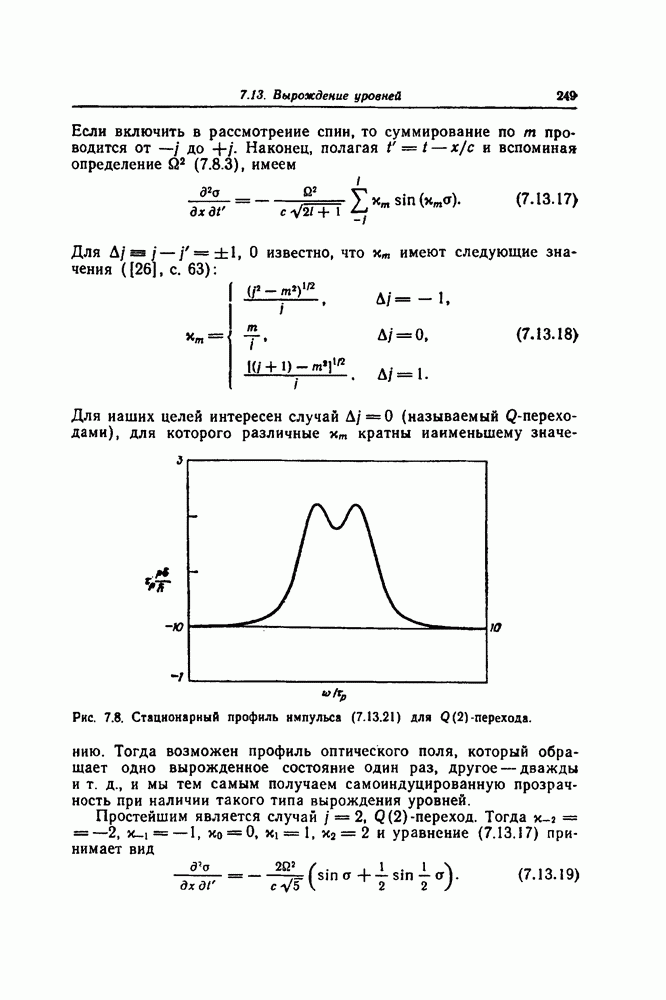
- 7.13. ВЫРОЖДЕНИЕ УРОВНЕЙ
- Глава 8. ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
- 8.2. ПРЕОБРАЗОВАНИЯ БЭКЛУНДА ДЛЯ НЕКОТОРЫХ ДРУГИХ ЭВОЛЮЦИОННЫХ УРАВНЕНИЯ
- 8.3. БОЛЕЕ ОБЩИЕ ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
- Главе 9. ТЕОРИЯ ВОЗМУЩЕНИЯ
- УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 9.2. ВОЗМУЩЕНИЕ ОДНОСОЛИТОННОГО РЕШЕНИЯ
- КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЁДИНГЕРА
- 9.4. ЗАТУХАНИЕ ЕДИНИЧНОГО СОЛИТОНА