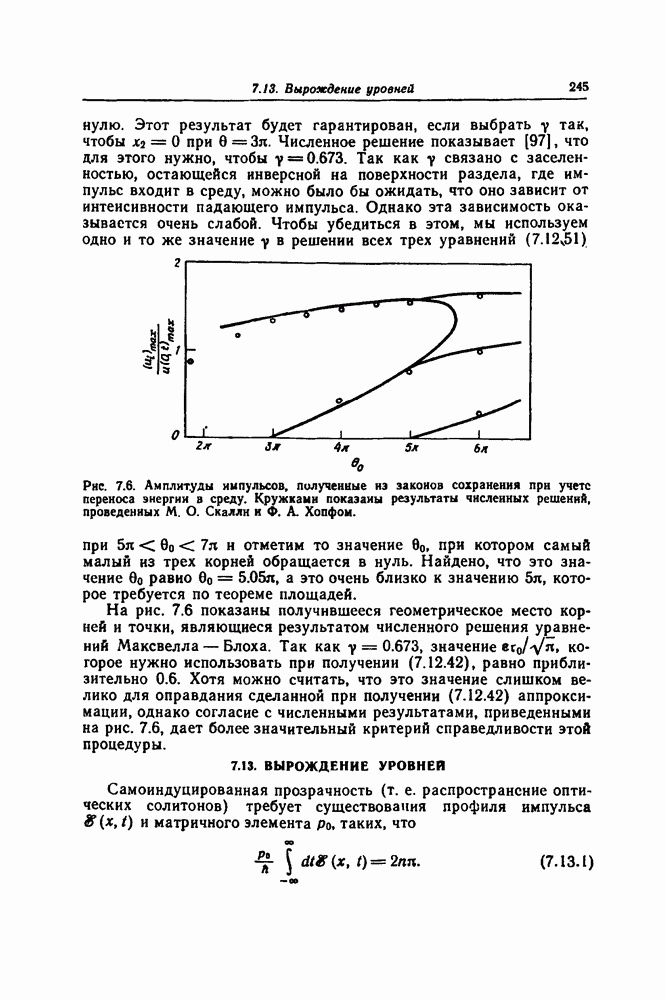
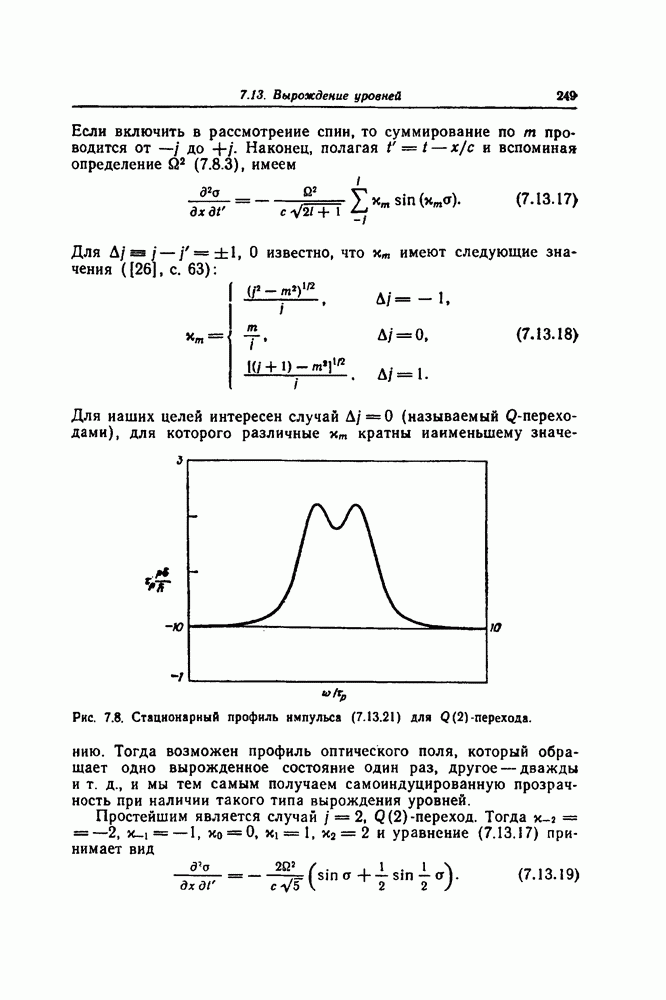
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 8. ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
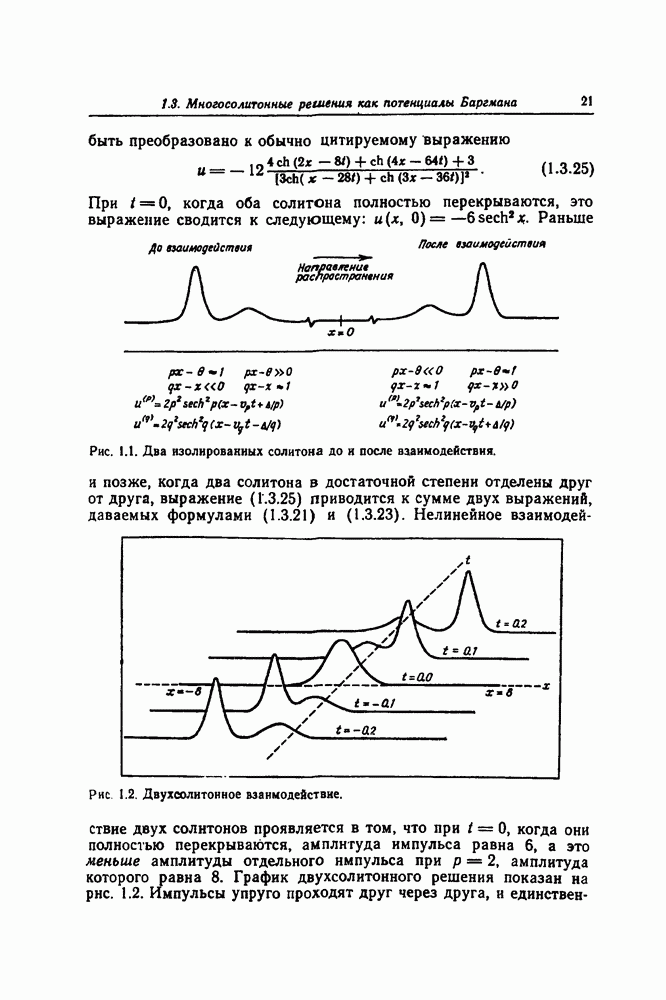
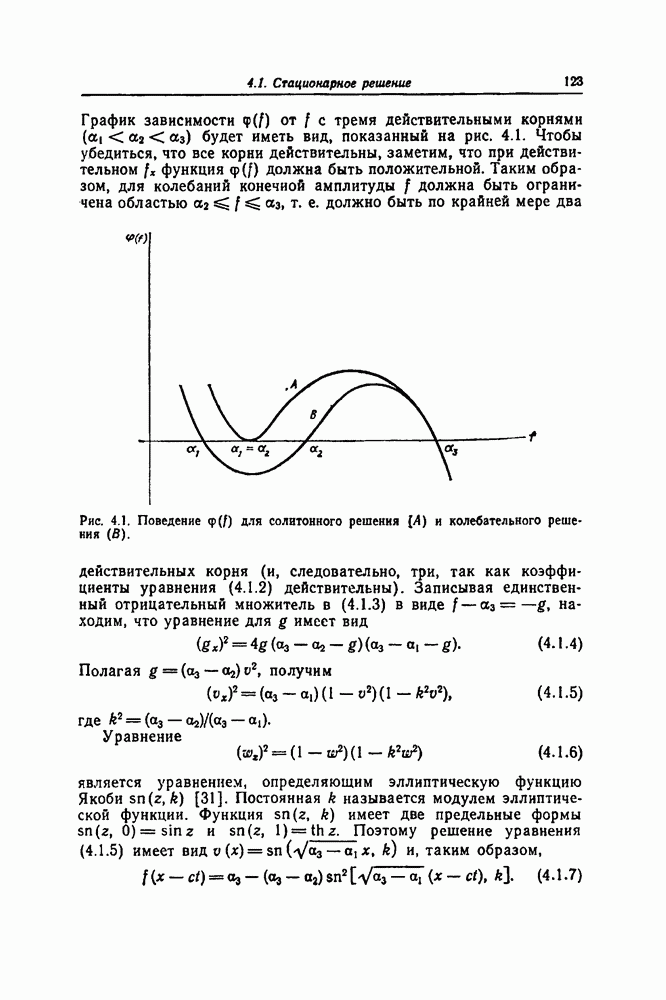
В гл. 2 мы видели, что решение уравнения Шрёдингера для потенциала  можно выразить через элементарные функции, если
можно выразить через элементарные функции, если  где
где  положительное целое число. Эти специальные значения
положительное целое число. Эти специальные значения  соответствуют безотражательным потенциалам и дают также начальные профили импульсов, развивающихся в чисто многосолитонные решения уравнения Кортевега — де Фриза. Начиная с
соответствуют безотражательным потенциалам и дают также начальные профили импульсов, развивающихся в чисто многосолитонные решения уравнения Кортевега — де Фриза. Начиная с  так что
так что  можно построить эти специальные потенциалы и решения соответствующих уравнений Шрёдингера с помощью простого метода, разработанного в гл. 2.
можно построить эти специальные потенциалы и решения соответствующих уравнений Шрёдингера с помощью простого метода, разработанного в гл. 2.
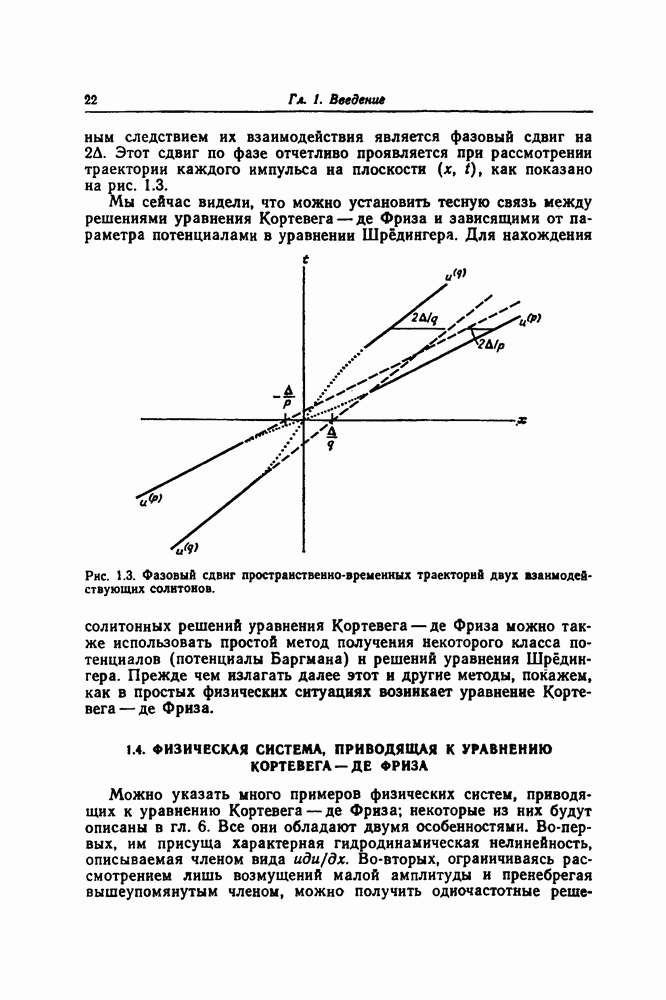
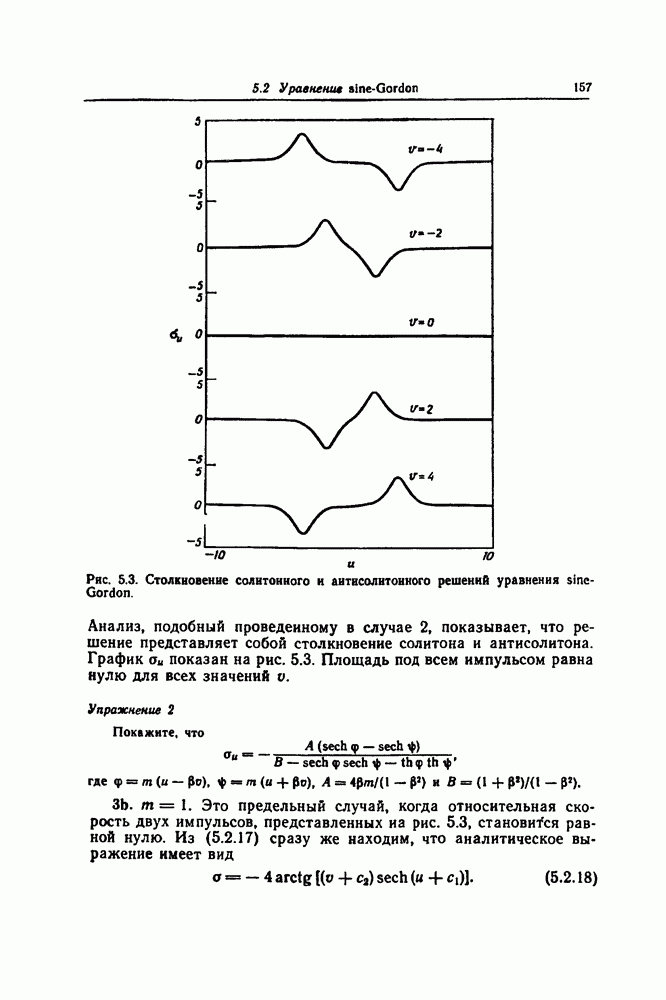
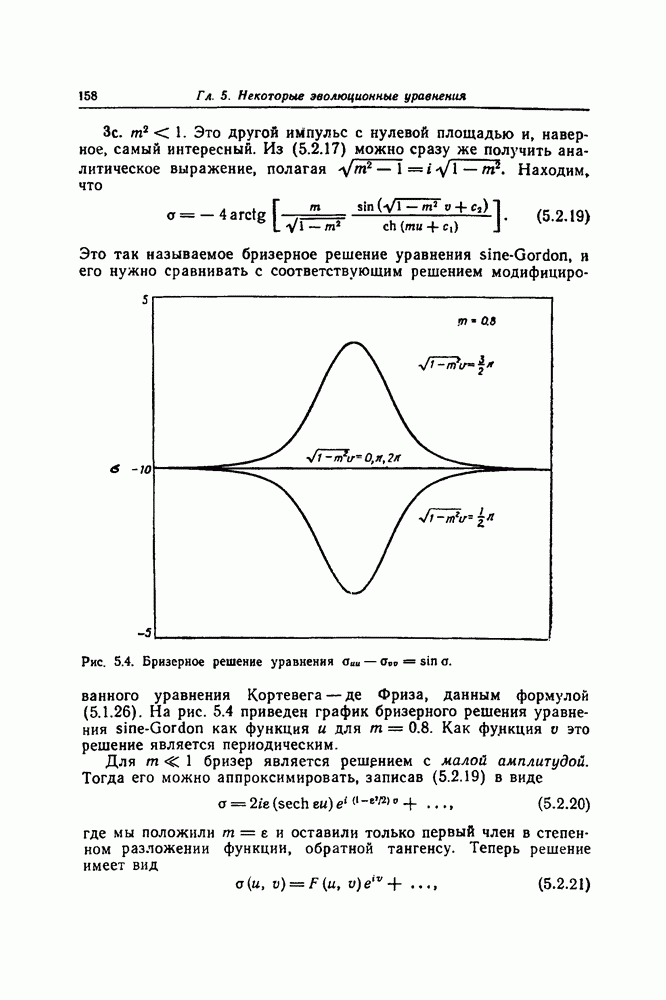
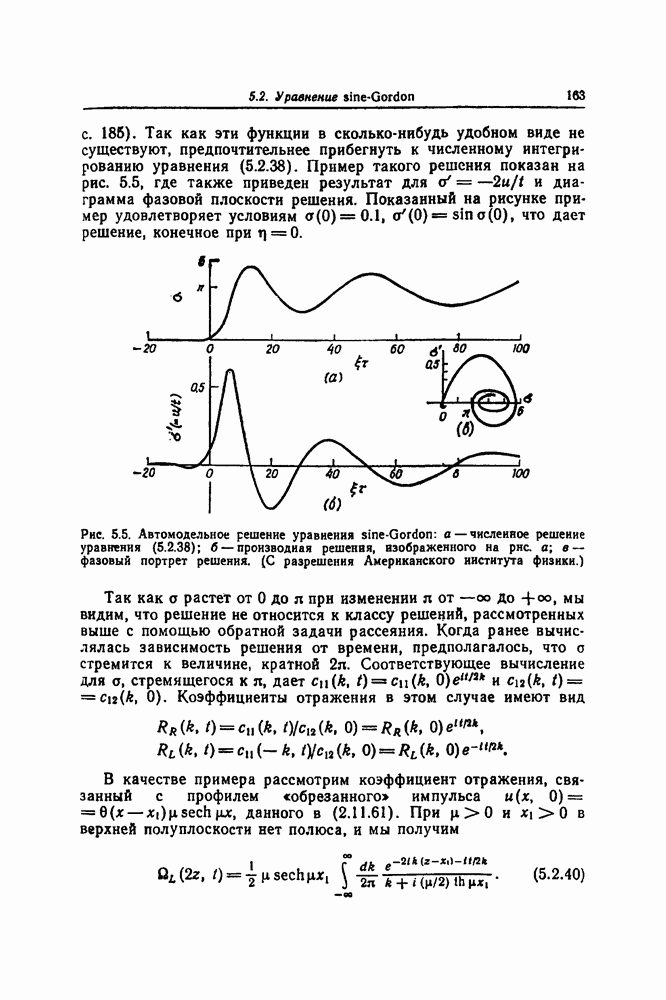
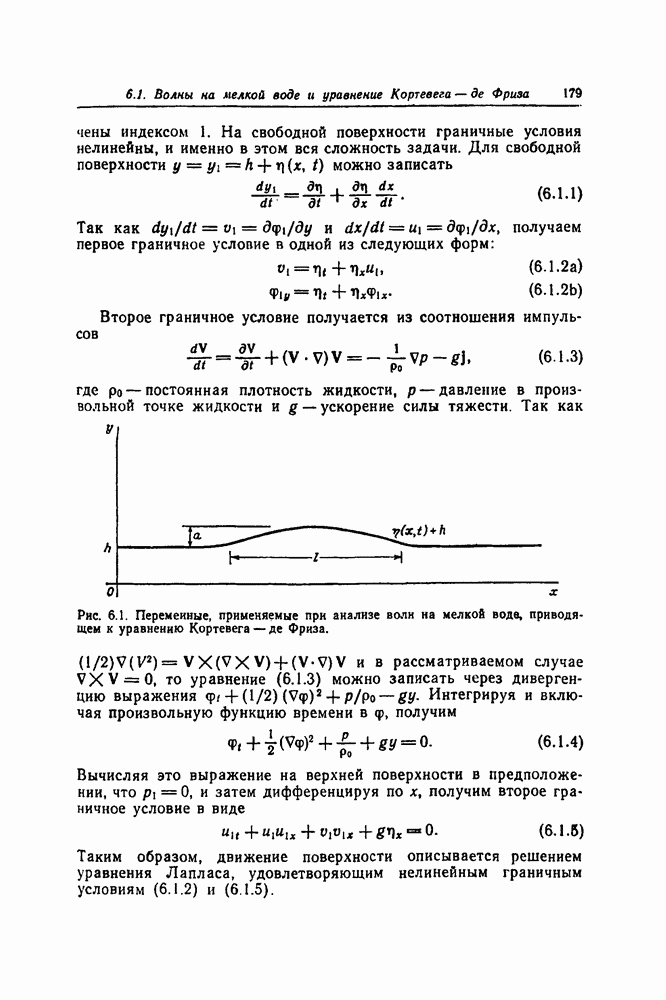
Представляется естественным вопрос, существует ли простая теория преобразований, связывающих эти решения в более поздние моменты времени их эволюции. Мы сейчас изложим такую теорию преобразований не только для уравнения Кортевега — де Фриза, но и для некоторых других наиболее известных солитонных уравнений. Для уравнения sine-Gordon, которое давно возникло в дифференциальной геометрии ([34], с. 284), уравнения соответствующих преобразований были получены А. В. Бэклундом, и преобразования того типа, с которыми мы будем встречаться стали известны как преобразования Бэклунда. Обзор литературы в этой области, относящийся к более раннему периоду, был дан в статье Гурса [46] и воспроизведен Миурой ([86], с. 77). Надежда на то, что другие солитонные уравнения также будут иметь преобразования Бэклунда, была реализована только недавно, после того как Уолквист и Эстабрук [116] получили преобразование Бэклунда для уравнения Кортевега — де Фриза.
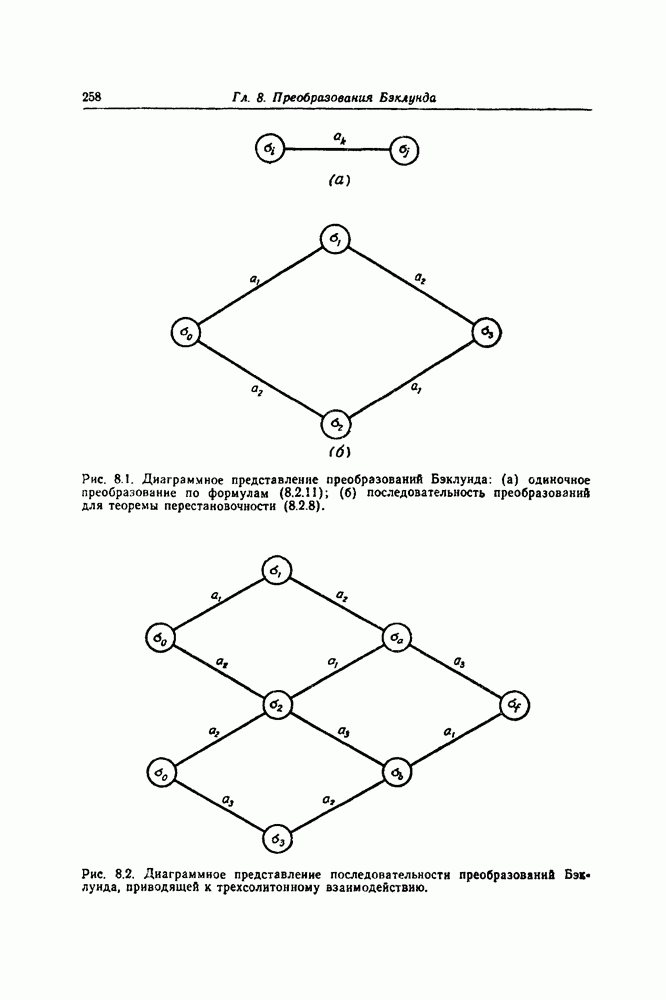
Один из наиболее интересных результатов этой теории преобразований состоит в том, что она приводит к простой формуле суперпозиции — теореме перестановочности, посредством которой из односолитонных решений можно простыми алгебраическими приемами построить многосолитонные решения.
8.1. ПРЕОБРАЗОВАНИЕ БЭКЛУНДА ДЛЯ УРАВНЕНИЯ КОРТЕВЕГА-ДЕ ФРИЗА
В разд. 2.6 мы рассмотрели соотношение между потенциалами в двух уравнениях Шрёдингера, которые были связаны таким образом, что решение одного уравнения являлось линейной комбинацией решения другого уравнения и первой производной этого решения Возникшие в результате потенциалы были начальными
условиями для чисто многосолитонных решений. Распространим теперь эти соображения на случай потенциалов, зависящих от параметра, причем потребуем, чтобы собственное значение от этого параметра не зависело [115]. Из наших предыдущих рассуждений мы знаем, что связь между двумя такими потенциалами означает соответствующую связь между двумя решениями уравнения Кортевега — де Фриза. Мы найдем, что эта связь является связью специального вида; она известна как преобразование Бэклунда.
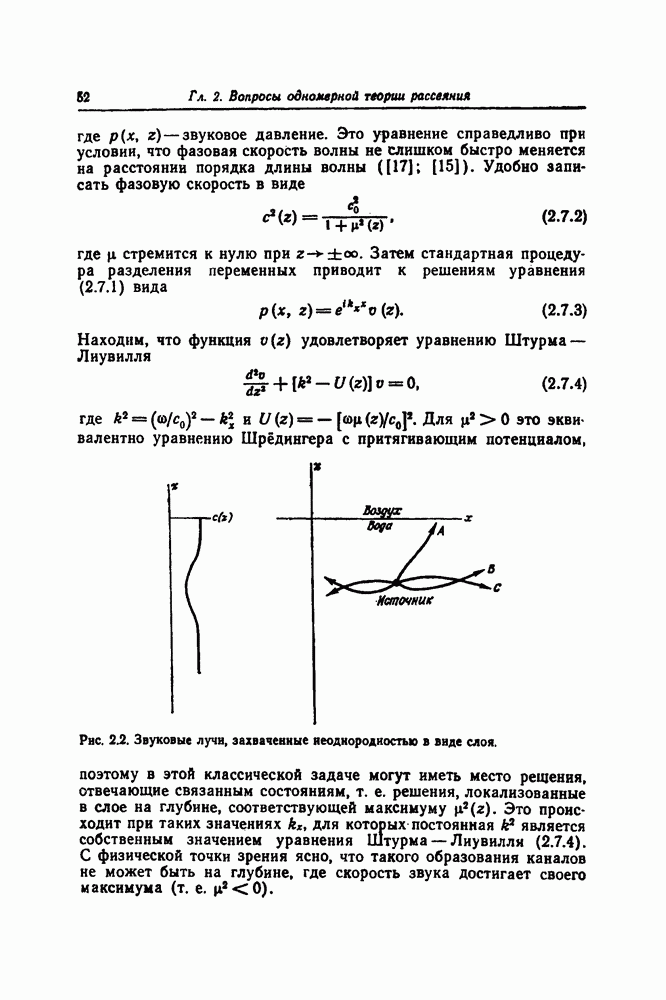
Рассмотрим два уравнения Штурма — Лиувилля

где  связаны соотношением
связаны соотношением

Если  функции
функции  могут, конечно, быть двумя решениями уравнения Кортевега — де Фриза. Так как в этих уравнениях
могут, конечно, быть двумя решениями уравнения Кортевега — де Фриза. Так как в этих уравнениях  является просто параметром, мы можем следовать в точности той же процедуре, которая была использована в разд. 2.6. Замечая, что теперь интегрирование вводит произвольную функцию времени, мы находим, что
является просто параметром, мы можем следовать в точности той же процедуре, которая была использована в разд. 2.6. Замечая, что теперь интегрирование вводит произвольную функцию времени, мы находим, что  должно удовлетворять уравнениям
должно удовлетворять уравнениям

которые соответствуют уравнениям (2.6.5) и (2.6.6). Если снова ввести линеаризующее преобразование  мы найдем, что у удовлетворяет уравнению (8.1.1), где А, заменено на
мы найдем, что у удовлетворяет уравнению (8.1.1), где А, заменено на  Так как мы налагаем ограничение, состоящее в том, что собственное значение не должно зависеть от времени, мы видим, что
Так как мы налагаем ограничение, состоящее в том, что собственное значение не должно зависеть от времени, мы видим, что  должно быть постоянным.
должно быть постоянным.
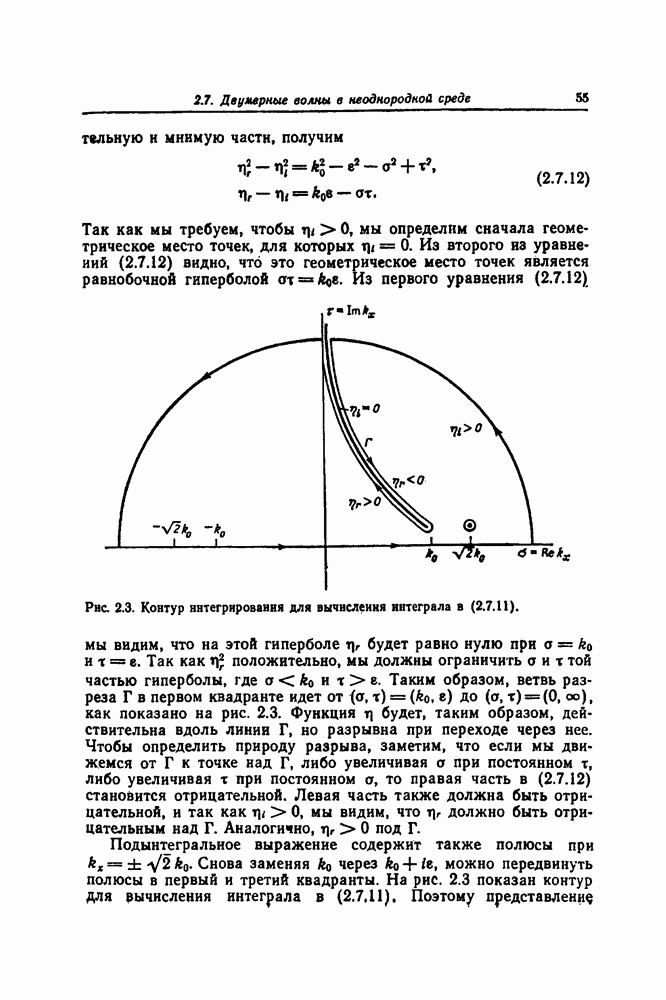
Если теперь ввести потенциальные функции с помощью определений  то (8.1.4) можно записать в виде
то (8.1.4) можно записать в виде

В конечном счете нас интересуют пространственные производные  дающие
дающие  Следовательно, можно в уравнении (8.1.6) отбросить произвольную функцию времени. Вводя обозначение
Следовательно, можно в уравнении (8.1.6) отбросить произвольную функцию времени. Вводя обозначение  находим, что уравнение (8.1.5) может быть записано в виде
находим, что уравнение (8.1.5) может быть записано в виде

где  конечно,
конечно,  Таким образом, мы получаем нелинейное дифференциальное уравнение первого порядка
Таким образом, мы получаем нелинейное дифференциальное уравнение первого порядка
(уравнение Риккати), связывающее две функции, которые тесно связаны с решениями уравнения Кортевега — де Фриза. Если предположить, что  удовлетворяет уравнению Кортевега — де Фриза вида
удовлетворяет уравнению Кортевега — де Фриза вида  то
то  удовлетворяет уравнению
удовлетворяет уравнению

аналогично для 
Уравнение (8.1.7) дает связь между пространственными производными  Чтобы получить выражение, связывающее их производные по времени, можно сначала продифференцировать (8.1.7) по времени, а затем проинтегрировать по
Чтобы получить выражение, связывающее их производные по времени, можно сначала продифференцировать (8.1.7) по времени, а затем проинтегрировать по 

Используя (8.1.8) и вводя обозначения  можно записать
можно записать

С помощью (8.1.7) и интегрирования по частям получим

Окончательный результат (8.1.11) вместе с (8.1.7) составляет преобразование Бэклунда для уравнения Кортевега — де Фриза. Если известно решение  уравнения третьего порядка (8.1.8), то другое решение
уравнения третьего порядка (8.1.8), то другое решение  можно получить, решая уравнения преобразования Бэклунда, т. е. уравнение первого порядка (8.1.7) и уравнение второго порядка (8.1.11).
можно получить, решая уравнения преобразования Бэклунда, т. е. уравнение первого порядка (8.1.7) и уравнение второго порядка (8.1.11).
В качестве простого примера использования теории этого преобразования можно начать с подстановки тривиального решения

где при получении последнего выражения в  мы использовали связь
мы использовали связь  из (8.1.12а). После интегрирования (8.1.12а) и определения произвольной функции времени по
из (8.1.12а). После интегрирования (8.1.12а) и определения произвольной функции времени по  имеем
имеем  в (8.1.7). Находим, что
в (8.1.7). Находим, что  удовлетворяет уравнениям
удовлетворяет уравнениям

где  Видно, что функция
Видно, что функция  является единичным солитоном уравнения Кортевега — де Фриза. Решение
является единичным солитоном уравнения Кортевега — де Фриза. Решение  в качестве односолитонного не интересно, поскольку при
в качестве односолитонного не интересно, поскольку при  оно расходится, но позже оно окажется полезным.
оно расходится, но позже оно окажется полезным.
Полученное решение (8.1.13а) могло бы теперь играть роль решения  в (8.1.7), а для
в (8.1.7), а для  могло бы быть получено другое решение. Эта процедура повлекла бы за собой интегрирование более сложного дифференциального уравнения, чем уравнение (8.1.12а). К счастью, более сложные решения можно построить намного проще. Их можно получить с помощью простой формулы суперпозиции, вообще не требующей дополнительного интегрирования. Чтобы получить такую формулу, которая известна для уравнения sine-Gordon как теорема перестановочности ([34], с. 286), мы рассмотрим сначала два решения
могло бы быть получено другое решение. Эта процедура повлекла бы за собой интегрирование более сложного дифференциального уравнения, чем уравнение (8.1.12а). К счастью, более сложные решения можно построить намного проще. Их можно получить с помощью простой формулы суперпозиции, вообще не требующей дополнительного интегрирования. Чтобы получить такую формулу, которая известна для уравнения sine-Gordon как теорема перестановочности ([34], с. 286), мы рассмотрим сначала два решения  получающиеся из (8.1.7), если исходить из решения
получающиеся из (8.1.7), если исходить из решения  с двумя различными значениями
с двумя различными значениями  Тогда мы имеем
Тогда мы имеем

Если снова использовать уравнение (8.1.7), но с  вместо
вместо  вместо
вместо  и обозначить новое решение через
и обозначить новое решение через  получим
получим

Аналогично можно использовать  вместо
вместо  вместо
вместо  чтобы получить решение, которое мы обозначим через
чтобы получить решение, которое мы обозначим через  Тогда имеем
Тогда имеем

Как мы увидим ниже, можно положить  Таким образом, если вычесть
Таким образом, если вычесть  из (8.1.14а), а также
из (8.1.14а), а также  из (8.1.15а), мы получим два различных выражения для
из (8.1.15а), мы получим два различных выражения для  Приравнивая два выражения для этой разности и полагая
Приравнивая два выражения для этой разности и полагая  мы придем к чисто алгебраическому соотношению
мы придем к чисто алгебраическому соотношению

Если мы начнем с решения  этот результат сразу же приводит к двухсолитонной формуле для уравнения Кортевега — де Фриза. Более конкретно, предположим, что
этот результат сразу же приводит к двухсолитонной формуле для уравнения Кортевега — де Фриза. Более конкретно, предположим, что  и затем используем вместо
и затем используем вместо  величину
величину  из
из  а вместо
а вместо  используем (8.1.13а). Такой выбор решений исключает появление нуля в знаменателе формулы суперпозиции (8.1.16). В частности, выбор постоянных
используем (8.1.13а). Такой выбор решений исключает появление нуля в знаменателе формулы суперпозиции (8.1.16). В частности, выбор постоянных  дает
дает

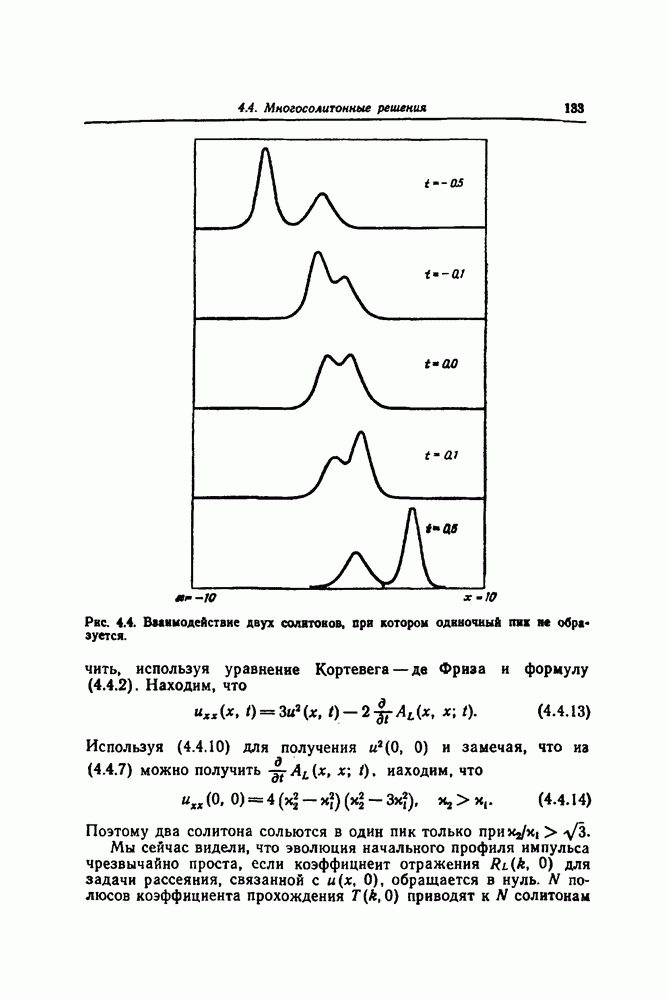
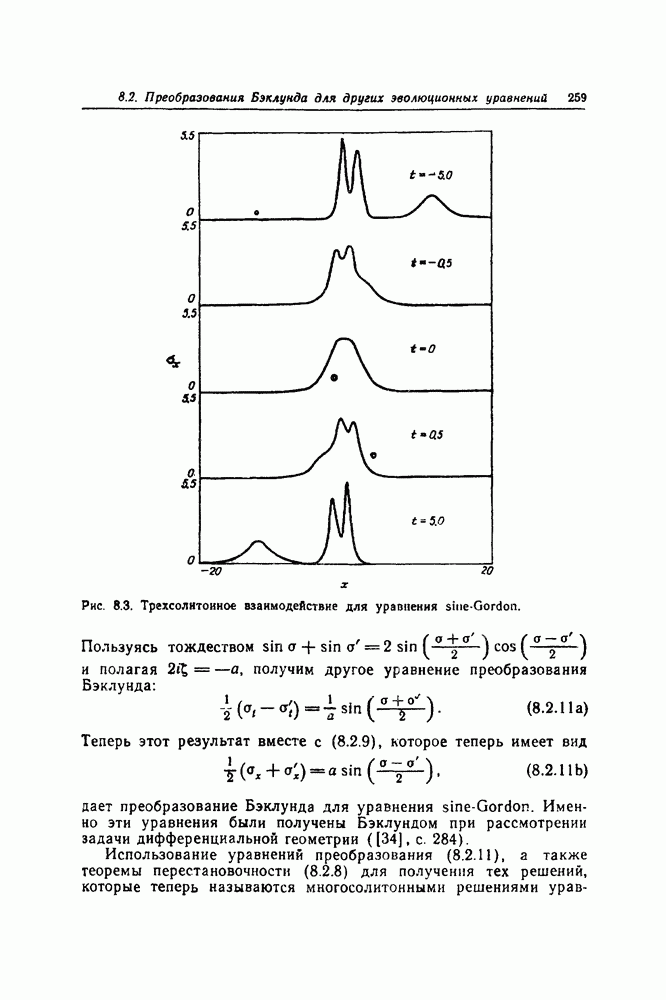
Пространственная производная этого решения является двухсолитонной формулой (1.3.25). Этот метод будет также использован в разд. 8.2 для порождения многосолитонных решений уравнения sine-Gordon.
Справедливость теоремы перестановочности
Любое доказательство теоремы перестановочности основано на равенстве  Это равенство легко устанавливается, если интерпретировать решения
Это равенство легко устанавливается, если интерпретировать решения  как представительные решения задач рассеяния. Если мы можем показать равенство некоторых данных рассеяния, то на основе теории обратной задачи рассеяния можно подтвердить, что в этом случае равны и сами рассеивающие потенциалы [38].
как представительные решения задач рассеяния. Если мы можем показать равенство некоторых данных рассеяния, то на основе теории обратной задачи рассеяния можно подтвердить, что в этом случае равны и сами рассеивающие потенциалы [38].
Предположим, что  решение уравнения (8.1.1), пронормировано так, как в (2.2.1), т. е.
решение уравнения (8.1.1), пронормировано так, как в (2.2.1), т. е.

где  .
.
Для локализованных потенциалов при  уравнение (8.1.5) принимает вид
уравнение (8.1.5) принимает вид  Записывая
Записывая  имеем решение для А в виде
имеем решение для А в виде  Таким образом,
Таким образом,

Можно получить аналогичным образом пронормированное решение для  соответствующего решению уравнения (8.1.2), записывая
соответствующего решению уравнения (8.1.2), записывая  где К должно быть выбрано так, чтобы снова получить падающую волну единичной амплитуды. Из (8.1.3) имеем соотношение
где К должно быть выбрано так, чтобы снова получить падающую волну единичной амплитуды. Из (8.1.3) имеем соотношение

которое показывает, что для получения падающей волны единичной амплитуды нужно выбрать К в виде  Тогда при
Тогда при

Очевидно, что последующее преобразование решения  в новое решение
в новое решение  даст коэффициент прохождения
даст коэффициент прохождения

Так как алгебраические множители коммутируют, тот же результат получился бы, если бы при получении  члены
члены  были взяты в обратном порядке. Нули двух коэффициентов прохождения также расположены в одних и тех же точках плоскости
были взяты в обратном порядке. Нули двух коэффициентов прохождения также расположены в одних и тех же точках плоскости  (с теми же вычетами), и, следовательно, можно сделать вывод, что рассеивающие потенциалы
(с теми же вычетами), и, следовательно, можно сделать вывод, что рассеивающие потенциалы  и
и  которые можно построить по этим данным рассеяния, также равны.
которые можно построить по этим данным рассеяния, также равны.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- 1.1. УРАВНЕНИЕ ШТУРМА-ЛИУВИЛЛЯ
- 1.2. УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 1.3. МНОГОСОЛИТОННЫЕ РЕШЕНИЯ КАК ПОТЕНЦИАЛЫ БАРГМАНА
- 1.4. ФИЗИЧЕСКАЯ СИСТЕМА, ПРИВОДЯЩАЯ К УРАВНЕНИЮ КОРТЕВЕГА — ДЕ ФРИЗА
- 1.5. РАСПРОСТРАНЕНИЕ НА СЛУЧАИ ДРУГИХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
- 1.6. ПЛАН ДАЛЬНЕЙШЕГО ИЗЛОЖЕНИЯ
- Глава 2. ВОПРОСЫ ОДНОМЕРНОЙ ТЕОРИИ РАССЕЯНИЯ
- 2.2. РАССЕЯНИЕ ОСЦИЛЛЯТОРОМ
- 2.3. УПРУГО ЗАКРЕПЛЕННАЯ СТРУНА
- 2.4. УРАВНЕНИЕ ШРЕДИНГЕРА
- 2.5. РАССЕЯНИЕ ПОТЕНЦИАЛОМ ВИДА sech
- 2.6. СООТВЕТСТВУЮЩИЕ УРАВНЕНИЯ ШТУРМА — ЛИУВИЛЛЯ
- 2.7. ДВУМЕРНЫЕ ВОЛНЫ В НЕОДНОРОДНОЙ СРЕДЕ
- 2.8. ОБЩИЙ ПОДХОД К ПРОБЛЕМЕ РАССЕЯНИЯ
- 2.9. «ОБРЕЗАННЫЕ» ПОТЕНЦИАЛЫ
- 2.10. РАССЕЯНИЕ ИМПУЛЬСОВ — УРАВНЕНИЯ МАРЧЕНКО
- 2.11. ЗАДАЧА РАССЕЯНИЯ ЗАХАРОВА — ШАБАТА
- 2.12. СВЯЗЬ МЕЖДУ УРАВНЕНИЕМ ШРЕДИНГЕРА И УРАВНЕНИЯМИ ЗАХАРОВА — ШАБЛТА: УРАВНЕНИЯ РИККАТИ
- Глава 3. ОДНОМЕРНАЯ ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ
- 3.2. НАЛИЧИЕ СВЯЗАННЫХ СОСТОЯНИЯ
- 3.3. БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ
- 3.4. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ-РАЦИОНАЛЬНАЯ ФУНКЦИЯ
- 3.5. ПОТЕНЦИАЛЫ БАРГМАНА
- 3.8. МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ ЗАХАРОВА — ШАБАТА ДЛЯ ДЕЙСТВИТЕЛЬНЫХ ПОТЕНЦИАЛОВ
- 3.7. БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ ДЛЯ СИСТЕМЫ ЗАХАРОВА — ШАБАТА
- 3.8. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ ДЛЯ СИСТЕМЫ ЗАХАРОВА — ШАБАТА В ВИДЕ РАЦИОНАЛЬНОЯ ФУНКЦИИ
- 3.9. СИСТЕМА ЗАХАРОВА — ШАБАТА С КОМПЛЕКСНЫМ ПОТЕНЦИАЛОМ
- Глава 4. УРАВНЕНИЕ КОРТЕВЕГА—ДЕ ФРИЗА
- 4.2. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РЕШЕНИЙ
- 4.3. ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
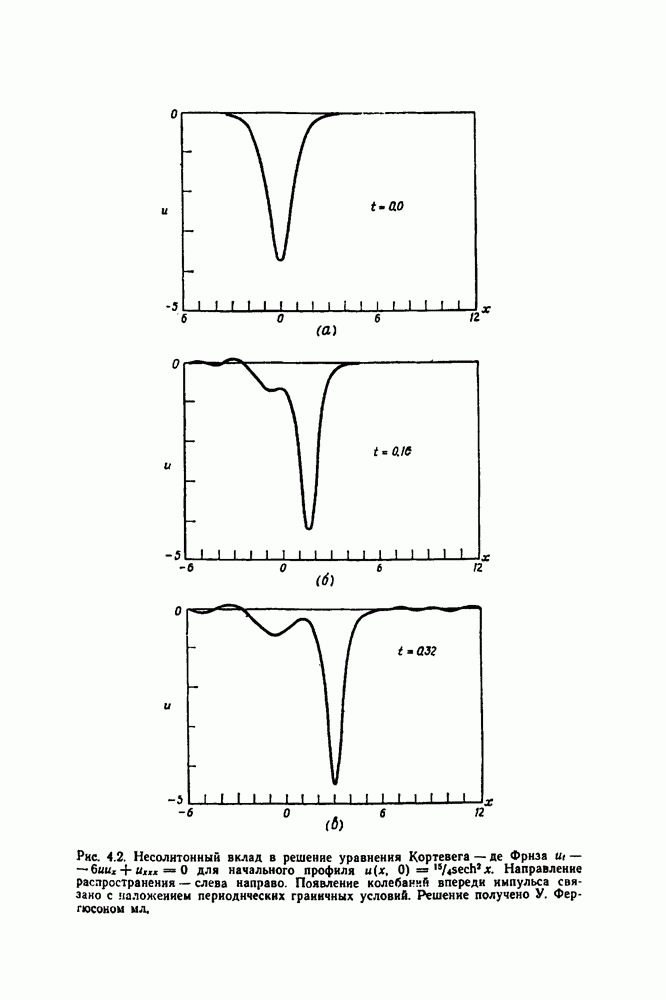
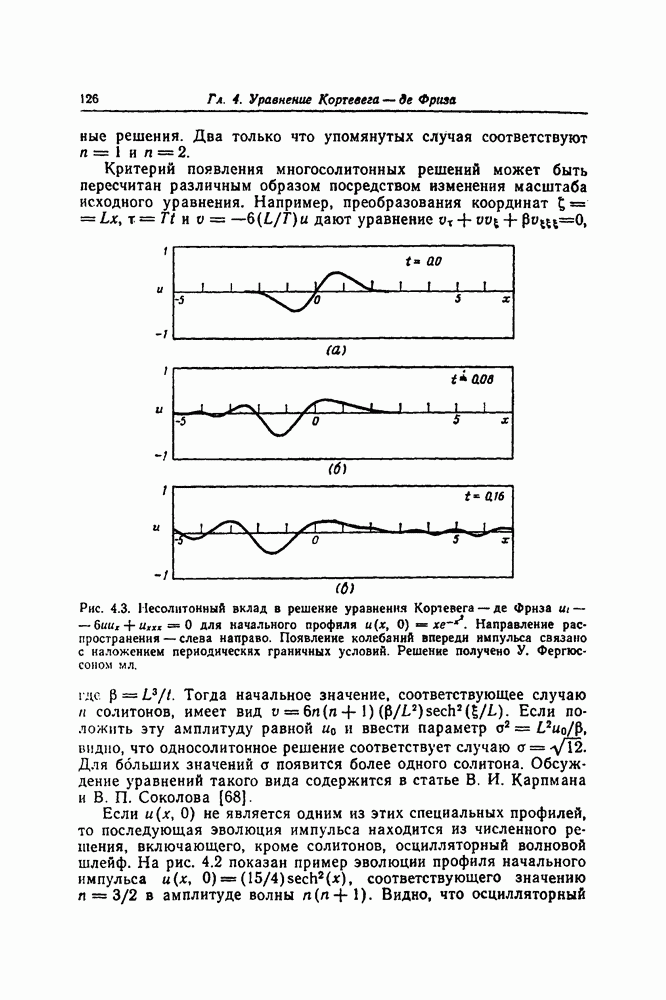
- 4.4. МНОГОСОЛИТОННЫЕ РЕШЕНИЯ
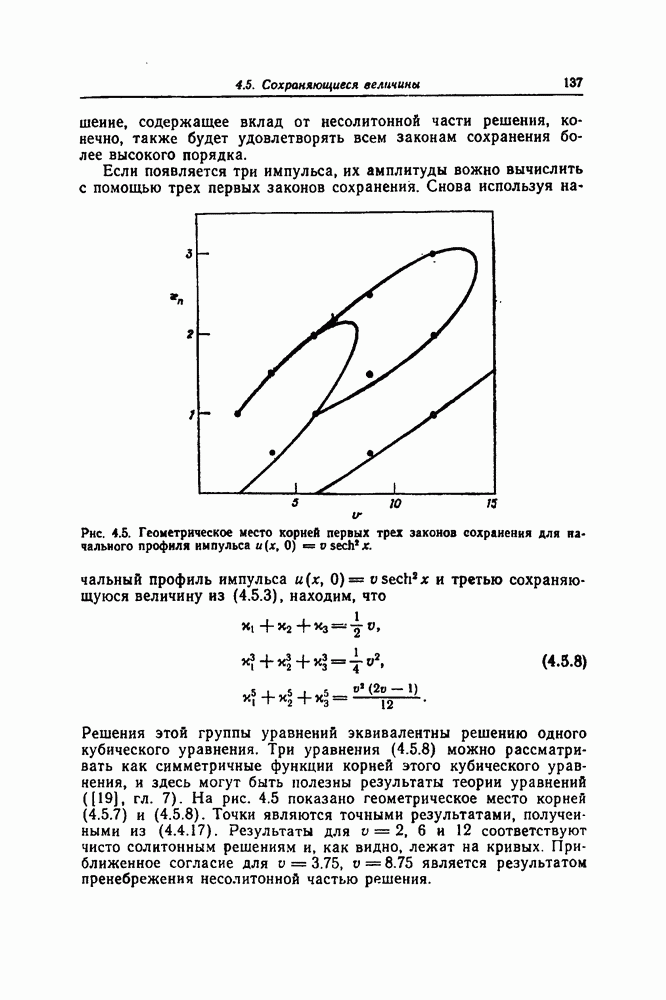
- 4.5. СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
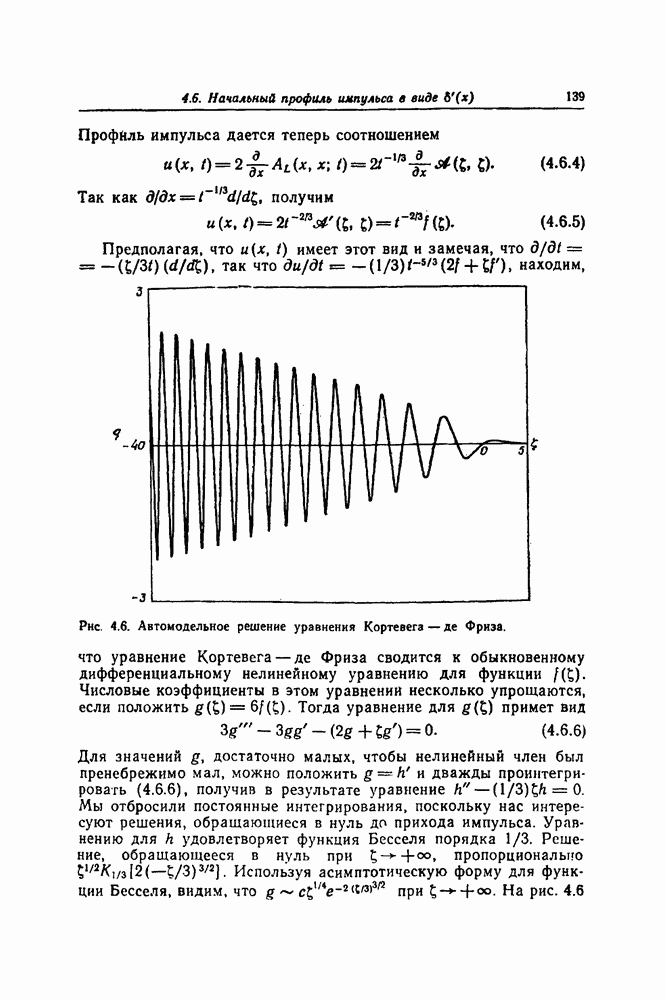
- 4.6. НАЧАЛЬНЫЙ ПРОФИЛЬ ИМПУЛЬСА В ВИДЕ ДЕЛЬТА-ФУНКЦИИ: АВТОМОДЕЛЬНОЕ РЕШЕНИЕ
- 4.7. ДРУГОЙ ПОДХОД К ЛИНЕЙНЫМ УРАВНЕНИЯМ ДЛЯ УРАВНЕНИЯ КОРТЕВЕГА-ДЕ ФРИЗА
- Глава 5. НЕКОТОРЫЕ ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ, СВЯЗАННЫЕ С СИСТЕМОЙ ЗАХАРОВА — ШАБАТА
- 5.1. МОДИФИЦИРОВАННОЕ УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 5.2. УРАВНЕНИЕ SINE-GORDON
- 5.3. КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- 5.4. ОБЩИЙ КЛАСС РАЗРЕШИМЫХ НЕЛИНЕЙНЫХ ЭВОЛЮЦИОННЫХ УРАВНЕНИЙ
- Глава 6. ПРИЛОЖЕНИЯ I
- 6.1. ВОЛНЫ НА МЕЛКОЙ ВОДЕ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 6.2. ВОЛНЫ НА МЕЛКОЙ ВОДЕ И КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- 6.3. ИОННО-ЗВУКОВЫЕ ВОЛНЫ В ПЛАЗМЕ И УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
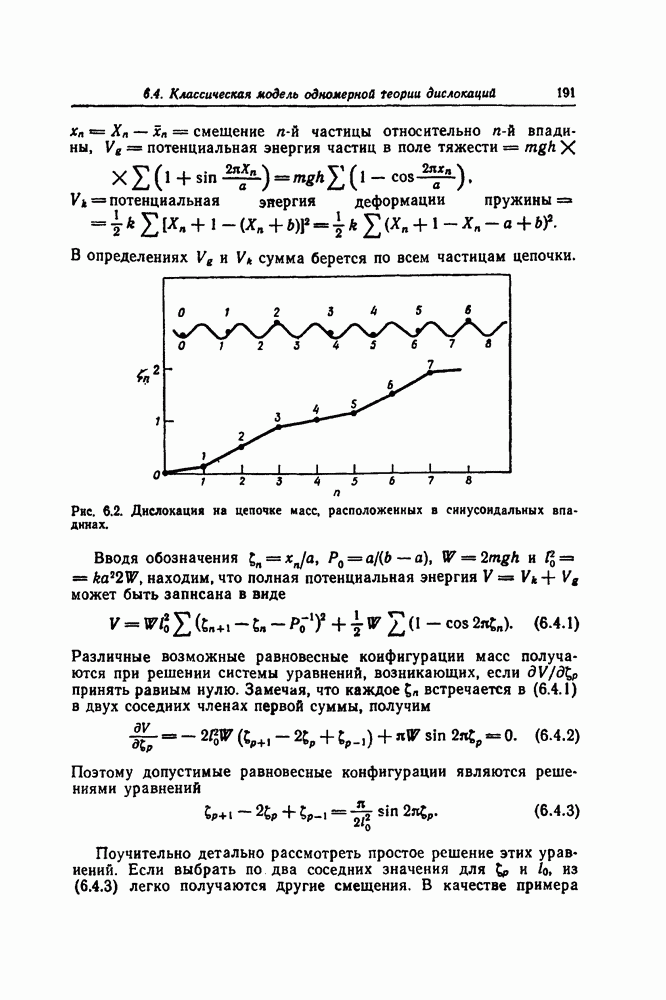
- 6.4. КЛАССИЧЕСКАЯ МОДЕЛЬ ОДНОМЕРНОЙ ТЕОРИИ ДИСЛОКАЦИИ — УРАВНЕНИЕ SINE-GORDON
- 6.5. ВЫБОР ПАРАМЕТРОВ РАЗЛОЖЕНИЯ
- Глава 7. ПРИЛОЖЕНИЯ II
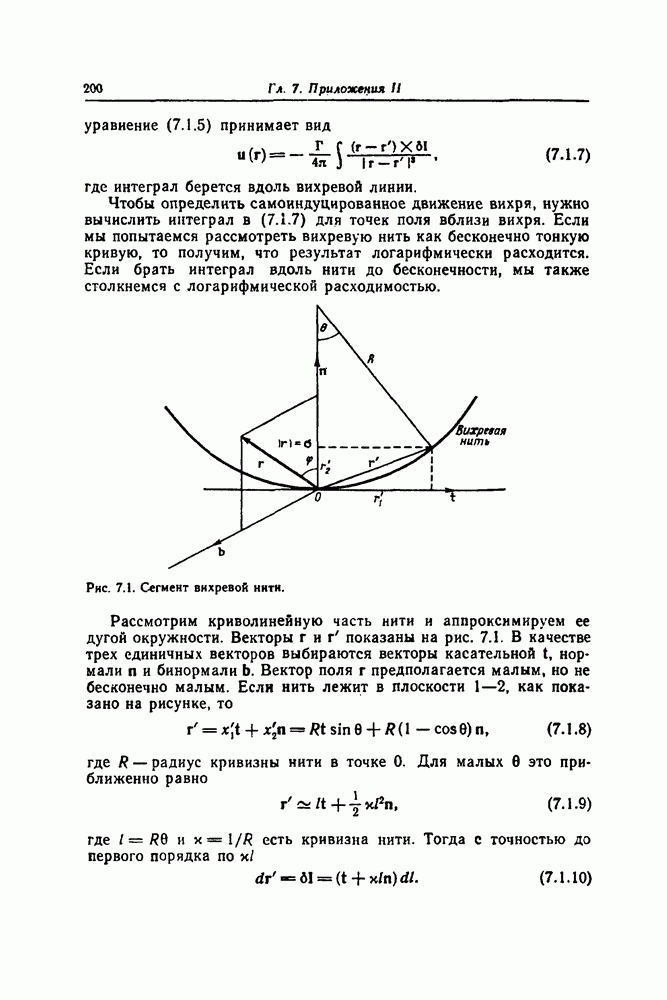
- 7.1. САМОИНДУЦИРОВАННЫЙ ВИХРЬ
- 7.2. ДВИЖЕНИЕ НИТИ
- 7.3. ФОРМА ОДНОСОЛИТОНИОИ НИТИ
- 7.4. ДРУГИЕ СОЛИТОННЫЕ УРАВНЕНИЯ
- 7.5. ОПИСАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 7.6. ДВУХУРОВНЕВЫЙ АТОМ
- 7.7. УРАВНЕНИЯ МОДЕЛИ
- 7.8. НЕПОДВИЖНЫЕ АТОМЫ — ПРЕДЕЛ SINE-CORDON
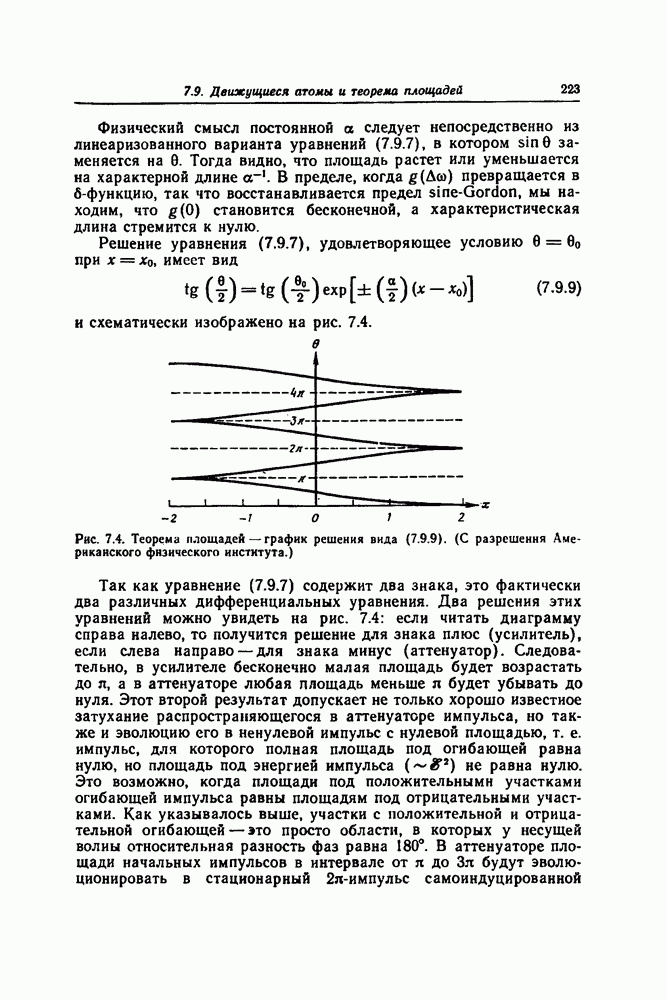
- 7.9. ДВИЖУЩИЕСЯ АТОМЫ И ТЕОРЕМА ПЛОЩАДЕЙ
- 7.10. РЕШЕНИЕ МЕТОДОМ ОБРАТНОЙ ЗАДАЧИ
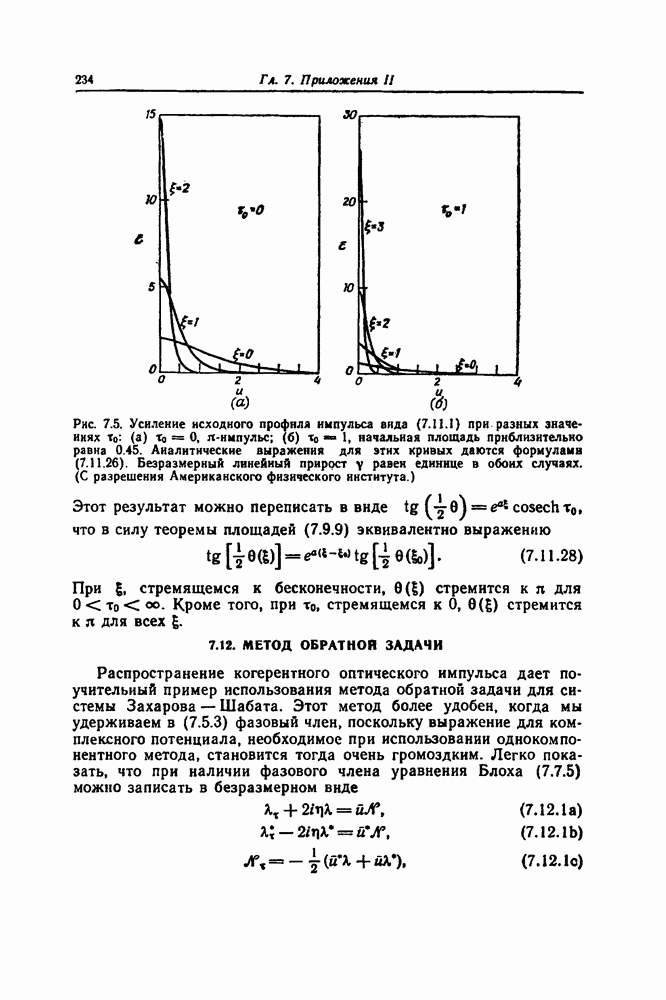
- 7.11. РАСПРОСТРАНЕНИЕ В УСИЛИТЕЛЕ
- 7.12. МЕТОД ОБРАТНОЙ ЗАДАЧИ
- 7.13. ВЫРОЖДЕНИЕ УРОВНЕЙ
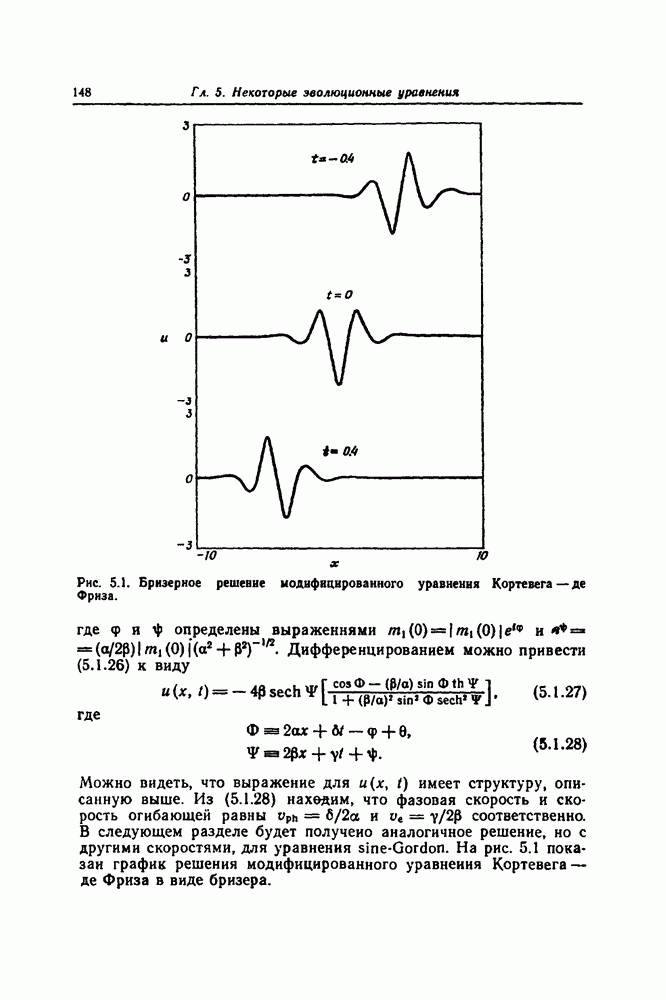
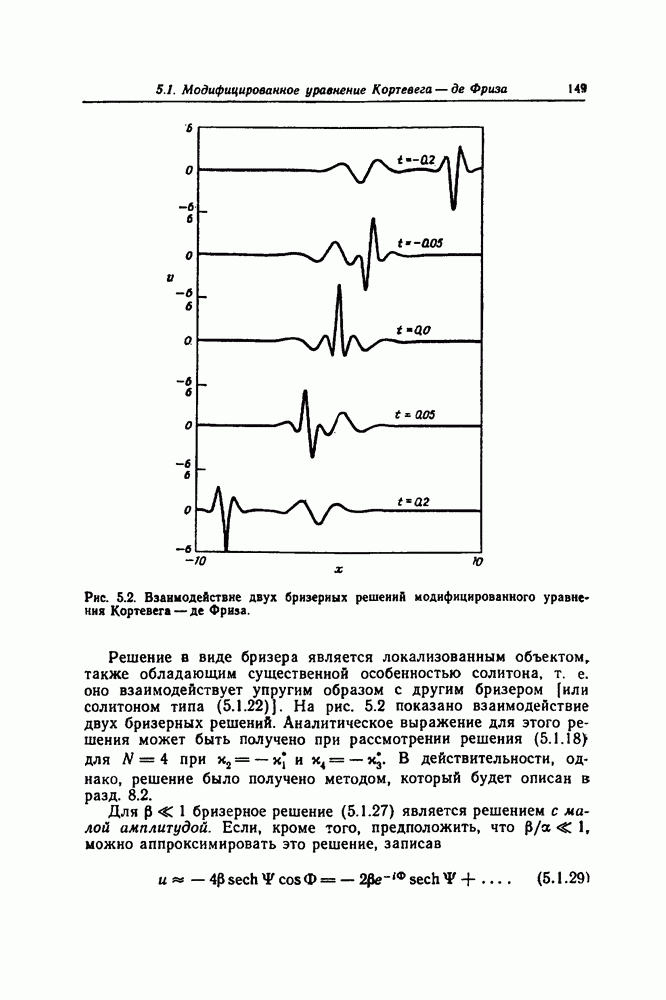
- Глава 8. ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
- 8.2. ПРЕОБРАЗОВАНИЯ БЭКЛУНДА ДЛЯ НЕКОТОРЫХ ДРУГИХ ЭВОЛЮЦИОННЫХ УРАВНЕНИЯ
- 8.3. БОЛЕЕ ОБЩИЕ ПРЕОБРАЗОВАНИЯ БЭКЛУНДА
- Главе 9. ТЕОРИЯ ВОЗМУЩЕНИЯ
- УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
- 9.2. ВОЗМУЩЕНИЕ ОДНОСОЛИТОННОГО РЕШЕНИЯ
- КУБИЧЕСКОЕ УРАВНЕНИЕ ШРЁДИНГЕРА
- 9.4. ЗАТУХАНИЕ ЕДИНИЧНОГО СОЛИТОНА