| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
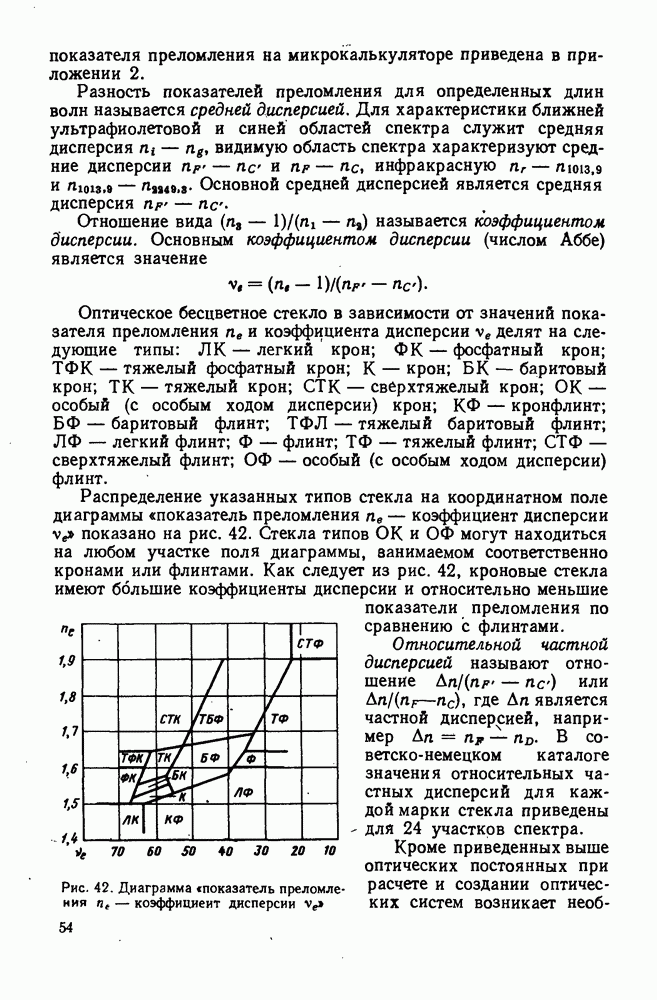
98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
В оптических фотоэлектрических системах источниками излучения часто являются нагретые тела, дающие сплошной спектр излучения. Силу и спектральный состав излучения тепловых источников определяют путем спектрофотометрического сравнения с излучением черного тела (ЧТ).
Излучение ЧТ, подчиняющееся закону Ламберта, описывается формулой Планка, позволяющей вычислить спектральную плотность энергетической светимости:

где  длина волны,
длина волны,  температура по абсолютной шкале. Длина волны, на которую приходится максимум излучения ЧТ, определяется по закону смещения Вина-Голицына:
температура по абсолютной шкале. Длина волны, на которую приходится максимум излучения ЧТ, определяется по закону смещения Вина-Голицына:

Подставив значение  в формулу Планка (429), получим максимальное значение спектральной плотности энергетической светимости
в формулу Планка (429), получим максимальное значение спектральной плотности энергетической светимости 

Энергетическая светимость ЧТ во всем спектре электромагнитных волн определяется путем интегрирования

или по закону Стефана — Больцмана

где
В формуле Планка спектральная плотность энергетической светимости ЧТ является функцией двух переменных: длины волны  и температуры
и температуры  Поэтому для упрощения вычислений формулу Планка преобразуют в уравнение единой изотермической кривой. Для этого вводят новые переменные
Поэтому для упрощения вычислений формулу Планка преобразуют в уравнение единой изотермической кривой. Для этого вводят новые переменные

и

в которых  определяется по формуле (430),
определяется по формуле (430),  по формуле (431). Подставив в уравнение Планка величину
по формуле (431). Подставив в уравнение Планка величину  выраженную по (433) через
выраженную по (433) через  выраженную по (434) через у, получим уравнение единой изотермической кривой
выраженную по (434) через у, получим уравнение единой изотермической кривой

Эту кривую (рис. 234) или соответствующие уравнению (435) таблицы [32, 37] используют при вычислении спектральной плотности энергетической светимости ЧТ для данной температуры в выбранном интервале длин волн. Сначала по формулам (430) и (431) вычисляют величины  и
и  а затем для каждого выбранного значения
а затем для каждого выбранного значения  находят соответствующее ему значение х по формуле (433). Пользуясь единой изотермической
находят соответствующее ему значение х по формуле (433). Пользуясь единой изотермической

Рис. 234. Единан изотермическая кривая

Рис. 235. Спектральная плотность энергетической светимости ЧТ и реального тела
кривой (см. рис. 233) или таблицами, находят для каждого х соответствующие значения у, по которым вычисляют согласно (434) спектральную плотность энергетической светимости 

Таким образом, с помощью уравнения единой изотермической кривой можно построить спектральную кривую излучения ЧТ для любой температуры.
Реальные тепловые источники излучают энергии меньше, чем ЧТ при той же температуре. В зависимости от свойств реальных источников их подразделяют на селективные и серые.
Селективные излучатели характеризуются спектральным коэффициентом теплового излучения, под которым понимают отношение спектральных плотностей энергетических светимостей реального тела и ЧТ при одинаковых температурах и длинах волн:

Эта величина меньше единицы и является функцией длины волны и температуры. Примером селективного излучателя служит вольфрам, широко используемый для изготовления нитей ламп накаливания. На рис. 235 приведены кривые спектральной плотности энергетической светимости ЧТ и селективного источника при одинаковых температурах. Характерной особенностью этих кривых является то, что длина волны, на которую приходится максимум излучения,  и селективного источника разная. В частности, у металлов максимум излучения приходится на меньшую длину волны, чем
и селективного источника разная. В частности, у металлов максимум излучения приходится на меньшую длину волны, чем 
Серые тела характеризуются коэффициентом теплового излучения

который не зависит от длины волны и изменяется только при изменении температуры. Поэтому отношение (437) справедливо и для интегральных величин.
Коэффициент теплового излучения реальных источников определяют экспериментально. Результаты этих экспериментов приводятся в виде таблиц или графиков [7, 161.
Таким образом, рассчитав спектральную плотность энергетической светимости ЧТ и зная величину  или
или  можно определить спектральную плотность энергетической светимости селективного излучателя по формуле (436):
можно определить спектральную плотность энергетической светимости селективного излучателя по формуле (436):

или серого излучателя по формуле (437)

При расчете оптической фотоэлектрической системы с учетом спектральных характеристик для теплового источника должны быть известны его температура, спектральный коэффициент теплового излучения и размеры излучаемой поверхности.
Принципиальная схема оптической фотоэлектрической системы остается, очевидно, такой же, как и при расчете по интегральным характеристикам (см. рис. 233).
Будем считать известными: характеристики источника излучения [площадь источника  его температура
его температура  и спектральный коэффициент теплового излучения
и спектральный коэффициент теплового излучения  характеристики приемника излучения [минимальная реакция
характеристики приемника излучения [минимальная реакция  относительная спектральная чувствительность
относительная спектральная чувствительность  и максимальная спектральная чувствительность
и максимальная спектральная чувствительность  спектральный коэффициент пропускания атмосферы
спектральный коэффициент пропускания атмосферы  спектральный коэффициент пропускания светофильтра
спектральный коэффициент пропускания светофильтра  спектральный коэффициент пропускания оптической системы
спектральный коэффициент пропускания оптической системы  Обычно спектральные коэффициенты пропускания оптических, сред даются в виде графиков.
Обычно спектральные коэффициенты пропускания оптических, сред даются в виде графиков.
Пусть источник излучения расположен на оптической оси и имеет одинаковую по всем направлениям энергетическую яркость. Если оптическая система не имеет виньетирования, то с учетом спектральных коэффициентов пропускания атмосферы, светофильтра и оптической системы по аналогии с формулой (425) получим выражение для монохроматического потока излучения, выходящего из оптической системы:

где
Так как энергетическая яркость источника одинакова по всем направлениям, то с учетом формулы (436) будем иметь:

Следовательно,

Если этот поток полностью попадает на светочувствительную поверхность приемника, то реакция приемника на монохроматический поток излучения будет:

Полная реакция приемника на поток излучения сложного спектрального состава определяется интегрированием выражения (439). Эту реакцию приравниваем величине 

Таким образом, находим синус апертурного угла в пространстве предметов

и диаметр входного зрачка 
Пределы интегрирования в формуле (440) зависят от спектральной характеристики приемника и спектральных коэффициентов пропускания оптических сред. Интеграл, стоящий в знаменателе формулы (440), выполняют графическим интегрированием. Приведем способ вычисления интеграла, изложенный в [37]. Рассмотрим отношение

где интеграл, стоящий в знаменателе, равен энергетической светимости ЧТ, определяемой по закону Стефана — Больцмана  формулу (432)]:
формулу (432)]:

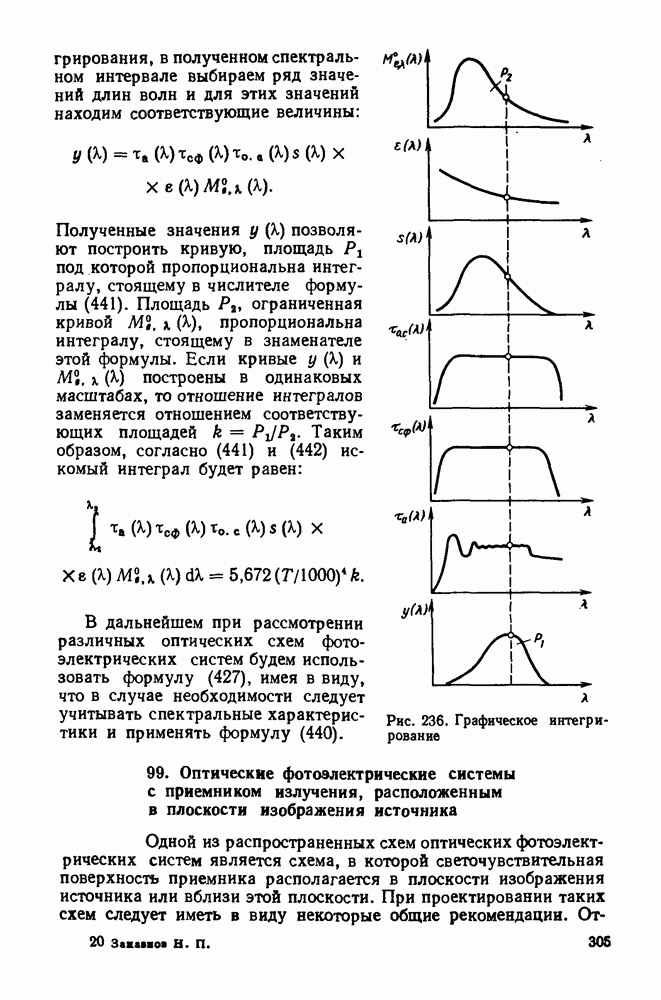
Для вычисления величины  необходимо построить график всех функций, стоящих под интегралом в числителе. Так как температура источника задана, то спектральная плотность энергетической светимости ЧТ определяется с помощью единой изотермической кривой. Спектральные кривые остальных безразмерных величин, стоящих под интегралом, известны по техническим условиям на расчет системы (рис. 236). Установив пределы
необходимо построить график всех функций, стоящих под интегралом в числителе. Так как температура источника задана, то спектральная плотность энергетической светимости ЧТ определяется с помощью единой изотермической кривой. Спектральные кривые остальных безразмерных величин, стоящих под интегралом, известны по техническим условиям на расчет системы (рис. 236). Установив пределы
интегрирования, в полученном спектральном интервале выбираем ряд значений длин волн и для этих значений находим соответствующие величины:

Полученные значения  позволяют построить кривую, площадь
позволяют построить кривую, площадь  под которой пропорциональна интегралу, стоящему в числителе формулы (441). Площадь
под которой пропорциональна интегралу, стоящему в числителе формулы (441). Площадь  ограниченная кривой
ограниченная кривой  пропорциональна интегралу, стоящему в знаменателе этой формулы. Если кривые
пропорциональна интегралу, стоящему в знаменателе этой формулы. Если кривые  и
и  построены в одинаковых масштабах, то отношение интегралов заменяется отношением соответствующих площадей
построены в одинаковых масштабах, то отношение интегралов заменяется отношением соответствующих площадей  Таким образом, согласно (441) и (442) искомый интеграл будет равен:
Таким образом, согласно (441) и (442) искомый интеграл будет равен:

В дальнейшем при рассмотрении различных оптических схем фотоэлектрических систем будем использовать формулу (427), имея в виду, что в случае необходимости следует учитывать спектральные характеристики и применять формулу (440).

Рис. 236. Графическое интегрирование
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
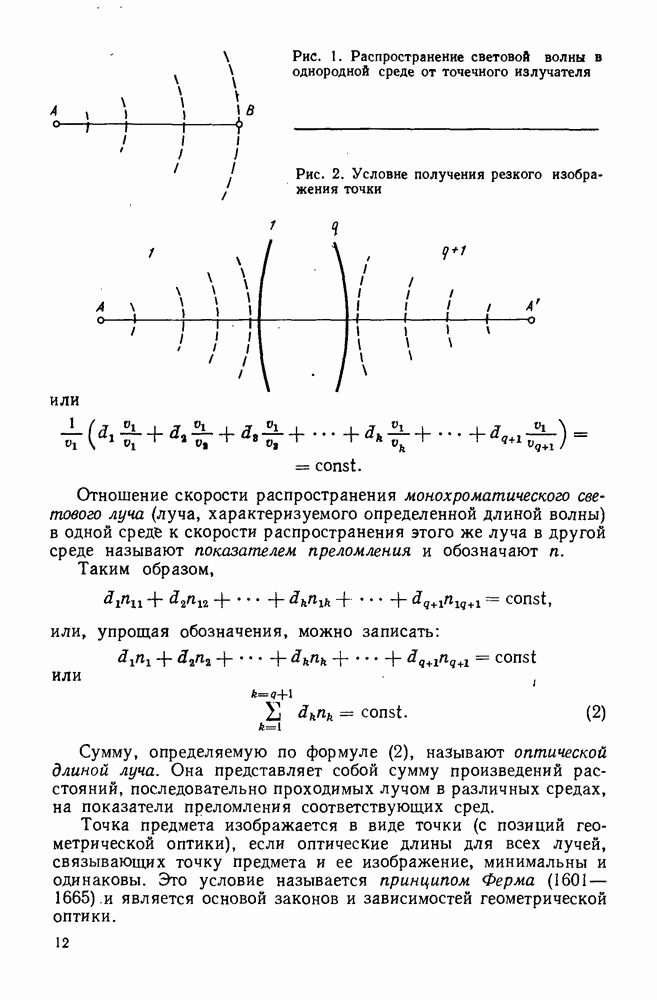
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
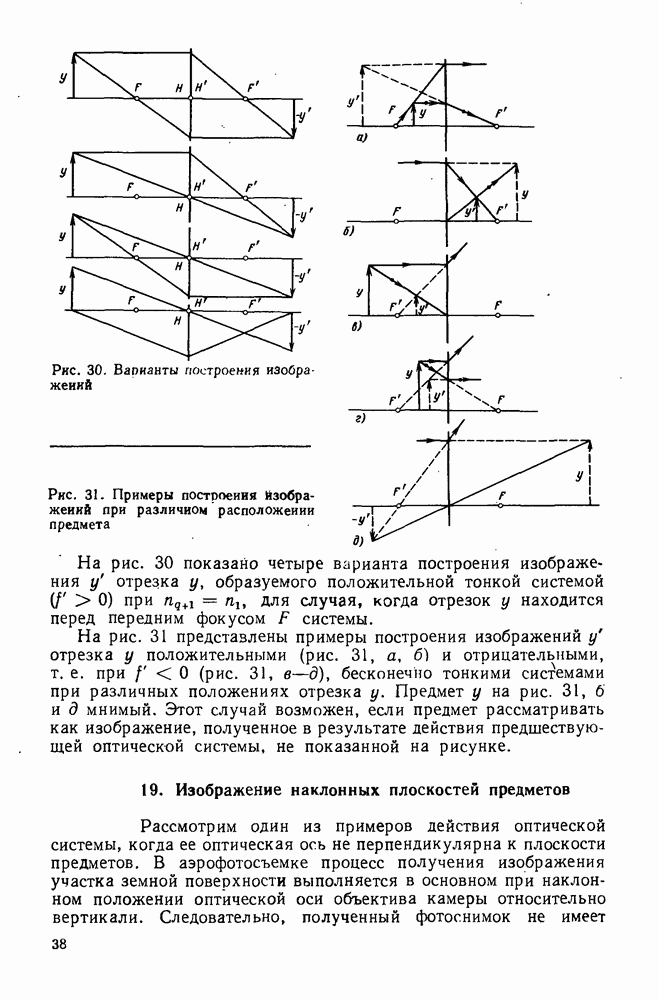
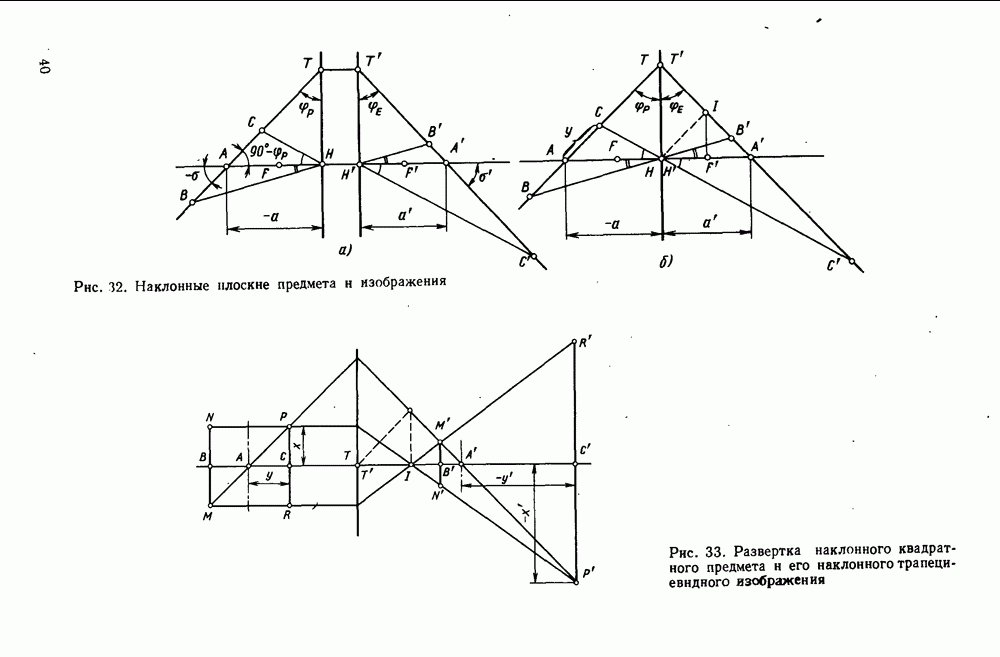
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
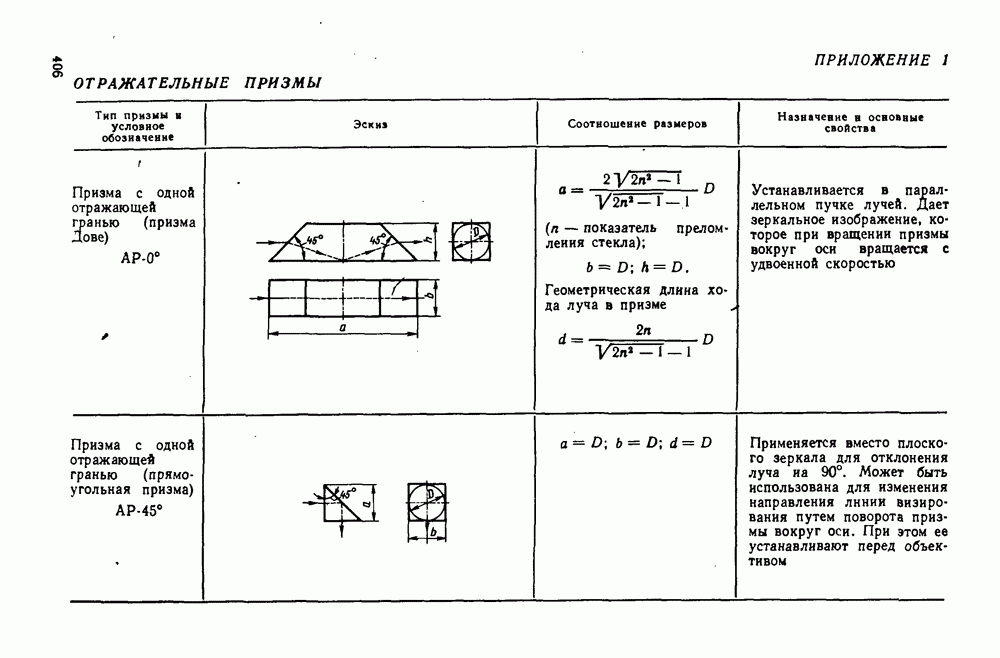
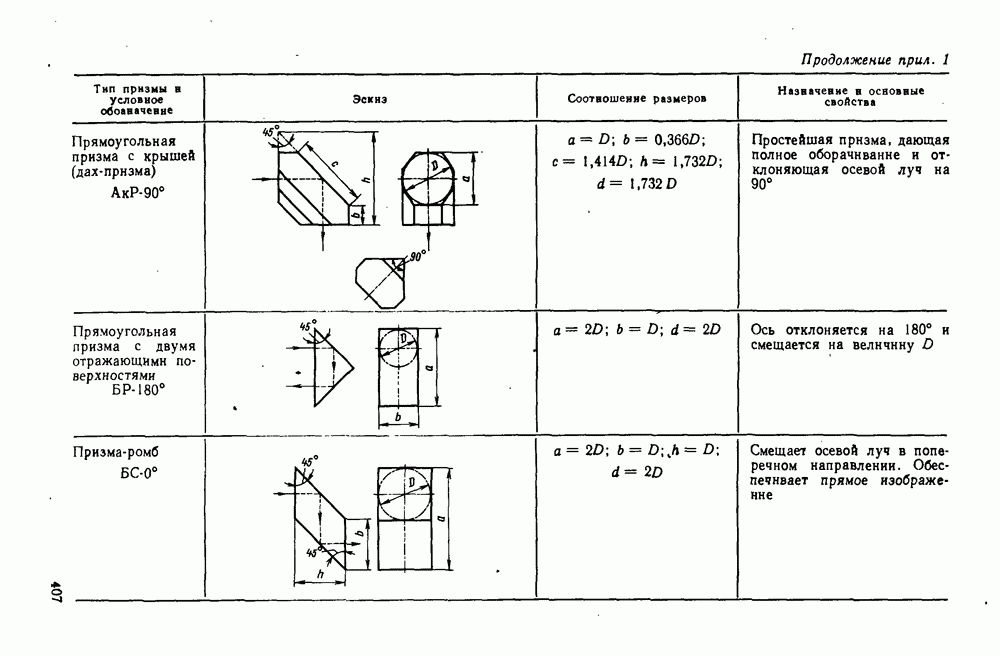
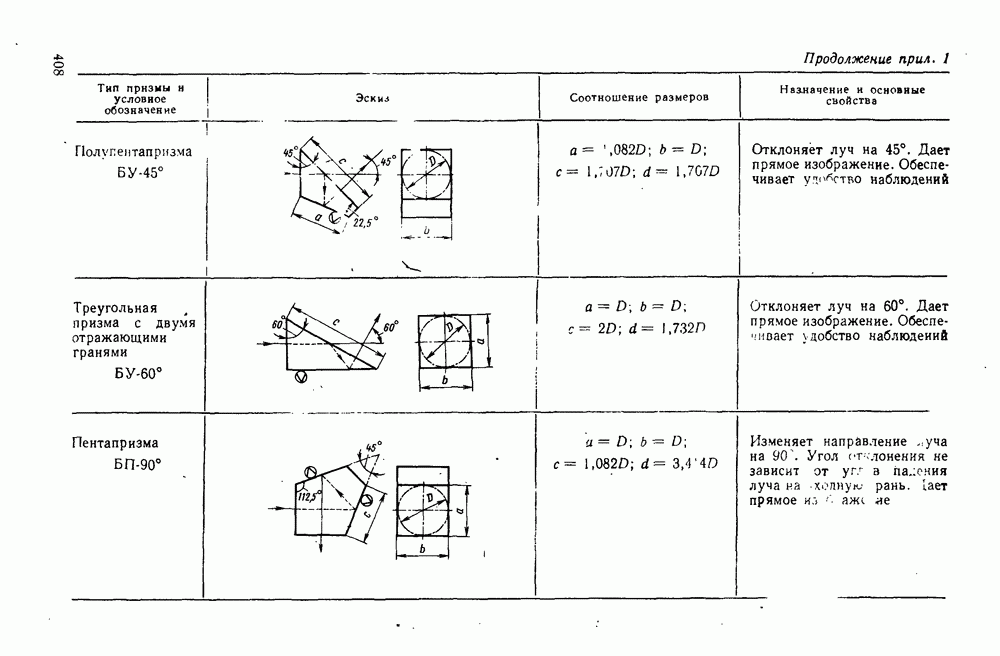
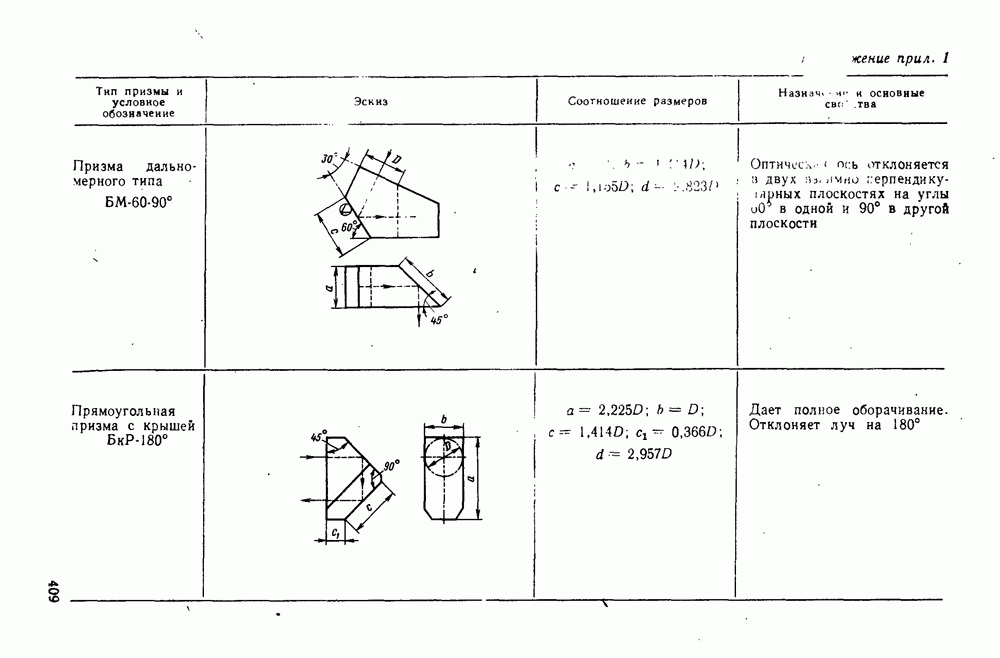
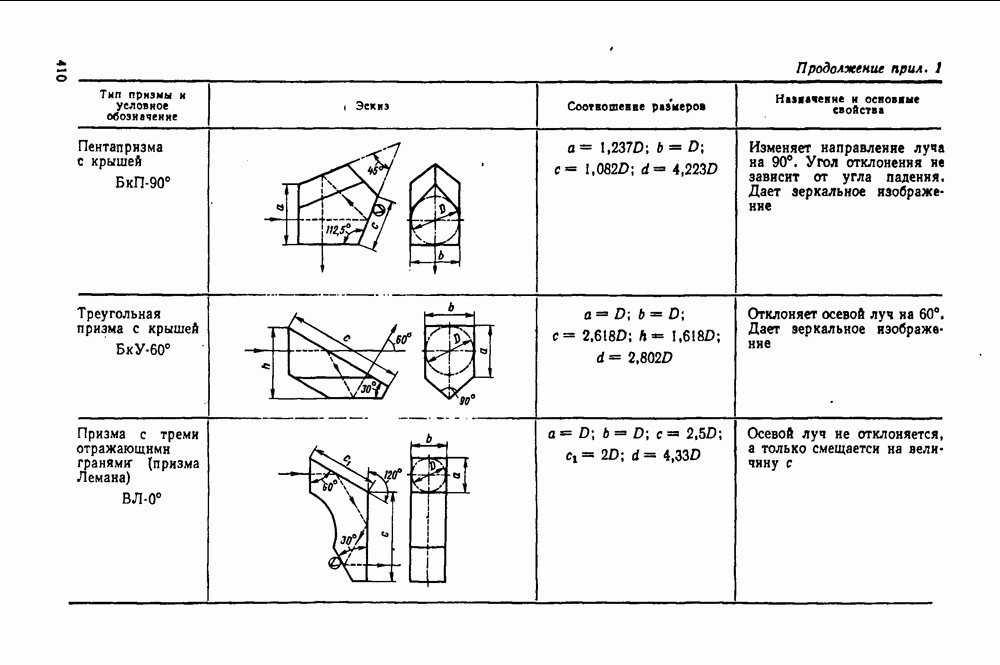
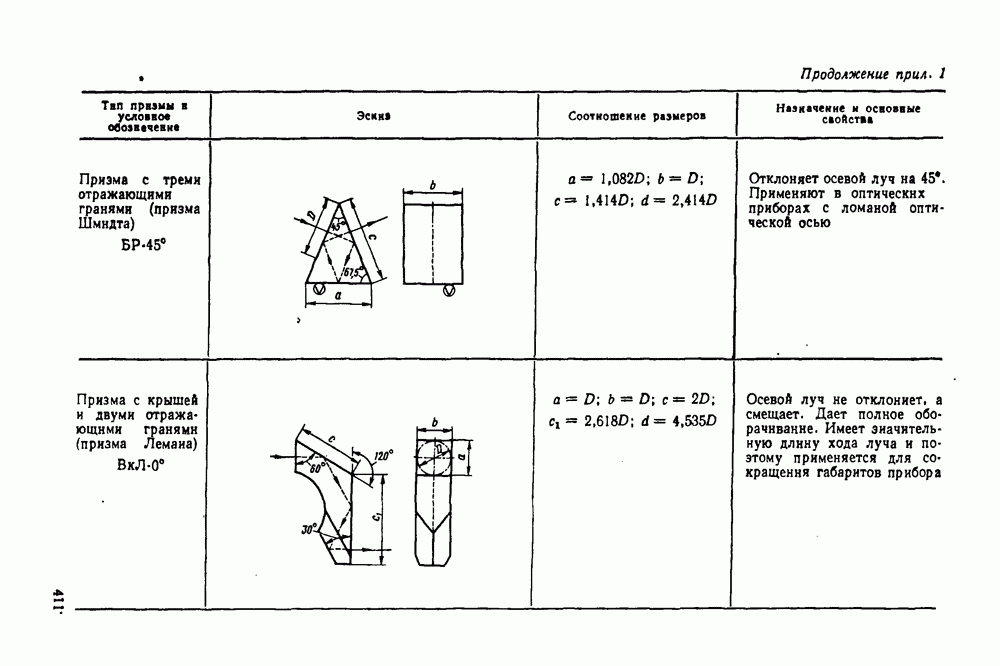
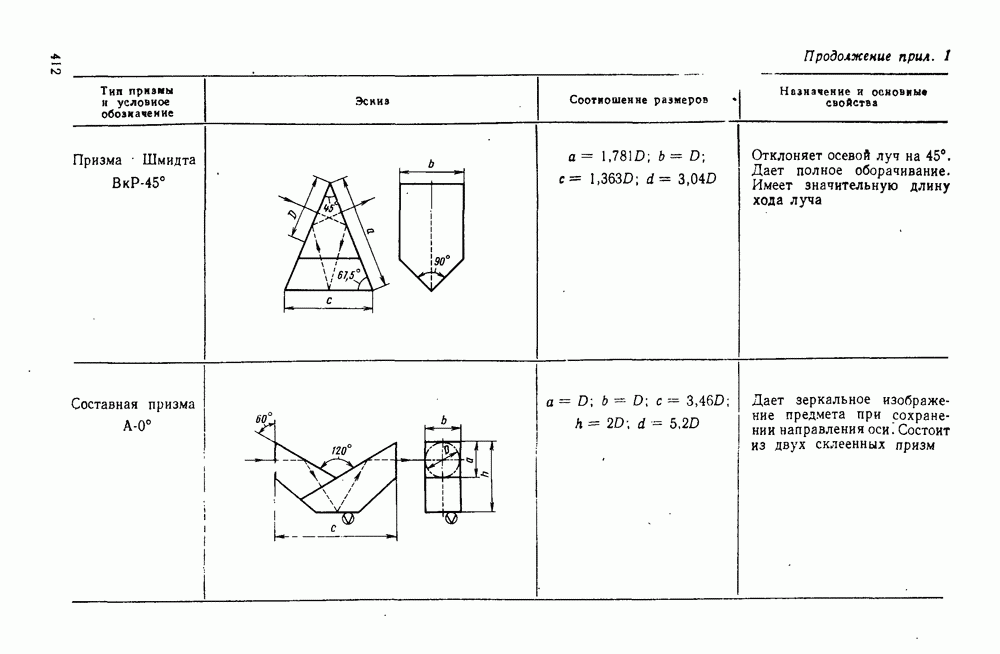
- 29. Отражательные призмы
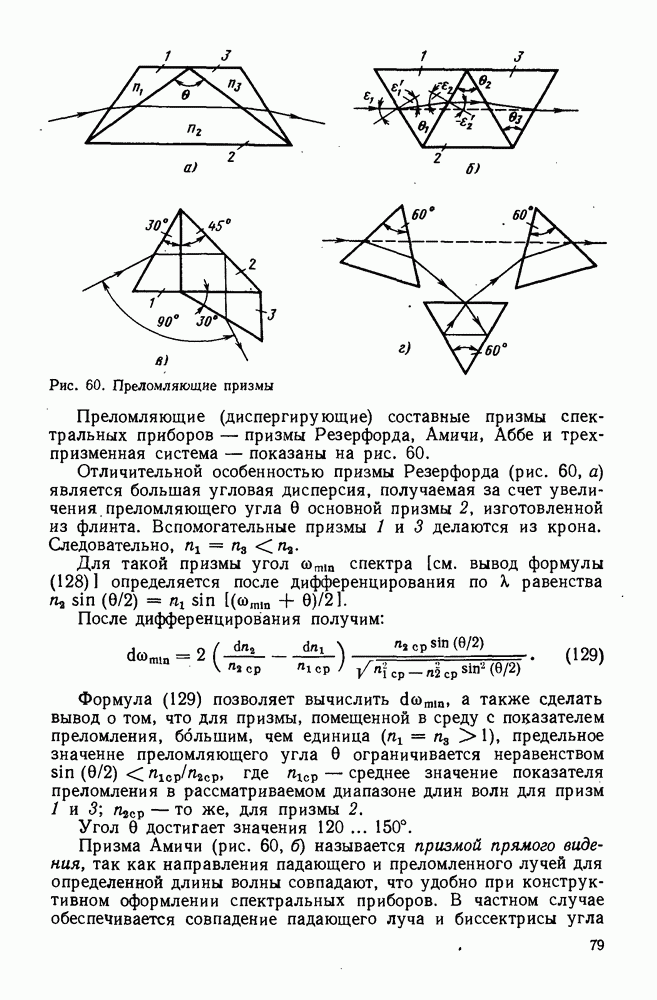
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
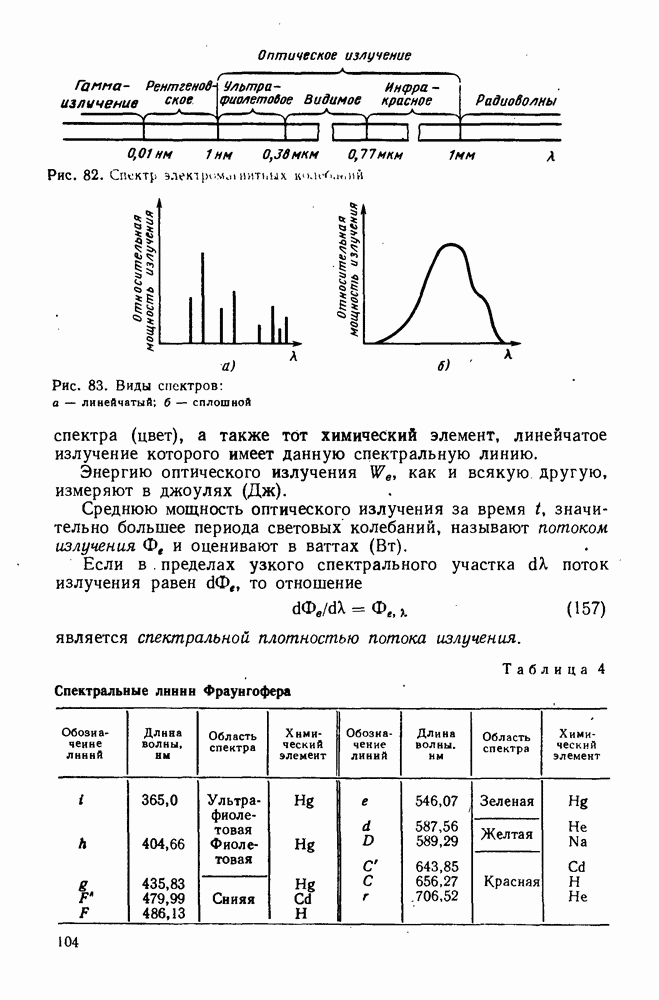
- 37. Оптическое излучение. Поток излучения
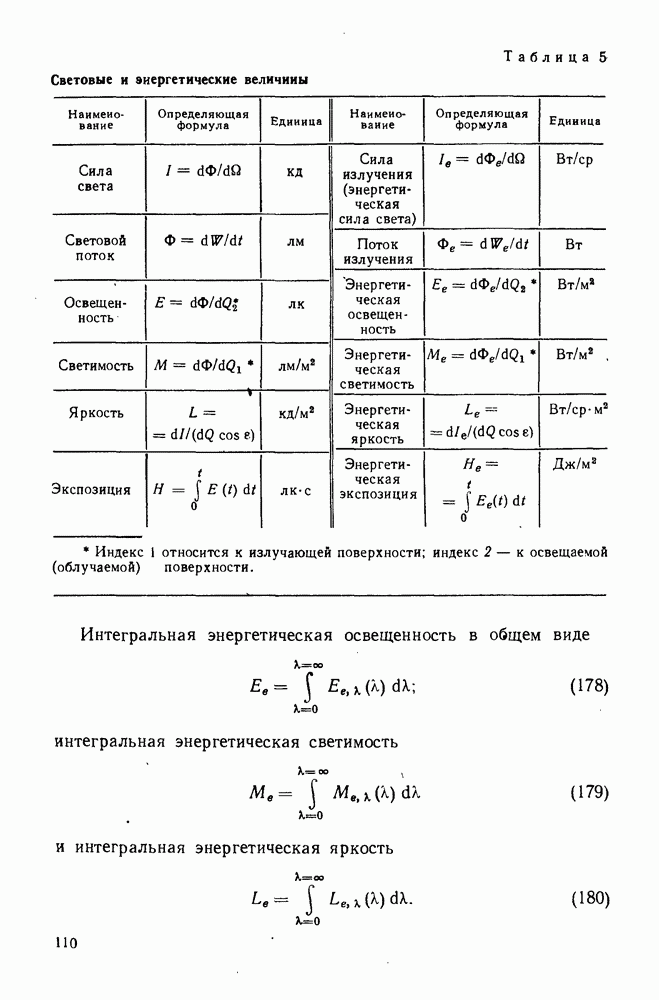
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
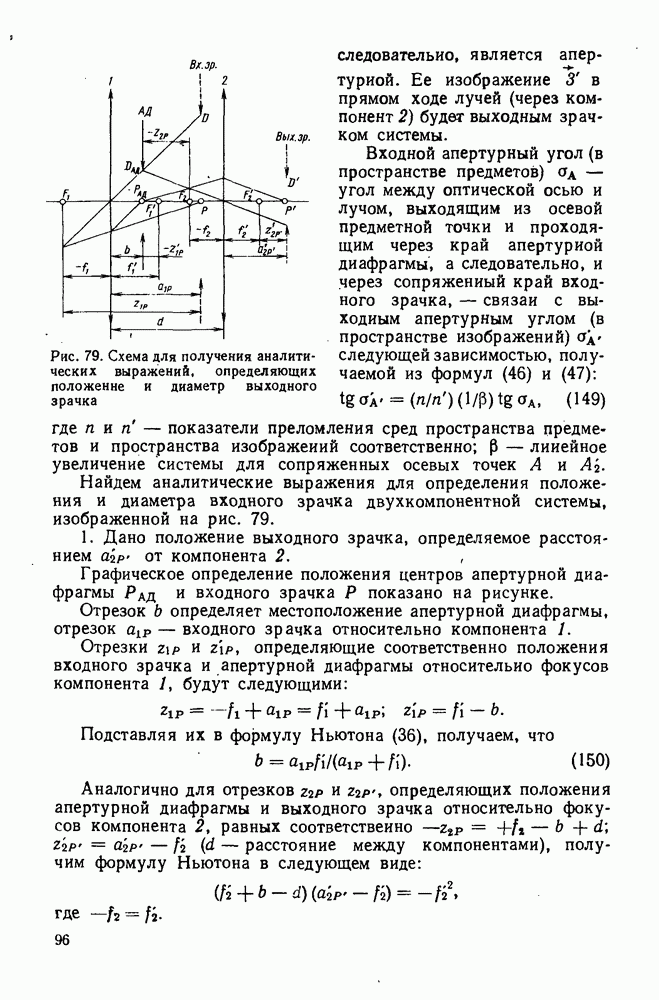
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы